Saltar al contenido principal
LibreTexts Español

3.4: La Forma Punto-Pendiente de una Línea

  1. Última actualización
  2. Guardar como PDF
  • Page ID
    110769

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    En la última sección, desarrollamos la forma pendiente-intercepción de una línea (y = mx + b). La forma pendiente-intercepción de una línea es aplicable cuando se le da la pendiente y la intercepción y de la línea. No obstante, habrá momentos en que se desconozca la intercepción y.

    Supongamos por ejemplo, que se le pide encontrar la ecuación de una línea que pasa por un punto determinado\(P\left(x_{0}, y_{0}\right)\) con pendiente = m. Esta situación se representa en la Figura\(\PageIndex{1}\).

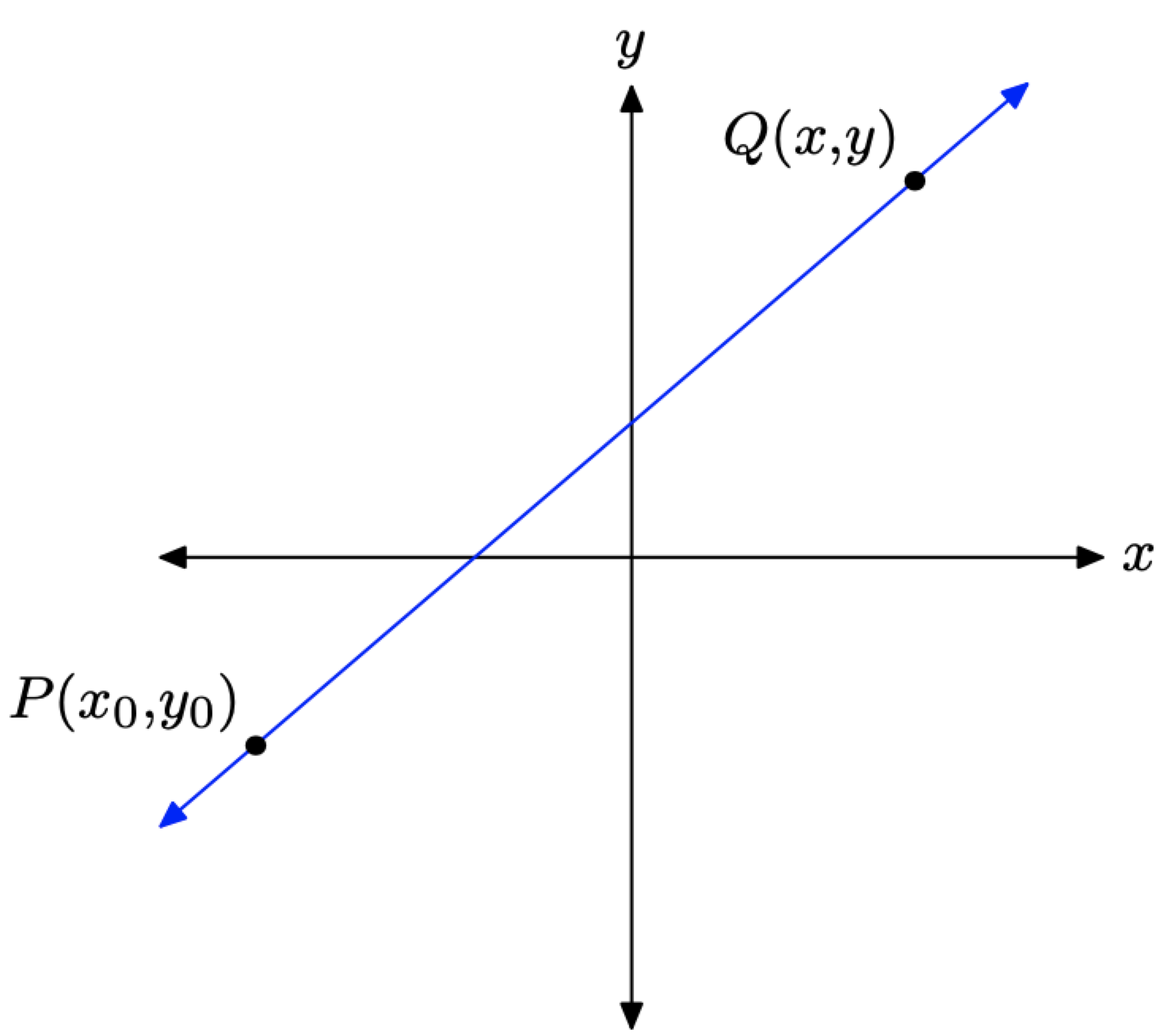
    WeChat7ae165dfc8321137635b442d6de2add0.png
    Figura\(\PageIndex{1}\). Una línea a través\(\left(x_{0}, y_{0}\right)\) con pendiente m.

    Deje que el punto Q (x, y) sea un punto arbitrario en la línea. Podemos determinar la ecuación de la línea usando la fórmula de pendiente con los puntos P y Q. Por lo tanto,

    \[\text { Slope }=\frac{\Delta y}{\Delta x}=\frac{y-y_{0}}{x-x_{0}}\]

    Debido a que la pendiente es igual a m, podemos establecer Pendiente = m en este último resultado para obtener

    \[m=\frac{y-y_{0}}{x-x_{0}}\]

    Si multiplicamos ambos lados de esta última ecuación por\(x-x_{0}\), obtenemos

    \[m\left(x-x_{0}\right)=y-y_{0}\]

    o intercambiando lados de esta última ecuación,

    \[y-y_{0}=m\left(x-x_{0}\right)\]

    Este último resultado es la ecuación de la línea.

    La forma de punto-pendiente de una línea

    Si la línea L pasa por el punto\(\left(x_{0}, y_{0}\right)\) y tiene pendiente m, entonces la ecuación de la línea es\[y-y_{0}=m\left(x-x_{0}\right)\] Esta forma de la ecuación de una línea se llama la forma punto-pendiente.

    Para utilizar la forma punto-pendiente de una línea, siga estos pasos.

    Procedimiento para usar la forma de punto-pendiente de una línea

    Cuando se le da la pendiente de una línea y un punto en la línea, utilice la forma de pendiente de punto de la siguiente manera:

    1. Sustituir la pendiente dada por m en la fórmula\(y-y_{0}=m\left(x-x_{0}\right)\).
    2. Sustituir las coordenadas del punto dado por x0 e y0 en la fórmula\(y-y_{0}=m\left(x-x_{0}\right)\).

    Por ejemplo, si la línea tiene pendiente −2 y pasa por el punto (3, 4), entonces sustituya\(m=-2, x_{0}=3,\) y\(y_{0}=4\) en la fórmula\(y-y_{0}=m\left(x-x_{0}\right)\) para obtener\[y-4=-2(x-3)\].

    Ejemplo\(\PageIndex{1}\)

    Dibuja la línea que pasa por el punto P (−3, −2) y tiene pendiente m = 1/2. Utilice la forma punto-pendiente para determinar la ecuación de la línea.

    Solución

    Primero, grafica el punto P (−3, −2), como se muestra en la Figura\(\PageIndex{2}\) (a). Comenzando desde el punto P (−3, −2), mueva 2 unidades a la derecha y 1 unidad hasta el punto Q (−1, −1). La línea que atraviesa los puntos P y Q de la Figura\(\PageIndex{2}\) (a) ahora tiene pendiente m = 1/2.

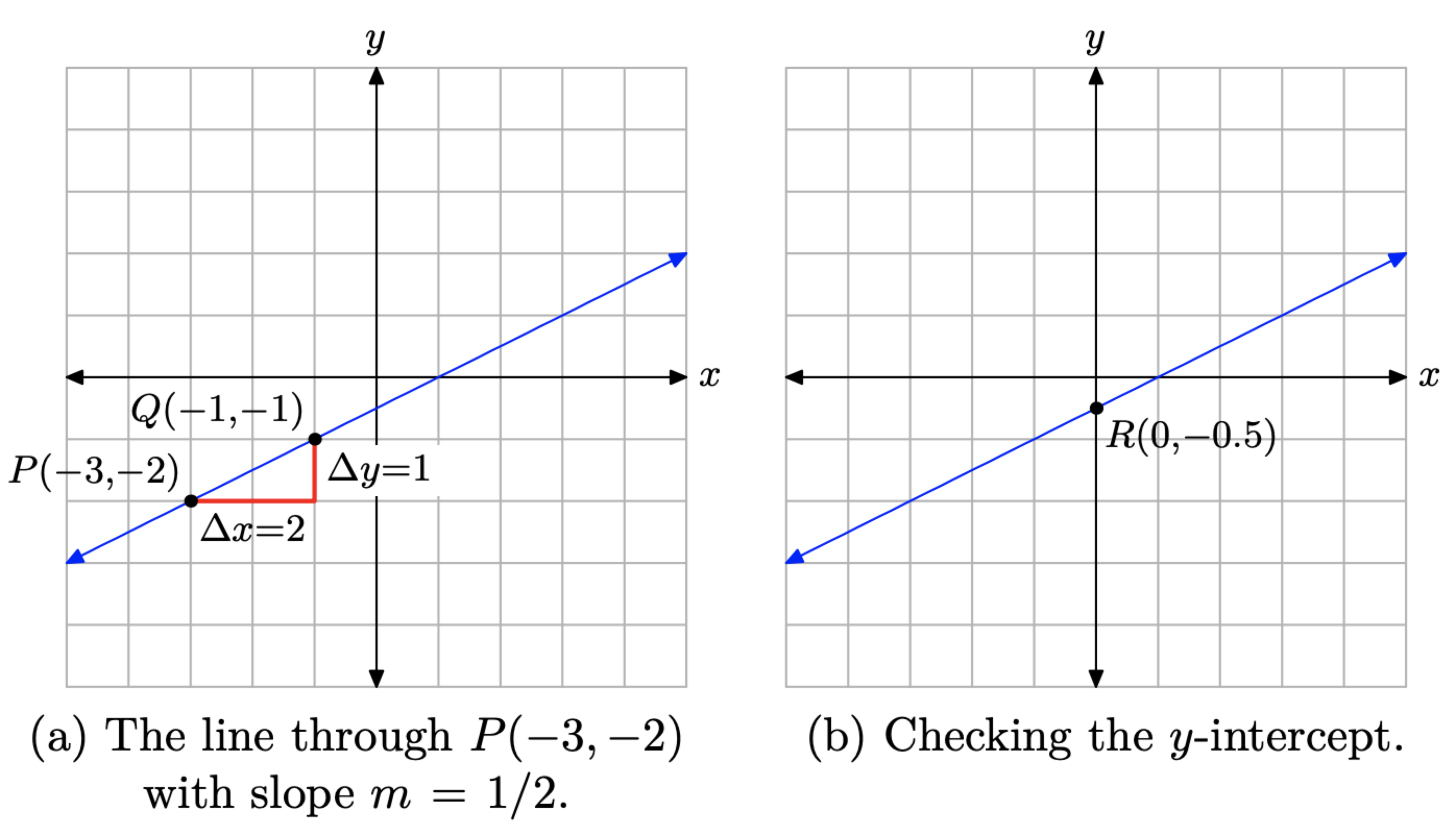
    WeChatb11c39993f9ab17a0098dc9991df0cb7.png
    Figura\(\PageIndex{2}\)

    Para determinar la ecuación de la línea en la Figura\(\PageIndex{2}\) (a), utilizaremos la forma punto-pendiente de la línea

    \[y-y_{0}=m\left(x-x_{0}\right)\]

    La pendiente de la línea es m = 1/2 y el punto dado es P (−3, −2), entonces\(\left(x_{0}, y_{0}\right)=(−3, −2)\). En la ecuación (3), establecer\(m=1 / 2, x_{0}=-3,\) y\(y_{0}=-2\), obtener

    \[y-(-2)=\frac{1}{2}(x-(-3))\]

    o equivalentemente,

    \[y+2=\frac{1}{2}(x+3)\]

    Esta es la ecuación de la línea en la Figura\(\PageIndex{2}\) (a).

    Como comprobación, hemos estimado la intercepción y de la línea en la Figura\(\PageIndex{2}\) (b) como R (0, −0.5). Coloquemos la ecuación (4) en forma de pendiente-intercepción para determinar el valor exacto de la intercepción y. Primero, distribuye 1/2 para obtener

    \[y+2=\frac{1}{2} x+\frac{3}{2}\]

    Restar 2 de ambos lados de esta última ecuación.

    \[y=\frac{1}{2} x+\frac{3}{2}-2\]

    Hacer fracciones equivalentes con un denominador común y simplificar.

    \[\begin{array}{l}{y=\frac{1}{2} x+\frac{3}{2}-\frac{4}{2}} \\ {y=\frac{1}{2} x-\frac{1}{2}}\end{array}\]

    Al comparar la ecuación (5) con y = mx+b nos da b = −1/2. Este es el valor y exacto de la intercepción y. Obsérvese que este resultado se compara exactamente con el valor y del punto R en la Figura\(\PageIndex{2}\) (b). Esto es un poco afortunado. No esperes obtener una comparación exacta cada vez. No obstante, si la comparación no está cerca, busca un error en tu trabajo, ya sea en tus cálculos o en tu gráfica.

    Veamos otro ejemplo.

    Ejemplo\(\PageIndex{2}\)

    Encuentra la ecuación de la línea que pasa por los puntos P (−3, 2) y Q (2, −1). Coloca tu respuesta final en forma estándar.

    Solución

    Nuevamente, para ayudar a mantener nuestro enfoque, trazamos la línea que pasa por los puntos P (−3, 2) y Q (2, −1) en la Figura\(\PageIndex{3}\).

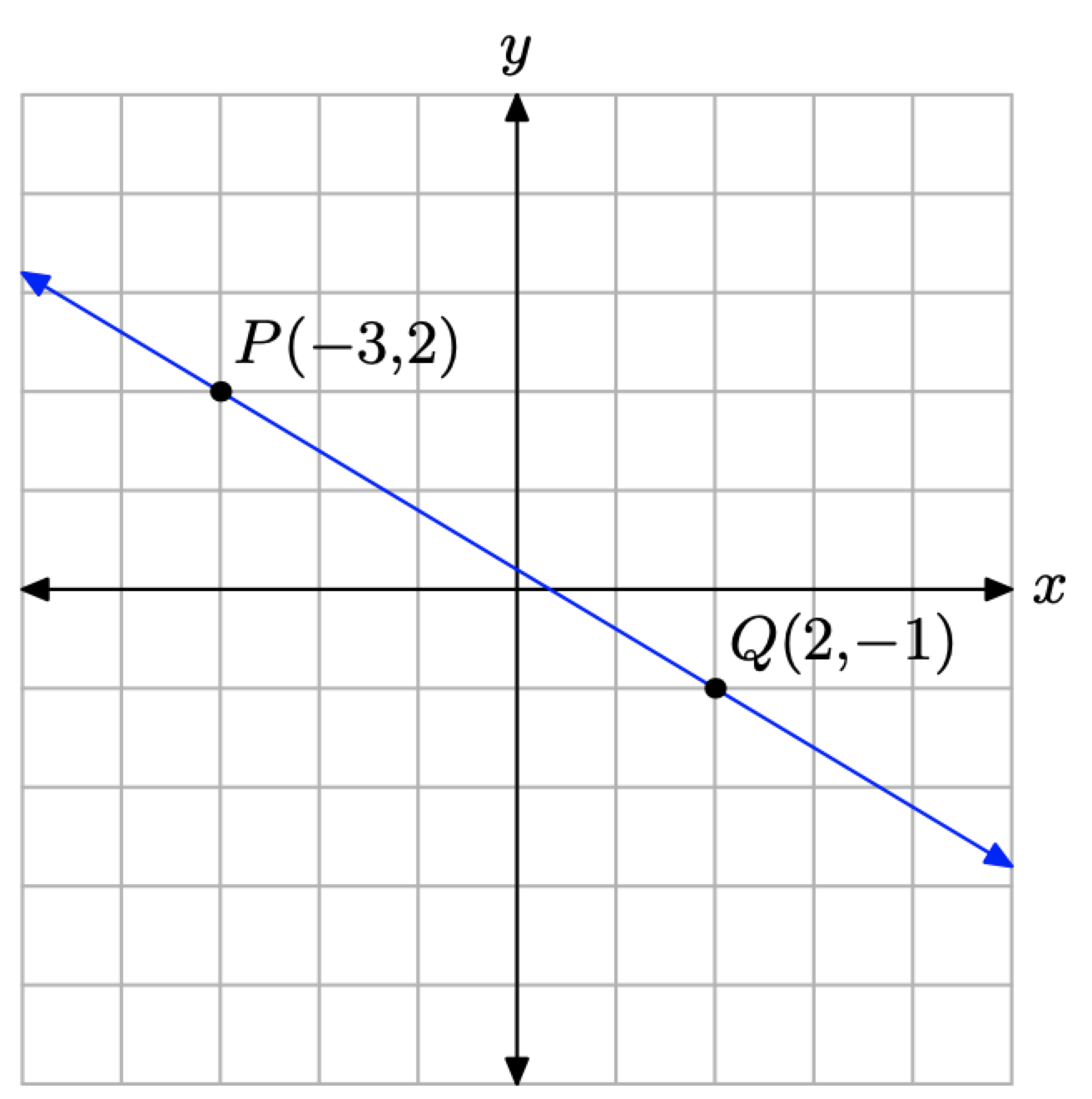
    WeChata0d7e316a7412734afa037efaf06e7b9.png
    Figura\(\PageIndex{3}\). La línea a través de los puntos P (−3, 2) y Q (2, −1).

    Utilice la fórmula de pendiente para determinar la pendiente de la línea a través de los puntos P (−3, 2) y Q (2, −1).

    \[m=\frac{\Delta y}{\Delta x}=\frac{-1-2}{2-(-3)}=-\frac{3}{5}\]

    Usaremos la forma punto-pendiente de la línea

    \[y-y_{0}=m\left(x-x_{0}\right)\]

    Vamos a usar el punto P (−3, 2) como el punto dado\(\left(x_{0}, y_{0}\right)\). Es decir,\(\left(x_{0}, y_{0}\right)=(-3,2)\). Sustituto\(m=-3 / 5, x_{0}=-3,\) y\(y_{0}=2\) en la ecuación (7), obteniendo

    \[y-2=-\frac{3}{5}(x-(-3))\]

    Esta es la ecuación de la línea que pasa por los puntos P y Q.

    Alternativamente, también podríamos usar el punto Q (2, −1) como punto dado\(\left(x_{0}, y_{0}\right)\). Es decir,\(\left(x_{0}, y_{0}\right)=(2,-1)\). Sustituto\(m=-3 / 5, x_{0}=2,\) y\(y_{0}=-1\) en forma de punto-pendiente (7), obteniendo

    \[y-(-1)=-\frac{3}{5}(x-2)\]

    Esta también, es la ecuación de la línea que pasa por los puntos P y Q.

    ¿Cómo pueden las ecuaciones (8) y (9) ser ambas la ecuación de la línea a través de P y Q, sin embargo, verse tan claramente diferentes? Coloquemos cada ecuación en forma estándar\(Ax + By = C\) y comparemos los resultados.

    Si partimos con la ecuación (8) y distribuimos la pendiente,

    \[\begin{array}{l}{y-2=-\frac{3}{5}(x-(-3))} \\ {y-2=-\frac{3}{5} x-\frac{9}{5}}\end{array}\]

    Multiplica ambos lados por el denominador común 5 para borrar las fracciones.

    \[\begin{aligned} 5(y-2) &=5\left(-\frac{3}{5} x-\frac{9}{5}\right) \\ 5 y-10 &=-3 x-9 \end{aligned}\]

    Agregue 3x a ambos lados de la ecuación, luego agregue 10 a ambos lados de la ecuación para obtener

    \[3 x+5 y=1\]

    Colocar la ecuación (9) en forma estándar de manera similar. Primero, comenzar con la ecuación (9) y distribuir la pendiente,

    \[\begin{aligned} y-(-1) &=-\frac{3}{5}(x-2) \\ y+1 &=-\frac{3}{5} x+\frac{6}{5} \end{aligned}\]

    A continuación, multiplica ambos lados de este último resultado por 5 para borrar las fracciones de la ecuación.

    \[\begin{aligned} 5(y+1) &=5\left(-\frac{3}{5} x+\frac{6}{5}\right) \\ 5 y+5 &=-3 x+6 \end{aligned}\]

    Finalmente, suma 3x a ambos lados de la ecuación, luego resta 5 de ambos lados de la ecuación para obtener

    \[3 x+5 y=1\]

    Obsérvese que la ecuación (11) es idéntica a la ecuación (10). Por lo tanto, no importa qué punto utilice en la forma de punto-pendiente. Ambos llevan al mismo resultado.

    Líneas Paralelas

    Recordemos que la pendiente controla la “inclinación” de una línea. En consecuencia, si dos líneas son paralelas, deben tener la misma “pendiente” o pendiente. Veamos un ejemplo de líneas paralelas.

    Ejemplo\(\PageIndex{3}\)

    Encuentra la ecuación de la línea que pasa por el punto P (−2, 2) que es paralelo a la línea que pasa por los puntos Q (−3, −1) y R (2, 1).

    Solución

    Primero, para ayudarnos a mantenernos enfocados, trazamos la línea a través de los puntos Q (−3, −1) y R (2, 1), luego trazamos el punto P (−2, 2), como se muestra en la Figura\(\PageIndex{4}\) (a).

    Podemos usar la fórmula de pendiente para calcular la pendiente de la línea que pasa por los puntos Q (−3, −1) y R (2, 1).

    \[m=\frac{\Delta y}{\Delta x}=\frac{1-(-1)}{2-(-3)}=\frac{2}{5}\]

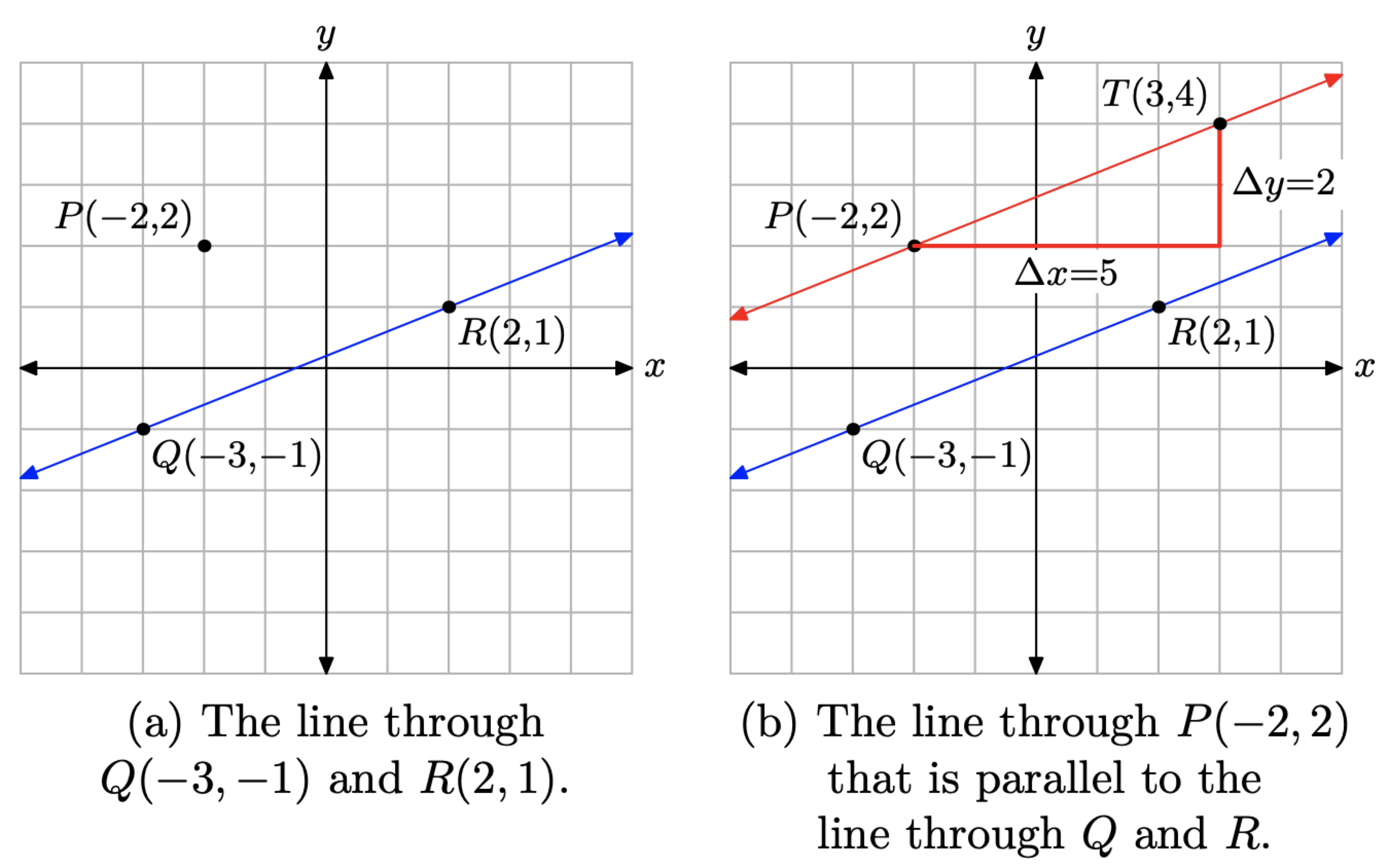
    WeChatf91e04129da47aa1d1b93440e15a29bd.png
    Figura\(\PageIndex{4}\).

    Ahora dibujamos una línea por el punto P (−2, 2) que es paralela a la línea a través de los puntos Q y R. Las líneas paralelas deben tener la misma pendiente, así que partimos en el punto P (−2, 2), “corremos” 5 unidades a la derecha, luego “elevamos” 2 unidades hasta el punto T (3, 4), como se muestra en la Figura\(\PageIndex{4}\) (b).

    Buscamos la ecuación de la línea a través de los puntos P y T. Utilizaremos la forma de pendiente puntual de la línea

    \[y-y_{0}=m\left(x-x_{0}\right)\]

    Usaremos el punto P (−2, 2) como punto dado\(\left(x_{0}, y_{0}\right)\). Es decir,\(\left(x_{0}, y_{0}\right) = (−2, 2)\). La línea a través de P tiene pendiente 2/5. Sustituto\(m=2 / 5, x_{0}=-2,\) y\(y_{0}=2\) en la ecuación (13) para obtener

    \[y-2=\frac{2}{5}(x-(-2))\]

    Coloquemos la ecuación (14) en forma estándar. Distribuya la pendiente, luego despeje las fracciones multiplicando ambos lados de la ecuación resultante por 5.

    \[\begin{aligned} y-2 &=\frac{2}{5} x+\frac{4}{5} \\ 5(y-2) &=5\left(\frac{2}{5} x+\frac{4}{5}\right) \\ 5 y-10 &=2 x+4 \end{aligned}\]

    Finalmente, restar 5y de ambos lados de la última ecuación, luego restar 4 de ambos lados de la ecuación, obteniendo

    \[-14=2 x-5 y\]

    o equivalentemente,

    \[2 x-5 y=-14\]

    Esta es la forma estándar de la ecuación de la línea que pasa por el punto P y paralela a la línea que pasa por los puntos Q y R.

    Líneas perpendiculares

    Supongamos que dos líneas\(L_{1}\) y\(L_{2}\) tienen pendientes\(m_{1}\) y\(m_{2}\), respectivamente. Recordemos (ver la sección sobre Pendiente) que si\(L_{1}\) y\(L_{2}\) son perpendiculares, entonces el producto de sus pendientes es\(m_{1} m_{2}=-1\). Alternativamente, la pendiente de la primera línea es el recíproco negativo de la segunda línea, y viceversa; es decir,\(m_{1}=-1 / m_{2}\) y\(m_{2}=-1 / m_{1}\). Veamos un ejemplo de líneas perpendiculares.

    Ejemplo\(\PageIndex{4}\)

    Encuentra la ecuación de la línea que pasa por el punto P (−4, −4) que es perpendicular a la línea 4x + 3y = 12.

    Solución

    Ayudará a nuestro enfoque si dibujamos la línea dada 4x + 3y = 12. La forma más fácil de trazar una línea en forma estándar Ax + By = C es encontrar las intercepciones x e y.

    \[\begin{array}{rlrrll}{4 x+3 y} & {=}&{12} & {4 x+3 y} & {=}&{12} \\ {4 x+3(0)} & {=}&{12} & {4(0)+3 y} & {=}&{12} \\ {4 x} & {=}&{12} & {3 y} & {=}&{12} \\ {x} & {=}&{3} & {y} & {=}&{4}\end{array}\]

    Trazar las intercepciones x e y R (3, 0) y S (0, 4) como se muestra en la Figura\(\PageIndex{5}\) (a). La línea a través de los puntos R y S es la gráfica de la ecuación 4x + 3y = 12.

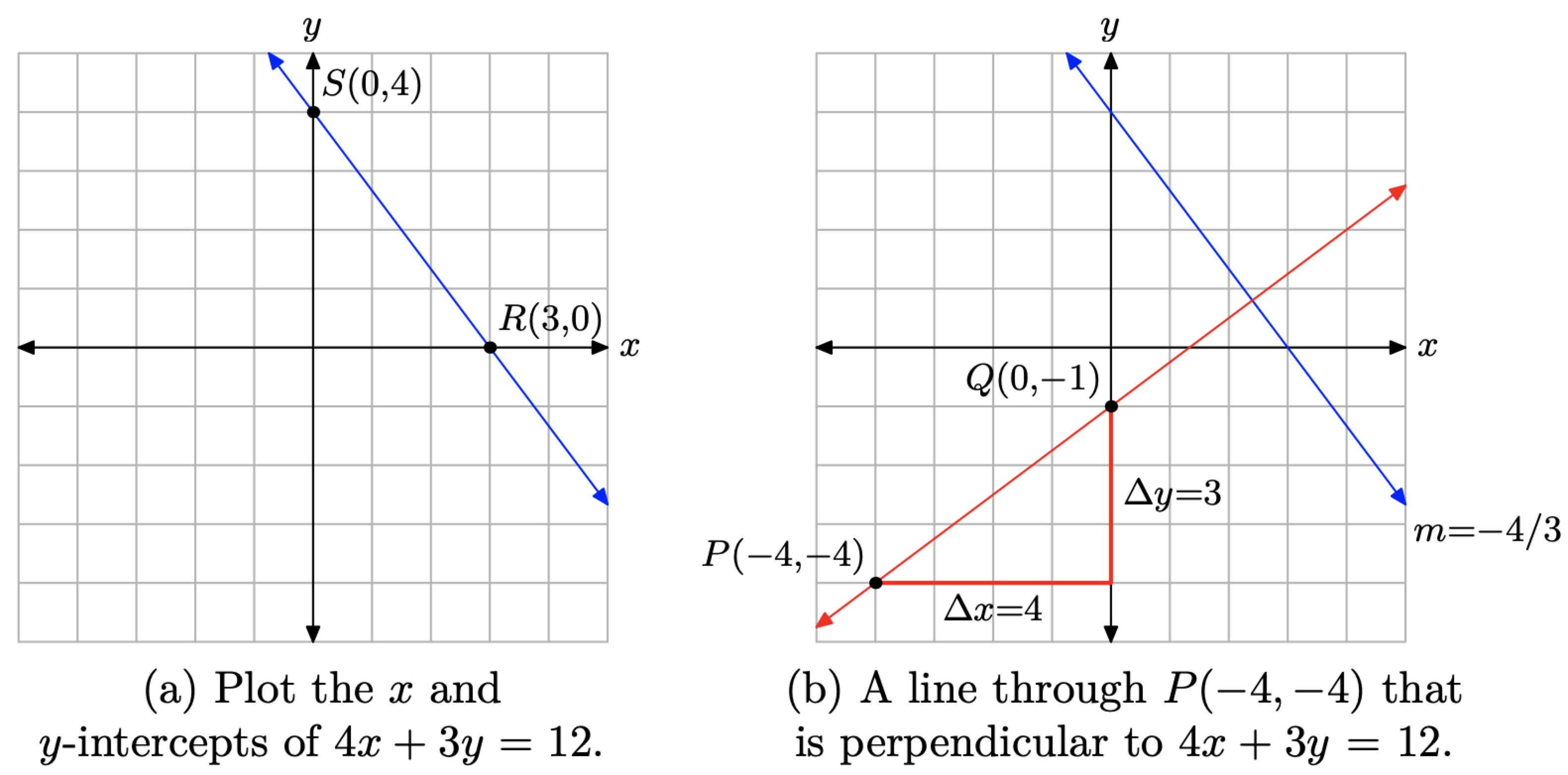
    WeChatf5a79539226b56f42d05801aae5a4375.png
    Figura\(\PageIndex{5}\)

    A continuación, determine la pendiente de la línea 4x + 3y = 12 colocando esta ecuación en forma pendiente-intercepción (es decir, resolver la ecuación 4x + 3y = 12 para y)

    \[\begin{aligned} 4 x+3 y &=12 \\ 3 y &=-4 x+12 \\ y &=-\frac{4}{3} x+4 \end{aligned}\]

    Si dos líneas son perpendiculares, entonces sus pendientes son recíprocos negativos entre sí. Por lo tanto, la pendiente de la línea que es perpendicular a la línea 4x + 3y = 12 (que tiene pendiente −4/3) es m = 3/4. Nuestra segunda línea debe pasar por el punto P (−4, −4). Para dibujar esta segunda línea, primero grafica el punto P (−4, −4), luego mueve 4 unidades a la derecha y 3 unidades hacia arriba hasta el punto Q (0, −1), como se muestra en la Figura\(\PageIndex{5}\) (b). La línea que atraviesa los puntos P y Q es perpendicular a la línea 4x + 3y = 12.

    Para determinar la ecuación de la línea a través de los puntos P y Q, usaremos la forma punto-pendiente de la línea, a saber

    \[y-y_{0}=m\left(x-x_{0}\right)\]

    La pendiente de la línea a través de los puntos P y Q es m = 3/4. Si usamos el punto P (−4, −4), entonces\(\left(x_{0}, y_{0}\right)=(-4,-4)\). Establecer\(m=3 / 4, x_{0}=-4,\) y\(y_{0}=-4\) en la ecuación (16), obteniendo

    \[y-(-4)=\frac{3}{4}(x-(-4))\]

    o equivalentemente,

    \[y+4=\frac{3}{4}(x+4)\]

    Alternativamente, podríamos usar la forma pendiente-intercepción de la línea. Sabemos que la línea a través de los puntos P y Q en la Figura\(\PageIndex{5}\) (b) cruza el eje y en Q (0, −1). Entonces, con pendiente m = 3/4 y coordenada y de la intercepción y b = −1, la forma pendiente-intercepción y = mx + b se convierte

    \[y=\frac{3}{4} x-1\]

    Por otro lado, si resolvemos la ecuación (17) para y,

    \[\begin{aligned} y+4 &=\frac{3}{4}(x+4) \\ y+4 &=\frac{3}{4} x+3 \\ y &=\frac{3}{4} x-1 \end{aligned}\]

    Tenga en cuenta que esto es idéntico al resultado encontrado usando la forma pendiente-intercepción anterior.

    Es reconfortante observar que las dos formas (punto-pendiente y pendiente-intercepción) dan el mismo resultado, pero ¿cómo determinamos la forma más eficiente a utilizar para un problema en particular? Aquí hay una buena pista.

    Determinación de la Forma de la Línea a Usar

    Aquí hay algunos consejos sólidos cuando está tratando de determinar si usar la forma pendiente-intercepción o la forma pointslope de una línea.

    • Si se le da la pendiente y la intercepción y, utilice la forma pendiente-intercepción y = mx + b.
    • Si se le da un punto (que no sea la intercepción y) y la pendiente, utilice la forma punto-pendiente\(y-y_{0}=m\left(x-x_{0}\right)\).

    Aplicaciones de Funciones Lineales

    En esta sección veremos algunas aplicaciones de funciones lineales. Comenzamos desarrollando una función relacionada con la temperatura Fahrenheit y Celsius.

    Ejemplo\(\PageIndex{5}\)

    El agua se congela en\(32^{\circ} F\) y\(0^{\circ} \mathrm{C}\). El agua hierve en\(212^{\circ} F\) y\(100^{\circ} \mathrm{C}\). F y C son abreviaturas para escalas de temperatura Fahrenheit y Celsius, respectivamente. Asumiendo una relación lineal, desarrollar un modelo relativo a la temperatura Fahrenheit y Celsius.

    Solución

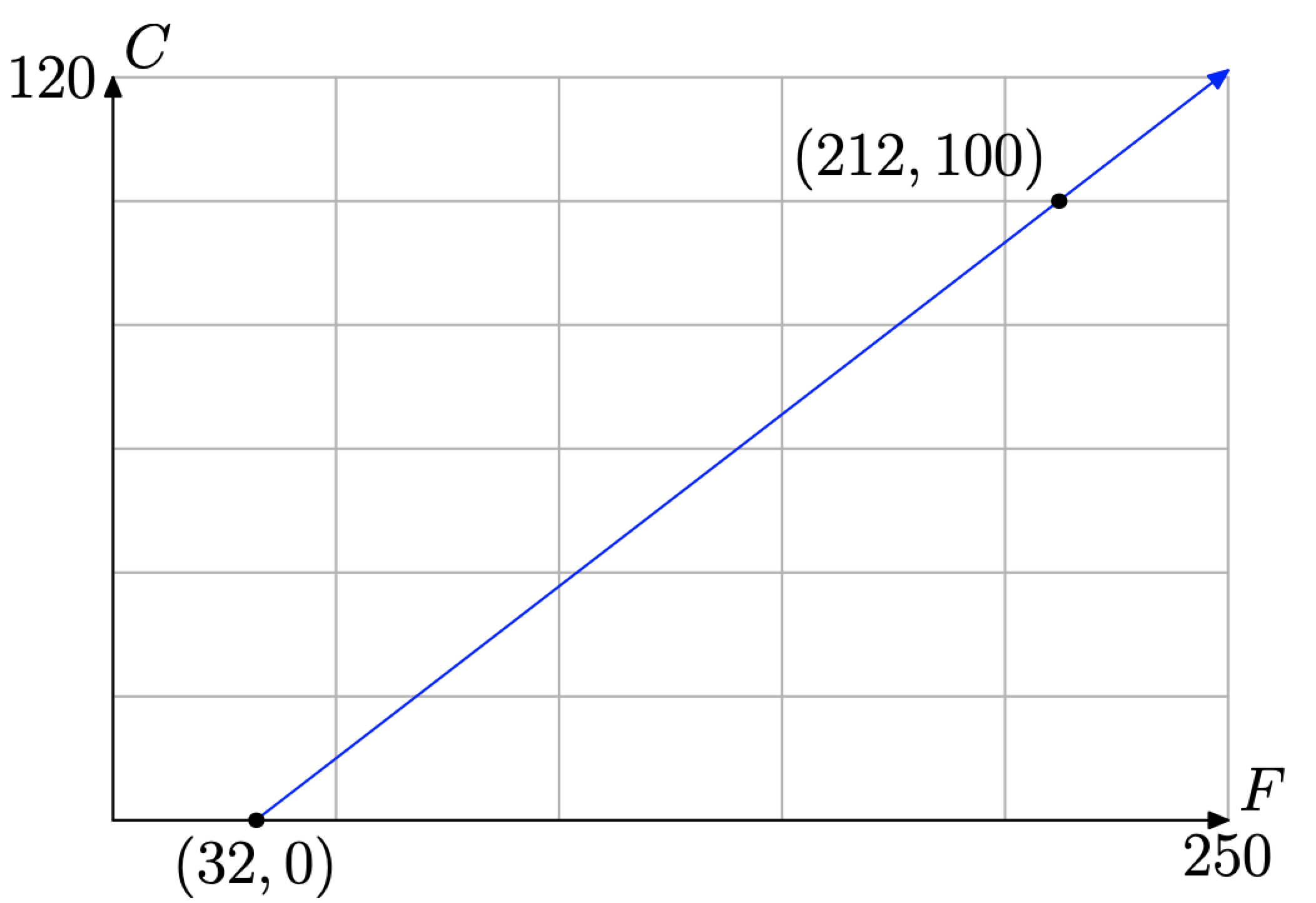
    Primero, para ayudar a mantener nuestro enfoque, configuramos un sistema de coordenadas en una hoja de papel cuadriculado. En Figura\(\PageIndex{6}\), hemos decidido hacer de la temperatura Celsius la variable dependiente y hemos asignado la temperatura Celsius al eje vertical. De igual manera, hemos declarado la temperatura Fahrenheit como la variable independiente y la hemos asignado al eje horizontal.

    Interpretar los datos dados:

    • El agua se congela en\(32^{\circ} F\) y\(0^{\circ} C\). Esto nos da el punto (F, C) = (32, 0), que trazamos en la Figura\(\PageIndex{6}\).
    • El agua hierve en\(212^{\circ} F\) y\(100^{\circ} C\). Esto nos da el punto (F, C) = (212, 100), que trazamos en la Figura\(\PageIndex{6}\).

    Ahora estamos en terreno familiar. Queremos encontrar la ecuación de la línea a través de estos dos puntos, que es el mismo tipo de problema que abordamos en el Ejemplo 6. Primero, usa los puntos (32, 0) y (212, 100) para determinar la pendiente de la línea.

    \[m=\frac{\Delta C}{\Delta F}=\frac{100-0}{212-32}=\frac{100}{180}=\frac{5}{9}\]

    Ahora utilizaremos la forma punto-pendiente de la línea,\(y-y_{0}=m\left(x-x_{0}\right)\) con m = 5/9 y\(\left(x_{0}, y_{0}\right)=(32,0)\). Sustituto\(m=5 / 9, x_{0}=32,\) y\(y_{0}=0\) en\(y-y_{0}=m\left(x-x_{0}\right)\) obtener

    WeChat592ee9ac052697196b626cb1b26fab84.png
    Figura\(\PageIndex{6}\). Trazar la temperatura Celsius versus la temperatura Fahrenheit

    \[y-0=\frac{5}{9}(x-32)\]

    Sin embargo, nuestro eje dependiente está etiquetado C, no y, y nuestro eje independiente está etiquetado F, no x Entonces, debemos reemplazar y y x en la ecuación (20) con C y F, respectivamente, obteniendo

    \[C=\frac{5}{9}(F-32)\]

    Este resultado en la ecuación (21) expresa la temperatura Celsius en función de la temperatura de Fahrenheit. Alternativamente, también podríamos usar la notación de funciones y escribir

    \[C(F)=\frac{5}{9}(F-32)\]

    Supongamos que sabemos que la temperatura de Fahrenheit exterior es\(80^{\circ} \mathrm{F}\) y deseamos expresarlo usando la escala Celsius. Para ello, simplemente evaluamos C (80), como en

    \[C(80)=\frac{5}{9}(80-32) \approx 26.6\]

    De ahí que la temperatura Celsius sea aproximadamente\(26.6^{\circ} \mathrm{C}\).

    Por otro lado, supongamos que sabemos que la temperatura Celsius en un techo metálico es\(80^{\circ} \mathrm{C}\) y deseamos encontrar la temperatura Fahrenheit. Para ello, tenemos que resolver

    \[C(F)=80\]

    para F, o equivalentemente,

    \[\frac{5}{9}(F-32)=80\]

    Multiplica ambos lados por 9 para obtener

    \[5(F-32)=720\]

    luego divide ambos lados del resultado por 5 para obtener

    \[F-32=144\]

    Al sumar 32 a ambos lados de este último resultado se produce la temperatura de Fahrenheit\(F = 176^{\circ} \mathrm{F}\). ¡Guau, eso está caliente!

    This page titled 3.4: La Forma Punto-Pendiente de una Línea is shared under a CC BY-NC-SA 2.5 license and was authored, remixed, and/or curated by David Arnold.