3.3: Ecuaciones de Líneas
- Page ID
- 110758
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)En esta sección desarrollaremos la forma pendiente-interceptación de una línea. Cuando hayas completado el trabajo en esta sección, deberías poder mirar la gráfica de una línea y determinar su ecuación en forma de pendiente-intercepción.
La forma de pendiente-interceptación
En el apartado anterior, desarrollamos la fórmula para la pendiente de una línea. Supongamos que la variable dependiente es y y la variable independiente es x y tenemos una línea que pasa por los puntos\(P\left(x_{1}, y_{1}\right)\) y\(Q\left(x_{2}, y_{2}\right)\), como se muestra en la Figura\(\PageIndex{1}\).
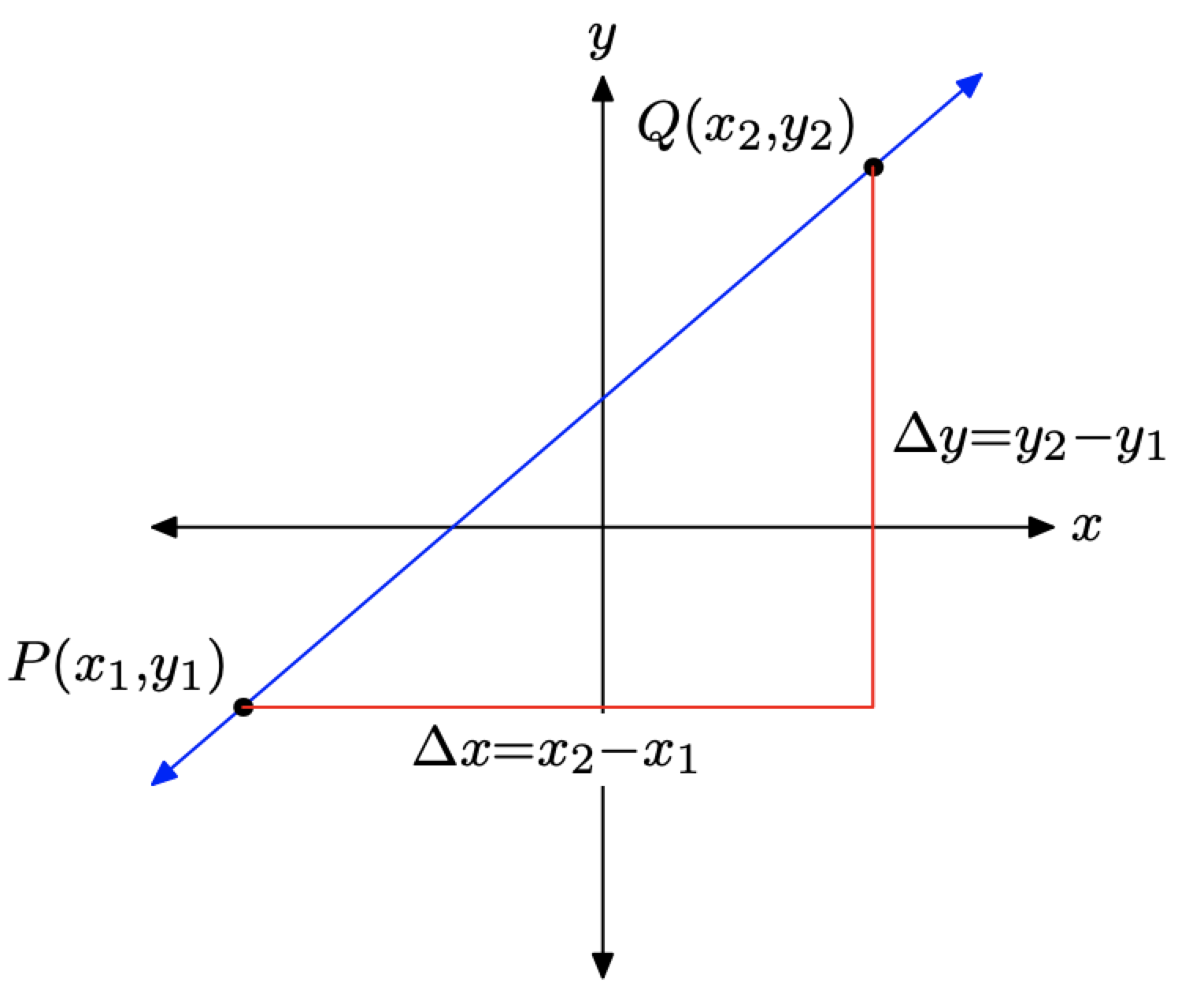
Al barrer los ojos de izquierda a derecha, tenga en cuenta que el cambio en x es\(\Delta x=x_{2}-x_{1}\) y el cambio en y es\(\Delta y=y_{2}-y_{1}\). Así, la pendiente de la línea está determinada por la fórmula
\[\text { Slope }=\frac{\Delta y}{\Delta x}=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\]
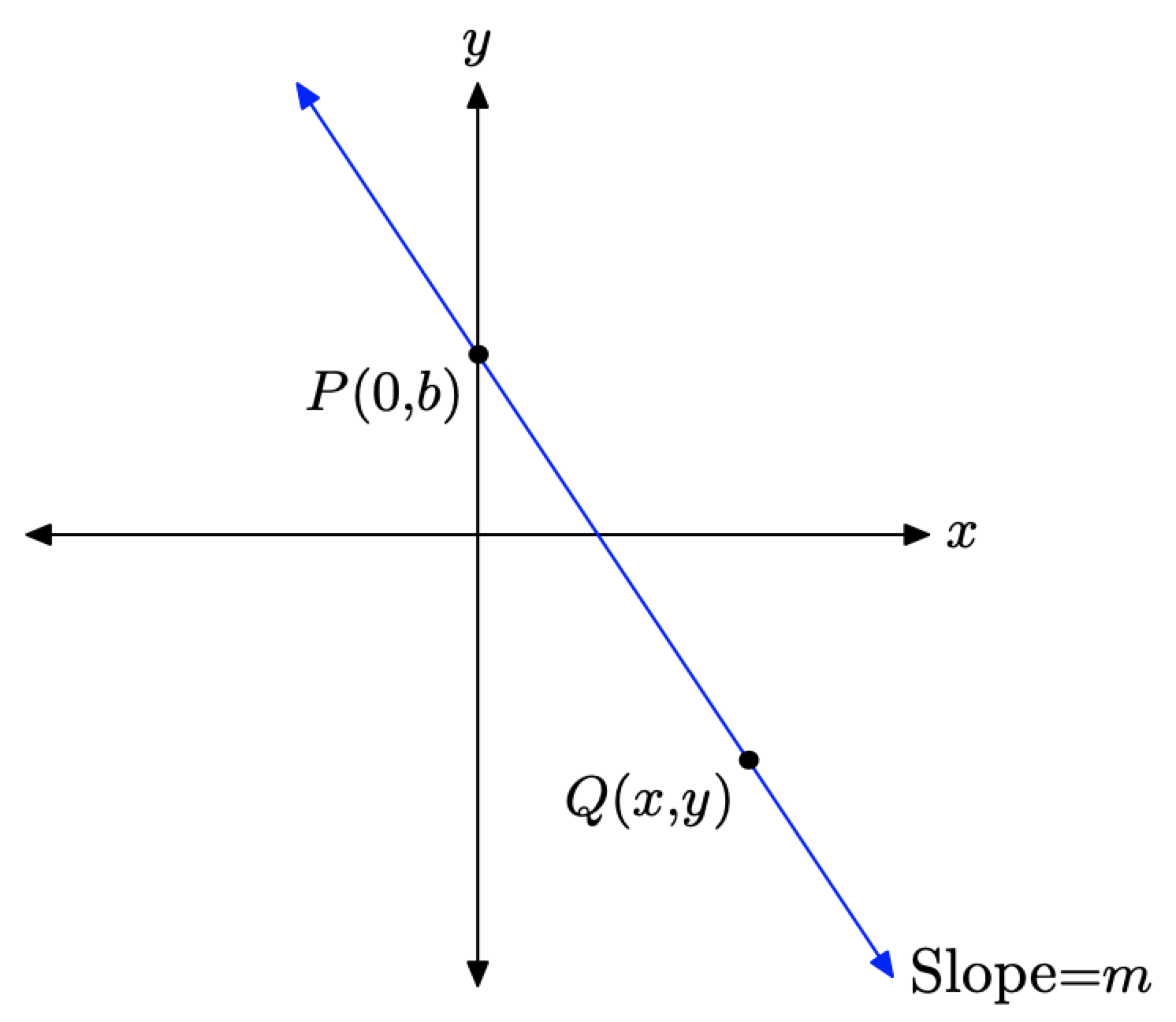
Ahora considere la línea en la Figura\(\PageIndex{2}\). Supongamos que se nos dan dos datos sobre esta línea:
- El punto donde la línea cruza el eje y (la intercepción y) es (0, b).
- La “pendiente” de la línea es algún número m.
Para encontrar la ecuación de la línea que se muestra en la Figura\(\PageIndex{2}\), seleccione un punto arbitrario Q (x, y) en la línea, luego calme la pendiente de la línea usando\(\left(x_{1}, y_{1}\right)=P(0, b)\) y\(\left(x_{2}, y_{2}\right)=Q(x, y)\) en la fórmula de pendiente (1).
\[\text { Slope }=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}=\frac{y-b}{x-0}\]
Simplificar.
\[\text { Slope }=\frac{y-b}{x}\]
Se nos da que la pendiente es el número m, así que sustituya este número por la palabra “Pendiente” en el último resultado.
\[m=\frac{y-b}{x}\]
Multiplique ambos lados de la última ecuación por\(x\).
\[m x=y-b\]
Agrega b a ambos lados de la última ecuación para obtener
\[m x+b=y\]
o al intercambiar lados de la ecuación,
\[y=m x+b\]
La discusión anterior lleva al siguiente resultado.
Definición: La forma pendiente-interceptación de una línea
Si la línea\(L\) intercepta el eje y en el punto (0, b) y tiene pendiente m, entonces la ecuación de la línea es
\[y=m x+b. \label{slopeintercept eq}\]
Esta forma de la ecuación de una línea se llama la forma pendiente-intercepción. La función definida por la ecuación\[f(x)=m x+b\] se llama función lineal.
Es importante señalar dos datos clave sobre la forma pendiente-intercepción y = mx + b.
- El coeficiente de x (la m en y = mx + b) es la pendiente de la línea.
- El término constante (el b en y = mx+b) es la coordenada y de la intercepción y (0, b).
Procedimiento para el uso de la forma pendiente-intercepción de una línea
Cuando se le da la pendiente de una línea y la intercepción y de la línea, utilice la forma pendiente-intercepción de la siguiente manera:
- Sustituir la pendiente dada por m en la fórmula\(y = mx + b\).
- Sustituya la coordenada y de la intercepción y por b en la fórmula\(y = mx + b\).
Por ejemplo, si la línea tiene pendiente −2 y la intercepción y (el punto donde la línea cruza el eje y) es (0, 3), entonces sustituya m = −2 y b = 3 en Ecuación\ ref {slopeintercept eq} para obtener
\[y = −2x + 3\].
Veamos algunos ejemplos de uso de esta fórmula tan importante.
Ejemplo\(\PageIndex{1}\)
¿Cuál es la ecuación de la línea que tiene pendiente −2/3 e intercepción y en (0, 3)? Boceto de la línea en papel cuadriculado
Solución
La ecuación de la línea es
\[y=m x+b\]
Se nos da que la pendiente es −2/3. De ahí que m = −2/3. En segundo lugar, se nos da que la línea intercepta el eje y en el punto (0, 3). En la forma pendiente-intercepción y = mx + b, recuerde que b representa la coordenada y de la intercepción y. De ahí que b = 3. Sustituir m = −2/3 y b = 3 en la ecuación (4), obteniendo
\[y=-\frac{2}{3} x+3\]
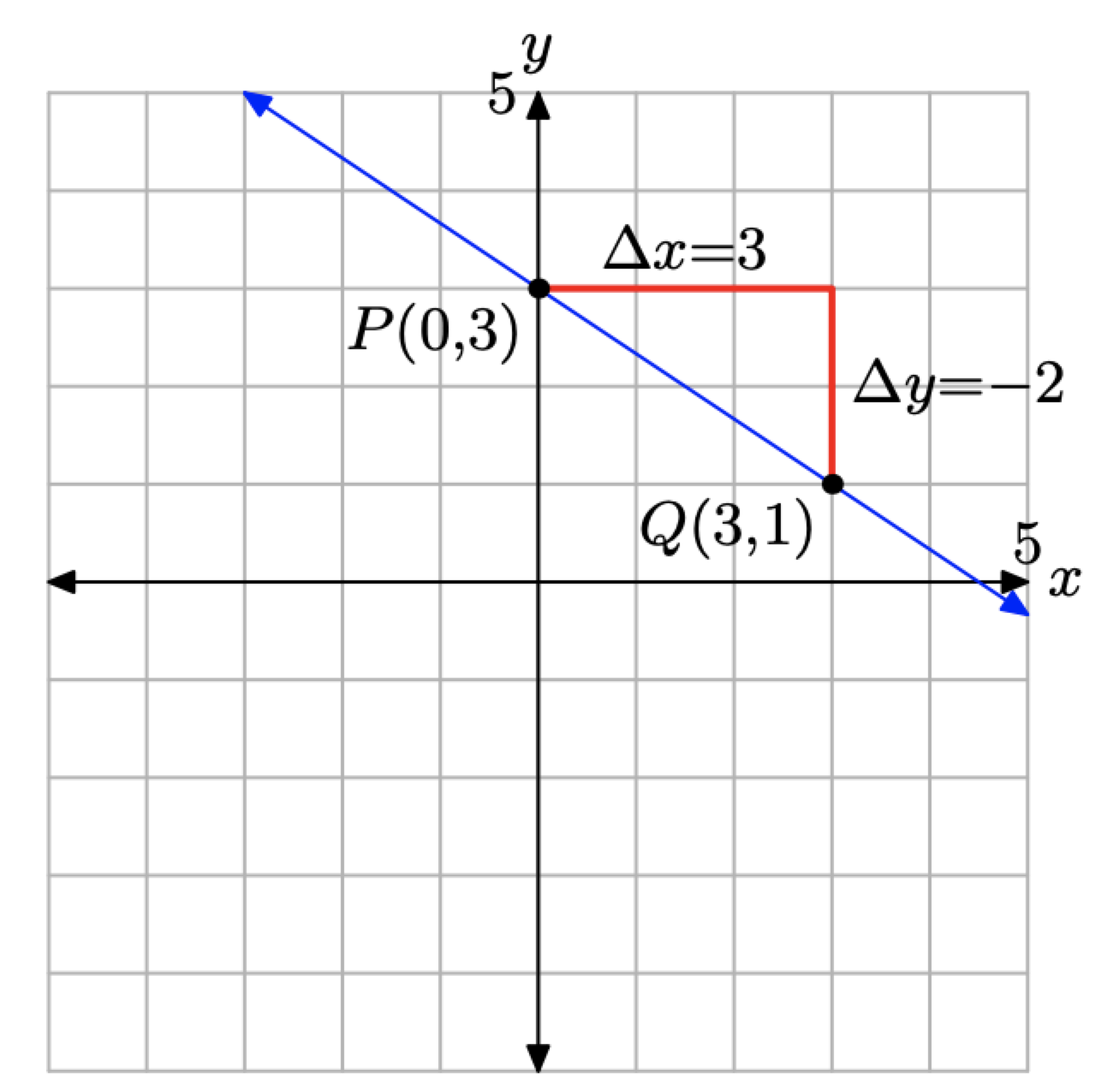
Para bosquejar la gráfica de la línea, primero localice la intercepción y en P (0, 3), como se muestra en la Figura\(\PageIndex{3}\). Partiendo de la intercepción y en P (0, 3), mueva 3 unidades a la derecha y 2 unidades hacia abajo hasta el punto Q (3, 1). La línea requerida pasa por los puntos P y Q.
Tenga en cuenta que la línea “intercepta” el eje y en 3 y se inclina cuesta abajo, de acuerdo con el hecho de que la pendiente es negativa en este ejemplo.
Ejemplo\(\PageIndex{2}\)
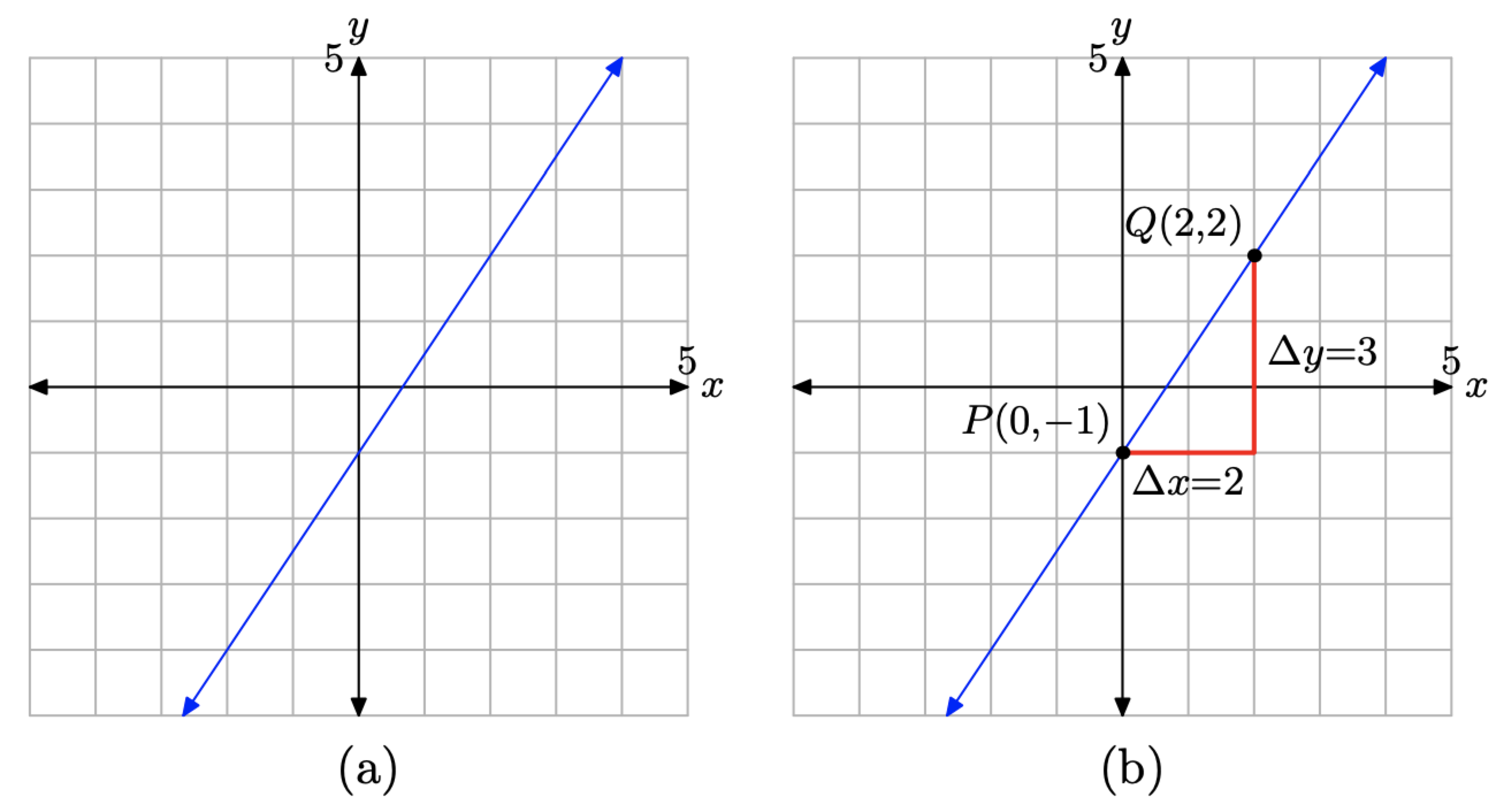
Dada la gráfica de la línea en la Figura\(\PageIndex{4}\) (a), determinar la ecuación de la línea.
Solución
Primero, localice la intercepción y de la línea, que hemos etiquetado como P (0, −1) en la Figura\(\PageIndex{4}\) (b). En la fórmula y = mx + b, recuerde que b representa la coordenada y de la intercepción y. Así, b = −1.
En segundo lugar, necesitamos determinar la pendiente de la línea. En la Figura\(\PageIndex{4}\) (b), comience en el punto P, mueva 2 unidades a la derecha, luego 3 unidades hacia arriba hasta el punto Q (2, 2). Esto hace que la pendiente\[m=\frac{\Delta y}{\Delta x}=\frac{3}{2}\]
Sustituye m = 3/2 y b = −1 en la forma pendiente-intercepción y = mx + b para obtener
\[y=\frac{3}{2} x-1\]
que es la ecuación deseada de la línea.
Hacer conexiones
Si la conexión entre tasa y pendiente aún no está clara, recordemos un ejemplo que hicimos anteriormente en el capítulo.
Sebastián se despide de su hermano, quien está platicando con un grupo de sus amigos aproximadamente a 20 pies de distancia. Entonces Sebastián comienza a alejarse de su hermano a un ritmo constante de 4 pies por segundo.
La distancia entre los hermanos depende de la cantidad de tiempo que haya pasado, por lo que establecemos la distancia d en el eje vertical y el tiempo t en el eje horizontal, como se muestra en la Figura\(\PageIndex{5}\). Tenga en cuenta que d y t están tomando el lugar “habitual” de y y x, respectivamente. La distancia que separa a los hermanos en el tiempo t = 0 es d = 20 pies. Esto se indica con la “intercepción d” en P (0, 20) en la Figura\(\PageIndex{5}\).
A continuación, la distancia entre los hermanos va aumentando a una velocidad de 4 pies por segundo. Comenzando en el punto P (0, 20), mueva 1 segundo a la derecha (2 cajas) y 4 unidades hacia arriba (1 caja) hasta el punto Q (1, 24), como se muestra en la Figura\(\PageIndex{5}\). La línea a través de los puntos P y Q modela entonces la distancia entre los hermanos en función del tiempo.
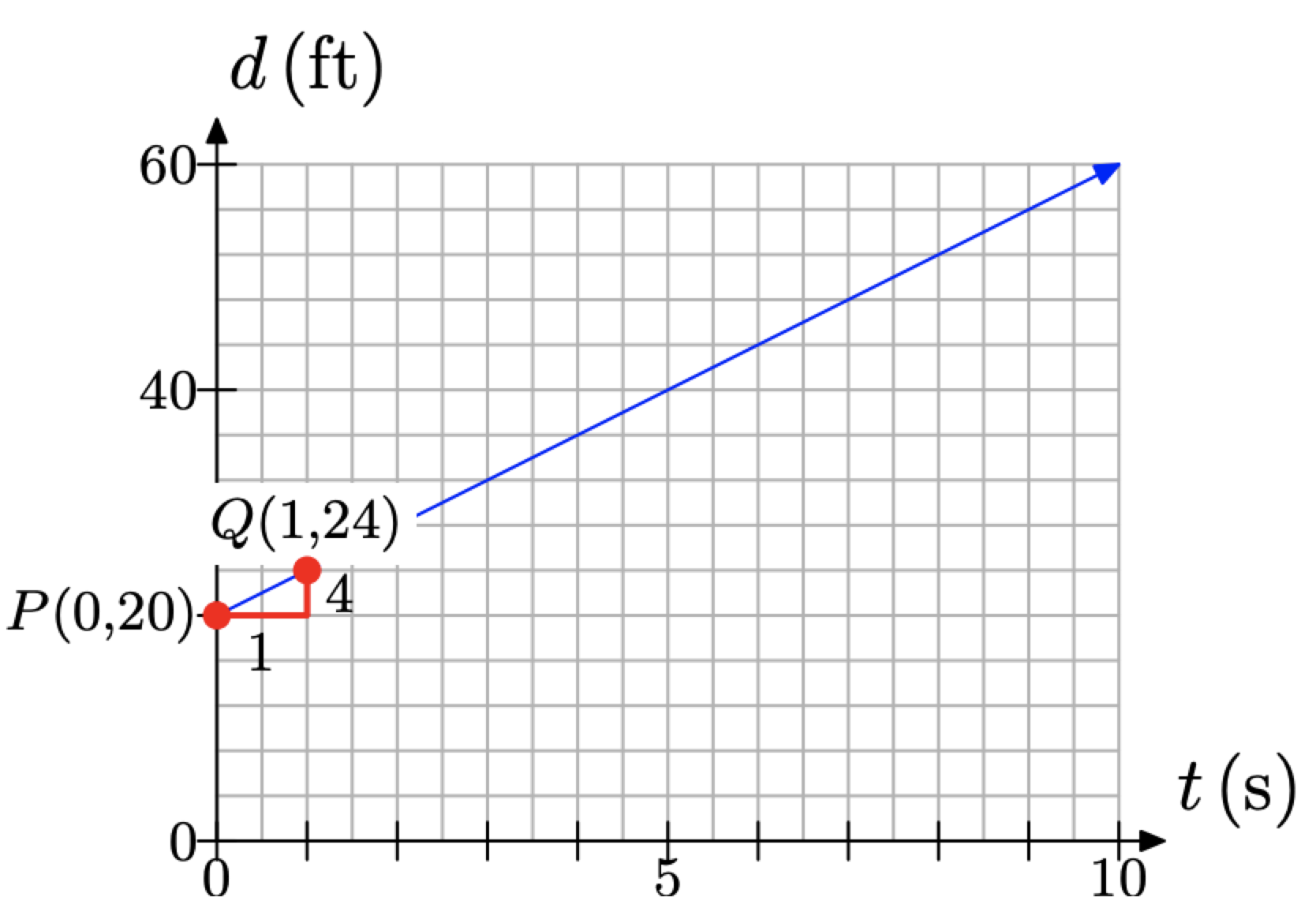
Si recuerda, entonces determinamos una relación entre la distancia d y el tiempo t examinando la distancia entre los hermanos en los tiempos t = 0, 1, 2 y 3, y resumiendo los resultados en la Tabla\(\PageIndex{1}\).
| t | d |
|---|---|
| 0 | 20 |
| 1 | 20+4 (1) |
| 2 | 20+4 (2) |
| 3 | 20+4 (3) |
La intuición condujo entonces al siguiente modelo, que proporciona la distancia d entre los hermanos en función del tiempo t.
\[d=20+4 t\]
Nuevamente, los lectores deben verificar que la ecuación (6) produce los resultados en la Tabla\(\PageIndex{1}\) a t = 0, 1, 2 y 3.
Alternativamente, con la teoría desarrollada en esta sección, desarrollaríamos la ecuación de la línea usando la forma pendiente-intercepción de la línea; es decir,
\[y=m x+b\]
Sin embargo, en este caso, la variable dependiente es d, no y, y la variable independiente es t, no x Entonces, reemplace y y x en la ecuación (7) por d y t, respectivamente, obteniendo
\[d=m t+b\]
A continuación, la línea intercepta el eje d en P (0, 20), así que b = 20. Además, la pendiente de la línea es de 4 pies por segundo, por lo que m = 4. Sustituir m = 4 y b = 20 en la ecuación (8) para obtener
\[d=4 t+20\]
o usando notación de funciones,\(d(t) = 4t + 20\). Obsérvese que la ecuación (9) es idéntica al modelo de ecuación generado intuitivamente (6).
Ojalá, este desarrollo debería cimentar para siempre la idea de que la pendiente de la línea es la velocidad a la que la variable dependiente está cambiando con respecto a la variable independiente.
La forma estándar de una línea
Ahora sabemos que si nuestra ecuación tiene la forma\(y=m x+b\) (o puede ser manipulada en esta forma), la gráfica será una línea. Tomemos un momento para demostrar que la gráfica de la ecuación\(A x+B y=C\), donde A, B y C son constantes, es una línea.
Si podemos colocar el formulario\(A x+B y=C\) en forma pendiente-intercepción\(y=m x+b\), entonces eso demostrará que la gráfica de\(A x+B y=C\) es una línea. Entonces, empieza con\(A x+B y=C\) y resta Ax de ambos lados de la ecuación.
\[B y=-A x+C\]
Dividir ambos lados de esta última ecuación por B. Obsérvese que aquí hay una suposición que\(B \neq 0\). Nosotros manejaremos el caso cuando B = 0 por separado, al final de esta sección.
\[\begin{aligned} \frac{B y}{B} &=\frac{-A x+C}{B} \\ y &=-\frac{A}{B} x+\frac{C}{B} \end{aligned}\]
Cuando comparamos\(y=-(A / B) x+(C / B)\) con y = mx + b, observamos que la pendiente es m = −A/B y la coordenada y de la intercepción y es b = C/B. Debido a que tuvimos éxito en colocar la ecuación\(A x+B y=C\) en forma pendiente-intercepción, ahora sabemos que la gráfica de\(A x+B y=C\) es una línea (necesitaremos este resultado en trabajos posteriores).
La forma estándar de una línea
El gráfico de la ecuación Ax + By = C es una línea. El formulario\[A x+B y=C\] se llama la forma estándar de una línea.
Veamos un ejemplo.
Ejemplo\(\PageIndex{3}\)
La ecuación 3x+4y = 12 está en forma estándar. Coloque esta ecuación en forma de pendiente-intercepción, determine la pendiente y la intercepción y, luego, use estos resultados para dibujar la gráfica de la línea.
Solución
Primero, resolver la ecuación 3x + 4y = 12 para y.
\[\begin{aligned} 3 x+4 y &=12 \\ 4 y &=-3 x+12 \\ y &=-\frac{3}{4} x+3 \end{aligned}\]
Anote en el último paso cómo entró en juego la propiedad distributiva. Cuando dividimos −3x + 12 por 4, dividimos cada término por 4, obteniendo (−3/4) x + 3.
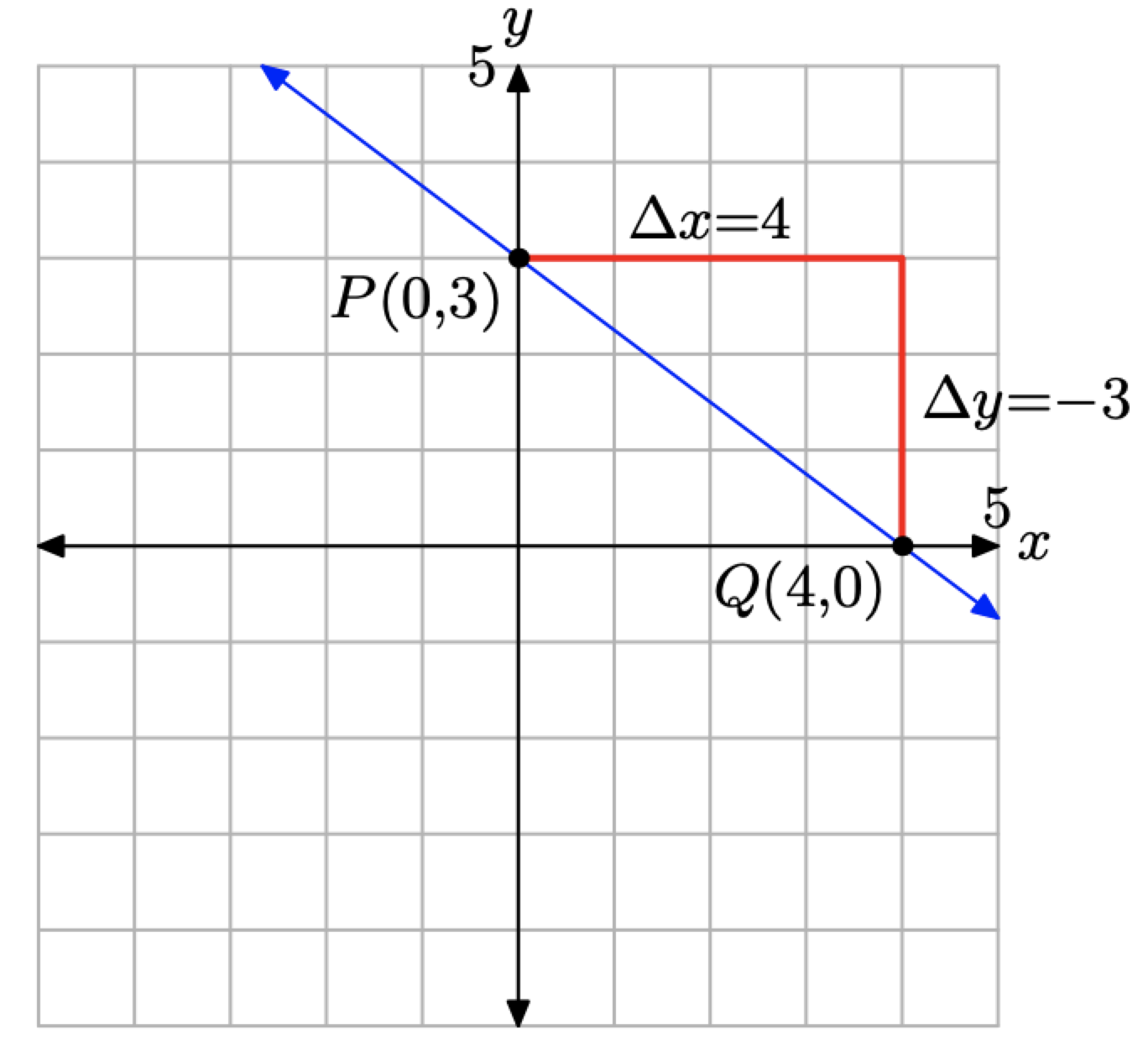
Cuando comparamos y = (−3/4) x+3 con la forma de pendiente-intercepción general y = mx+b, determinamos que la pendiente es m = −3/4 y la coordenada y de la intercepción y es b = 3. Para bosquejar la gráfica de la línea, como hemos hecho en la Figura\(\PageIndex{6}\), trazar la intercepción y en P (0, 3), luego mover 4 unidades a la derecha y 3 unidades hacia abajo al punto Q (4, 0). La línea que pasa por los puntos P y Q es la línea requerida.
Observe nuevamente que la pendiente es m = −3/4 y la línea se inclina “cuesta abajo”. Además, b = 3 y la línea “intercepta” el eje y en P (0, 3).
Veamos otro ejemplo.
Ejemplo\(\PageIndex{4}\)
En Ejemplo\(\PageIndex{1}\), determinamos que la línea dada tenía la ecuación
\[y=\frac{3}{2} x-1\]
Coloque esta ecuación en estándar de\(Ax + By = C\), donde A, B y C son números enteros y\(A > 0\).
Solución
Se nos pide que coloquemos la ecuación\(y = (3/2)x − 1\) en la forma\(Ax + By = C\), donde A, B y C son números enteros, así que comencemos por borrar fracciones de la ecuación. Multiplique ambos lados de la ecuación por el denominador común 2.
\[\begin{aligned} y &=\frac{3}{2} x-1 \\ 2 y &=2\left(\frac{3}{2} x-1\right) \\ 2 y &=3 x-2 \end{aligned}\]
Ahora, resta 2y de ambos lados de la ecuación, luego suma 2 a ambos lados de la ecuación para obtener
\[2=3 x-2 y\]
o equivalentemente,
\[3 x-2 y=2\]
Tenga en cuenta que este último resultado está en forma estándar\(Ax + By = C\), donde A, B y C son números enteros y A > 0.
Intercepta
Ahora sabemos que la gráfica de la ecuación\(Ax + By = C\), donde A, B y C son constantes, es una línea. Debido a que la gráfica de\(Ax + By = C\) es una línea, para dibujar la gráfica de la línea, solo necesitamos encontrar dos puntos que satisfagan la ecuación, trazarlos, luego trazar una línea a través de ellos. Nuestros dos puntos favoritos para trabajar son las intercepciones x e y, porque cada uno involucra el número cero, un número fácil para trabajar.
Considera la gráfica de la Figura\(\PageIndex{7}\) (a). Tenga en cuenta que la gráfica pasa por el eje x tres veces. Los puntos donde la gráfica intercepta el eje x se denominan intercepciones x. Tenga en cuenta que cada uno de estos puntos tiene un valor definitorio en común: el valor y de cada una de estas intercepciones x es igual a cero.
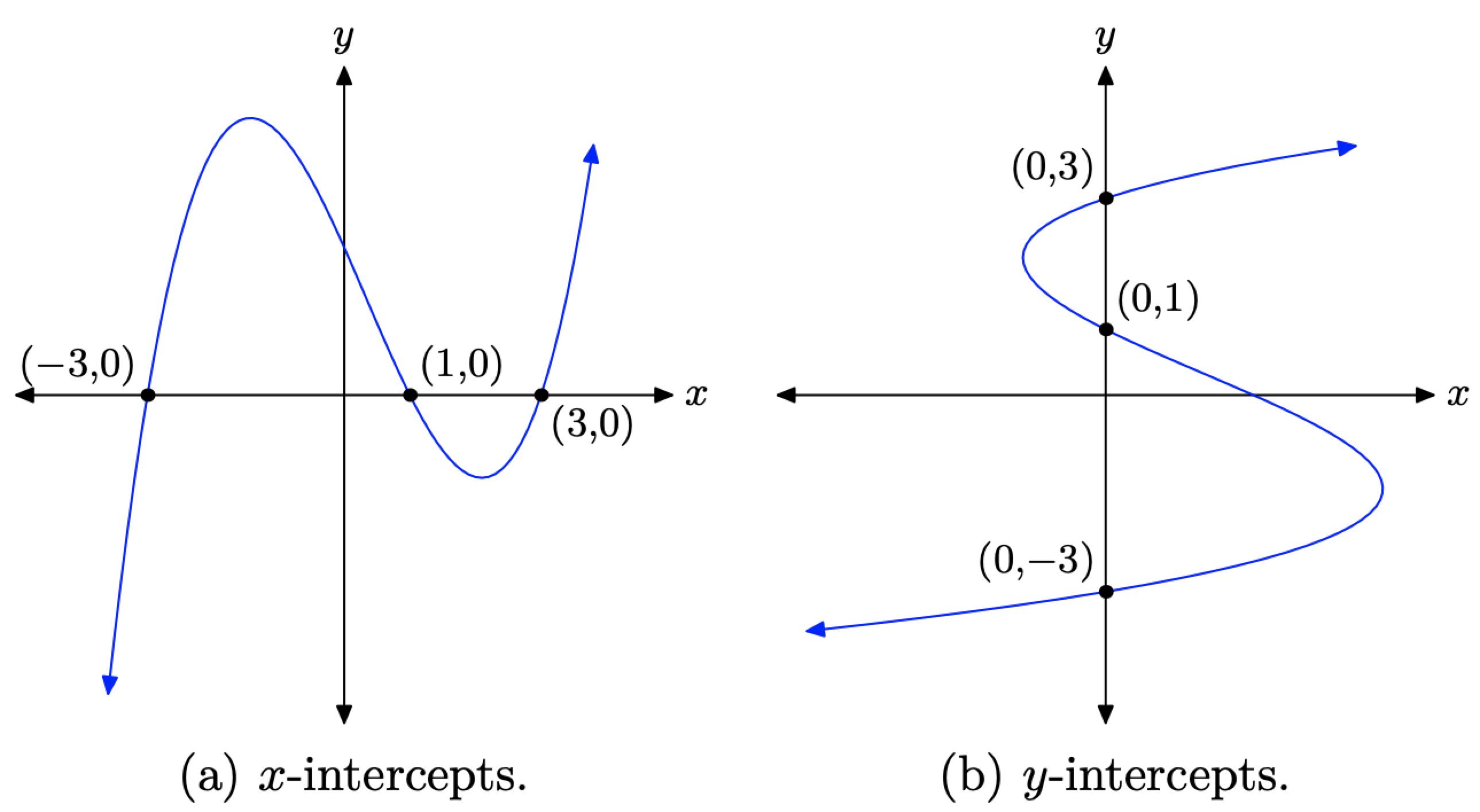
Cómo encontrar una intercepción x
Para encontrar una intercepción x, deje y = 0 en la ecuación y resuelva para x.
Por otro lado, considere la gráfica en la Figura\(\PageIndex{7}\) (b). Tenga en cuenta que esta no es una función (falla la prueba de línea vertical) sino que la gráfica intercepta el eje y tres veces separadas. Los puntos donde la gráfica intercepta el eje y se denominan intercepciones y. Tenga en cuenta que cada una de las intercepciones y en la Figura\(\PageIndex{7}\) (b) tiene un valor definitorio en común: el valor x de cada una de las intercepciones y es igual a cero.
Cómo encontrar una intercepción en Y
Para encontrar una intercepción y, deje x = 0 en la ecuación y resuelva para y.
Pongamos en práctica lo que hemos aprendido.
Ejemplo\(\PageIndex{5}\)
Esboza la gráfica de 3x + 4y = 12.
Solución
Dibujamos la gráfica de la ecuación 3x + 4y = 12 en la Figura\(\PageIndex{6}\). Allí resolvimos la ecuación para y para determinar la pendiente y la intercepción y. Estos, a su vez, se utilizaron para dibujar la gráfica de 3x + 4y = 12 en la Figura\(\PageIndex{6}\).
Aquí, nuestro enfoque será diferente. Primero determinaremos las intercepciones x e y, las trazaremos, luego trazaremos una línea a través de estas intercepciones. Ojalá, obtengamos un resultado que coincida con el de la Figura\(\PageIndex{6}\).
Para encontrar la intercepción x, deje\(y = 0\) entrar\(3x + 4y = 12\) y resolver para x.
\[\begin{aligned} 3 x+4 y &=12 \\ 3 x+4(0) &=12 \\ 3 x &=12 \\ x &=4 \end{aligned}\]
De ahí que la intercepción x sea el punto Q (4, 0). Para encontrar la intercepción y, deje x = 0 in\(3x + 4y = 12\) y resuelva para y.
\[\begin{aligned} 3 x+4 y &=12 \\ 3(0)+4 y &=12 \\ 4 y &=12 \\ y &=3 \end{aligned}\]
De ahí que la intercepción y sea el punto P (0, 3). En Figura\(\PageIndex{8}\), hemos trazado ambas intercepciones x e y dibujamos una línea a través de ellas. Tenga en cuenta que la línea resultante en la Figura\(\PageIndex{8}\) coincide con la misma línea dibujada en la Figura\(\PageIndex{6}\) (donde usamos un método diferente).
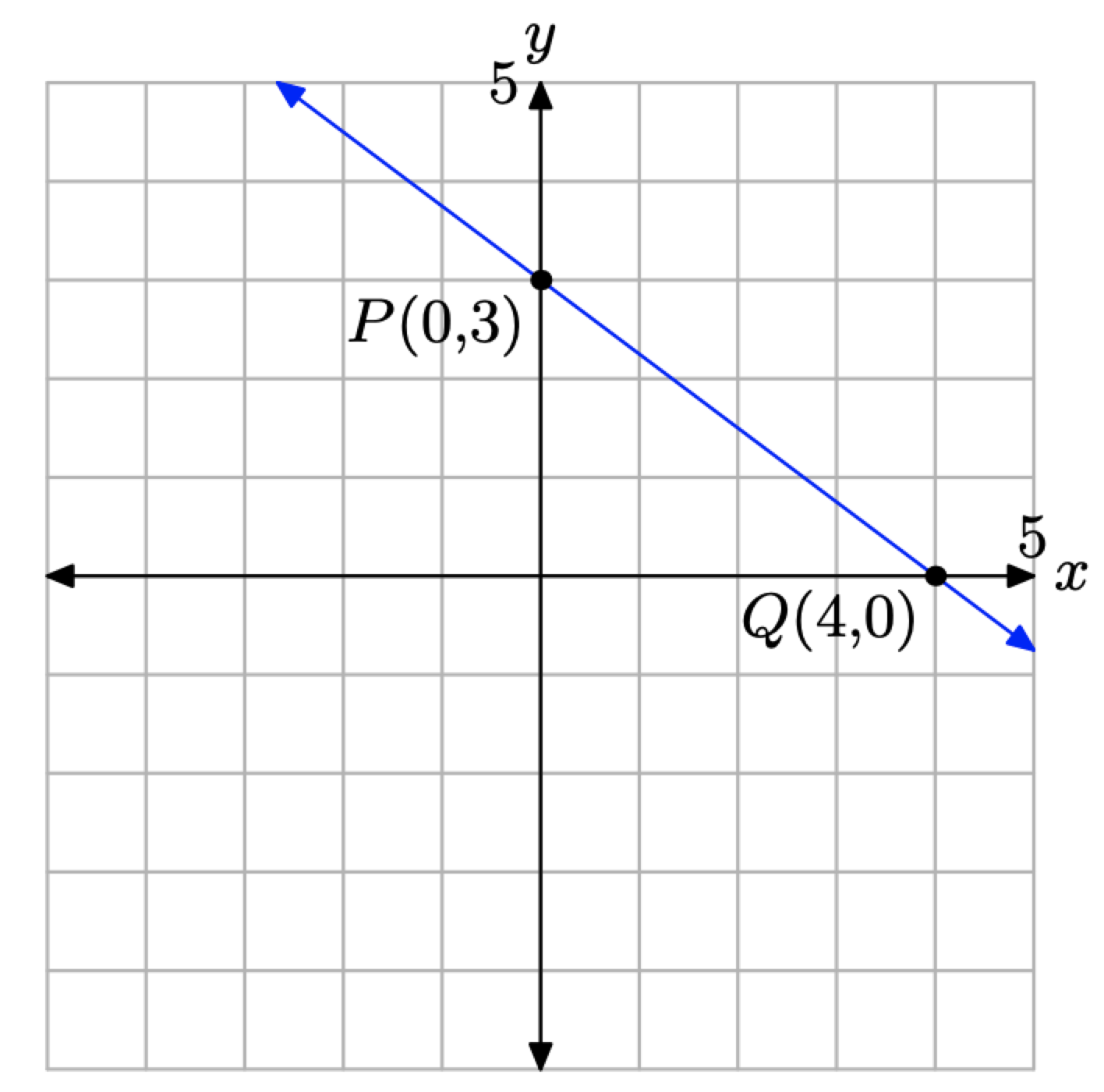
Figura\(\PageIndex{8}\). Trazando las intercepciones x e y.
Recomendamos que siempre que la línea se dé en Forma Estándar\(Ax + By = C\), encuentre las intercepciones x e y, las trazar, luego dibuje una línea a través de ellas. Esta técnica es bastante eficiente porque trabajar con el número cero simplifica enormemente los cálculos.
Líneas Horizontales y Verticales
Hemos introducido la forma estándar de la línea\(Ax + By = C\). El caso en el que A y B son simultáneamente iguales a cero no es muy interesante.4 Sin embargo, los dos casos siguientes son de interés.
- Si dejamos A = 0 y B 6= 0 en la forma estándar\(Ax + By = C\), entonces By = C, o equivalentemente y = C/B.Obsérvese que ésta tiene la forma y = b, donde b es alguna constante.
- De igual manera, si dejamos que B = 0 y A 6= 0 en la forma estándar\(Ax + By = C\), entonces Ax = C, o equivalentemente, x = C/A.Obsérvese que ésta tiene la forma x = a, donde a es alguna constante.
Las líneas que tienen la forma x = a e y = b son dos de las líneas más fáciles de trazar. Veamos un ejemplo de cada uno.
Ejemplo\(\PageIndex{6}\)
Esboza la gráfica de la ecuación x = 3.
Solución
La dirección “bosquejar la gráfica de la ecuación x = 3” puede ser bastante fastidiosa a menos que uno recuerde que una gráfica de una ecuación es el conjunto de todos los puntos que satisfacen la ecuación. Así, la dirección se plantea mejor si decimos “bosquejar el conjunto de todos los puntos (x, y) que satisfacen x = 3”, o equivalentemente, “bosquejar el conjunto de todos los puntos (x, y) que tienen un valor x de 3”. Entonces es una cuestión fácil esbozar la línea vertical que se muestra en la Figura\(\PageIndex{9}\).
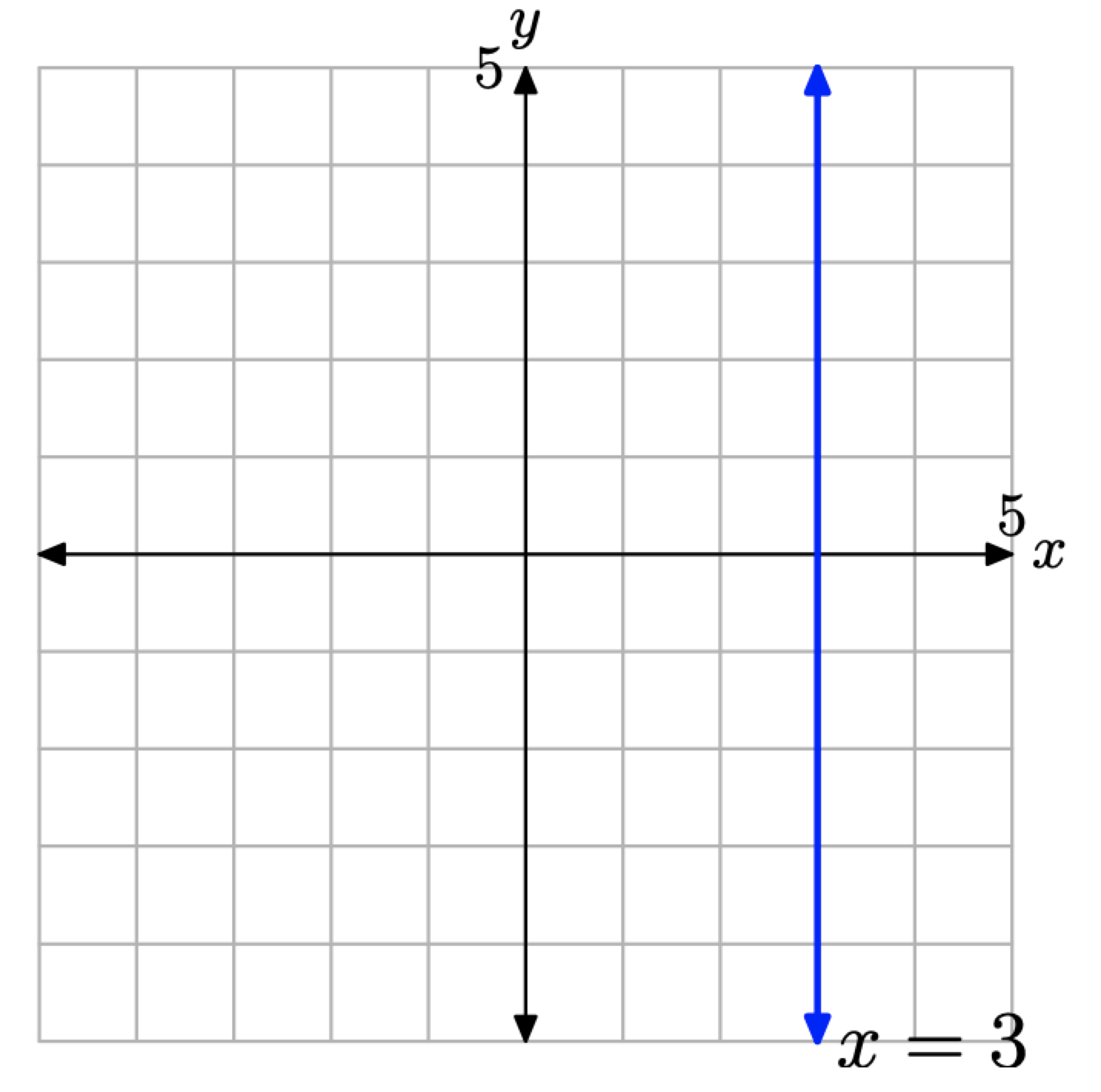
Tenga en cuenta que cada punto de la línea tiene un valor x igual a 3. También, tenga en cuenta que la pendiente de esta línea vertical es indefinida.
Ejemplo\(\PageIndex{7}\)
Esbozar la gráfica de la ecuación y = 3.
Solución
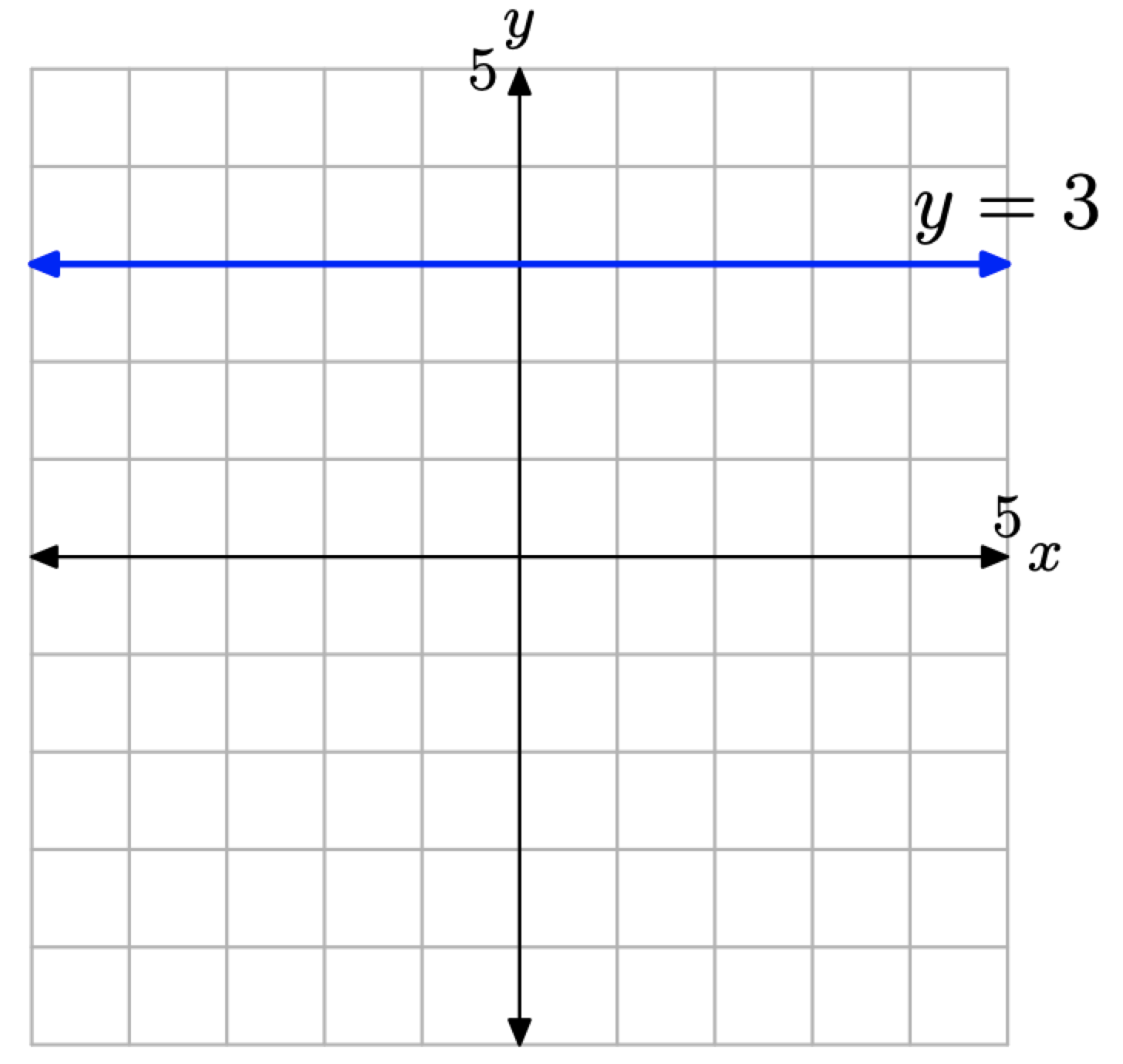
Esta dirección se plantea mejor si decimos “bosquejar el conjunto de todos los puntos (x, y) que satisfacen y = 3”, o equivalentemente, “bosquejar el conjunto de todos los puntos (x, y) que tienen un valor y de 3”. Entonces es una cuestión fácil esbozar la línea horizontal que se muestra en la Figura\(\PageIndex{10}\).
Tenga en cuenta que cada punto de la línea tiene un valor y igual a 3. También, tenga en cuenta que esta línea horizontal tiene pendiente cero.
Dos comentarios finales están en regla. Debido a que la línea en la Figura 10 tiene pendiente cero e intercepción y (0, 3), podemos insertar m = 0 y b = 3 en la forma de intercepción de pendiente y = mx + b y obtener
\[y=0 x+3\]
que por supuesto, equivale a y = 3. Sin embargo, la línea vertical mostrada en la Figura\(\PageIndex{9}\) tiene pendiente “indefinida”, por lo que este enfoque no está disponible. Simplemente debemos reconocer que la línea vertical en la Figura\(\PageIndex{9}\) consiste en todos los puntos que tienen un valor x igual a 3, y luego intuir que su ecuación es x = 3.


