3.5: La Línea de Mejor Ajuste

Al recopilar datos en el mundo real, una gráfica de los datos a menudo revela una “tendencia lineal”, pero los datos no caen precisamente en una sola línea. En este caso, se busca encontrar un modelo lineal que se aproxime a los datos. Empecemos por mirar un ejemplo extendido.

Aditya y Tami son compañeros de laboratorio en la clase de física del Dr. Miller. Están colgando masas de un resorte y midiendo el estiramiento resultante en la primavera. Consulte la Tabla\(\PageIndex{1}\) para conocer sus datos.

Mesa\(\PageIndex{1}\). Conjunto de datos de Aditya y Tami.

m (masa en gramos)	10	20	30	40	50
x (estiramiento en cm)	6.8	10.2	13.9	21.2	24.2

El objetivo es encontrar un modelo que describa los datos, tanto en forma de gráfica como de ecuación. El primer paso es trazar los datos. Recordemos algunos de los lineamientos previstos en la primera sección del capítulo actual.

Lineamientos

Al trazar datos reales, seguimos estas pautas.

1. No quieres gráficas pequeñas. Lo mejor es escalar tu gráfica para que llene una hoja completa de papel cuadriculado. Esto hará que sea mucho más fácil leer e interpretar la gráfica.
2. Es posible que tengas diferentes escalas en cada eje, pero una vez elegidas, debes seguir siendo consistente.
3. Se quiere elegir una escala que facilite nuestro primer objetivo, pero que también haga que los datos sean fáciles de trazar.

Aditya y Tami son libres de elegir las masas que cuelgan en la primavera. De ahí que la masa m sea la variable independiente. En consecuencia, escalaremos el eje horizontal para acomodar la masa. La distancia que estira el resorte depende de la cantidad de masa que cuelga del resorte, por lo que la distancia estirada x es la variable dependiente. Escalaremos el eje vertical para acomodar la distancia estirada.

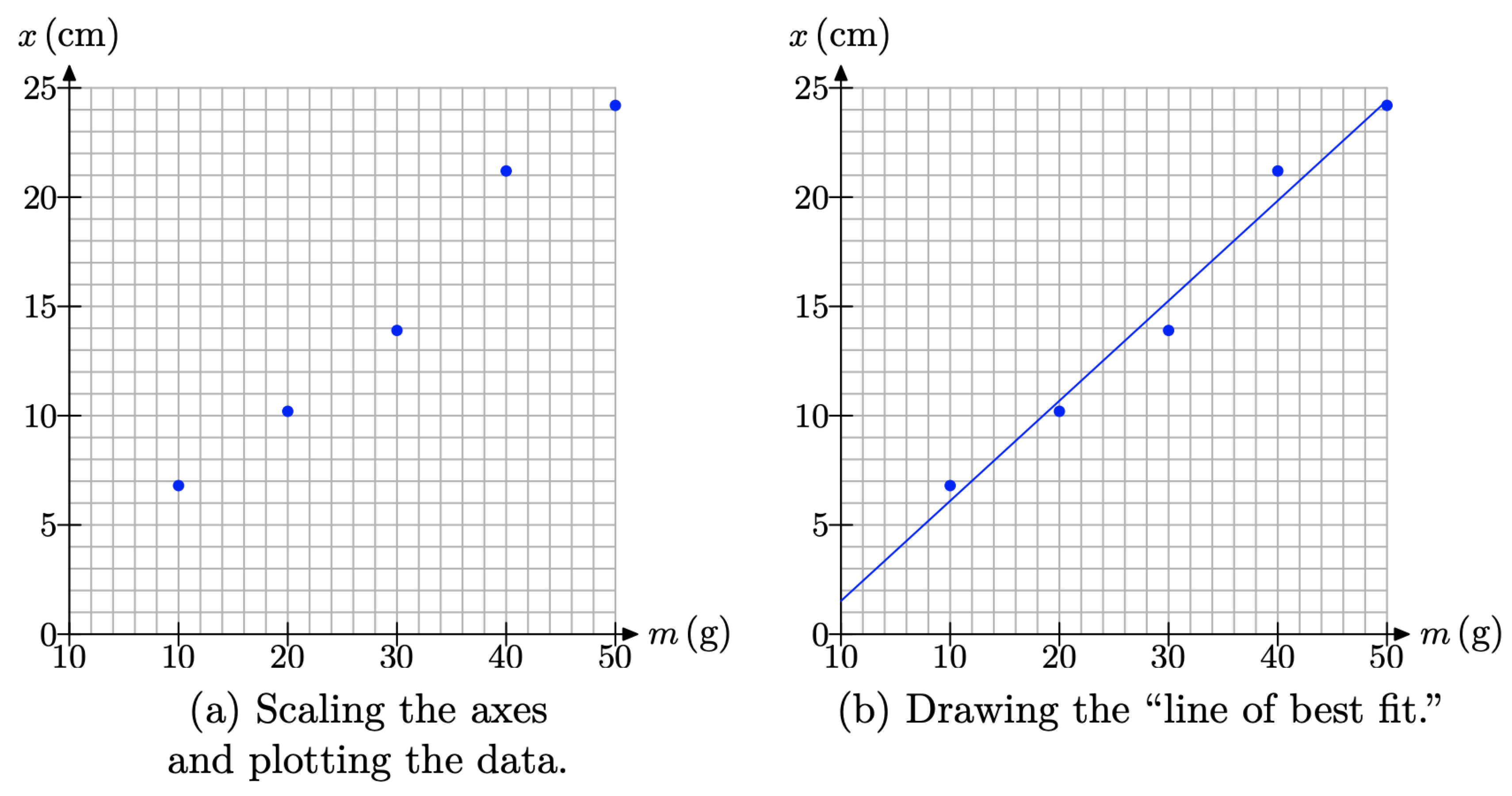
En el eje horizontal, necesitamos ajustar las masas de 10, 20, 30, 40 y 50 gramos. Para evitar una gráfica más pequeña, dejaremos que cada 5 cajas representen 10 gramos. En el eje vertical, necesitamos ajustar distancias que van desde 6.8 centímetros hasta e incluyendo 24.2 centímetros. Hacer que cada caja represente 1 cm da un gráfico de buen tamaño y permitirá trazar fácilmente nuestros puntos de datos, lo que hemos hecho en la Figura\(\PageIndex{1}\) (a).

Observe la tendencia lineal que muestran los datos de la Figura\(\PageIndex{1}\) (a). No es posible dibujar una sola línea que pase por cada uno de los puntos de datos, por lo que un modelo lineal no “encajará” exactamente con los datos. Sin embargo, los datos son “aproximadamente lineales”, así que intentemos dibujar una línea que “casi se ajuste” a los datos.

No es nuestro objetivo aquí tratar de trazar una línea que pase por tantos puntos de datos como sea posible. Si lo hacemos, entonces estamos diciendo esencialmente que los puntos por los que no pasa la línea no tienen influencia en el modelo general, ni tienen influencia alguna en ninguna predicción que podamos hacer con nuestro modelo. Esto no es una suposición razonable.

En efecto, el objetivo es trazar una línea que se acerque lo más a tantos puntos como sea posible. Algunos puntos estarán por encima de la línea, otros estarán por debajo, y lo que intentaremos hacer es “equilibrar” las sobreestimaciones y las subestimaciones en un intento de minimizar el error general. La mejor manera de hacerlo es tomar una regla de plástico transparente, algo que puedas ver a través, y rotar y desplazar la regla hasta que creas que tienes una línea que equilibra las sobreestimaciones y subestimaciones. Esto lo hemos hecho por ti en la Figura\(\PageIndex{1}\) (b). La línea resultante se llama la “línea de mejor ajuste”.

Figura\(\PageIndex{1}\).

Podemos usar la “línea de mejor ajuste” en la Figura\(\PageIndex{1}\) (b) para hacer predicciones. Por ejemplo, si quisiéramos predecir cuánto se estirará el resorte cuando Aditya y Tami unan una masa de 22 gramos, entonces ubicaríamos 22 gramos en el eje horizontal, dibujaríamos una línea vertical hacia arriba a la “línea de mejor ajuste”, seguida de una línea horizontal al eje vertical, como se muestra en la Figura\(\PageIndex{2}\) (a). Tenga en cuenta que el valor x en el eje vertical parece ser de aproximadamente 11.6 centímetros.

Alternativamente, desarrollaremos un modelo de ecuaciones. Primero, seleccione dos puntos en la “línea de mejor ajuste” usando las siguientes pautas.

Nota

1. Elija dos puntos en la “línea de mejor ajuste” que no sean puntos de datos.
2. Intenta escoger puntos que pasen por un punto de celosía de la cuadrícula. Facilita mucho la interpretación de las coordenadas del punto.
3. Cuanto más separados estén los dos puntos seleccionados, mejor será la precisión. No escojas puntos que estén demasiado juntos.

Figura\(\PageIndex{2}\).

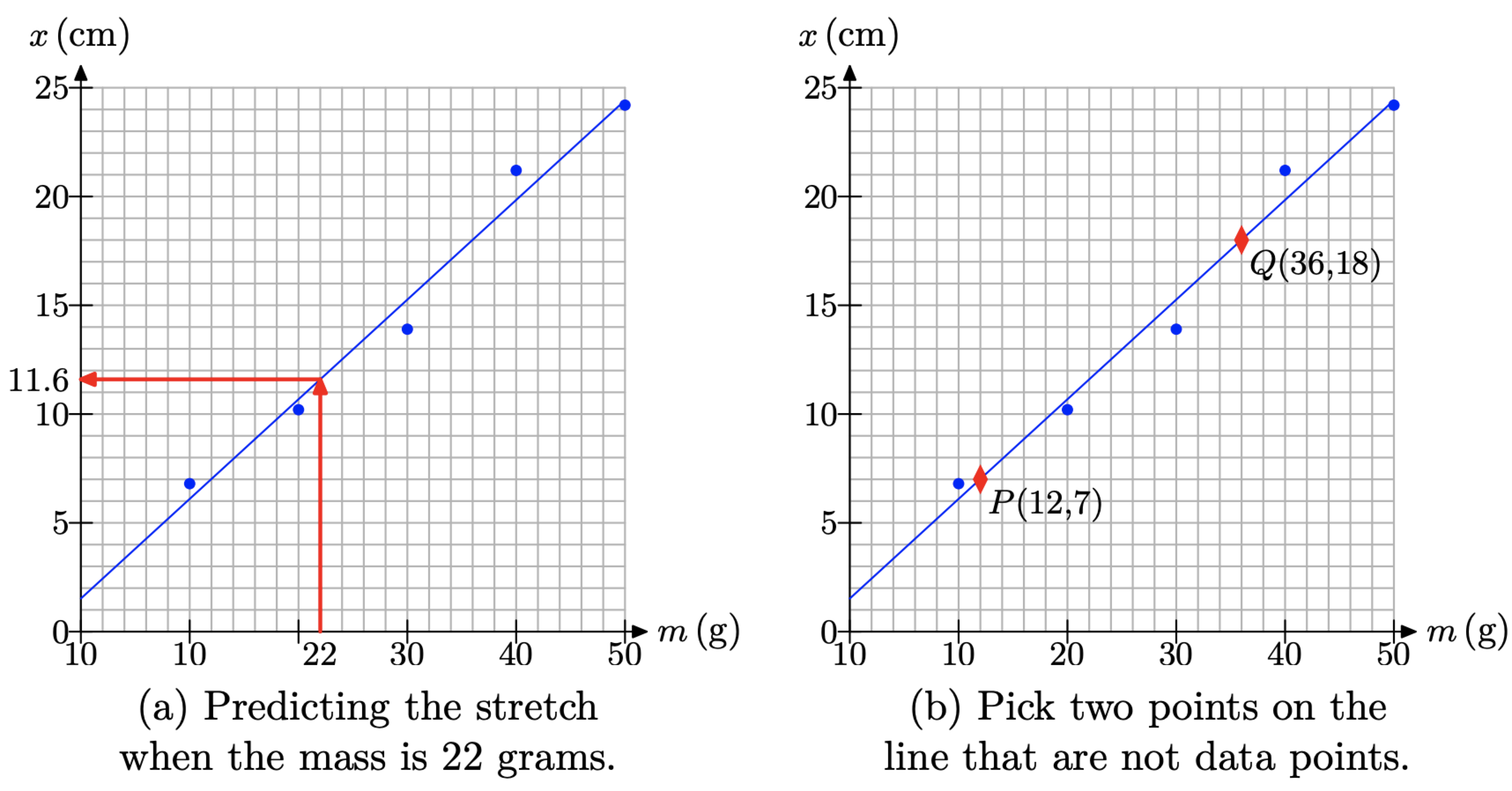
En la Figura\(\PageIndex{2}\) (b), hemos seleccionado los puntos P (12, 7) y Q (36, 18). El primer punto indica que una masa de 12 gramos estira la primavera 7 centímetros. La interpretación para el segundo punto es similar. Podemos encontrar la pendiente de la línea a través de los puntos P y Q con la fórmula de pendiente.

\[m=\frac{\Delta x}{\Delta m}=\frac{18 \mathrm{cm}-7 \mathrm{cm}}{36 \mathrm{g}-12 \mathrm{g}}=\frac{11}{24} \frac{\mathrm{cm}}{\mathrm{g}}\]

La pendiente de la línea es la velocidad a la que la distancia estirada está cambiando con respecto a cómo está cambiando la masa. En este caso, por cada 24 gramos adicionales de masa que se cuelga, el resorte estira 11 centímetros adicionales.

El siguiente paso es usar la fórmula de punto-pendiente para determinar la ecuación de la línea.

\[y-y_{0}=m\left(x-x_{0}\right)\]

Usemos el punto P (12, 7). Es decir, set\(\left(x_{0}, y_{0}\right)=(12,7)\). Sustituir\(m=11 / 24, x_{0}=12\), y\(y_{0}=7\) en la ecuación (1) para obtener

\[y-7=\frac{11}{24}(x-12)\]

En la aplicación de masa de resorte, la variable dependiente es x, no y, y la variable independiente es m, no x. Reemplace la y en el lado izquierdo de la ecuación (2) por x, luego reemplace x en el lado derecho de la ecuación (2) con m para obtener

\[x-7=\frac{11}{24}(m-12)\]

Resolver ecuación (3) para x

\[\begin{aligned} x-7 &=\frac{11}{24} m-\frac{132}{24} \\ x &=\frac{11}{24} m-\frac{132}{24}+7 \\ x &=\frac{11}{24} m-\frac{132}{24}+\frac{168}{24} \\ x &=\frac{11}{24} m+\frac{36}{24} \end{aligned}\]

Reducir 36/24 a 3/2 para obtener

\[x=\frac{11}{24} m+\frac{3}{2}\]

Recordemos que x representa la distancia estirada y m representa la cantidad de masa colgada del resorte. Es decir, x es una función de m. Podemos usar la notación de funciones para escribir la última ecuación de la siguiente manera.

\[x(m)=\frac{11}{24} m+\frac{3}{2}\]

Podemos usar el modelo en la ecuación (4) para determinar la cantidad de estiramiento cuando se une una masa de 22 gramos al resorte. Sustituye m = 22 en la ecuación (4), luego usa una calculadora para aproximar el estiramiento en la primavera.

\[x(22)=\frac{11}{24}(22)+\frac{3}{2} \approx 11.6 \mathrm{cm}\]

Observe el acuerdo con la solución gráfica que se encuentra en la Figura\(\PageIndex{2}\) (a). Los lectores deben entender que este tipo de precisión no es la norma habitual. Hay una serie de factores que pueden introducir errores.

• Aditya y Tami podrían no haber tomado medidas precisas en el laboratorio, por lo que los datos podrían ser defectuosos para empezar.
• Podría haber errores cuando escalamos los ejes y trazamos los datos.
• La línea “globo ocular” de mejor ajuste que dibujamos fue muy subjetiva. Una ligera rotación o traslación de la regla durante el dibujo de la supuesta “línea de mejor ajuste” puede producir diferentes resultados.
• Nuestros cálculos podrían contener errores y errores de redondeo.

Uso de la calculadora gráfica para encontrar la línea de mejor ajuste

Los estadísticos han desarrollado un método particular, llamado el “método de mínimos cuadrados”, que se utiliza para encontrar una “línea de mejor ajuste” para un conjunto de datos que muestran una tendencia lineal. El algoritmo busca encontrar la línea que minimice el error total. Estos algoritmos están programados en la calculadora gráfica y están disponibles para uso estudiantil.

Para utilizar la calculadora gráfica para determinar la línea de mejor ajuste, lo primero que tienes que aprender a hacer es cargar los datos de Table\(\PageIndex{1}\) en tu calculadora.

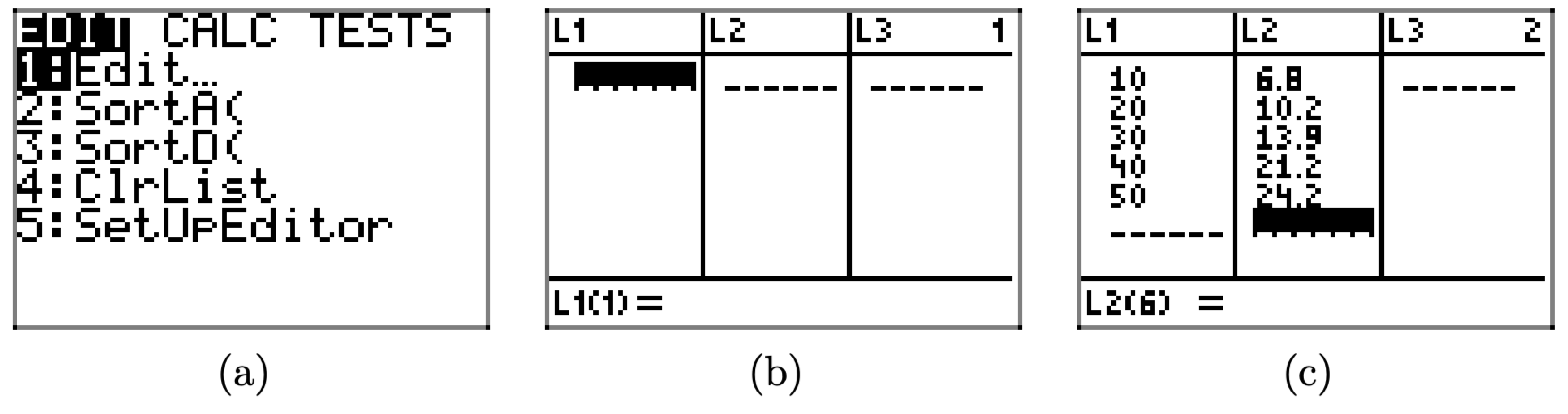
• Localice y presione el botón STAT en su teclado, que abrirá el menú que se muestra en la Figura\(\PageIndex{3}\) (a).

• Seleccione 1:Editar en este menú, que abrirá la ventana de edición que se muestra en la Figura\(\PageIndex{3}\) (b).

• Ingresar los datos de la Tabla\(\PageIndex{1}\) en listas\(L_{1}\) y\(L_{2}\), como se muestra en la Figura\(\PageIndex{3}\) (c)

Figura\(\PageIndex{3}\). Ingresa los datos de Table\(\PageIndex{1}\) en listas\(L_{1}\) y\(L_{2}\) en tu calculadora gráfica.

El siguiente paso es trazar los datos que has ingresado en listas\(L_{1}\) y\(L_{2}\).

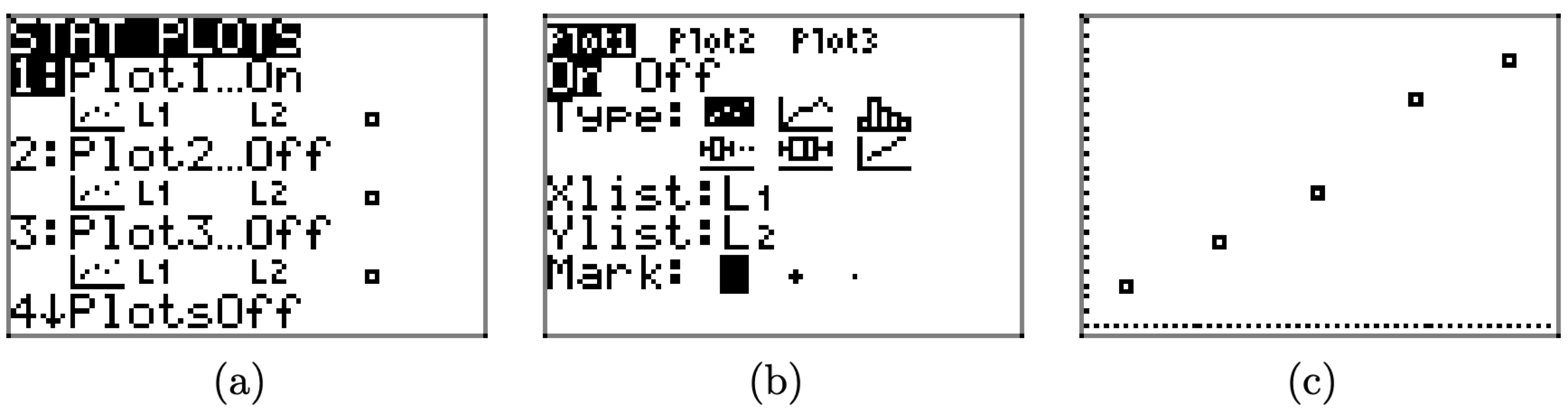
• Presione la tecla 2ND, seguida de STAT PLOT (ubicada encima del menú Y=). Esto abre la ventana que se muestra en la Figura\(\PageIndex{4}\) (a).
• Seleccione 1:Traza1 para abrir la ventana de selección de trazado que se muestra en la Figura\(\PageIndex{4}\) (b).
• En la ventana de selección de parcela de la Figura\(\PageIndex{4}\) (b), hay varias cosas que debes verificar.

1. Usa las teclas de flecha para colocar el cursor sobre la palabra “On” y presiona la tecla ENTRAR para resaltar esta selección.
2. Hay seis “Tipos” de parcelas: gráfica de dispersión, gráfica lineal, histograma, gráfica de caja modificada, gráfica de caja y gráfica de probabilidad normal. Estas opciones están dispuestas en dos filas de tres parcelas. Mueve el cursor a la primera gráfica de la primera fila, la gráfica de dispersión, luego presiona la tecla ENTRAR para resaltar tu selección.
3. La siguiente selección es la XList. Esta es la lista que va sobre el eje horizontal. En el caso del Cuadro 1, queremos colocar los datos de masa en el eje horizontal. Ingresamos los datos de masa en la lista L1, así que ingresamos 2ND L1 (L1 se encuentra por encima del 1 en el teclado).
4. La siguiente selección es la Ylist. Ingresa 2ND L2 (L2 se encuentra por encima del 2 en el teclado). Esto enumera la distancia estirada y se colocará en el eje vertical.
5. El último elemento es el marcador. Elige la primera con las teclas de flecha (es la más fácil de ver) y presiona la tecla ENTRAR para resaltar esta opción.

• Presiona el botón ZOOM en la primera fila de teclas de tu teclado. Use las teclas de flecha para desplazar el menú hacia abajo hasta que pueda seleccionar 9:ZoomStat. Esto producirá la imagen mostrada en la Figura\(\PageIndex{4}\) (c).

Figura\(\PageIndex{4}\). Trazar los puntos de datos de la Tabla\(\PageIndex{1}\)

El paso final es calcular y trazar la línea de mejor ajuste.

• Vuelva a presionar el botón STAT, pero luego use la flecha derecha para seleccionar el submenú CALC resaltado en la Figura\(\PageIndex{5}\) (a).
• Seleccione 4:LinReg (ax+b) en el submenú CALC. Esto coloca el comando LinReg (ax+b) en su pantalla de inicio, como se muestra en la Figura\(\PageIndex{5}\) (b). Luego debe escribir 2ND\(L_{1}\), una coma (ubicada en su propia clave justo encima de la tecla 7), luego 2ND\(L_{2}\), como se muestra en la Figura\(\PageIndex{5}\) (b).
• Pulse la tecla ENTER para ejecutar el comando LinReg\(L_{1}\)\(L_{2}\), que produce la ecuación de la línea de mejor ajuste que se muestra en la Figura\(\PageIndex{5}\) (c).

Figura\(\PageIndex{5}\). Encontrar la ecuación de la línea de mejor ajuste.

La pantalla de la Figura\(\PageIndex{5}\) (c) es bastante informativa. Nos dice dos cosas.

1. La ecuación de la línea de mejor ajuste es y = ax + b.
2. La pendiente es a = .458 y la intercepción y es b = 1.52.

Sustituir a = 0.458 y b = 1.52 en la ecuación y = ax + b nos da la ecuación de la línea de mejor ajuste.

\[y=0.458 x+1.52\]

Podemos superponer la gráfica de la línea de mejor ajuste en nuestro conjunto de datos en dos sencillos pasos.

• Presione la tecla Y= e ingrese la ecuación 0.458*X+1.52 in\(\boldsymbol{Y}_{1}\), como se muestra en la Figura\(\PageIndex{6}\) (a).
• Presiona el botón GRAPH en la fila superior de teclas de tu teclado para producir la línea que mejor se ajuste en la Figura\(\PageIndex{6}\) (b).

Figura\(\PageIndex{6}\). Superponer la línea de mejor ajuste en la gráfica de dispersión de los datos de Table\(\PageIndex{1}\).

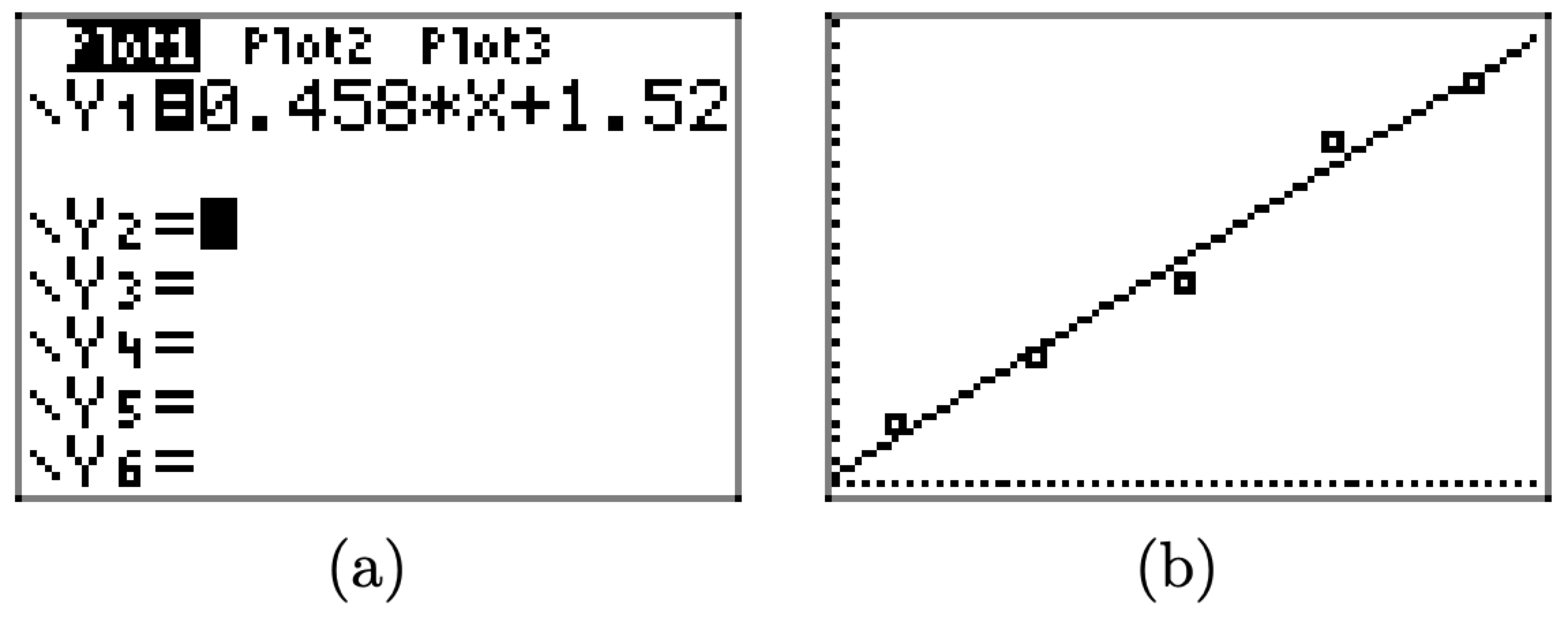
En el lado izquierdo de la ecuación (5), reemplace y por x (la distancia estirada); en el lado derecho, reemplace x por m (cantidad de masa). Esto lleva al resultado\[x=0.458 m+1.52\]

Tal vez recuerde que nuestro cálculo manual produjo la ecuación (4), que repetimos aquí por conveniencia.

\[x=\frac{11}{24} x+\frac{3}{2}\]

Tenga en cuenta que 11\(/ 24 \approx 0.4583\) y 3/2 = 1.5, por lo que la ecuación (6) concuerda estrechamente con nuestra ecuación calculada a mano de la línea de mejor ajuste.

Es bastante inusual tener una línea calculada a mano de mejor ajuste que concuerde tan estrechamente con el resultado sofisticado y muy preciso producido por la calculadora gráfica. Entonces, no se decepcione cuando los resultados de sus tareas no coincidan tan bien como lo han hecho en este ejemplo. Si estás en el estadio de béisbol con tu ecuación calculada a mano para la línea de mejor ajuste, esa suele ser lo suficientemente buena. Sin embargo, si su ecuación calculada a mano ni siquiera está cerca de lo que produce su calculadora, es “volver al tablero de dibujo”. Recomprueba tu parcela y tus cálculos. ¡Sé terco! No te conformes con tus resultados hasta que tengas un acuerdo razonable.