3.6: Capítulo 3 Ejercicios con Soluciones

3.1 Ejercicios

Ejercicio\(\PageIndex{1}\)

Jodiah está ahorrando su dinero para comprar un sistema de juego Playstation 3. Estima que necesitará 950 dólares para comprar la propia unidad, accesorios, y algunos juegos. Tiene 600 dólares ahorrados en este momento, y razonablemente puede poner 60 dólares en sus ahorros al final de cada mes. Ya que la cantidad de dinero ahorrado depende de cuántos meses hayan pasado, elija el tiempo, en meses, como su variable independiente y colóquelo en el eje horizontal. Que t represente el número de meses transcurridos, y haga una marca para cada mes. Elija el dinero ahorrado, en dólares, como su variable dependiente y colóquelo en el eje vertical. Que A represente la cantidad ahorrada en dólares. Dado que Jodiah ahorra $60 cada mes, será conveniente dejar que cada caja represente $60. Copia el siguiente sistema de coordenadas en una hoja de papel cuadriculado.

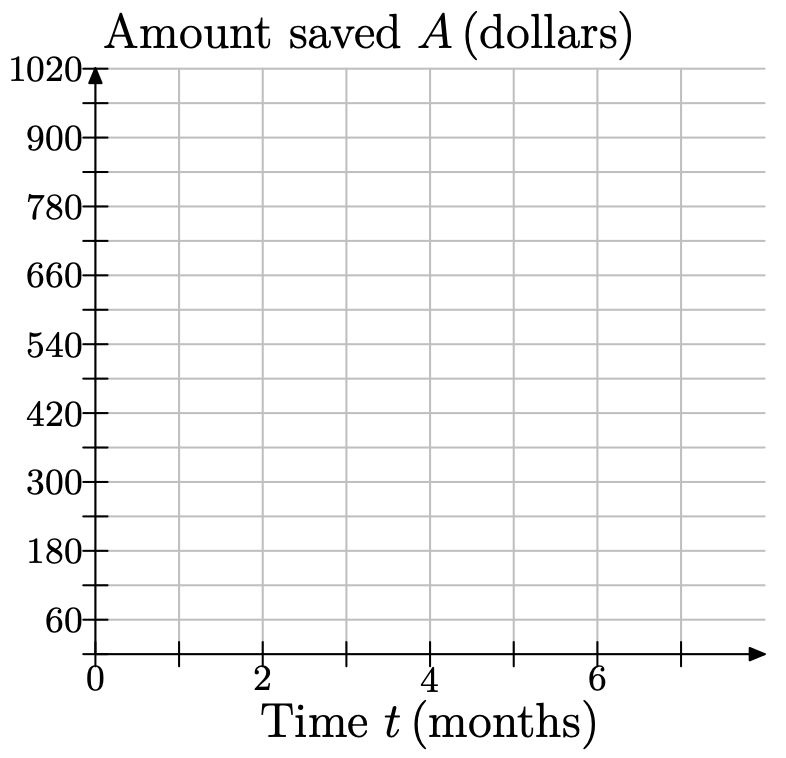
a) Al mes 0, Jodiah tiene 600 dólares ahorrados. Esto corresponde al punto (0, 600). Trace este punto en su sistema de coordenadas.

b) Para el mes siguiente, ahorró 60 dólares más. Comenzando en el punto (0, 600), muévase 1 mes a la derecha y $60 hacia arriba y trazar un nuevo punto de datos. ¿Cuáles son las coordenadas de este punto?

c) Cada vez que vayas a la derecha 1 mes, debes subir por $60 y trazar un nuevo punto de datos. Repita este proceso hasta llegar al borde del sistema de coordenadas.

d) Teniendo en cuenta que estamos modelando esta situación discreta continuamente, dibuja una línea a través de tus puntos de datos.

e) Usa tu gráfica para estimar cuánto dinero habrá ahorrado Jodiah después de 7 meses. f) Usando tu gráfica, estima cuántos meses le llevará haber ahorrado suficiente dinero para comprar su sistema de juego, accesorios y juegos.

Contestar

d)

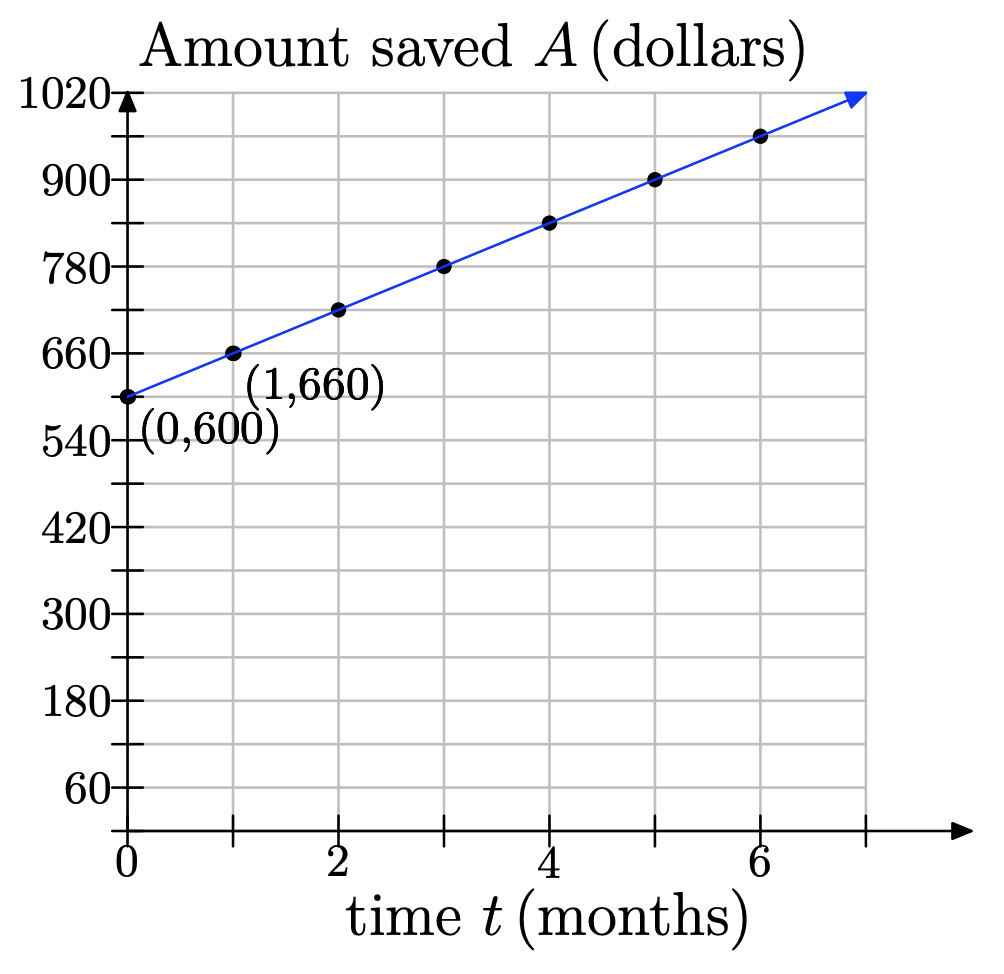
e)

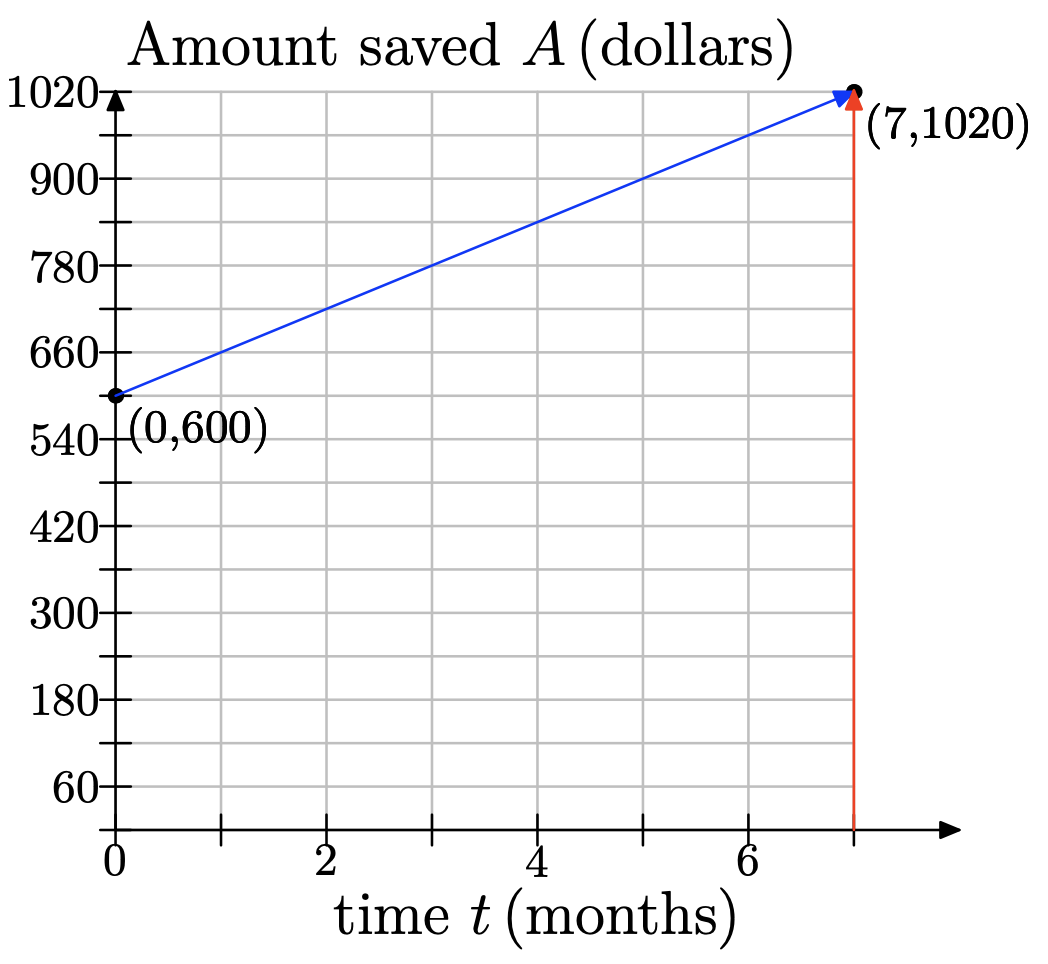
De la gráfica, cuando t = 7 meses, habrá ahorrado $1020.

f)

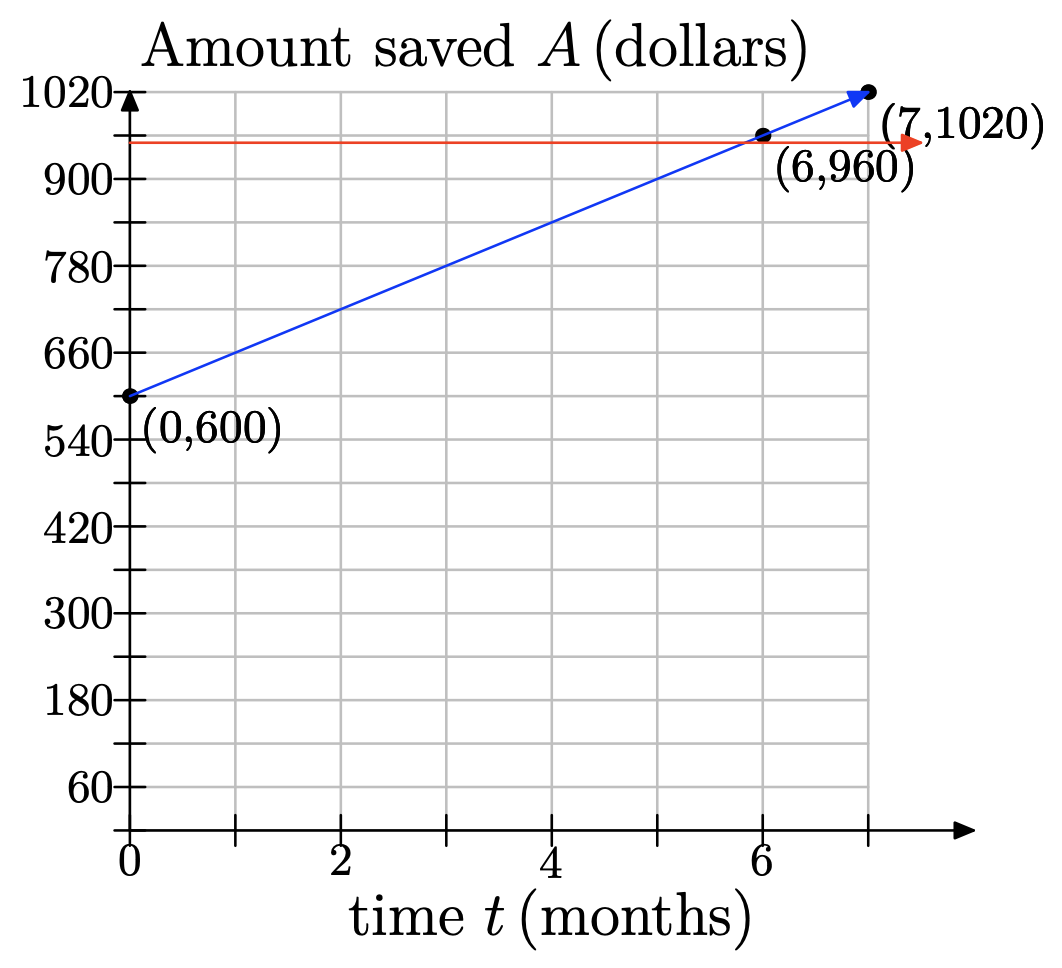
Tenga en cuenta que hemos modelado un problema discreto continuamente: Él ahorra 60 dólares al final de cada mes, y tendrá 900 dólares al final del mes cinco; y luego $960 al final del mes seis. No habrá tiempo en el que tenga exactamente 950 dólares, por lo que la respuesta es de 6 meses, momento en el que tendrá 960 dólares.

Ejercicio\(\PageIndex{2}\)

El letrero de arriba muestra los precios de un viaje en taxi de Liberty Cab Company. Dado que el costo depende de la distancia recorrida, haga que la distancia sea la variable independiente y colóquelo en el eje horizontal. Que d represente la distancia recorrida, en millas. Debido a que la compañía de taxi cobra por 1/6 millas, es conveniente marcar cada 1/6 millas. Haz precio, en $, tu variable dependiente y colócala sobre el eje vertical. Que C represente el costo, en $. Debido a que el costo ocurre en incrementos de 40c, marque cada 40c a lo largo del eje vertical. Copia el siguiente sistema de coordenadas en una hoja de papel cuadriculado.

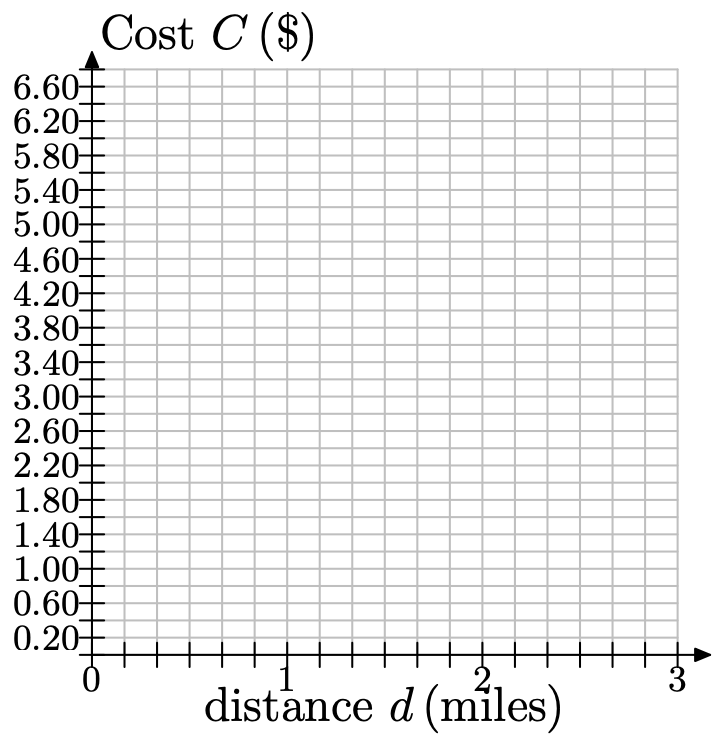
a) Para la primera 1/6 milla de recorrido, el costo es de $2.30. Esto corresponde al punto (1/6, $2.30). Trace este punto en su sistema de coordenadas.

b) Para el siguiente 1/6 de milla, el costo sube 40\(\cent\). Comenzando en el punto (1/6, $2.30), mueve 1/6 de milla a la derecha y 40c hacia arriba y traza un nuevo punto de datos. ¿Cuáles son las coordenadas de este punto?

c) Cada vez que vayas a la derecha 1/6 de milla, debes subir 40\(\cent\) y trazar un nuevo punto de datos. Repita este proceso hasta llegar al borde de su sistema de coordenadas.

d) Teniendo en cuenta que estamos modelando esta situación discreta continuamente, dibuja una línea a través de tus puntos de datos.

e) Melissa se sube a un taxi en la ciudad de Niagara Falls, a unas 2 millas del Parque Estatal de las Cataratas del Niágara. Usa tu gráfica para estimar la tarifa al parque.

f) En otros lugares de la zona, Georgina toma un taxi. Ella solo tiene $5 por la tarifa. Usa la gráfica para estimar hasta dónde puede viajar, en millas, con solo $5 por la tarifa.

Ejercicio\(\PageIndex{3}\)

Un barco está a 200 pies de una boya en el mar. Se acerca a la boya a una velocidad promedio de 15 pies/s.

a) Elegir el tiempo, en segundos, como su variable independiente y la distancia desde la boya, en pies, como su variable dependiente, hacer una gráfica de un sistema de coordenadas en una hoja de papel cuadriculado que muestre los ejes y unidades. Usa marcas de graduación para identificar tus básculas.

b) En el tiempo t=0, la embarcación se encuentra a 200 pies de la boya. ¿A qué punto corresponde esto? Trace este punto en su sistema de coordenadas.

c) Después de 1 segundo, la embarcación se ha acercado 15 pies a la boya. Comenzando en el punto anterior, mueva 1 segundo a la derecha y 15 pies hacia abajo (ya que la distancia es decreciente) y traza un nuevo punto de datos. ¿Cuáles son las coordenadas de este punto?

d) Cada vez que vayas a la derecha 1 segundo, debes bajar 15 pies y trazar un nuevo punto de datos. Repite este proceso hasta llegar a los 12 segundos.

e) Dibuja una línea a través de tus puntos de datos.

f) Cuando la embarcación se encuentra a menos de 50 pies de la boya, el conductor quiere comenzar a disminuir la velocidad. Usa tu gráfica para estimar qué tan pronto estará el barco a menos de 50 pies de la boya.

Contestar

e)

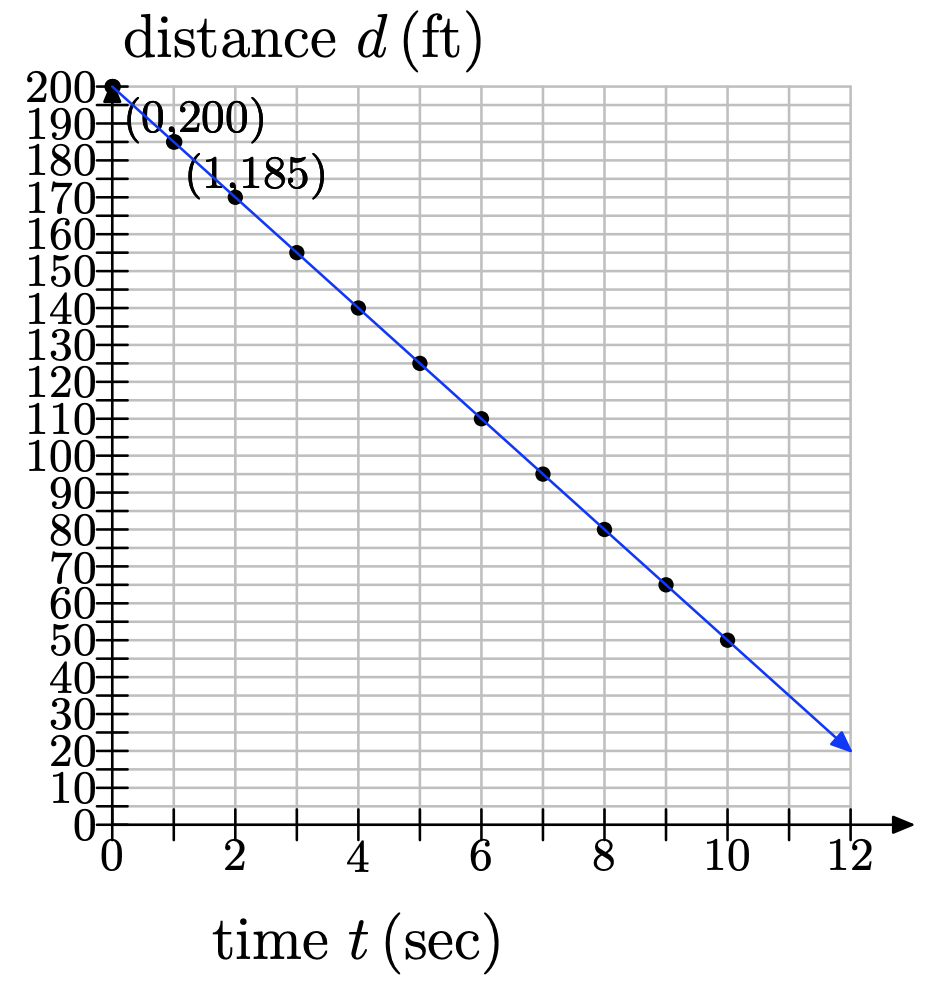
f) Dibujamos una línea a 50 pies y vemos que ocurre a los 10 segundos:

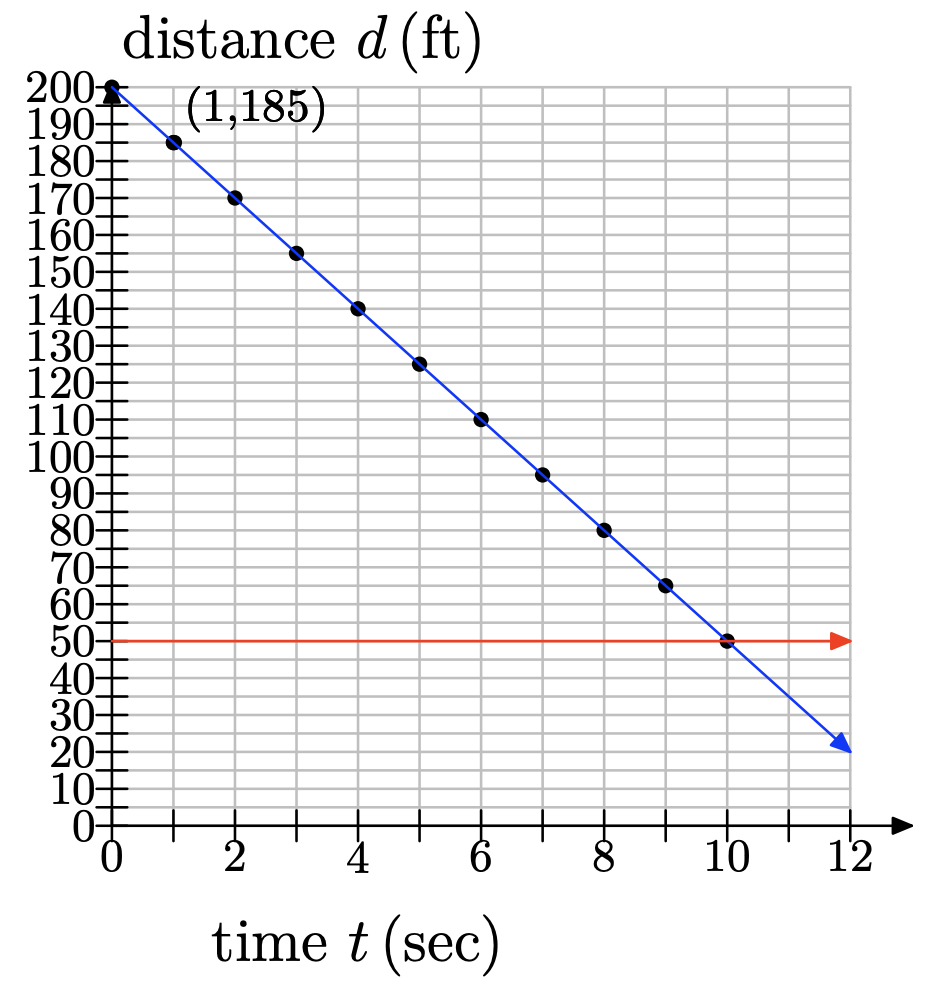
Ejercicio\(\PageIndex{4}\)

Joe debe $24,000 en préstamos estudiantiles. Ha terminado la universidad y ahora está trabajando. Él puede darse el lujo de pagar 1500 dólares mensuales para sus préstamos.

a) Elija el tiempo en meses como su variable independiente y el monto adeudado, en $, como variable dependiente. En una hoja de papel cuadriculado, haga un boceto del sistema de coordenadas, utilizando marcas de graduación y etiquetando los ejes de manera apropiada.

b) En el tiempo t = 0, Joe aún no ha pagado nada por sus préstamos. ¿A qué punto corresponde esto? Trace este punto en su sistema de coordenadas.

c) Después de un mes, paga 1500 dólares. Comenzando en el punto anterior, muévase 1 mes a la derecha y $1500 hacia abajo (a la baja porque la deuda está disminuyendo). Trazar este punto. ¿Cuáles son sus coordenadas?

d) Cada vez que vayas 1 mes a la derecha, debes mover $1500 hacia abajo. Continúa haciendo esto hasta que sus préstamos hayan sido pagados.

e) Teniendo en cuenta que estamos modelando esta situación discreta continuamente, trazar una línea a través de sus puntos de datos.

f) Utilizar la gráfica para determinar cuántos meses le llevará pagar el monto total de sus préstamos.

Ejercicio\(\PageIndex{5}\)

Earl la ardilla sólo tiene diez días más para la hibernación. Necesita ahorrar 50 bellotas más. Está cansado de recoger bellotas y así sólo es capaz de reunir 8 bellotas cada 2 días.

a) Que t represente el tiempo en días y conviértelo en su variable independiente. Deje que N represente el número de bellotas recolectadas y conviértalo en su variable dependiente. Configura un sistema de coordenadas apropiadamente escalado en una hoja de papel cuadriculado.

b) En el tiempo t = 0, Earl ha recogido cero de las bellotas que necesita. ¿A qué punto corresponde esto? Trace este punto en su sistema de coordenadas.

c) Después de dos días (t = 2), Earl ha recolectado 8 bellotas. Comenzando en el punto anterior, muévete 2 días a la derecha y 8 bellotas hacia arriba. Trazar este punto. ¿Cuáles son sus coordenadas?

d) Cada vez que vayas 2 días a la derecha, debes mover 8 bellotas hacia arriba y trazar un punto. Continúa haciendo esto hasta que llegues a los 14 días.

e) Teniendo en cuenta que estamos modelando esta situación discreta continuamente, trazar una línea a través de sus puntos de datos.

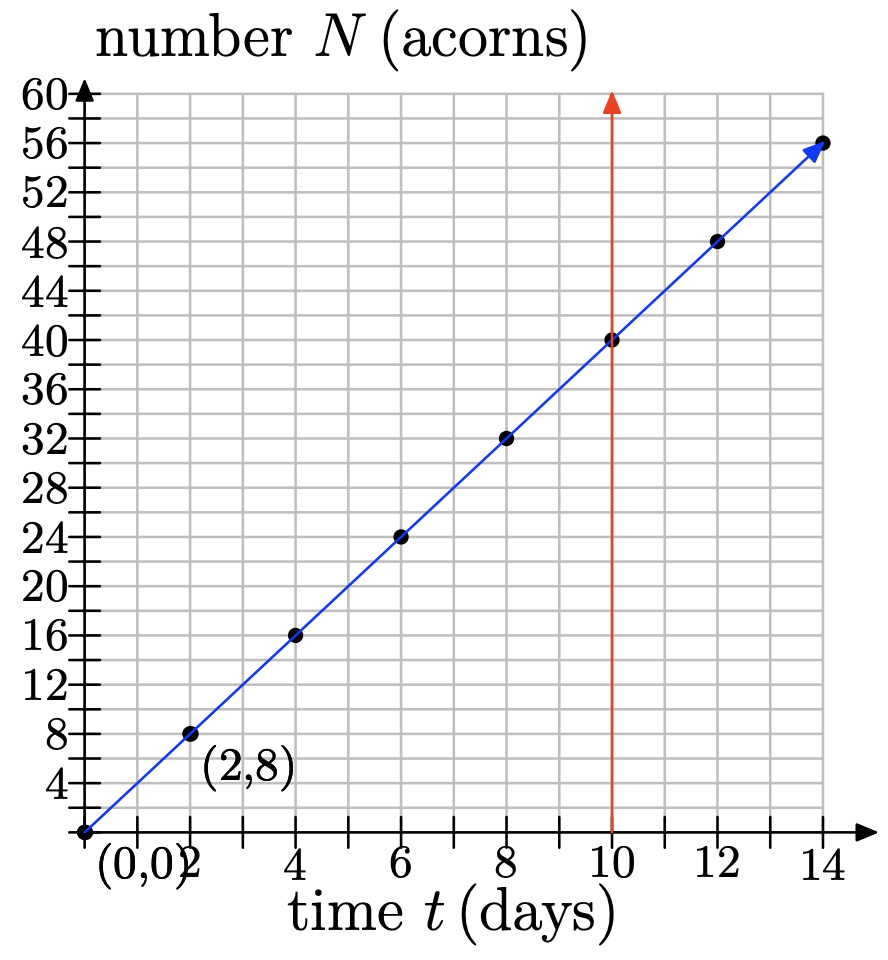
f) Utilice la gráfica para determinar cuántas bellotas habrá recolectado después de 10 días. ¿Earl habrá recogido suficientes bellotas para su hibernación invernal?

g) Observe que el número de bellotas recolectadas está aumentando a razón de 8 bellotas cada 2 días. Reducir esto a una tasa que indique el número promedio de bellotas que se recolecta cada día.

h) La siguiente tabla enumera el número de bellotas que Earl habrá recolectado en diversos momentos. Algunas de las entradas han sido completadas para ti. Por ejemplo, a t = 0, Earl no tiene bellotas, entonces N = 0. Después de un día, la cantidad aumenta en 4, por lo que N = 0 + 4 (1). Después de dos días, se han producido dos aumentos, por lo que N = 0+4 (2). El patrón continúa. Rellene las entradas faltantes.

t	N
0	0
1	0 + 4 (1)
2	0 + 4 (2)
3	0 + 4 (3)
4
6
8
10
12
14

i) Expresar el número de bellotas recolectadas, N, en función del tiempo t, en días.

j) Usa tu función para predecir el número de bellotas que Earl tendrá después de 10 días. ¿Esta respuesta concuerda con tu estimación de la parte (f)?

Contestar

e)

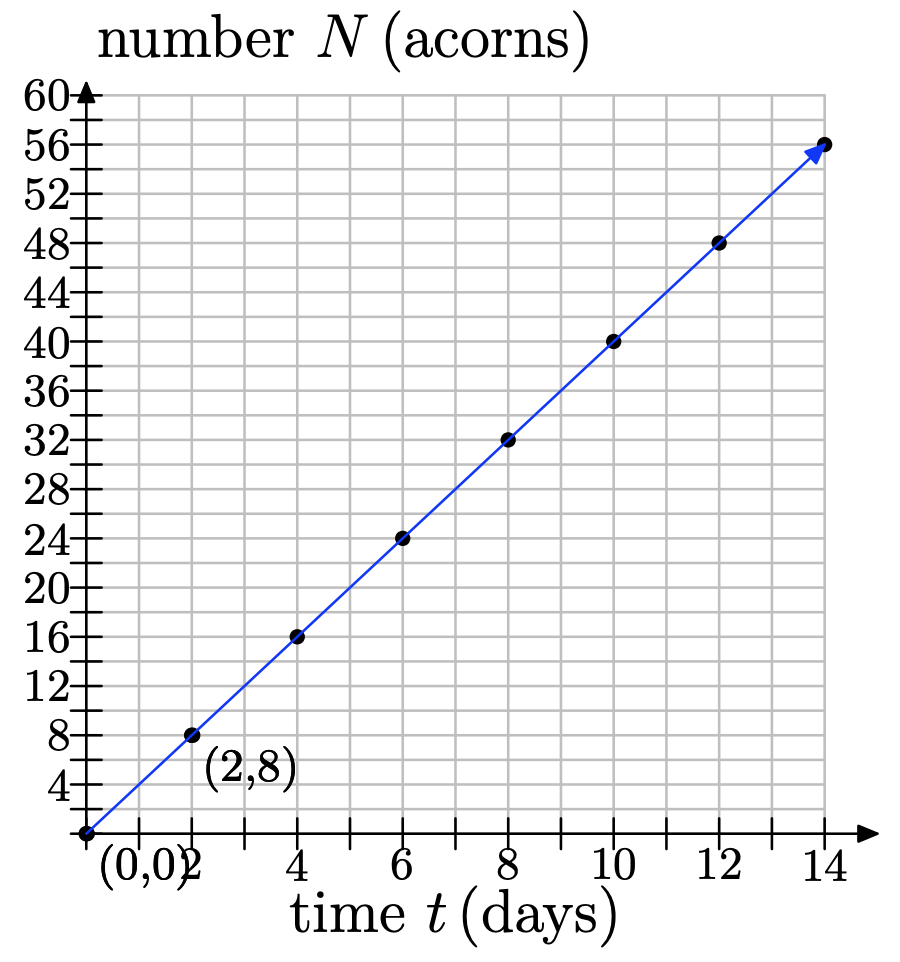
f) Si dibujas una línea a los 10 días, entonces podrás ver que habrá recogido 40 bellotas.

g)\(\frac{8}{2}\) bellotas/día = 4 bellotas/día

h) Siguiendo el patrón, obtenemos:

t	N
0	0
1	0 + 4 (1)
2	0 + 4 (2)
3	0 + 4 (3)
4	0+4 (4)
6	0+4 (6)
8	0+4 (8)
10	0+4 (10)
12	0+4 (12)
14	0+4 (14)

i) N = 0 + 4t o N = 4t

j) A t = 10, N = 0 + 4 (10) = 40 bellotas.

Ejercicio\(\PageIndex{6}\)

En la televisión en red, una hora típica de programación contiene 15 minutos de comerciales y anuncios y 45 minutos del programa en sí.

a) Elija la cantidad de televisión vista como su variable independiente y colóquelo en el eje horizontal. Que T represente la cantidad de televisión vista, en horas. Elija la cantidad total de comerciales/anuncios vistos como su variable dependiente y colóquelo en el eje vertical. Que C represente la cantidad total de comerciales/anuncios vistos, en minutos. Usando una hoja de papel cuadriculado, haga un boceto de un sistema de coordenadas y etiquete apropiadamente.

b) Durante 0 horas de programación vistas, se han visto 0 minutos de comerciales. ¿A qué punto corresponde esto? Trócalo en tu sistema de coordenadas.

c) Después de ver 1 hora de programación-ming, se han visto 15 minutos de comerciales/anuncios. Comenzando en el punto anterior, muévase 1 hora a la derecha y 15 minutos hacia arriba. Trazar este punto. ¿Cuáles son sus coordenadas?

d) Cada vez que vayas 1 hora a la derecha, debes moverte 15 minutos hacia arriba y trazar un punto. Continúa haciendo esto hasta llegar a las 5 horas de programación.

e) Dibuja una línea a través de tus puntos de datos.

f) Billy ve la televisión durante cinco horas el lunes. Usa la gráfica para determinar cuántos minutos de comerciales ha visto durante este tiempo.

g) Supongamos que una persona ha visto una hora de comerciales/anuncios. Usa la gráfica para estimar cuántas horas de televisión vio.

h) En la siguiente tabla se muestran los números de horas de programación vistas, ya que se relaciona con el número de minutos de comerciales/anuncios vistos. Por 0 horas de TV, se ven 0 minutos de comerciales/anuncios. Por cada hora de televisión vista, debemos contar 15 minutos de comerciales/anuncios. Entonces, durante 1 hora, se ven 0 + 15 (1) minutos de comerciales. Por 2 horas, 0 + 15 (2) minutos; y así sucesivamente. Rellene las entradas faltantes.

T (hrs)	C (minutos)
0	0
1	0 + 15 (1)
2	0 + 15 (2)
3
4
5

i) Exprese la cantidad de comerciales/anuncios vistos, C, en función de la cantidad de televisión vista T. Utilice su ecuación para predecir la cantidad de comerciales/anuncios vistos durante 5 horas de programación televisiva. ¿Esta respuesta concuerda con tu estimación de la parte (f)?

Ejercicio\(\PageIndex{7}\)

Según la OTAN (la Asociación Nacional de Propietarios de Teatro), el precio promedio de una entrada de cine fue de 5.65 dólares en el año 2001. Desde entonces, el precio promedio ha ido subiendo cada año en alrededor de 20\(\cents\).

a) Elegir año, a partir del 2000, como variable independiente y hacer marcas cada año en el eje. Elige el precio promedio del boleto, en dólares, como tu variable dependiente y comienza en 5.65 dólares, con marcas cada 10\(\cents\) arriba. Haga un boceto de un sistema de coordenadas y etiquete adecuadamente.

b) En 2001, el precio promedio del boleto fue de 5.65 dólares, correspondientes al punto (2001, 5.65). Trócalo en tu sistema de coordenadas.

c) En 2002, un año después, el precio medio subió alrededor de 20\(\cents\). Comenzando en el punto anterior, muévete a la derecha por 1 año y arriba por 20\(\cents\) y trazar el punto. ¿Cuáles son sus coordenadas?

d) Cada vez que vayas 1 año a la derecha, debes moverte hacia arriba por 20\(\cents\) y trazar un punto. Continuar haciendo esto hasta el año 2010.

e) Teniendo en cuenta que estamos modelando esta situación discreta continuamente, trazar una línea a través de sus puntos de datos.

f) Utilice la gráfica para estimar en qué año pasará el precio promedio de un boleto 7.00 dólares.

Contestar

e)

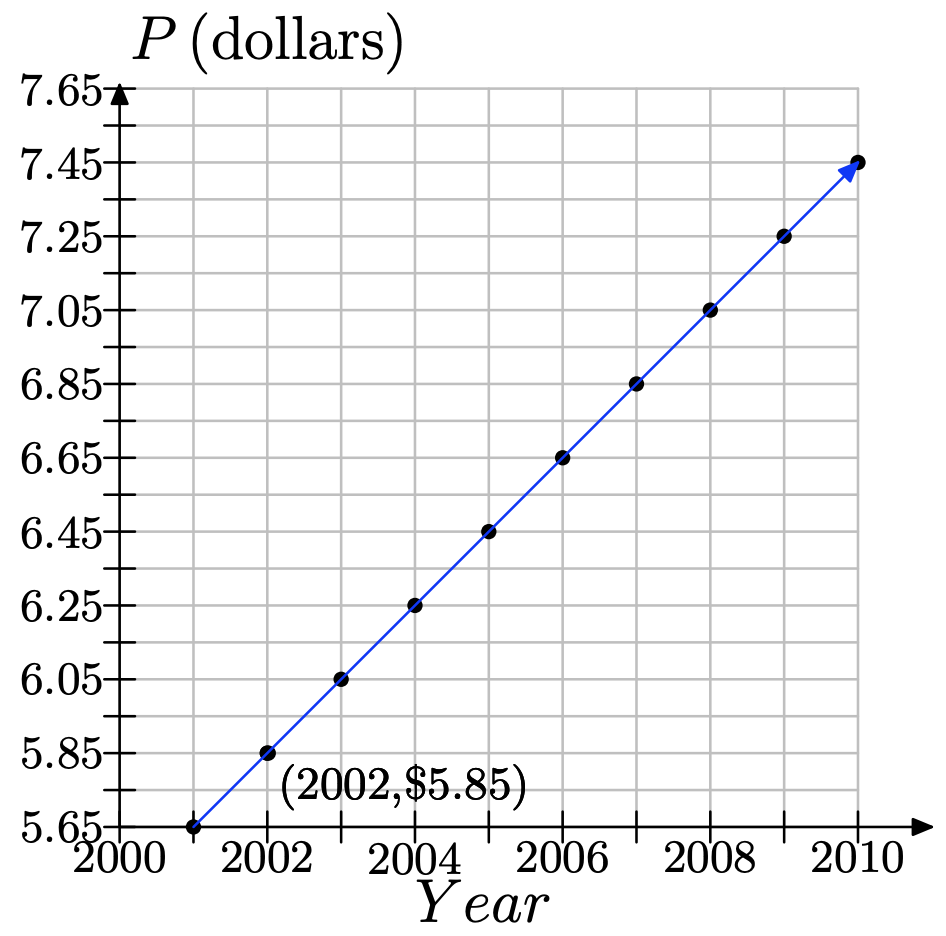
f) Dibuja una línea por $7.00 y busca el año.

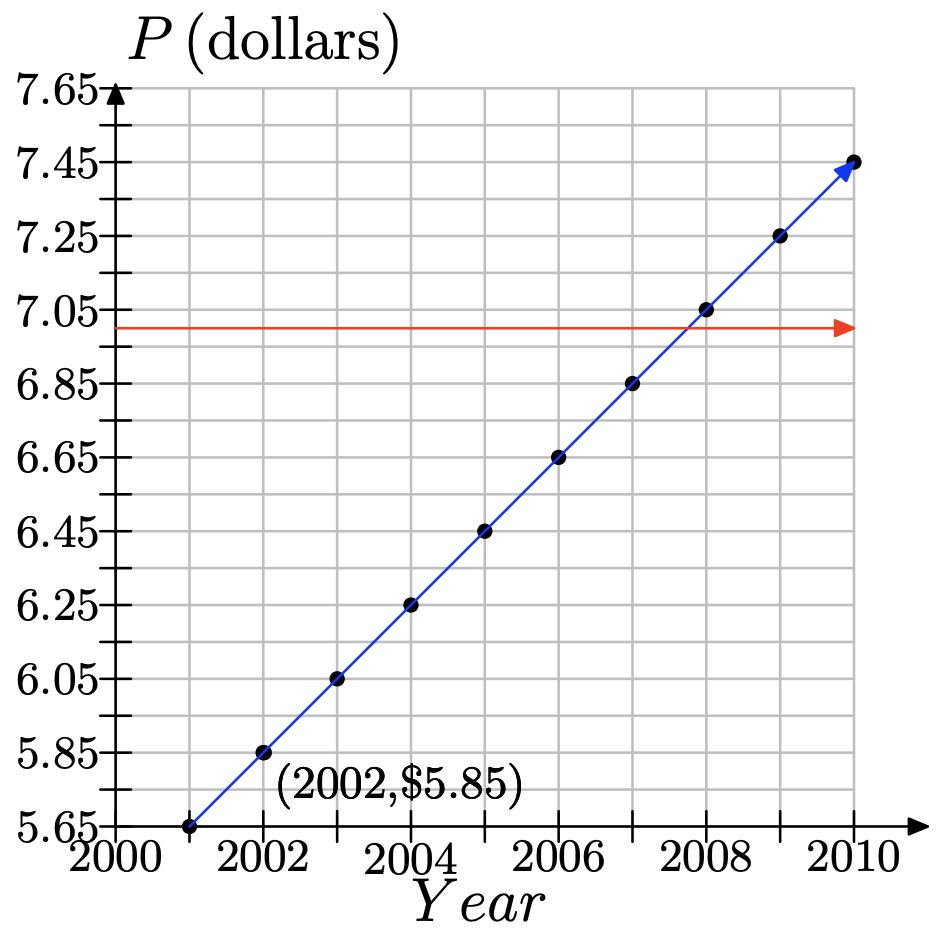
Observe que el año es entre 2007 y 2008. Pero este es un problema discreto, ya que sólo estamos lidiando con años enteros. Así, la respuesta es 2008.

Ejercicio\(\PageIndex{8}\)

Cuando Jessica conduce su automóvil a una conferencia relacionada con el trabajo, su empleador le reembolsa aproximadamente 45 centavos por milla para cubrir el costo de la gasolina y el desgaste del vehículo.

a) Utilizando la distancia recorrida d, en millas, como la variable independiente y el monto reembolsado A, en dólares, como variable dependiente, hacer un boceto de un sistema de coordenadas y etiquetar adecuadamente. Marque la distancia cada 5 millas y el monto reembolsado cada $0.45.

b) Por viajar 0 millas, el reembolso es 0. Esto corresponde al punto (0, 0). Trócalo en tu sistema de coordenadas.

c) Para un viaje que le requiera conducir un total de 5 millas, se le reembolsan 5 (0.45) = $2.25. Esto corresponde al punto (5, $2.25). Trazar.

d) Por cada 5 millas que vayas a la derecha, debes subir $2.25 y trazar el punto. Haz esto hasta llegar a 20 millas.

e) Teniendo en cuenta que estamos modelando esta situación discreta continuamente, trazar una línea a través de sus puntos de datos.

f) En marzo, Jessica asiste a una conferencia que está a solo 5 millas de distancia. Contando el viaje de ida y vuelta, recorre 10 millas totales. Usa la gráfica para determinar cuánto se le reembolsa.

g) En diciembre, asiste a una conferencia a 10 millas de distancia. ¿Cuánto dura su viaje en total? Usa la gráfica para determinar cuánto se le reembolsará.

h) Para viajes más largos, como 200 millas totales, probablemente necesitarás hacer una gráfica mucho más grande. ¿Y si viaja 400 millas? ¿O más? Son limitaciones como estas las que hacen útil encontrar una ecuación que describa lo que muestra la gráfica. Para encontrar la ecuación, partimos de una tabla que nos ayuda a entender la relación entre las variables dependientes e independientes. Complete la siguiente tabla.

d (millas)	A ($)
0	0
1	0 + 0.45 (1)
2	0 + 0.45 (2)
3
4
5
10
20
50
100

i) Usa la tabla de la parte (h) para elaborar una ecuación que relacione d y A.

j) Ahora, utilice la ecuación para determinar los montos de reembolso para viajes de 200 millas y 400 millas.

Ejercicio\(\PageIndex{9}\)

La temperatura se mide típicamente en grados Fahrenheit en los Estados Unidos; pero se mide en grados Celsius en muchos otros países. La relación entre Fahrenheit y Celsius es lineal. Escojamos la medición de grados en Celsius para ser nuestra variable independiente y la medición de grados en Fahrenheit para ser nuestra variable dependiente. El agua se congela a 0 grados Celsius, lo que corresponde a 32 grados Fahrenheit; y el agua hierve a 100 grados Celsius, lo que corresponde a 212 grados Fahrenheit. Podemos trazar esta información como los dos puntos (0,32) y (100,212). La relación es lineal, así que tenga la siguiente gráfica:

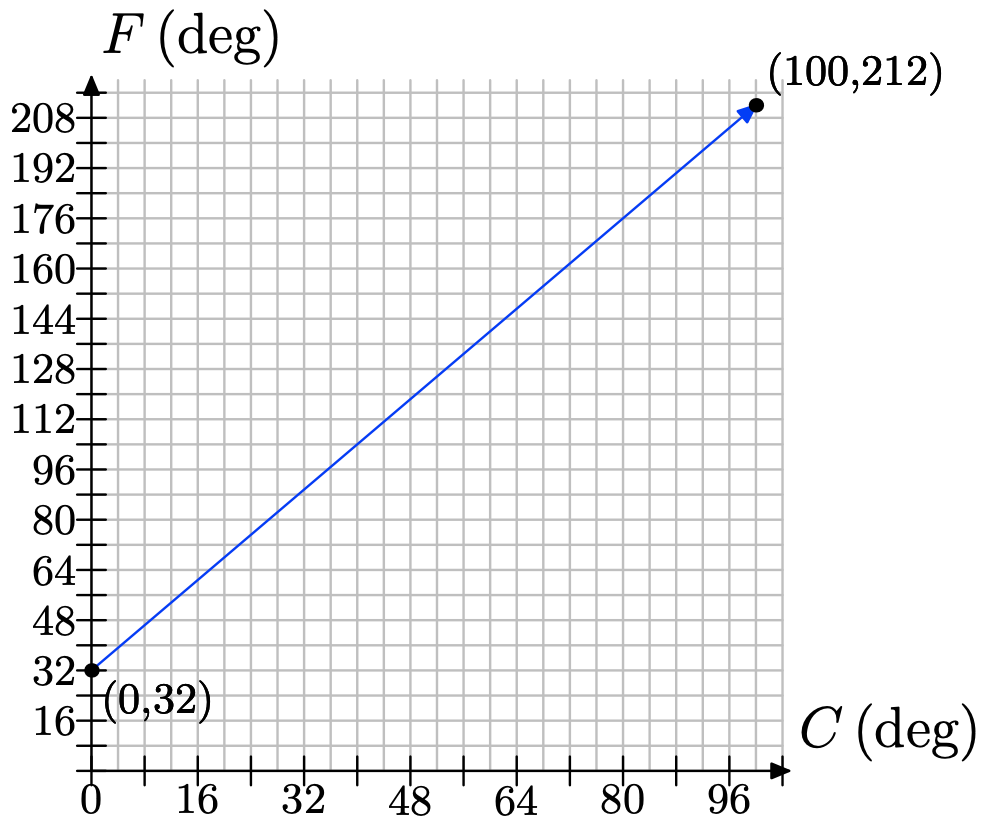
a) Utilice la gráfica para aproximar la temperatura equivalente a Fahrenheit para 48 grados Celsius.

b) Para determinar la tasa de cambio de Fahrenheit con respecto a Celsius, dibujamos un triángulo rectángulo con lados paralelos a los ejes que conecta los dos puntos que conocemos...

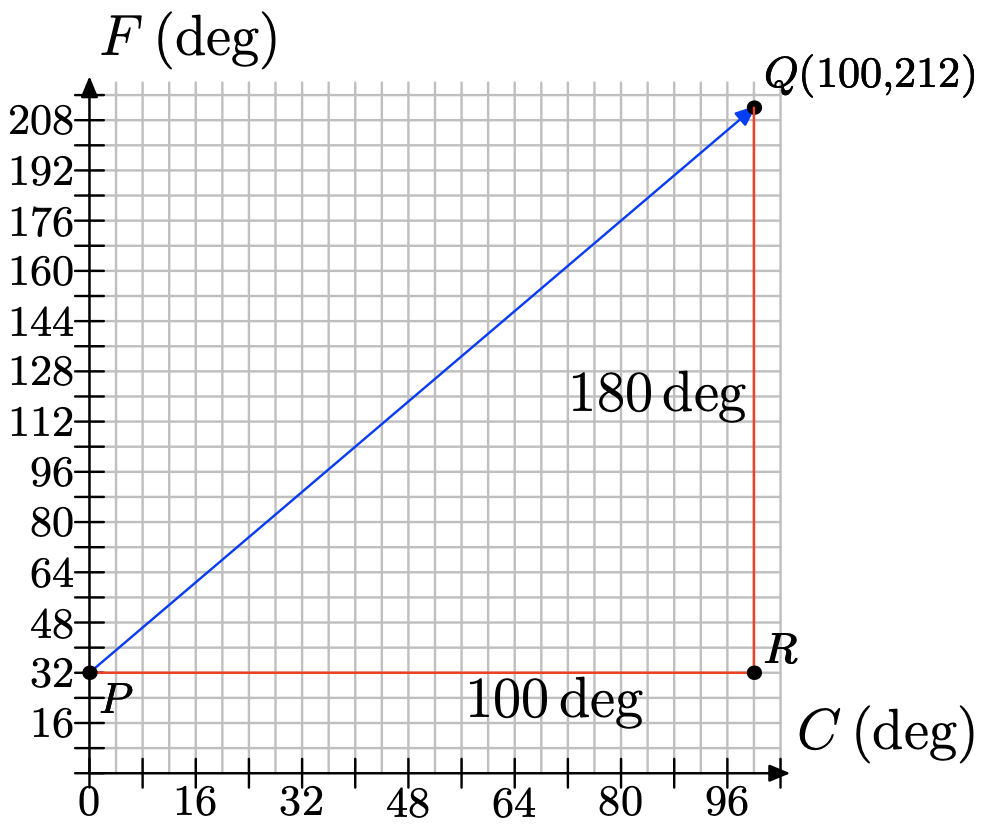
La PR lateral tiene 100 grados de largo, lo que representa un incremento en 100 grados Celsius. El RQ lateral es de 180 grados, lo que representa un incremento en 180 grados Fahrenheit. Encuentra la tasa de incremento de Fahrenheit por Celsio. c) La siguiente tabla muestra algunos valores de temperaturas en Celsius y sus correspondientes lecturas de Fahrenheit. Cero grados Celsius corresponde a 32 grados Fahrenheit. Nuestra tarifa es de 9 grados Fahrenheit por cada 5 grados Celsius, o 9/5 de un grado Fahrenheit por cada 1 grado Celsius. Entonces, para 1 grado Celsius, aumentamos la lectura de Fahrenheit en 9/5 grados, obteniendo 32 + 9/5 (1). Para 2 grados Celsius, aumentamos en dos ocurrencias de 9/5 grados para obtener 32 + 9/5 (2). Rellene las entradas faltantes, siguiendo el patrón.

C (grados)	F (grados)
0	32
1	\(32 + \frac{9} {5} (1)\)
2	\(32 + \frac{9} {5} (2)\)
3	\(32 + \frac{9} {5} (3)\)
4
5
10
20
48
100

d) Utilice la tabla para formar una ecuación que dé grados Fahrenheit en términos de grados Celsius.

Contestar

a) Hacemos una línea a 48 grados Celsius y leemos la estimación de Fahrenheit.

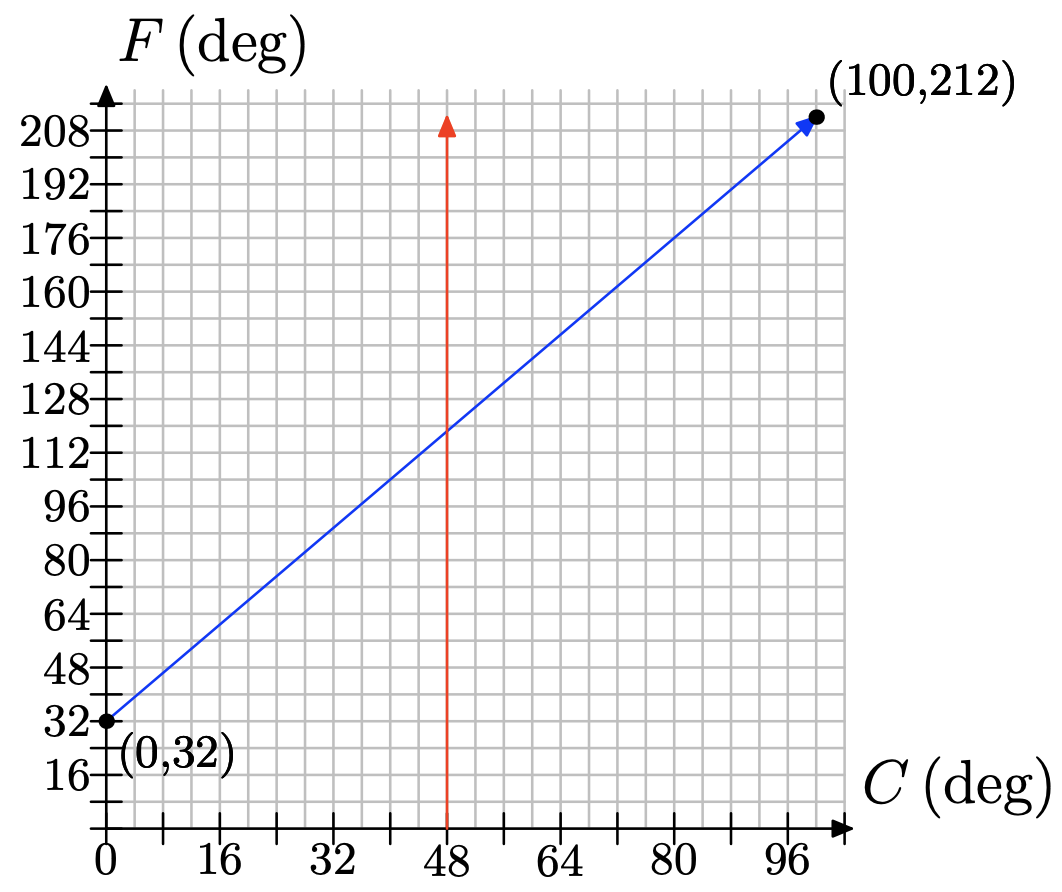
La estimación debe ser aproximadamente de 120 grados Fahrenheit.

b)\(\dfrac{changeinF}{ changeinC} = \dfrac{180}{ 100 }= \dfrac{9}{ 5}\)

c)

C (grados)	F (grados)
0	32
1	\(32 + \frac{9} {5} (1)\)
2	\(32 + \frac{9} {5} (2)\)
3	\(32 + \frac{9} {5} (3)\)
4	\(32 + \frac{9} {5} (4)\)
5	\(32 + \frac{9} {5} (5)\)
10	\(32 + \frac{9} {5} (10)\)
20	\(32 + \frac{9} {5} (20)\)
48	\(32 + \frac{9} {5} (48)\)
100	\(32 + \frac{9} {5} (100)\)

d) F = 9 5C + 32

Ejercicio\(\PageIndex{10}\)

El 16 de junio de 2006, la tasa de conversión de Euro a dólares estadounidenses fue de aproximadamente 0.8 a 1, lo que significa que cada 0.8 Euros valían 1 dólar estadounidense.

a) Elegir dólares para ser la variable independiente y Euros para ser la variable dependiente, hacer una gráfica de sistema de coordenadas. Marcar cada dólar en el eje del dólar y cada 0.8 euros en el eje Euro. Etiquete apropiadamente.

b) Cero dólares valen 0 Euros. Esto corresponde al punto (0, 0). Trócalo en tu sistema de coordenadas.

c) Un dólar vale 0.8 Euros. Traza esto como un punto en tu sistema de coordenadas.

d) Por cada dólar que te muevas a la derecha, debes subir 0.8 Euros y trazar un punto. Haz esto hasta llegar a los $10.

e) Dibuja una línea a través de tus puntos de datos.

f) Utilice la gráfica para estimar cuántos euros valen $8.

g) Utilice la gráfica para estimar cuántos dólares valen 5 Euros.

h) En la siguiente tabla se muestran algunos valores de dólares y su valor correspondiente en Euros. Rellene las entradas faltantes.

Dólares	Euros
0	0
1	0 + 0.8 (1)
2	0 + 0.8 (2)
3
4
5
10

i) Usa la tabla para hacer una ecuación que pueda ser utilizada para convertir dólares a Euros.

j) Utilice la ecuación de (i) para convertir $8 a Euros. ¿Tu respuesta concuerda con la respuesta de (f) que obtuviste usando la gráfica?

Ejercicio\(\PageIndex{11}\)

La Torre de Pisa en Italia tiene su famosa inclinación hacia el sur porque el suelo arcilloso y arenoso sobre el que se construye es más suave en el lado sur que en el norte. La inclinación se encuentra a menudo midiendo la distancia que la parte superior de la torre sobresale de la base, indicada por h en la siguiente figura. En 1980, la torre tuvo una inclinación de h = 4.49m, y esta inclinación se incrementó en aproximadamente 1 mm/año.

Figura\(\PageIndex{1}\). h mide la inclinación de la Torre de Pisa.

Investigaremos cómo cambió la inclinación de la torre de 1980 a 1995.

a) Primero, señalar que nuestras unidades no coinciden: La inclinación en 1980 se dio como 4.49 m, pero el incremento anual en la inclinación se da como 1 mm/año. Nuestro primer objetivo es hacer que las unidades sean iguales. Utilizaremos milímetros (mm). Convertir 4.49 m a mm.

b) Obtener una hoja de papel cuadriculado. Ya que la inclinación de la torre depende del año, haga del año la variable independiente y colóquelo en el eje horizontal. Que t represente el año. Haga que la inclinación sea la variable dependiente y colóquelo en el eje vertical. Dejar que h represente la inclinación, medida en milímetros (mm). Elija 1980 como primer año en el eje horizontal y marque cada año a partir de entonces, hasta 1995. Dejemos que el eje vertical comience en 4.49 m, convertido a mm de la parte (a), ya que esa fue nuestra primera medición; y luego marcamos cada 1 mm a partir de entonces hasta 4510 mm.

c) Piense en 1980 como el año de inicio. Junto con la medición de inclinación de ese año, forma un punto. ¿Cuáles son las coordenadas de este punto? Trace el punto en su sistema de coordenadas.

d) Comenzando en el primer punto, de la parte (c), mover un año a la derecha (a 1981) y 1 mm hacia arriba (porque la inclinación aumenta) y traza un nuevo punto de datos.

e) Cada vez que te muevas un año a la derecha, debes moverte 1 mm hacia arriba y trazar un nuevo punto. Repita este proceso hasta llegar al año 1995.

f) Teniendo en cuenta que estamos modelando esta situación discreta continuamente, dibuja una línea a través de tus puntos de datos. Podemos utilizar este modelo para hacer predicciones.

g) Según los modelos de simulación por computadora, que utilizan matemáticas sofisticadas, la torre estaría en peligro de colapsar cuando h alcance aproximadamente los 4495 mm. Usa tu gráfica para estimar en qué año sucedería esto.

h) En realidad, la inclinación de la torre pasó de 4495 mm y la torre no colapsó. De hecho, la inclinación aumentó a 4500 mm antes de que la torre se cerrara el 7 de enero de 1990, para someterse a renovaciones para disminuir la inclinación. (La torre se reabrió en 2001, luego de que los ingenieros usaron pesos y eliminaron la suciedad de debajo de la base para disminuir la inclinación en 450 mm.) ¿Cuáles podrían ser algunas razones por las que la predicción del modelo de computadora fue incorrecta?

i) La siguiente tabla enumera la inclinación de la torre, h, el año, y el número de años desde 1980. En 1980, la inclinación era de 4490 mm y aún no se habían producido ocurrencias del incremento de 1 mm, por lo que rellenamos 4490 + 0 (1) = 4490. En 1981, una ocurrencia del incremento de 1 mm se había dado porque había pasado un año desde 1980. Por lo tanto, la inclinación fue de 4490 + 1 (1). En 1982 se habían producido dos ocurrencias del incremento de 1 mm, debido a que habían pasado 2 años desde 1980. Así, la inclinación fue de 4490 + 2 (1). Y el patrón continúa de esta manera. Rellene las entradas restantes.

Año	años x después del '80	inclinación h
1980	0	4490 + 0 (1)
1981	1	4490 + 1 (1)
1982	2	4490 + 2 (1)
1983
1984
1985
1986
1987
1988
1989
1990
1991
1992
1993
1994
1995

j) Dejar x representar el número de años desde 1980 y h representar la inclinación. Usando la tabla anterior, escribe una ecuación que relacione h y x.

k) Usa tu ecuación para predecir la inclinación en 1990. ¿Está de acuerdo con el valor real a partir de 1990? ¿Concuerda con el valor que se muestra en la gráfica que hiciste?

l) En la parte (g), utilizó la gráfica para predecir el año en el que la inclinación sería de 4495mm. Usa tu ecuación para hacer la misma predicción. ¿Están de acuerdo las respuestas?

Contestar

a) Hay 1000mm en 1m, por lo que 4.49 = 4.49 (1000) = 4490 mm.

f)

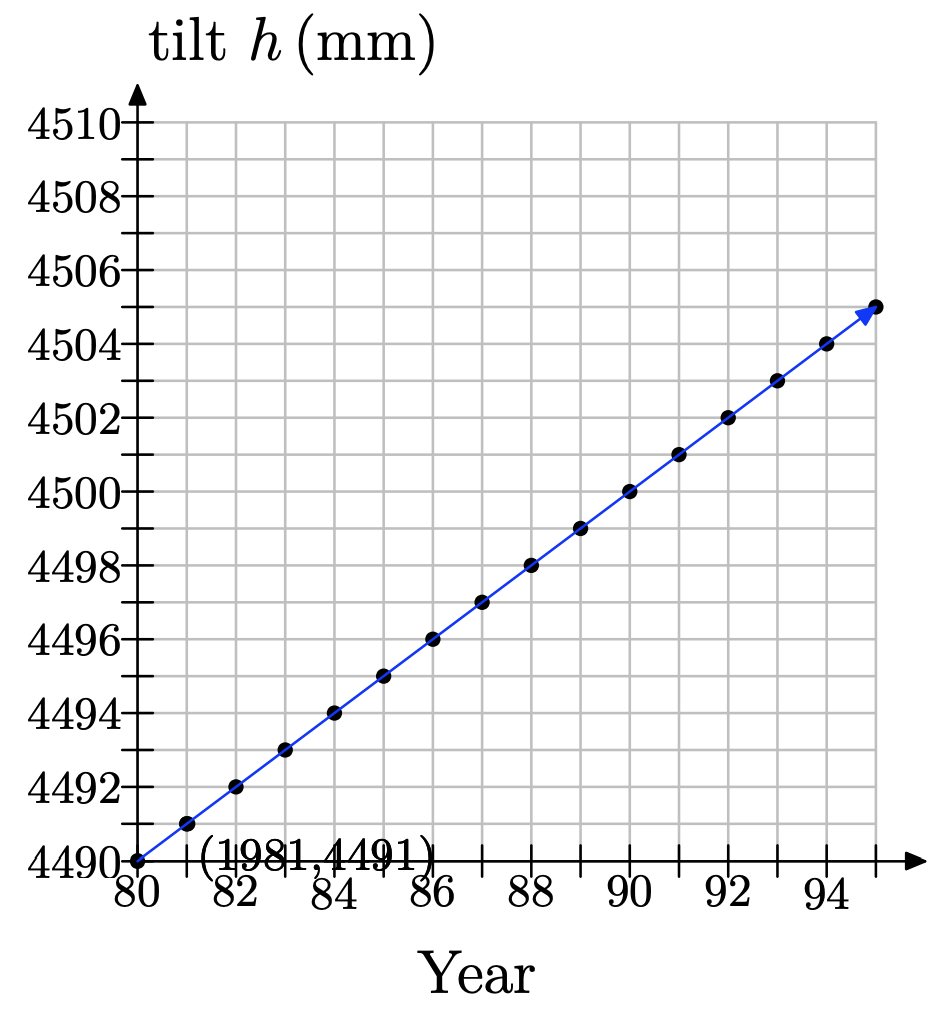
g) Dibujamos una línea para h = 4495 y vemos que corresponde a 1985.

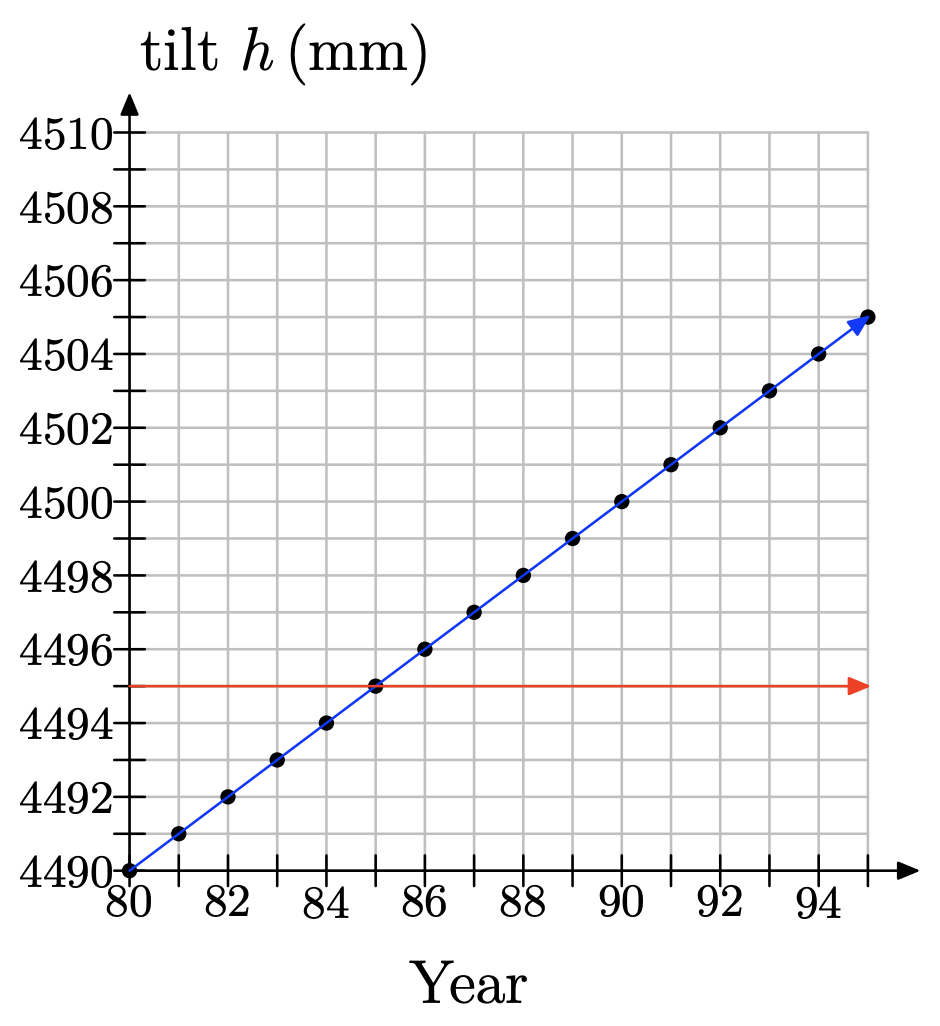
h) Ningún modelo es perfecto. El modelo de computadora no debe haber tomado en consideración ciertos factores inesperados.

i)

Año	años x después del '80	inclinación h
1980	0	4490 + 0 (1)
1981	1	4490 + 1 (1)
1982	2	4490 + 2 (2)
1983	3	4490 + 2 (3)
1984	4	4490 + 2 (4)
1985	5	4490 + 2 (5)
1986	6	4490 + 2 (6)
1987	7	4490 + 2 (7)
1988	8	4490 + 2 (8)
1989	9	4490 + 2 (9)
1990	10	4490 + 2 (10)
1991	11	4490 + 2 (11)
1992	12	4490 + 2 (12)
1993	13	4490 + 2 (13)
1994	14	4490 + 2 (14)
1995	15	4490 + 2 (15)

j) h = 4490 + 1x

k) En 1990, x = 10, y así h = 4490+1 (10) = 4500mm. Sí, concuerda con el valor real en 1990.

l) Para encontrar cuando la inclinación será 4495, establecer h = 4495 y resolver para x. 4495 = 4490 + 1x lleva a 5 = x, y así nuestra respuesta es 1985. Esto concuerda con la respuesta de (g).

Ejercicio\(\PageIndex{12}\)

Según el Statistical Abstract of the United States (www.census.gov), hubo aproximadamente 31, 000 delitos reportados en Estados Unidos en 1998, y esto estaba bajando en una tasa de alrededor de 2900 por año.

a) En una hoja de papel cuadriculado, hacer un sistema de coordenadas y trazar los datos de 1998 como punto. Tenga en cuenta que solo necesitará graficar el primer cuadrante de un sistema de coordenadas, ya que no hay datos para años anteriores a 1998 y no puede haber un número negativo de delitos denunciados. Utilice la tasa dada para encontrar puntos de 1999 a 2006, y luego trazar una línea a través de sus datos. Estamos construyendo un modelo continuo para nuestra situación discreta.

b) La siguiente tabla enumera el número de delitos denunciados, C, el año y el número de años desde 1998. En 1998, el número era de 31, 000 y aún no se habían producido ocurrencias de la disminución de 2900, por lo que llenamos 31000 − 2900 (0). En 1999, una ocurrencia de la disminución de 2900 había ocurrido porque había pasado un año desde 1998. Por lo tanto, el número de delitos denunciados fue de 31000−2900 (1). Y el patrón continúa de esta manera. Rellene las entradas restantes.

Año	años x después de 1998	No. de delitos C
1998	0	31000 − 2900 (0)
1999	1	31000 − 2900 (1)
2000
2001
2002

c) Observando el patrón en la tabla, se obtiene la ecuación C = 31000 − 2900x para relacionar el número de delitos C con el número de años x después de 1998. Aquí, C es una función de x, y así podemos usar la notación C (x) = 31000 − 2900x para enfatizar esto.

i. Cómputos C (5).

ii. En una oración completa, explique lo que representa C (5).

iii. Calcular C (8).

iv. En una oración completa, explique lo que representa C (8).

Ejercicio\(\PageIndex{13}\)

Según el Statistical Abstract of the United States (www.census.gov), en 1999 había aproximadamente 606, 000 internos en las cárceles de Estados Unidos, y esto estaba aumentando en una tasa de alrededor de 14, 000 por año.

a) En una hoja de papel cuadriculado, hacer un sistema de coordenadas y trazar los datos de 1999 como punto. Tenga en cuenta que solo necesitará graficar el primer cuadrante de un sistema de coordenadas, ya que no hay datos para años anteriores a 1999 y no puede haber un número negativo de delitos denunciados. Use la tasa dada para encontrar puntos de 2000 a 2006, y luego dibuje una línea a través de sus datos. Estamos construyendo un modelo continuo para nuestra situación discreta.

b) La siguiente tabla enumera el número de internos, N, el año y el número de años transcurridos desde 1999. En 1999, el número era de 606, 000 y aún no se habían producido ocurrencias del incremento de 14, 000, por lo que llenamos 606000 + 14000 (0). En el año 2000, una ocurrencia del incremento de 14, 000 había ocurrido porque había pasado un año desde 1999. Por lo tanto, el número de delitos denunciados fue de 606000 + 14000 (1). Y el patrón continúa de esta manera. Rellene las entradas restantes.

Año	años x después de '99	No. de internos N
1999	0	606000+14000 (0)
2000	1	606000+14000 (1)
2001
2002

c) Observando el patrón en la tabla, se obtiene la ecuación N = 606000+14000x para relacionar el número de delitos C con el número de años x después de 1999. Aquí, N es una función de x, y así podemos usar la notación N (x) = 606000+14000x para enfatizar esto.

i. Calcular N (5).

ii. En una oración completa, explique lo que representa N (5).

iii. Calcular N (7).

iv. En una oración completa, explique lo que representa N (7).

Contestar

a)

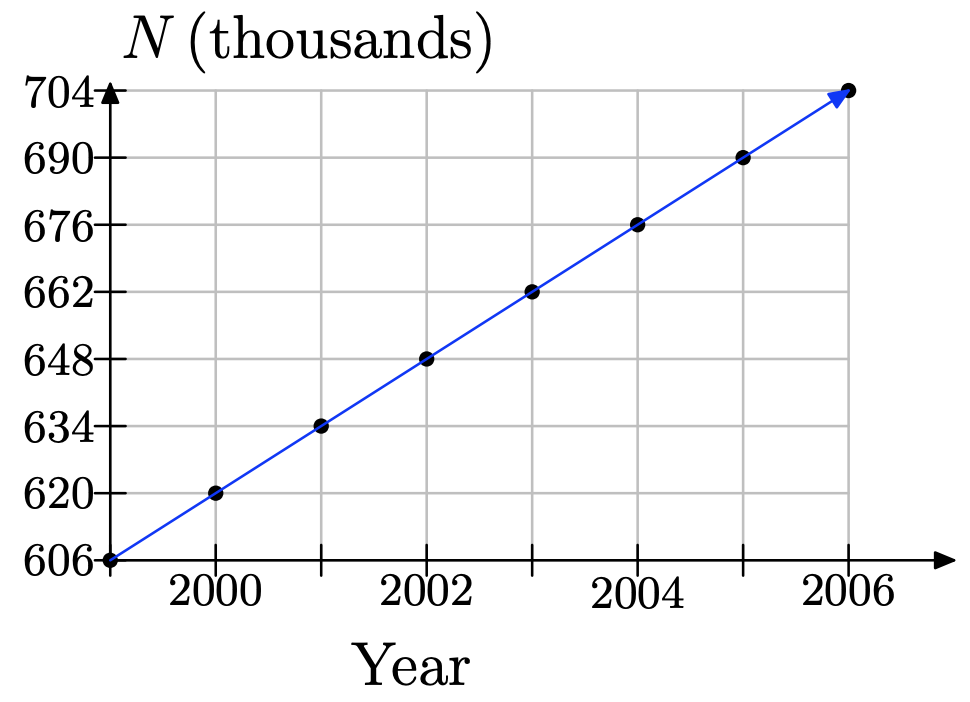
b)

Año	años x después de '99	No. de internos N
1999	0	606000+14000 (0)
2000	1	606000+14000 (1)
2001	2	606000+14000 (2)
2002	3	606000+14000 (3)

c)

i. N (5) = 606000 + 14000 (5) = 676000.

ii. Significa que, según nuestro modelo, 5 años después de 1999 (es decir, en 2004), el número de internos será de 676, 000.

iii. N (7) = 606000 + 14000 (7) = 704000.

iv. Significa que, según nuestro modelo, en 2006, el número de internos será de 704, 000

3.2 Ejercicios

Ejercicio\(\PageIndex{1}\)

Supongamos que está montando una bicicleta cuesta arriba, como se muestra a continuación.

Figura\(\PageIndex{1}\). Montar en bicicleta cuesta arriba de una colina.

a) Si el cerro es recto como se muestra, considere la inclinación, o inclinación, de su inclinación. Al subir la colina, ¿qué puedes decir de la inclinación? ¿Cambia? Si es así, ¿cómo?

b) La inclinación es lo que los matemáticos llaman la pendiente. Para confirmar su respuesta a la parte (a), colocará el cerro en un sistema de coordenadas y calculará su pendiente a lo largo de varios segmentos del cerro. Consulte la figura a continuación.

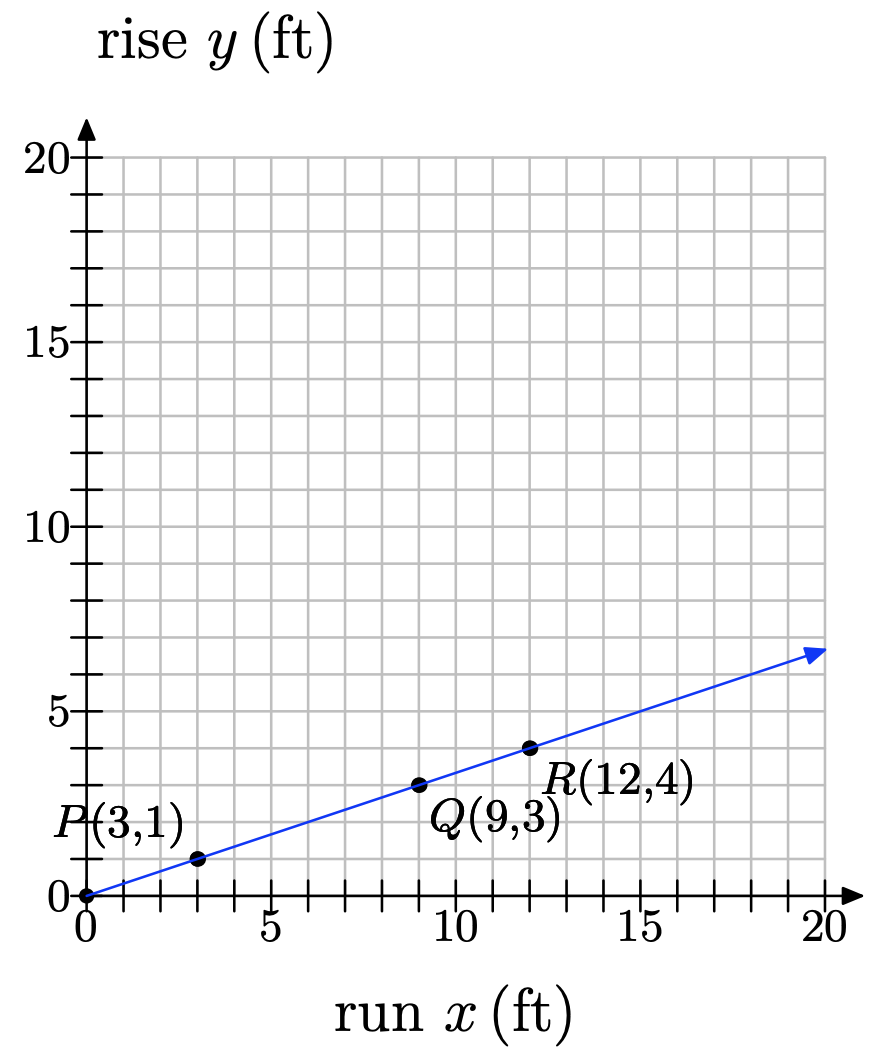
Tres puntos —P, Q y R— han sido etiquetados a lo largo del cerro. Llamamos a la distancia vertical (altura) la subida y la distancia horizontal la carrera. Al subir la colina del punto P al punto Q, ¿cuál es la subida? ¿Cuál es la carrera? Utilice estos valores para calcular la pendiente de P a Q.

c) Ahora considera a medida que montas de P a R. ¿Cuál es el ascenso? ¿Cuál es la carrera? Utilice estos valores para calcular la pendiente de P a R.

d) Por último, considera a medida que montas de Q a R. ¿Cuál es el ascenso? ¿Cuál es la carrera? Utilice estos valores para calcular la pendiente de Q a R.

e) ¿Cómo se comparan los valores de pendiente de las partes (b) - (d)? ¿Estos resultados confirman su respuesta a la parte (a)?

f) Observe que la pendiente es positiva en este ejemplo. En este contexto de andar en bicicleta sobre una colina, ¿qué significaría la pendiente negativa?

Contestar

a) No, no cambia. La inclinación es la misma en todas partes a lo largo del cerro recto.

b)\(m_{PQ} = \dfrac{3−1 }{9−3} = \dfrac{2}{6} = \dfrac{1}{3}\)

c)\(m_{PR} = \dfrac{4−1 }{12−3} = \dfrac{3}{9} = \dfrac{1}{3}\)

d)\(m_{QR} = \dfrac{4-3}{12−9} = \dfrac{1}{3}\)

e) Todos son iguales. Esto tiene sentido porque la inclinación o inclinación del cerro es la misma en todas partes.

f) Pendiente positiva significa que estás montando cuesta arriba; pendiente negativa significaría que estás montando cuesta abajo.

Ejercicio\(\PageIndex{2}\)

Establecer un sistema de coordenadas en una hoja de papel cuadriculado, trazando los puntos P (3, 4) y Q (−2, −7) y dibujando la línea a través de ellos.

a) ¿Qué se puede decir de la pendiente de la línea? ¿Es positivo, cero, negativo o indefinido? ¿La pendiente es la misma en todas partes a lo largo de la línea, o cambia en lugares? Si cambia, ¿dónde son diferentes las pendientes?

b) Usa tu gráfica para determinar el cambio en y (subida) y el cambio en x (carrera). Utilice estos resultados para calcular la pendiente de la línea.

c) Utilice la fórmula de pendiente para calcular la pendiente de la línea.

d) ¿Su solución numérica de la parte (c) concuerda con su solución gráfica de la parte (b)? Si no, revisa tu trabajo para ver si hay errores.

Ejercicio\(\PageIndex{3}\)

Establecer un sistema de coordenadas en una hoja de papel cuadriculado, trazando los puntos P (−1, 3) y Q (5, −3) y dibujando la línea a través de ellos.

a) ¿Qué se puede decir de la pendiente de la línea? ¿Es positivo, cero, negativo o indefinido? ¿La pendiente es la misma en todas partes a lo largo de la línea, o cambia en lugares? Si cambia, ¿dónde son diferentes las pendientes?

b) Usa tu gráfica para determinar el cambio en y (subida) y el cambio en x (carrera). Utilice estos resultados para calcular la pendiente de la línea.

c) Utilice la fórmula de pendiente para calcular la pendiente de la línea.

d) ¿Su solución numérica de la parte (c) concuerda con su solución gráfica de la parte (b)? Si no, revisa tu trabajo para ver si hay errores.

Contestar

a) La pendiente es negativa porque la línea se inclina cuesta abajo. La pendiente es la misma en todas partes a lo largo de la línea porque la inclinación de la línea no cambia.

b)

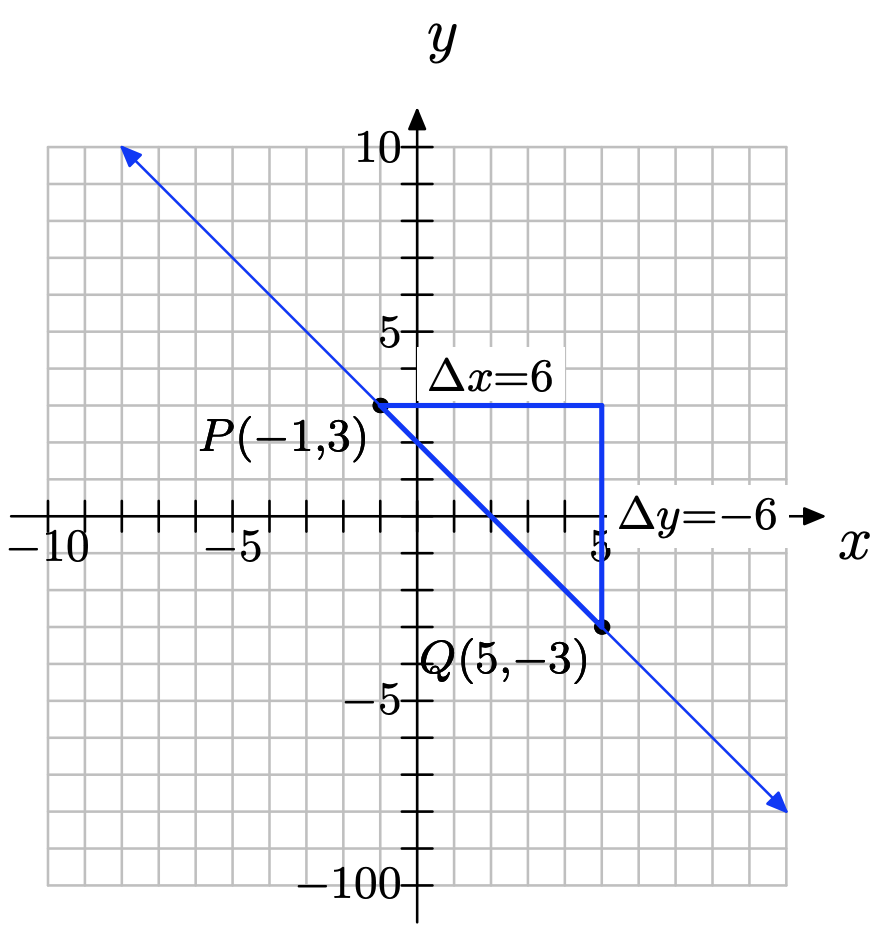
pendiente = −6/6 = −1

c) ∆y = −3 − (3) = −6; ∆x = 5 − (−1) = 6; pendiente =\ dfrac {\ delta y} {\ delta x}\) =\( \dfrac{−6 }{6}\) = −1

d) Sí.

En Ejercicios\(\PageIndex{4}\) -\(\PageIndex{10}\), realizar cada una de las siguientes tareas.

i. Hacer un boceto de un sistema de coordenadas; trazar los puntos dados y dibujar la línea a través de los puntos.

ii. Utilice la fórmula de pendiente para calcular la pendiente de la línea a través de los puntos dados. Reducir la pendiente donde sea posible.

Ejercicio\(\PageIndex{4}\)

(0, 0) y (3, 4)

Ejercicio\(\PageIndex{5}\)

(−5, 2) y (0, 3)

Contestar

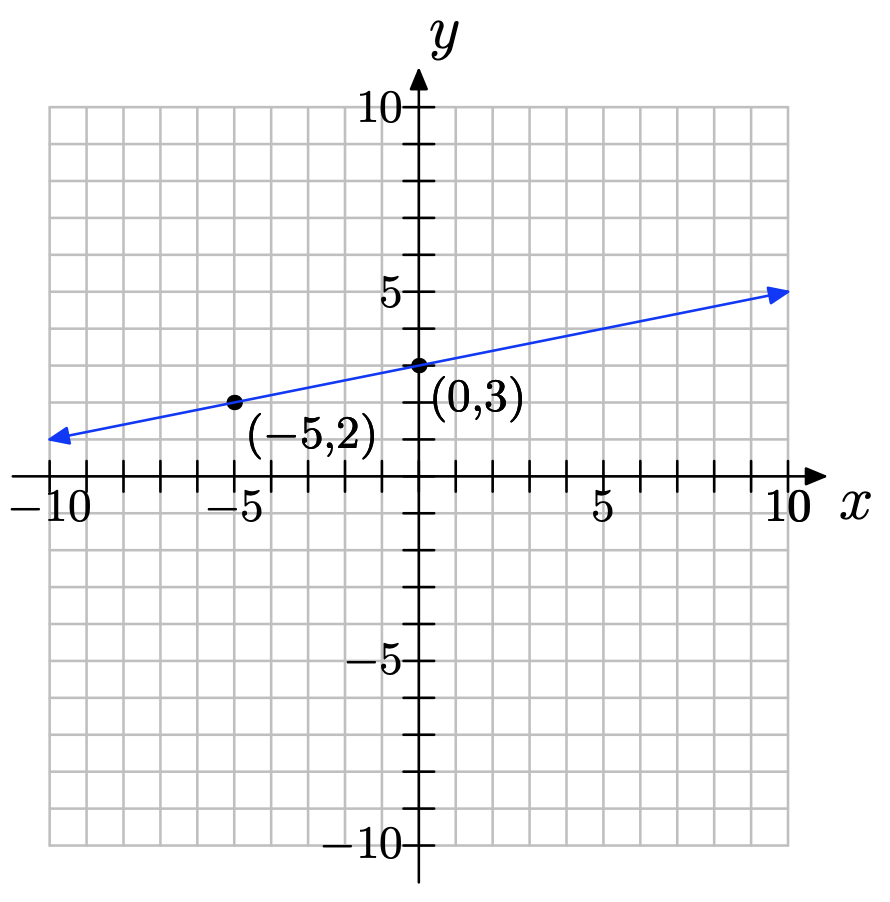
\(slope = \dfrac{3−2}{ 0−(−5)} = \dfrac{1}{5}\)

Ejercicio\(\PageIndex{6}\)

(−3, −3) y (6, −5)

Ejercicio\(\PageIndex{7}\)

(2, 0) y (2, 2)

Contestar

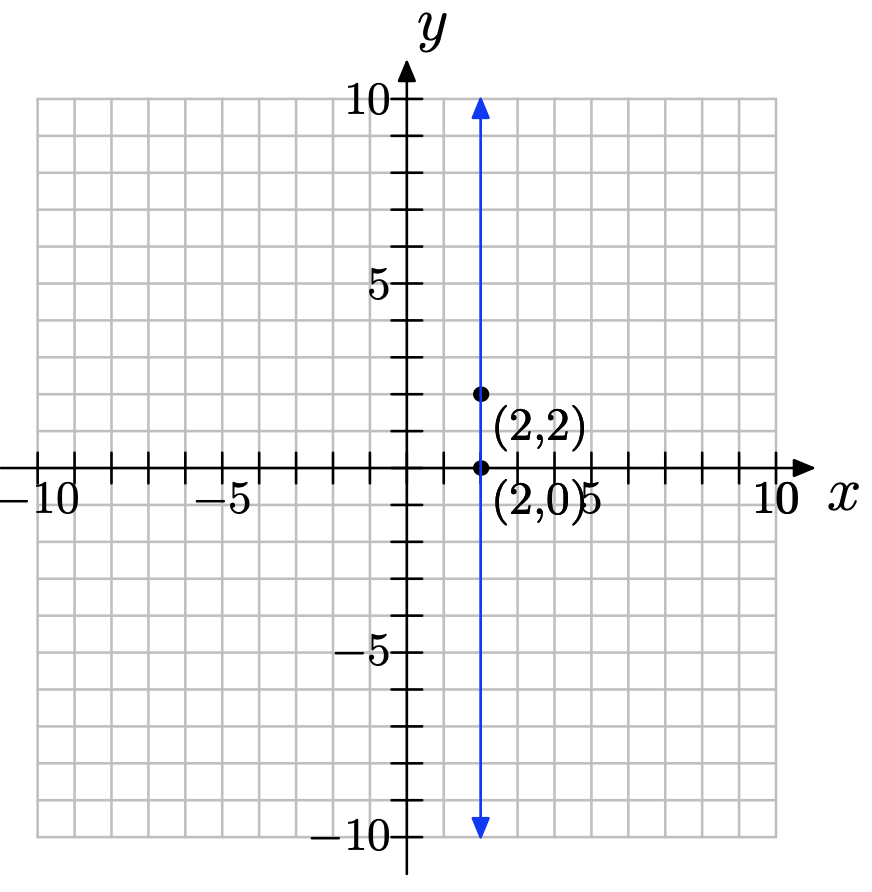
\(slope = \dfrac{2−0 }{2−2} = \dfrac{2}{0}\)= indefinido

Ejercicio\(\PageIndex{8}\)

(−9, −3) y (6, −3)

Ejercicio\(\PageIndex{9}\)

(−8, 4) y (3, −8)

Contestar

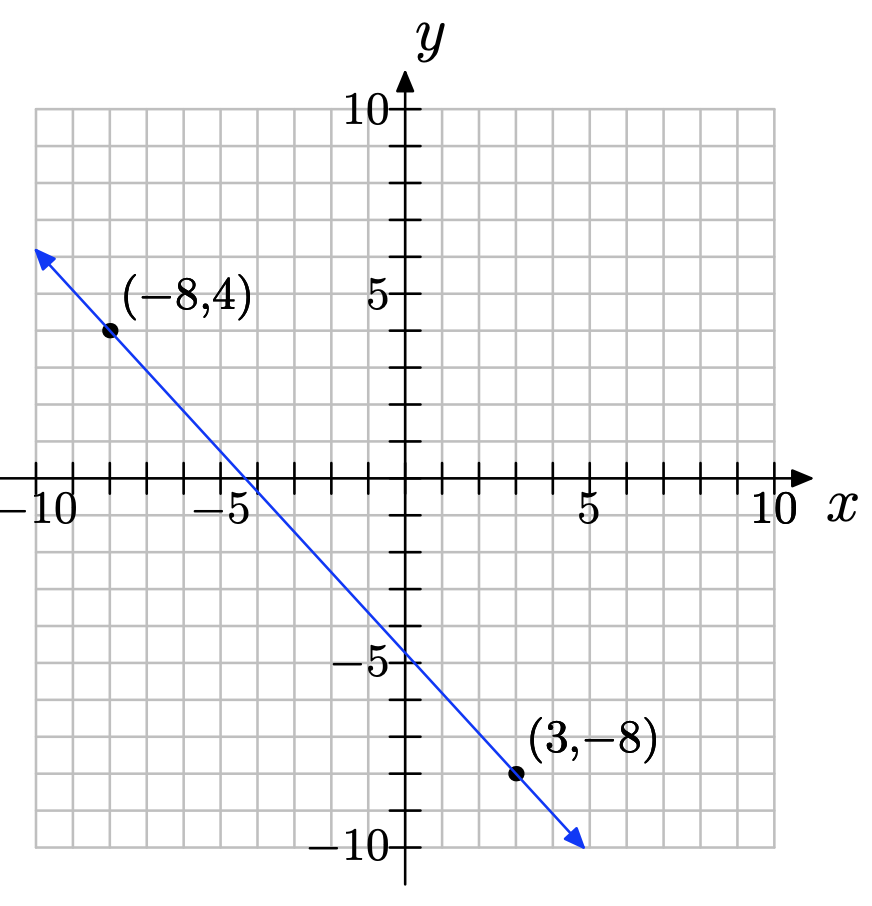
\(slope = \dfrac{−8−4}{ 3−(−8)} = \dfrac{−12}{ 11}\)

Ejercicio\(\PageIndex{10}\)

(−2, 6) y (5, −2)

Ejercicio\(\PageIndex{11}\)

Para la siguiente línea, se han elegido dos puntos convenientes P y Q. Elegimos dos puntos que estaban en las esquinas de cajas en nuestra cuadrícula para que sus coordenadas sean fáciles de leer.

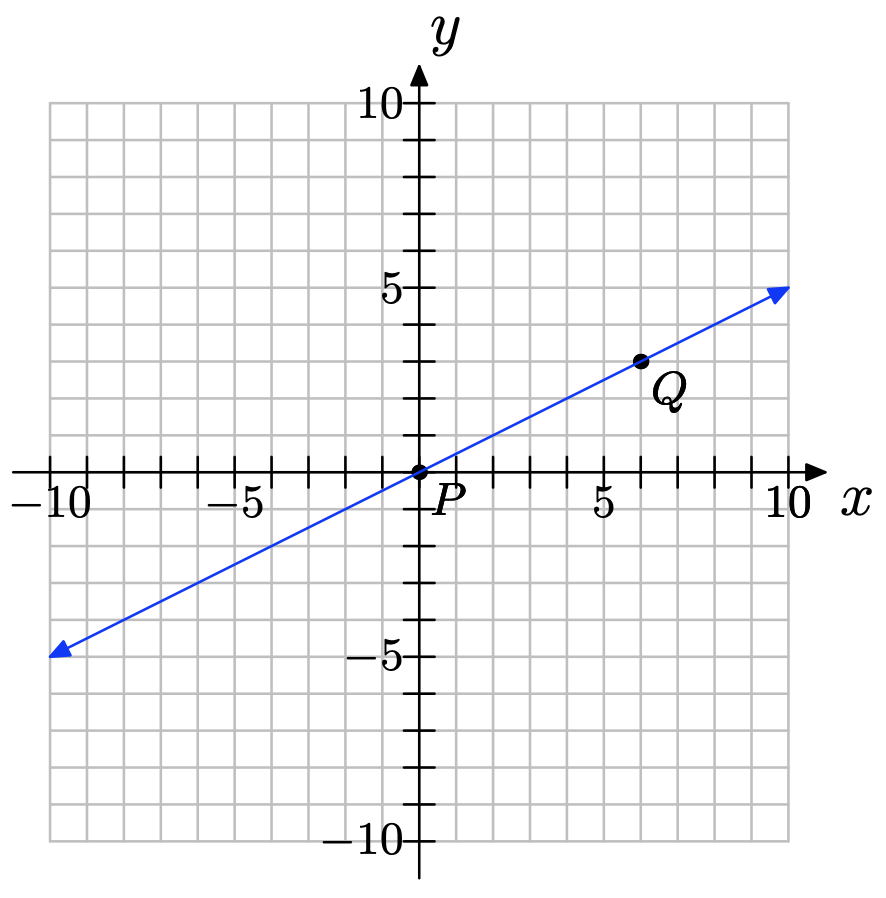
a) Etiquetar sus coordenadas.

b) Pensando en P como punto de partida y Q como punto final, dibuja un triángulo rectángulo uniendo los puntos.

c) Indique claramente el cambio en y (subida) y el cambio en x (carrera) de P a Q.

d) Computar la pendiente.

Contestar

a) Los puntos son (0, 0) y (6, 3).

b)

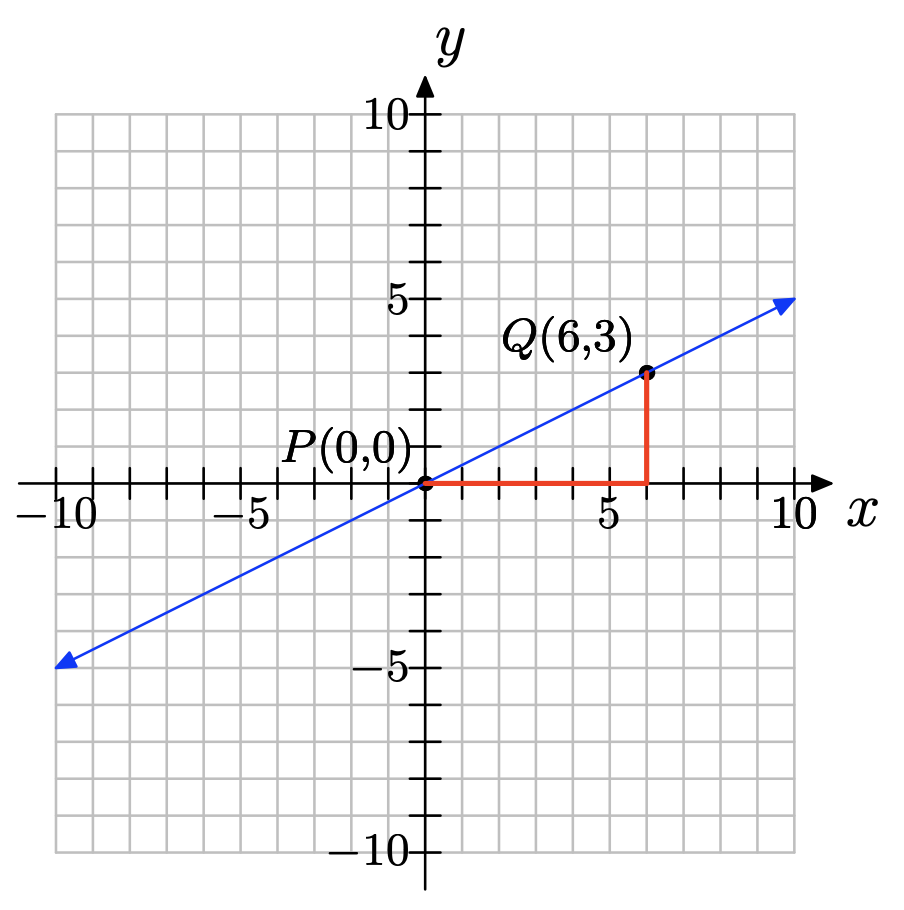
c) ∆y = 3 − 0 = 3; ∆x = 6 − 0 = 6

d) pendiente =\(\dfrac{\delta y}{\delta x} =\dfrac{3}{6} = \dfrac{1}{ 2}\)

Ejercicio\(\PageIndex{12}\)

Para la siguiente línea, se han elegido dos puntos convenientes A y B. Elegimos dos puntos que estaban en las esquinas de cajas en nuestra cuadrícula para que sus coordenadas sean fáciles de leer.

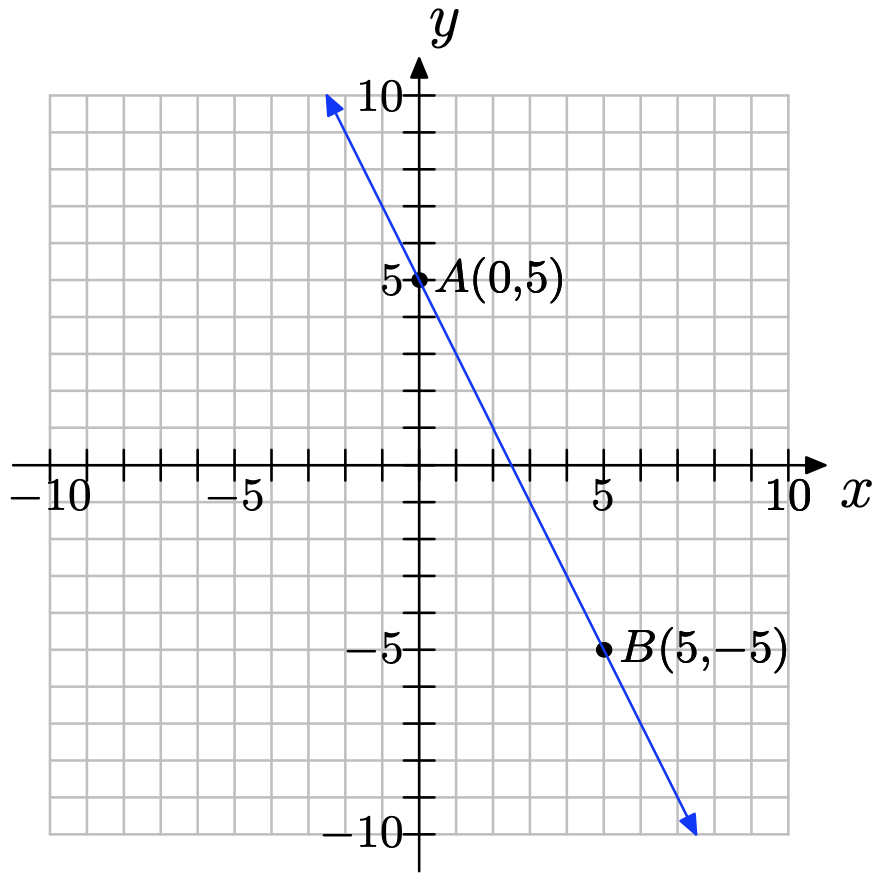
a) Etiquetar sus coordenadas.

b) Pensando en A como punto de partida y B como punto final, dibuja un triángulo rectángulo uniendo los puntos.

c) Indique claramente el cambio en y (subida) y el cambio en x (carrera) de A a B.

d) Computar la pendiente.

Ejercicio\(\PageIndex{13}\)

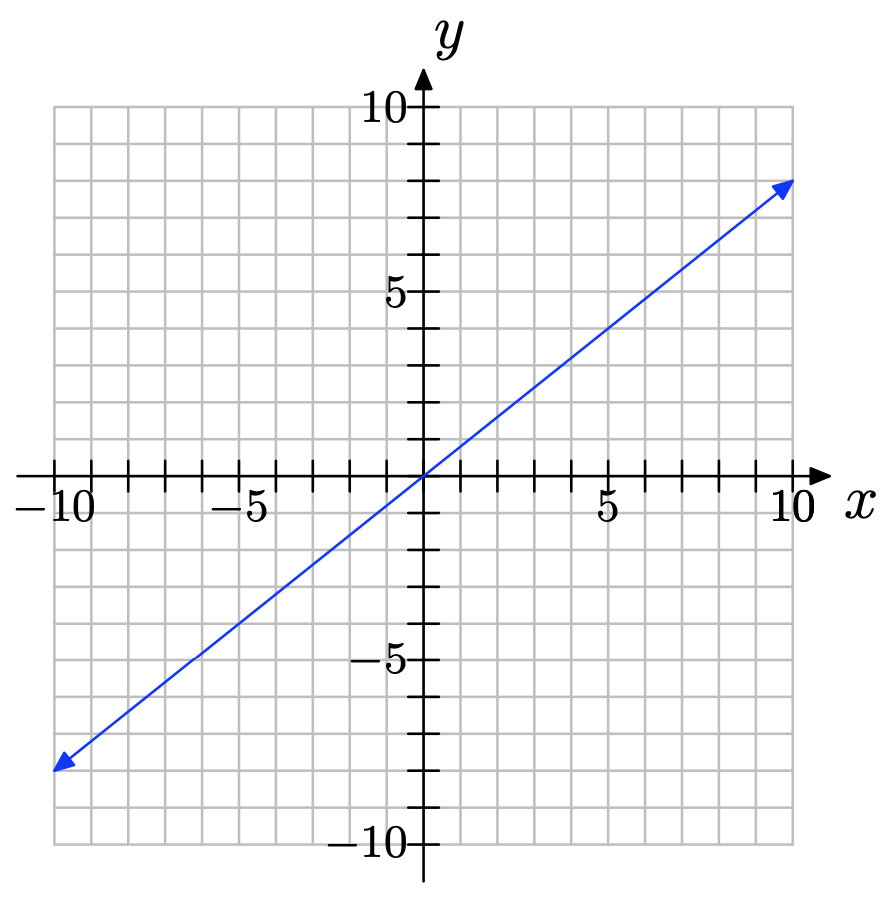
Copia el sistema de coordenadas a continuación en una hoja de papel cuadriculado. Luego haga lo siguiente:

a) Seleccione cualquiera de los dos puntos convenientes P y Q en la gráfica de la línea. Etiquete cada punto con sus coordenadas.

b) Indicar claramente el cambio en y (subida) y el cambio en x (carrera). Calcular la pendiente de la línea.

Contestar

NOTA: Las soluciones pueden variar dependiendo de qué dos puntos convenientes fueron elegidos.

a) Se pueden escoger dos puntos cualesquiera de la línea; por ejemplo, (0, 0) y (5, 4) como se muestra a continuación.

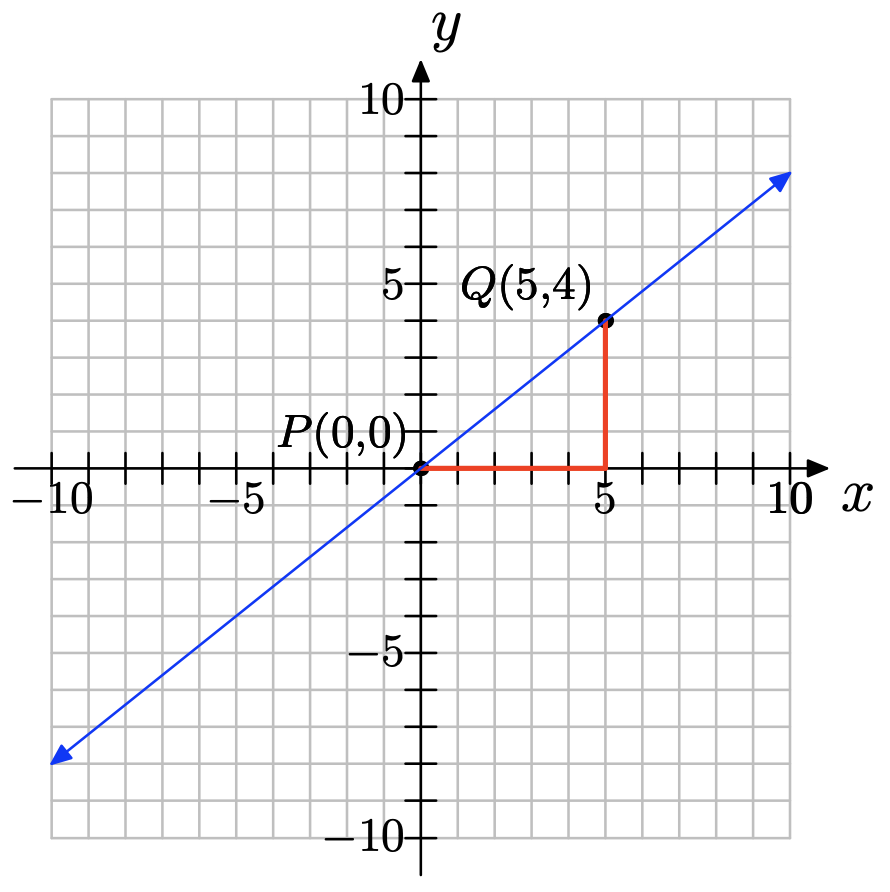
b) ∆y = 4 − 0 = 4; ∆x = 5 − 0 = 5; pendiente =\(\dfrac{\delta y }{\delta x} = \dfrac{4}{5}\)

Ejercicio\(\PageIndex{14}\)

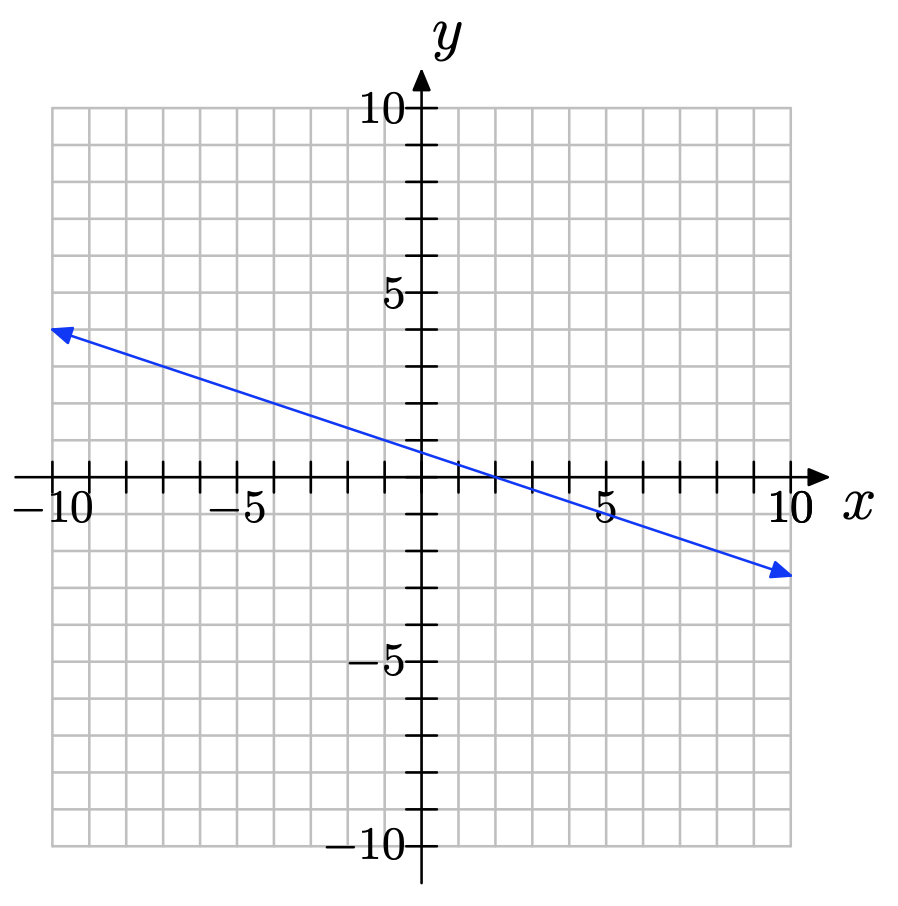
Copia el sistema de coordenadas a continuación en una hoja de papel cuadriculado. Luego haga lo siguiente:

a) Seleccione cualquiera de los dos puntos convenientes P y Q en la gráfica de la línea. Etiquete cada punto con sus coordenadas.

b) Indicar claramente el cambio en y (subida) y el cambio en x (carrera). Calcular la pendiente de la línea.

Ejercicio\(\PageIndex{15}\)

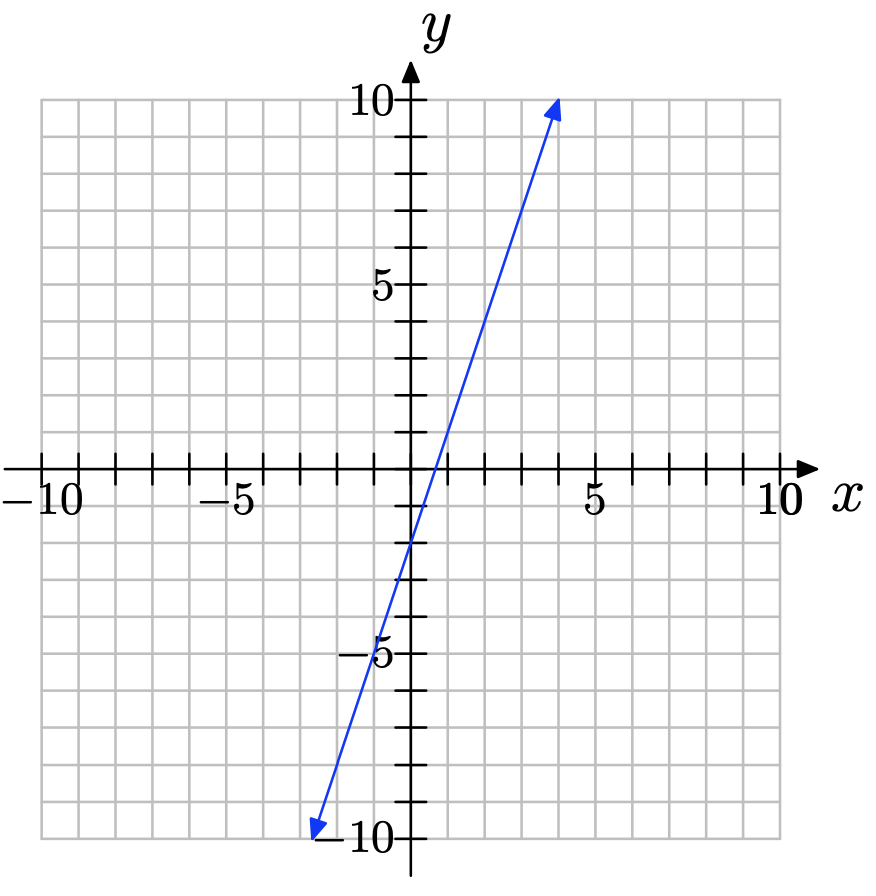
Copia el sistema de coordenadas a continuación en una hoja de papel cuadriculado. Luego haga lo siguiente:

a) Seleccione cualquiera de los dos puntos convenientes P y Q en la gráfica de la línea. Etiquete cada punto con sus coordenadas.

b) Indicar claramente el cambio en y (subida) y el cambio en x (carrera). Calcular la pendiente de la línea.

Contestar

NOTA: Las soluciones pueden variar dependiendo de qué dos puntos convenientes fueron elegidos.

a) Se pueden escoger dos puntos cualesquiera de la línea; por ejemplo, (1, 1) y (3, 7) como se muestra a continuación.

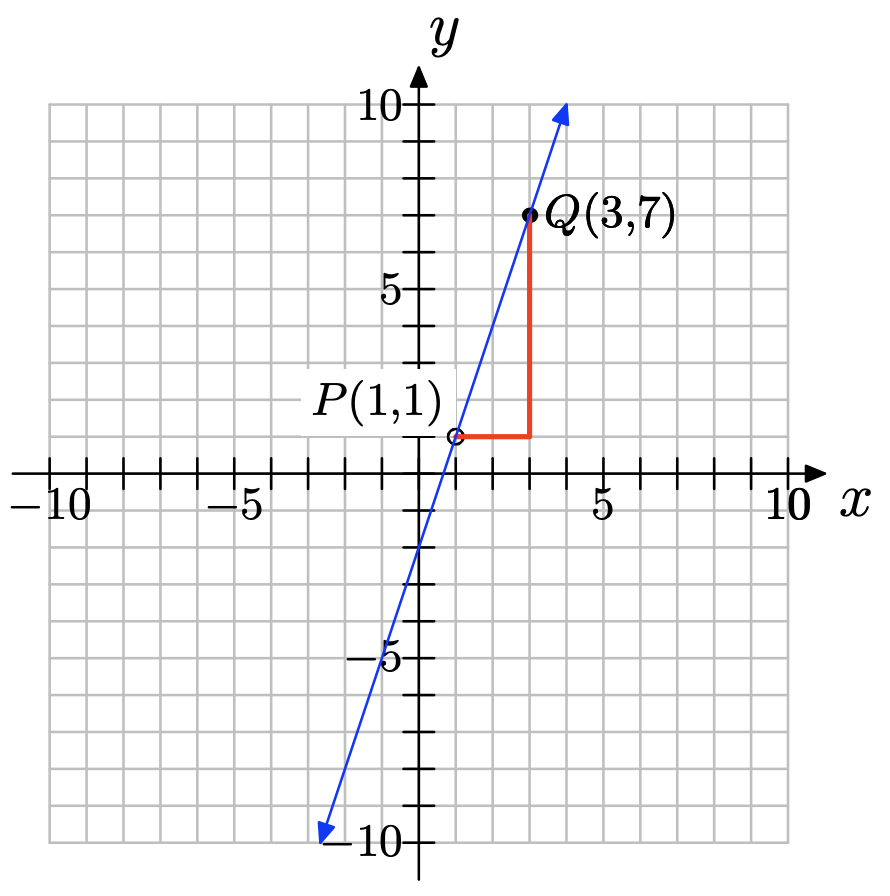
b) ∆y = 7 − 1 = 6; ∆x = 3 − 1 = 2; pendiente =\( \dfrac{\delta y }{\delta x} = \dfrac{6}{2} = 3\)

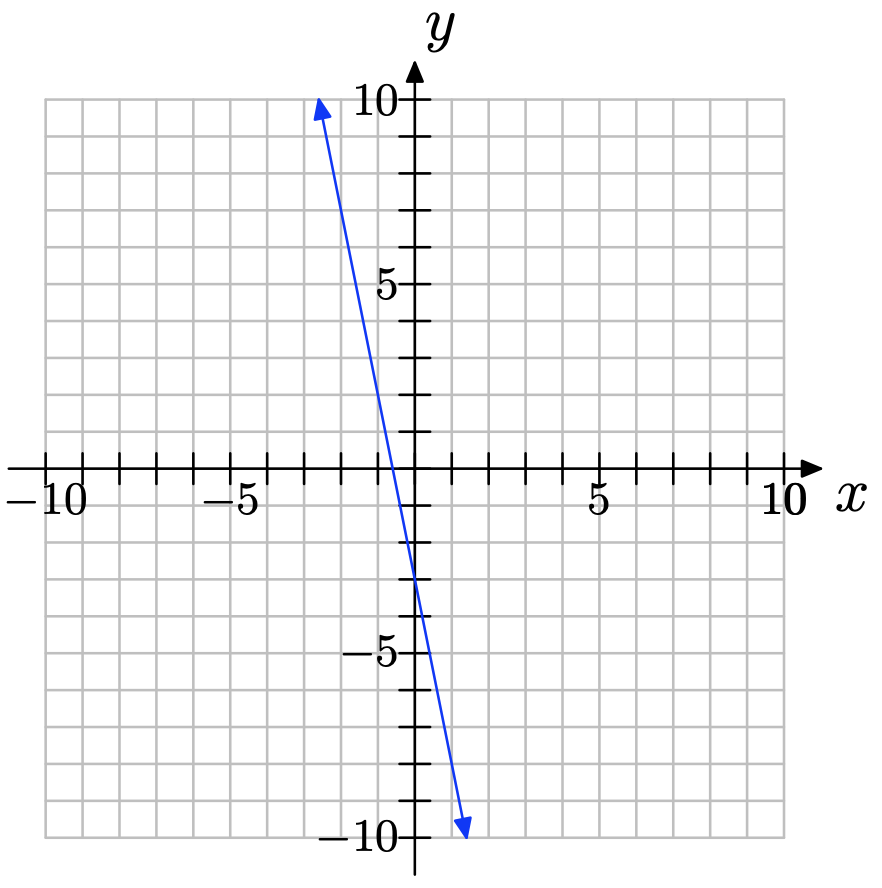
Ejercicio\(\PageIndex{16}\)

Copia el sistema de coordenadas a continuación en una hoja de papel cuadriculado. Luego haga lo siguiente:

a) Seleccione cualquiera de los dos puntos convenientes P y Q en la gráfica de la línea. Etiquete cada punto con sus coordenadas.

b) Indicar claramente el cambio en y (subida) y el cambio en x (carrera). Calcular la pendiente de la línea.

Ejercicio\(\PageIndex{17}\)

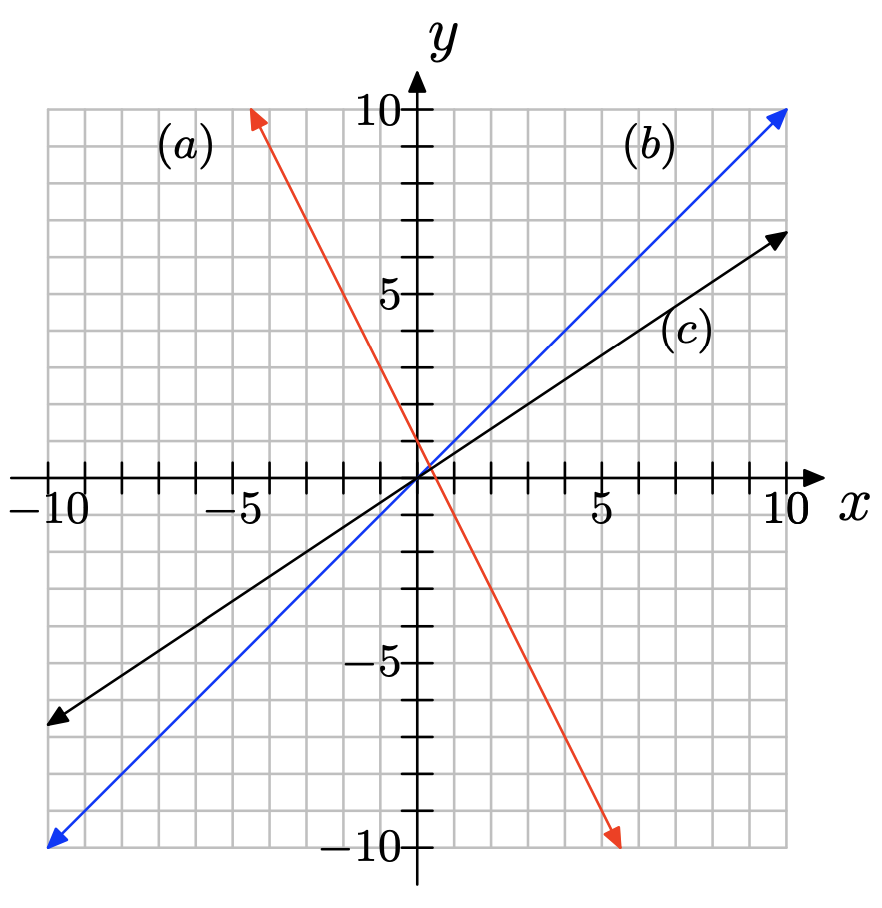
El siguiente sistema de coordenadas muestra las gráficas de tres líneas, cada una con diferente pendiente. Haga coincidir cada pendiente con (a), (b) o (c) apropiadamente.

pendiente = 1

pendiente = 2/3

pendiente = −2

Contestar

pendiente = 1: (b)

pendiente = 2/3: (c)

pendiente = −2: (a)

Ejercicio\(\PageIndex{18}\)

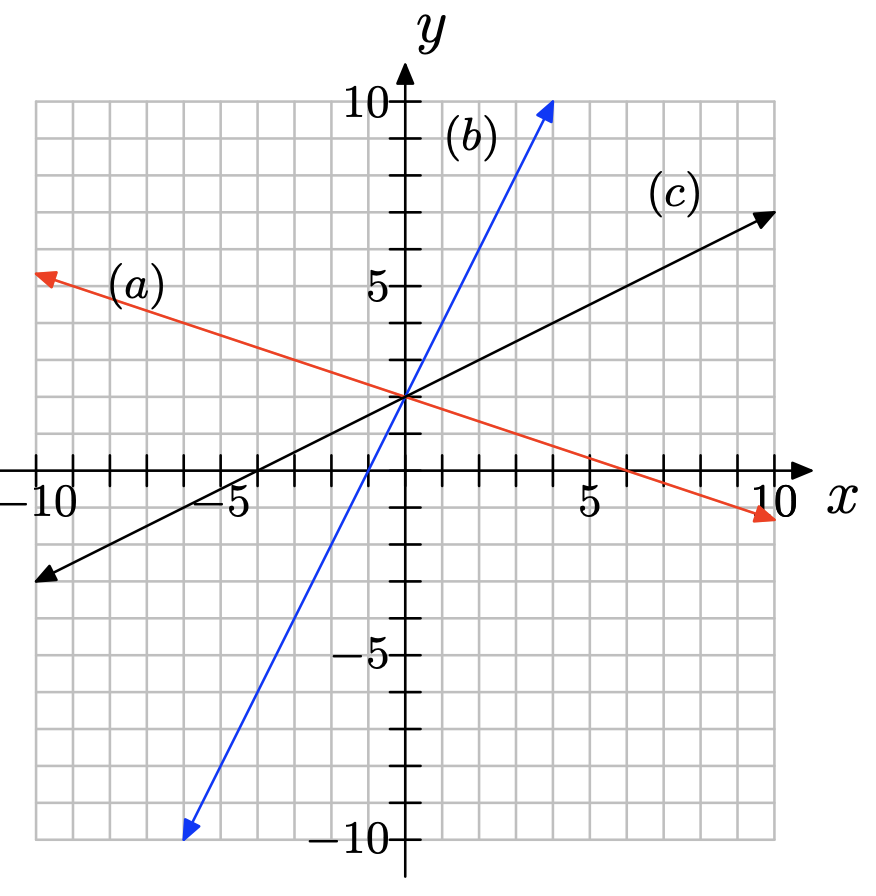
El siguiente sistema de coordenadas muestra las gráficas de tres líneas, cada una con diferente pendiente. Haga coincidir cada pendiente con (a), (b) o (c) apropiadamente.

pendiente = 2

pendiente = −1/3

pendiente = 1/2

Ejercicio\(\PageIndex{19}\)

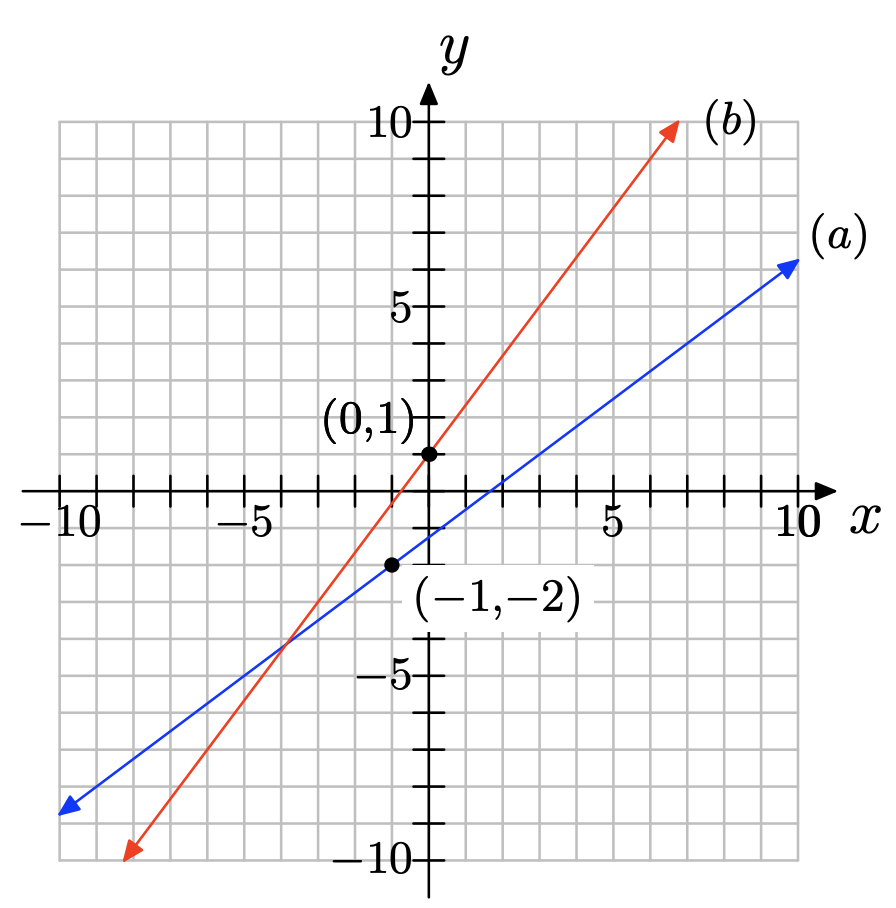
Dibuje un sistema de coordenadas en una hoja de papel cuadriculado para la cual los ejes x e y oscilan entre −10 y 10.

a) Dibuja una línea que contenga el punto (0, 1) y tenga pendiente 2. Etiquete la línea como (a).

b) En el mismo sistema de coordenadas, dibuje una línea que contenga el punto (0, 1) y tenga pendiente −1/2. Etiquetarlo como (b).

c) Utilizar las pendientes de estas dos líneas para mostrar que son perpendiculares.

Contestar

b)

c)\(m_{1}m_{2} = 2(−1/2) = −1\), por lo que las líneas son perpendiculares.

Ejercicio\(\PageIndex{20}\)

Dibuje un sistema de coordenadas en una hoja de papel cuadriculado para la cual los ejes x e y oscilan entre −10 y 10.

a) Dibuja una línea que contenga el punto (1, −2) y tenga pendiente 1/3. Etiquete la línea como (a).

b) En el mismo sistema de coordenadas, dibuje una línea que contenga el punto (0, 1) y tenga pendiente −3. Etiquetarlo como (b).

c) Utilizar las pendientes de estas dos líneas para mostrar que son perpendiculares.

Ejercicio\(\PageIndex{21}\)

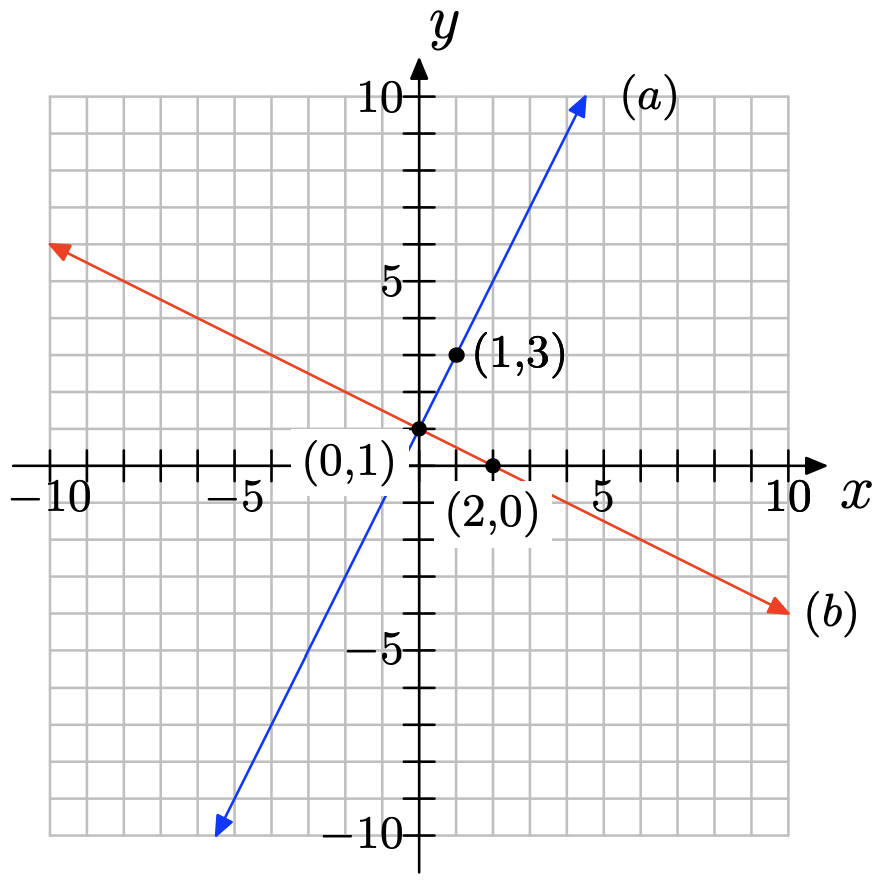
Dibuja una línea a través del punto P (1, 3) que sea paralela a la línea a través del origen con pendiente −1/4.

Contestar

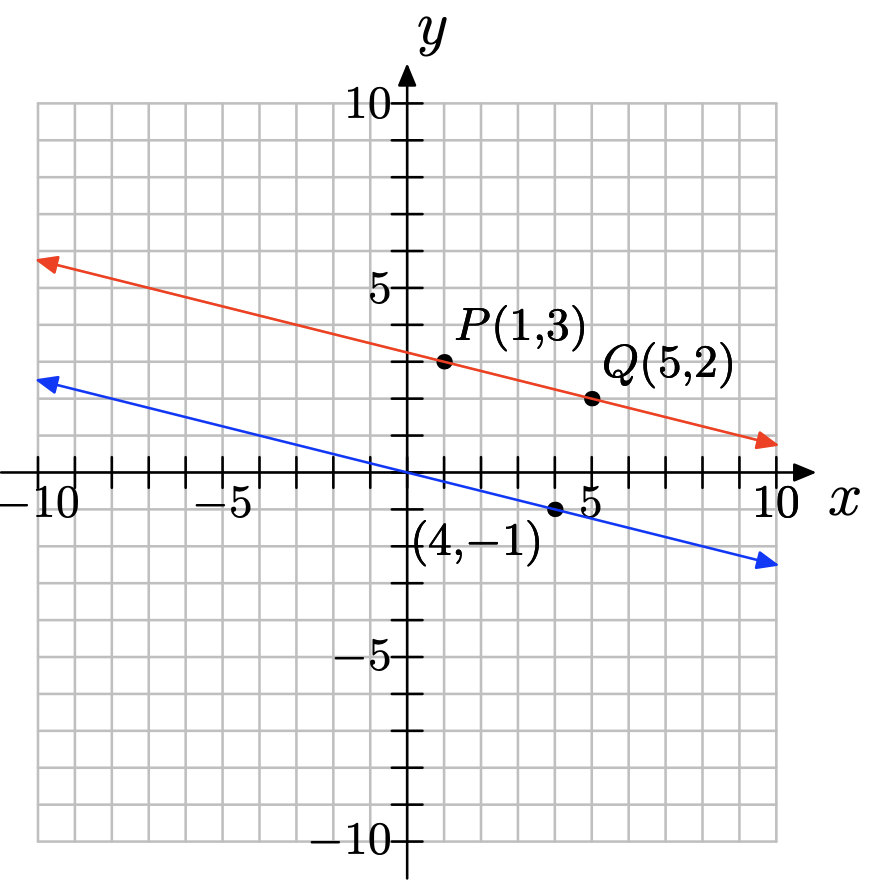
Ejercicio\(\PageIndex{22}\)

Dibuja una línea a través del punto P (1,3) que sea paralela a la línea a través del origen con pendiente 3/5.

Ejercicio\(\PageIndex{23}\)

Dibuje un sistema de coordenadas en una hoja de papel cuadriculado para la cual los ejes x e y oscilan entre −10 y 10.

a) Dibuja una línea que contenga el punto (−1, −2) y tenga pendiente 3/4. Etiquete la línea como (a).

b) En el mismo sistema de coordenadas, dibuje una línea que contenga el punto (0, 1) y tenga pendiente 4/3. Etiquetarlo como (b).

c) ¿Estas líneas son paralelas, perpendiculares o ninguna? Espectáculo usando sus pendientes.

Contestar

b)

c)\(m_{1}m_{2} = (4/3)(3/4) = 1 \neq −1\), por lo que las líneas no son perpendiculares; las pendientes no son iguales, por lo que las líneas tampoco son paralelas. Así, las líneas pueden clasificarse como no paralelas ni perpendiculares.

Ejercicio\(\PageIndex{24}\)

Grafique un sistema de coordenadas en una hoja de papel cuadriculado para la cual los ejes x e y oscilan entre −10 y 10.

a) Dibuja una línea que contenga el punto (−4, 0) y tenga pendiente 1. Etiquete la línea como (a).

b) En el mismo sistema de coordenadas, dibuje una línea que contenga el punto (0, 2) y tenga pendiente −1. Etiquetarlo como (b).

c) ¿Estas líneas son paralelas, perpendiculares o ninguna? Espectáculo usando sus pendientes.

Ejercicio\(\PageIndex{25}\)

Figura\(\PageIndex{2}\). Una pendiente es una forma de expresar pendiente.

En la carretera de Fort Bragg a Willits o de Fort Bragg a Santa Rosa, a menudo se pasan señales como la que se muestra arriba. Una calificación es solo pendiente expresada como un porcentaje en lugar de una fracción o decimal. Es decir, la pendiente mide la pendiente de la carretera tal como lo hace la pendiente.

a) Una pendiente de 80 /0 significa que, por cada distancia horizontal de 100 pies, la carretera sube o baja 8 pies (dependiendo de si vas cuesta arriba o cuesta abajo). Escribir grado 80 /0 como pendiente en forma fraccional reducida.

b) Supongamos que una colina cae 16 pies por cada 180 pies horizontalmente. Encuentra el grado del cerro al décimo de un por ciento más cercano.

c) Explique en una oración o oraciones completas lo que representaría una calificación de 00 /0.

Contestar

a) grado\(=\dfrac{ 8}{ 100} = \dfrac{2}{ 25}\)

b) grado\(= \dfrac{16}{ 180} = \dfrac{4}{ 45} = 8.90 \)%

c) El 0% de pendiente representa sin pendiente ni pendiente; es decir, un camino plano.

3.3 Ejercicios

En Ejercicios\(\PageIndex{1}\) -\(\PageIndex{6}\), realice cada una de las siguientes tareas para la función lineal dada.

i. Establecer un sistema de coordenadas en una hoja de papel cuadriculado. Etiquetar y escalar cada eje. Recuerda dibujar todas las líneas con una regla.

ii. Identificar la pendiente e intercepción y de la gráfica de la función lineal dada.

iii. Utilice la pendiente y la intercepción y para dibujar la gráfica de la función lineal dada en su sistema de coordenadas. Etiquete la intercepción y con su coordenada y la gráfica con su ecuación.

Ejercicio\(\PageIndex{1}\)

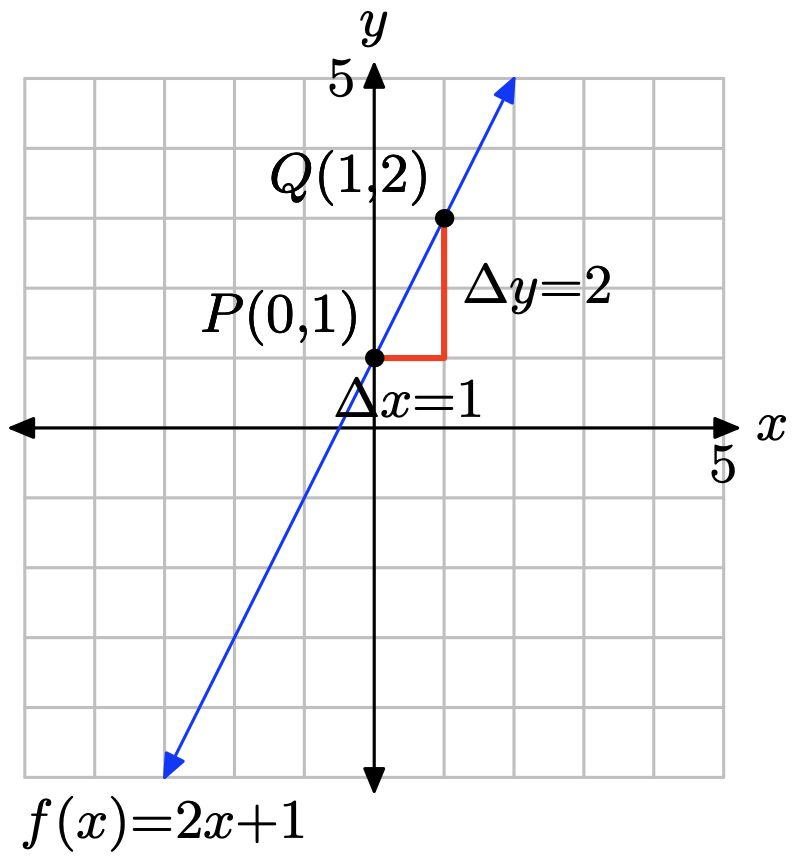
f (x) = 2x + 1

Contestar

Compara f (x) = 2x + 1 con f (x) = mx + b Obsérvese que la pendiente es m = 2 y la coordenada y de la intercepción y es b = 1. Por lo tanto, la intercepción y será el punto (0, 1). Trazar el punto P (0, 1). Para obtener una línea de pendiente m = 2/1, iniciar en el punto P (0, 1), luego mover 1 unidad a la derecha y 2 unidades hacia arriba, llegando al punto Q (1, 3), como se muestra en la siguiente figura. La línea que pasa por los puntos P y Q es la línea requerida.

Ejercicio\(\PageIndex{2}\)

f (x) = −2x + 3

Ejercicio\(\PageIndex{3}\)

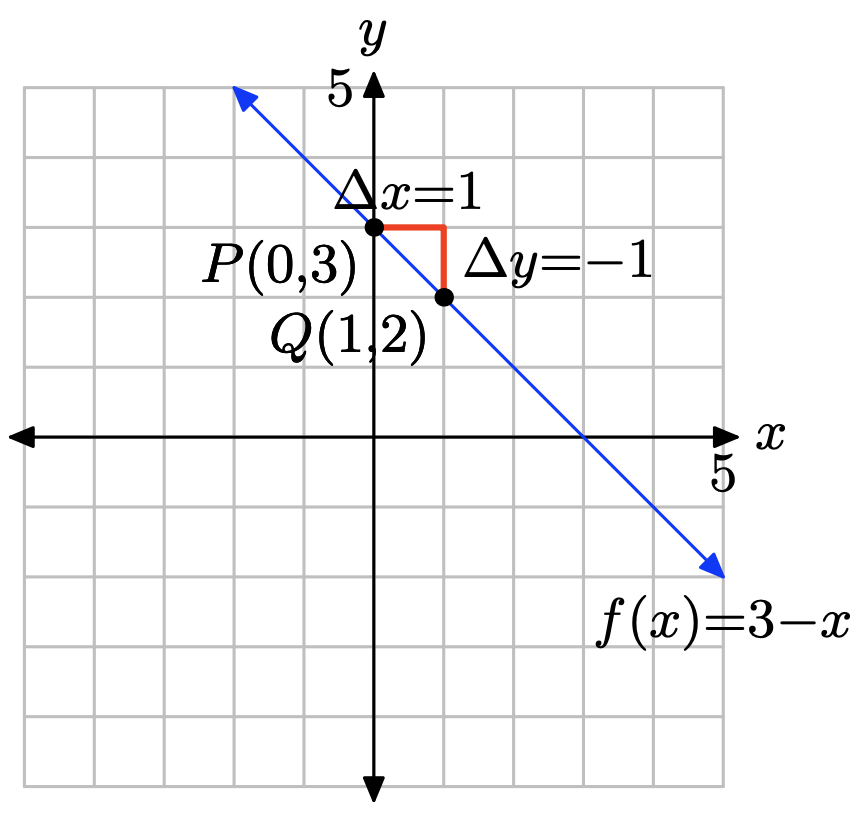
f (x) = 3 − x

Contestar

Compare f (x) = 3 − x, o equivalentemente f (x) = −x + 3, con f (x) = mx + b. Observe que la pendiente es m = −1 y la coordenada y de la intersección y es b = 3. Por lo tanto, la intercepción y será el punto (0, 3). Trazar el punto P (0, 3). Para obtener una línea de pendiente m = −1, comience en el punto P (0, 3), luego mueva 1 unidad a la derecha y 1 unidades hacia abajo, llegando al punto Q (1, 2), como se muestra en la siguiente figura. La línea que pasa por los puntos P y Q es la línea requerida.

Ejercicio\(\PageIndex{4}\)

f (x) = 2 − 3x

Ejercicio\(\PageIndex{5}\)

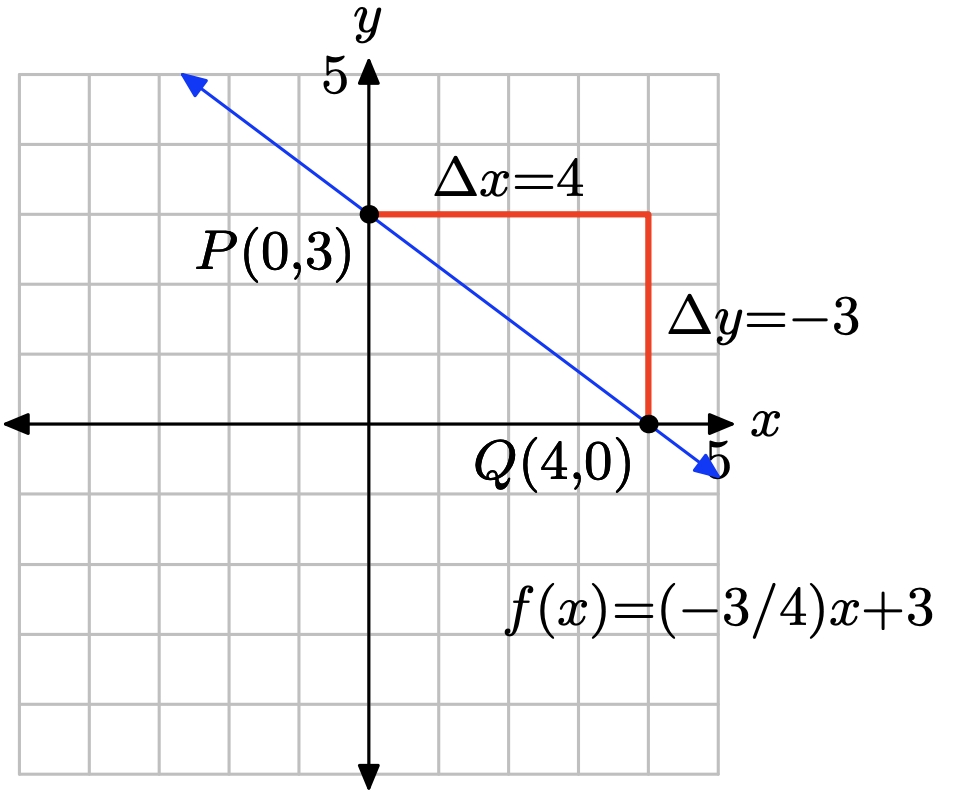
\(f(x) = −\frac{3}{4} x + 3\)

Contestar

Compare f (x) = (−3/4) x+3 con f (x) = mx+b Observe que la pendiente es m = −3/4 y la coordenada y de la intersección y es b = 3. Por lo tanto, la intercepción y será el punto (0, 3). Trazar el punto P (0, 3). Para obtener una línea de pendiente m = −3/4, comience en el punto P (0, 3), luego mueva 4 unidades a la derecha y 3 unidades hacia abajo, llegando al punto Q (4, 0), como se muestra en la siguiente figura. La línea que pasa por los puntos P y Q es la línea requerida.

Ejercicio\(\PageIndex{6}\)

\(f(x) = \frac{2}{3} x − 2\)

En Ejercicios\(\PageIndex{7}\) -\(\PageIndex{12}\), realizar cada una de las siguientes tareas.

i. Hacer una copia de la gráfica dada en una hoja de papel cuadriculado.

ii. Etiquete la intercepción y con sus coordenadas, luego dibuje un triángulo rectángulo y etiquete los lados para ayudar a identificar la pendiente.

iii. Etiquete la línea con su ecuación.

Ejercicio\(\PageIndex{7}\)

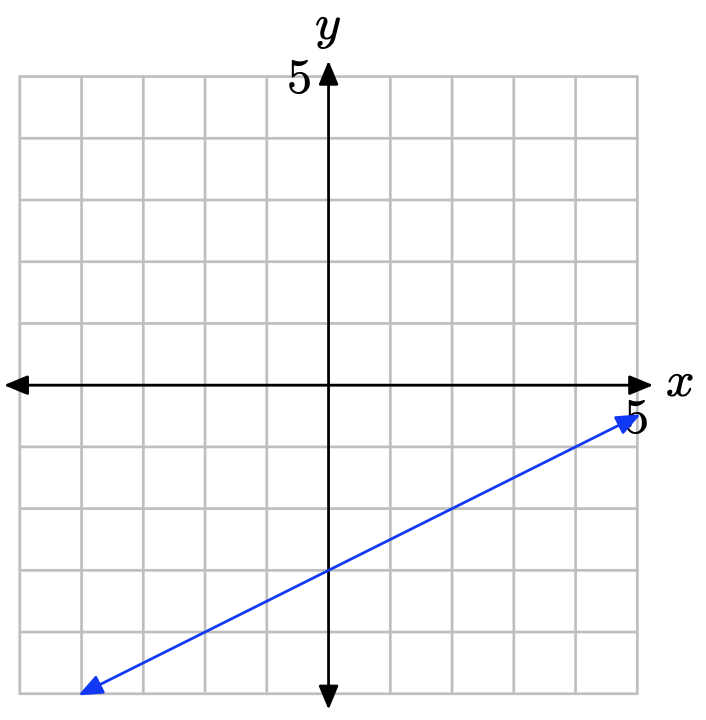
Contestar

La pendiente se encuentra dividiendo la subida por la carrera (ver figura). De ahí que la pendiente sea 1/2. La intercepción y se encuentra anotando dónde la gráfica de la línea cruza el eje y (ver figura), en este caso, en (0, −3). Por lo tanto, m = 1/2 y b = −3, por lo que la ecuación de la línea en forma de intercepción de pendiente es

\[y = mx + b \quad \text{or} \quad y = \frac{1}{2}x − 3\]

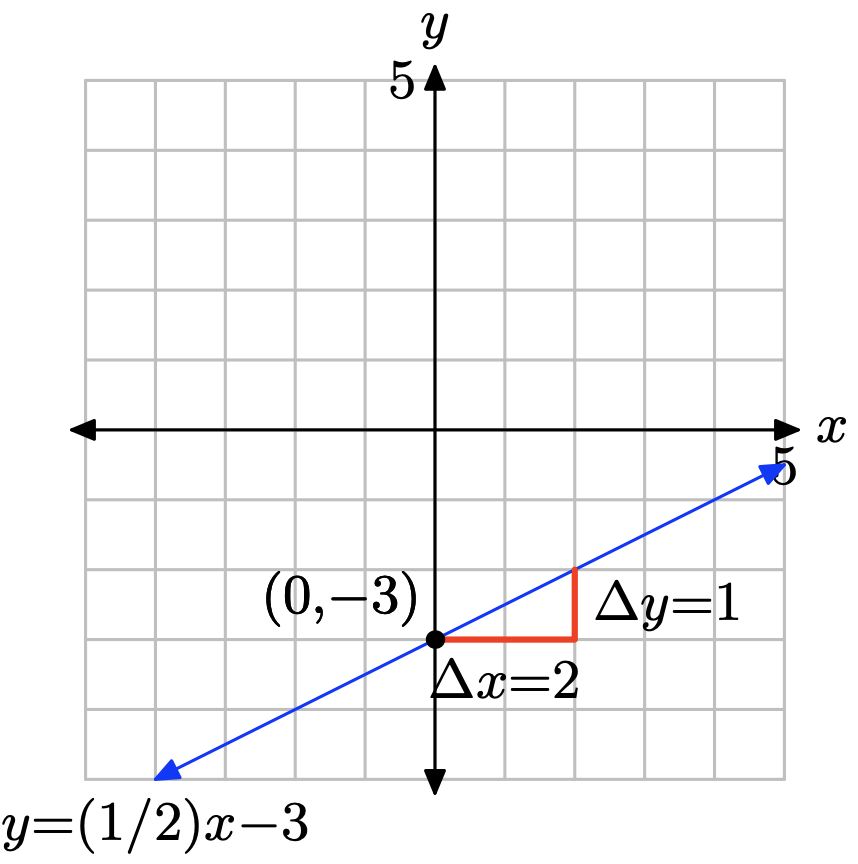
Ejercicio\(\PageIndex{8}\)

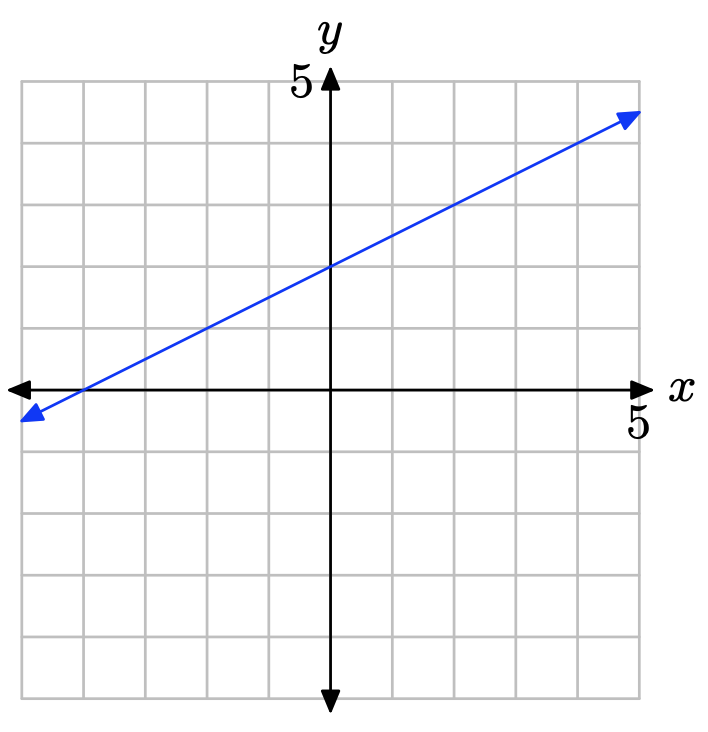
Ejercicio\(\PageIndex{9}\)

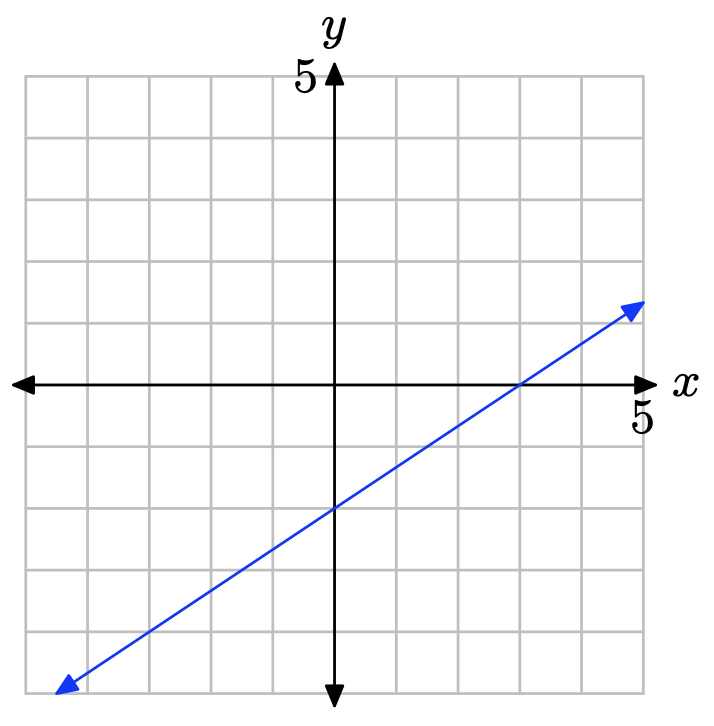
Contestar

La pendiente se encuentra dividiendo la subida por la carrera (ver figura). De ahí que la pendiente sea 2/3. La intercepción y se encuentra anotando dónde la gráfica de la línea cruza el eje y (ver figura), en este caso, en (0, −2). Por lo tanto, m = 2/3 y b = −2, por lo que la ecuación de la línea en forma de intercepción de pendiente es

\[y = mx + b \quad \text{or} \quad y = \frac{2}{3}x − 2\]

Ejercicio\(\PageIndex{10}\)

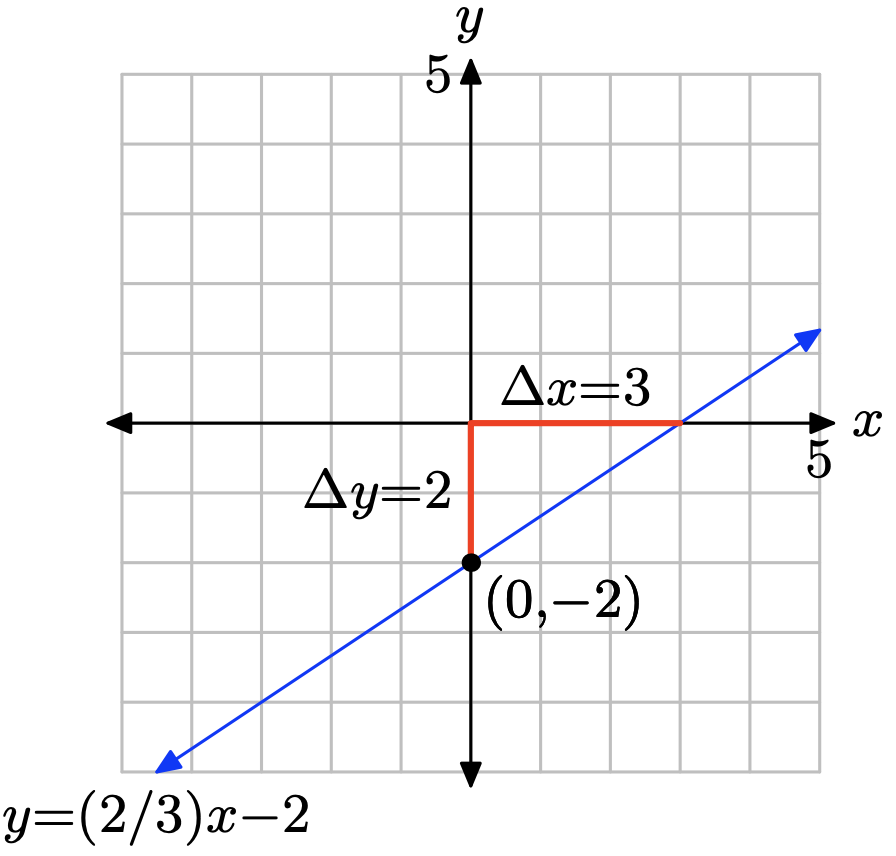
Ejercicio\(\PageIndex{11}\)

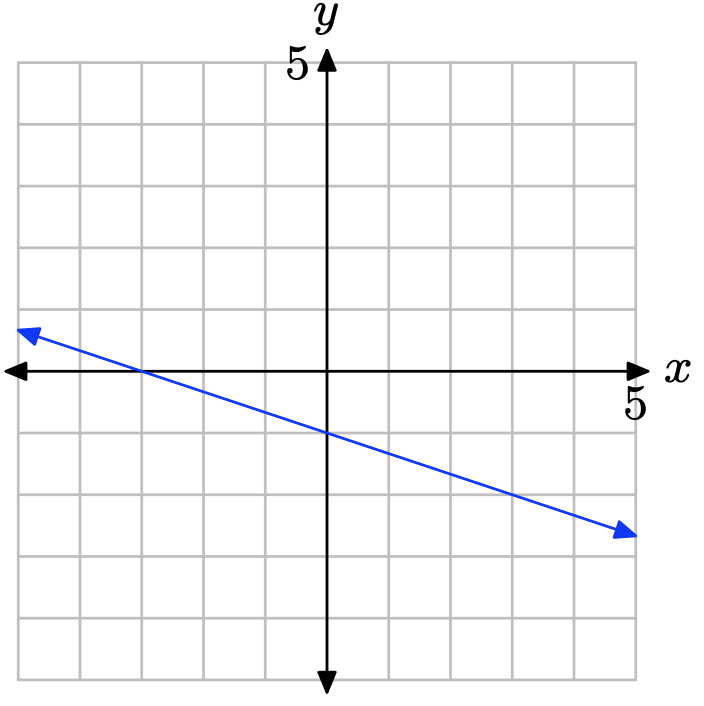
Contestar

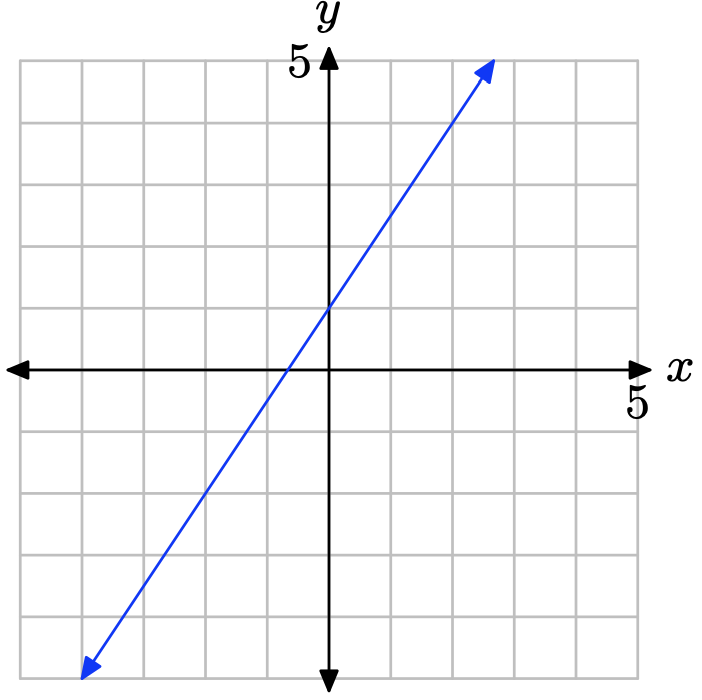
La pendiente se encuentra dividiendo la subida por la carrera (ver figura). De ahí que la pendiente sea 3/2. La intercepción y se encuentra señalando dónde la gráfica de la línea cruza el eje y (ver figura), en este caso, en (0, 1). Por lo tanto, m = 3/2 y b = 1, por lo que la ecuación de la línea en forma de intercepción de pendiente es

\[y = mx + b \quad \text{or} \quad y = \frac{3}{2}x + 1\]

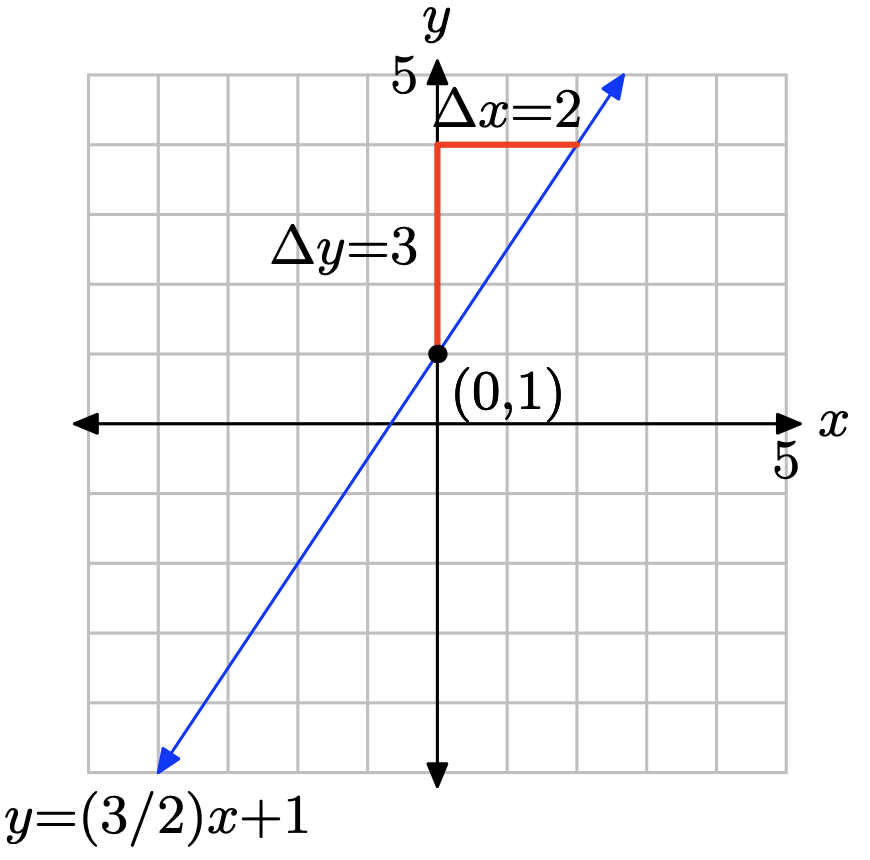
Ejercicio\(\PageIndex{12}\)

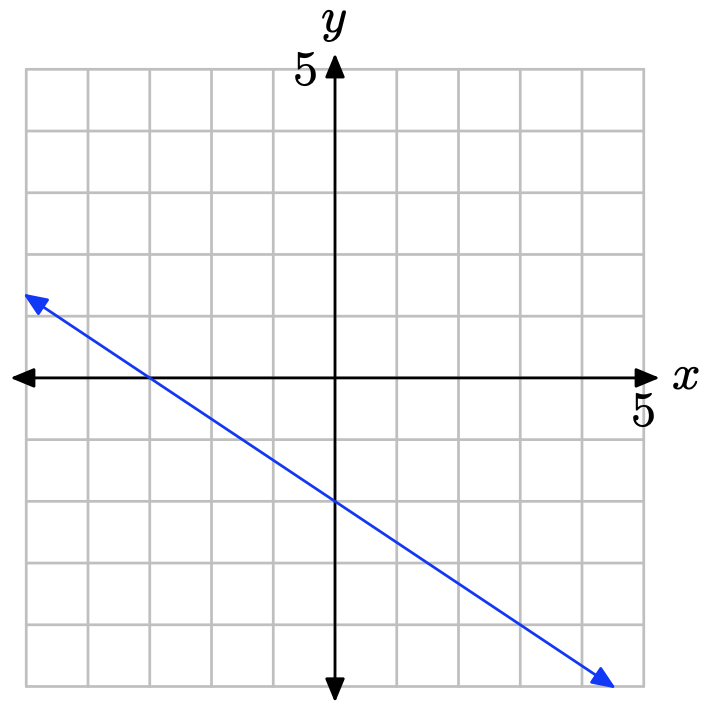
Ejercicio\(\PageIndex{13}\)

Kate gana $39, 000 al año y recibe un aumento de $1000 cada año. Ya que su salario depende del año, deje que el tiempo t represente el año, siendo t = 0 el año presente, y colóquelo a lo largo del eje horizontal. Que el salario S, en miles de dólares, sea la variable dependiente y colóquelo a lo largo del eje vertical. Supondremos que la tasa de incremento de $1000 anuales es constante, por lo que podemos modelar esta situación con una función lineal.

a) En una hoja de papel cuadriculado, hacer una gráfica para modelar esta situación, llegando hasta t = 10 años.

b) ¿Qué es la S-intercepción?

c) ¿Cuál es la pendiente?

d) Supongamos que queremos predecir el salario de Kate en 20 años o 30 años. No podemos usar el modelo gráfico porque solo muestra hasta t = 10 años. Podríamos dibujar una gráfica más grande, pero ¿y si entonces quisiéramos predecir 50 años en el futuro? El punto es que un modelo gráfico se limita a lo que muestra. Un modelo de función algebraica, sin embargo, se puede utilizar para predecir para cualquier año! Encuentra la forma pendiente-intercepción de la función lineal que modela el salario de Kate.

e) Escribir la función usando notación de función, lo que enfatiza que S es una función de t.

f) Ahora use el modelo algebraico de (e) para predecir el salario de Kate a los 10 años, 20 años, 30 años y 50 años en el futuro.

g) Calcular S (40).

h) En una oración completa, explicar lo que significa el valor de S (40) de la parte (g) en el contexto del problema.

Contestar

a)

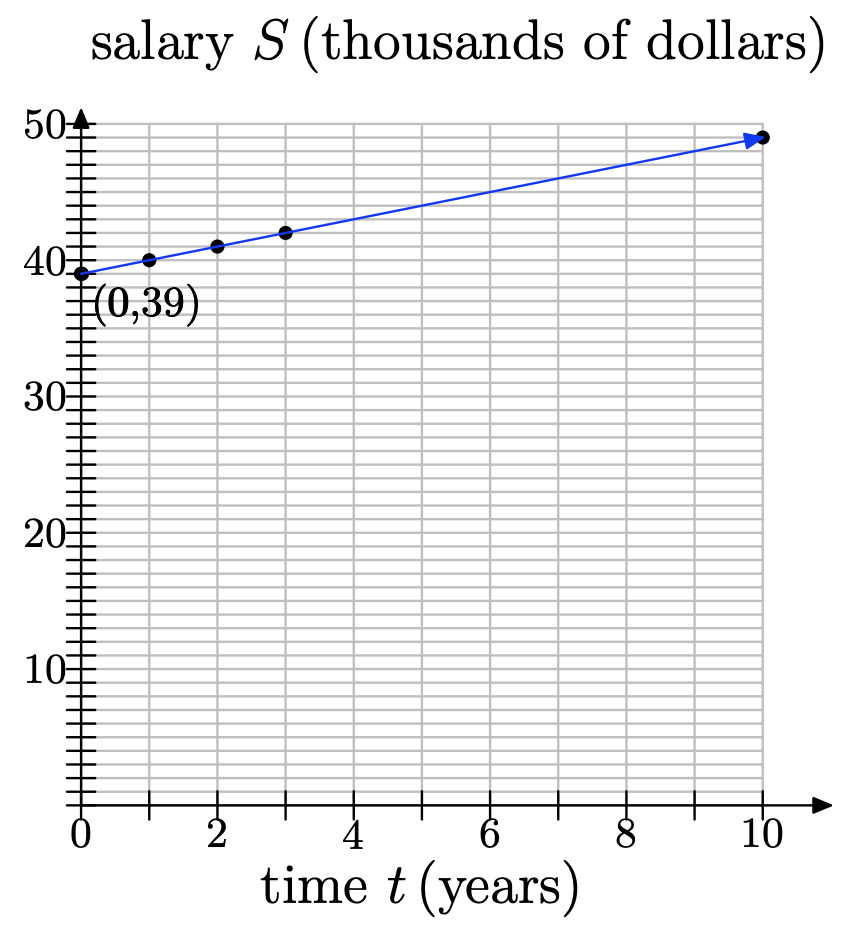
b) A t = 0 (año presente), su salario es de $39, 000. Ya que S está en miles de dólares, S = 39 cuando t = 0. Entonces la S-intercepción es (0, 39).

c) El incremento en el salario de Kate es de $1, 000 anuales, pero S es en miles de dólares, por lo que la tasa de incremento en S es de 1. Es decir, la pendiente es 1.

d) Usando la forma pendiente-intercepción, obtenemos S = t + 39.

e) S (t) = t + 39.

f)

• Para encontrar el salario de Kate en 10 años, cómpule S (10) = 10 + 39 = 49, lo que significa que estará ganando 49, 000 dólares anuales.
• Para encontrar el salario de Kate en 20 años, cómpule S (20) = 20 + 39 = 59, lo que significa que estará ganando 59, 000 dólares anuales.
• Para encontrar el salario de Kate en 30 años, cómpule S (30) = 30 + 39 = 69, lo que significa que estará ganando $69, 000 anuales.
• Para encontrar el salario de Kate en 50 años, cómpule S (50) = 50 + 39 = 89, lo que significa que estará ganando $89, 000 anuales.

g) S (40) = 40 + 39 = 79. h) Si la tasa actual de incremento continúa, en 40 años el salario de Kate será de $79, 000.

Ejercicio\(\PageIndex{14}\)

Por cada DVD que vende Blue Charles Co. obtienen ganancias 5c. El beneficio depende del número de DVD's vendidos, así que dejemos que el número vendido n sea la variable independiente y el beneficio P, en $, sea la variable dependiente.

a) En una hoja de papel cuadriculado, hacer una gráfica para modelar esta situación, llegando hasta n = 15.

b) Utilizar la gráfica para predecir el beneficio si se venden n = 10 DVD's.

c) El modelo gráfico se limita a predecir valores de n en su gráfica. Cualquier valor mayor de n requiere una gráfica más grande, o un tipo diferente de modelo. Para comenzar a encontrar un modelo algebraico, identifique la intercepción P de la gráfica.

d) ¿Cuál es la pendiente de la línea en su modelo gráfico?

e) Encontrar una forma pendiente-intersección de una función lineal que modele las ventas de Blue Charles Co.

f) Escribir la función usando notación de función.

g) Explicar por qué este modelo no tiene la misma limitación que el modelo gráfico.

h) Encuentra P (100), P (1000) y P (10000).

i) En oraciones completas, explique qué significan los valores de P (100), P (1000) y P (10000) en el contexto del problema.

Ejercicio\(\PageIndex{15}\)

Enrique tenía mil dólares ahorrados cuando comenzó a guardar 25 dólares adicionales cada mes.

a) Que t represente el tiempo, en meses, y S representa el ahorro de Enrique, en $. Identificar cuáles deben ser las variables independientes y dependientes.

b) Para comenzar a encontrar una función lineal para modelar esta situación, identificar la intercepción S y la pendiente.

c) Encontrar una forma de pendiente-intersección de una función lineal para modelar los ahorros de Enrique a lo largo del tiempo.

d) Escribir la función lineal en notación de funciones.

e) Utilizar el modelo de función para predecir cuánto habrá en sus ahorros en un año.

f) Utilizar el modelo de función para predecir cuándo tendrá $2000 ahorrados.

g) Graficar la función en un sistema de coordenadas.

h) Al mismo tiempo, Anne-Marie también comienza a ahorrar 25 dólares mensuales, pero comienza con 1200 dólares ya en sus ahorros. Haga un modelo gráfico de su situación y colóquelo en el mismo sistema de coordenadas que el modelo gráfico para el ahorro de Enrique. Etiquételo de manera apropiada.

i) ¿Cómo se comparan las líneas entre sí? Di algo de sus pendientes.

j) Encontrar una forma pendiente-intersección de una función lineal que modele el ahorro de Anne-Marie. Usa las mismas variables que hiciste para el modelo de Enrique.

k) Escribir la función usando notación de función.

l) Demostrar que las gráficas de las dos funciones son líneas paralelas.

m) Para Anne-Marie, mirando las gráficas, ¿crees que le tomará más tiempo o menos tiempo que Enrique ahorrar hasta 2000 dólares?

n) Utilice el modelo de función lineal para Anne-Marie para predecir cuánto tiempo le llevará ahorrar $2000. ¿Esto concuerda con su expectativa de (m)?

Contestar

a) t debe ser la variable independiente y S debe ser la variable dependiente.

b) S-intercepción = (0, 1000); pendiente = 25

c) S = 25t + 1000

d) S (t) = 25t + 1000

e) S (12) = 25 (12) + 1000 = 1300

f) Establecer S=2000 y resolver para t. 2000 = 25t + 1000 1000 = 25t 40 = t Así que le tomará 40 meses llegar a los 2000 dólares.

h)

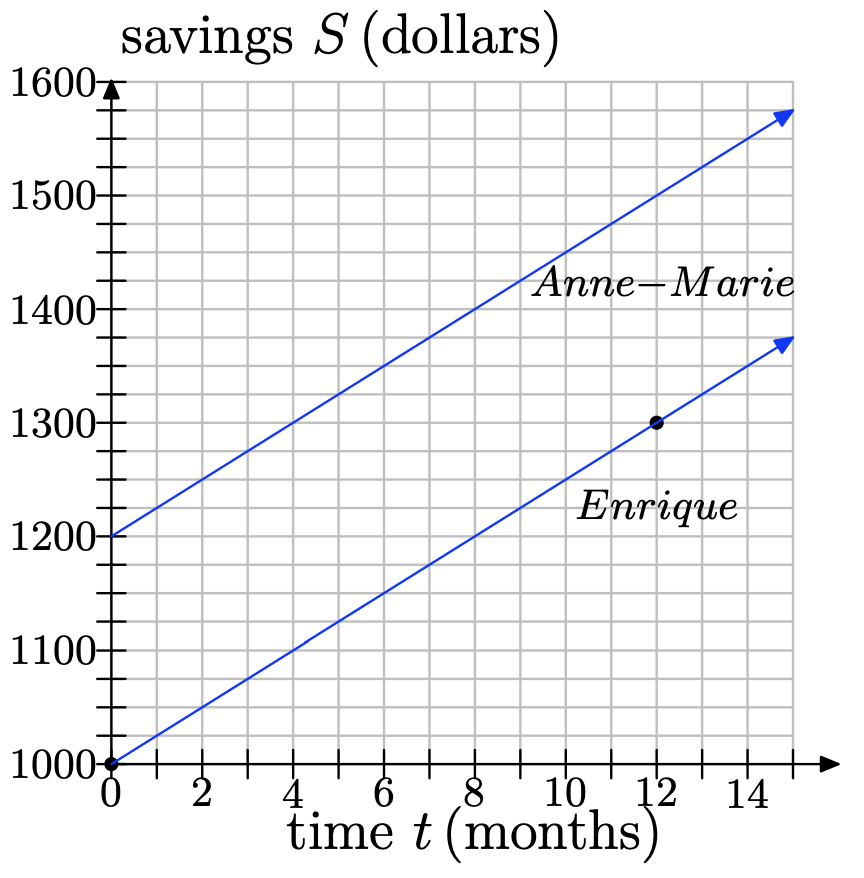
i) Las líneas tienen la misma pendiente; son paralelas.

j) S = 25t + 1200

k) S (t) = 25t + 1200

l) Son líneas porque están en la forma y = mx + b. Son paralelos porque sus pendientes son iguales (ambos son 25).

m) Debería llevarle menos tiempo porque su gráfica está por encima de la gráfica de Enrique. Esto tiene sentido intuitivamente ya que ella comenzó con más dinero que él.

n) Establecer S=2000 y resolver para t. 2000 = 25t + 1200 800 = 25t 32 = t Así que le tomará 32 meses llegar a los 2000 dólares. Esto concuerda con nuestra expectativa de (m): Le toma menos tiempo que Enrique

Ejercicio\(\PageIndex{16}\)

José se encuentra inicialmente a 400 metros de la parada de autobús. Comienza a correr hacia la parada a una velocidad de 5 metros por segundo.

a) Expresar la distancia d de José desde la parada de autobús en función del tiempo t.

b) Utilice su modelo para determinar la distancia de José a la parada de autobús después de un minuto.

c) Usa tu modelo para determinar el tiempo que tardará José en llegar a la parada del autobús.

Ejercicio\(\PageIndex{17}\)

Una bola se deja caer del reposo sobre la superficie de la tierra. A medida que cae, su velocidad aumenta a una velocidad constante de 32 pies por segundo por segundo.

a) Expresar la velocidad v de la pelota en función del tiempo t.

b) Usa tu modelo para determinar la velocidad de la pelota después de 5 segundos.

c) Usa tu modelo para determinar el tiempo que tardará la pelota en alcanzar una velocidad de 256 pies por segundo.

Contestar

a) Haremos una gráfica “aproximada” de velocidad v versus tiempo t. La velocidad depende del tiempo, por lo que colocamos la velocidad en el eje vertical y el tiempo en el eje horizontal en la figura que sigue. La velocidad inicial es de 0 pies/s, lo que nos da el v-intercept en P (0, 0). La velocidad a la que aumenta la velocidad (aceleración) es constante y será la pendiente de la línea; es decir, la pendiente de la línea es m = 32 pies/s2 (32 pies por segundo por segundo).

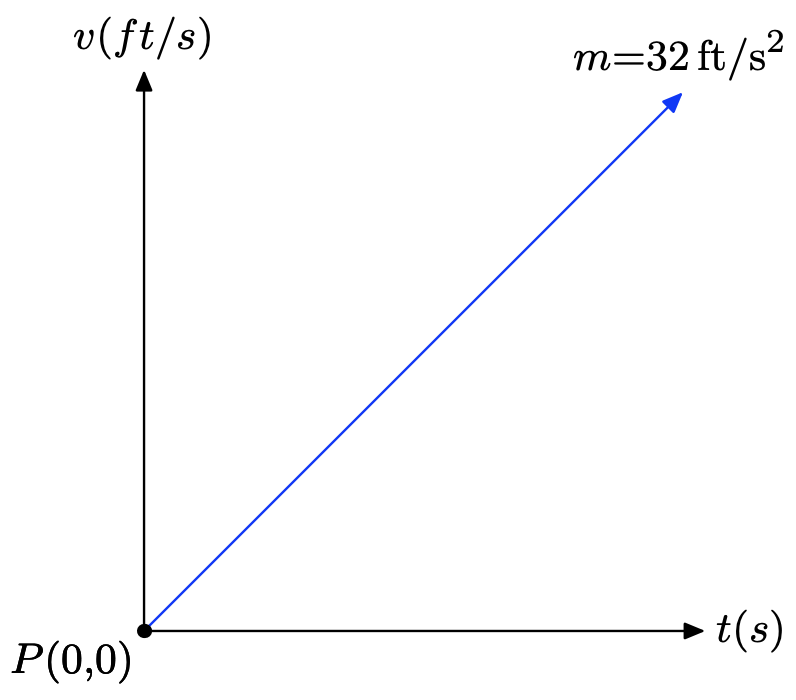
Debido a que conocemos la pendiente e intercepción de la línea, podemos usar la forma de intercepción de pendiente y = mx + b y sustituto m = 32 y b = 0 para obtener

\[y = mx + b\\ y = 32x + 0 \\y = 32x\]

Sin embargo, estamos usando v y t en lugar de y y x, por lo que reemplazamos estos en la última fórmula para obtener

\[v = 32t\]

o usando notación de función,

\[v(t) = 32t\]
b) Para encontrar la velocidad del balón después de 5 segundos, sustituya t = 5 en la ecuación desarrollada en la parte anterior.

\[v(t) = 32t \\ v(5) = 32(5) \\ v(5) = 160\]

De ahí que la velocidad de la pelota después de 5 segundos sea de 160 pies por segundo.

c) Para encontrar el tiempo que tarda la pelota en llegar a 256 pies por segundo, debemos encontrar t para que v (t) = 256.

\[v(t) = 256\\ 32t = 256\\ t = 8\]

De esta manera, la pelota tarda 8 segundos en alcanzar una velocidad de 256 pies por segundo.

Ejercicio\(\PageIndex{18}\)

Se lanza una pelota al aire con una velocidad inicial de 200 metros por segundo. Inmediatamente comienza a perder velocidad a una velocidad de 9.5 metros por segundo por segundo.

a) Expresar la velocidad v de la pelota en función del tiempo t.

b) Usa tu modelo para determinar la velocidad de la pelota después de 5 segundos.

c) Usa tu modelo para determinar el tiempo que tardará la pelota en alcanzar su altura máxima.

En Ejercicios\(\PageIndex{19}\) -\(\PageIndex{24}\), se da una función lineal en forma estándar Ax + By = C. En cada caso, resuelve la ecuación dada para y, colocando la ecuación en forma pendiente-intercepción. Utilice la pendiente e intercepción para dibujar la gráfica de la ecuación en una hoja de papel cuadriculado.

Ejercicio\(\PageIndex{19}\)

3x − 2 años = 6

Contestar

Colocar 3x − 2y = 6 en forma pendiente-intercepción. Primero resta 3x de ambos lados de la ecuación, luego divide ambos lados de la ecuación resultante por −2.

\[\begin{array} {lll} 3x − 2y & = &6 −2 \\ y &=& −3x + 6 \\ y &= &\frac{3}{2}x − 3 \end{array}\]

Compara y = (3/2) x − 3 con y = mx + b para ver que la pendiente es m = 3/2 y la coordenada y de la intersección y es b = −3. Por lo tanto, la intercepción y será el punto (0, −3). Trazar el punto P (0, −3). Para obtener una línea de pendiente m = 3/2, comience en el punto P (0, −3), luego mueva 3 unidades hacia arriba y 2 unidades a la derecha, llegando al punto Q (2, 0), como se muestra en la siguiente figura. La línea que pasa por los puntos P y Q es la línea requerida.

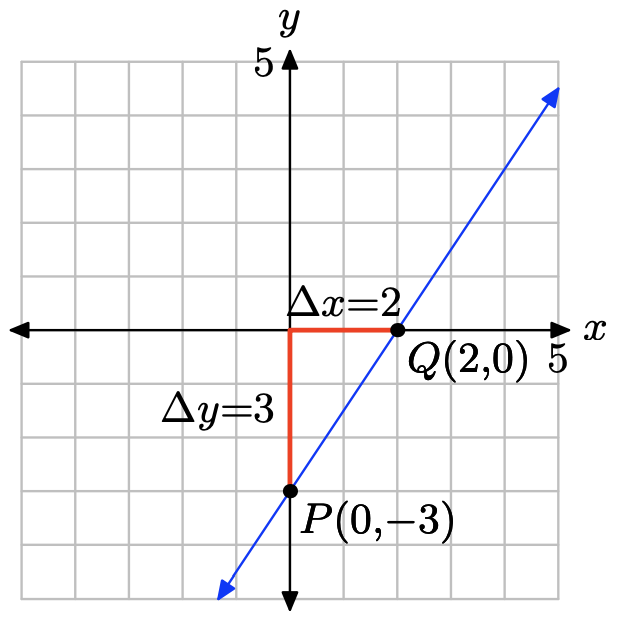
Ejercicio\(\PageIndex{20}\)

3x + 5 años = 15

Ejercicio\(\PageIndex{21}\)

3x + 2 años = 6

Contestar

Coloca 3x + 2y = 6 en forma pendiente-intercepción. Primero resta 3x de ambos lados de la ecuación, luego divide ambos lados de la ecuación resultante por 2.

\[\begin{array}{lll} 3x + 2y & =& 6 \\ 2y &=& −3x + 6 \\ y &=& −\frac{3}{2} x + 3 \end{array}\]

Compara y = (−3/2) x + 3 con y = mx + b para ver que la pendiente es m = −3/2 y la coordenada y de la intersección y es b = 3. Por lo tanto, la intercepción y será el punto (0, 3). Trazar el punto P (0, 3). Para obtener una línea de pendiente m = −3/2, iniciar en el punto P (0, 3), luego mover 3 unidades hacia abajo y 2 unidades a la derecha, llegando al punto Q (2, 0), como se muestra en la siguiente figura. La línea que pasa por los puntos P y Q es la línea requerida.

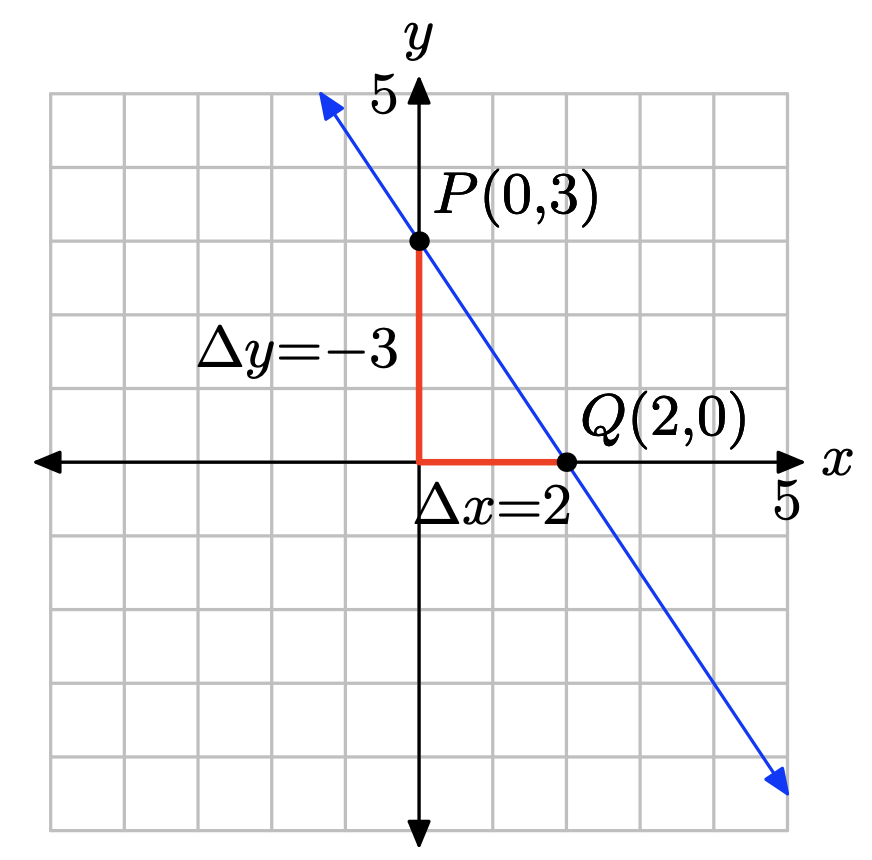
Ejercicio\(\PageIndex{22}\)

4x − y = 4

Ejercicio\(\PageIndex{23}\)

x − 3y = −3

Contestar

Coloque x − 3y = −3 en forma de pendiente-intercepción. Primero resta x de ambos lados de la ecuación, luego divide ambos lados de la ecuación resultante por −3.

\[\begin{array} {lll} x − 3y &=& −3 \\ −3y &=& −x − 3 \\ y &=& \frac{1}{3} x + 1 \end{array}\]

Compara y = (1/3) x + 1 con y = mx + b para ver que la pendiente es m = 1/3 y la coordenada y de la intercepción y es b = 1. Por lo tanto, la intercepción y será el punto (0, 1). Trazar el punto P (0, 1). Para obtener una línea de pendiente m = 1/3, iniciar en el punto P (0, 1), luego mover 1 unidad hacia arriba y 3 unidades a la derecha, llegando al punto Q (3, 2), como se muestra en la siguiente figura. La línea que pasa por los puntos P y Q es la línea requerida.

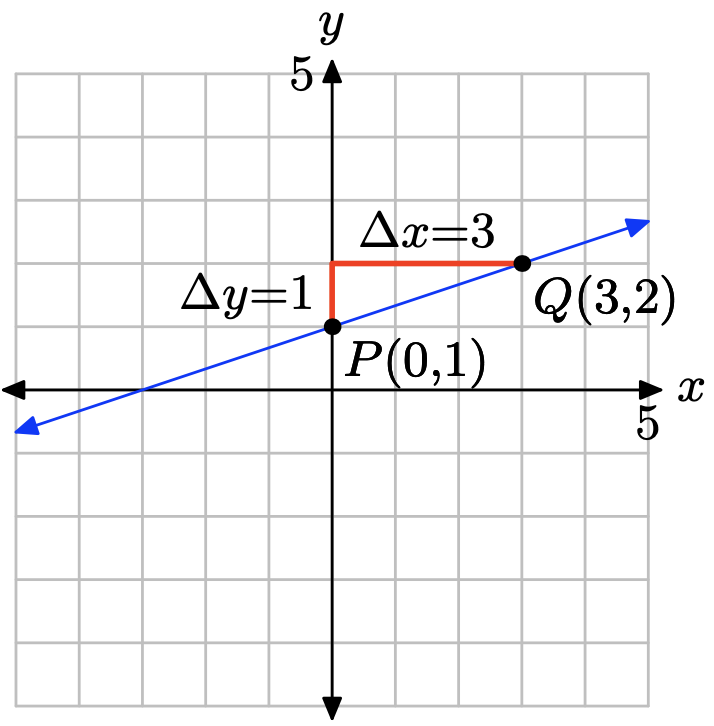
Ejercicio\(\PageIndex{24}\)

x + 4y = −4

En Ejercicios\(\PageIndex{25}\) -\(\PageIndex{30}\), se le da una función lineal en forma de pendiente-intercepción. Coloque la función lineal en forma estándar Ax+ By = C, donde A, B y C son números enteros y A > 0.

Ejercicio\(\PageIndex{25}\)

\(y = \frac{2}{3}x − 5\)

Contestar

Comienza con\[y =\frac{ 2}{ 3} x − 5\] y multiplica ambos lados por 3 para despejar las fracciones.

\[3y = 2x − 15\]

Finalmente, restar 3y de ambos lados de la ecuación, luego sumar 15 a ambos lados de la ecuación para obtener\[15 = 2x − 3y\], o equivalentemente,\[2x − 3y = 15\].

Ejercicio\(\PageIndex{26}\)

\(y = \frac{5}{6}x + 1\)

Ejercicio\(\PageIndex{27}\)

\(y = −\frac{4}{ 5} x + 3\)

Contestar

Comienza con\[y = −\frac{4}{5} x + 3\] y multiplica ambos lados por 5 para despejar las fracciones. \[5y = −4x + 15\]

Finalmente, agregue 4x a ambos lados de la ecuación.

\[4x + 5y = 15\]

Ejercicio\(\PageIndex{28}\)

\(y = −\frac{3}{7} x + 2\)

Ejercicio\(\PageIndex{29}\)

\(y = −\frac{2}{5} x − 3\)

Contestar

Comienza con\[y = −\frac{2}{5} x − 3\] y multiplica ambos lados por 5 para despejar las fracciones.

\[5y = −2x − 15\]

Por último, agregue 2x a ambos lados de la ecuación.

\[2x + 5y = −15\]

Ejercicio\(\PageIndex{30}\)

\(y = −\frac{1}{4}x + 2\)

Ejercicio\(\PageIndex{31}\)

¿Cuál es la intercepción x de la línea?

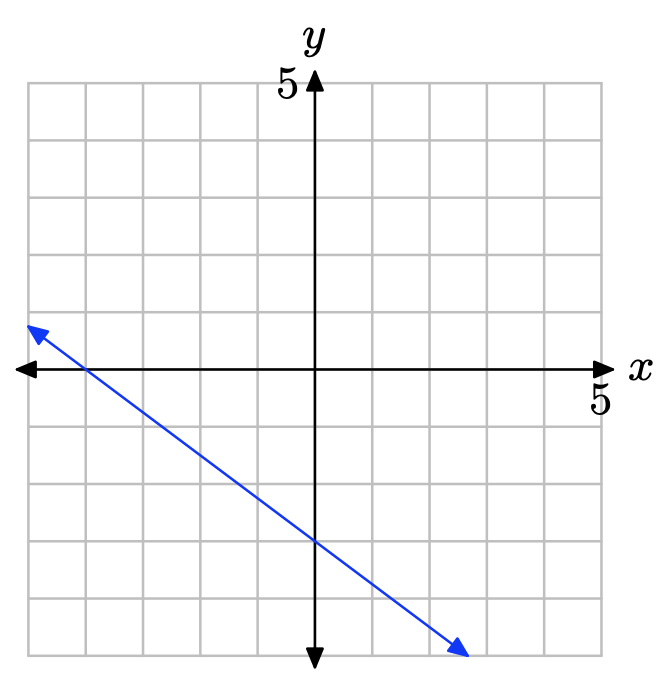
Contestar

La intercepción x es la ubicación donde la línea cruza el eje x.

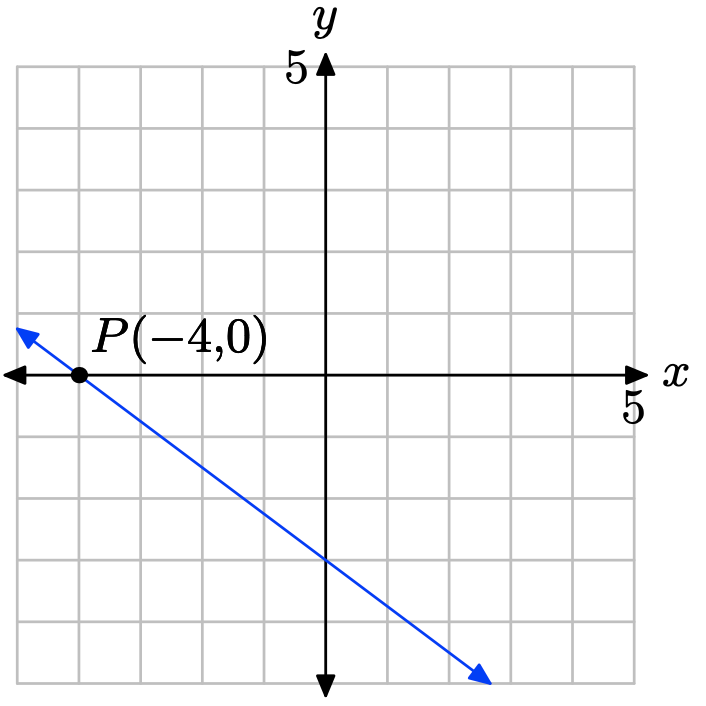
Por lo tanto, la intercepción x es (−4, 0).

Ejercicio\(\PageIndex{32}\)

¿Cuál es la intercepción y de la línea?

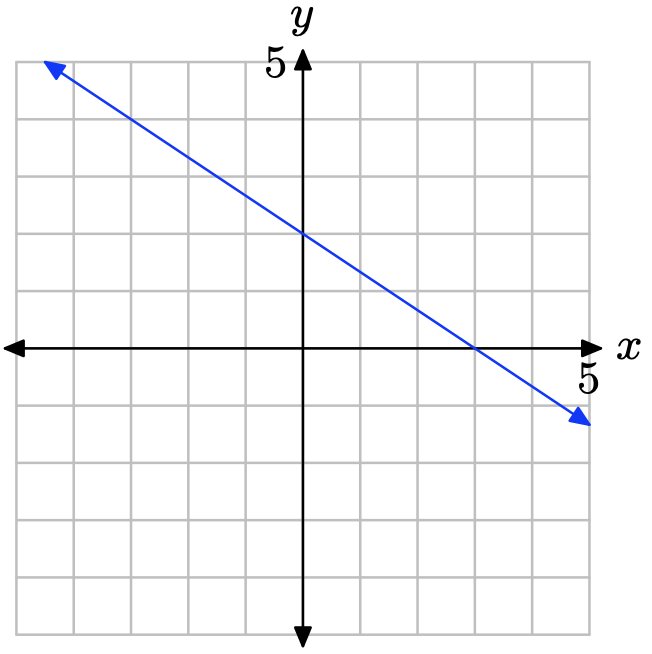
Ejercicio\(\PageIndex{33}\)

¿Cuál es la intercepción y de la línea?

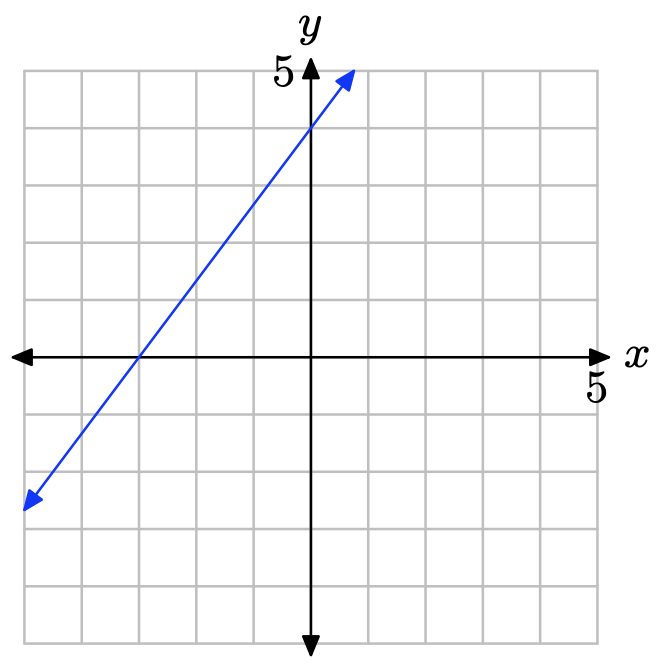
Contestar

La intercepción y es la ubicación donde la línea cruza el eje y.

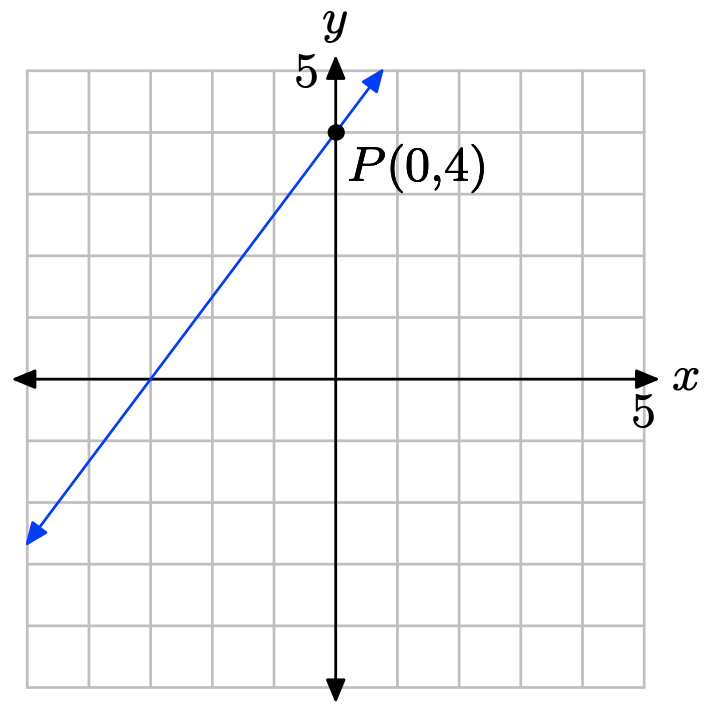
Por lo tanto, la intercepción y es (0, 4).

Ejercicio\(\PageIndex{34}\)

¿Cuál es la intercepción x de la línea?

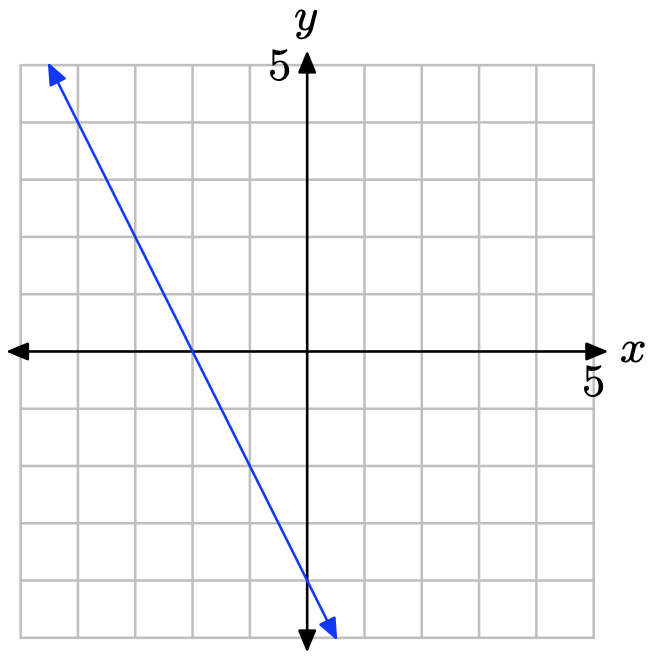
En Ejercicios\(\PageIndex{35}\) -\(\PageIndex{40}\), encuentra las intercepciones x e y de la función lineal que se da en forma estándar. Utilice las intercepciones para trazar la gráfica de la línea en una hoja de papel cuadriculado.

Ejercicio\(\PageIndex{35}\)

3x − 2 años = 6

Contestar

Establezca x = 0 en 3x − 2y = 6 para obtener −2y = 6 o y = −3. La intercepción y es (0, −3). Establecer y = 0 en 3x − 2y = 6 para obtener 3x = 6 o x = 2. La intercepción x es (2, 0). Trazar las intercepciones. La línea a través de las intercepciones es la línea requerida.

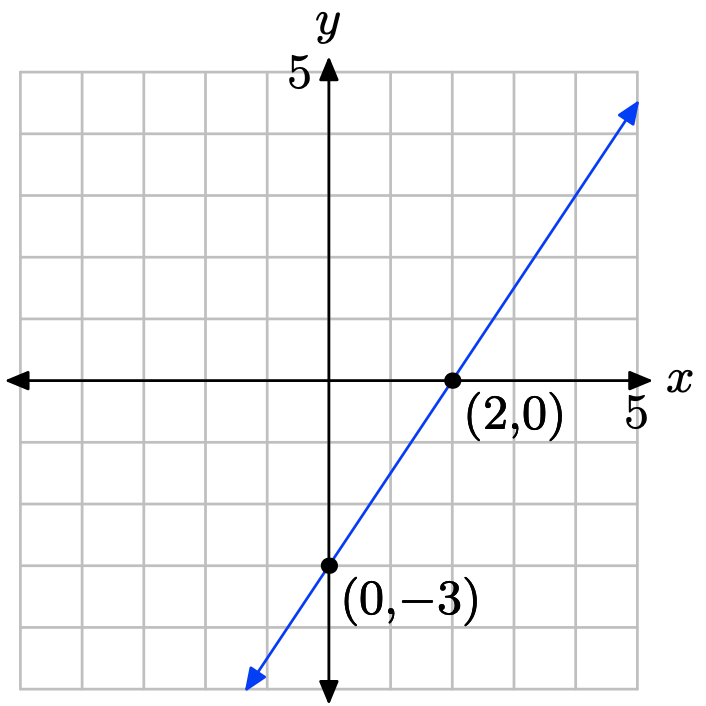
Ejercicio\(\PageIndex{36}\)

4x + 5 años = 20

Ejercicio\(\PageIndex{37}\)

x − 2y = −2

Contestar

Establezca x = 0 en x−2y = −2 para obtener −2y = −2 o y = 1. La intercepción y es (0, 1). Establezca y = 0 en x − 2y = −2 para obtener x = −2. La intercepción x es (−2, 0). Trazar las intercepciones. La línea a través de las intercepciones es la línea requerida.

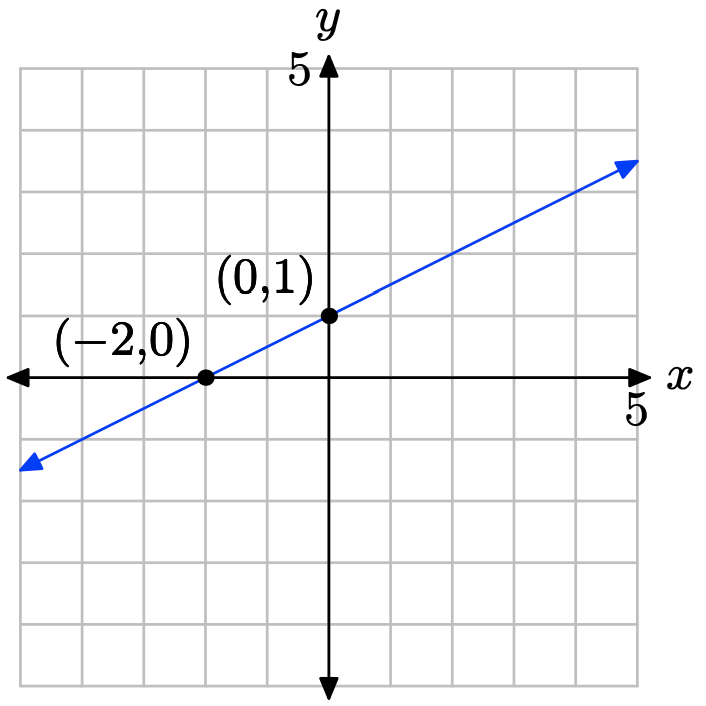
Ejercicio\(\PageIndex{38}\)

6x + 5 años = 30

Ejercicio\(\PageIndex{39}\)

2x − y = 4

Contestar

Establezca x = 0 en 2x − y = 4 para obtener −y = 4 o y = −4. La intercepción y es (0, −4). Establecer y = 0 en 2x − y = 4 para obtener 2x = 4. La intercepción x es (2, 0). Trazar las intercepciones. La línea a través de las intercepciones es la línea requerida.

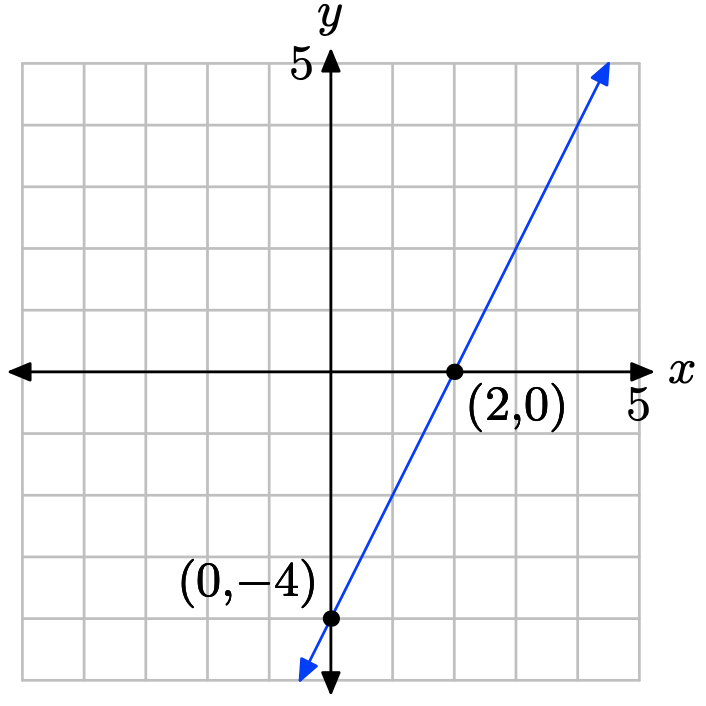
Ejercicio\(\PageIndex{40}\)

8x − 3 años = 24

Ejercicio\(\PageIndex{41}\)

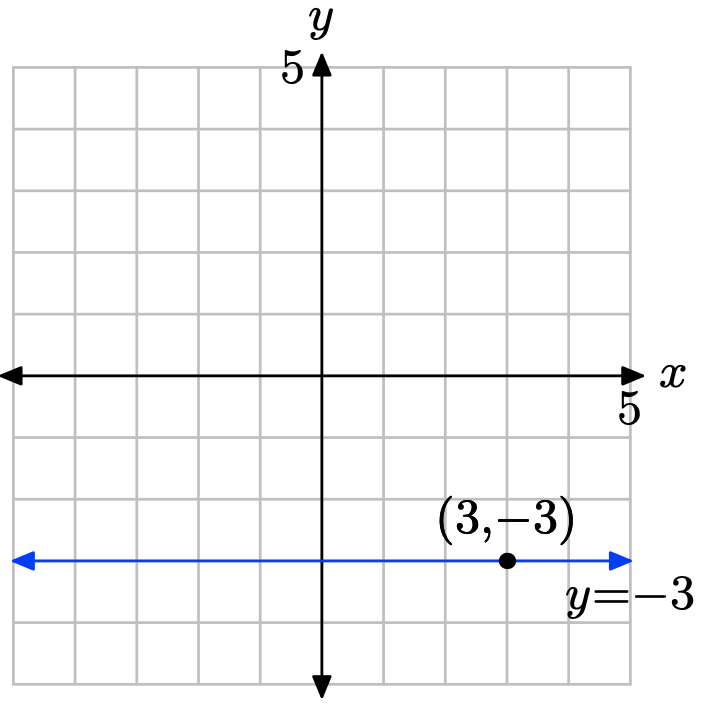
Dibuje la gráfica de la línea horizontal que pasa por el punto (3, −3). Etiquete la línea con su ecuación.

Contestar

Cada línea horizontal tiene una ecuación de la forma y = d. Como esta línea debe pasar por el punto (3, −3), se deduce que la ecuación es y = −3.

Ejercicio\(\PageIndex{42}\)

Dibuje la gráfica de la línea horizontal que pasa por el punto (−9, 9). Etiquete la línea con su ecuación.

Ejercicio\(\PageIndex{43}\)

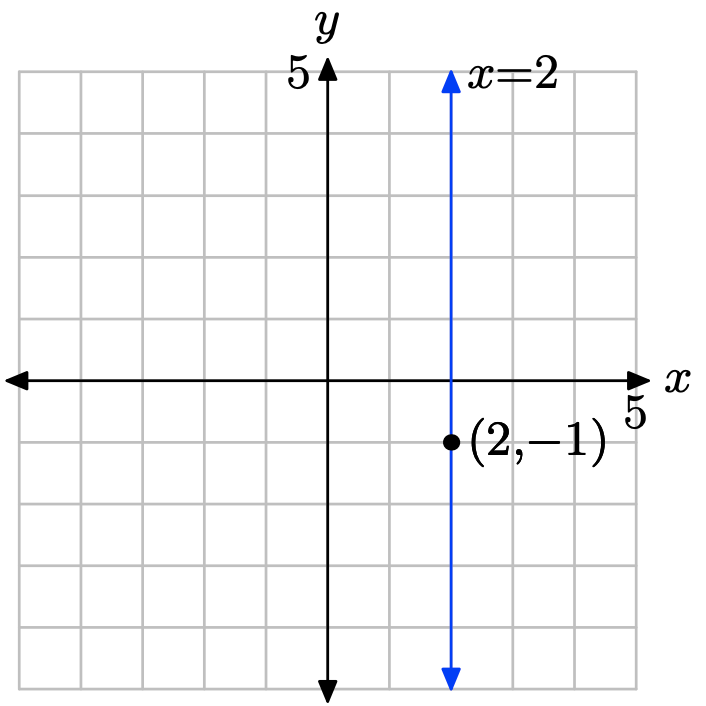
Dibuje el gráfico de la línea vertical que pasa por el punto (2, −1). Etiquete la línea con su ecuación.

Contestar

Cada línea vertical tiene una ecuación de la forma x = c. Como esta línea debe pasar por el punto (2, −1), se deduce que la ecuación es x = 2.

Ejercicio\(\PageIndex{44}\)

Dibuje la gráfica de la línea vertical que pasa por el punto (15, −16). Etiquete la línea con su ecuación.

En Ejercicios\(\PageIndex{45}\) -\(\PageIndex{48}\), encuentra el dominio y el rango de la función lineal dada.

Ejercicio\(\PageIndex{45}\)

f (x) = −37x − 86

Contestar

El dominio de cada función lineal es\((−\infty,\infty)\). Dado que la pendiente de la gráfica de f es\(−37 \neq 0\), el rango también lo es\((−\infty,\infty)\).

Ejercicio\(\PageIndex{46}\)

f (x) = 98

Ejercicio\(\PageIndex{47}\)

f (x) = −12

Contestar

El dominio de cada función lineal es\((−\infty,\infty)\). Dado que f (x) = −12 para cada x, el rango es {−12}.

Ejercicio\(\PageIndex{48}\)

f (x) = −2x + 8

3.4 Ejercicios

En Ejercicios\(\PageIndex{1}\) -\(\PageIndex{4}\), realizar cada una de las siguientes tareas.

i. Dibujar la línea sobre una hoja de papel cuadriculado con la pendiente dada m que pasa por el punto dado\((x_{0}, y_{0})\).

ii. Estimar la intercepción y de la línea.

iii. Utilice la forma punto-pendiente para determinar la ecuación de la línea. Coloque su respuesta en forma de pendiente-intercepción resolviendo para y. Compare el valor exacto de la intersección y con la aproximación encontrada en la parte (ii).

Ejercicio\(\PageIndex{1}\)

m = 2/3 y\((x_{0}, y_{0}) = (−1, −1)\)

Contestar

Trazar el punto P (−1, −1). Para dibujar una línea por P con pendiente m = 2/3, comience en el punto P, luego mueva hacia arriba 2 unidades y derecha 3 unidades hasta el punto Q (2, 1). La línea que pasa por los puntos P y Q es la línea requerida.

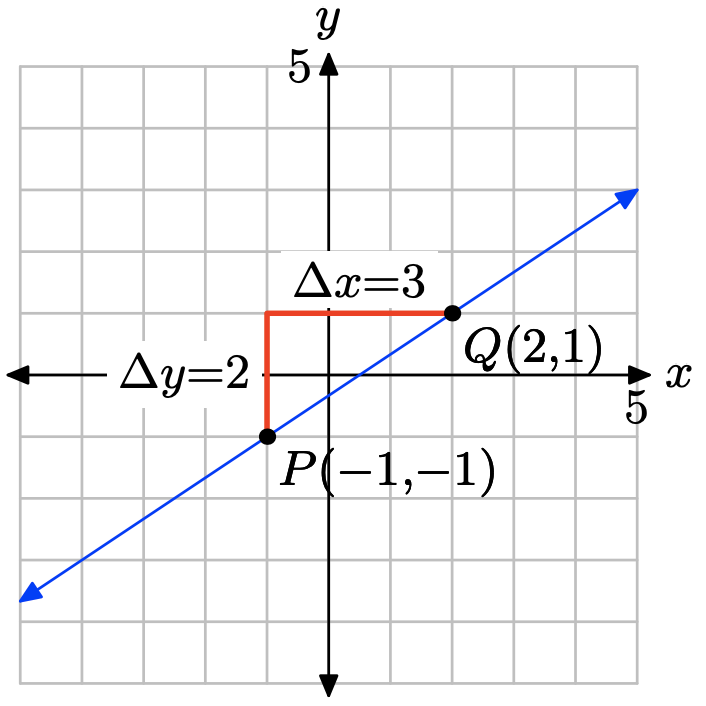
A partir de la gráfica anterior, estimaríamos la intercepción y como (0, −0.3). Para encontrar la ecuación de la línea, sustituya m = 2/3 y\((x_{0}, y_{0}) = (−1, −1)\) en la forma punto-pendiente de la línea.

\[y − y0 = m(x − x0) \\ y − (−1) = \frac{2}{ 3} (x − (−1))\\ y + 1 = \frac{2}{ 3} (x + 1)\]

Para colocar esto en forma pendiente-intercepción y = mx + b, resolver para y.

\[y = \frac{2}{ 3} x + \frac{2}{ 3} − 1\\ y = \frac{2}{ 3} x + \frac{2}{ 3} − \frac{3}{ 3} \\ y = \frac{2}{ 3} x − \frac{1}{ 3}\]

Al comparar este resultado con y = mx + b, vemos que la coordenada y exacta del yintercepto es b = −1/3, lo que está muy de acuerdo con la aproximación −0.3 encontrada anteriormente.

Ejercicio\(\PageIndex{2}\)

m = -2/3 y\((x_{0}, y_{0}) = (1, −1)\)

Ejercicio\(\PageIndex{3}\)

m = -3/4 y\((x_{0}, y_{0}) = (−2, 3)\)

Contestar

Trazar el punto P (−2, 3). Para dibujar una línea a través de P con pendiente m = −3/4, comience en el punto P, luego baje 3 unidades y derecha 4 unidades hasta el punto Q (2, 0). La línea que pasa por los puntos P y Q es la línea requerida.

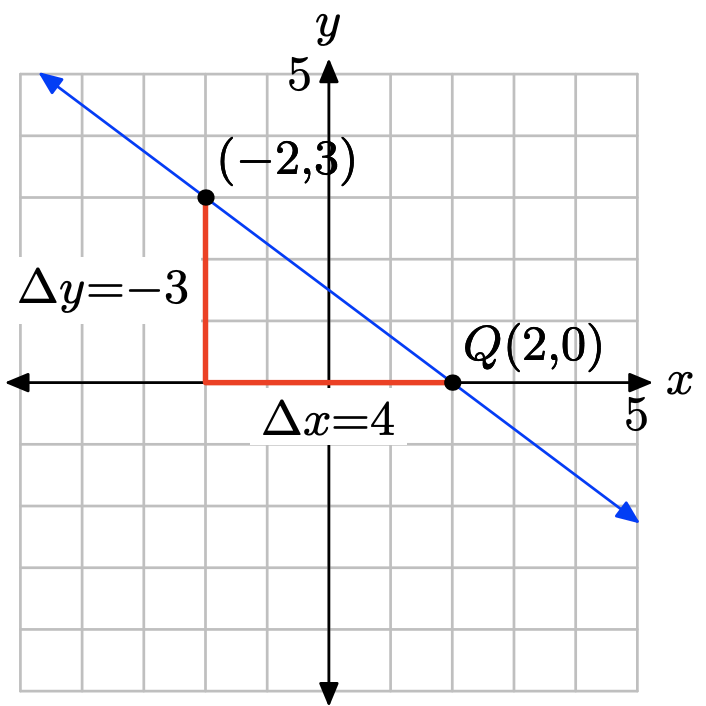
A partir de la gráfica anterior, estimaríamos la intercepción y como (0, 1.5). Para encontrar la ecuación de la línea, sustituya m = −3/4 y\((x_{0}, y_{0}) = (−2, 3)\) en la forma punto-pendiente de la línea.

\[y − y_{0} = m(x − x_{0}) \\ y − 3 = −\frac{3}{ 4} (x − (−2)) \\ y − 3 = −\frac{3}{ 4} (x + 2)\]

Para colocar esto en forma pendiente-intercepción y = mx + b, resolver para y.

\[y = −\frac{3}{ 4} x − \frac{3}{ 2} + 3 \\ y = −\frac{3}{ 4} x − \frac{3}{ 2} + \frac{6}{ 2} \\ y = −\frac{3}{ 4} x + \frac{3}{ 2} \]

Al comparar este resultado con y = mx + b, vemos que la coordenada y exacta de la intersección y es b = 3/2, lo que está muy de acuerdo con la aproximación 1.5 encontrada anteriormente.

Ejercicio\(\PageIndex{4}\)

m = 2/5 y\((x_{0}, y_{0}) = (−3, -2)\)

Ejercicio\(\PageIndex{5}\)

Encuentra la ecuación de la línea en forma pendiente-intercepción que pasa por el punto (1, 3) y tiene una pendiente de 1.

Contestar

Sustituya 1 por m, 1 para\(x_{1}\), y 3 para\(y_{1}\) en la forma de pendiente de punto\(y − y_{1} = m(x − x_{1})\) para obtener y − 3 = 1 (x − 1). Para colocar esto en forma pendiente-intercepción y = mx + b, resolver para y.\[y = x − 1 + 3 \\ y = x + 2\]

Ejercicio\(\PageIndex{6}\)

Encuentra la ecuación de la línea en forma pendiente-intercepción que pasa por el punto (0, 2) y tiene una pendiente de 1/4.

Ejercicio\(\PageIndex{7}\)

Encuentra la ecuación de la línea en forma pendiente-intercepción que pasa por el punto (1, 9) y tiene una pendiente de −2/3.

Contestar

Sustituya −2/3 para m, 1 para x1 y 9 para y1 en la forma de pendiente puntual\(y − y_{1} = m(x − x_{1})\)

para obtener\[y − 9 = −\frac{2}{3} (x − 1)\].

Para colocar esto en forma pendiente-intercepción y = mx + b, resolver para y.

\[y = −\frac{2}{3} x + \frac{2}{3} + 9 \\ y = −\frac{2}{3} x + \frac{2}{3} + \frac{27}{3} \\ y = −\frac{2}{3} x + \frac{29}{3}\]

Ejercicio\(\PageIndex{8}\)

Encuentra la ecuación de la línea en forma pendiente-intercepción que pasa por el punto (1, 9) y tiene una pendiente de −3/4.

En Ejercicios\(\PageIndex{9}\) -\(\PageIndex{12}\), realizar cada una de las siguientes tareas.

i. Establecer un sistema de coordenadas en una hoja de papel cuadriculado y trazar la línea a través de los dos puntos dados.

ii. Utilice la forma punto-pendiente para determinar la ecuación de la línea.

iii. Coloque la ecuación de la línea en forma estándar Ax+By = C, donde A, B y C son números enteros y A > 0. Etiquete la línea en su parcela con este resultado.

Ejercicio\(\PageIndex{9}\)

(−2, −1) y (3, 2)

Contestar

Traza los puntos P (−2, −1) y Q (3, 2) y dibuja una línea a través de ellos.

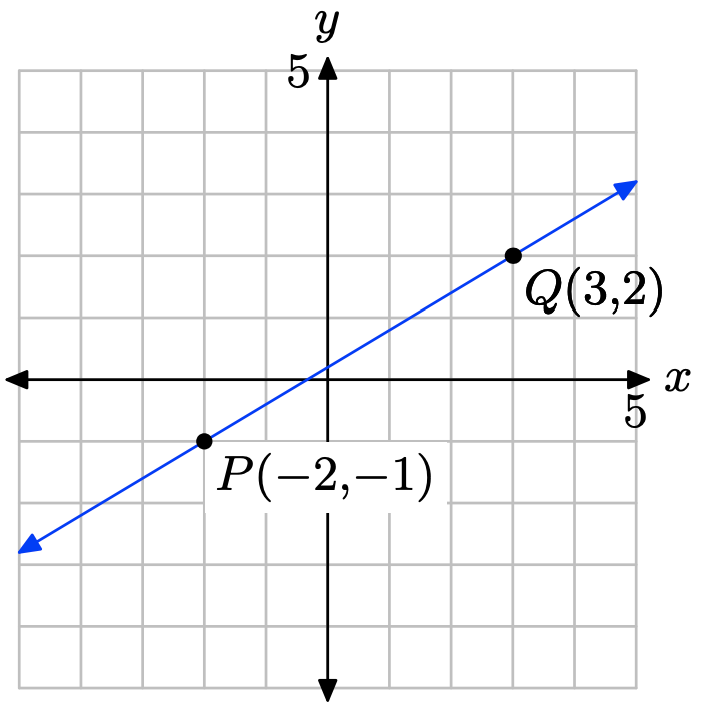
Calcular la pendiente de la línea a través de los puntos P y Q.

\[m = \dfrac{\delta y }{\delta x} = \dfrac{2 − (−1)}{ 3 − (−2)} = \dfrac{3}{5}\]

Sustituir m = 3/5 y\((x_{0}, y_{0}) = (−2, −1)\) en la forma punto-pendiente de la línea

\[y − y_{0} = m(x − x_{0}) \\ y − (−1) = \dfrac{3}{5} (x − (−2)) \\ y + 1 =\dfrac{3}{5} (x + 2)\]

Colocar este resultado en forma estándar. Primero despeja las fracciones multiplicando por 5.

\[y + 1 = \dfrac{3}{5} x + \dfrac{6}{5} \\ 5y + 5 = 3x + 6 \\ 3x − 5y = −1\]

Por lo tanto, la forma estándar de la línea es 3x − 5y = −1.

Ejercicio\(\PageIndex{10}\)

(−1, 4) y (2, −3)

Ejercicio\(\PageIndex{11}\)

(−2, 3) y (4, −3)

Contestar

Traza los puntos P (−2, 3) y Q (4, −3) y dibuja una línea a través de ellos.

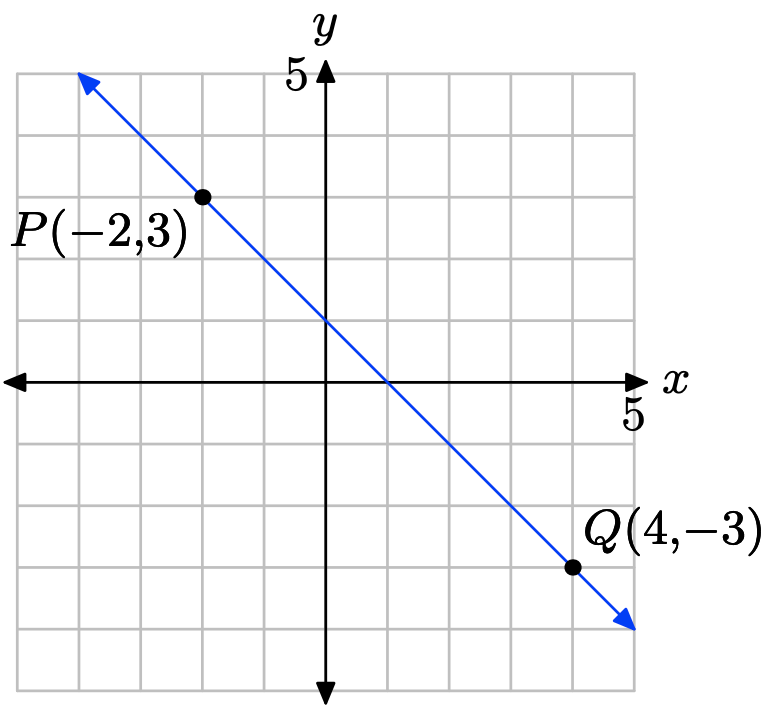
Calcular la pendiente de la línea a través de los puntos P y Q.

\[m = \dfrac{\delta y}{\delta x} = \dfrac{−3 − 3}{4 − (−2)}= \dfrac{−6}{ 6} = −1\]

Sustituya m = −1 y\((x_{0}, y_{0}) = (−2, 3)\) en la forma punto-pendiente de la línea.

\[y − y_{0} = m(x − x_{0}) \\ y − 3 = −1(x − (−2)) \\ y − 3 = −1(x + 2) \]

Colocar este resultado en forma estándar.

\[y − 3 = −x − 2 \\ x + y = 1 \]

De ahí que la forma estándar de la línea sea x + y = 1.

Ejercicio\(\PageIndex{12}\)

(−4, 4) y (2, −4)

Ejercicio\(\PageIndex{13}\)

Encuentra la ecuación de la línea en forma pendiente-intercepción que pasa por los puntos (−5, 5) y (6, 8).

Contestar

Sustituya 5 por\(y_{1}\), 8 para\(y_{2}\), −5 para\(x_{1}\), y 6 para\(x_{2}\) en la fórmula de pendiente para encontrar la pendiente m:

\[m = \dfrac{y_{1} − y_{2}}{x_{1} − x_{2} }= \dfrac{5 − 8}{−5 − 6} = \dfrac{3}{11}\]

Ahora sustituya\(\dfrac{3}{11}\) m, −5 por x1 y 5 por y1 en la forma de pendiente puntual

\[y − y_{1} = m(x − x_{1})\]

y luego resolver para y para obtener la ecuación

\[y = \dfrac{3}{ 11} x + \dfrac{70}{ 11}\]

Ejercicio\(\PageIndex{14}\)

Encuentra la ecuación de la línea en forma pendiente-intercepción que pasa por los puntos (6, −6) y (9, −7).

Ejercicio\(\PageIndex{15}\)

Encuentra la ecuación de la línea en forma pendiente-intercepción que pasa por los puntos (−4, 6) y (2, −4).

Contestar

Sustituya 6 por\(y_{1}\), −4 para\(y_{2}\), −4 para\(x_{1}\), y 2 para\(x_{2}\) en la fórmula de pendiente para encontrar la pendiente m:

\[m = \dfrac{ y_{1} − y_{2}}{ x_{1} − x_{2} }= \dfrac{6 − (−4) }{−4 − 2} = \dfrac{−5}{ 3}\]

Ahora sustituya\(\dfrac{−5}{ 3}\) m, −4 por x1 y 6 por\(y_{1}\) en la forma de pendiente puntual

\[y − y_{1} = m(x − x_{1})\]

y luego resolver para y para obtener la ecuación

\[y = \dfrac{−5}{3} x − \dfrac{2}{ 3}\]

Ejercicio\(\PageIndex{16}\)

Encuentra la ecuación de la línea en forma pendiente-intercepción que pasa por los puntos (−1, 5) y (4, 4).

En Ejercicios\(\PageIndex{17}\) -\(\PageIndex{20}\), realizar cada una de las siguientes tareas.

i. Dibujar la gráfica de la ecuación lineal dada en papel cuadriculado y etiquetarla con su ecuación.

ii. Determine la pendiente de la ecuación dada, luego use esta pendiente para dibujar una segunda línea a través del punto P dado que sea paralela a la primera línea.

iii. Estima la intercepción y de la segunda línea a partir de su gráfica.

iv. Utilice la forma punto-pendiente para determinar la ecuación de la segunda línea. Coloque este resultado en forma de pendiente-intercepción y = mx + b, luego indique el valor exacto de la intercepción y. Marque la segunda línea con la forma pendiente-intercepción de su ecuación.

Ejercicio\(\PageIndex{17}\)

2x + 3y = 6, P = (−2, −3)

Contestar

Traza los puntos Q (0, 2) y R (3, 0) y dibuja una línea a través de ellos como se muestra en (a) a continuación. Puede calcular la pendiente de esta línea a partir de la gráfica, o puede usar la fórmula de pendiente de la siguiente manera.

\[m = \dfrac{\delta y}{\delta x} = \dfrac{0 − 2 }{3 − 0} = −\dfrac{2}{ 3}\]

La segunda línea debe ser paralela a la primera, por lo que debe tener la misma pendiente; es decir, m = −2/3. La segunda línea debe pasar por el punto P (−2, −3), así que trazar el punto P. Para obtener la pendiente correcta, comience en el punto P, luego mueva 3 unidades a la derecha y 2 unidades hacia abajo, como se muestra en (b). Parecería que esta línea cruza el eje y cerca de (0, −4.3).

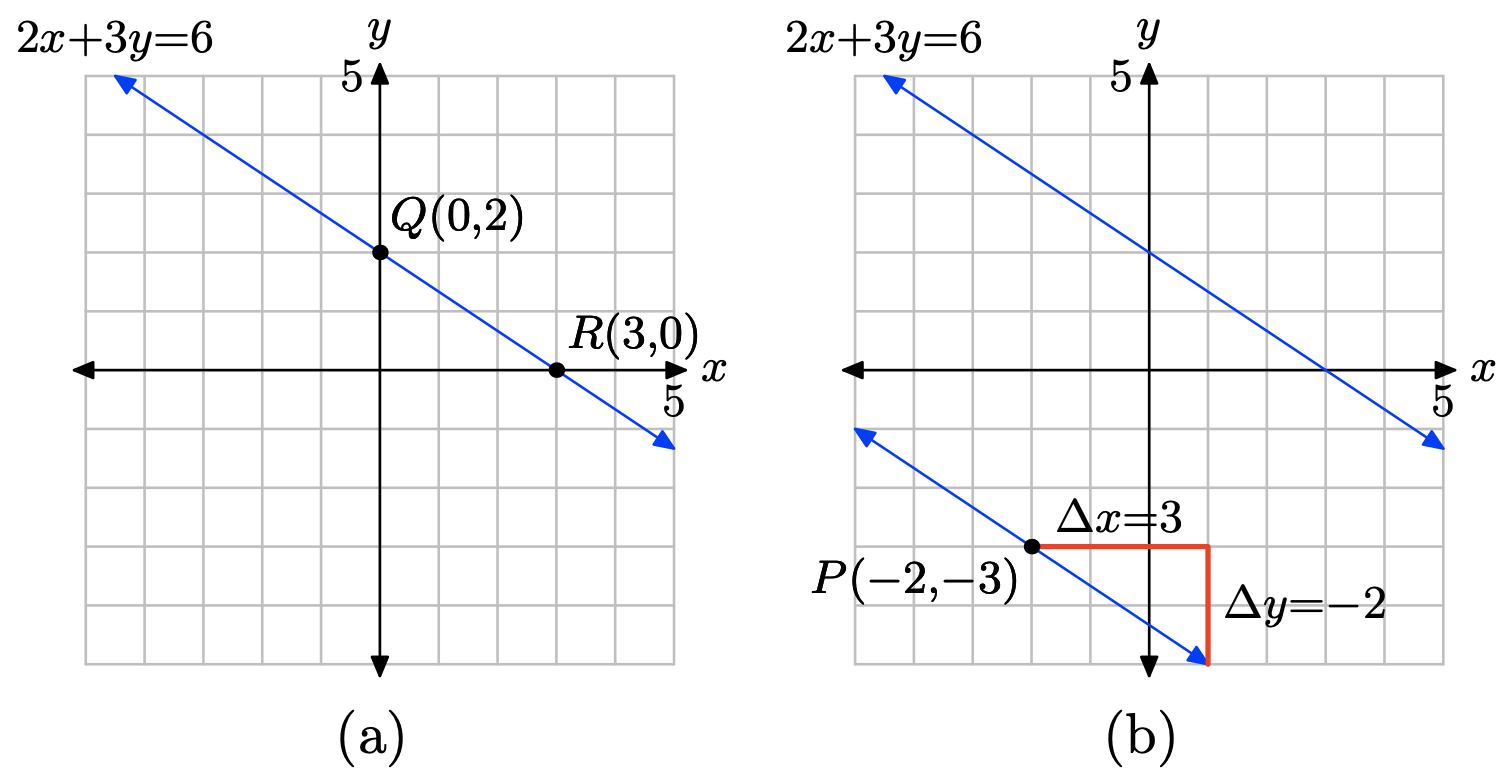
Para encontrar la ecuación de la segunda línea, utilice la forma de pendiente de punto de la línea y m = −2/3 y\((x_{0}, y_{0}) = (−2, −3)\), de la siguiente manera.

\[y − y_{0} = m(x − x_{0}) \\ y − (−3) = −\dfrac{2}{ 3} (x − (−2)) \\ y + 3 = −\dfrac{2}{ 3}(x + 2)\]

Para colocar esto en forma pendiente-intercepción y = mx + b, debemos resolver para y.

\[y + 3 = −\dfrac{2}{ 3}x − \dfrac{4}{ 3} \\ y = −\dfrac{2}{ 3} x − \dfrac{4}{ 3} − 3 \\ y = −\dfrac{2}{ 3} x − \dfrac{4}{ 3} −\dfrac{9}{ 3}\\ y = −\dfrac{2}{ 3} x − \dfrac{13}{ 3}\]

Por lo tanto, la ecuación en forma pendiente-intercepción es y = (−2/3) x − 13/3, haciendo la coordenada y exacta de la intercepción y b = −13/3, que está bastante de acuerdo (consulte su calculadora) con nuestra estimación de −4.3.

Ejercicio\(\PageIndex{18}\)

3x − 4y = 12, P = (−3, 4)

Ejercicio\(\PageIndex{19}\)

x + 2y = −4, P = (3, 3)

Contestar

Traza los puntos Q (−4, 0) y R (0, −2) y dibuja una línea a través de ellos como se muestra en (a) a continuación. Puede calcular la pendiente de esta línea a partir de la gráfica, o puede usar la fórmula de pendiente de la siguiente manera.

\[m = \dfrac{\delta y}{\delta x} = \dfrac{−2 − 0 }{0 − (−4)} = −\dfrac{1}{2}\]

La segunda línea debe ser paralela a la primera, por lo que debe tener la misma pendiente; es decir, m = −1/2. La segunda línea debe pasar por el punto P (3, 3), así que trazar el punto P. Para obtener la pendiente correcta, comience en el punto P, luego mueva 1 unidad hacia abajo y 2 unidades a la derecha, como se muestra en (b). Parecería que esta línea cruza el eje y cerca de (0, 4.5).

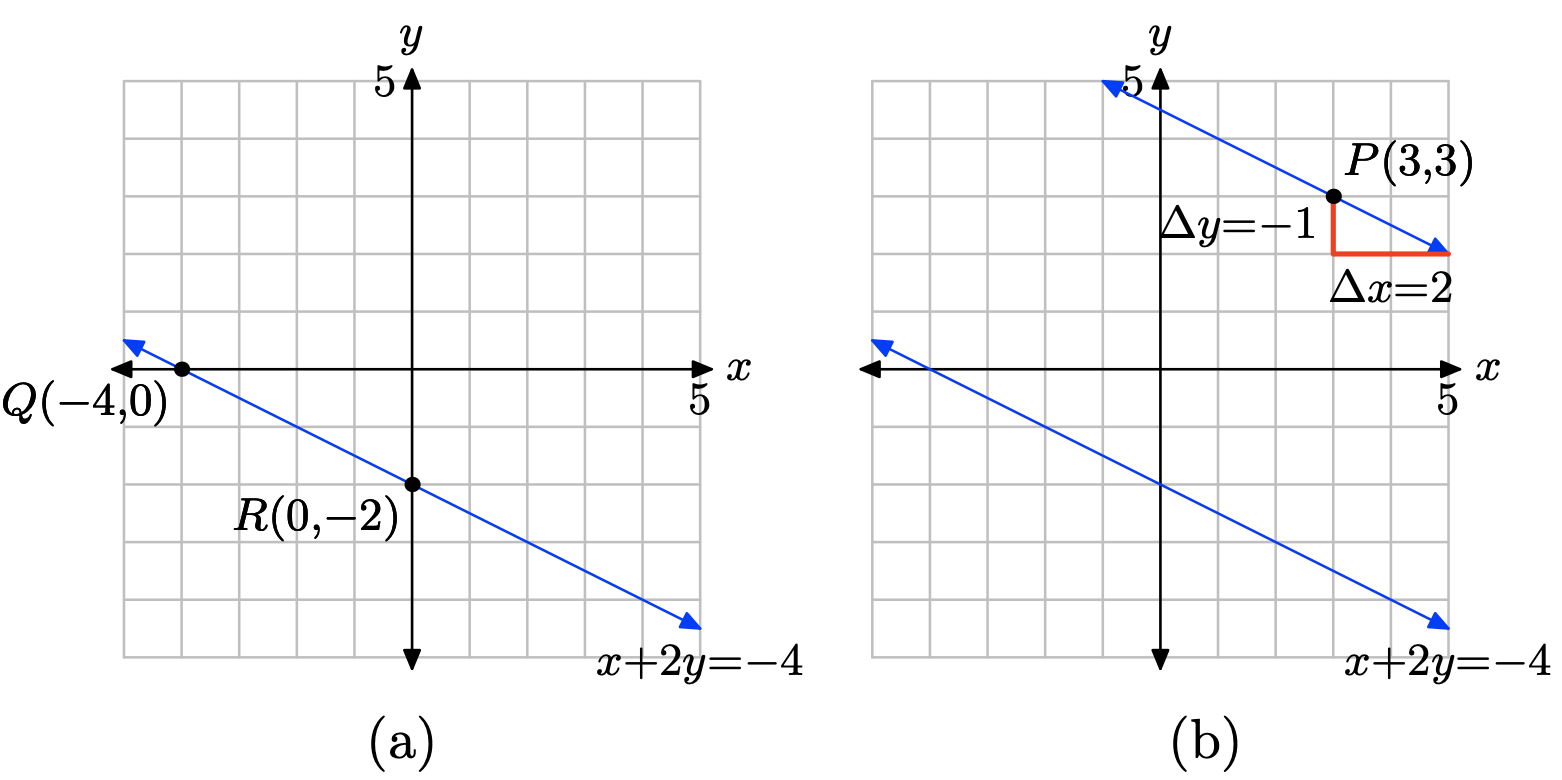
Para encontrar la ecuación de la segunda línea, utilice la forma de pendiente de punto de la línea y m = −1/2 y\((x_{0}, y_{0}) = (3, 3)\), de la siguiente manera.

\[y − y_{0} = m(x − x_{0}) \\ y − 3 = −\dfrac{1}{ 2} (x − 3) \]

Para colocar esto en forma pendiente-intercepción y = mx + b, debemos resolver para y.

\[− 3 = −\dfrac{1}{ 2} x + \dfrac{3}{ 2} \\ y = −\dfrac{1}{ 2} x + \dfrac{3}{ 2} + 3 \\ y = −\dfrac{1}{ 2} x + \dfrac{3}{ 2} + \dfrac{6}{ 2} \\ y = −\dfrac{1}{ 2} x + \dfrac{9}{ 2}\]

De ahí que la ecuación en forma pendiente-intercepción es y = (−1/2) x + 9/2, haciendo la coordenada y exacta de la intercepción y b = 9/2, que está bastante de acuerdo (consulte su calculadora) con nuestra estimación de 4.5.

Ejercicio\(\PageIndex{20}\)

5x + 2y = 10, P = (−3, −5)

En Ejercicios\(\PageIndex{21}\) -\(\PageIndex{24}\), realizar cada una de las siguientes tareas.

i. Dibujar la gráfica de la ecuación lineal dada en papel cuadriculado y etiquetarla con su ecuación.

ii. Determine la pendiente de la ecuación dada, luego use esta pendiente para dibujar una segunda línea a través del punto P dado que es prependicular a la primera línea.

iii. Utilice la forma punto-pendiente para determinar la ecuación de la segunda línea. Coloca este resultado en forma estándar Ax+By = C, donde A, B, C son números enteros y A > 0. Etiquete la segunda línea con esta forma estándar de su ecuación.

Ejercicio\(\PageIndex{21}\)

x − 2y = −2, P = (3, −4)

Contestar

Dejar x = 0 en x − 2y = −2. Entonces −2y = −2 e y = 1. Este cálculo nos da la intercepción y R (0, 1). Dejar y = 0 en x − 2y = −2 y x = −2. Esto nos da la intercepción x Q (−2, 0). Traza los puntos Q (−2, 0) y R (0, 1) y dibuja una línea a través de ellos como en (a) abajo.

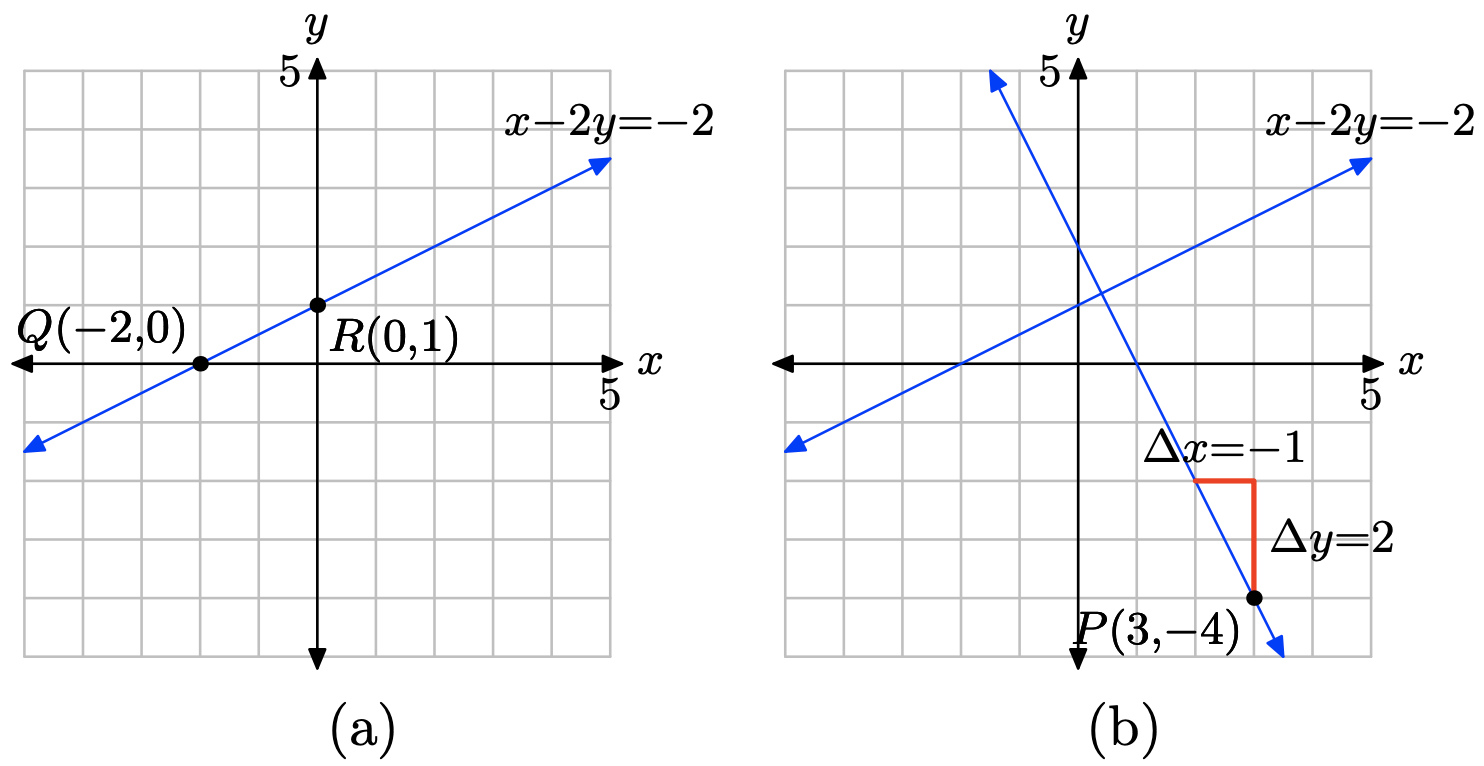
Se puede calcular la pendiente de la primera línea a partir de la gráfica o se puede obtener con la fórmula de pendiente de la siguiente manera.

\[m1 = \dfrac{\delta y}{\delta x} = \dfrac{1 − 0}{ 0 − (−2)} = \dfrac{1}{ 2}\]

La segunda línea es perpendicular a esta primera línea, por lo que la pendiente de la segunda línea debe ser el recíproco negativo de la pendiente de la primera línea; es decir, la pendiente de la segunda línea debe ser\(m = −1/m_{2} = −1/(1/2)\), o m = −2. Para dibujar una línea a través del punto P (3, −4) que es perpendicular a la línea en (a), primero grafica el punto P (3, −4), luego mueve hacia arriba 2 unidades y hacia la izquierda 1 unidad como se muestra en (b). Esto nos da una línea a través de P (3, −4) con pendiente m = −2, por lo que esta línea será perpendicular a la primera línea. Para encontrar la ecuación de la línea perpendicular, sustituya m = −2 y\((x_{0}, y_{0}) = (3, −4)\) en la fórmula punto-pendiente, luego coloque la ecuación resultante en forma estándar.

\[y − y_{0} = m(x − x_{0}) \\ y − (−4) = −2(x − 3) \\ y + 4 = −2x + 6 \\ 2x + y = 2 \]

Así, la ecuación de la línea que pasa por P (3, −4) y es perpendicular a la línea x − 2y = −2 es 2x + y = 2.

Ejercicio\(\PageIndex{22}\)

3x + y = 3, P = (−3, −4)

Ejercicio\(\PageIndex{23}\)

x − 2y = 4, P = (−3, 3)

Contestar

Establecer x = 0 en x − 2y = 4 para obtener −2y = 4. Por lo tanto, y = −2 y la intercepción y es Q (0, −2). Establecer y = 0 en x − 2y = 4 para obtener x = 4. De ahí que la intercepción x sea R (4, 0). Trace Q (0, −2) y R (4, 0) y dibuje una línea a través de ellos como en (a) abajo.

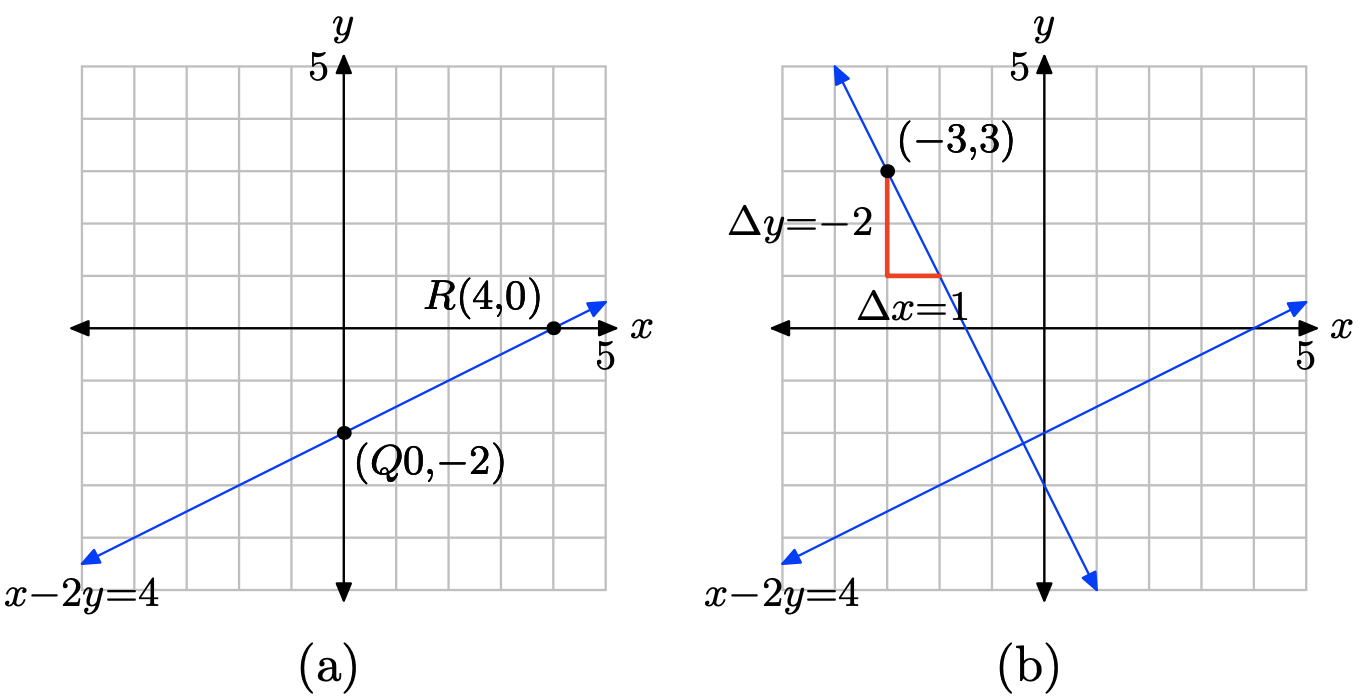
Se puede calcular la pendiente de la primera línea a partir de la gráfica o se puede obtener con la fórmula de pendiente de la siguiente manera.

\[m_{1} = \dfrac{\delta y}{\delta x} = \dfrac{0 − (−2)}{ 4 − 0 }= \dfrac{1}{2}\]

La segunda línea es perpendicular a esta primera línea, por lo que la pendiente de la segunda línea debe ser el recíproco negativo de la pendiente de la primera línea; es decir, la pendiente de la segunda línea debe ser m = −1/m2 = −1/ (1/2), o m = −2. Para dibujar una línea a través del punto P (−3, 3) que es perpendicular a la línea en (a), primero grafica el punto P (−3, 3), luego mueve hacia abajo 2 unidades y hacia la derecha 1 unidad como se muestra en (b). Esto nos da una línea a través de P (−3, 3) con pendiente m = −2, por lo que esta línea será perpendicular a la primera línea. Para encontrar la ecuación de la línea perpendicular, sustituya m = −2 y\((x_{0}, y_{0}) = (−3, 3)\) en la fórmula punto-pendiente, luego coloque la ecuación resultante en forma estándar.

\[y − y_{0} = m(x − x_{0}) \\ y − 3 = −2(x − (−3)) \\ y − 3 = −2(x + 3) \\ y − 3 = −2x − 6 \\ 2x + y = −3\]

Así, la ecuación de la línea que pasa por P (−3, 3) y es perpendicular a la línea x − 2y = 4 es 2x + y = −3.

Ejercicio\(\PageIndex{24}\)

x − 4y = 4, P = (−3, 4)

Ejercicio\(\PageIndex{25}\)

Encuentra la ecuación de la línea en forma pendiente-intersección que pasa por el punto (7, 8) y es paralela a la línea x − 5y = 4.

Contestar

Primero resolver x − 5y = 4 para y para obtener\(y = \dfrac{1 }{5} x − \dfrac{4}{5} \) La pendiente de esta línea es\(\dfrac{1}{5}\). Por lo tanto, cada línea paralela también tiene pendiente\(\dfrac{1}{5}\).

Ahora para encontrar la ecuación de la línea paralela que pasa por el punto (7, 8), sustituya\(\dfrac{1}{5}\) m, 7 para\(x_{1}\), y 8 para\(y_{1}\) en la forma de punto-pendiente

\[y − y_{1} = m(x − x_{1})\]para obtener

\[y − 8 = \dfrac{1}{5}(x − 7)\]. Entonces resuelve para y:

\[y = \dfrac{1}{5} x − \dfrac{7}{5} + 8 \\ y = \dfrac{1}{5}x − \dfrac{7}{5} +\dfrac{40}{5} y = \dfrac{1}{5} x + \dfrac{33}{5}\]

Ejercicio\(\PageIndex{26}\)

Encuentra la ecuación de la línea en forma pendiente-intersección que pasa por el punto (3, −7) y es perpendicular a la línea 7x − 2y = −8.

Ejercicio\(\PageIndex{27}\)

Encuentra la ecuación de la línea en forma pendiente-intersección que pasa por el punto (1, −2) y es perpendicular a la línea −7x + 5y = 4.

Contestar

Primero resuelve −7x + 5y = 4 para que y obtenga

\[y = \dfrac{7}{5} x + 4 5\]

La pendiente de esta línea es\ dfrac {7} {5}. Por lo tanto, cada línea perpendicular tiene pendiente −\(\dfrac{7}{5}\) (el recíproco negativo de\(\dfrac{7}{5}\). Ahora, para encontrar la ecuación de la línea perpendicular que pasa por el punto (1, −2), sustituya −\ dfrac {5} {7} por m, 1 para\(x_{1}\) y −2 para\(y_{1}\) en la forma punto-pendiente

\[y − y1 = m(x − x1)\]para obtener\[y − (−2) = −\dfrac{5}{7} (x − 1)\]. Entonces resuelve para y:

\[y = −\dfrac{5}{7}x +\dfrac{5}{7} − 2 \\ y = −\dfrac{5}{7} x + \dfrac{5}{7} − \dfrac{14}{7} \\ y = −\dfrac{5}{7} x − \dfrac{9}{7}\]

Ejercicio\(\PageIndex{28}\)

Encuentra la ecuación de la línea en forma pendiente-intersección que pasa por el punto (4, −9) y es paralela a la línea 9x + 3y = 5.

Ejercicio\(\PageIndex{29}\)

Encuentra la ecuación de la línea en forma pendiente-intersección que pasa por el punto (2, −9) y es perpendicular a la línea −8x + 3y = 1.

Contestar

Primero resuelve −8x + 3y = 1 para que y obtenga\[y = \dfrac{8}{3} x + \dfrac{1}{3} \]

La pendiente de esta línea es\(\dfrac{8}{3}\). Por lo tanto, cada línea perpendicular tiene pendiente\(−\dfrac{3}{8}\) (el recíproco negativo de\(\dfrac{8}{3}\)). Ahora, para encontrar la ecuación de la línea perpendicular que pasa por el punto (2, −9), sustituya\(−\dfrac{3}{8}\) m, 2 para\(x_{1}\) y −9 para\(y_{1}\) en la forma punto-pendiente\[y − y1 = m(x − x1)\]

para obtener\[y − (−9) = −\dfrac{3}{8} (x − 2)\]

Entonces resuelve para y:

\[y = −\dfrac{3}{8} x + \dfrac{3}{4} − 9 \\ y = −\dfrac{3}{8} x + \dfrac{3}{4}− \dfrac{36}{4} \\ y = −\dfrac{3}{8} x − \dfrac{33}{4}\]

Ejercicio\(\PageIndex{30}\)

Encuentra la ecuación de la línea en forma pendiente-intersección que pasa por el punto (−7, −7) y es paralela a la línea 8x + y = 2.

Contestar

Agrega textos aquí. No elimine primero este texto.

Ejercicio\(\PageIndex{31}\)

Una pelota es lanzada verticalmente hacia arriba sobre un planeta distante. Después de 1 segundo, su velocidad es de 100 metros por segundo. Después de 5 segundos, la velocidad es de 50 metros por segundo. Supongamos que la velocidad v de la bola es una función lineal del tiempo t.

a) En papel cuadriculado, dibuje el gráfico de la velocidad v versus el tiempo t. Supongamos que la velocidad es la variable dependiente y colócala en el eje vertical.

b) Determinar la pendiente de la línea, incluyendo sus unidades, luego dar una explicación del mundo real del significado de esta pendiente.

c) Determinar una ecuación que modele la velocidad v de la bola en función del tiempo t.

d) Determinar el tiempo que tarda la pelota en alcanzar su máxima altura.

Contestar

a) A 1 segundo, la velocidad es de 100 metros por segundo. Este es el punto (1, 100) en la trama de abajo. A los 5 segundos, la velocidad es de 50 metros por segundo. Este es el punto (5, 50) en la trama de abajo.

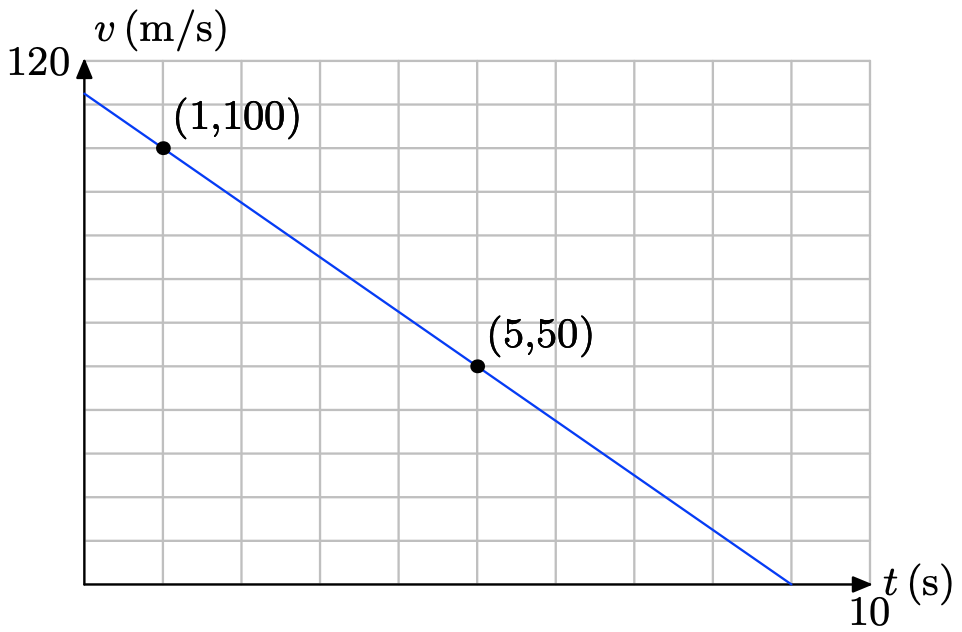
b) Mantendremos las unidades en nuestro cálculo de pendiente para proporcionar un significado real para la tasa.

\[m = \dfrac{\delta v}{\delta t} = \dfrac{50 m/s − 100 m/s}{ 5 s − 1 s} = −12.5 (m/s)/s.\]

Es decir, la pendiente es\(−12.5 m/s^2\). Se trata de la aceleración, la velocidad a la que la velocidad está cambiando con respecto al tiempo. Cada segundo, la velocidad disminuye 12.5 metros por segundo.

c) Utilizamos la forma punto-pendiente de la línea, a saber

\[y − y_{0} = m(x − x_{0})\]

Sin embargo, v y t están tomando el lugar de y y x, respectivamente, por lo que la ecuación se convierte\[v − v_{0} = m(t − t_{0})\], Ahora, sustituir la pendiente m = −12.5 y el punto\((t_{0}, v_{0}) = (1, 100)\) a obtener\[v − 100 = −12.5(t − 1)\]. Resolver esto para v, obteniendo\[v − 100 = −12.5t + 12.5 \\ v = −12.5t + 112.5\]. Equivalentemente, podríamos usar la notación de funciones y escribir\[v(t) = −12.5t + 112.5\].

d) Cuando la bola alcanza su altura máxima, su velocidad será igual a cero. En consecuencia, para encontrar el tiempo de este evento, debemos resolver v (t) = 0. Reemplazar v (t) por −12.5t + 112.5 y resolver para t\[−12.5t + 112.5 = 0 \\ −12.5t = −112.5 \\ t = 9\]. De ahí que la pelota tardará 9 segundos en alcanzar su máxima altura.

Ejercicio\(\PageIndex{32}\)

Una pelota es lanzada verticalmente hacia arriba sobre un planeta distante. Después de 2 segundos, su velocidad es de 320 pies por segundo. Después de 8 segundos, la velocidad es de 200 pies por segundo. Supongamos que la velocidad v de la bola es una función lineal del tiempo t.

a) En papel cuadriculado, dibuje el gráfico de la velocidad v versus el tiempo t. Supongamos que la velocidad es la variable dependiente y colócala en el eje vertical.

b) Determinar la pendiente de la línea, incluyendo sus unidades, luego dar una explicación del mundo real del significado de esta pendiente.

c) Determinar una ecuación que modele la velocidad v de la bola en función del tiempo t.

d) Determinar el tiempo que tarda la pelota en alcanzar su máxima altura.

Ejercicio\(\PageIndex{33}\)

Un automóvil está viajando por la autopista y el conductor aplica sus frenos. Después de 2 segundos, la velocidad del automóvil es de 60 km/h, después de 4 segundos, la velocidad del automóvil es de 50 km/h.

a) En papel cuadriculado, dibuje el gráfico de la velocidad v versus el tiempo t. Supongamos que la velocidad es la variable dependiente y colócala en el eje vertical.

b) Determinar la pendiente de la línea, incluyendo sus unidades, luego dar una explicación del mundo real del significado de esta pendiente.

c) Determinar una ecuación que modele la velocidad v del automóvil en función del tiempo t. d) Determinar el tiempo que tarda el automóvil en detenerse.

Contestar

a) Después de 2 segundos, la velocidad del automóvil es de 60 km/h Este es el punto (2, 60). Después de 4 segundos, la velocidad del auto es de 50 km/h Este es el punto (4, 50). Traza estos dos puntos y dibuja una línea a través de ellos, como se muestra en la gráfica de abajo.

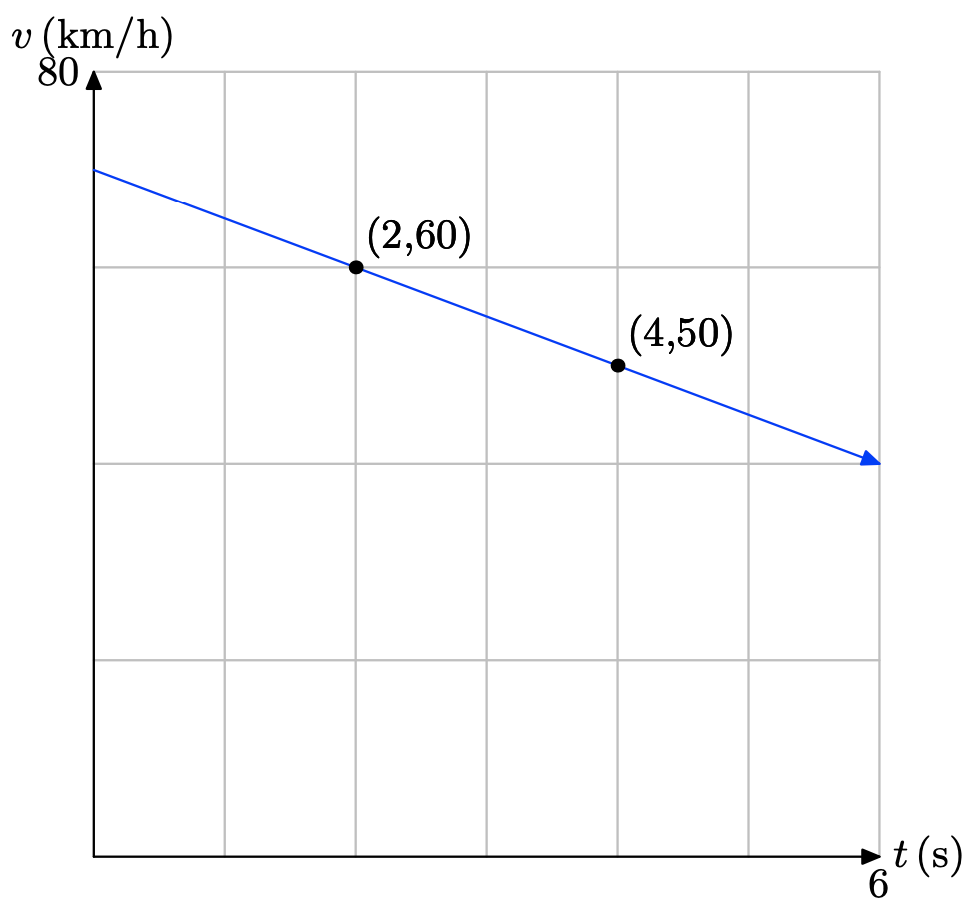
b) Mantendremos las unidades en nuestro cálculo de pendiente para proporcionar un significado real para la tasa.

\[m = \dfrac{\delta v}{\delta t} = \dfrac{50 km/h − 60 km/h}{ 4 s − 2 s }= −5 (km/h)/s\]

Es decir, la pendiente es −5 (km/h) /s, es decir, la aceleración, la velocidad a la que la velocidad está cambiando con respecto al tiempo. Cada segundo, la velocidad disminuye 5 kilómetros por hora.

c) Utilizamos la forma punto-pendiente de la línea, es decir\[y − y_{0} = m(x − x_{0})\], Sin embargo, v y t están tomando el lugar de y y x, respectivamente, por lo que la ecuación se convierte\[v − v_{0} = m(t − t_{0})\], Ahora, sustituir la pendiente m = −5 y el punto\((t_{0}, v_{0}) = (2, 60)\) a obtener\[v − 60 = −5(t − 2)\]. Resolver esto para v, obteniendo\[v − 60 = −5t + 10 \\ v = −5t + 70\]. Equivalentemente, podríamos usar la notación de funciones y escribir\[v(t) = −5t + 70\].

d) Para encontrar el tiempo que tarda el auto en detenerse, debemos determinar el tiempo t para que\[v(t) = 0\]. Reemplazar v (t) por −5t + 70 y resolver para t.

\[−5t + 70 = 0\\ −5t = −70 \\ t = 14\]. De ahí que tarde 14 segundos para que el frene hasta detenerse.

Ejercicio\(\PageIndex{34}\)

Un automóvil viaja por la autobahn y su conductor pisa el acelerador. Después de 2 segundos, la velocidad del automóvil es de 30 km/h, después de 4 segundos, la velocidad del automóvil es de 40 km/h.

a) En papel cuadriculado, dibuje el gráfico de la velocidad v versus el tiempo t. Supongamos que la velocidad es la variable dependiente y colócala en el eje vertical.

b) Determinar la pendiente de la línea, incluyendo sus unidades, luego dar una explicación del mundo real del significado de esta pendiente.

c) Determinar una ecuación que modele la velocidad v del automóvil en función del tiempo t.

d) Determinar la velocidad del vehículo después de 8 segundos.

Ejercicio\(\PageIndex{35}\)

Supongamos que la demanda d de una determinada marca de teakettle es una función lineal de su precio unitario p. Cuando el precio unitario se fija en $30, la demanda de teteras es de 100. Esto significa que el público compra 100 teteeras. Si el precio unitario se fija en $50, entonces la demanda de teteras es de 60.

a) En papel cuadriculado, esbozar la gráfica de la demanda d versus el precio unitario p. Supongamos que la demanda es la variable dependiente y colocarla en el eje vertical.

b) Determinar la pendiente de la línea, incluyendo sus unidades, luego dar una explicación del mundo real del significado de esta pendiente.

c) Determinar una ecuación que modele la demanda d de teteras en función del precio unitario p.

d) Calcular la demanda si el precio unitario se fija en $40.

Contestar

a) Cuando el precio unitario es de $30, la demanda es de 100 tetederas. Este es el punto (30, 100). Cuando el precio unitario es de $50, la demanda es de 60 tetederas. Este es el punto (50, 60). Traza los puntos (30, 100) y (50, 60) y dibuja una línea a través de ellos, como se muestra en la trama de abajo.

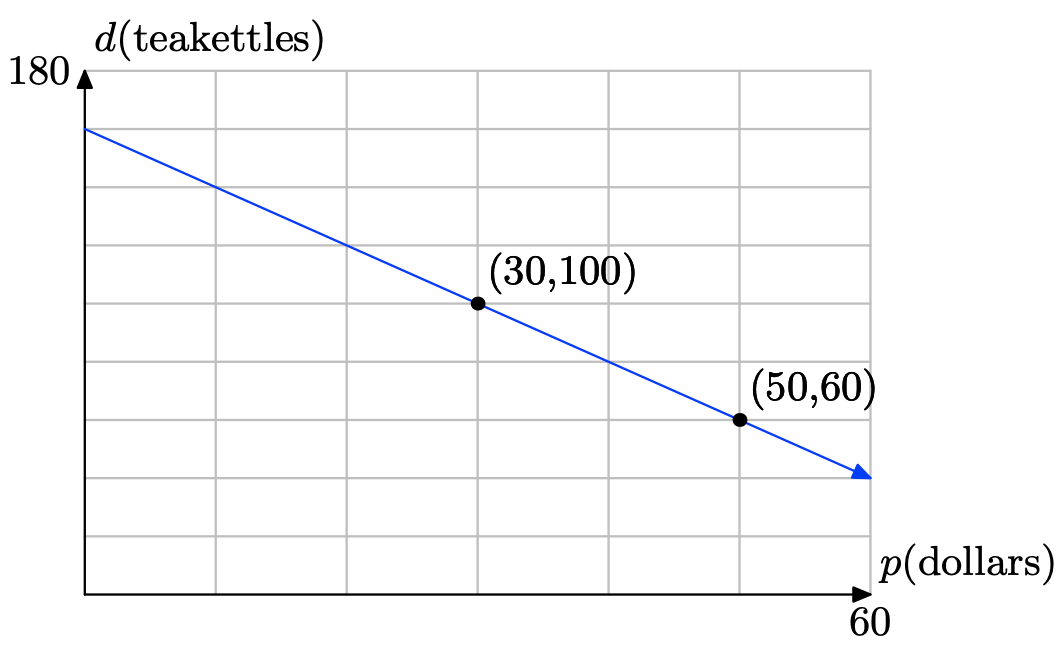
b) Mantendremos las unidades en nuestro cálculo de pendiente para proporcionar un significado real para la tasa.

\[m = \dfrac{\delta d}{\delta p} = \dfrac{60 teakettles − 100 teakettles}{ 50 dollars − 30 dollars } = −2 teakettles/dollar\]

Es decir, la pendiente es −2 teakettles/dólar. Esta es la tasa a la que la demanda está cambiando con respecto al precio unitario. Por cada incremento en el precio unitario de un dólar, la demanda se baja en 2 teteras (se compran 2 teteras menos).

c) Utilizamos la forma punto-pendiente de la línea, es decir, Sin embargo\[ y − y_{0} = m(x − x_{0})\], d y p están tomando el lugar de y y y x, respectivamente, por lo que la ecuación se convierte en

\[d − d_{0} = m(p − p_{0})\]

Ahora, sustituya la pendiente m = −2 y el punto\((p_{0}, d_{0}) = (30, 100)\) a obtener\[d − 100 = −2(p − 30)\]. Resolver esto para d, obteniendo

\[d − 100 = −2p + 60 \\ d = −2p + 160\]

Equivalentemente, podríamos usar notación de función y escribir d (p) = −2p + 160.

d) Para determinar la demanda si el precio unitario es de $40, cómpule\[ d(40) = −2(40) + 160 = 80\]

De ahí que la demanda sea de 80 teteras si el precio por tetera se fija en $40.

Ejercicio\(\PageIndex{36}\)

Es un clima perfecto para volar cometas en la costa de Oregón. Annie agarra su cometa, se sube al techo de su casa de dos pisos y comienza a tocar cuerda de cometa. En 10 segundos, la cometa de Annie se encuentra a 120 pies sobre el suelo. Después de 20 segundos, se encuentra a 220 pies sobre el suelo. Supongamos que la altura h de la cometa sobre el suelo es una función lineal de la cantidad de tiempo t que ha pasado desde que Annie comenzó a tocar cuerda de cometa.

a) En papel cuadriculado, dibuje la gráfica de la altura h de la cometa sobre el suelo versus el tiempo t. Supongamos que la altura es la variable dependiente y colócala sobre el eje vertical.

b) Determinar la pendiente de la línea, incluyendo sus unidades, luego dar una explicación del mundo real del significado de esta pendiente.

c) Determinar una ecuación que modele la altura h de la cometa en función del tiempo t.

d) Determinar la altura de la cometa después de 20 segundos.

e) Determinar la altura del techo del segundo piso de Annie sobre el suelo.

3.5 Ejercicios

Ejercicio\(\PageIndex{1}\)

El siguiente conjunto de datos sobre crédito al consumo (deuda) revolvente en Estados Unidos es de Google.com. Esto se compone principalmente de deuda de tarjetas de crédito, pero también incluye otros créditos de consumo no hipotecarios, como los que ofrecen los bancos comerciales, las cooperativas de crédito, Sallie Mae y el gobierno federal.

Año	años x después de 2001	todos los créditos rotatorios C en miles de millones de $
2001	0	721.0
2002	1	741.2
2003	2	759.3
2004	3	786.1
2005	4	805.4

a) Establecer un sistema de coordenadas en papel cuadriculado, colocando el crédito C en el eje vertical, y los años x posteriores a 2001 en el eje horizontal. Etiquete y escale cada eje de manera apropiada. Dibuja lo que sientes es la línea de mejor ajuste. Recuerda dibujar todas las líneas con una regla.

b) Seleccione dos puntos en su línea de mejor ajuste que no sean de la tabla de datos anterior. Utilice estos dos puntos para determinar la pendiente de la línea. Incluye unidades con tu respuesta. Escribe una oración o dos explicando el significado real de la pendiente de la línea de mejor ajuste en el mundo real.

c) Utilizar uno de los dos puntos de la línea y la pendiente para determinar la ecuación de la línea de mejor ajuste en forma de punto-pendiente. Utilice C y x para las variables dependientes e independientes, respectivamente. Resuelve la ecuación resultante para C y escribe tu resultado usando la notación de funciones.

d) Utilizar la ecuación desarrollada en la parte (c) para predecir la deuda crediticia revolvente en el año 2008.

e) Si continúa la tendencia lineal pronosticada por la línea de mejor ajuste, ¿en qué año la deuda crediticia revolvente alcanzará 1.0 billones de dólares?

Contestar

a) Escalar y etiquetar los ejes, trazar los puntos, luego dibujar la línea de mejor ajuste.

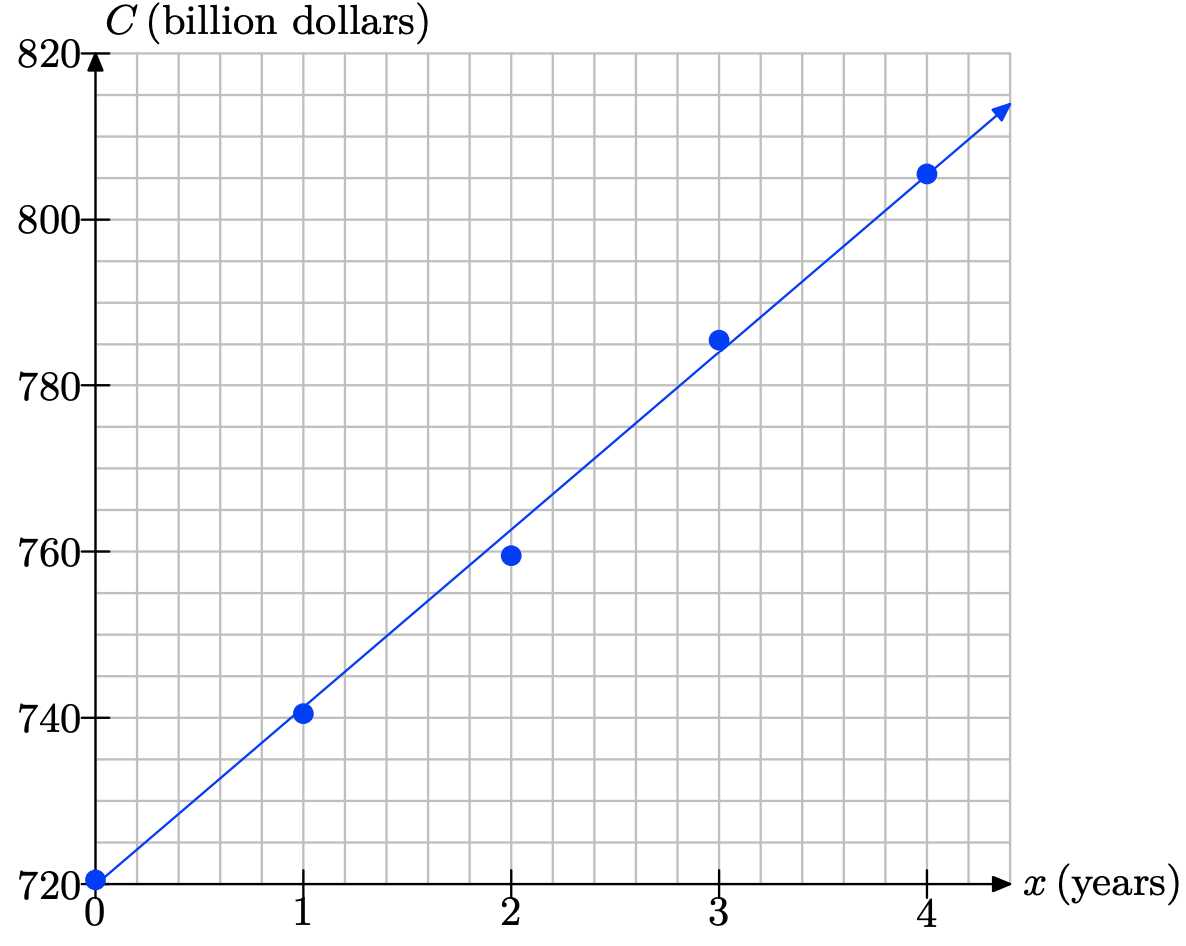
b) Seleccionar dos puntos, P (1.4, 750) y Q (2.8, 780) que sean puntos en la línea pero no puntos en la tabla de datos original.

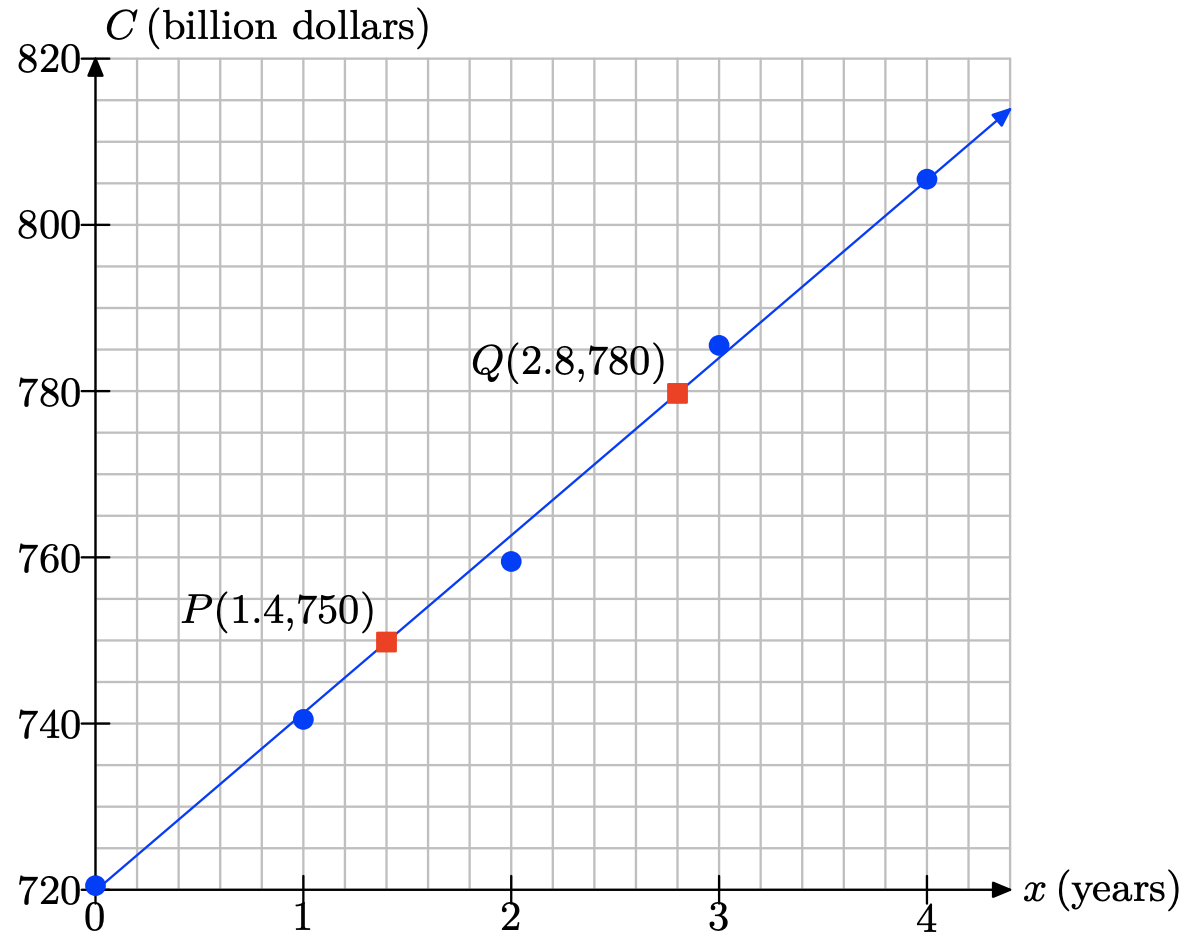
Usa estos dos puntos para calcular la pendiente de la línea de mejor ajuste.

\[m = \dfrac{\delta C}{\delta x} = \dfrac{780 − 750}{ 2.8 − 1.4}\]mil millones de dólares/año

Utilizando una calculadora, la pendiente es de aproximadamente 21.42 mil millones de dólares al año. Lo que esto significa es que la deuda crediticia está aumentando a una tasa de 21.42 mil millones de dólares al año. c) Para encontrar la ecuación de la línea, utilice el punto P (1.4, 750) y la pendiente m = 21.42 en la forma punto-pendiente de la línea.

\[y − y_{0} = m(x − x_{0}) \\ y − 750 = 21.42(x − 1.4)\]

Reemplace y y x por C y x, respectivamente, luego resuelva para C en términos de x.

\[C − 750 = 21.42(x − 1.4) \\ C − 750 = 21.42x − 29.988 \\ C = 21.42x + 720.012\]

En notación de funciones, C (x) = 21.42x + 720.012. Nota: Las respuestas variarán algo debido a la naturaleza subjetiva de dibujar la línea de mejor ajuste y elegir puntos en la línea.

d) El año 2008 da x = 2008−2001 = 7 años desde 2001. De ahí que para encontrar la deuda crediticia en 2008, utilizamos C (x) = 21.42x + 720.012 y evaluamos

\[C(7) = 21.42(7) + 720.012 = 869.952\]

De ahí que la deuda crediticia en 2008 sea de aproximadamente 869 mil millones de dólares.

e) Un billón de dólares es de 1000 mil millones de dólares. De ahí que para encontrar cuando la deuda crediticia es de 1000 mil millones de dólares, debemos resolver C (x) = 1000 para x.

\[C(x) = 1000 \\ 21.42x + 720.012 = 1000 \\ 21.42x = 279.988 \\ x \approx 13.07\]De ahí que la deuda crediticia alcance un billón de dólares aproximadamente 13 años después del año 2001, o un poco en el año 2014.

Ejercicio\(\PageIndex{2}\)

El siguiente conjunto de datos sobre crédito no revolvente (deuda) en Estados Unidos proviene de Google.com. El mayor componente del crédito no revolvente son los préstamos para automóviles, pero también incluye préstamos estudiantiles y otros préstamos de consumo a plazo definido.

Año	años x después de 2001	Deuda no revolvente D en miles de millones de $
2001	0	1121.3
2002	1	1184.1
2003	2	1247.3
2004	3	1305.0
2005	4	1342.3

a) Establecer un sistema de coordenadas sobre papel cuadriculado, colocando la deuda crediticia no revolvente D en el eje vertical, y los años x posteriores a 2001 en el eje horizontal. Etiquete y escale cada eje de manera apropiada. Dibuja lo que sientes es la línea de mejor ajuste. Recuerda dibujar todas las líneas con una regla.

b) Seleccione dos puntos en su línea de mejor ajuste que no sean de la tabla de datos anterior. Utilice estos dos puntos para determinar la pendiente de la línea. Incluye unidades con tu respuesta. Escribe una oración o dos explicando el significado real de la pendiente de la línea de mejor ajuste en el mundo real.

c) Utilizar uno de los dos puntos de la línea y la pendiente para determinar la ecuación de la línea de mejor ajuste en forma de pendiente puntual. Utilice D y x para las variables dependientes e independientes, respectivamente. Resuelve la ecuación resultante para D y escribe tu resultado usando la notación de funciones.

d) Utilizar la ecuación desarrollada en la parte (c) para predecir la deuda crediticia no revolvente en el año 2008. e) Si la tendencia lineal pronosticada por la línea de mejor ajuste continúa, ¿en qué año la deuda crediticia no revolvente alcanzará 2.0 billones de dólares?

Ejercicio\(\PageIndex{3}\)

Según la Oficina de Transporte de Estados Unidos (www.bts.gov), las ventas minoristas de autos nuevos disminuyeron cada año entre 2000 y 2004, como se muestra en la siguiente tabla.

Año	años x después de 2000	Ventas S en miles
2001	0	8847
2002	1	8423
2003	2	8103
2004	3	7610
2005	4	7506

a) Establecer un sistema de coordenadas sobre papel cuadriculado, colocando las ventas S en el eje vertical, y los años x después de 2000 en el eje horizontal. Etiquete y escale cada eje de manera apropiada. Dibuja lo que sientes es la línea de mejor ajuste. Recuerda dibujar todas las líneas con una regla.

b) Seleccione dos puntos en su línea de mejor ajuste que no sean de la tabla de datos anterior. Utilice estos dos puntos para determinar la pendiente de la línea. Incluye unidades con tu respuesta. Escribe una oración o dos explicando el significado real de la pendiente de la línea de mejor ajuste en el mundo real.

c) Utilizar uno de los dos puntos de la línea y la pendiente para determinar la ecuación de la línea de mejor ajuste en forma de punto-pendiente. Utilice S y x para las variables dependientes e independientes, respectivamente. Resuelve la ecuación resultante para S y escribe tu resultado usando la notación de funciones.

d) Utilizar la ecuación desarrollada en la parte (c) para predecir las ventas en el año 2006.

e) Si continúa la tendencia lineal pronosticada por la línea de mejor ajuste, ¿cuándo bajarán las ventas a 7 millones de autos al año?

Contestar

a) Escalar y etiquetar los ejes, trazar los puntos, luego dibujar la línea de mejor ajuste.

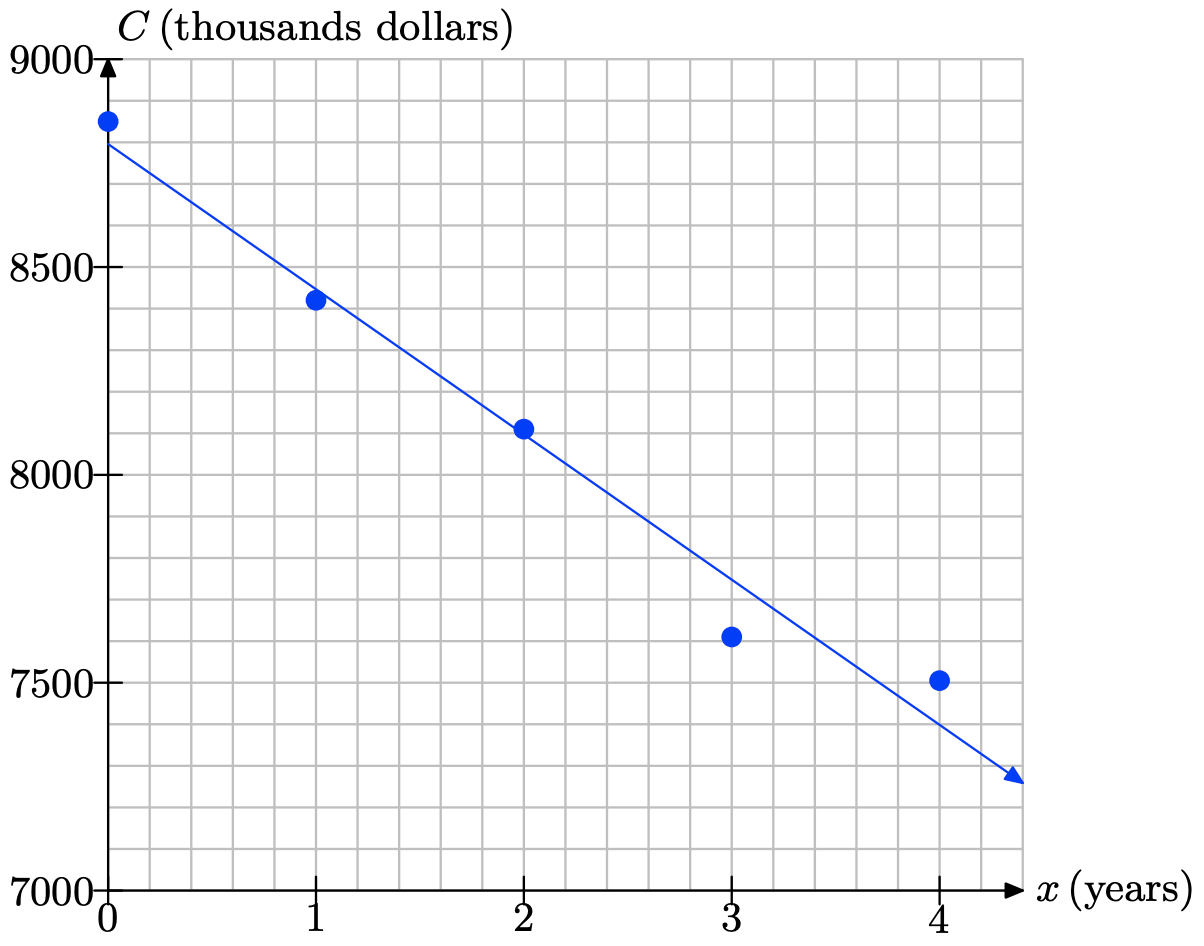
b) Seleccionar dos puntos, P (1.4, 8300) y Q (4.0, 7400) que sean puntos en la línea pero no puntos en la tabla de datos original.

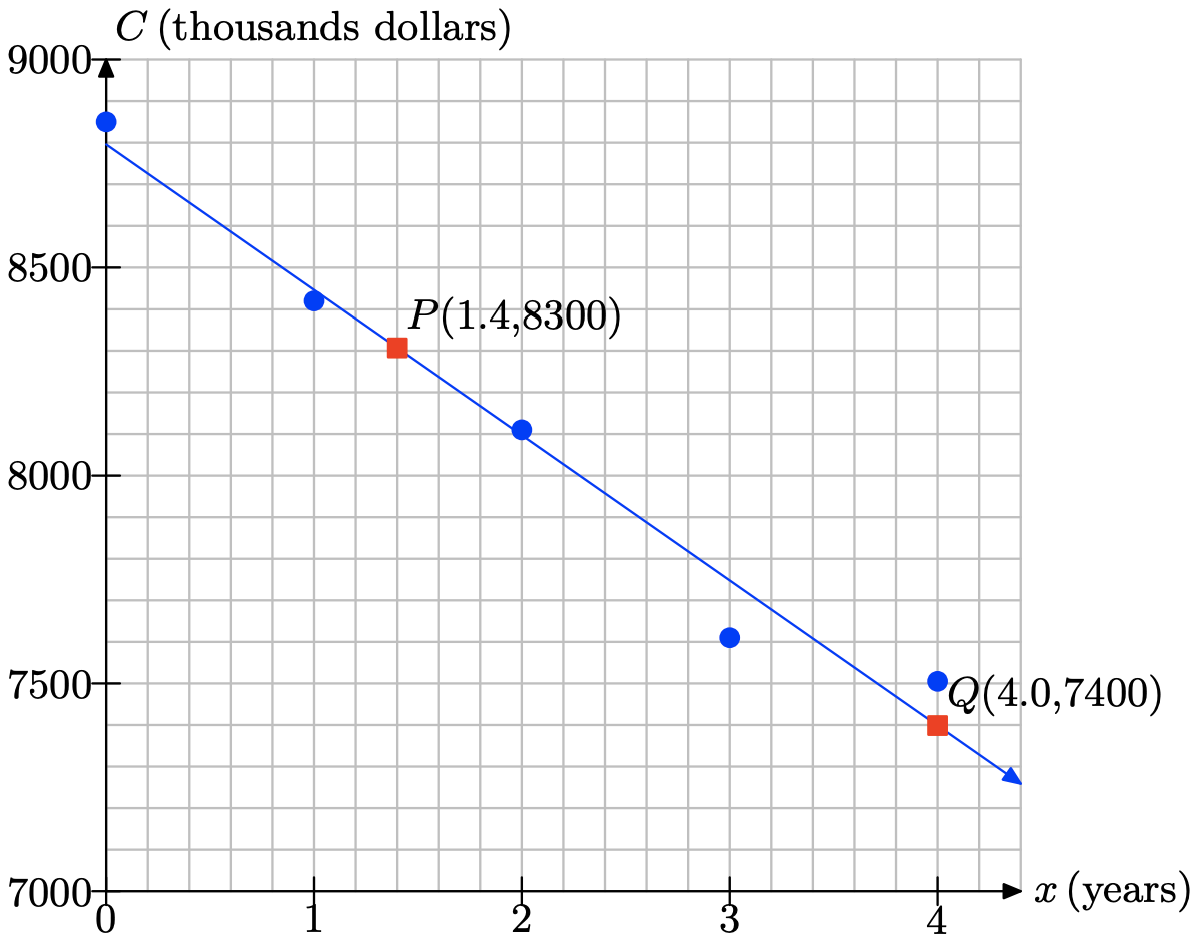
Usa estos dos puntos para calcular la pendiente de la línea de mejor ajuste.

\[m = \dfrac{\delta C }{\delta x} = \dfrac{8300 − 7400 }{4.0 − 1.4}\]mil coches/año Utilizando una calculadora, la pendiente es de aproximadamente −346.15 mil autos al año. Lo que esto significa es que las ventas de autos nuevos están disminuyendo a una tasa aproximada de 346 mil autos al año.

c) Para encontrar la ecuación de la línea, utilice el punto P (1.4, 8300) y la pendiente m = −346.15 en la forma punto-pendiente de la línea.

\[y − y_{0} = m(x − x_{0}) \\ y − 8300 = −346.15(x − 1.4)\]

Reemplace y y x por S y x, respectivamente, luego resuelva para S en términos de x.

\[S − 8300 = −346.15(x − 1.4) \\ S − 8300 = −346.15x + 484.61 \\ S = −346.15x + 8784.61\]

En notación de funciones, S (x) = −346.15x + 8784.61. Nota: Las respuestas variarán algo debido a la naturaleza subjetiva de dibujar la línea de mejor ajuste y elegir puntos en la línea.

d) Para determinar las ventas en 2006, evaluar S (x) = −346.15x+8784.61 a x = 2006− 2000 = 6.

\[S(6) = −346.15(6) + 8784.61 = 6707.71\]

De esta manera, las ventas serán aproximadamente de 6,707,710 autos nuevos.

e) Para determinar cuándo bajarán las ventas de autos nuevos a 7 millones, debemos resolver

\[S(x) = 7000. −346.15x + 8784.61 = 7000 \\ −346.15x = −1784.61 \\ x \approx 5.16\]

De ahí que las ventas alcancen los 7 millones de autos en algún lugar del año 2005-2006.

Ejercicio\(\PageIndex{4}\)

La siguiente tabla muestra la población total del mundo a mitad de año según la Oficina del Censo de Estados Unidos, (www.census.gov) para los últimos años.

Año	años x después de 2000	Población P en miles de millones
2000	0	6.08
2001	1	6.16
2002	2	6.23
2003	3	6.30
2004	4	6.38
2005	5	6.45
2006	6	6.53

a) Establecer un sistema de coordenadas en papel cuadriculado, colocando la población P en el eje vertical, y los años x después de 2000 en el eje horizontal. Etiquete y escale cada eje de manera apropiada. Dibuja lo que sientes es la línea de mejor ajuste. Recuerda dibujar todas las líneas con una regla.

b) Seleccione dos puntos en su línea de mejor ajuste que no sean de la tabla de datos anterior. Utilice estos dos puntos para determinar la pendiente de la línea. Incluye unidades con tu respuesta. Escribe una oración o dos explicando el significado real de la pendiente de la línea de mejor ajuste en el mundo real.

c) Utilizar uno de los dos puntos de la línea y la pendiente para determinar la ecuación de la línea de mejor ajuste en forma de punto-pendiente. Utilice P y x para las variables dependientes e independientes, respectivamente. Resuelve la ecuación resultante para P y escribe tu resultado usando la notación de funciones.

d) Utilizar la ecuación desarrollada en la parte (c) para predecir la población en 2010.

e) Si continúa la tendencia lineal predicha por la línea de mejor ajuste, ¿cuándo llegará la población mundial a los 7 mil millones?

Ejercicio\(\PageIndex{5}\)

La siguiente tabla muestra un extracto de los datos de 2005 de la Oficina del Censo de Estados Unidos (www.census.gov) sobre las ventas anuales de casas nuevas en Estados Unidos.

Rango de precios (miles de $)	Número vendido (miles)
150 − 199	246
200 − 249	200
250 − 299	152

No podemos usar rangos de precios como valores de coordenadas (debemos tener valores únicos), por lo que reemplazamos cada rango de precios de la tabla con un solo precio en el medio del rango, el valor promedio de una vivienda en ese rango. Esto nos da la siguiente tabla modificada:

Precio Promedio P (miles de $)	Número vendido N (miles)
175	246
225	200
275	152

Ahora podemos trazar los datos en un sistema de coordenadas.

a) Ingresa los datos en tu calculadora y haz un diagrama de dispersión. Cópielo en su papel, etiquetándolo adecuadamente.

b) Usa tu calculadora para determinar una línea que mejor se ajuste. A esto se le llama función de demanda lineal, ya que permite predecir la demanda de casas con un precio determinado. Escríbalo usando notación de funciones y redondea a la milésima más cercana. Grafíquelo en su calculadora y cópielo en su sistema de coordenadas.

c) Utilizar la función de demanda lineal para predecir las ventas anuales de viviendas con un precio de $200, 000. Intente utilizar la función TABLE en su calculadora para hacer esta predicción.

Contestar

a) Seleccione STAT, luego 1:Editar e ingrese los datos como se muestra en (a). Seleccione 2da PARCELA STAT, luego encienda Trazo1 como se muestra en (b). Seleccione la gráfica de dispersión, elija las listas que utilizó para los datos, luego un marcador, como se muestra en (b). Finalmente, seleccione 9:ZoomStat en el menú ZOOM para producir la parcela en (c).

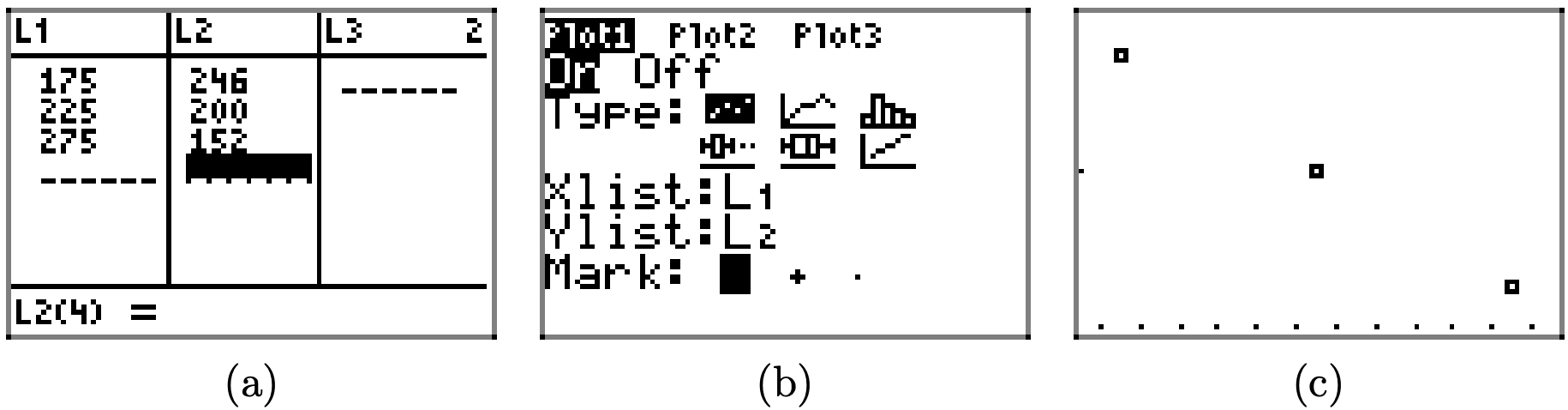
b) Presione el botón STAT, flecha derecha hacia el menú CALC, luego seleccione 4:LinReg (ax+b), seguido de L1, una coma, L2, una coma e Y1 en el menú VARS (seleccione Y-VARS luego 1:Submenús de función). El resultado se muestra en (a). Pulse INTRO para producir el cálculo que se muestra en (b). Esta es la línea de mejor ajuste. Este procedimiento también almacena la línea de mejor ajuste en Y1, por lo que al presionar el botón GRAPH se obtiene la línea de mejor ajuste que se muestra en (c).

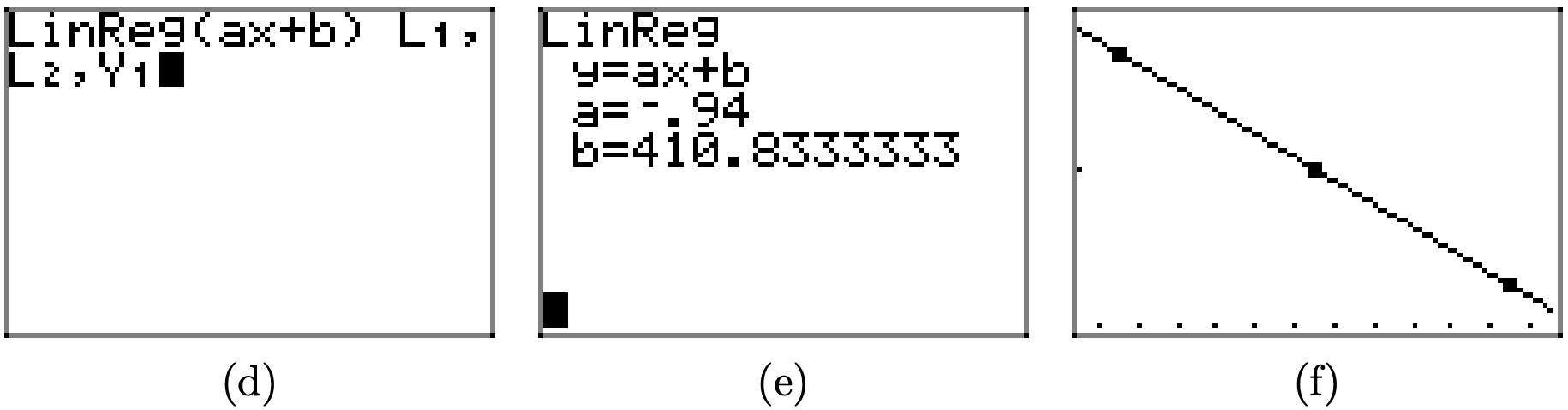
En (b) anterior, vemos que el número vendido N, en función del precio promedio P viene dado por la función lineal N (P) = −0.94P + 410.833.

c) Si todo salió bien en la parte (b), entonces podemos presionar 2nd TBL SET y configurar los parámetros de la tabla como se muestra en (g). Asegúrese de que la variable independiente esté establecida en ASK. Selecciona 2da TABLA, luego ingresa 200 (lo que representa un precio promedio p = $200, 000) como se muestra en (h).

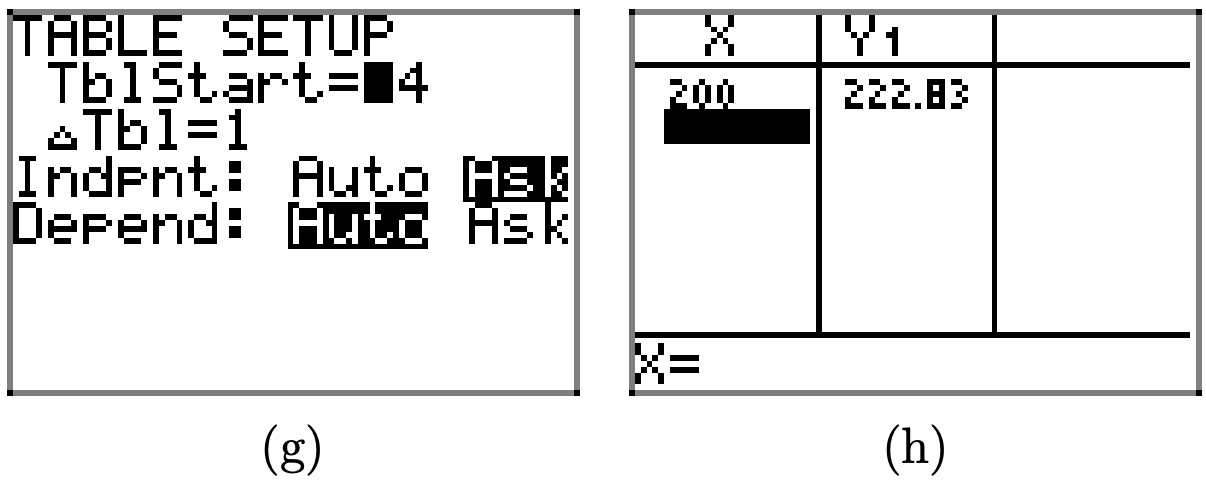
Así, N (200) = 222.83, por lo que aproximadamente 222.83 mil o 222, 830 viviendas se venden al precio promedio de $200,000.

Ejercicio\(\PageIndex{6}\)

En la siguiente tabla se muestran datos de la Asociación Nacional de Constructores de Viviendas (www.nahb.org), indicando el precio medio de las viviendas nuevas en Estados Unidos.

Año	Precio medio (miles de $)
2000	169
2001	175
2002	188
2003	195
2004	221
2005	238

a) Ingresa los datos en tu calculadora y haz un diagrama de dispersión. Cópielo en su papel, etiquetándolo adecuadamente.

b) Utilice su calculadora para determinar una línea de mejor ajuste que pueda usarse para predecir el precio medio de las casas nuevas en años futuros. Escríbelo usando la notación de funciones. Grafíquelo en su calculadora y cópielo en su sistema de coordenadas.

c) Utilizar la función de demanda lineal para predecir el precio medio de una vivienda nueva en 2010. Intente utilizar la función TABLE en su calculadora para hacer esta predicción.

d) Mirando la gráfica, ¿cree que la función de demanda lineal modela bien los puntos de datos reales? Si no, ¿por qué no? ¿Qué significa esto sobre la predicción que hiciste en la parte (c)?

Ejercicio\(\PageIndex{7}\)

Jim está colgando bloques de varias masas en un resorte en el laboratorio de física. Se da cuenta de que el resorte se estirará aún más si agrega más masa al final del resorte. Pronto está convencido de que la distancia que estirará el resorte depende de la cantidad de masa que se le adhiera. Decide tomar algunas medidas. Registra la cantidad de masa adherida al final del resorte y luego mide la distancia que estiró el resorte. Aquí están los datos de Jim.

Masa (gramos)	Distancia Estirada (cm)
50	1.2
100	1.9
150	3.1
200	4.0
250	4.8
300	6.2

a) Ingresa los datos en tu calculadora y haz un diagrama de dispersión. Cópielo en su papel, etiquetándolo adecuadamente.

b) Use su calculadora para determinar una línea de mejor ajuste que pueda usarse para predecir la distancia que estira el resorte. Escríbelo usando la notación de funciones. Grafíquelo en su calculadora y cópielo en su sistema de coordenadas.

c) Utilice la función de la parte (c) para predecir la distancia que estirará el resorte si 175 gramos están unidos al resorte. Intente utilizar la función TABLE en su calculadora para hacer esta predicción.

Contestar

a) Seleccione STAT, luego 1:Editar e ingrese los datos como se muestra en (a). Seleccione 2da PARCELA STAT, luego encienda Trazo1 como se muestra en (b). Seleccione la gráfica de dispersión, elija las listas que utilizó para los datos, luego un marcador, como se muestra en (b). Finalmente, seleccione 9:ZoomStat en el menú ZOOM para producir la parcela en (c).

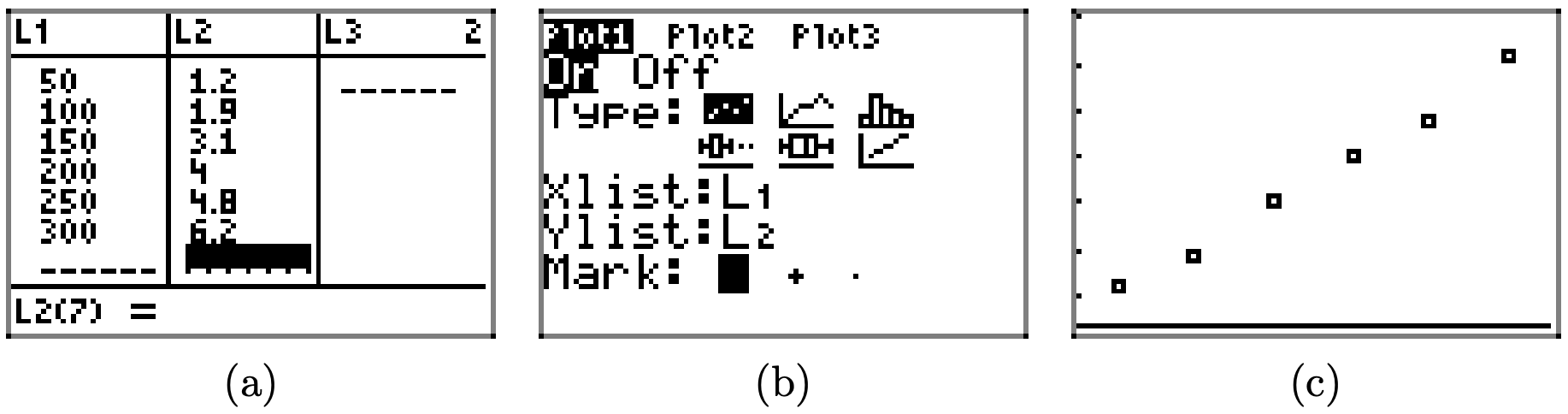
b) Presione el botón STAT, flecha derecha hacia el menú CALC, luego seleccione 4:LinReg (ax+b), seguido de L1, una coma, L2, una coma e Y1 en el menú VARS (seleccione Y-VARS luego 1:Submenús de función). El resultado se muestra en (a). Pulse INTRO para producir el cálculo que se muestra en (b). Esta es la línea de mejor ajuste. Este procedimiento también almacena la línea de mejor ajuste en Y1, por lo que al presionar el botón GRAPH se obtiene la línea de mejor ajuste que se muestra en (c).

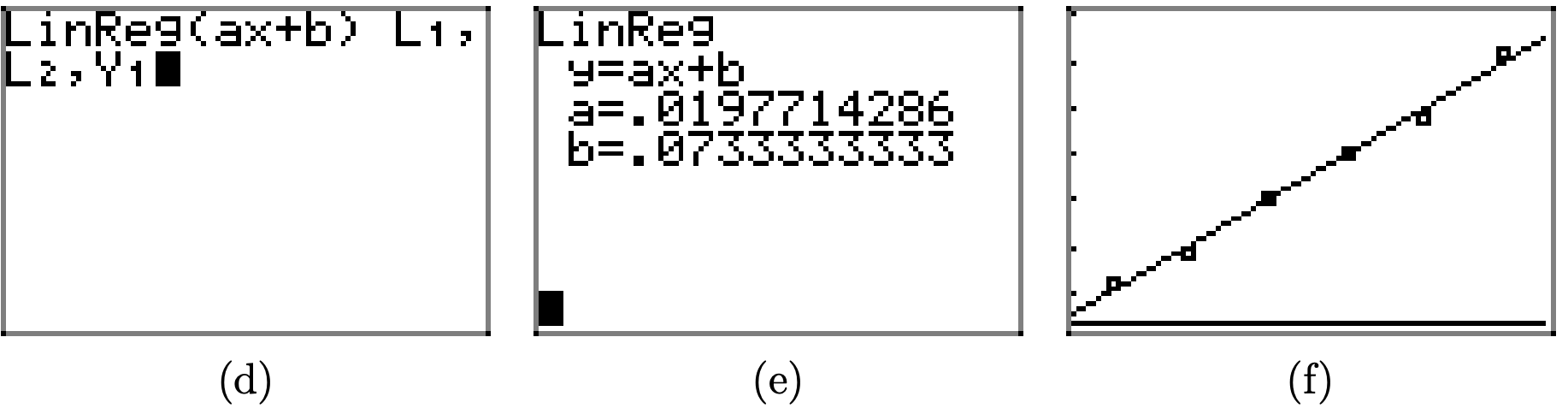
En (b) anterior, vemos que la distancia estirada d, en función de la masa m viene dada por la función lineal d (m) = 0.01977m + 0.07333.

c) Si todo salió bien en la parte (b), entonces podemos presionar 2nd TBL SET y configurar los parámetros de la tabla como se muestra en (g). Asegúrese de que la variable independiente esté establecida en ASK. Seleccione 2da TABLA, luego ingrese 175 (que representa una masa de 175 gramos) como se muestra en (h).

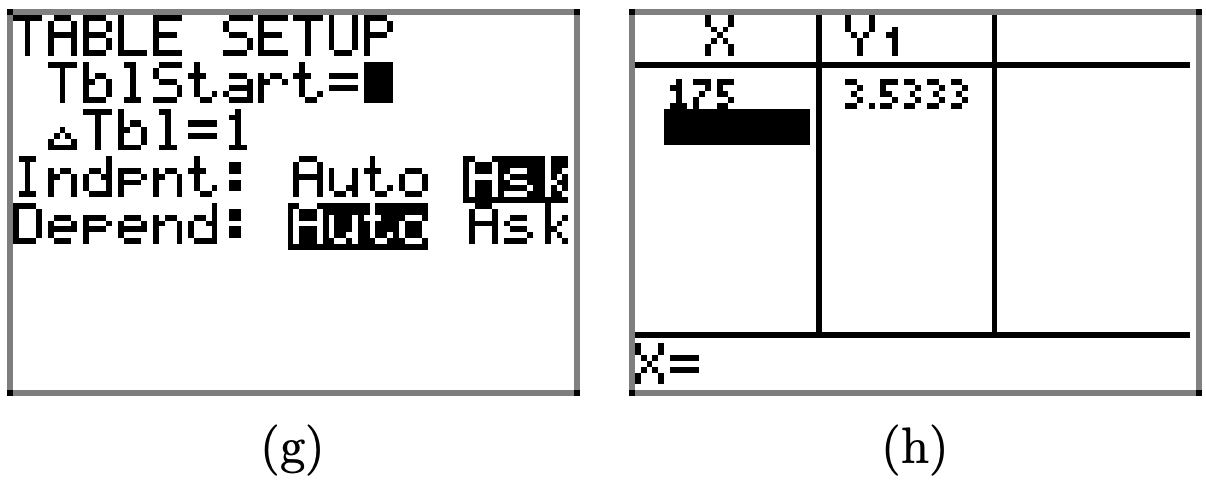
Así, d (175) = 3.5333, por lo que el resorte se estira aproximadamente 3.53 centímetros cuando se une una masa de 175 gramos.

Ejercicio\(\PageIndex{8}\)

Dave y Melody son compañeros de laboratorio en el laboratorio de química de Tony Sartori por la tarde. El profesor Sartori ha preparado un experimento para ayudarles a descubrir la relación entre las escalas de temperatura Celsius y Fahrenheit. El experimento consiste en un vaso lleno de hielo y dos termómetros, uno calibrado en la escala Fahrenheit y el otro en la escala Celsius. Dave y Melody usan un quemador Bunsen para calentar el vaso de precipitados, eventualmente llevando el agua en el vaso al punto de ebullición. Cada pocos minutos hacen dos lecturas de temperatura, una en Fahrenheit, otra en Celsius. A continuación se indican los datos que registran durante la sesión de laboratorio.

Celsius	Fahrenheit
4.0	39
18	65
30	85
51	122
70	159
85	186
100	210

a) Ingresa los datos en tu calculadora y haz un diagrama de dispersión. Cópielo en su papel, etiquetándolo adecuadamente.

b) Use su calculadora para determinar una línea de mejor ajuste que pueda usarse para predecir la temperatura Fahrenheit en función de la temperatura Celsius. Escríbelo usando la notación de funciones. Grafíquelo en su calculadora y cópielo en su sistema de coordenadas.

c) Utilizar la función de la parte (c) para predecir la temperatura Fahrenheit si la temperatura Celsius es 40. Intente utilizar la función TABLE en su calculadora para hacer esta predicción.

d) Utilizar la función de la parte (c) para predecir la temperatura Celsius si la temperatura Fahrenheit es 100.

Ejercicio\(\PageIndex{9}\)

En la siguiente tabla se muestran datos sobre las ventas de viviendas en la Costa Mendocino en 2005.

Rango de precios (miles de $)	Número vendido (miles)
200 − 299	14
300 − 399	55
400 − 499	62

No podemos usar rangos de precios como valores de coordenadas (debemos tener valores únicos), por lo que reemplazamos cada rango de precios de la tabla con un solo precio en el medio del rango, el valor promedio de una vivienda en ese rango. Esto nos da la siguiente tabla modificada:

Precio Promedio P (miles de $)	Número vendido N (miles)
250	14
350	55
450	62

Ahora podemos trazar los datos en un sistema de coordenadas.

a) Ingresa los datos en tu calculadora y haz un diagrama de dispersión. Cópielo en su papel, etiquetándolo adecuadamente.

b) Usa tu calculadora para determinar una línea que mejor se ajuste. Escríbalo usando notación de funciones y redondea a la milésima más cercana. Grafíquelo en su calculadora y cópielo en su sistema de coordenadas.

c) Utilizar la función lineal para predecir las ventas de casas en el rango de precios $500, 000− $599, 000. Utilice el precio promedio de $550, 000 para esta estimación.

d) El número real de casas vendidas en el rango de precios $500, 000 − $599, 000 fue 41. Trace esto como un punto en su sistema de coordenadas y compárelo con la predicción de su modelo de función lineal. Observe que este valor real es bastante diferente de la predicción.

e) ¡Lo que esto significa es que un modelo lineal no es muy bueno para los datos para las ventas de viviendas! Dibuja una curva simple que recorra cada uno de los puntos de datos. ¡Observe que no se parece mucho a la forma de una línea! Se requieren funciones más sofisticadas para modelar este ejemplo, como las funciones cuadráticas, que estudiamos en un capítulo posterior. ¡La moraleja de la historia aquí es que no todos los conjuntos de datos se pueden modelar linealmente!

Contestar

a) Seleccione STAT, luego 1:Editar e ingrese los datos como se muestra en (a). Seleccione 2da PARCELA STAT, luego encienda Trazo1 como se muestra en (b). Seleccione la gráfica de dispersión, elija las listas que utilizó para los datos, luego un marcador, como se muestra en (b). Finalmente, seleccione 9:ZoomStat en el menú ZOOM para producir la parcela en (c).

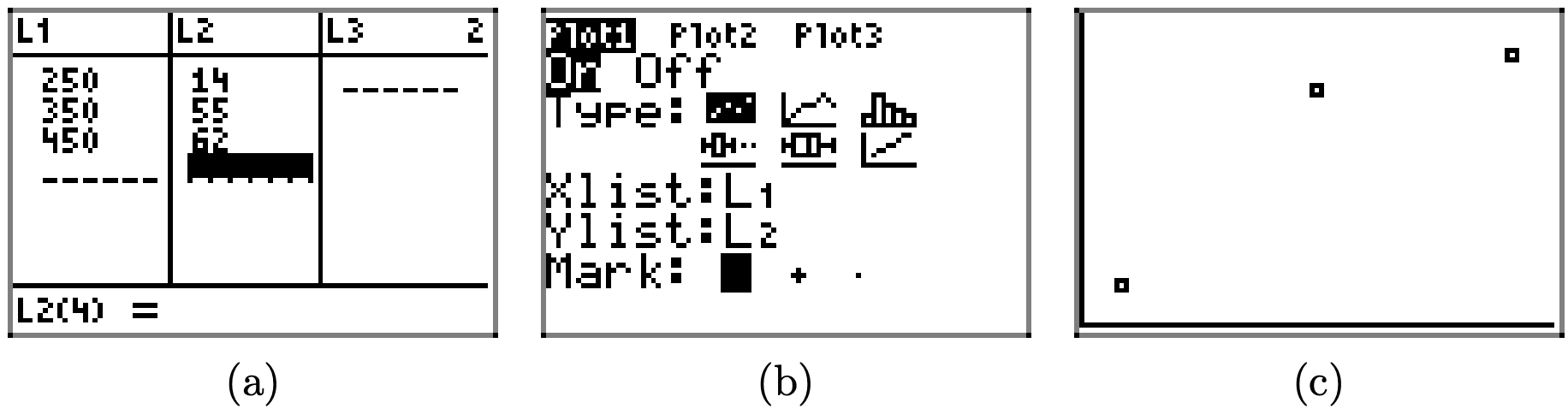
b) Presione el botón STAT, flecha derecha hacia el menú CALC, luego seleccione 4:LinReg (ax+b), seguido de L1, una coma, L2, una coma e Y1 en el menú VARS (seleccione Y-VARS luego 1:Submenús de función). El resultado se muestra en (a). Pulse INTRO para producir el cálculo que se muestra en (b). Esta es la línea de mejor ajuste. Este procedimiento también almacena la línea de mejor ajuste en Y1, por lo que al presionar el botón GRAPH se obtiene la línea de mejor ajuste que se muestra en (c).

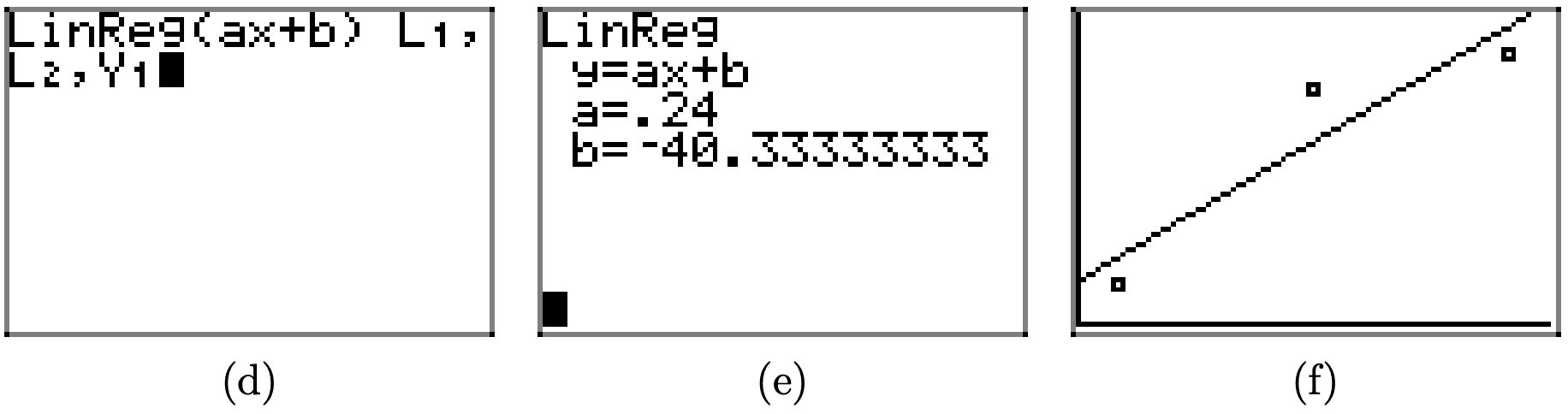
En (b) anterior, vemos que el número vendido N, en función del precio promedio P viene dado por la función lineal N (P) = 0.24P − 40.33.

c) Si todo salió bien en la parte (b), entonces podemos presionar 2nd TBL SET y configurar los parámetros de la tabla como se muestra en (g). Asegúrese de que la variable independiente esté establecida en ASK. Selecciona 2da TABLA, luego ingresa 550 (que representa un precio promedio P = $550, 000) como se muestra en (h).

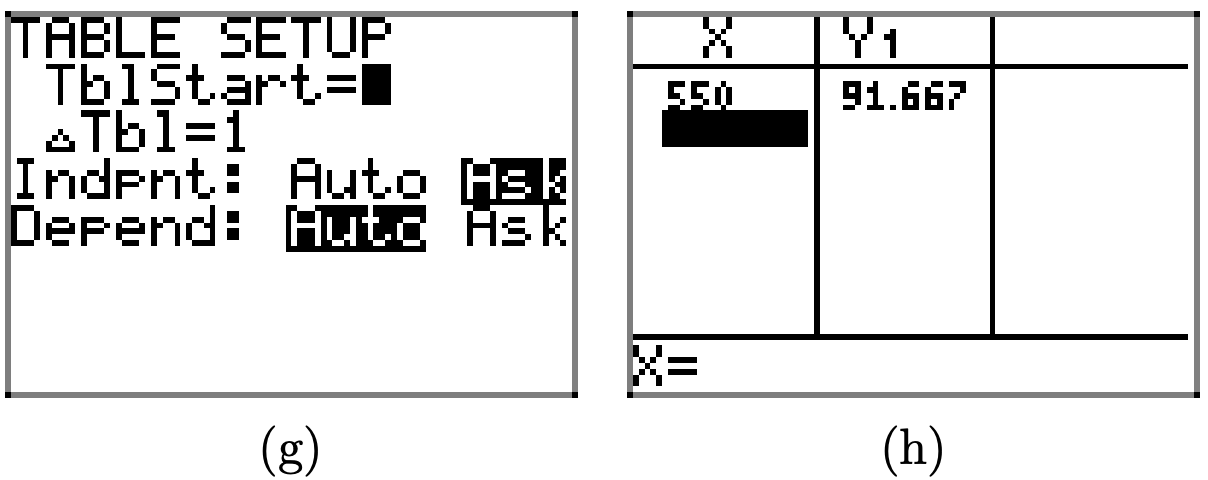
Así, N (550) = 91.667, por lo que aproximadamente 91.667 mil o 91, 667 viviendas se venden al precio promedio de $550,000. d) Presiona el botón STAT, selecciona 1:Editar y agrega el punto (550, 41) a la tabla, como se muestra en (i). Seleccione 9:ZoomStat en el menú ZOOM para producir la imagen en (j). Tenga en cuenta que los datos ya no representan una tendencia lineal, sino algo más no lineal (curvilíneo)

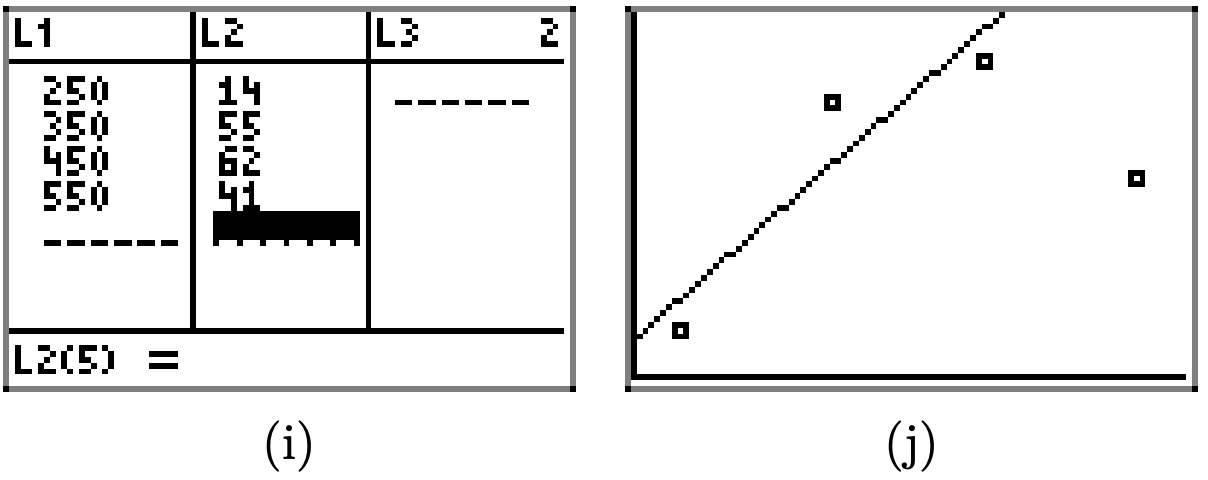
e) En (k) hemos dibujado una curva suave de mejor ajuste.

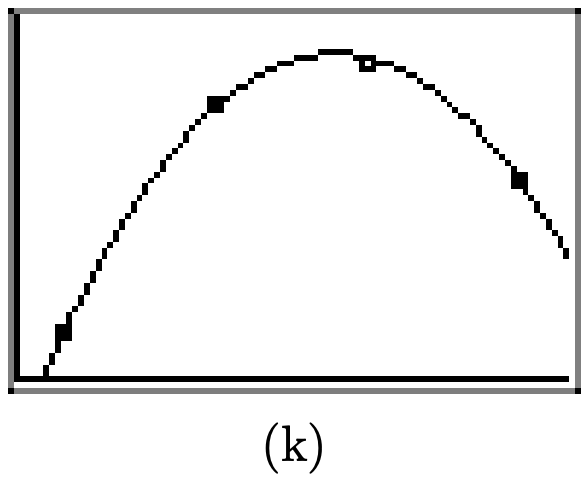
Ejercicio\(\PageIndex{10}\)

Lo siguiente de la edición del 14 de julio de 2006 del periódico Being Today muestra cómo los tacones altos afectan la bola del pie. En la tabla se muestra el incremento en porcentaje de presión sobre la bola del pie para determinadas alturas de talones.

Altura del tacón h (pulgadas)	% de aumento en la presión
1	22
2	57

a) Ingresa los datos en tu calculadora y haz un diagrama de dispersión. Cópielo en su papel, etiquetándolo adecuadamente.

b) Observe que, debido a que tenemos exactamente dos puntos de datos, la línea de mejor ajuste es la línea que pasa por ambos puntos. Para comenzar a encontrar la ecuación, utilice la fórmula de pendiente para calcular la pendiente.

c) Utilice la forma punto-pendiente para encontrar una ecuación para la línea. Escríbelo en forma de pendiente-intercepción.

d) Utilizar la función lineal para predecir el porcentaje de aumento de tensión para un talón de 3 pulgadas.

e) El porcentaje real de aumento de presión para un talón de 3 pulgadas es del 76%. Trace esto como un punto en su sistema de coordenadas y compárelo con la predicción de su modelo de función lineal. Observe que este valor real es bastante diferente de la predicción.

f) ¡Lo que esto significa es que un modelo lineal no es muy bueno para los datos! Dibuja una curva simple que recorra cada uno de los puntos de datos. ¡Observe que no se parece mucho a la forma de una línea! Se requieren funciones más sofisticadas para modelar este ejemplo. ¡No todos los conjuntos de datos deben modelarse linealmente!