5.3: Ceros de la Cuadrática

Hemos visto cómo la forma de vértice y el uso inteligente del eje de simetría pueden ayudar a dibujar una gráfica precisa de la función cuadrática definida por la ecuación\(f(x) = ax^2+bx+c\). Al dibujar la gráfica de la parábola es útil saber dónde la gráfica de la parábola cruza el eje x. Ese es el objetivo principal de esta sección, encontrar los cruces cero o intercepciones x de la parábola.

Antes de comenzar, deberás revisar las técnicas que te permitirán facturar la expresión cuadrática\(ax^2 + bx + c\).

Factorización\(ax^2 + bx + c\) cuando a = 1

Nuestra intención en esta sección es proporcionar una revisión rápida de las técnicas utilizadas para facturar trinomios cuadráticos. Comenzamos mostrando cómo factorial trinomios que tienen la forma\(ax^2 + bx + c\), donde el coeficiente principal es a = 1; es decir, trinomios que tienen la forma\(x^2+bx+c\). En la siguiente sección, abordaremos la técnica utilizada para factorial\(ax^2+bx+c\) cuándo\(a \neq 1\).

Empecemos con un ejemplo.

Ejemplo\(\PageIndex{1}\)

Factor\(x^{2}+16 x-36\)

Solución

Obsérvese que el coeficiente principal, el coeficiente de\(x^2\), es un 1. Esta es una observación importante, porque la técnica aquí presentada no funcionará cuando el coeficiente principal no sea igual a 1.

Obsérvese que el término constante del trinomio\(x^2 + 16x − 36\) es −36. Enumere todos los pares enteros cuyo producto sea igual a −36.

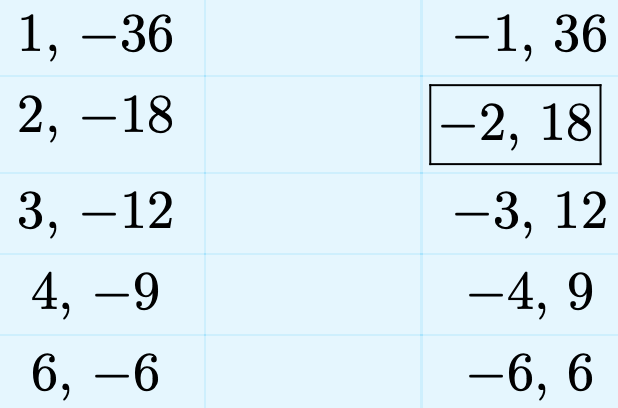
Tenga en cuenta que hemos enmarcado el par −2, 18. Hemos hecho esto porque la suma de este par de enteros es igual al coeficiente de x en la expresión trinomial\(x^2 + 16x − 36\). Usa este par enmarcado para factorizar el trinomio.

\[x^{2}+16 x-36=(x-2)(x+18)\]

Es importante que revises tu resultado. Utilice la propiedad distributiva para multiplicar.

\[\begin{aligned}(x-2)(x+18) &=x(x+18)-2(x+18) \\ &=x^{2}+18 x-2 x-36 \\ &=x^{2}+16 x-36 \end{aligned}\]

Así, nuestra factorización es correcta.

Resumimos la técnica.

Algorithm

Para factorizar la cuadrática\(x^2 + bx + c\), proceda de la siguiente manera:

1. Enumere todos los pares enteros cuyo producto es igual a c.
2. Circular o encuadrar el par cuya suma es igual al coeficiente de x, es decir, b. Utilice este par para facturar el trinomio.

Veamos otro ejemplo.

Ejemplo\(\PageIndex{2}\)

Factorizar el trinomio\(x^{2}-25 x-84\)

Solución

Enumere todos los pares enteros cuyo producto es −84.

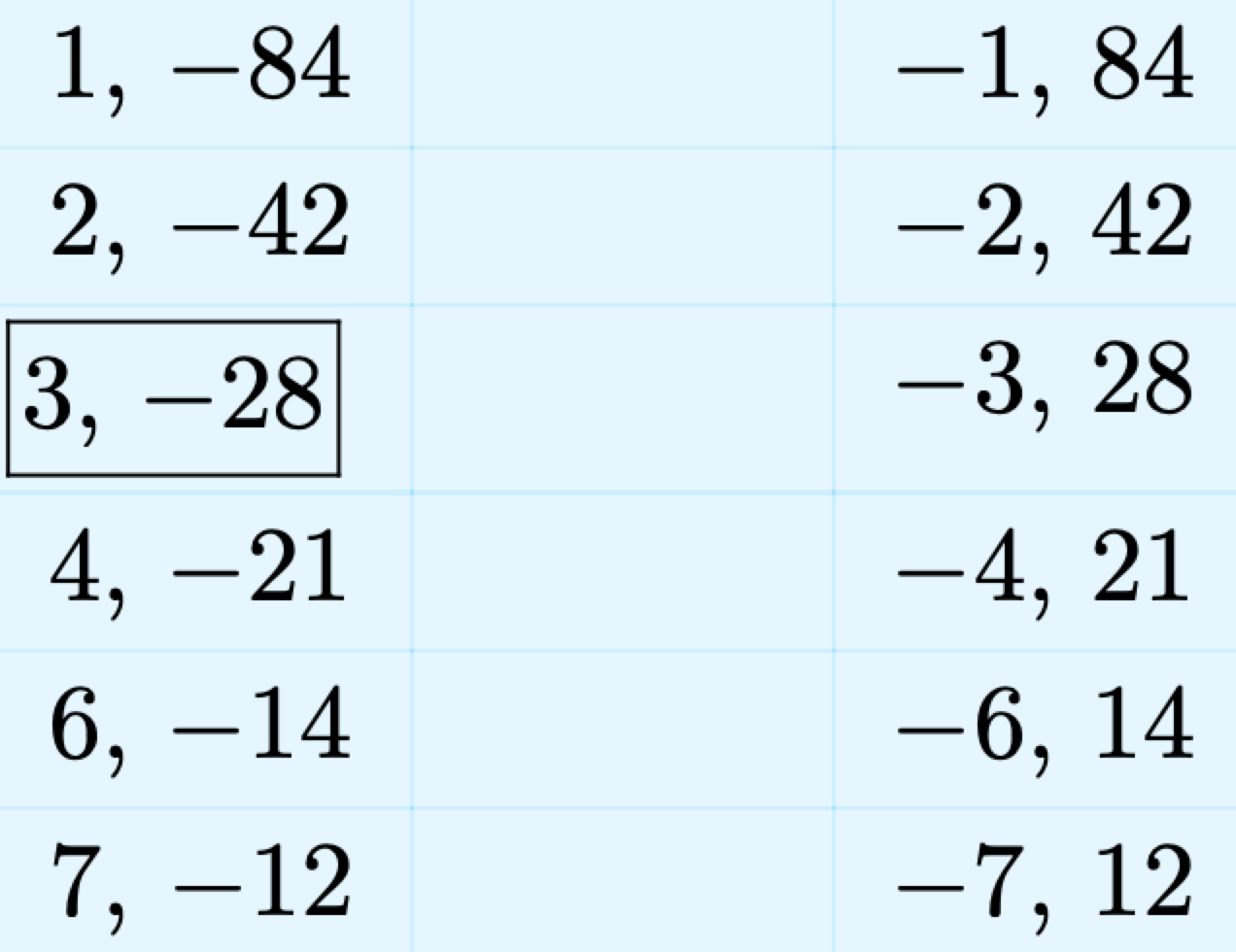
Hemos enmarcado el par cuya suma es igual al coeficiente de x, es decir, −25. Usa este par para factorizar el trinomio.

\[x^{2}-25 x-84=(x+3)(x-28) \nonumber\]

Cheque

\[\begin{aligned}(x+3)(x-28) &=x(x-28)+3(x-28) \\ &=x^{2}-28 x+3 x-84 \\ &=x^{2}-25 x-84 \end{aligned}\]

Con experiencia, hay una serie de ideas que acelerarán el proceso.

• Como estás listando los pares enteros, si por casualidad observas que el par actual tiene la suma apropiada, no hay necesidad de enumerar los pares enteros restantes. Simplemente detenga el proceso de enumerar los pares enteros y use el par actual para factorial el trinomio.
• Algunos alumnos están perfectamente contentos de que se les pregunte “¿Se puede pensar en un par entero cuyo producto es c y cuya suma es b (donde b y c se refieren a los coeficientes de\(x^2 +bx+c\))?” Si puedes escoger el par “fuera del aire” así, todo está bien y bien.

Usa el par entero para factorial el trinomio y no te molestes en enumerar ningún par entero.

Ahora, investiguemos cómo proceder cuando el coeficiente principal no es 1.

Factorización\(a x^{2}+b x+c\) cuando\(a \neq 1\)

Cuando\(a \neq 1\), utilizamos una técnica llamada prueba ac para facturar el trinomio\(ax^2 + bx + c\). El proceso se explica mejor con un ejemplo.

Ejemplo\(\PageIndex{3}\)

Factor\(2x^2 + 13x − 24\).

Solución

Obsérvese que el coeficiente principal no es igual a 1. En efecto, el coeficiente de\(x^2\) en este ejemplo es un 2. Por lo tanto, la técnica de los ejemplos anteriores no funcionará. Así, recurrimos a una técnica similar llamada ac-test.

Primero, compare\[2 x^{2}+13 x-24 \qquad \text { and } \qquad a x^{2}+b x+c\]

y tenga en cuenta que a = 2, b = 13 y c = −24. Calcular el producto de a y c. Así es como la técnica gana su nombre “ac-test”.

\[a c=(2)(-24)=-48 \nonumber\]

Enumere todos los pares enteros cuyo producto es ac = −48.

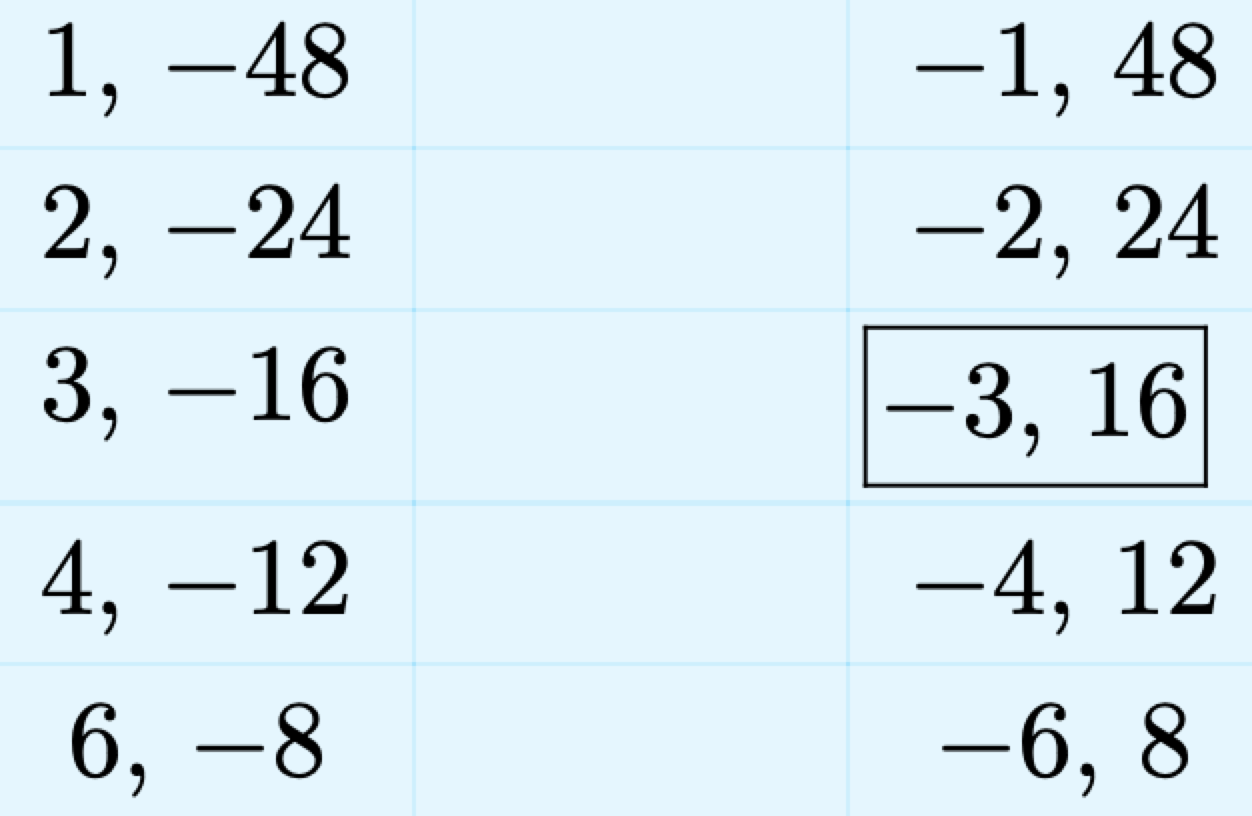
Hemos enmarcado al par cuya suma es b = 13. El siguiente paso es reescribir el trinomio\(2x^2 + 13x − 24\), dividiendo el término medio en una suma, usando nuestro par entero enmarcado.

\[2 x^{2}+13 x-24=2 x^{2}-3 x+16 x-24 \nonumber\]

Facturamos una x de los dos primeros términos, luego un 8 de los dos últimos términos. Este proceso se llama factorización por agrupación.

\[2 x^{2}-3 x+16 x-24=x(2 x-3)+8(2 x-3) \nonumber\]

Ahora factorizamos un factor común de 2x − 3.

\[x(2 x-3)+8(2 x-3)=(x+8)(2 x-3) \nonumber\]

Es útil ver el proceso completo como una unidad coherente.

\[\begin{aligned} 2 x^{2}+13 x-24 &=2 x^{2}-3 x+16 x-24 \\ &=x(2 x-3)+8(2 x-3) \\ &=(x+8)(2 x-3) \end{aligned}\]

Cheque

Nuevamente, es importante verificar la respuesta por multiplicación.

\[\begin{aligned}(x+8)(2 x-3) &=x(2 x-3)+8(2 x-3) \\ &=2 x^{2}-3 x+16 x-24 \\ &=2 x^{2}+13 x-24 \end{aligned}\]

Debido a que este es el trinomio original, nuestra solución comprueba.

Resumimos este proceso.

Algoritmo: Prueba AC

Para factorizar la cuadrática\(ax^2 + bx + c\), proceda de la siguiente manera:

1. Enumere todos los pares enteros cuyo producto sea igual a ac.
2. Circular o encuadrar el par cuya suma es igual al coeficiente de x, es decir, b.
3. Utilice el par con un círculo para expresar el término medio bx como una suma.
4. Factorizar por “agrupación”.

Veamos otro ejemplo.

Ejemplo\(\PageIndex{4}\)

Factor\(3 x^{2}+34 x-24\)

Solución

Comparar

\[3 x^{2}+34 x-24 \quad \text { and } \quad a x^{2}+b x+c \nonumber\]

y tenga en cuenta que a = 3, b = 34 y c = −24. Enumere todos los pares enteros cuyo producto es igual a ac = (3) (−24) = −72.

Hemos enmarcado el par cuya suma es la misma que b = 34, el coeficiente de x in\(3x^2 + 34x − 24\). Nuevamente, los posibles atajos son posibles. Si puedes “pensar” en un par cuyo producto es ac = −72 y cuya suma es b = 34, entonces no es necesario enumerar ningún par entero. Alternativamente, si te encuentras con el par necesario mientras los estás listando, entonces puedes detener el proceso. No es necesario enumerar los pares restantes si tienes el que necesitas.

Use el par enmarcado para expresar el término medio como una suma, luego factifique por agrupación.

\[\begin{aligned} 3 x^{2}+34 x-24 &=3 x^{2}-2 x+36 x-24 \\ &=x(3 x-2)+12(3 x-2) \\ &=(x+12)(3 x-2) \end{aligned}\]

Dejamos que el lector verifique este resultado.

Intercepta

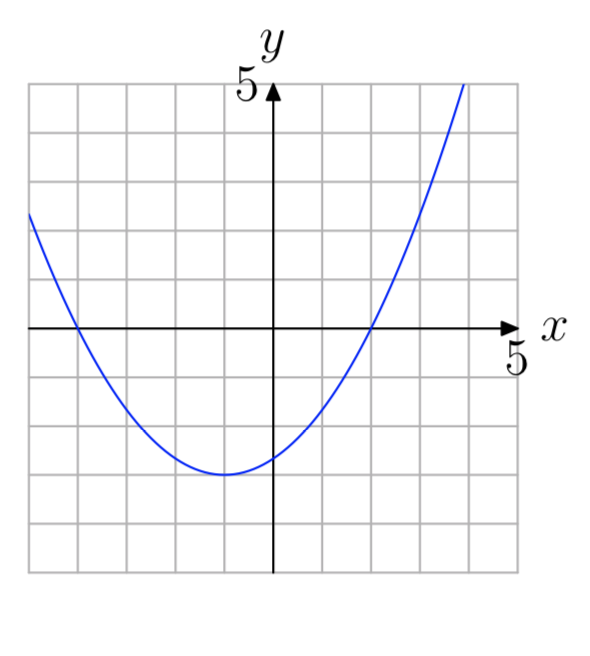
Los puntos donde la gráfica de una función cruza el eje x se denominan las intercepciones x de la gráfica de la función. Considere la gráfica de la función cuadrática f en la Figura\(\PageIndex{1}\).

Figura\(\PageIndex{1}\): Las intercepciones x e y son características clave de cualquier gráfica.

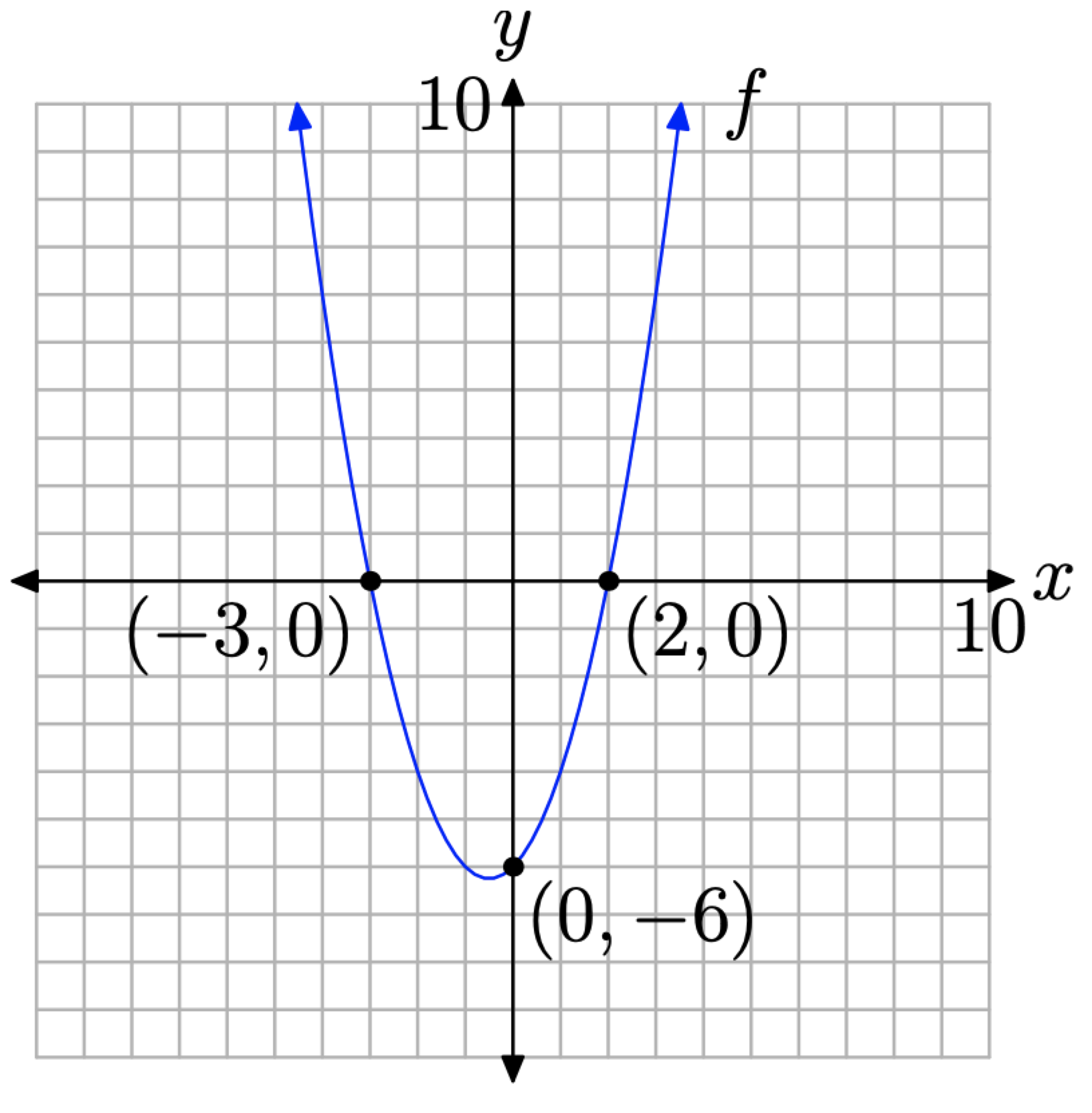
Tenga en cuenta que la gráfica de la f cruza el eje x en (−3, 0) y (2, 0). Estas son las intercepciones x de la parábola. Tenga en cuenta que la coordenada y de cada intercepción x es cero.

En notación de funciones, las soluciones de f (x) = 0 (observe la similitud con y = 0) son las coordenadas x de los puntos donde la gráfica de f cruza el eje x. Analizando la gráfica de f en la Figura\(\PageIndex{1}\), vemos que tanto −3 como 2 son soluciones de f (x) = 0.

Por lo tanto, el proceso para encontrar las intercepciones x es claro.

Encontrar intercepciones x

Para encontrar las intercepciones x de la gráfica de cualquier función, establezca y = 0 y resuelva para x. Alternativamente, si se usa la notación de función, establezca f (x) = 0 y resuelva para x.

Veamos un ejemplo.

Ejemplo\(\PageIndex{5}\)

Encuentra las intercepciones x de la gráfica de la función cuadrática definida por\(y = x^2 + 2x − 48\).

Solución

Para encontrar las intercepciones x, primero establece y = 0.

\[0=x^{2}+2 x-48\]

A continuación, factorizar el trinomio a la derecha. Tenga en cuenta que el coeficiente de\(x^2\) es 1. Solo necesitamos pensar en dos enteros cuyo producto sea igual al término constante −48 y cuya suma sea igual al coeficiente de x, a saber, 2. Los números 8 y −6 vienen a la mente, por lo que los factores trinomiales de la siguiente manera (los lectores deben verificar este resultado).

\[0=(x+8)(x-6)\]

Para completar la solución, necesitamos usar una propiedad importante de los números reales llamada propiedad cero del producto.

Propiedad de Producto Cero

Si a y b son algunos números reales tales que\[ab = 0\], entonces ya sea a = 0 o b = 0.

En nuestro caso, tenemos 0 = (x + 8) (x − 6). Por lo tanto, debe darse el caso de que

\[x+8=0 \qquad \text { or } \qquad x-6=0\]

Estas ecuaciones se pueden resolver de forma independiente para producir

\[x=-8 \quad \text { or } \quad x=6\]

Así, las intercepciones x de la gráfica de\(y = x^2 + 2x−48\) se ubican en (−8, 0) y (6, 0).

Veamos otro ejemplo.

Ejemplo\(\PageIndex{6}\)

Encuentra las intercepciones x de la gráfica de la función cuadrática\(f(x) = 2x^2 − 7x − 15\).

Solución

Para encontrar las intercepciones x de la gráfica de la función cuadrática f, comenzamos configurando

\[f(x)=0\nonumber\]

Por supuesto,\(f(x) = 2x^2 − 7x − 15\), así podemos sustituir para obtener

\[2 x^{2}-7 x-15=0 \nonumber\]

Ahora usaremos la prueba ac para facturar el trinomio de la izquierda. Tenga en cuenta que ac = (2) (−15) = −30. Enumere los pares enteros cuyos productos son iguales a −30.

Tenga en cuenta que el par enmarcado suma al coeficiente de x in\(2x^2 − 7x − 15\). Use el par enmarcado para expresar el término medio como una suma, luego factifique agrupando

\[\begin{aligned} 2 x^{2}-7 x-15 &=0 \\ 2 x^{2}+3 x-10 x-15 &=0 \\ x(2 x+3)-5(2 x+3) &=0 \\(x-5)(2 x+3) &=0 \end{aligned}\]

Ahora podemos usar la propiedad cero del producto. O bien

\[x-5=0 \qquad \text { or } \qquad 2 x+3=0 \nonumber\]

Cada uno de estos se puede resolver de forma independiente para obtener

\[x=5 \qquad \text { or } \qquad x=-3 / 2 \nonumber\]

Así, las intercepciones x de la gráfica de la función cuadrática\(f(x) = 2x^2 − 7x − 15\) se ubican en (−3/2, 0) y (5, 0).

Una definición más está en orden.

Definición 7: Ceros de una función

a las soluciones de f (x) = 0 se llaman los ceros de la función f.

Así, en el último ejemplo, tanto −3/2 como 5 son ceros de la función cuadrática\(f(x) = 2x^2−7x−15\). Observe la relación íntima entre los ceros de la función cuadrática y las intercepciones x de la gráfica. Tenga en cuenta que −3/2 es un cero y (−3/2, 0) es una intercepción x. Del mismo modo, 5 es un cero y (5, 0) es una intercepción x.

La calculadora gráfica se puede utilizar para encontrar los ceros de una función.

Ejemplo\(\PageIndex{7}\)

Usa la calculadora gráfica para encontrar los ceros de la función\(f(x) = 2x^2 − 7x − 15\).

Solución

Ingresa la función\(f(x) = 2x^2 − 7x − 15\_ into Y1 in the Y= menu; then adjust the window parameters as shown in Figure \(\PageIndex{2}\) (b). Presione el botón GRAPH para producir la parábola que se muestra en la Figura\(\PageIndex{2}\) (c).

Para encontrar un cero de la función, proceda de la siguiente manera:

Figura\(\PageIndex{2}\). Trazando la función cuadrática\(f(x) = 2x^2 − 7x − 15\).

• Presione 2nd TRACE para abrir la ventana CALCULAR que se muestra en la Figura\(\PageIndex{3}\) (a). En este menú, seleccione 2:cero.
• La calculadora responde pidiendo un “Izquierda”. Utilice las teclas de flecha para mover el cursor ligeramente hacia la izquierda de la intercepción x más a la izquierda, como se muestra en la Figura\(\PageIndex{3}\) (b). Presione la tecla ENTER.
• La calculadora responde pidiendo un “Encuadernado a la derecha”. Utilice las teclas de flecha para mover el cursor ligeramente hacia la derecha de la intercepción x más a la izquierda, como se muestra en la Figura\(\PageIndex{3}\) (c). Presione la tecla ENTER.
• La calculadora responde pidiendo un “Guess”. Puede usar las teclas de flecha para seleccionar un valor x inicial en cualquier lugar entre los límites izquierdo y derecho que haya seleccionado (tenga en cuenta que la calculadora los marca en la pantalla en la Figura\(\PageIndex{3}\) (d)). Sin embargo, el cursor ya se encuentra entre estas marcas, por lo que normalmente solo golpeamos ENTRAR en este punto. Te sugerimos que lo hagas también.

Figura\(\PageIndex{3}\). Usando la utilidad cero para encontrar una intercepción x.

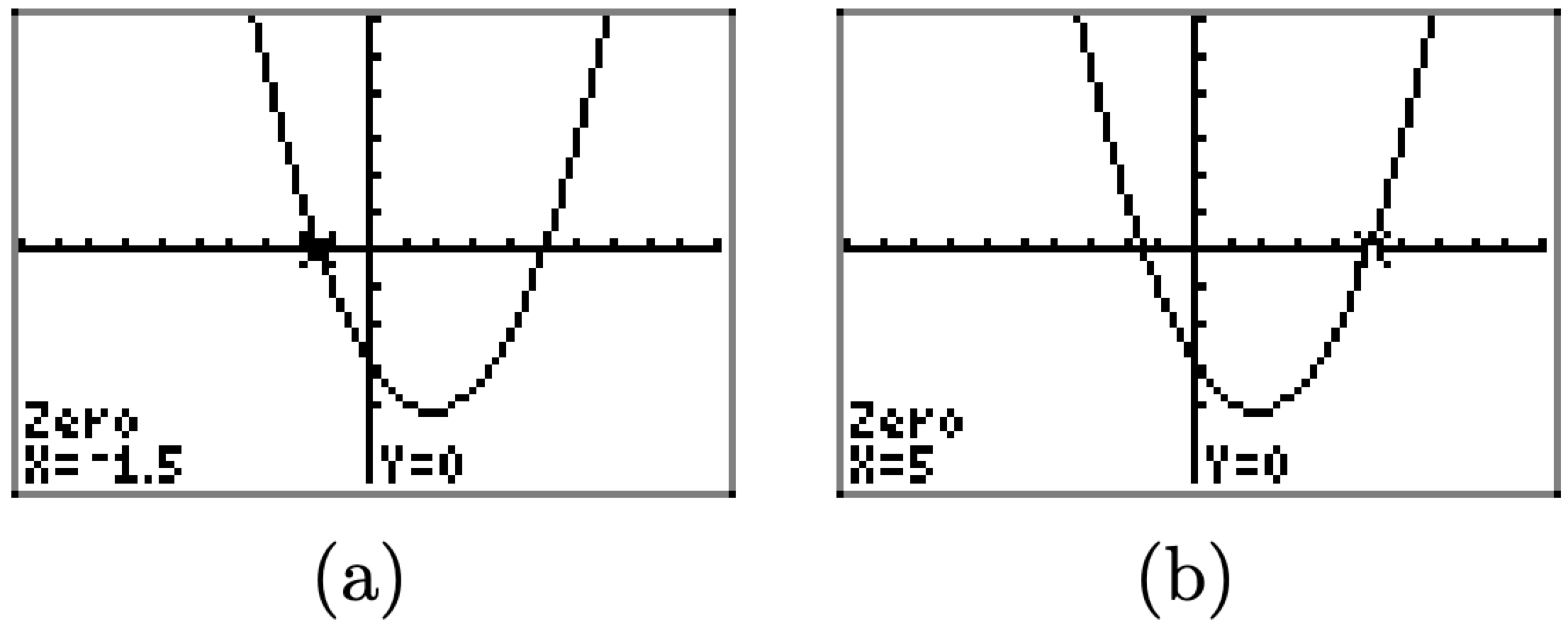
La calculadora responde marcando la intercepción x e informando su valor x en la parte inferior de la pantalla, como se muestra en la Figura\(\PageIndex{4}\) (a). Este es uno de los ceros de la función. Tenga en cuenta que este valor de −1.5 concuerda muy bien con nuestro resultado calculado a mano −3/2 en el Ejemplo\(\PageIndex{6}\). Se siguió precisamente el mismo procedimiento descrito anteriormente para encontrar la segunda intercepción x mostrada en la Figura\(\PageIndex{4}\) (b). Obsérvese que también concuerda con la solución calculada a mano de Ejemplo\(\PageIndex{6}\).

En una línea similar, el punto donde la gráfica de una función cruza el eje y se llama la intercepción y de la gráfica de la función. En\(\PageIndex{1}\) la Figura la intercepción y de la parábola es (0, −6). Tenga en cuenta que la coordenada x de esta intercepción y es cero.

Por lo tanto, el proceso para encontrar intercepciones y debe ser claro.

Figura\(\PageIndex{4}\): Los ceros de\(f(x) − 2x^2 − 7x − 15\).

Encontrar intercepciones en Y

Para encontrar las intercepciones y de la gráfica de cualquier función, establecer\(x = 0\) y resolver para\(y\). Alternativamente, si se usa notación de función, simplemente evalúe f (0).

Ejemplo\(\PageIndex{8}\)

Encuentra la intercepción y de la función cuadrática definida por\(f(x) = x^2 − 3x − 11\).

Solución

Evaluar la función en x = 0.

\[f(0)=(0)^{2}-3(0)-11=-11\]

Las coordenadas de la intercepción y son (0, −11).

Poniéndolo todo junto

Encontraremos que tanto las intercepciones x como las y son extremadamente útiles a la hora de dibujar la gráfica de una función cuadrática.

Ejemplo\(\PageIndex{9}\)

Colocar la función cuadrática\(y = x^2 + 2x − 24\) en forma de vértice. Trazar el vértice y el eje de simetría y etiquetarlos con sus coordenadas y ecuación, respectivamente. Encuentra y traza las intercepciones x e y de la parábola y etiquétalas con sus coordenadas.

Solución

Toma la mitad del coeficiente de x, cuadrado, luego suma y resta esta cantidad para equilibrar la ecuación. Factorizar y combinar coeficientes.

\[\begin{array}{l}{y=x^{2}+2 x+1-1-24} \\ {y=(x+1)^{2}-25}\end{array}\]

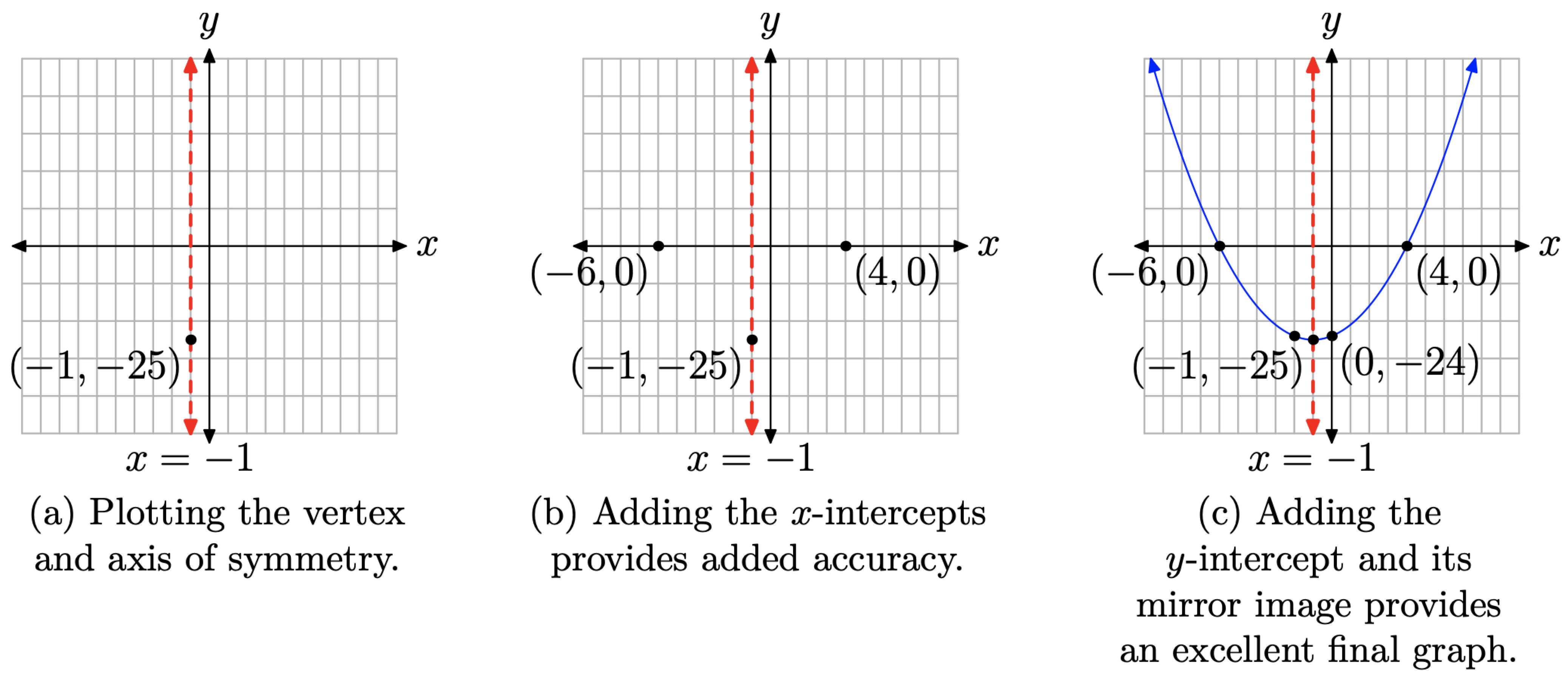
El gráfico es una parábola que se abre hacia arriba; se desplaza 1 unidad a la izquierda y 25 unidades hacia abajo. Esta información es suficiente para trazar y etiquetar el vértice, luego trazar y etiquetar el eje de simetría, como se muestra en la Figura\(\PageIndex{5}\) (a).

Para encontrar las intercepciones x, deje y = 0 in\(y = x^2 + 2x − 24\).

\[0=x^{2}+2 x-24 \nonumber\]

El coeficiente principal es un 1. El par entero −4 y 6 tiene el producto −24 y la suma 2. Así, el lado derecho factoriza de la siguiente manera.

\[0=(x+6)(x-4) \nonumber\]

Para que este producto sea igual a cero, ya sea

\[x+6=0 \qquad \text { or } \qquad x-4=0 \nonumber\]

Resuelve cada una de estas ecuaciones lineales de forma independiente.

\[x=-6 \qquad \text { or } \qquad x=4 \nonumber\]

Recordemos que dejamos y = 0. Hemos encontrado dos soluciones, x = −6 y x = 4. Así, tenemos intercepciones x en (−6, 0) y (4, 0), como se muestra en la Figura\(\PageIndex{5}\) (b).

Finalmente, para encontrar la intercepción y, dejar x = 0 in\(y = x^2+2x−24\). Con esta sustitución, y = −24. Así, la intercepción y es (0, −24), como se muestra en la Figura\(\PageIndex{5}\) (c). Tenga en cuenta que también hemos incluido la imagen especular de la intercepción y a través del eje de simetría.

Figura\(\PageIndex{5}\)

Veamos un último ejemplo.

Ejemplo\(\PageIndex{10}\)

Trazar la parábola representada por la ecuación\(f(x) = −2x^2−7x+15\). Trazar y etiquetar el vértice, el eje de simetría y las intercepciones x e y.

Solución

Primero, factorizar un −2.

\[f(x)=-2\left[x^{2}+\frac{7}{2} x-\frac{15}{2}\right] \nonumber\]

La mitad de 7/2 es 7/4. Al cuadrado, esto asciende a 49/16. Sumar y restar esta última cantidad para mantener equilibrada la ecuación.

\[f(x)=-2\left[x^{2}+\frac{7}{2} x+\frac{49}{16}-\frac{49}{16}-\frac{15}{2}\right]\]

Los tres primeros términos dentro de los paréntesis forman un trinomio cuadrado perfecto. Las dos últimas constantes se combinan con un denominador común.

\[\begin{array}{l}{f(x)=-2\left[\left(x^{2}+\frac{7}{2} x+\frac{49}{16}\right)-\frac{49}{16}-\frac{120}{16}\right]} \\ {f(x)=-2\left[\left(x+\frac{7}{4}\right)^{2}-\frac{169}{16}\right]}\end{array}\]

Finalmente, redistribuya el −2.

\[f(x)=-2\left(x+\frac{7}{4}\right)^{2}+\frac{169}{8}\]

El gráfico de esta última ecuación es una parábola que se abre hacia abajo, traducida 7/4 unidades a la izquierda y 169/8 unidades hacia arriba. Esta es información suficiente para trazar y etiquetar el vértice y el eje de simetría, como se muestra en la Figura\(\PageIndex{6}\) (a).

Para encontrar las intercepciones y, establezca f (x) = 0 in\(f(x) = −2x^2 − 7x + 15\). También multiplicaremos ambos lados de la ecuación resultante por −1.

\[\begin{array}{l}{0=-2 x^{2}-7 x+15} \\ {0=2 x^{2}+7 x-15}\end{array}\]

Después de comparar\(2x^2 + 7x − 15\) con\(ax^2 + bx + c\), observamos que el par entero −3 y 10 tienen producto igual a ac = −30 y suma igual a b = 7. Utilice este par para expresar el término medio de\(2x^2 + 7x − 15\) como una suma y luego factizar por agrupación.

\[\begin{array}{l}{0=2 x^{2}-3 x+10 x-15} \\ {0=x(2 x-3)+5(2 x-3)} \\ {0=(x+5)(2 x-3)}\end{array}\]

Por la propiedad cero del producto, ya sea\[x+5=0 \qquad \text { or } \qquad 2 x-3=0\]

Resuelve estas ecuaciones lineales de forma independiente. \[x=-5 \qquad \text { or } \qquad x=\frac{3}{2}\]

Estos valores x son los ceros de f (hacen f (x) = 0), así que tenemos intercepciones x en (−5, 0) y (3/2, 0), como se muestra en la Figura\(\PageIndex{6}\) (b).

Figura\(\PageIndex{6}\)

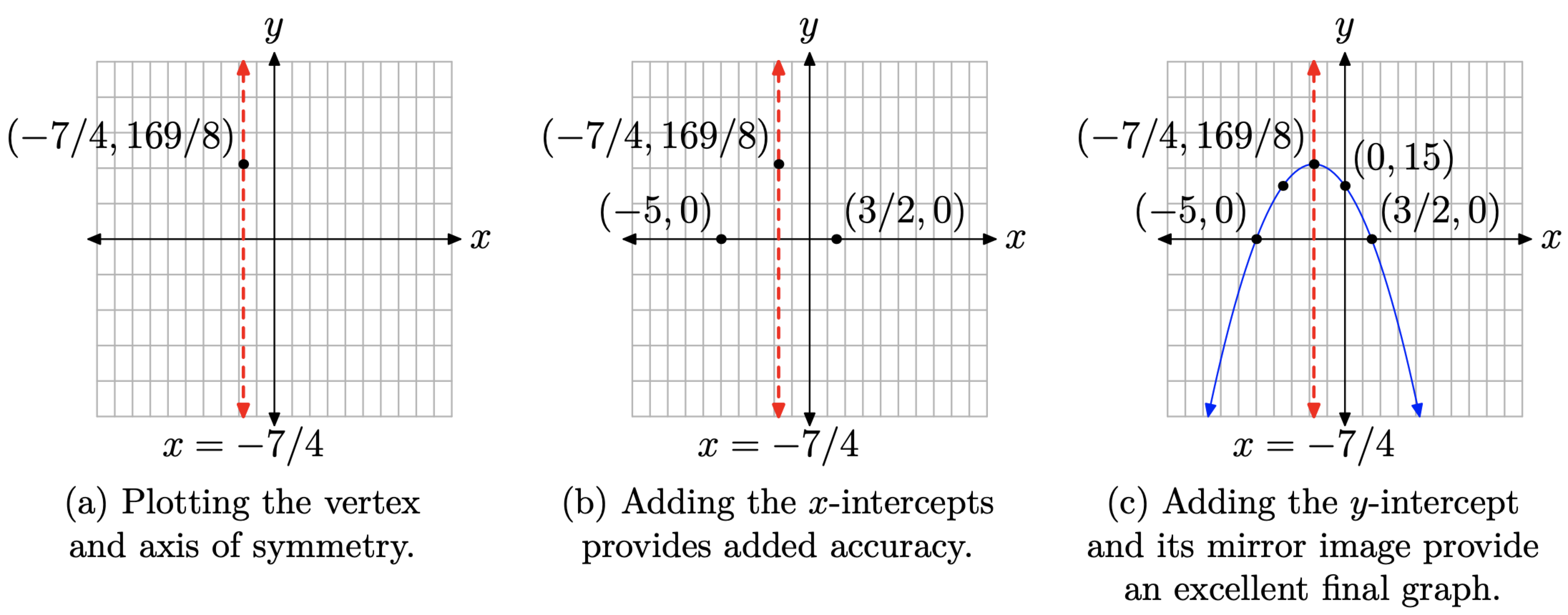
Finalmente, para encontrar la intercepción y, establezca x = 0 in\(f(x) = −2x^2 − 7x + 15\) para obtener f (0) = 15. Observe el posicionamiento de la intercepción y (0, 15) y su imagen especular a través del eje de simetría en la Figura\(\PageIndex{6}\) (c).

Ejercicio

En los Ejercicios 1 - 8, factorial el polinomio cuadrático dado.

Ejercicio\(\PageIndex{1}\)

\(x^2+9x+14\)

Responder

(x+2) (x+7)

Ejercicio\(\PageIndex{2}\)

\(x^2+6x+5\)

Ejercicio\(\PageIndex{3}\)

\(x^2+10x+9\)

Responder

(x+9) (x+1)

Ejercicio\(\PageIndex{4}\)

\(x^2+4x−21\)

Ejercicio\(\PageIndex{5}\)

\(x^2−4x−5\)

Responder

(x−5) (x+1)

Ejercicio\(\PageIndex{6}\)

\(x^2+7x−8\)

Ejercicio\(\PageIndex{7}\)

\(x^2−7x+12\)

Responder

(x−4) (x−3)

Ejercicio\(\PageIndex{8}\)

\(x^2+5x−24\)

En los Ejercicios 9 - 16, encuentra los ceros de la función cuadrática dada.

Ejercicio\(\PageIndex{9}\)

\(f(x) = x^2−2x−15\)

Responder

Ceros: x = −3, x = 5

Ejercicio\(\PageIndex{10}\)

\(f(x) = x^2+4x−32\)

Ejercicio\(\PageIndex{11}\)

\(f(x) = x^2+10x−39\)

Responder

Ceros: x = −13, x = 3

Ejercicio\(\PageIndex{12}\)

\(f(x) = x^2+4x−45\)

Ejercicio\(\PageIndex{13}\)

\(f(x) = x^2−14x+40\)

Responder

Ceros: x = 4, x = 10

Ejercicio\(\PageIndex{14}\)

\(f(x) = x^2−5x−14\)

Ejercicio\(\PageIndex{15}\)

\(f(x) = x^2+9x−36\)

Responder

Ceros: x = −12, x = 3

Ejercicio\(\PageIndex{16}\)

\(f(x) = x^2+11x−26\)

En los Ejercicios 17 - 22, realizar cada una de las siguientes tareas para las funciones cuadráticas.

1. Cargue la función en Y1 del Y= de su calculadora gráfica. Ajuste los parámetros de la ventana para que el vértice sea visible en la ventana de visualización.
2. Configure un sistema de coordenadas en su papel de tarea. Etiquete y escale cada eje con xmin, xmax, ymin e ymax. Haga una copia razonable de la imagen en la ventana de visualización de su calculadora en este sistema de coordenadas y etiquételo con su ecuación.
3. Utilice la utilidad cero en su calculadora gráfica para encontrar los ceros de la función. Utilice estos resultados para trazar las intercepciones x en su sistema de coordenadas y etiquetarlas con sus coordenadas.
4. Utilizar una técnica estrictamente algebraica (sin calculadora) para encontrar los ceros de la función cuadrática dada. Muestra tu trabajo junto a tu sistema de coordenadas. ¡Sé terco! Trabaja el problema hasta que tus ceros algebraicos y gráficamente sean una coincidencia razonable.

Ejercicio\(\PageIndex{17}\)

\(f(x) = x^2+5x−14\)

Responder

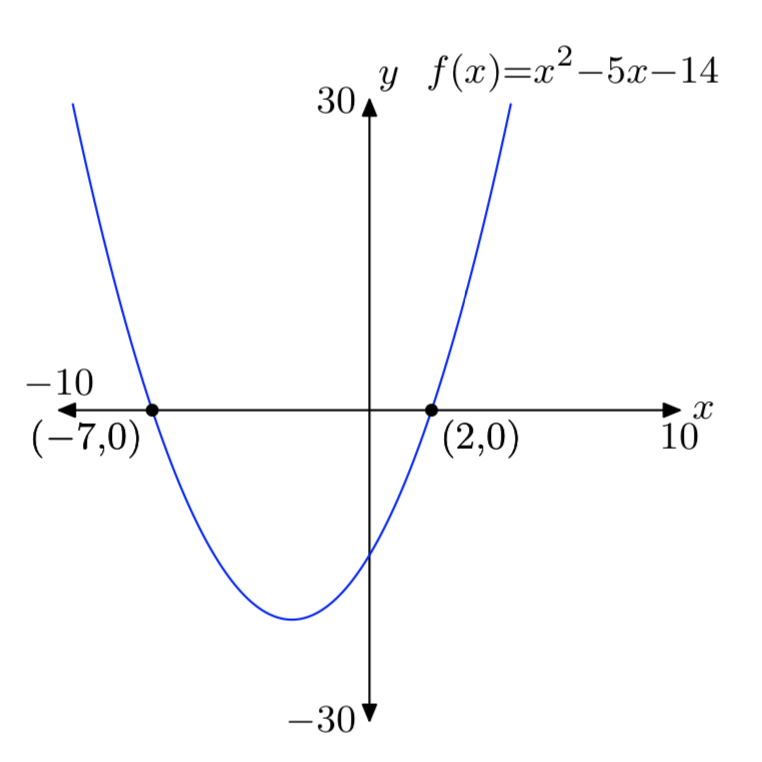
Ejercicio\(\PageIndex{18}\)

\(f(x) = x^2+x−20\)

Ejercicio\(\PageIndex{19}\)

\(f(x) = −x^2+3x+18\)

Responder

Ejercicio\(\PageIndex{20}\)

\(f(x) = −x^2+3x+40\)

Ejercicio\(\PageIndex{21}\)

\(f(x) = x^2−16x−36\)

Responder

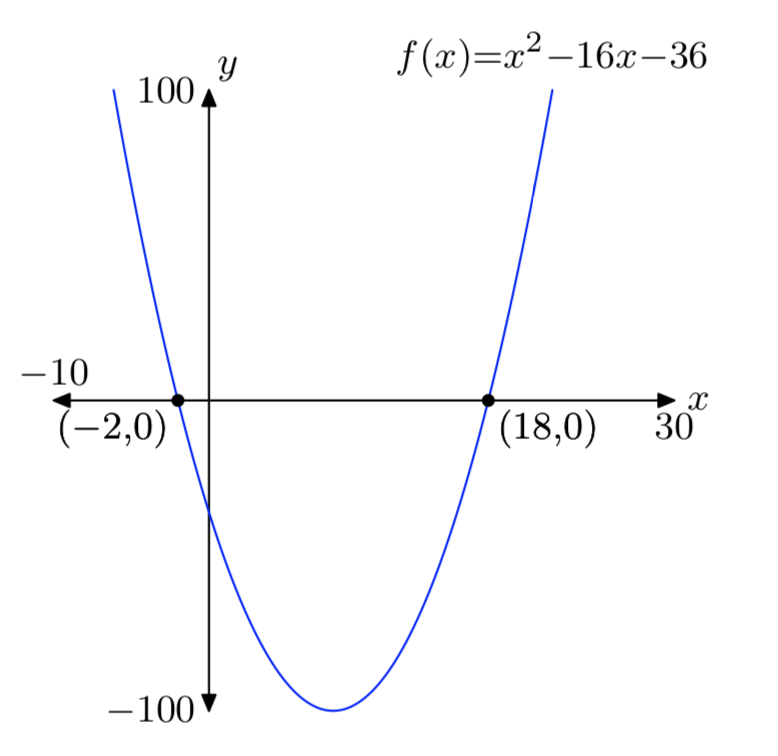
Ejercicio\(\PageIndex{22}\)

\(f(x) = x^2+4x−96\)

En los Ejercicios 23 - 30, realice cada una de las siguientes tareas para la función cuadrática dada.

1. Configura un sistema de coordenadas en papel cuadriculado. Etiquetar y escalar cada eje. Recuerda dibujar todas las líneas con una regla.
2. Utiliza la técnica de completar el cuadrado para colocar la función cuadrática en forma de vértice. Trace el vértice en su sistema de coordenadas y etiquételo con sus coordenadas. Dibuja el eje de simetría en tu sistema de coordenadas y etiquételo con su ecuación.
3. Utilice una técnica estrictamente algebraica (sin calculadoras) para encontrar las intercepciones x de la gráfica de la función cuadrática dada. Trócalos en tu sistema de coordenadas y etiquétalos con sus coordenadas.
4. Encuentra la intercepción y de la gráfica de la función cuadrática. Trace la intercepción y en su sistema de coordenadas y su imagen especular a través del eje de simetría, luego etiquete estos puntos con sus coordenadas.
5. Usando toda la información trazada, dibuja el gráfico de la función cuadrática y etiquételo con la forma de vértice de su ecuación. Utilice la notación de intervalos para describir el dominio y el rango de la función cuadrática.

Ejercicio\(\PageIndex{23}\)

\(f(x) = x^2+2x−8\)

Responder

Dominio = (\(−\infty, \infty\)), Rango = [−9,\(\infty\))

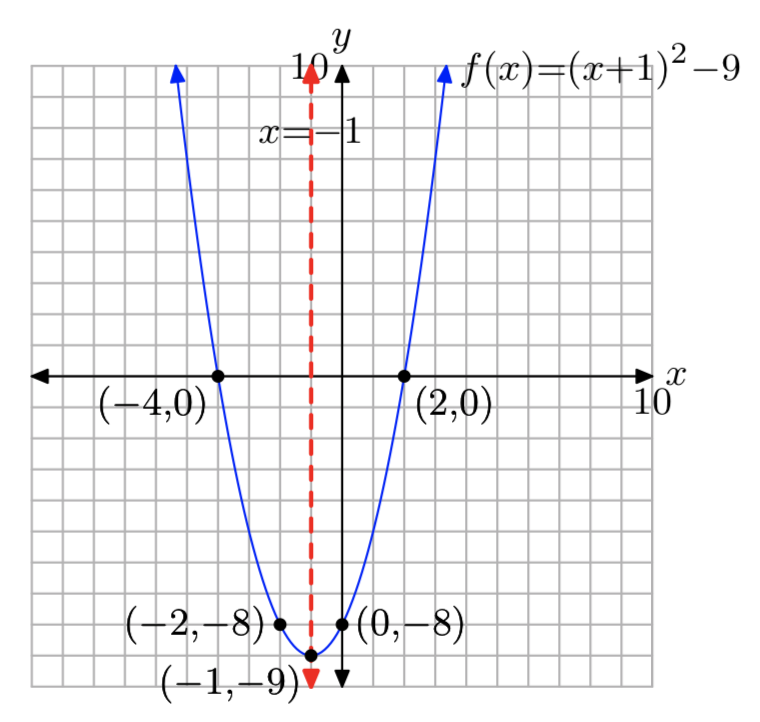
Ejercicio\(\PageIndex{24}\)

\(f(x) = x^2−6x+8\)

Ejercicio\(\PageIndex{25}\)

\(f(x) = x^2+4x−12\)

Responder

Dominio = (\(−\infty, \infty\)), Rango = [−16,\(\infty\))

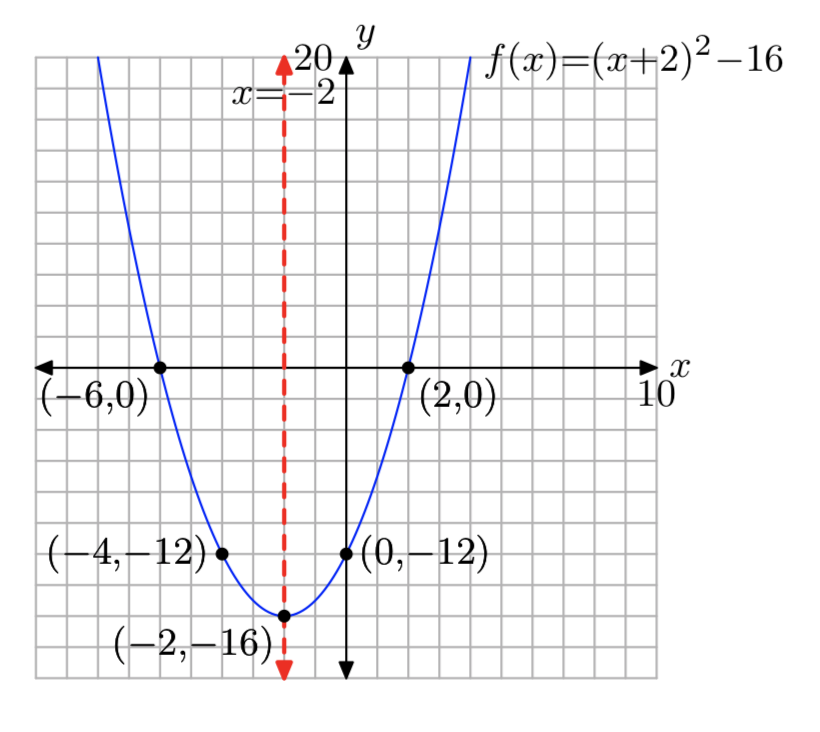
Ejercicio\(\PageIndex{26}\)

\(f(x) = x^2+8x+12\)

Ejercicio\(\PageIndex{27}\)

\(f(x) = −x^2−2x+8\)

Responder

Dominio = (\(−\infty, \infty\)), Rango = (\(−\infty\), 9]

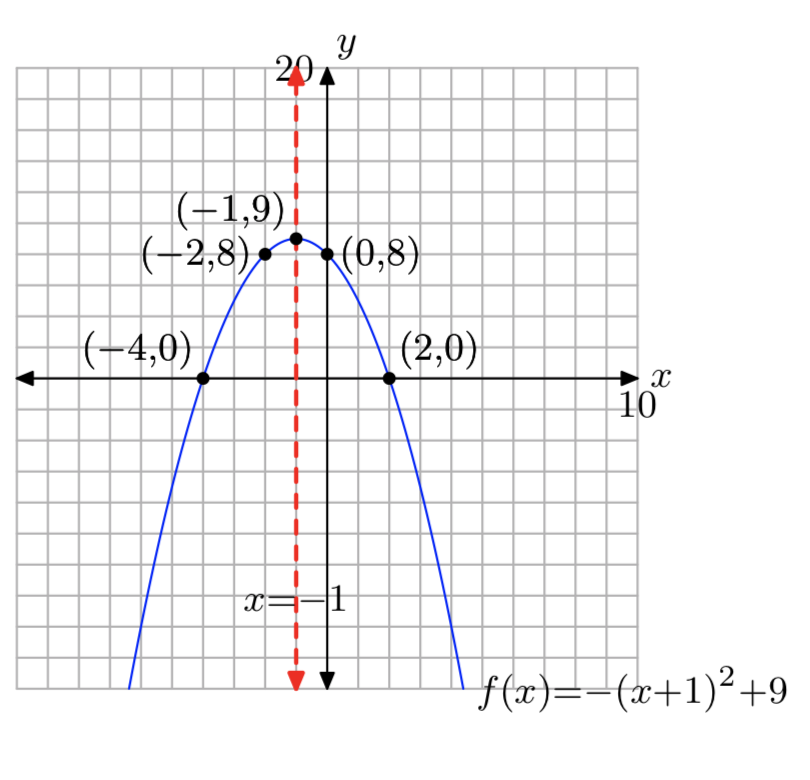
Ejercicio\(\PageIndex{28}\)

\(f(x) = −x^2−2x+24\)

Ejercicio\(\PageIndex{29}\)

\(f(x) = −x^2−8x+48\)

Responder

Dominio = (\(−\infty, \infty\)), Rango = (\(−\infty\), 64]

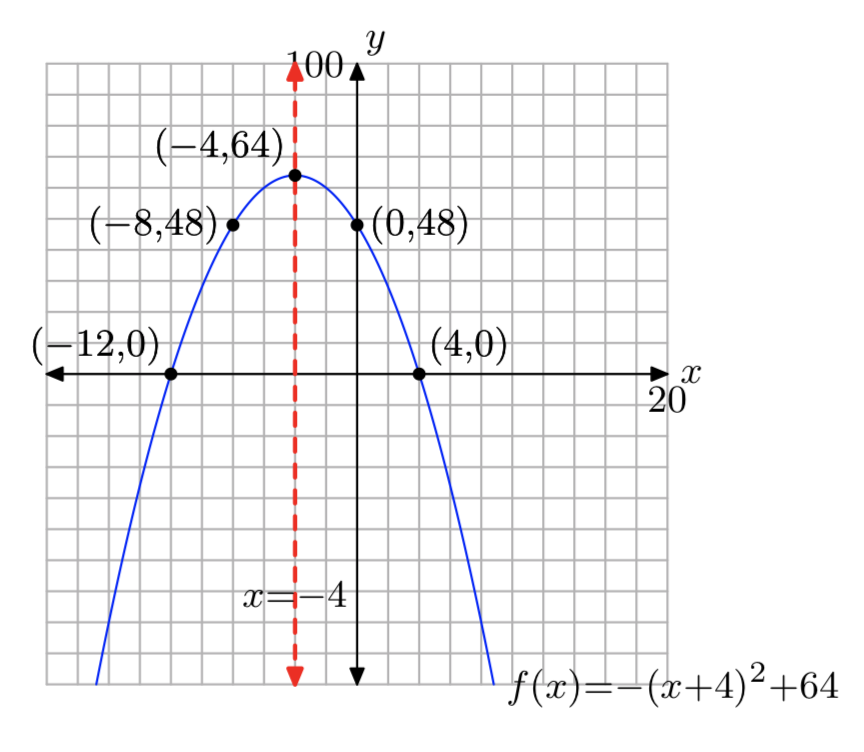
Ejercicio\(\PageIndex{30}\)

\(f(x) = −x^2−8x+20\)

En los Ejercicios 31 - 38, factorial el polinomio cuadrático dado.

Ejercicio\(\PageIndex{31}\)

\(42x^2+5x−2\)

Responder

(7x+2) (6x−1)

Ejercicio\(\PageIndex{32}\)

\(3x^2+7x−20\)

Ejercicio\(\PageIndex{33}\)

\(5x^2−19x+12\)

Responder

(x−3) (5x−4)

Ejercicio\(\PageIndex{34}\)

\(54x^2−3x−1\)

Ejercicio\(\PageIndex{35}\)

\(−4x^2+9x−5\)

Responder

(4x−5) (−x+1)

Ejercicio\(\PageIndex{36}\)

\(3x^2−5x−12\)

Ejercicio\(\PageIndex{37}\)

\(2x^2−3x−35\)

Responder

(2x+7) (x−5)

Ejercicio\(\PageIndex{38}\)

\(−6x^2+25x+9\)

En los Ejercicios 39 - 46, encuentra los ceros de las funciones cuadráticas dadas.

Ejercicio\(\PageIndex{39}\)

\(f(x) = 2x^2−3x−20\)

Responder

Ceros:\(x = −\frac{5}{2}\), x = 4

Ejercicio\(\PageIndex{40}\)

\(f(x) = 2x^2−7x−30\)

Ejercicio\(\PageIndex{41}\)

\(f(x) = −2x^2+x+28\)

Responder

Ceros:\(x = −\frac{7}{2}\), x = 4

Ejercicio\(\PageIndex{42}\)

\(f(x) = −2x^2+15x−22\)

Ejercicio\(\PageIndex{43}\)

\(f(x) = 3x^2−20x+12\)

Responder

Ceros:\(x = \frac{2}{3}\), x = 6

Ejercicio\(\PageIndex{44}\)

\(f(x) = 4x^2+11x−20\)

Ejercicio\(\PageIndex{45}\)

\(f(x) = −4x^2+4x+15\)

Responder

Ceros:\(x = −\frac{3}{2}\),\(x = \frac{5}{2}\)

Ejercicio\(\PageIndex{46}\)

\(f(x) = −6x^2−x+12\)

En los Ejercicios 47 - 52, realizar cada una de las siguientes tareas para las funciones cuadráticas dadas.

1. Cargue la función en Y1 del Y= de su calculadora gráfica. Ajuste los parámetros de la ventana para que el vértice sea visible en la ventana de visualización.
2. Configure un sistema de coordenadas en su papel de tarea. Etiquete y escale cada eje con xmin, xmax, ymin e ymax. Haga una copia razonable de la imagen en la ventana de visualización de su calculadora en este sistema de coordenadas y etiquételo con su ecuación.
3. Utilice la utilidad cero en su calculadora gráfica para encontrar los ceros de la función. Utilice estos resultados para trazar las intercepciones x en su sistema de coordenadas y etiquetarlas con sus coordenadas.
4. Utilizar una técnica estrictamente algebraica (sin calculadora) para encontrar los ceros de la función cuadrática dada. Muestra tu trabajo junto a tu sistema de coordenadas. ¡Sé terco! Trabaja el problema hasta que tus ceros algebraicos y gráficamente sean una coincidencia razonable.

Ejercicio\(\PageIndex{47}\)

\(f(x) = 2x^2+3x−35\)

Responder

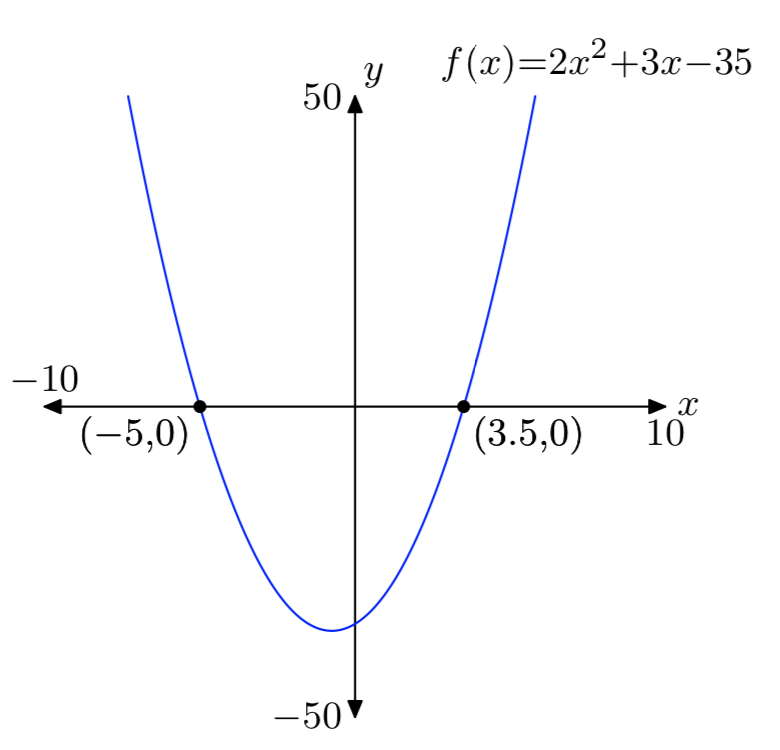
Ejercicio\(\PageIndex{48}\)

\(f(x) = 2x^2−5x−42\)

Ejercicio\(\PageIndex{49}\)

\(f(x) = −2x^2+5x+33\)

Responder

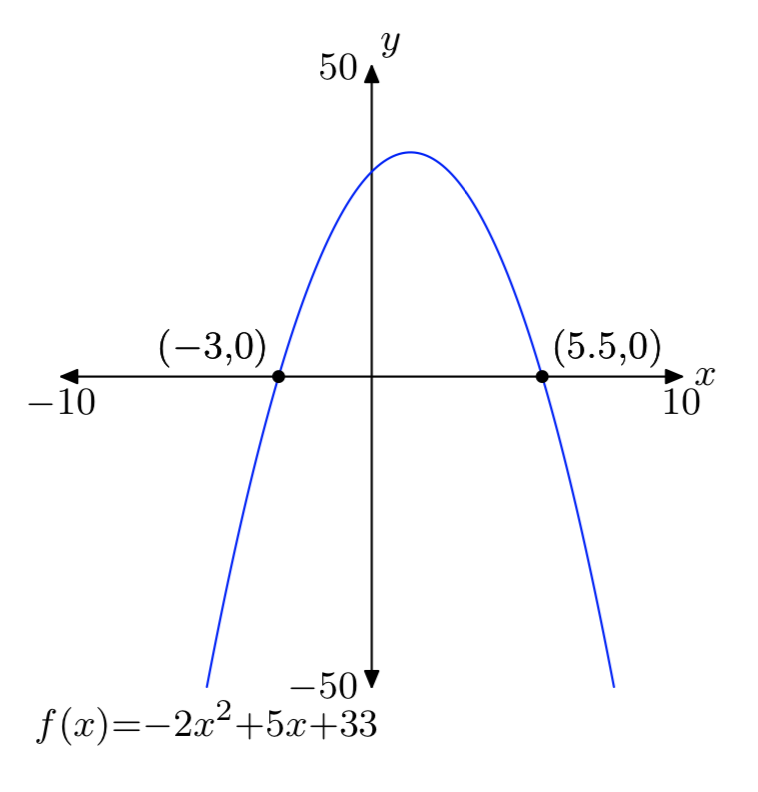
Ejercicio\(\PageIndex{50}\)

\(f(x) = −2x^2−5x+52\)

Ejercicio\(\PageIndex{51}\)

\(f(x) = 4x^2−24x−13\)

Responder

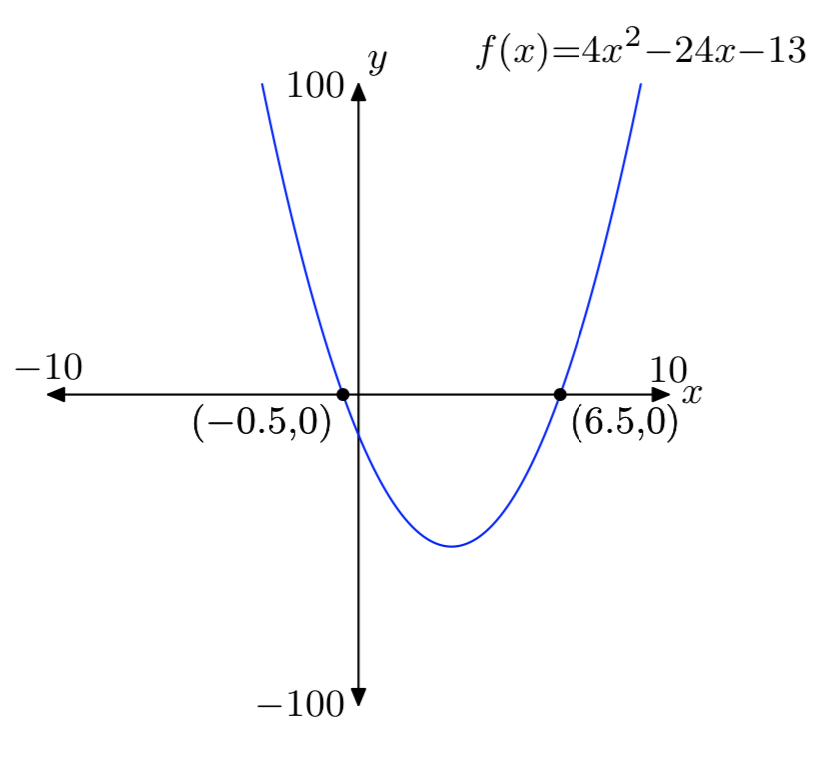
Ejercicio\(\PageIndex{52}\)

\(f(x) = 4x^2+24x−45\)

En los Ejercicios 53 - 60, realizar cada una de las siguientes tareas para las funciones cuadráticas dadas.

1. Configura un sistema de coordenadas en papel cuadriculado. Etiquetar y escalar cada eje. Recuerda dibujar todas las líneas con una regla.
2. Utiliza la técnica de completar el cuadrado para colocar la función cuadrática en forma de vértice. Trace el vértice en su sistema de coordenadas y etiquételo con sus coordenadas. Dibuja el eje de simetría en tu sistema de coordenadas y etiquételo con su ecuación.
3. Utilice un método estrictamente algebraico (sin calculadoras) para encontrar las intercepciones x de la gráfica de la función cuadrática. Trócalos en tu sistema de coordenadas y etiquétalos con sus coordenadas.
4. Encuentra la intercepción y de la gráfica de la función cuadrática. Trace la intercepción y en su sistema de coordenadas y su imagen especular a través del eje de simetría, luego etiquete estos puntos con sus coordenadas.
5. Usando toda la información trazada, dibuja el gráfico de la función cuadrática y etiquételo con la forma de vértice de su ecuación. Utilice la notación de intervalos para describir el dominio y el rango de la función cuadrática.

Ejercicio\(\PageIndex{53}\)

\(f(x) = 2x^2−8x−24\)

Responder

Dominio = (\(−\infty, \infty\)), Rango = [−32,\(\infty\))

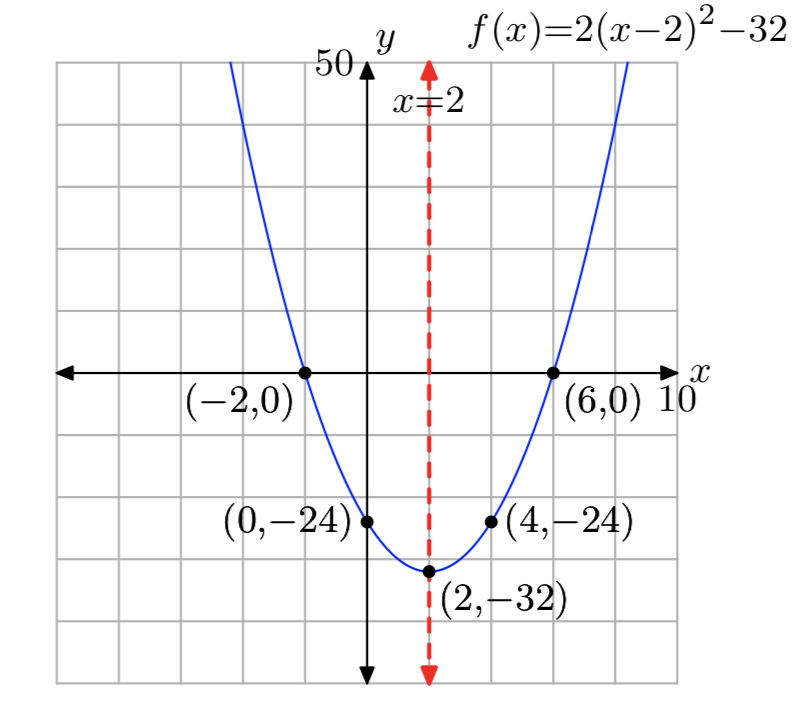
Ejercicio\(\PageIndex{54}\)

\(f(x) = 2x^2−4x−6\)

Ejercicio\(\PageIndex{55}\)

\(f(x) = −2x^2−4x+16\)

Contestar

Dominio = (\(−\infty, \infty\)), Rango = (\(−\infty\), 18]

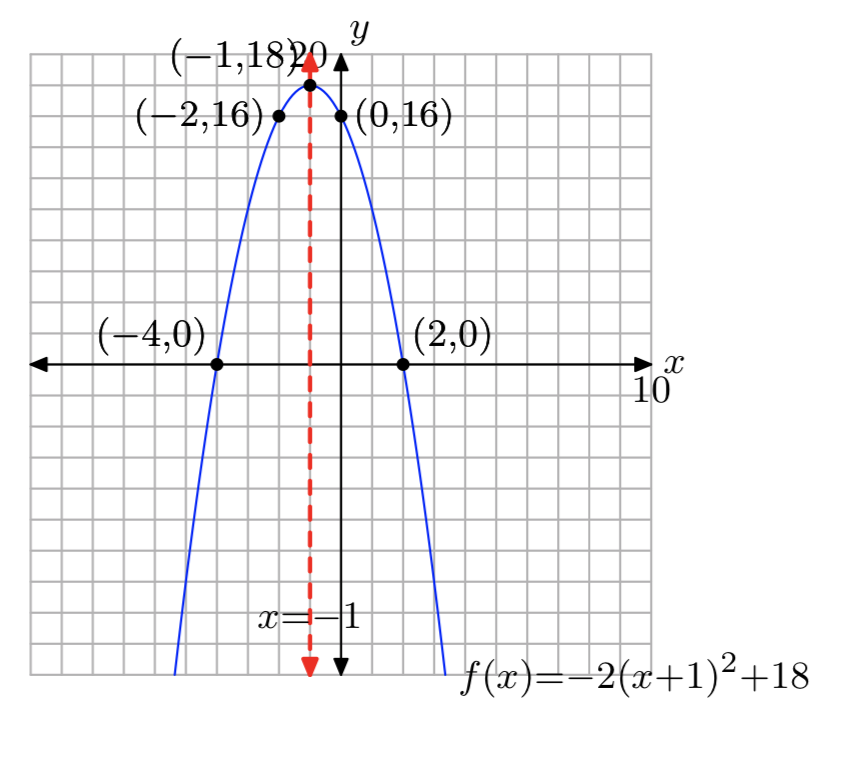
Ejercicio\(\PageIndex{56}\)

\(f(x) = −2x^2−16x+40\)

Ejercicio\(\PageIndex{57}\)

\(f(x) = 3x^2+18x−48\)

Contestar

Dominio = (\(−\infty, \infty\)), Rango = [−75,\(\infty\))

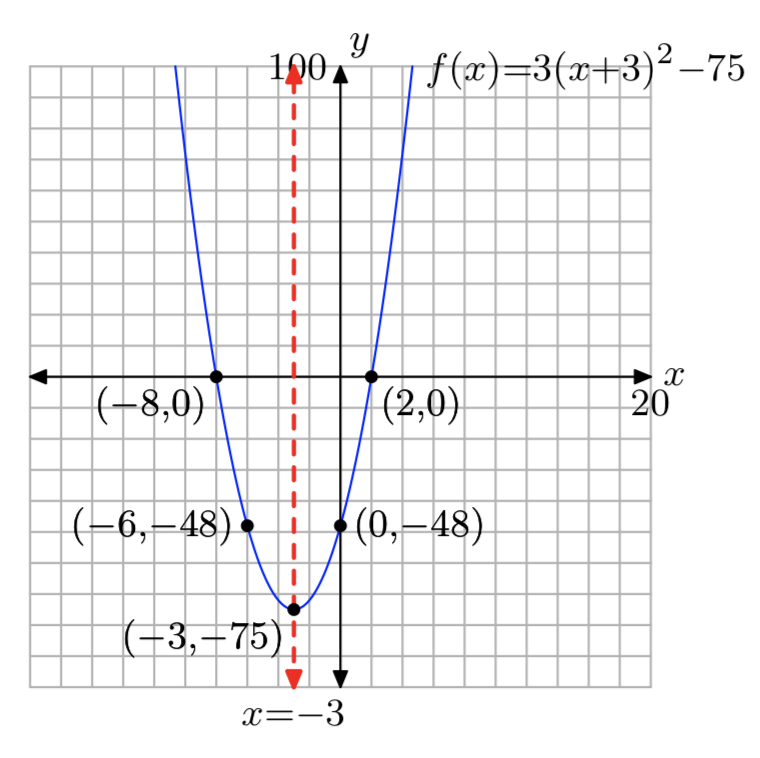
Ejercicio\(\PageIndex{58}\)

\(f(x) = 3x^2+18x−216\)

Ejercicio\(\PageIndex{59}\)

\(f(x) = 2x^2+10x−48\)

Contestar

Dominio = (\(−\infty, \infty\)), Rango = [−\(\frac{121}{2}\),\(\infty\))

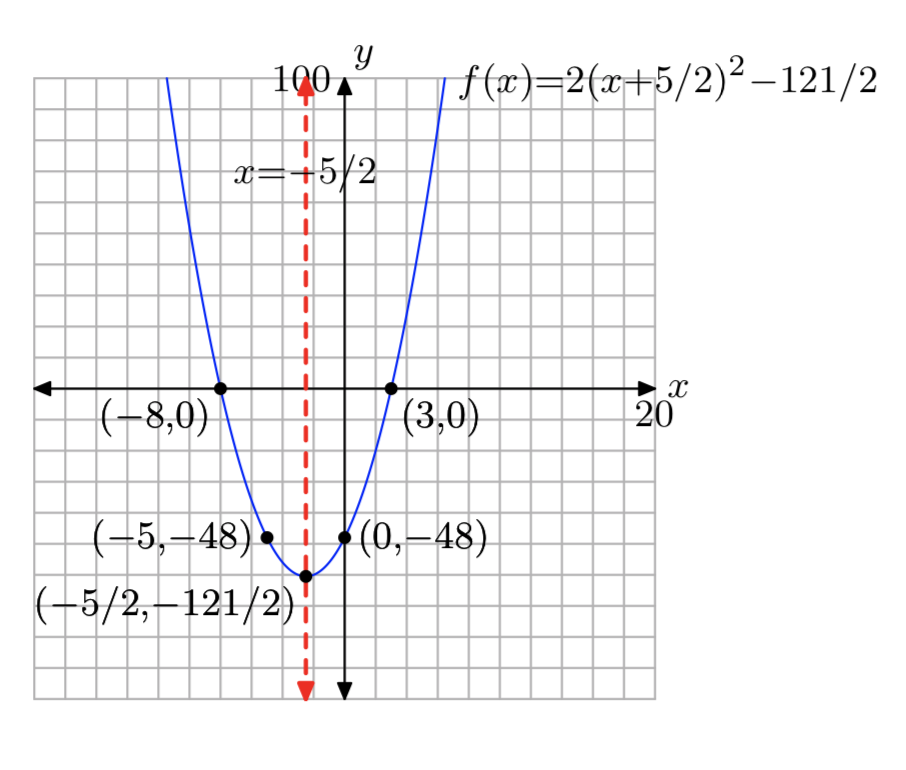
Ejercicio\(\PageIndex{60}\)

\(f(x) = 2x^2−10x−100\)

En Ejercicios 61 - 66, Usa la gráfica de\(f(x) = ax^2+bx+c\) mostrado para encontrar todas las soluciones de la ecuación f (x) = 0. (Nota: Cada solución es un número entero.)

Ejercicio\(\PageIndex{61}\)

Contestar

−2, 3

Ejercicio\(\PageIndex{62}\)

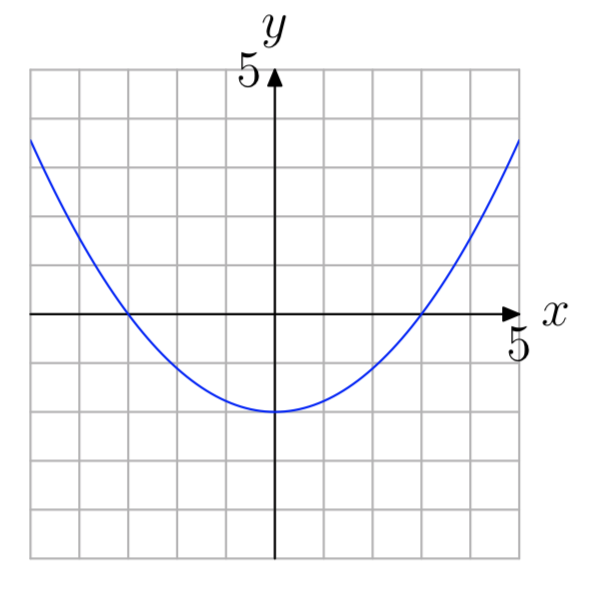
Ejercicio\(\PageIndex{63}\)

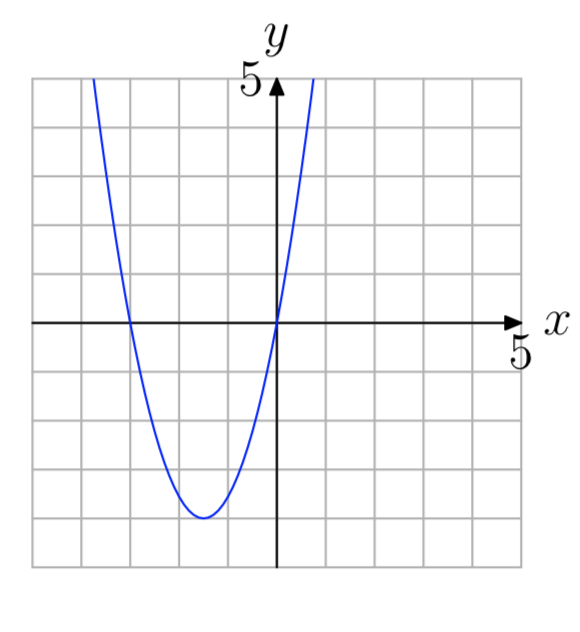
Contestar

−3, 0

Ejercicio\(\PageIndex{64}\)

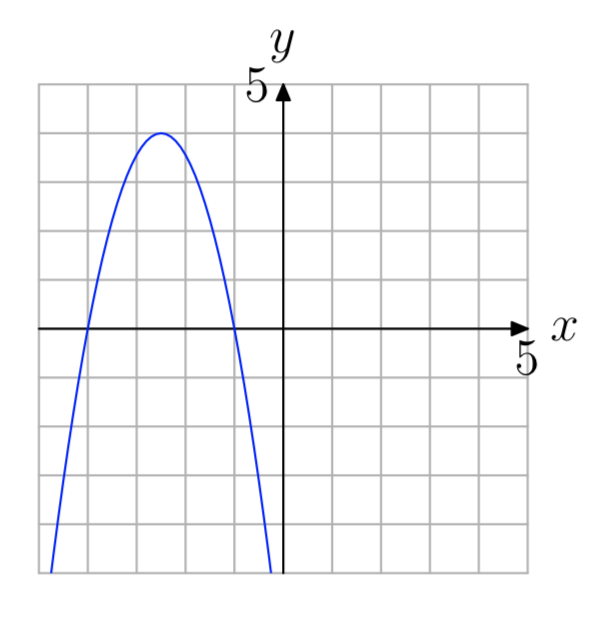
Ejercicio\(\PageIndex{65}\)

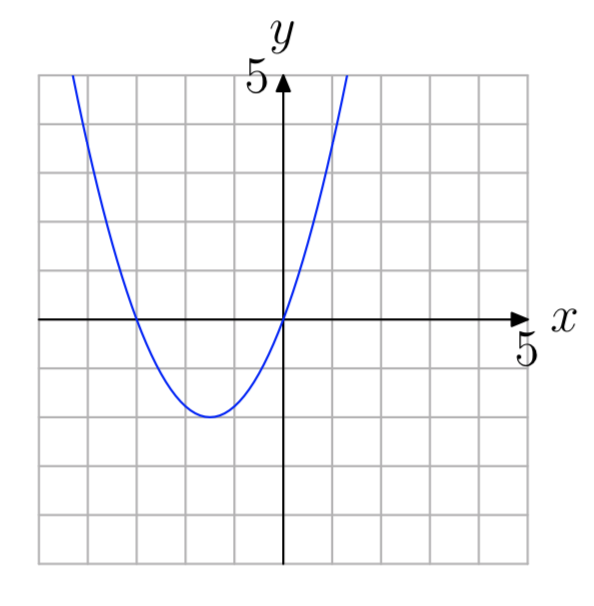
Contestar

−3, 0

Ejercicio\(\PageIndex{66}\)