5.2: Forma de vértice
- Page ID
- 110738
En la sección anterior, aprendiste que es una tarea sencilla bosquejar la gráfica de una función cuadrática si se presenta en forma de vértice
\[f(x)=a(x-h)^{2}+k \nonumber \]
El objetivo de la sección actual es comenzar con la forma más general de la función cuadrática, a saber
\[f(x)=a x^{2}+b x+c \nonumber \]
y manipular la ecuación en forma de vértice. Una vez que tengas tu función cuadrática en forma de vértice, la técnica de la sección anterior debería permitirte construir la gráfica de la función cuadrática. Sin embargo, antes de dirigir nuestra atención a la tarea de convertir la cuadrática general en forma de vértice, necesitamos revisar los fundamentos algebraicos necesarios. Comencemos con una revisión de un importante atajo algebraico llamado cuadrar un binomio.
Al cuadrado de un binomio
Un monomio es un solo término algebraico, generalmente construido como un producto de un número (llamado coeficiente) y una o más variables elevadas a potencias integrales no negativas, como\(-3 x^{2}\) o 14\(y^{3} z^{5}\). La frase clave aquí es “término único”. Un binomio es una suma o diferencia algebraica de dos monomios (o términos), tales como\(x+2 y\) o\(3 a b^{2}-2 c^{3}\). La frase clave aquí es “dos términos”.
Para “cuadrar un binomio”, comenzar con un binomio arbitrario, como a+b, luego multiplicarlo por sí mismo para producir su cuadrado (a + b) (a + b), o, de manera más compacta,\((a+b)^{2}\). Podemos utilizar la propiedad distributiva para ampliar el cuadrado del binomio a + b.
\[\begin{aligned}(a+b)^{2} &=(a+b)(a+b) \\ &=a(a+b)+b(a+b) \\ &=a^{2}+a b+b a+b^{2} \end{aligned}\]
Porque ab = ba, podemos agregar los dos términos medios para llegar a la siguiente propiedad.
Propiedad 3
El cuadrado del binomio a + b se expande de la siguiente manera.
\[(a+b)^{2}=a^{2}+2 a b+b^{2}\]
Ejemplo\(\PageIndex{1}\)
Ampliar\((x+4)^{2}\)
Solución
Podríamos proceder de la siguiente manera.
\[\begin{align*}(x+4)^{2} &=(x+4)(x+4) \\ &=x(x+4)+4(x+4) \\ &=x^{2}+4 x+4 x+16 \\ &=x^{2}+8 x+16 \end{align*}\]
Aunque es correcta, esta técnica no nos ayudará con nuestra próxima tarea. Lo que tenemos que hacer es seguir el algoritmo sugerido por la Propiedad 3.
Algoritmo para cuadrar un binomio
Para cuadrar el binomio a + b, proceda de la siguiente manera:
- Cuadrado el primer término para obtener\(a^2\).
- Multiplica el primer y segundo términos juntos, y luego multiplica el resultado por dos para obtener 2ab.
- Cuadrado el segundo término para obtener\(b^2\).
Así, para ampliar\((x + 4)^2\), debemos proceder de la siguiente manera.
- Cuadrado el primer término para obtener\(x^2\)
- Multiplica el primer y segundo términos juntos y luego multiplica por dos para obtener 8x.
- Cuadrarse el segundo término para obtener 16.
Proceder de esta manera nos permite realizar la expansión mentalmente y simplemente anotar la solución.
\[(x+4)^{2}=x^{2}+2(x)(4)+4^{2}=x^{2}+8 x+16 \nonumber\]
Aquí hay algunos ejemplos más. En cada uno, hemos escrito un paso extra para ayudar a aclarar el procedimiento. En la práctica, simplemente debes anotar la solución sin ningún paso intermedio.
\[\begin{array}{l}{(x+3)^{2}=x^{2}+2(x)(3)+3^{2}=x^{2}+6 x+9} \\ {(x-5)^{2}=x^{2}+2(x)(-5)+(-5)^{2}=x^{2}-10 x+25} \\ {\left(x-\frac{1}{2}\right)^{2}=x^{2}+2(x)\left(-\frac{1}{2}\right)+\left(-\frac{1}{2}\right)^{2}=x^{2}-x+\frac{1}{4}}\end{array}\]
Es imperativo que domines este atajo antes de pasar al resto del material de esta sección.
Trinomios Cuadrados Perfectos
Una vez que hayas dominado la cuadratura de un binomio, como en
\[(a+b)^{2}=a^{2}+2 a b+b^{2} \nonumber\]
es una cuestión sencilla identificar y factorizar trinomios (tres términos) teniendo la forma\(a^{2}+2 a b+b^{2}\). Simplemente “deshaces” la multiplicación. Siempre que veas un trinomio cuyos términos primero y tercero son cuadrados perfectos, debes sospechar que factoriza de la siguiente manera.
\[a^{2}+2 a b+b^{2}=(a+b)^{2} \nonumber\]
Un trinomio que factoriza según esta regla o patrón se denomina trinomio cuadrado perfecto.
Por ejemplo, el primer y último término del siguiente trinomio son cuadrados perfectos.
\[x^{2}+16 x+64 \nonumber\]
Las raíces cuadradas del primer y último término son x y 8, respectivamente. De ahí que tenga sentido intentar lo siguiente.
\[x^{2}+16 x+64=(x+8)^{2} \nonumber\]
Es importante que compruebes tu resultado usando la multiplicación. Entonces, siguiendo el algoritmo de tres pasos para cuadrar un binomio:
- Cuadrado x para obtener\(x^2\).
- Multiplica x y 8 para obtener 8x, luego multiplica este resultado por 2 para obtener 16x.
- Cuadrado 8 para obtener 64.
De ahí,\(x^2 + 16x + 64\) es un trinomio cuadrado perfecto y factores como\((x + 8)^2\).
Como otro ejemplo, considere\(x^2 − 10x + 25\). Las raíces cuadradas del primer y último término son x y 5, respectivamente. Por lo tanto, tiene sentido intentar
\[x^{2}-10 x+25=(x-5)^{2} \nonumber\]
Nuevamente, deberías revisar este resultado. Tenga en cuenta especialmente que dos veces el producto de x y −5 es igual al término medio a la izquierda, es decir, −10x.
Completando la Plaza
Si se da una función cuadrática en forma de vértice, es una cuestión sencilla esbozar la parábola representada por la ecuación. Por ejemplo, considere la función cuadrática
\[f(x)=(x+2)^{2}+3\]
que está en forma de vértice. El gráfico de esta ecuación es una parábola que se abre hacia arriba. Se traduce 2 unidades a la izquierda y 3 unidades hacia arriba. Esta es la ventaja de la forma de vértice. Las transformaciones requeridas para dibujar la gráfica de la función son fáciles de detectar cuando la ecuación está escrita en forma de vértice.
Es una cuestión sencilla transformar la ecuación\(f(x) = (x + 2)^2 + 3\) en la forma general de una función cuadrática,\(f(x) = ax^2 + bx + c\). Simplemente usamos el algoritmo de tres pasos para cuadrar el binomio; luego combinamos términos similares.
\[\begin{array}{l}{f(x)=(x+2)^{2}+3} \\ {f(x)=x^{2}+4 x+4+3} \\ {f(x)=x^{2}+4 x+7}\end{array}\]
Obsérvese, sin embargo, que el resultado de esta manipulación\(f(x) = x^2 + 4x+ 7\),, no es tan útil como la forma de vértice, ya que es difícil identificar las transformaciones requeridas para dibujar la parábola representada por la ecuación\(f(x) = x^2 + 4x + 7\).
Es realmente lo contrario de la manipulación anterior lo que se necesita. Si se nos presenta una ecuación en la forma\(f(x) = ax^2 + bx + c\), tal como\(f(x) = x^2 + 4x + 7\), entonces se necesita un método algebraico para convertir esta ecuación a forma de vértice\(f(x) = a(x−h)^2+k\); o en este caso, volver a su forma de vértice original\(f(x) = (x + 2)^2 + 3\).
El procedimiento que buscamos se llama completar la plaza. El nombre se deriva del hecho de que necesitamos “completar” el trinomio en el lado derecho de\(y = x^2 + 4x + 7\) para que se convierta en un trinomio cuadrado perfecto.
Algoritmo para completar el cuadrado
El procedimiento para completar el cuadrado implica tres pasos clave.
- Toma la mitad del coeficiente de x y cuadra el resultado.
- Sumar y restar la cantidad del paso uno para que el lado derecho de la ecuación no cambie.
- Factorizar el trinomio cuadrado perfecto resultante y combinar términos constantes.
Sigamos este procedimiento y coloquemos\(f(x) = x^2 + 4x + 7\) en forma de vértice.
- Toma la mitad del coeficiente de x. Así, (1/2) (4) = 2. Cuadrando este resultado. Así,\(2^2 = 4\).
- Suma y resta 4 en el lado derecho de la ecuación\(f(x) = x^2 + 4x + 7\)\[f(x)=x^{2}+4 x+4-4+7\]
- Agrupe los tres primeros términos en el lado derecho. Estos forman un trinomio cuadrado perfecto.
\[f(x)=\left(x^{2}+4 x+4\right)-4+7 \nonumber\]
Ahora factoriza el trinomio cuadrado perfecto y combina las constantes al final para obtener
\[f(x)=(x+2)^{2}+3 \nonumber\]
¡Eso es, ya terminamos! Hemos devuelto la cuadrática\(f(x) = x^2 + 4x + 7\) general a la forma de vértice\(f(x) = (x + 2)^2 + 3\).
Probemos eso una vez más.
Ejemplo\(\PageIndex{2}\)
Colocar la función cuadrática\(f(x) = x^2 − 8x − 9\) en forma de vértice.
Solución
Seguimos el algoritmo de tres pasos para completar el cuadrado.
- Tome la mitad del coeficiente de x y cuadrado: i.e.,\[[(1 / 2)(-8)]^{2}=[-4]^{2}=16 \nonumber\]
- Suma y resta esta cantidad al lado derecho de la función. \[f(x)=x^{2}-8 x+16-16-9 \nonumber\]
- Agrupe los tres primeros términos en el lado derecho. Estos forman un trinomio cuadrado perfecto. \[f(x)=\left(x^{2}-8 x+16\right)-16-9 \nonumber\]
Factorizar el trinomio cuadrado perfecto y combinar los coeficientes al final.
\[f(x)=(x-4)^{2}-25 \nonumber\]
Ahora, veamos cómo podemos utilizar la técnica de completar el cuadrado para ayudar a dibujar las gráficas de las funciones cuadráticas generales.
Trabajar con\(f(x) = x^2 + bx + c\)
Los ejemplos de esta sección tendrán la forma\(f(x) = x^2 + bx + c\). Tenga en cuenta que el coeficiente de\(x^2\) es 1. En la siguiente sección, trabajaremos con una forma más dura,\(f(x) = ax^2 + bx + c\), dónde\(a \neq 1\).
Ejemplo\(\PageIndex{3}\)
Completa el cuadrado para colocarlo\(f(x) = x^2 + 6x + 2\) en forma de vértice y bosquejar su gráfica.
Solución
Primero, toma la mitad del coeficiente de x y cuadrado; es decir,\([(1/2)(6)]^2 = 9\). En el lado derecho de la ecuación, sumar y restar esta cantidad para no cambiar la ecuación.
\[f(x)=x^{2}+6 x+9-9+2 \nonumber\]
Agrupe los tres primeros términos en el lado derecho.
\[f(x)=\left(x^{2}+6 x+9\right)-9+2 \nonumber\]
Los tres primeros términos del lado derecho forman un trinomio cuadrado perfecto que se factoriza fácilmente. Además, combine las constantes al final.
\[f(x)=(x+3)^{2}-7 \nonumber\]
Se trata de una parábola que se abre hacia arriba. Necesitamos desplazar la parábola 3 unidades hacia la izquierda y luego 7 unidades hacia abajo, colocando el vértice en (−3, −7) como se muestra en la Figura\(\PageIndex{1}\) (a). El eje de simetría es la línea vertical x = −3. La tabla de la Figura\(\PageIndex{1}\) (b) calcula dos puntos a la derecha del eje de simetría, y los puntos especulares a la izquierda del eje de simetría hacen una gráfica precisa de la parábola.
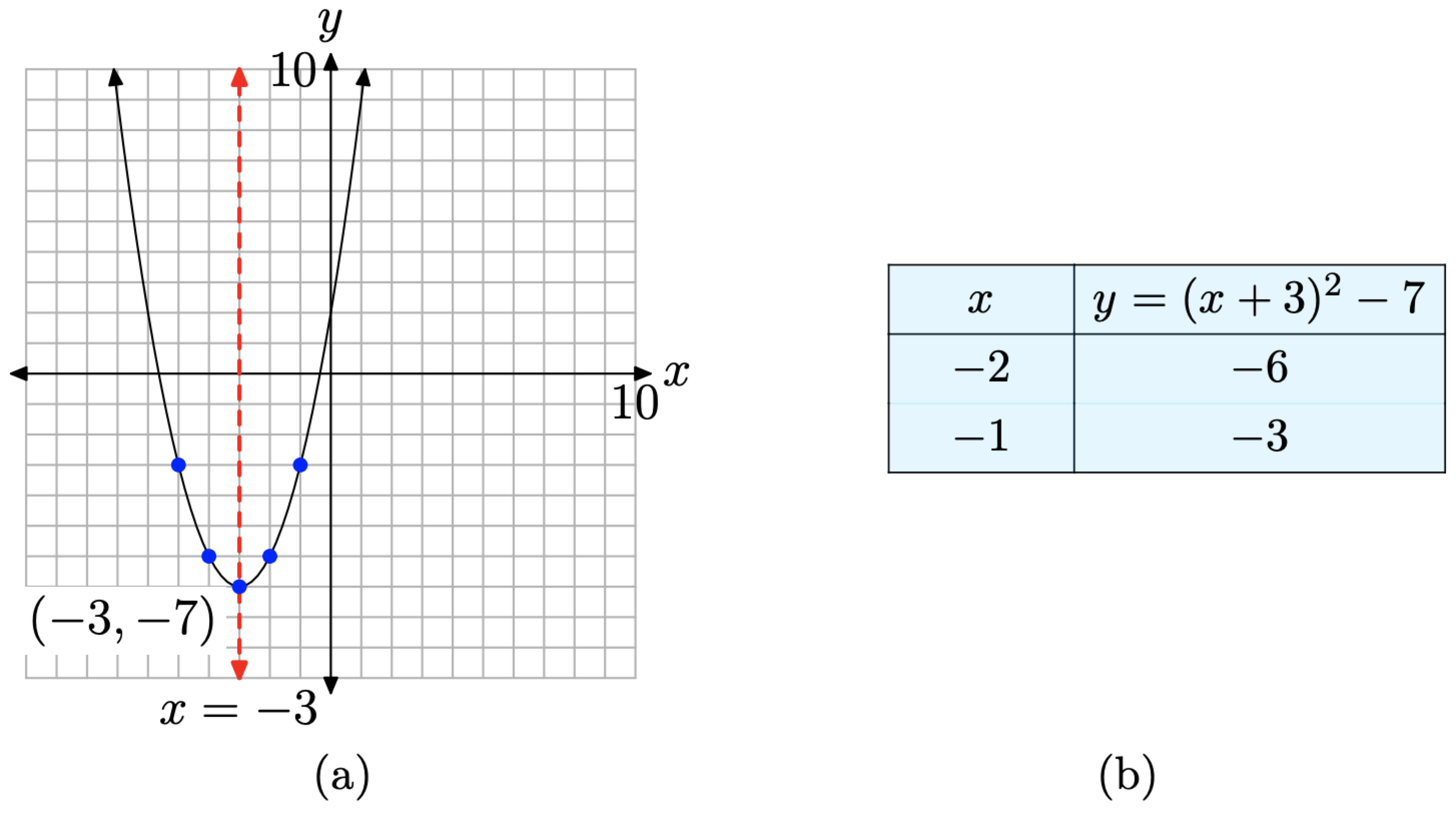
Veamos otro ejemplo.
Ejemplo\(\PageIndex{4}\)
Completa el cuadrado para colocarlo\(f(x) = x^2 − 8x + 21\) en forma de vértice y bosquejar su gráfica.
Solución
Primero, toma la mitad del coeficiente de x y cuadrado; es decir,\([(1/2)(−8)]^2 = 16\). En el lado derecho de la ecuación, sumar y restar esta cantidad para no cambiar la ecuación.
\[f(x)=x^{2}-8 x+16-16+21 \nonumber\]
Agrupe los tres primeros términos en el lado derecho de la ecuación.
\[f(x)=\left(x^{2}-8 x+16\right)-16+21 \nonumber\]
Los tres primeros términos forman un trinomio cuadrado perfecto que se factoriza fácilmente. Además, combine constantes al final.
\[f(x)=(x-4)^{2}+5 \nonumber\]
Se trata de una parábola que se abre hacia arriba. Necesitamos desplazar la parábola 4 unidades hacia la derecha y luego 5 unidades hacia arriba, colocando el vértice en (4, 5), como se muestra en la Figura\(\PageIndex{2}\) (a). La tabla de la Figura\(\PageIndex{2}\) (b) calcula dos puntos a la derecha del eje de simetría, y los puntos especulares a la izquierda del eje de simetría hacen una gráfica precisa de la parábola.
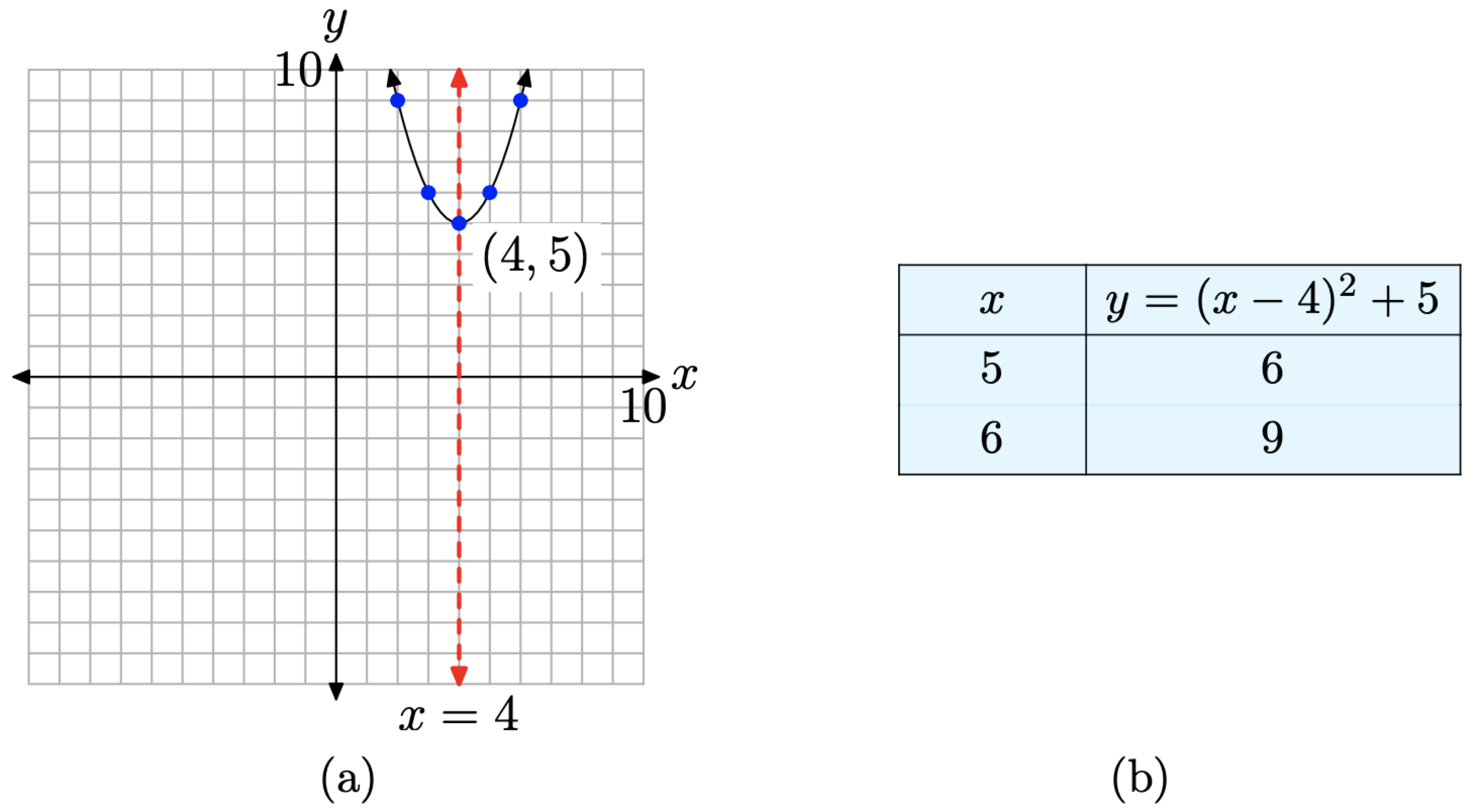
Trabajar con\(f(x) = ax^2 + bx + c\)
En los dos últimos ejemplos, el coeficiente de\(x^2\) fue 1. En esta sección, aprenderemos a completar el cuadrado cuando el coeficiente de\(x^2\) sea algún número distinto de 1.
Ejemplo\(\PageIndex{5}\)
Completa el cuadrado para colocarlo\(f(x)=2 x^{2}+4 x-4\) en forma de vértice y bosquejar su gráfica.
Solución
En los dos últimos ejemplos, obtuvimos cierta medida de éxito cuando el coeficiente de\(x^2\) fue un 1. Nos estábamos poniendo cómodos con esa situación y nos gustaría seguir estando cómodos, así que comencemos factorizando un 2 de cada término en el lado derecho de la ecuación.
\[f(x)=2\left[x^{2}+2 x-2\right] \nonumber\]
Si ignoramos el factor de 2 por delante, el coeficiente de\(x^2\) en la expresión trinomial dentro de los paréntesis es un 1. ¡Ah, suelo familiar! Procederemos como hicimos antes, pero llevaremos el factor de 2 fuera de los paréntesis en cada paso. Comience tomando la mitad del coeficiente de x y cuadrando el resultado; es decir,\([(1/2)(2)]^2 = 1\).
Sumar y restar esta cantidad dentro de los paréntesis para no cambiar la ecuación.
\[f(x)=2\left[x^{2}+2 x+1-1-2\right] \nonumber\]
Agrupe los tres primeros términos dentro de los paréntesis y combine constantes.
\[f(x)=2\left[\left(x^{2}+2 x+1\right)-3\right] \nonumber\]
Los términos agrupados dentro de los paréntesis forman un trinomio cuadrado perfecto que se factoriza fácilmente.
\[f(x)=2\left[(x+1)^{2}-3\right] \nonumber\]
Por último, redistribuir el 2.
\[f(x)=2(x+1)^{2}-6 \nonumber\]
Se trata de una parábola que se abre hacia arriba. Además, se estira por un factor de 2, por lo que será algo más estrecho que nuestros ejemplos anteriores. La parábola también se desplaza 1 unidad hacia la izquierda, luego 6 unidades hacia abajo, colocando el vértice en (−1, −6), como se muestra en la Figura\(\PageIndex{3}\) (a). La tabla de la Figura\(\PageIndex{3}\) (b) calcula dos puntos a la derecha del eje de simetría, y los puntos especulares a la izquierda del eje de simetría hacen una gráfica precisa de la parábola.
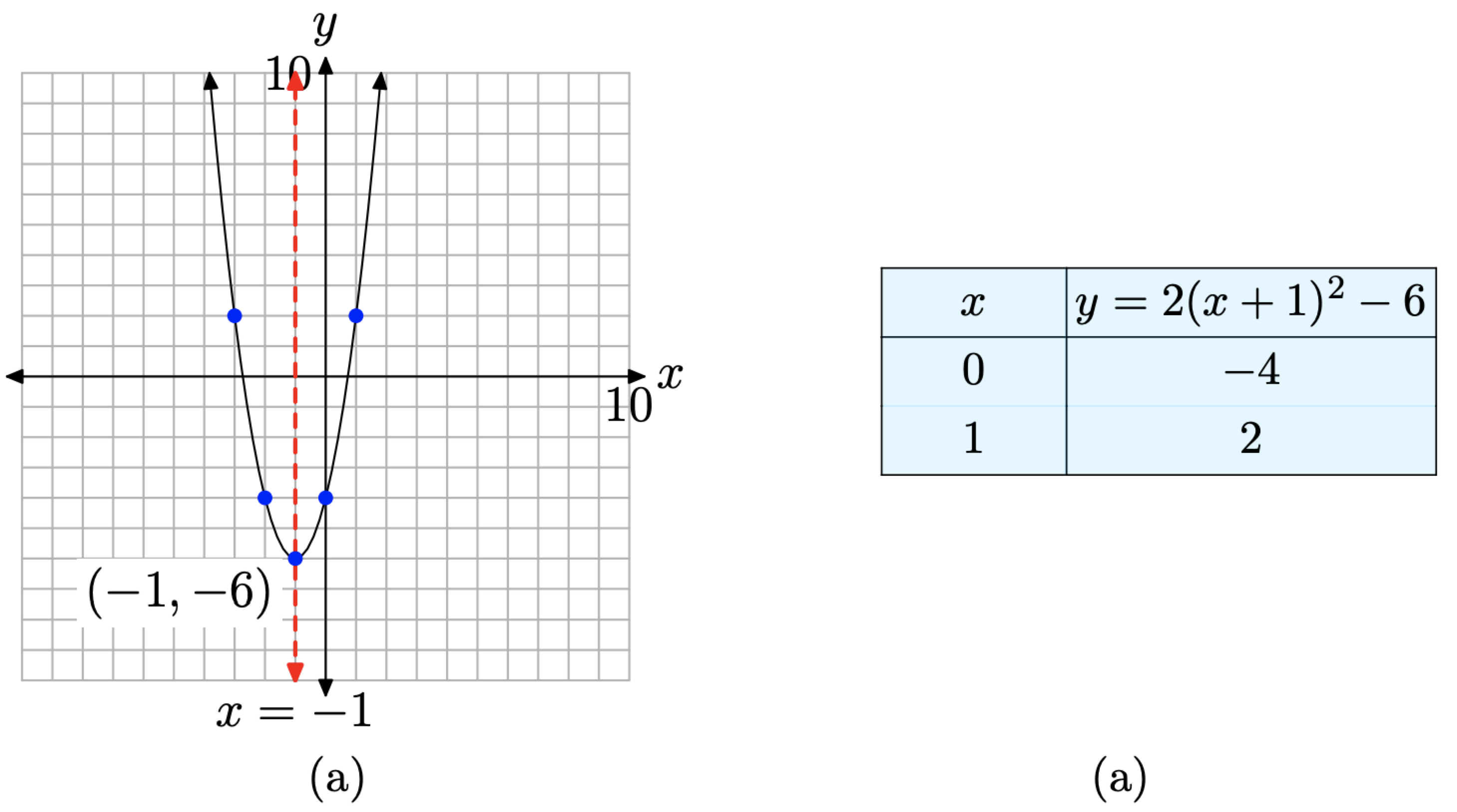
Veamos un ejemplo donde el coeficiente de\(x^2\) es negativo.
Ejemplo\(\PageIndex{6}\)
Completa el cuadrado para colocarlo\(f(x) = −x^2 + 6x − 2\) en forma de vértice y bosquejar su gráfica.
Solución
En el último ejemplo, factorizamos el coeficiente de\(x^2\). Esto nos dejó con un trinomio con coeficiente principal 1, lo que nos permitió proceder mucho como lo hacíamos antes: reducir a la mitad el coeficiente medio y cuadrado, sumar y restar esta cantidad, factorizar el trinomio cuadrado perfecto resultante. Como tuvimos éxito con esta técnica en el último ejemplo, comencemos de nuevo factorizando el coeficiente principal, en este caso un −1.
\[f(x)=-1\left[x^{2}-6 x+2\right] \nonumber\]
Si ignoramos el factor de −1 al frente, el coeficiente de\(x^2\) en la expresión trinomial dentro de los paréntesis es un 1. De nuevo, terreno familiar! Procederemos como hicimos antes, pero llevaremos el factor de −1 fuera de los paréntesis en cada paso. Comience tomando la mitad del coeficiente de x y cuadrando el resultado; es decir,\([(1/2)(−6)]^2 = 9\).
Sumar y restar esta cantidad dentro de los paréntesis para no cambiar la ecuación.
\[f(x)=-1\left[x^{2}-6 x+9-9+2\right] \nonumber\]
Agrupe los tres primeros términos dentro de los paréntesis y combine constantes.
\[f(x)=-1\left[\left(x^{2}-6 x+9\right)-7\right] \nonumber\]
Los términos agrupados dentro de los paréntesis forman un trinomio cuadrado perfecto que se factoriza fácilmente.
\[f(x)=-1\left[(x-3)^{2}-7\right] \nonumber\]
Finalmente, redistribuya el −1.
\[f(x)=-(x-3)^{2}+7 \nonumber\]
Se trata de una parábola que se abre hacia abajo. La parábola también se desplaza 3 unidades hacia la derecha, luego 7 unidades hacia arriba, colocando el vértice en (3, 7), como se muestra en la Figura\(\PageIndex{4}\) (a). La tabla de la Figura\(\PageIndex{4}\) (b) calcula dos puntos a la derecha del eje de simetría, y los puntos especulares a la izquierda del eje de simetría hacen una gráfica precisa de la parábola.
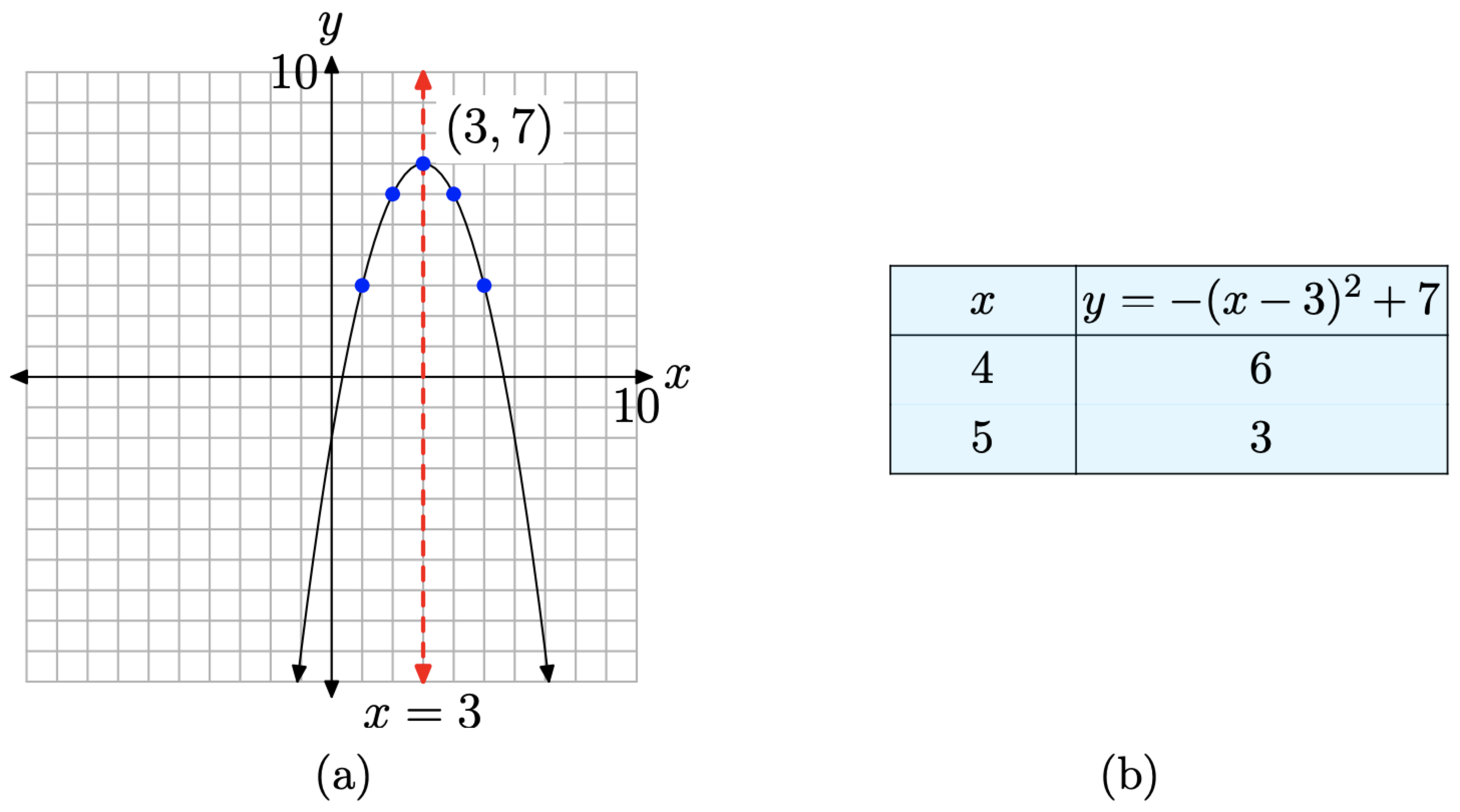
Probemos un ejemplo más.
Ejemplo\(\PageIndex{7}\)
Completa el cuadrado para colocarlo\(f(x) = 3x^2 + 4x − 8\) en forma de vértice y bosquejar su gráfica.
Solución
Comencemos de nuevo factorizando el coeficiente principal, en este caso un 3.
\[f(x)=3\left[x^{2}+\frac{4}{3} x-\frac{8}{3}\right] \nonumber\]
Las fracciones agregan un grado de dificultad, pero, si sigues la misma rutina que en los ejemplos anteriores, deberías poder obtener el resultado necesario. Tomar la mitad del coeficiente de x y cuadrar el resultado; es decir,\([(1/2)(4/3)]^2 = [2/3]^2 = 4/9\).
Sumar y restar esta cantidad dentro de los paréntesis para no cambiar la ecuación.
\[f(x)=3\left[x^{2}+\frac{4}{3} x+\frac{4}{9}-\frac{4}{9}-\frac{8}{3}\right] \nonumber\]
Agrupar los tres primeros términos dentro de los paréntesis. Necesitarás un denominador común para combinar constantes.
\[f(x)=3\left[\left(x^{2}+\frac{4}{3} x+\frac{4}{9}\right)-\frac{4}{9}-\frac{24}{9}\right] \nonumber\]
Los términos agrupados dentro de los paréntesis forman un trinomio cuadrado perfecto que se factoriza fácilmente.
\[f(x)=3\left[\left(x+\frac{2}{3}\right)^{2}-\frac{28}{9}\right] \nonumber\]
Por último, redistribuir el 3.
\[f(x)=3\left(x+\frac{2}{3}\right)^{2}-\frac{28}{3} \nonumber\]
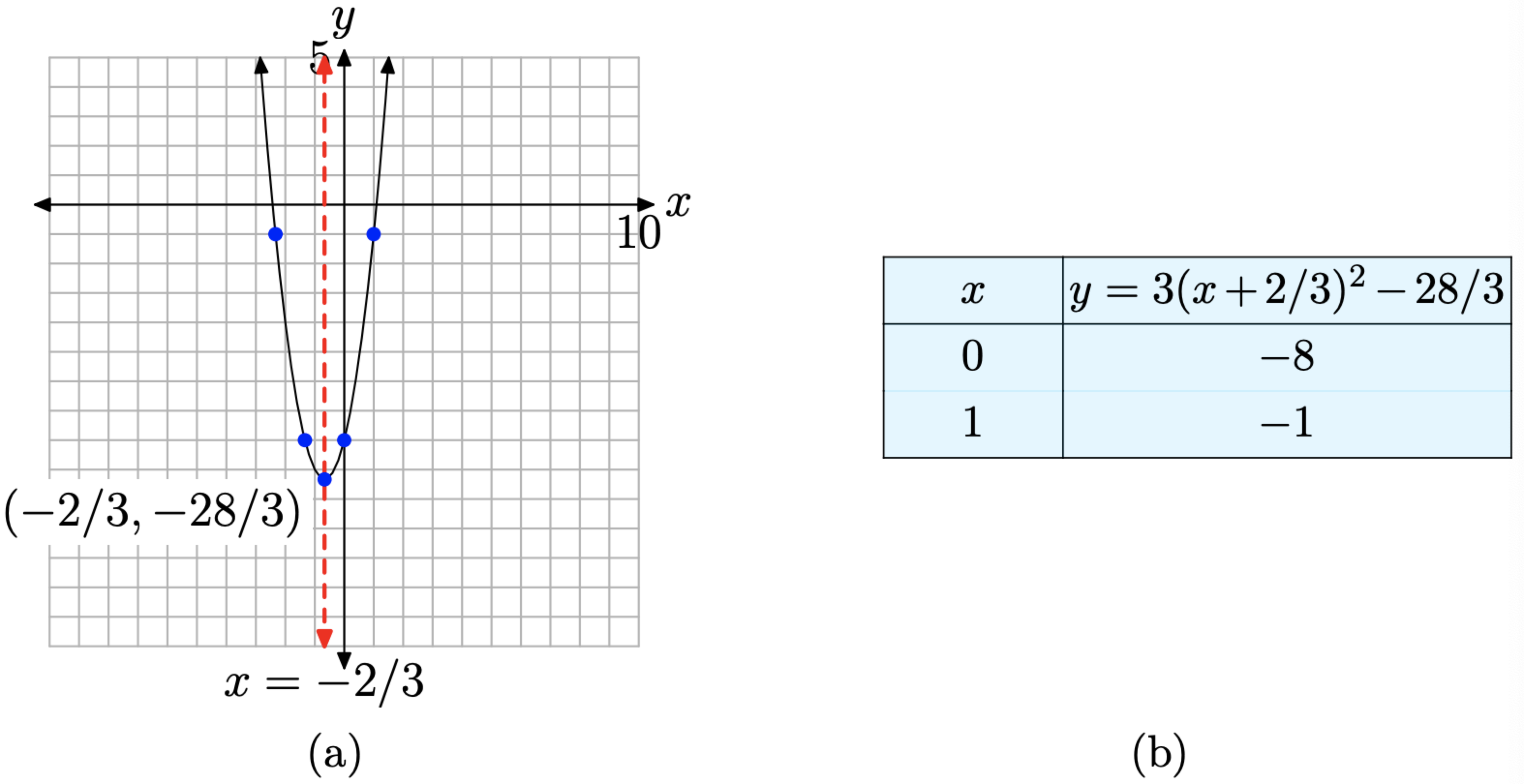
Se trata de una parábola que se abre hacia arriba. También se estira en un factor de 3, por lo que será más estrecho que todos nuestros ejemplos anteriores. La parábola también se desplaza 2/3 unidades hacia la izquierda, luego 28/3 unidades hacia abajo, colocando el vértice en (−2/3, −28/3), como se muestra en la Figura\(\PageIndex{5}\) (a). La tabla de la Figura\(\PageIndex{5}\) (b) calcula dos puntos a la derecha del eje de simetría, y los puntos especulares a la izquierda del eje de simetría hacen una gráfica precisa de la parábola.
Ejercicio
En los Ejercicios 1 - 8, ampliar el binomio.
Ejercicio\(\PageIndex{1}\)
\((x+\frac{4}{5})^2\)
- Contestar
-
\(x^2+\frac{8}{5}x+\frac{16}{25}\)
Ejercicio\(\PageIndex{2}\)
\((x−\frac{4}{5})^2\)
Ejercicio\(\PageIndex{3}\)
\((x+3)^2\)
- Contestar
-
\(x^2+6x+9\)
Ejercicio\(\PageIndex{4}\)
\((x+5)^2\)
Ejercicio\(\PageIndex{5}\)
\((x−7)^2\)
- Contestar
-
\(x^2−14x+49\)
Ejercicio\(\PageIndex{6}\)
\((x−\frac{2}{5})^2\)
Ejercicio\(\PageIndex{7}\)
\((x−6)^2\)
- Contestar
-
\(x^2−12x+36\)
Ejercicio\(\PageIndex{8}\)
\((x−\frac{5}{2})^2\)
En los Ejercicios 9 - 16, factorizar el trinomio cuadrado perfecto.
Ejercicio\(\PageIndex{9}\)
\(x^2−\frac{6}{5}x+\frac{9}{25}\)
- Contestar
-
\((x−\frac{3}{5})^2\)
Ejercicio\(\PageIndex{10}\)
\(x^2+5x+\frac{25}{4}\)
Ejercicio\(\PageIndex{11}\)
\(x^2−12x+36\)
- Contestar
-
\((x−6)^2\)
Ejercicio\(\PageIndex{12}\)
\(x^2+3x+\frac{9}{4}\)
Ejercicio\(\PageIndex{13}\)
\(x^2+12x+36\)
- Contestar
-
\((x+6)^2\)
Ejercicio\(\PageIndex{14}\)
\(x^2−\frac{3}{2}x+\frac{9}{16}\)
Ejercicio\(\PageIndex{15}\)
\(x^2+18x+81\)
- Contestar
-
\((x+9)^2\)
Ejercicio\(\PageIndex{16}\)
\(x^2+10x+25\)
En los Ejercicios 17 - 24, transforma la función cuadrática dada en forma de vértice\(f(x) = (x−h)^2+k\) completando el cuadrado.
Ejercicio\(\PageIndex{17}\)
\(f(x) = x^2−x+8\)
- Contestar
-
\((x−\frac{1}{2})^2+\frac{31}{4}\)
Ejercicio\(\PageIndex{18}\)
\(f(x) = x^2+x−7\)
Ejercicio\(\PageIndex{19}\)
\(f(x) = x^2−5x−4\)
- Contestar
-
\((x−\frac{5}{2})^2−\frac{41}{4}\)
Ejercicio\(\PageIndex{20}\)
\(f(x) = x^2+7x−1\)
Ejercicio\(\PageIndex{21}\)
\(f(x) = x^2+2x−6\)
- Contestar
-
\((x+1)^2−7\)
Ejercicio\(\PageIndex{22}\)
\(f(x) = x^2+4x+8\)
Ejercicio\(\PageIndex{23}\)
\(f(x) = x^2−9x+3\)
- Contestar
-
\((x−\frac{9}{2})−\frac{69}{4}\)
Ejercicio\(\PageIndex{24}\)
\(f(x) = x^2−7x+8\)
En los Ejercicios 25 - 32, transforma la función cuadrática dada en forma de vértice\(f(x) = a(x−h)^2+k\) completando el cuadrado.
Ejercicio\(\PageIndex{25}\)
\(f(x) = −2x^2−9x−3\)
- Contestar
-
\(−2(x+\frac{9}{4})^2+\frac{57}{8}\)
Ejercicio\(\PageIndex{26}\)
\(f(x) = −4x^2−6x+1\)
Ejercicio\(\PageIndex{27}\)
\(f(x) = 5x^2+5x+5\)
- Contestar
-
\(5(x+\frac{1}{2})^2+\frac{15}{4}\)
Ejercicio\(\PageIndex{28}\)
\(f(x) = 3x^2−4x−6\)
Ejercicio\(\PageIndex{29}\)
\(f(x) = 5x^2+7x−3\)
- Contestar
-
\(5(x+\frac{7}{10})^2−\frac{109}{20}\)
Ejercicio\(\PageIndex{30}\)
\(f(x) = 5x^2+6x+4\)
Ejercicio\(\PageIndex{31}\)
\(f(x) = −x^2−x+4\)
- Contestar
-
\(−1(x+\frac{1}{2})^2+\frac{17}{4}\)
Ejercicio\(\PageIndex{32}\)
\(f(x) = −3x^2−6x+4\)
En Ejercicios 33 - 38, encuentra el vértice de la gráfica de la función cuadrática dada.
Ejercicio\(\PageIndex{33}\)
\(f(x) = −2x^2+5x+3\)
- Contestar
-
\((\frac{5}{4}, \frac{49}{8})\)
Ejercicio\(\PageIndex{34}\)
\(f(x) = x^2+5x+8\)
Ejercicio\(\PageIndex{35}\)
\(f(x) = −4x^2−4x+1\)
- Contestar
-
\((−\frac{1}{2}, 2)\)
Ejercicio\(\PageIndex{36}\)
\(f(x) = 5x^2+7x+8\)
Ejercicio\(\PageIndex{37}\)
\(f(x) = 4x^2+2x+8\)
- Contestar
-
\((−\frac{1}{4}, \frac{31}{4})\)
Ejercicio\(\PageIndex{38}\)
\(f(x) = x^2+x−7\)
En los Ejercicios 39 - 44, encuentra el eje de simetría de la gráfica de la función cuadrática dada.
Ejercicio\(\PageIndex{39}\)
\(f(x) = −5x^2−7x−8\)
- Contestar
-
\(x = −\frac{7}{10}\)
Ejercicio\(\PageIndex{40}\)
\(f(x) = x^2+6x+3\)
Ejercicio\(\PageIndex{41}\)
\(f(x) = −2x^2−5x−8\)
- Contestar
-
\(x = −\frac{5}{4}\)
Ejercicio\(\PageIndex{42}\)
\(f(x) = −x^2−6x+2\)
Ejercicio\(\PageIndex{43}\)
\(f(x) = −5x^2+x+6\)
- Contestar
-
\(x = \frac{1}{10}\)
Ejercicio\(\PageIndex{44}\)
\(f(x) = x^2−9x−6\)
Para cada una de las funciones cuadráticas en los Ejercicios 45 - 66, realizar cada una de las siguientes tareas.
- Utilice la técnica de completar el cuadrado para colocar la función cuadrática dada en forma de vértice.
- Configura un sistema de coordenadas en una hoja de papel cuadriculado. Etiquetar y escalar cada eje.
- Dibuja el eje de simetría y etiquétalo con su ecuación. Trazar el vértice y etiquetarlo con sus coordenadas.
- Configure una tabla cerca de su sistema de coordenadas que calcule las coordenadas de dos puntos a cada lado del eje de simetría. Trazar estos puntos y sus imágenes especulares a través del eje de simetría. Dibujar la parábola y etiquetarla con su ecuación
- Utilice la gráfica de la parábola para determinar el dominio y el rango de la función cuadrática. Describir el dominio y el rango usando notación de intervalos.
Ejercicio\(\PageIndex{45}\)
\(f(x) = x^2−8x+12\)
- Contestar
-
\(f(x) = (x−4)^2−4\)
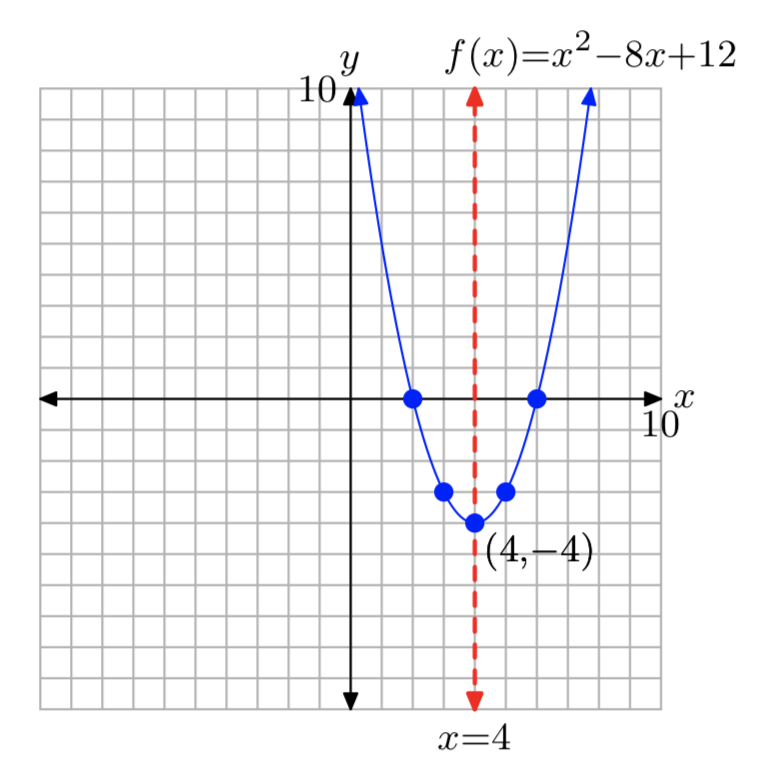
Dominio =\(\mathbb{R}\), Rango = [−4,\(\infty\))
Ejercicio\(\PageIndex{46}\)
\(f(x) = x^2+4x−1\)
Ejercicio\(\PageIndex{47}\)
\(f(x) = x^2+6x+3\)
- Contestar
-
\(f(x) = (x+3)^2−6\)
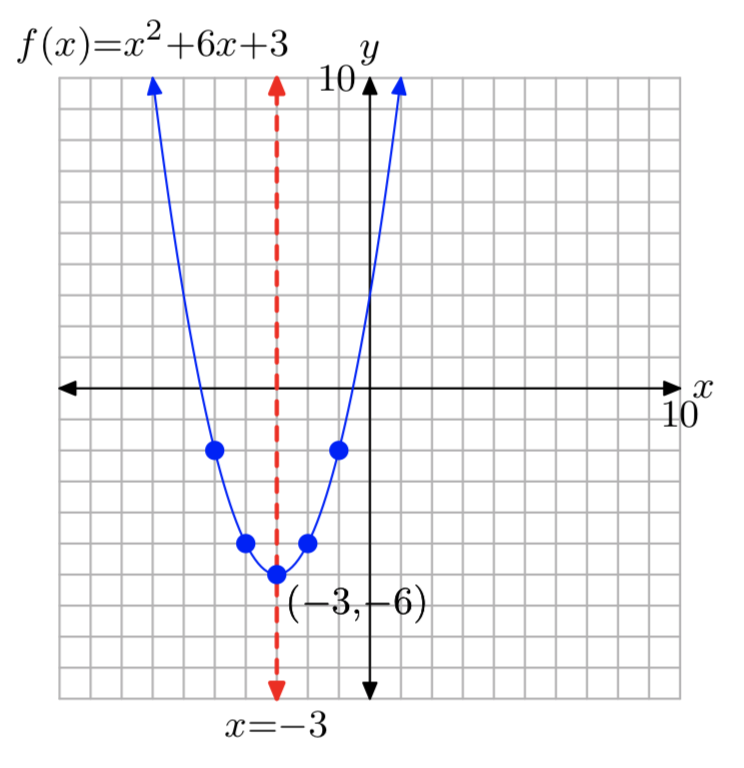
Dominio =\(\mathbb{R}\), Rango = [−6,\(\infty\))
Ejercicio\(\PageIndex{48}\)
\(f(x)=x^2−4x+1\)
Ejercicio\(\PageIndex{49}\)
\(f(x) = x^2−2x−6\)
- Contestar
-
\(f(x) = (x−1)^2−7\)
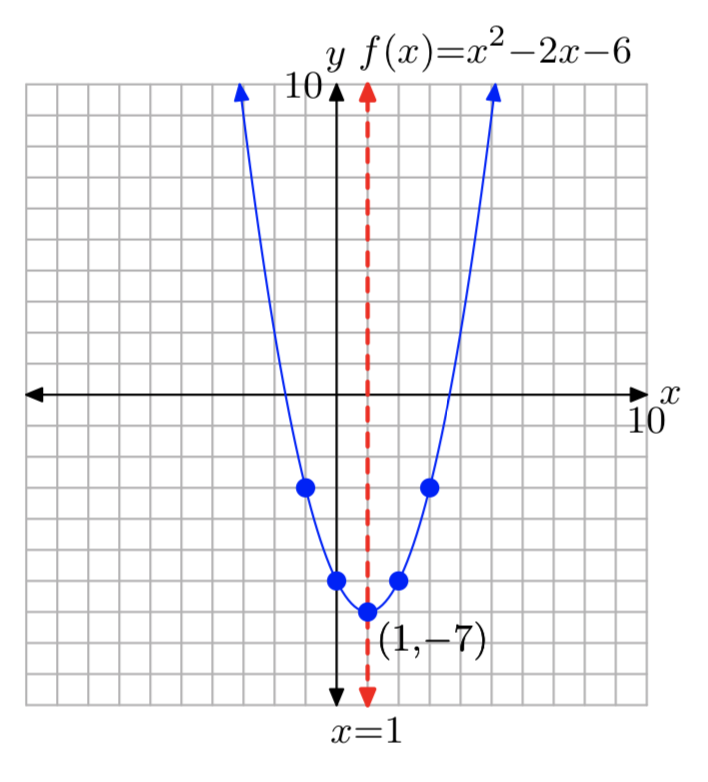
Dominio =\(\mathbb{R}\), Rango = [−7,\(\infty\))
Ejercicio\(\PageIndex{50}\)
\(f(x) = x^2+10x+23\)
Ejercicio\(\PageIndex{51}\)
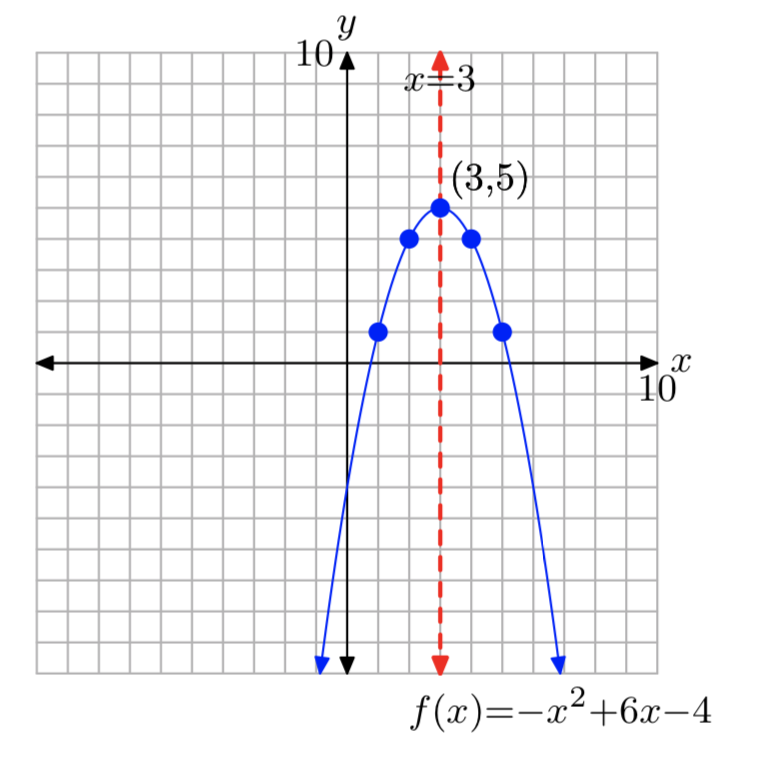
\(f(x) = −x^2+6x−4\)
- Contestar
-
\(f(x) = −(x−3)^2+5\)
Dominio =\(\mathbb{R}\), Rango = (−\(\infty\), 5]
Ejercicio\(\PageIndex{52}\)
\(f(x) = −x^2−6x−3\)
Ejercicio\(\PageIndex{53}\)
\(f(x) = −x^2−10x−21\)
- Contestar
-
\(f(x) = −(x+5)^2+4\)
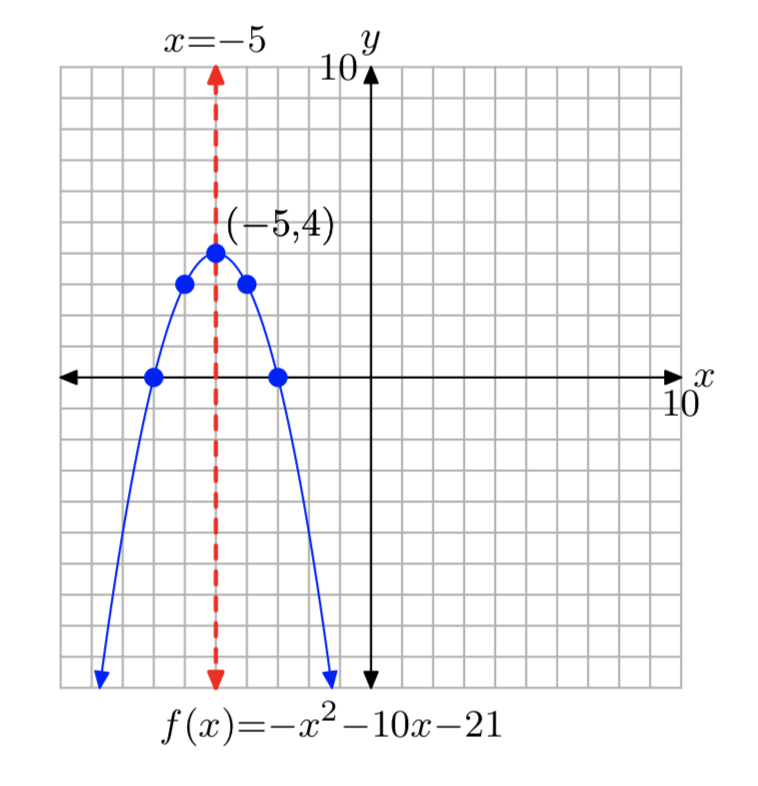
Dominio =\(\mathbb{R}\), Rango = (−\(\infty\), 4]
Ejercicio\(\PageIndex{54}\)
\(f(x) = −x^2+12x−33\)
Ejercicio\(\PageIndex{55}\)
\(f(x) = 2x^2−8x+3\)
- Contestar
-
\(f(x) = 2(x−2)^2−5\)
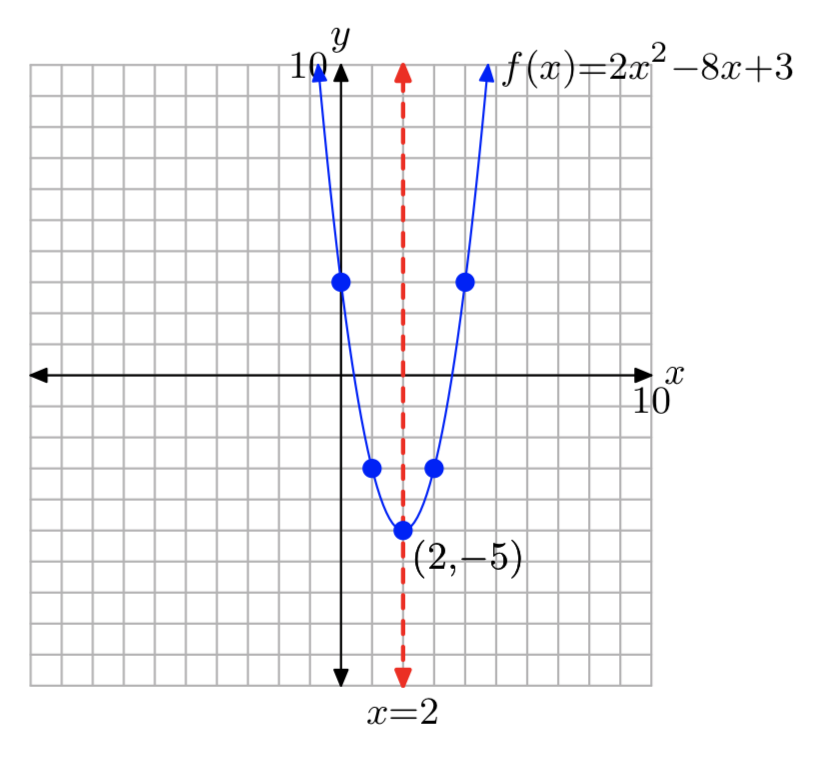
Dominio =\(\mathbb{R}\), Rango = [−5,\(\infty\))
Ejercicio\(\PageIndex{56}\)
\(f(x) = 2x^2+8x+4\)
Ejercicio\(\PageIndex{57}\)
\(f(x) = −2x^2−12x−13\)
- Contestar
-
\(f(x) = −2(x+3)^2+5\)
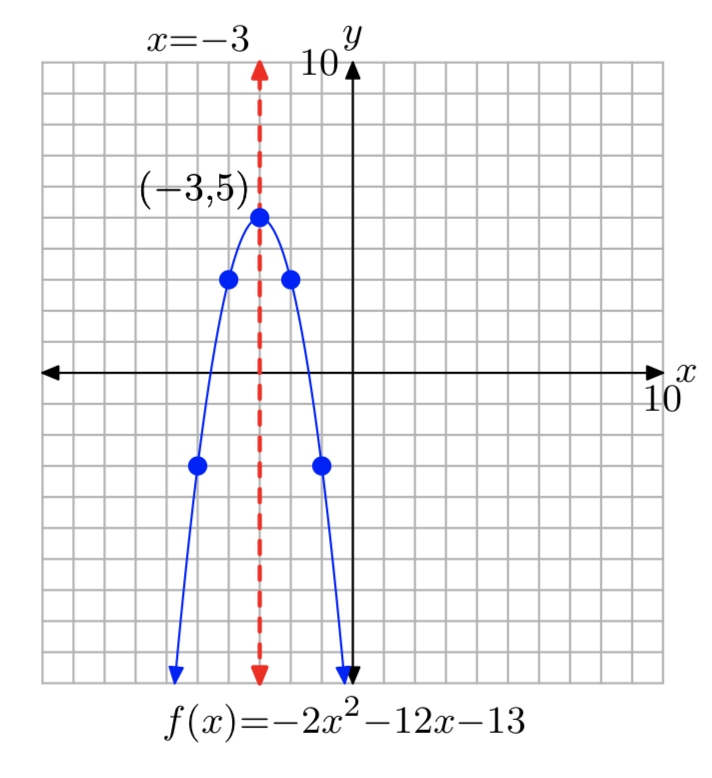
Dominio =\(\mathbb{R}\), Rango = (−\(\infty\), 5]
Ejercicio\(\PageIndex{58}\)
\(f(x) = −2x^2+24x−70\)
Ejercicio\(\PageIndex{59}\)
\(f(x) = \frac{1}{2}x^2−4x+5\)
- Contestar
-
\(f(x) = \frac{1}{2}(x−4)^2−3\)
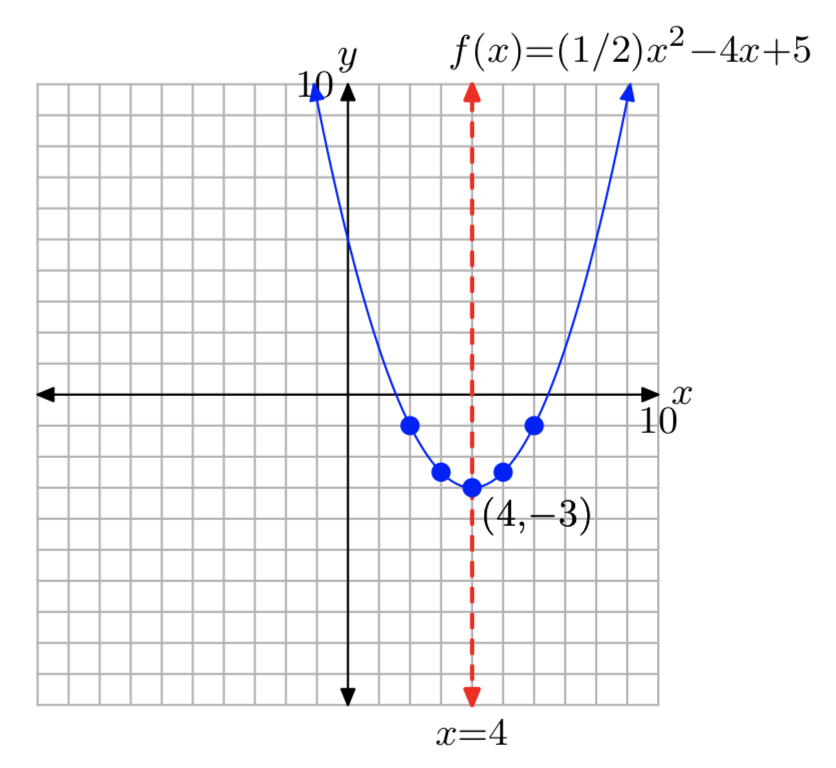
Dominio =\(\mathbb{R}\), Rango = [−3,\(\infty\))
Ejercicio\(\PageIndex{60}\)
\(f(x) = \frac{1}{2}x^2+4x+6\)
Ejercicio\(\PageIndex{61}\)
\(f(x) = −\frac{1}{2}x^2−3x+\frac{1}{2}\)
- Contestar
-
\(f(x) = −\frac{1}{2}(x+3)^2+5\)
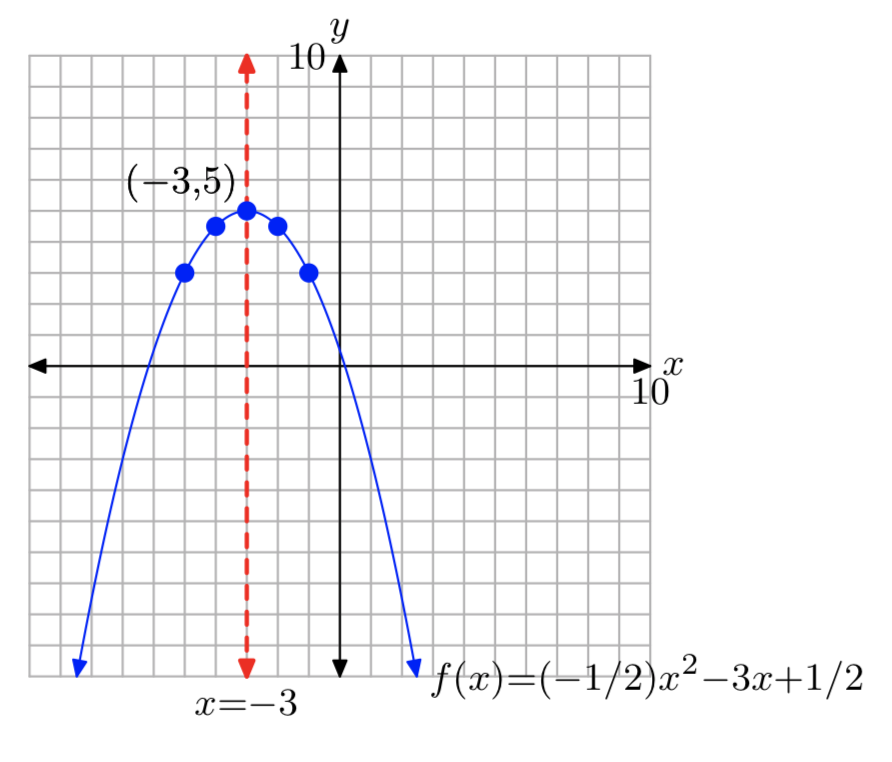
Dominio =\(\mathbb{R}\), Rango = (−\(\infty\), 5]
Ejercicio\(\PageIndex{62}\)
\(f(x) = −\frac{1}{2}x^2+4x−2\)
Ejercicio\(\PageIndex{63}\)
\(f(x) = 2x^2+7x−2\)
- Contestar
-
\(f(x) = 2(x+\frac{7}{4})^2− \frac{65}{8}\)
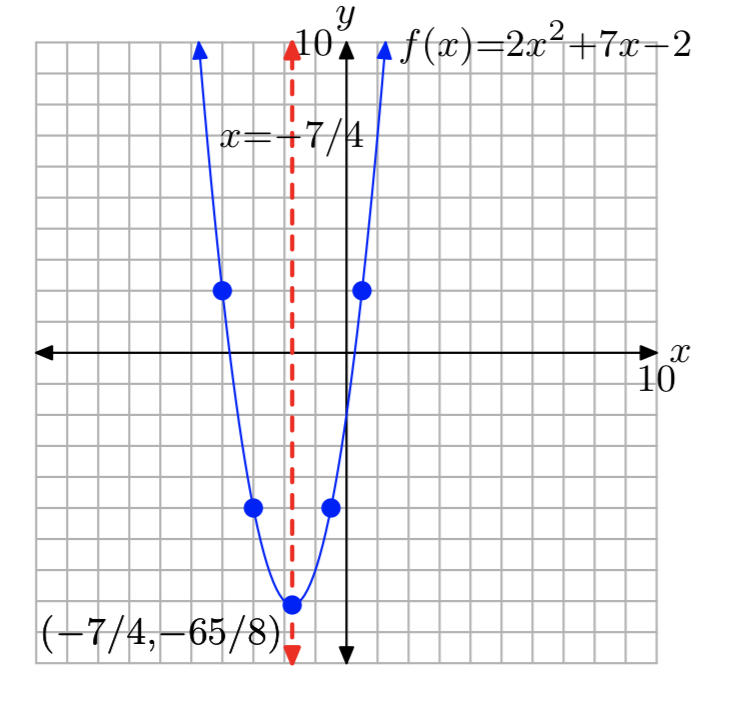
Dominio =\(\mathbb{R}\), Rango = [\(−\frac{65}{8}\),\(\infty\))
Ejercicio\(\PageIndex{64}\)
\(f(x) = −2x^2−5x−4\)
Ejercicio\(\PageIndex{65}\)
\(f(x) = −3x^2+8x−3\)
- Contestar
-
\(f(x) = −3(x−\frac{4}{3})^2+\frac{7}{3}\)
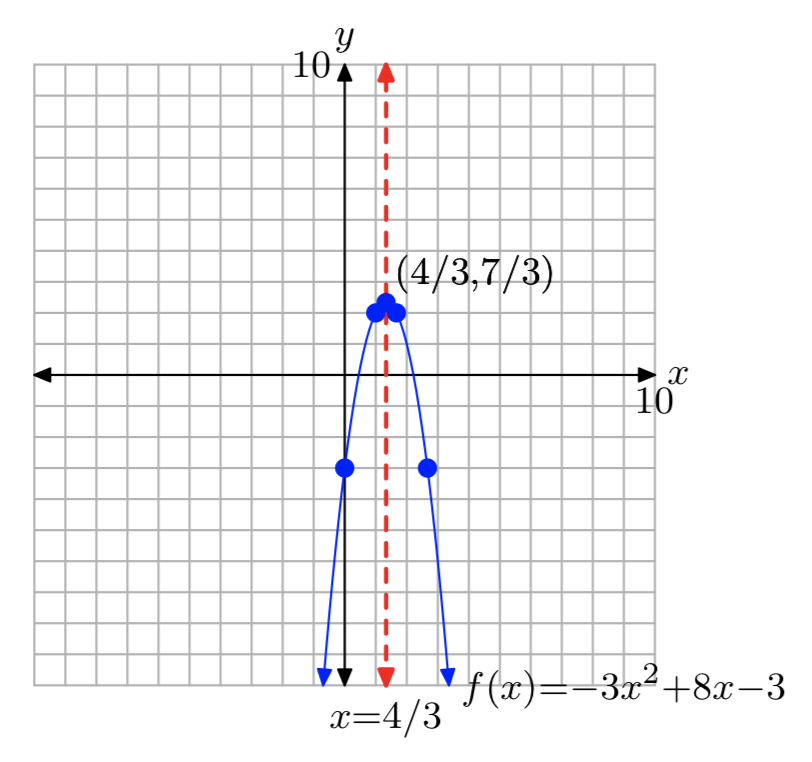
Dominio =\(\mathbb{R}\), Rango = (−\(\infty\),\(\frac{7}{3}\)]
Ejercicio\(\PageIndex{66}\)
\(f(x) = 3x^2+4x−6\)
En Ejercicios 67 - 72, encuentra el rango de la función cuadrática dada. Exprese su respuesta tanto en notación de intervalo como de conjunto.
Ejercicio\(\PageIndex{67}\)
\(f(x) = −2x^2+4x+3\)
- Contestar
-
(\(−\infty\), 5] = {x|\(x \le 5\)}
Ejercicio\(\PageIndex{68}\)
\(f(x) = x^2+4x+8\)
Ejercicio\(\PageIndex{69}\)
\(f(x) = 5x^2+4x+4\)
- Contestar
-
[\(\frac{16}{5}\),\(\infty\)) = {x|\(x \ge 5\)}
Ejercicio\(\PageIndex{70}\)
\(f(x) = 3x^2−8x+3\)
Ejercicio\(\PageIndex{71}\)
\(f(x) = −x^2−2x−7\)
- Contestar
-
(\(−\infty\), −6] = {x|\(x \le −6\)}
Ejercicio\(\PageIndex{72}\)
\(f(x) = x^2+x+9\)
Taladro para Habilidad. En los Ejercicios 73 - 76, evaluar la función al valor dado b.
Ejercicio\(\PageIndex{73}\)
\(f(x) = 9x^2−9x+4\); b = −6
- Contestar
-
382
Ejercicio\(\PageIndex{74}\)
\(f(x) = −12x^2+5x+2\); b = −3
Ejercicio\(\PageIndex{75}\)
\(f(x) = 4x^2−6x−4\); b = 11
- Contestar
-
414
Ejercicio\(\PageIndex{76}\)
\(f(x) = −2x^2−11x−10\); b = −12
Taladro para Habilidad. En Ejercicios 77 - 80, evaluar la función en la expresión dada.
Ejercicio\(\PageIndex{77}\)
Evaluar f (x+4) si\(f(x) = −5x^2+4x+2\).
- Contestar
-
\(−5x^2−36x−62\)
Ejercicio\(\PageIndex{78}\)
Evaluar f (−4x−5) si\(f(x) = 4x^2+x+1\).
Ejercicio\(\PageIndex{79}\)
Evaluar f (4x−1) si\(f(x) = 4x^2+3x−3\).
- Contestar
-
\(64x^2−20x−2\)
Ejercicio\(\PageIndex{80}\)
Evaluar f (−5x−3) si\(f(x) = −4x^2+x+4\).