5.5: Movimiento

Si una partícula se mueve con aceleración uniforme o constante, entonces debe comportarse de acuerdo con ciertas leyes estándar de la cinemática. En esta sección desarrollaremos estas leyes de movimiento y las aplicaremos a una serie de aplicaciones interesantes.

Velocidad Uniforme

Si un objeto viaja con una velocidad uniforme (constante) v, entonces la distancia d recorrida en el tiempo t viene dada por la fórmula

\[d=v t\]

o en palabras, “la distancia es igual a la velocidad por el tiempo”. Este concepto probablemente sea familiar para quienes manejamos nuestros autos en la carretera. Por ejemplo, si conduzco mi auto a una velocidad constante de 50 millas por hora, en 3 horas recorreré 150 millas. Es decir,

\[150 \mathrm{mi}=50 \frac{\mathrm{mi}}{\mathrm{h}} \times 3 \mathrm{h}\]

Tenga en cuenta que este cálculo tiene la forma “distancia es igual a velocidad por tiempo”. Es importante señalar cómo se equilibran las unidades en cada lado de este resultado. Esto se ve fácilmente cancelando unidades tanto como cancelaría números con fracciones ordinarias.

\[150 \mathrm{mi}=50 \frac{\mathrm{mi}}{\not{h}} \times 3 \not{h}\]

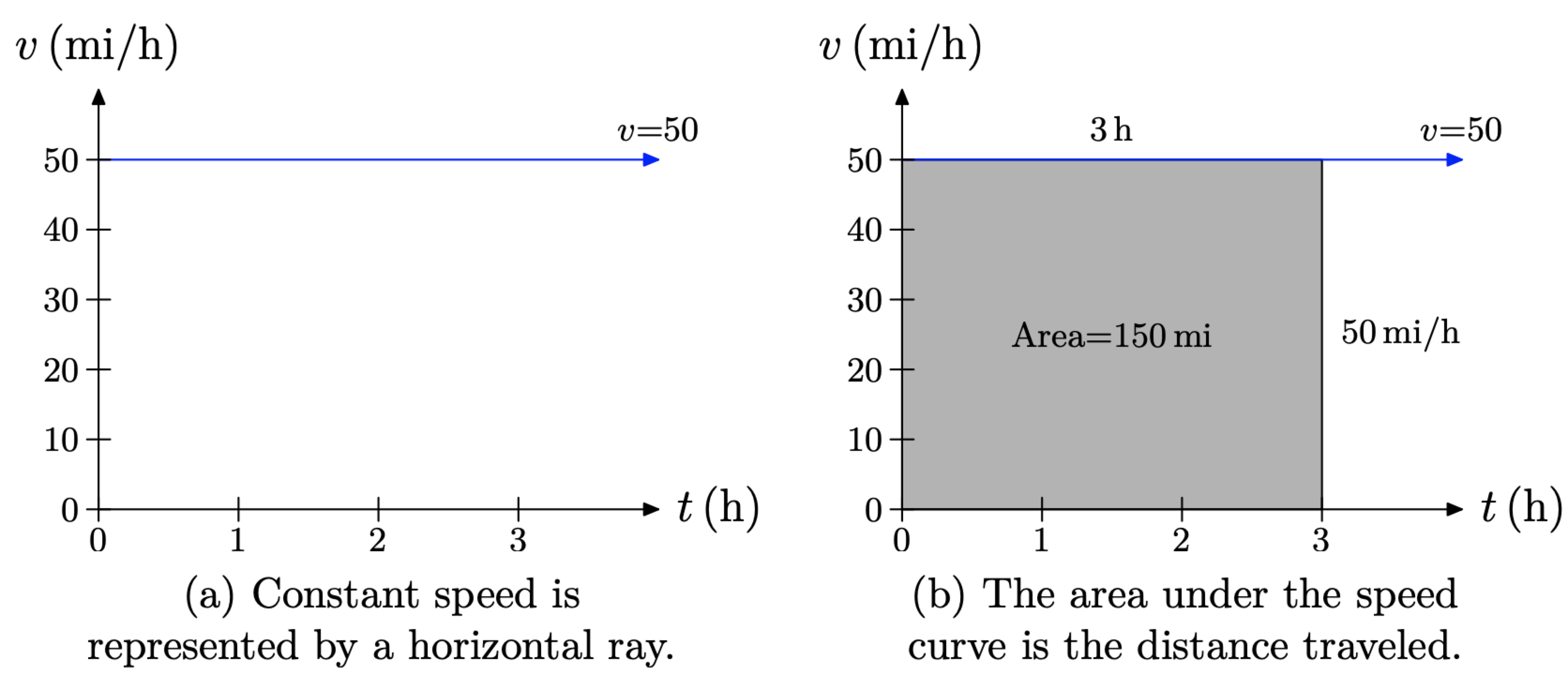
En la Figura\(\PageIndex{1}\) (a) hemos trazado la velocidad v del carro versus tiempo t. Debido a que la velocidad es uniforme (constante), la gráfica es un rayo horizontal, comenzando en el tiempo t = 0 y moviéndose hacia la derecha. En la Figura\(\PageIndex{1}\) (b), hemos sombreado el área bajo el rayo de velocidad constante durante el intervalo de tiempo [0, 3] horas. Tenga en cuenta que el área de la región rectangular sombreada tiene altura igual a 50 millas por hora (50 mi/h) y ancho igual a 3 horas (3 h), por lo que el área de este rectángulo es

\[\text { Area }=\text { height } \times \text { width }=50 \frac{\mathrm{mi}}{\mathrm{h}} \times 3 \mathrm{h}=150 \mathrm{mi}\]

Anote las unidades en la respuesta. El área bajo el rayo de velocidad constante es de 150 millas. Es decir, ¡el área bajo la curva de velocidad es la distancia recorrida!

Nuestro trabajo nos ha llevado al siguiente resultado.

Velocidad Uniforme

Supongamos que un objeto viaja con una velocidad uniforme (constante) v.

• La distancia recorrida d viene dada por la fórmula d = vt, donde t es el tiempo de viaje.
• El gráfico de velocidad v versus tiempo t será un rayo horizontal, comenzando en el tiempo t = 0 y moviéndose hacia la derecha.
• El área de la región rectangular bajo la gráfica de v durante el intervalo de tiempo [0, t] da la distancia recorrida durante ese período de tiempo.

Figura\(\PageIndex{1}\)

Veamos otro ejemplo.

Ejemplo\(\PageIndex{1}\)

Un objeto viaja con velocidad uniforme v. La gráfica de v versus t se muestra en la gráfica que sigue.

Figura\(\PageIndex{2}\). El gráfico de la velocidad del objeto versus tiempo.

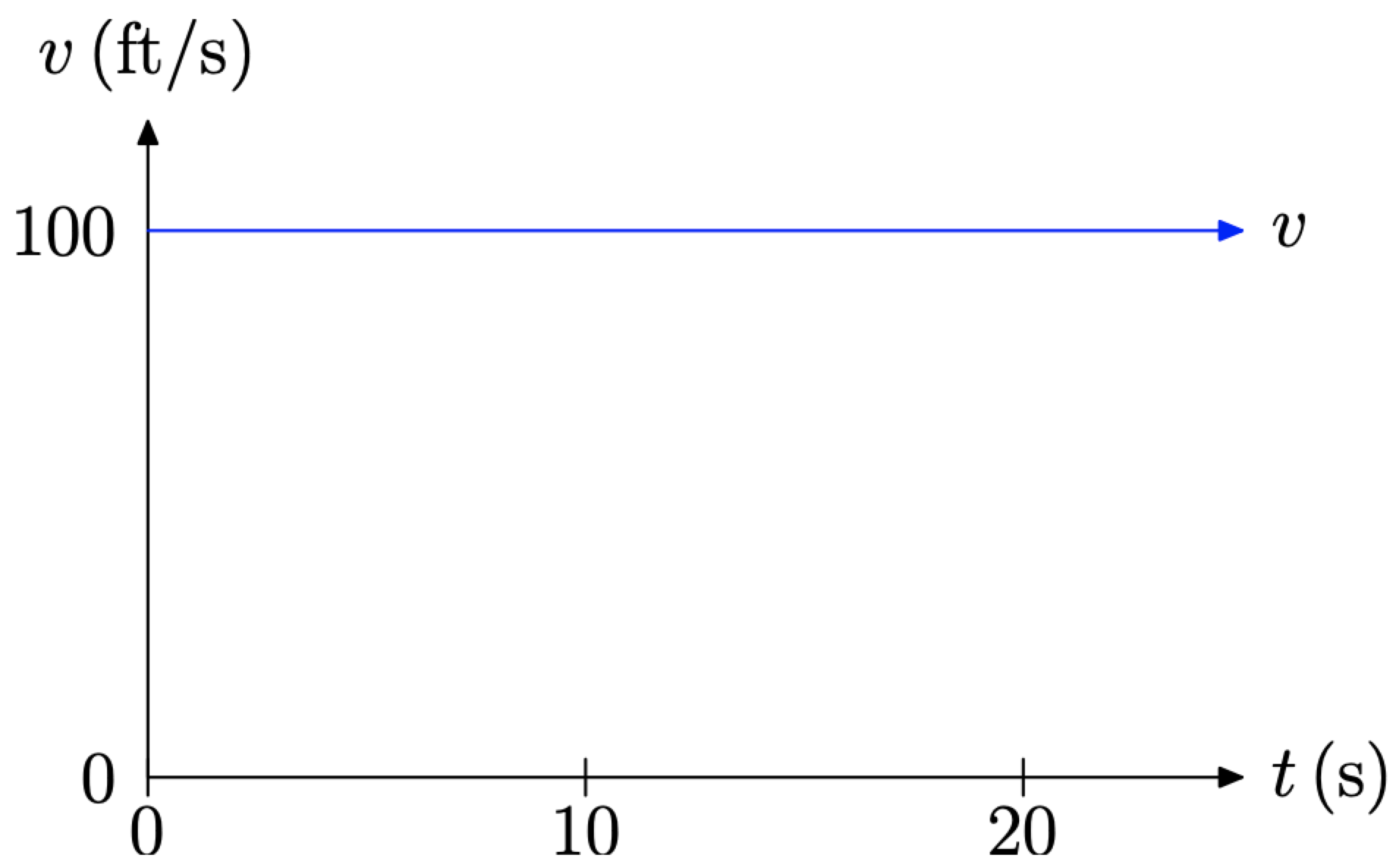
¿Cuál es la velocidad del objeto en cualquier momento t? ¿Hasta dónde viajará el objeto en 20 segundos?

Solución

Leemos la velocidad de la gráfica. Tenga en cuenta que el rayo que representa la velocidad es nivelado (constante) a 100 pies por segundo (100 pies/s). Por lo tanto, la velocidad en cualquier momento t es v = 100. En notación de funciones, escribiríamos v (t) = 100, siendo conscientes de que las unidades son pies por segundo (ft/s).

Para encontrar la distancia recorrida en 20 segundos, tenemos dos opciones:

1. Si usamos la fórmula d = vt, entonces

\[\begin{aligned} d &=v t \\ d &=100 \frac{\mathrm{ft}}{\not{s}} \times 20 \not{s} \\ d &=2000 \mathrm{ft} \end{aligned}\]

Es decir, el objeto recorre 2000 pies en los 20 segundos.

2. También podemos encontrar la distancia recorrida sombreando el área bajo la curva de velocidad uniforme durante el intervalo de tiempo de 20 segundos.

Figura\(\PageIndex{3}\). El área bajo la curva de velocidad uniforme representa la distancia recorrida.

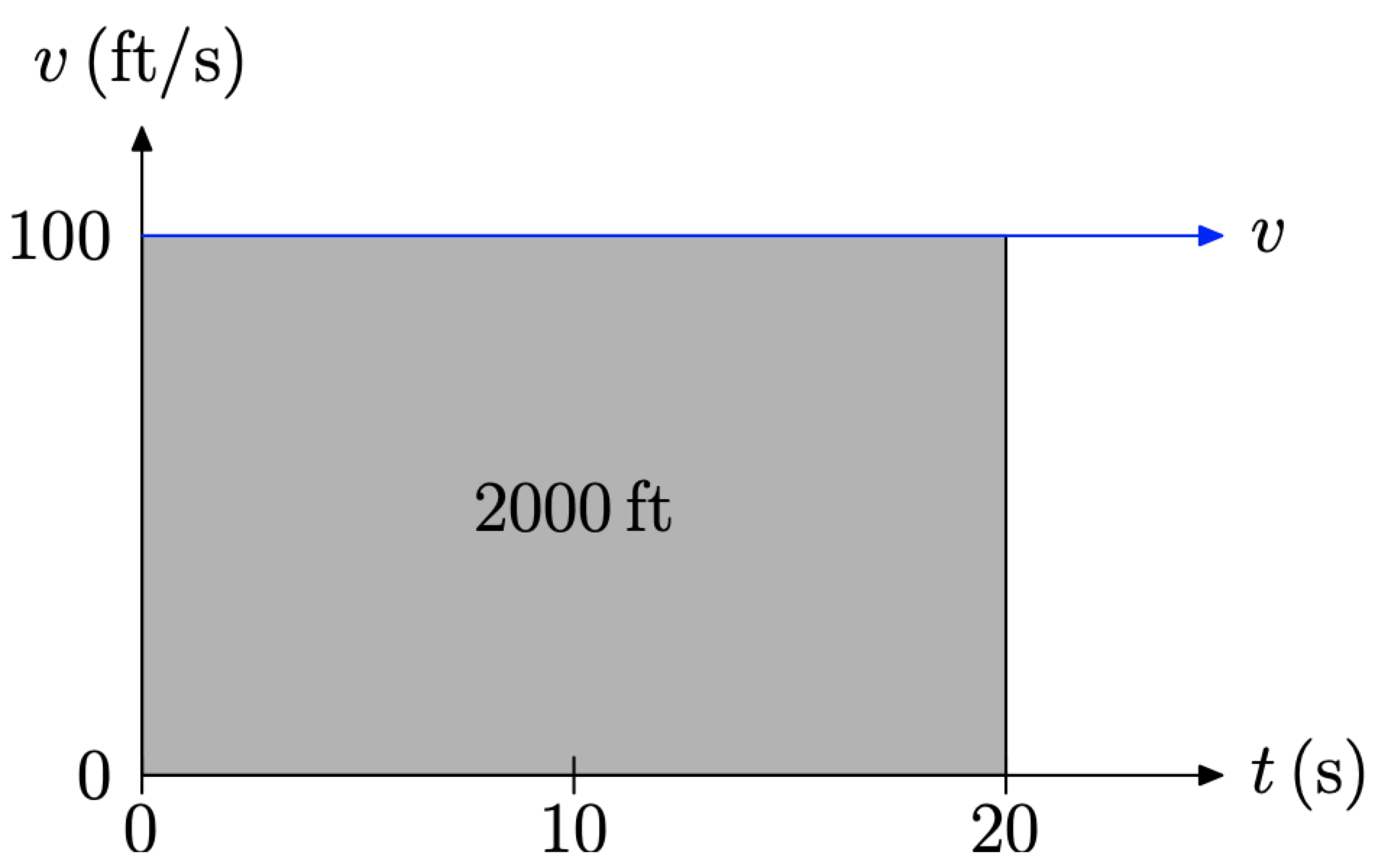
Tenga en cuenta que la altura de la región rectangular sombreada en la Figura\(\PageIndex{3}\) es de 100 pies por segundo (100 pies/s) y el ancho es de 20 segundos (20 s). Por lo tanto, el área de la región rectangular sombreada es

\[\text { Area }=100 \frac{\mathrm{ft}}{\not{s}} \times 20 \not{s}=2000 \mathrm{ft}\]

que es idéntico al resultado encontrado con la fórmula d = vt.

Aceleración uniforme

Volvamos a subir al auto y conduzcamos por la autopista a una velocidad constante (constante) de v = 30 millas por hora. Decidimos adelantar a un camión frente a nosotros, por lo que pisamos el acelerador del auto, lo que aumenta la velocidad del auto, permitiéndonos pasar el camión.

Definición

La aceleración es la velocidad a la que cambia la velocidad de un objeto con respecto al tiempo.

Por ejemplo, supongamos que cuando pisamos el acelerador del auto, la velocidad del auto cambia a una constante de 20 millas por hora por hora. Entonces diríamos que la aceleración es uniforme (constante) y escribiría

\[\text { Acceleration }=20 \frac{\mathrm{mi} / \mathrm{h}}{\mathrm{h}}\]

o, más sucintamente, como

\[\text { Acceleration }=20 \frac{\mathrm{mi}}{\mathrm{h}^{2}}\]

Esta última notación es la preferida por los científicos, pero la notación a = 20 (mi/h) /h es mucho más fácil de entender. Es decir, la velocidad está aumentando a un ritmo constante de 20 millas por hora cada hora.

• Por el momento pisamos el acelerador para pasar el camión, la velocidad inicial del auto es de v = 30 millas por hora. Si mantenemos una aceleración constante de 20 millas por hora por hora, después de 1 hora, la velocidad aumenta en 20 millas por hora, por lo que la velocidad del automóvil al final de 1 hora es\[v=30+20(1)\] o v = 50 millas por hora.
• Al cabo de dos horas, la velocidad del carro es\[v=30+20(2)\] o v = 70 millas por hora.
• Al cabo de tres horas, la velocidad del carro es\[v = 30 + 20(3)\], o v = 90 millas por hora.

Continuando de esta manera, es fácil ver que la velocidad del automóvil al final de las t horas estará dada por la fórmula\[v=30+20 t\]

Es importante señalar que estamos asumiendo que mantenemos nuestro pie en ese acelerador para mantener una aceleración uniforme (constante) de 20 millas por hora por hora. Concedido, este es un ejemplo bastante tonto con muy baja aceleración (¿es ese el auto de Fred Flintstone?) , pero sí nos permite concentrarnos en el concepto sin tener que lidiar con unidades desordenadas.

Si seguimos el argumento anterior, no es difícil desarrollar la primera ecuación de movimiento.

Primera Ecuación de Movimiento

Si un objeto que tiene velocidad inicial\(v_{0}\) experimenta una aceleración constante a, entonces su velocidad en el tiempo t viene dada por la fórmula\[v=v_{0}+a t\].

Seguimos la práctica científica de denotar la velocidad inicial por v0, la velocidad en el tiempo t = 0. Por eso subíndice v con cero.

Por supuesto, la primera ecuación de movimiento es válida sólo si cada cantidad posee las unidades adecuadas.

Ejemplo\(\PageIndex{2}\)

Supongamos que una partícula tiene una velocidad inicial de 20 pies por segundo (20 pies/s) y se le da una aceleración constante de 4 pies por segundo por segundo\(\left(4 f t / s^{2}\right)\). ¿Cuál será la velocidad de la partícula después de 3 minutos (3 min)?

Solución

Es tentador comenzar con la fórmula\[v=v_{0}+a t\]

y suplente\(v_{0}=20 \mathrm{ft} / \mathrm{s}, a=4 \mathrm{ft} / \mathrm{s}^{2},\) y\(t=3 \mathrm{min}\)

\[v=20 \frac{\mathrm{ft}}{\mathrm{s}}+4 \frac{\mathrm{ft}}{\mathrm{s}^{2}} \times 3 \mathrm{min}\]

No obstante, tenga en cuenta que las unidades no cancelarán porque el tiempo se mide en minutos. Lo que tenemos que hacer es cambiar el tiempo a segundos con la conversión

\[t=3 \not{min} \times 60 \frac{\mathrm{s}}{\not{min}}=180 \mathrm{s}\]

Ahora las unidades deben ser correctas. Sustituimos el tiempo en segundos en la fórmula\(v = v_{0} + at\) y obtenemos

\[\begin{aligned} v &=20 \frac{\mathrm{ft}}{\mathrm{s}}+4 \frac{\mathrm{ft} / \mathrm{s}}{\not{s}} \times 180 \not{\mathrm{s}} \\ &=20 \frac{\mathrm{ft}}{\mathrm{s}}+720 \frac{\mathrm{ft}}{\mathrm{s}} \\ &=740 \frac{\mathrm{ft}}{\mathrm{s}} \end{aligned}\]

De ahí que la velocidad de la partícula a los tres minutos sea v = 740 pies/s.

Veamos otro ejemplo.

Ejemplo\(\PageIndex{3}\)

Se lanza una pelota al aire con una velocidad inicial de 180 pies por segundo (180 pies/s). Inmediatamente comienza a desacelerar a una velocidad constante de 32 pies por segundo por segundo\((32 ft/s^2 )\). ¿A qué hora alcanzará la pelota su máxima altura?

Solución

Cuando la bola alcanza su altura máxima, su velocidad será igual a cero. Es decir, en el momento exacto en que el balón esté a su altura máxima, se detendrá antes de que regrese al suelo. Así, para encontrar el momento en que el balón está a su altura máxima, sustituya v = 0 en la fórmula\(v = v_{0} + at\) y resuelva por t.

\[\begin{aligned} 0 &=v_{0}+a t \\ a t &=-v_{0} \\ t &=-\frac{v_{0}}{a} \end{aligned}\]

Cuando decimos que la pelota desacelera a una velocidad constante de 32 pies/s cada segundo, estamos insinuando que la pelota pierde velocidad a una velocidad de 32 pies/s cada segundo. Así, la aceleración es negativa en este caso y escribimos\(a = −32 ft/s^2\).

Finalmente, solo necesitamos sustituir la velocidad inicial (v0 = 180 ft/s) y la aceleración\((a = −32 ft/s^2)\) en la ecuación (6) y simplificar.

\[t=-\frac{180 \mathrm{ft} / \mathrm{s}}{-32 \mathrm{ft} / \mathrm{s}^{2}}\]

Un análisis de las unidades es una buena comprobación de que estamos haciendo las cosas correctamente. Tenga en cuenta que\[\frac{\mathrm{ft} / \mathrm{s}}{\mathrm{ft} / \mathrm{s}^{2}}=\frac{\mathrm{ft}}{\mathrm{s}} \times \frac{\mathrm{s}^{2}}{\mathrm{ft}}=\mathrm{s}\]

Así, es el momento para que la pelota alcance su máxima altura\[t = 5 s\].

El área es la distancia recorrida

Si trazamos la gráfica de la velocidad v versus el tiempo t, tenga en cuenta que la ecuación\(v = v_{0} +at\) tiene la forma y = mx+b, particularmente si organizamos la ecuación en el orden\(v = at+v_{0}\). Entonces se ve fácilmente que la gráfica será una línea con intercepción igual a la velocidad inicial\(v_{0}\) y pendiente igual a la aceleración a. la gráfica de\(v = v_{0} + at\) se muestra en la Figura\(\PageIndex{4}\) (a).

En la Figura\(\PageIndex{4}\) (b), hemos sombreado el área bajo la gráfica de\(v = v_{0} + at\) durante el intervalo de tiempo [0, t]. Hay una pregunta natural que hacer. ¿El área bajo la gráfica de\(v = v_{0} + at\) la Figura\(\PageIndex{4}\) (b) representará la distancia recorrida durante el intervalo de tiempo [0, t]?

Figura\(\PageIndex{4}\). La gráfica de\(v = v_{0} + at\) es una línea con intercepción v0 y pendiente a.

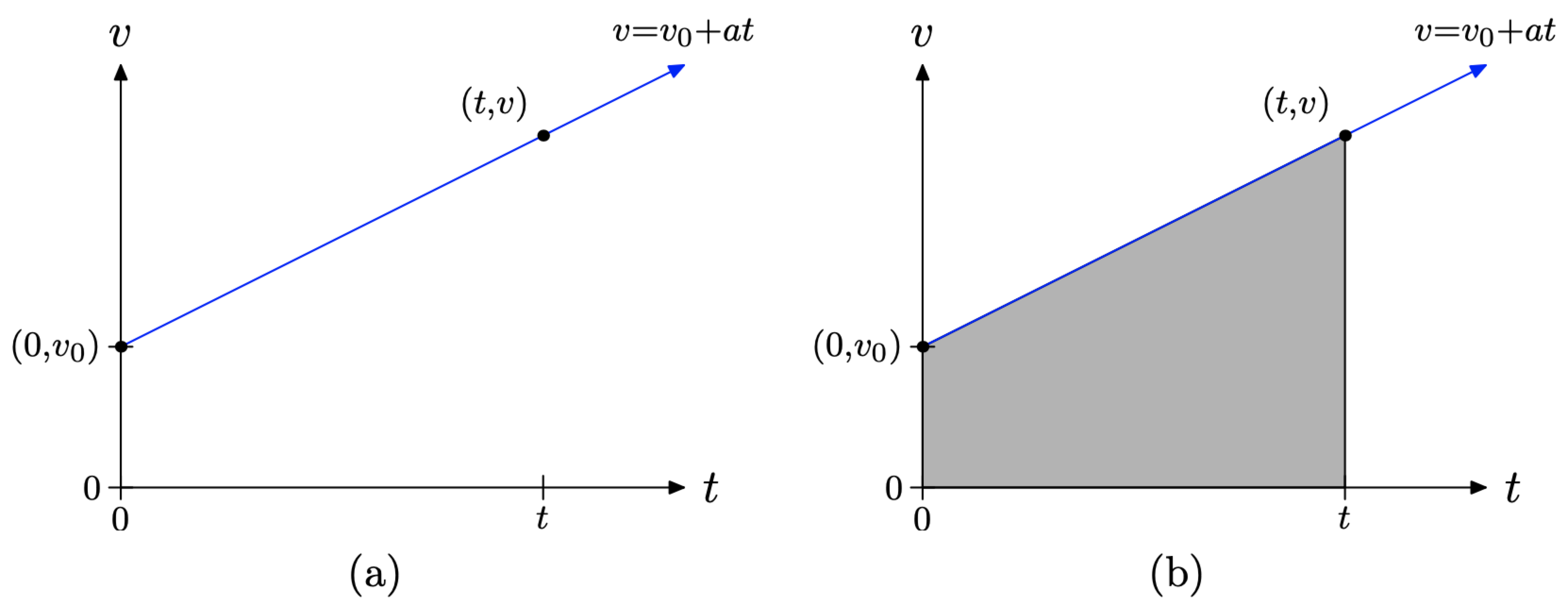
Sabemos que el área bajo un rayo de velocidad uniforme (constante) será igual a la distancia recorrida. ¿Podemos usar este hecho para responder a nuestra pregunta sobre la región triangular sombreada en la Figura\(\PageIndex{4}\) (b)?

Tomemos el intervalo de tiempo [0, t] en la Figura\(\PageIndex{4}\) (b) y lo dividemos en 4 subintervalos iguales de tiempo, como se muestra en la Figura\(\PageIndex{5}\) (a).

Figura\(\PageIndex{5}\). Subdividiendo el área en rectángulos.

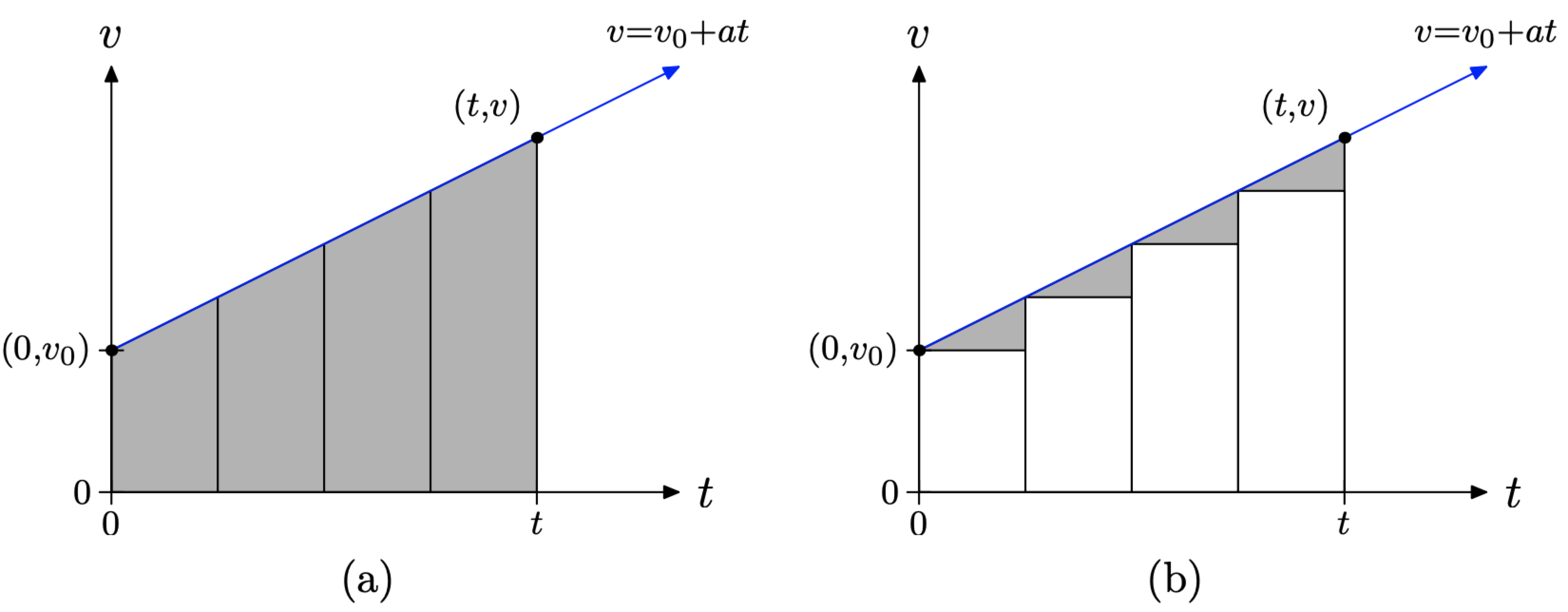
A continuación, utilice el punto final izquierdo de cada subintervalo de tiempo para dibujar cuatro rectángulos y rellenarlos con el color blanco, como se muestra en la Figura\(\PageIndex{5}\) (b). La parte superior de cada rectángulo es horizontal, por lo que sabemos que esto representa una velocidad uniforme (constante). Por lo tanto, el área de cada rectángulo blanco representa la distancia recorrida durante ese subintervalo de tiempo. Si sumamos las áreas de los cuatro rectángulos, entonces obtenemos la distancia total recorrida durante el lapso de tiempo [0, t], con, por supuesto, la suposición de que la velocidad es constante durante cada uno de los subintervalos de tiempo.

Sin embargo, la velocidad no es constante durante cada subintervalo de tiempo, por lo que la suma de las áreas de los rectángulos sólo se aproxima a la distancia total recorrida en el intervalo de tiempo [0, t].

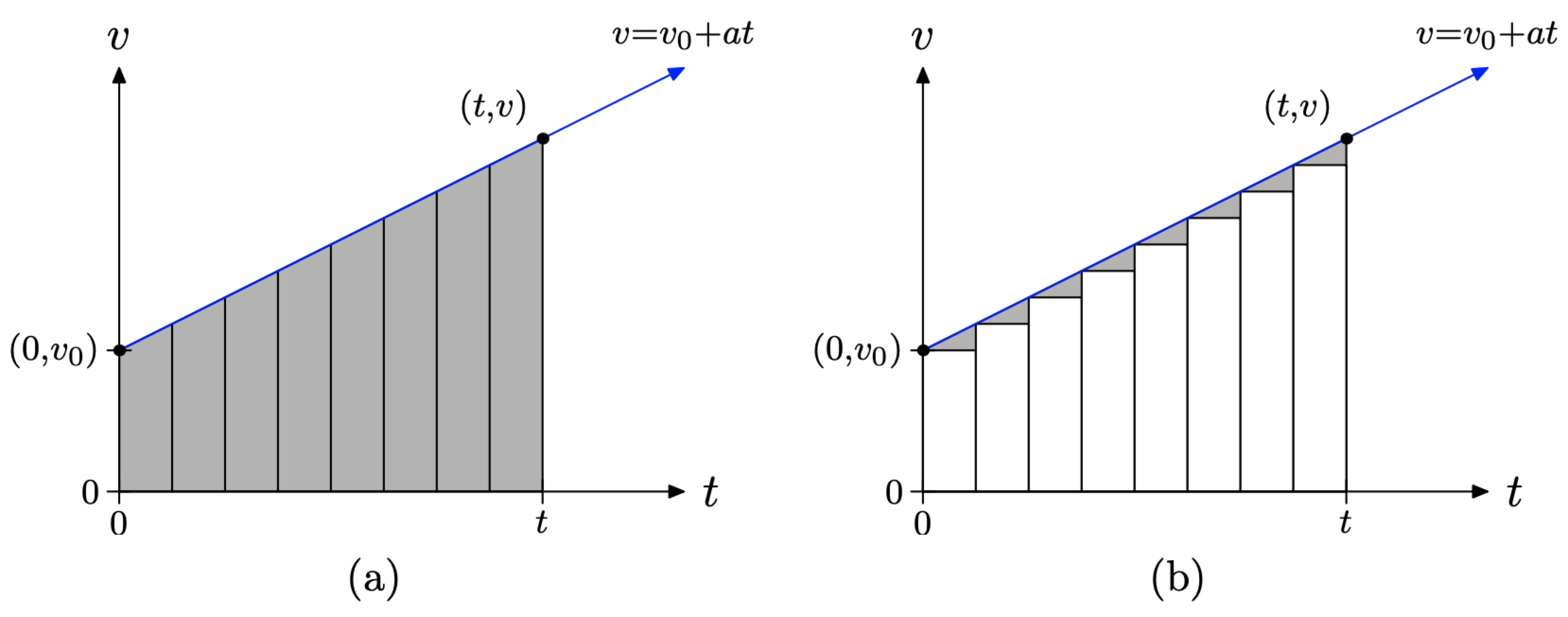
La idea clave es dibujar más rectángulos. En la Figura\(\PageIndex{6}\) (a), hemos dividido el intervalo de tiempo [0, t] en 8 subintervalos iguales de tiempo. En la Figura\(\PageIndex{6}\) (b), nuevamente usamos los extremos izquierdos de cada subintervalo de tiempo para dibujar rectángulos y los rellenamos con el color blanco.

Nuevamente, la parte superior de cada rectángulo blanco es horizontal, lo que representa una velocidad uniforme (constante) en ese subintervalo de tiempo. Por lo tanto, el área de cada rectángulo blanco nuevamente representa la distancia recorrida durante ese subintervalo de tiempo. La suma de los 8 rectángulos representa la distancia recorrida durante el intervalo de tiempo [0, t], asumiendo que la velocidad es constante durante cada uno de los subintervalos de tiempo.

Sin embargo, la velocidad no es constante en el intervalo de tiempo [0, t], por lo que la suma de los ocho rectángulos solo ofrece una aproximación de la distancia recorrida durante el intervalo de tiempo [0, t], aunque una mejor aproximación que la ofrecida por la suma de las áreas de sólo cuatro rectángulos en la Figura\(\PageIndex{5}\) (b).

A medida que subdividimos el intervalo de tiempo [0, t] más, sucederán dos cosas

Figura\(\PageIndex{6}\). Subdividiendo el área en rectángulos.

1. Los subintervalos de tiempo serán más pequeños (de hecho, infinitesimalmente pequeños). Cuando eso sucede, se vuelve cada vez más razonable asumir que la velocidad es constante durante ese subintervalo de tiempo. Por lo tanto, en el límite, la suma de las áreas de los rectángulos representará la distancia total recorrida a lo largo del intervalo de tiempo [0, t].
2. La suma de las áreas de los rectángulos converge al área de la región sombreada bajo la curva de velocidad en la Figura\(\PageIndex{4}\) (a).

Este argumento lleva a una conclusión convincente.

Área igual a distancia recorrida

El área bajo la curva\(v = v_{0} + at\) de velocidad en el intervalo de tiempo [0, t] representa la distancia recorrida durante el intervalo de tiempo [0, t].

En la Figura\(\PageIndex{7}\), la región sombreada debajo\(v = v_{0} + at\) es un trapecio. Para encontrar el área de este trapecio, sumamos las bases (lados paralelos) juntas, multiplicamos por la altura, luego tomamos la mitad del resultado.

Figura\(\PageIndex{7}\). El área de la región trapezoidal sombreada representa la distancia recorrida.

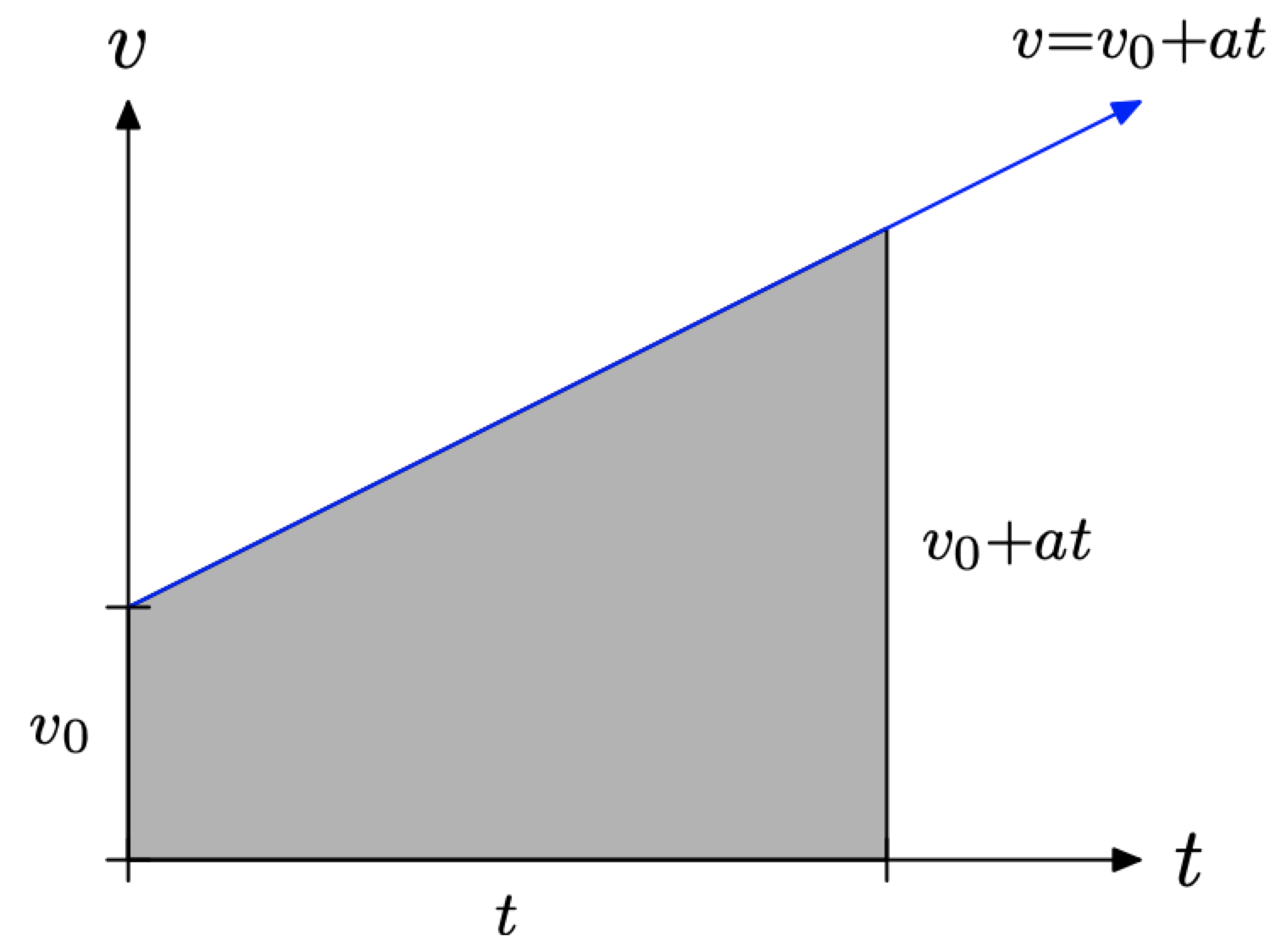
Así, el área de la región sombreada en la Figura\(\PageIndex{7}\) viene dada por la fórmula

\[\text { Area }=\frac{1}{2}\left[v_{0}+\left(v_{0}+a t\right)\right] t\]

Suma la cantidad dentro de los paréntesis, luego distribuya el 1/2 y el t para obtener

\[\text { Area }=v_{0} t+\frac{1}{2} a t^{2}\]

Movimiento en una dimensión

Supongamos que una partícula está obligada a moverse a lo largo de la línea real. Además, supongamos que en el tiempo t = 0, la posición inicial de la partícula está en\(x_{0}\) y la partícula tiene velocidad inicial\(v_{0}\) y se mueve hacia la derecha (como se muestra en la Figura\(\PageIndex{8}\)). Supongamos que la partícula experimenta una aceleración uniforme a que es positiva para que la partícula continúe moviéndose hacia la derecha al aumentar la velocidad. En el tiempo t, se denota la posición de la partícula por x y su velocidad por v (también se muestra en la Figura\(\PageIndex{8}\)).

Figura\(\PageIndex{8}\). Una partícula se mueve en la línea con aceleración uniforme.

Debido a que hemos asumido que la partícula se mueve hacia la derecha al aumentar la velocidad, la distancia recorrida por la partícula viene dada por la expresión\(x − x_{0}\). Sin embargo, también hemos aprendido que la distancia recorrida es el área bajo la gráfica de la velocidad (mostrada en la Figura\(\PageIndex{7}\)), que calculamos en la ecuación (7) para ser\(v_{0} t+ (1/2)at^2\). Concluimos que\[x-x_{0}=v_{0} t+\frac{1}{2} a t^{2}\]

lo que lleva a la segunda ecuación de movimiento.

Segunda Ecuación de Movimiento

Supongamos que una partícula se mueve sobre la línea real con una aceleración uniforme a. además, supongamos que la posición y velocidad de la partícula en el tiempo t = 0 están dadas por x0 y v0, respectivamente. Que x represente la posición de la partícula en el tiempo t. Luego, la posición de la partícula en el tiempo t viene dada por la fórmula

\[x=x_{0}+v_{0} t+\frac{1}{2} a t^{2}\]

Al desarrollar la ecuación de movimiento (9), hemos evitado la noción de velocidad. Sin embargo, si una partícula está obligada a moverse a lo largo de la línea real, puede moverse hacia la derecha o puede moverse hacia la izquierda. Esto agrega otra dimensión a la velocidad.

Dibujemos una recta numérica (como se muestra en la Figura\(\PageIndex{9}\)), localicemos el origen y coincidamos en que los desplazamientos positivos están a la derecha y los desplazamientos negativos a la izquierda.

Figura\(\PageIndex{9}\). Orientar la línea real

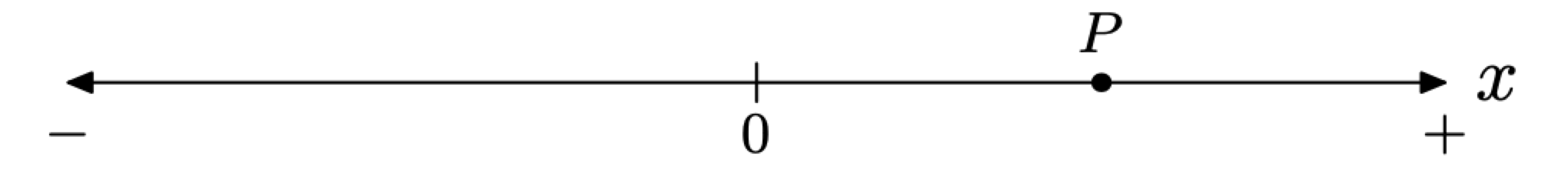
A continuación, definimos lo que se entiende por velocidad

Definición

La velocidad es la velocidad a la que cambia la posición de un objeto con respecto al tiempo.

Por ejemplo, supongamos que los desplazamientos en la línea orientada en la Figura\(\PageIndex{9}\) se miden en metros. Además, supongamos que la partícula en el punto P de la Figura\(\PageIndex{9}\) tiene velocidad v = 20 metros por segundo. Esto significaría que la posición de la partícula está cambiando en un positivo 20 metros cada segundo. Debido a la forma en que hemos orientado la línea Figura\(\PageIndex{9}\), esto significa que la partícula se mueve hacia la derecha a una velocidad de 20 metros por segundo.

Por otro lado, si la velocidad de la partícula en el punto P fuera de v = −20 metros por segundo, esto significaría que la posición de la partícula está cambiando en un negativo 20 metros cada segundo. Debido a la orientación que hemos elegido en la Figura\(\PageIndex{9}\), esto significaría que la partícula se mueve hacia la izquierda a una velocidad de 20 metros por segundo.

Tenga en cuenta que en cada caso (velocidad positiva o negativa) la velocidad es de 20 metros por segundo. Lo que la velocidad aporta a la mesa es un atributo adicional de orientación. El signo de la velocidad indica una dirección, mientras que la magnitud de la velocidad indica una velocidad.

Es importante para nosotros afirmar que las ecuaciones de movimiento se aplican igualmente bien cuando introducimos la noción de velocidad. Así, podemos resumir de la siguiente manera.

Las ecuaciones del movimiento

Supongamos que una partícula se mueve sobre una línea real orientada con una aceleración uniforme a. además, dejar\(x_{0}\) y\(v_{0}\) representar la posición inicial y la velocidad de la partícula en el tiempo t = 0.

• La velocidad v de la partícula en el tiempo t viene dada por la fórmula\(v = v_{0} + at\).
• La posición x de la partícula en el tiempo t viene dada por la fórmula\(x = x_{0} + v_{0} t + \frac{1}{2} at^2\).

Veamos algunas aplicaciones de estas Ecuaciones de Movimiento.

Ejemplo\(\PageIndex{4}\)

Orientar la línea real como en la Figura\(\PageIndex{9}\). Supongamos que en el tiempo t = 0 la partícula se ubica a 2 metros a la derecha del origen y se mueve a una velocidad de 3 metros por segundo. Además, supongamos que la partícula se está moviendo con una aceleración uniforme de\(1.5 m/s^2\). Encuentra la velocidad y posición de la partícula al cabo de 10 segundos.

Solución

Nos dan que\(v_{0} = 3\) m/s y\(a = 1.5 m/s^2\). Así, después de t = 10 segundos,

\[\begin{array}{l}{v=v_{0}+a t} \\ {v=3 \frac{\mathrm{m}}{\mathrm{s}}+1.5 \frac{\mathrm{m} / \mathrm{s}}{\not{s}} \times 10 \not{\mathrm{s}}} \\ {v=3 \frac{\mathrm{m}}{\mathrm{s}}+15 \frac{\mathrm{m}}{\mathrm{s}}} \\ {v=18 \frac{\mathrm{m}}{\mathrm{s}}}\end{array}\]

También se nos da que\(x_{0} = 2\) m. Así, después de t = 10 segundos

\[\begin{aligned} x &=x_{0}+v_{0} t+\frac{1}{2} a t^{2} \\ x &=2 \mathrm{m}+\left(3 \frac{\mathrm{m}}{\mathrm{s}}\right)(10 \mathrm{s})+\frac{1}{2}\left(1.5 \frac{\mathrm{m}}{\mathrm{s}^{2}}\right)(10 \mathrm{s})^{2} \\ x &=2 \mathrm{m}+\left(3 \frac{\mathrm{m}}{\not{s}}\right)(10 \mathrm{s})+\frac{1}{2}\left(1.5 \frac{\mathrm{m}}{\not{\mathrm{s}^{2}}}\right)\left(100 \not{\mathrm{s}^{2}}\right) \\ x &=2 \mathrm{m}+30 \mathrm{m}+75 \mathrm{m} \\ x &=107 \mathrm{m} \end{aligned}\]

Así, al final de t = 10 segundos, la partícula se ubica 107 metros a la derecha del origen y tiene velocidad 18 metros por segundo (se está moviendo hacia la derecha con velocidad 18 metros por segundo)

Veamos otra aplicación de las Ecuaciones de Movimiento.

Ejemplo\(\PageIndex{5}\)

Un automóvil viaja por la autopista a una velocidad de 60 millas por hora. De pronto, aparece un venado en la carretera por delante y el conductor aplica los frenos, desacelerando el auto a un ritmo constante de 12.9 pies por segundo cada segundo. ¿Cuánto tiempo tarda el auto en detenerse y qué tan lejos viaja durante este tiempo?

Solución

La velocidad del carro viene dada por la fórmula v = v0 + at. El auto parará cuando v = 0. Por lo tanto, sustituya v = 0 en la fórmula y resuelva por t

\[\begin{array}{l}{v=v_{0}+a t} \\ {0=v_{0}+a t} \\ {t=-\frac{v_{0}}{a}}\end{array}\]

En el tiempo t = 0, la velocidad inicial del automóvil es v0 = 60 mi/h. El automóvil está desacelerando por lo que está perdiendo velocidad a la velocidad dada de 12.9 pies por segundo cada segundo; es decir,\(a = −12.9 ft/s^2\). Podríamos intentar sustituir estos números en nuestro último resultado

\[t=-\frac{60 \mathrm{mi} / \mathrm{h}}{-12.9 \mathrm{ft} / \mathrm{s}^{2}}\]

El problema es inmediatamente evidente: las unidades no cancelarán. Tenemos dos opciones; podemos (1) cambiar la velocidad inicial a pies por segundo, o (2) cambiar la aceleración a millas por hora por hora. Haremos lo primero con el siguiente cálculo.

\[v_{0} = \frac{60\not{\text{mi}}}{\not{\text{h}}} \times \frac{5280\text{ft}}{\not{\text{mi}}} \times \frac{1\not{\text{h}}}{60\not{\text{min}}} \times \frac{1\not{\text{min}}}{60\not{\text{s}}} = 88\text{ft/s}\]

Sustituiremos este número en la ecuación (13).

\[\begin{aligned} t &=-\frac{v_{0}}{a} \\ t &=-\frac{88 \mathrm{ft} / \mathrm{s}}{-12.9 \mathrm{ft} / \mathrm{s}^{2}} \\ t & \approx 6.8 \mathrm{s} \end{aligned}\]

Nuevamente, es importante revisar las unidades. Tenga en cuenta que

\[\frac{\mathrm{ft} / \mathrm{s}}{\mathrm{ft} / \mathrm{s}^{2}}=\frac{\mathrm{ft}}{\mathrm{s}} \times \frac{\mathrm{s}^{2}}{\mathrm{ft}}=\mathrm{s}\]

que es la unidad correcta para el tiempo.

Ahora encontraremos la distancia de parada dejando que la posición inicial del carro sea\(x_{0} = 0\) pies. Así,\(x = x_{0} + v_{0} t + (1/2)at^2\) se convierte

\[x=v_{0} t+\frac{1}{2} a t^{2}\]

y x representará la distancia de detención.

Ahora, sustituya la velocidad inicial v0 = 88 pies por segundo, la aceleración a = −12.9 pies por segundo cada segundo, y el tiempo de parada t = 6.8 segundos. Por lo tanto,

\[\begin{aligned} x &=v_{0} t+\frac{1}{2} a t^{2} \\ x &=\left(\frac{88 \mathrm{ft}}{\mathrm{s}}\right)(6.8 \mathrm{s})+\frac{1}{2}\left(\frac{-12.9 \mathrm{ft} / \mathrm{s}}{\mathrm{s}}\right)(6.8 \mathrm{s})^{2} \\ x &=\left(\frac{88 \mathrm{ft}}{\not{s}}\right)(6.8 \not{\mathrm{s}})+\frac{1}{2}\left(\frac{-12.9 \mathrm{ft}}{\not{\mathrm{s}^{2}}}\right)\left(46.24 \not{\mathrm{s}^{2}}\right) \\ x &=598.4 \mathrm{ft}-298.248 \mathrm{ft} \\ x & \approx 300 \mathrm{ft} \end{aligned}\]

donde hemos redondeado la distancia de parada al pie más cercano.

La aceleración debido a la gravedad

Si descuidamos la resistencia al aire, entonces un cuerpo caerá a la superficie de la tierra con una aceleración uniforme. Los físicos utilizan la letra g para representar la aceleración debida a la gravedad. Cerca de la superficie de la tierra, esta aceleración viene dada por\(g=32 \mathrm{ft} / \mathrm{s}^{2}\) o, en el sistema métrico,\(g=9.8 \mathrm{m} / \mathrm{s}^{2}\).

Recuerde, la aceleración es la velocidad a la que la velocidad de un cuerpo está cambiando con respecto al tiempo. En consecuencia, si dejamos caer un cuerpo del reposo a una altura muy grande, después de 1 segundo, su velocidad será de 32 pies por segundo. Después de 2 segundos, su velocidad será de 64 pies por segundo. Después de 3 segundos, su velocidad será de 96 pies por segundo. Observe cómo la velocidad está cambiando a una velocidad de 32 pies por segundo cada segundo de tiempo.

La gravedad siempre atrae un objeto al centro de la tierra, por lo que tenemos que tener esto en cuenta al usar las Ecuaciones de Movimiento.

Veamos un ejemplo.

Ejemplo\(\PageIndex{6}\)

Una pelota es liberada del reposo de un globo de aire caliente que está flotando a una distancia de 2000 pies sobre la superficie de la tierra. ¿Cuánto tiempo tardará en que la pelota golpee el suelo?

Solución

En este ejercicio giraremos la línea real para que quede vertical, como se muestra en la Figura\(\PageIndex{10}\) (a). Estableceremos el origen a nivel del suelo y dejaremos que la dirección y positiva apunte hacia arriba (indicada por el signo + en la parte superior de la línea en la Figura\(\PageIndex{10}\) (a).

Figura\(\PageIndex{10}\).

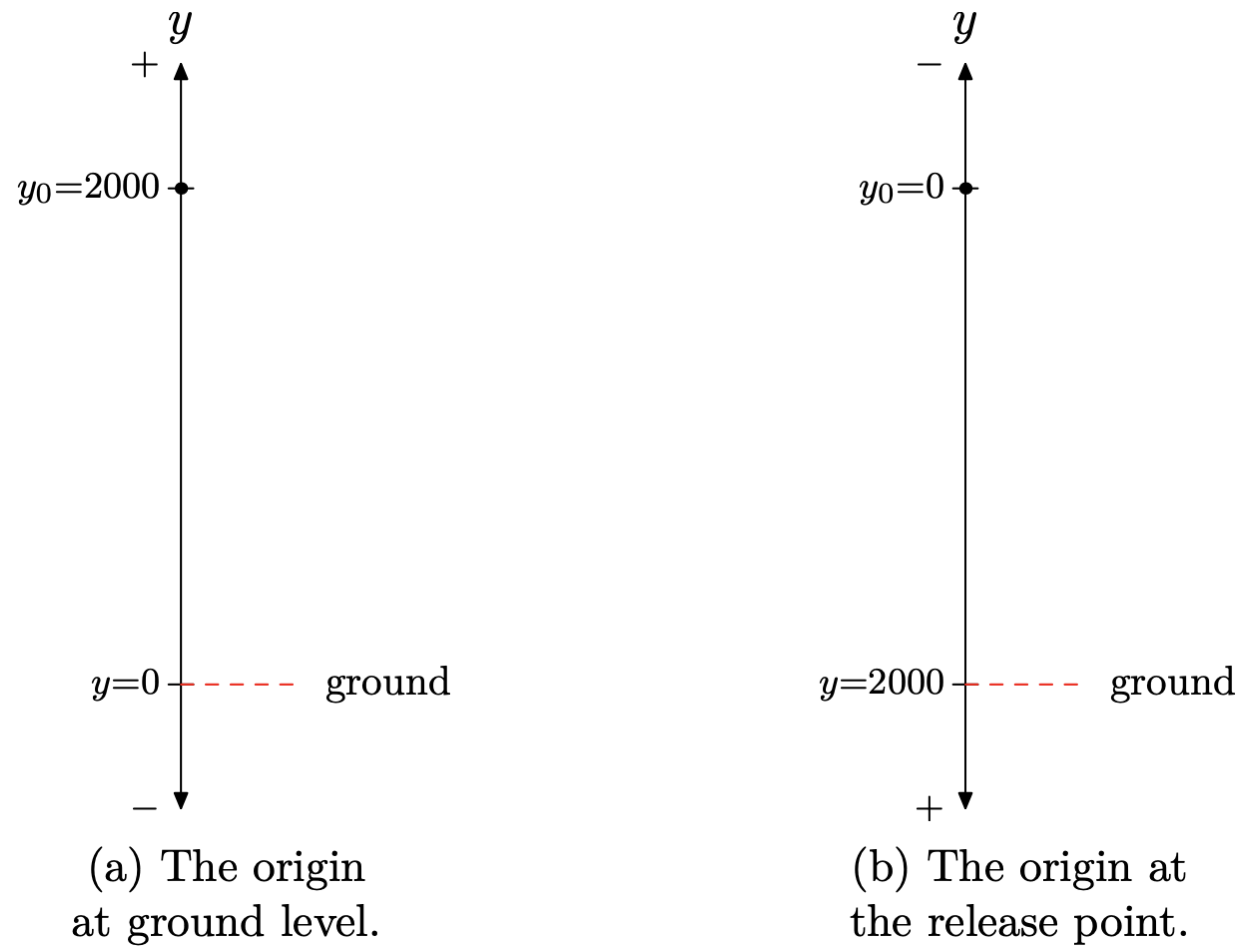
Comenzaremos con la ecuación\(y=y_{0}+v_{0} t+(1 / 2) a t^{2}\), y luego notaremos que la velocidad inicial es\(v_{0} = 0\) pies por segundo (la pelota se libera del reposo), por lo que la ecuación se convierte en\[y=y_{0}+\frac{1}{2} a t^{2}\]

Se nos pide encontrar cuándo la pelota golpea el suelo, así que eso significa que se nos pide encontrar cuando y = 0 (ver Figura\(\PageIndex{10}\) (a). Establecer y = 0 en la última ecuación y resolver para t.

\[\begin{aligned} 0 &=y_{0}+\frac{1}{2} a t^{2} \\ t^{2} &=-\frac{2 y_{0}}{a} \\ t &=\sqrt{-\frac{2 y_{0}}{a}} \end{aligned}\]

Obsérvese que los desplazamientos positivos son ascendentes (ver Figura 10 (a)). Si la velocidad es positiva, la bola se mueve hacia arriba. En nuestro caso, la pelota se mueve hacia abajo, por lo que la velocidad es negativa. A medida que la pelota se mueve hacia abajo, su velocidad se hace mayor, por lo que la velocidad se vuelve cada vez más negativa. De ahí que la aceleración debe ser negativa; es decir,\(a = −32 ft/s^2\). Sustituir esta aceleración y la posición inicial y0 = 2000 pies en el último resultado y simplificar

\[\begin{aligned} t &=\sqrt{-\frac{2(2000 \mathrm{ft})}{-32 \mathrm{ft} / \mathrm{s}^{2}}} \\ t & \approx 11.2 \mathrm{s} \end{aligned}\]
Hemos redondeado el resultado a la décima de segundo más cercana. Nuevamente, revisar las unidades es importante. En este caso,

\[\sqrt{\frac{\mathrm{ft}}{\mathrm{ft} / \mathrm{s}^{2}}}=\sqrt{\mathrm{ft} \times \frac{\mathrm{s}^{2}}{\mathrm{ft}}}=\sqrt{\mathrm{s}^{2}}=\mathrm{s}\]

Alternativamente, podríamos configurar la línea real como se muestra en la Figura 10 (b), donde hemos colocado el origen en el punto de liberación e invertido la orientación (la dirección positiva es ahora hacia abajo). Así, la posición inicial es\(y_{0} = 0\) pies y la velocidad inicial es\(v_{0} = 0\) pies por segundo (la pelota se libera del reposo). Establezca estos valores en la ecuación\(y=y_{0}+v_{0} t+(1 / 2) a t^{2}\) y resuelva para t.

\[\begin{aligned} y &=\frac{1}{2} a t^{2} \\ t^{2} &=\frac{2 y}{a} \\ t &=\sqrt{\frac{2 y}{a}} \end{aligned}\]

Los desplazamientos positivos están en dirección descendente (observe la inversión de orientación en la Figura\(\PageIndex{10}\) (b)). Esto significa que cuando la velocidad es positiva, la bola se mueve hacia abajo. Cuando soltemos la pelota, va a recoger más velocidad, por lo que la velocidad se vuelve cada vez más positiva. De ahí que la aceleración sea positiva en esta orientación; es decir,\(a = 32 ft/s^2\).

Cuando la pelota golpea el nivel del suelo, la posición es y = 2000 pies. Sustituir este valor de y y y la aceleración en el último resultado y simplificar (verificar las unidades).

\[t=\sqrt{\frac{2(2000 \mathrm{ft})}{32 \mathrm{ft} / \mathrm{s}^{2}}}\]

Tenga en cuenta que esto dará el mismo resultado que antes; es decir,\(t \approx 11.2\) segundos.

Ejemplo\(\PageIndex{7}\)

Se lanza una pelota al aire desde la altura del hombro (aproximadamente 5 pies) con una velocidad inicial ascendente de 100 pies por segundo. Encuentra el tiempo que tarda la pelota en regresar al suelo.

Solución

Busquemos una solución usando la calculadora gráfica. Usando la orientación de la Figura\(\PageIndex{10}\) (a), comience con la ecuación

\[y=y_{0}+v_{0} t+\frac{1}{2} a t^{2}\]

y tenga en cuenta que la posición inicial es\(y_{0}=5\) pies, la velocidad inicial es\(v_{0} = 100\) pies por segundo y la aceleración es a = −32 pies por segundo por segundo. Sustituir estos números en la ecuación anterior para obtener

\[\begin{array}{l}{y=5+100 t+\frac{1}{2}(-32) t^{2}} \\ {y=5+100 t-16 t^{2}}\end{array}\]

Ingrese esta ecuación en el menú Y= como se muestra en la Figura\(\PageIndex{11}\) (a). Ajustar los parámetros de la ventana como se muestra en la Figura\(\PageIndex{11}\) (b) para producir la imagen mostrada en la Figura\(\PageIndex{11}\) (c).

Figura\(\PageIndex{11}\) Uso de la calculadora gráfica para determinar el tiempo para regresar al suelo.

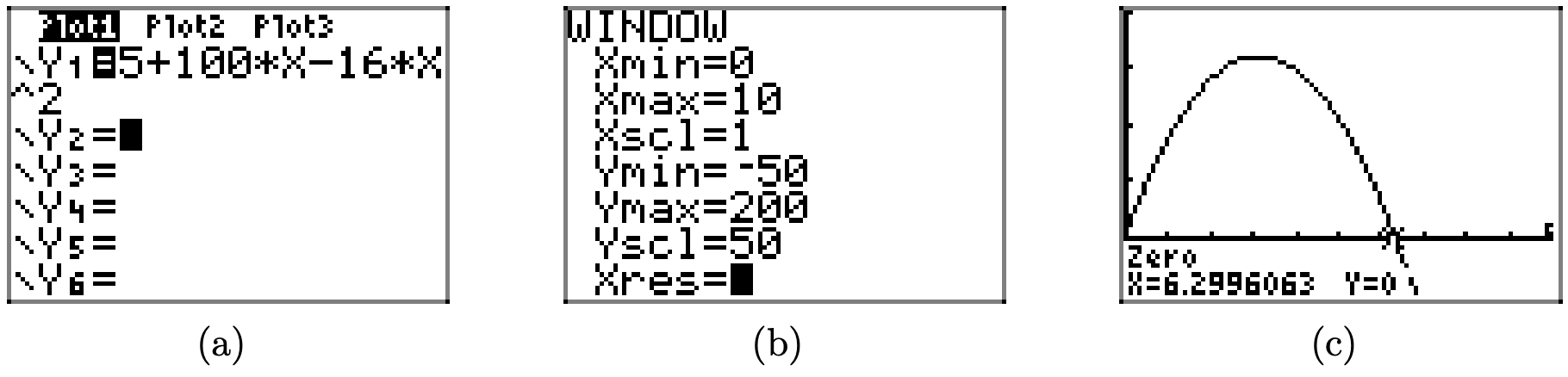
Para determinar el tiempo que tarda la pelota en regresar al suelo, debemos ubicar donde la altura de la pelota es y = 0 pies. Debido a que la gráfica de la Figura\(\PageIndex{11}\) (c) es una gráfica de altura o posición (en el eje vertical) versus tiempo (en el eje horizontal), esto ocurre cuando la gráfica de la Figura\(\PageIndex{11}\) (c) cruza el eje horizontal; es decir, a un cero de la función definida por\(y=5+100 t-16 t^{2}\). Para determinar este tiempo, utilice la utilidad 2:cero en el menú CALC para determinar el cero. El resultado se muestra en la Figura\(\PageIndex{11}\) (c), donde determinamos que tarda aproximadamente\(t \approx 6.29\) segundos para que la pelota regrese al suelo.

Alternativamente, podemos establecer y = 0 en la ecuación\(y=y_{0}+v_{0} t+(1 / 2) a t^{2}\) y usar la fórmula cuadrática para resolver para el tiempo t.

\[\begin{aligned} 0 &=y_{0}+v_{0} t+\frac{1}{2} a t^{2} \\ t &=\frac{-v_{0} \pm \sqrt{v_{0}^{2}-4\left(\frac{1}{2} a\right)\left(y_{0}\right)}}{2\left(\frac{1}{2} a\right)} \\ t &=\frac{-v_{0} \pm \sqrt{v_{0}^{2}-2 a y_{0}}}{a} \end{aligned}\]

Ahora podemos insertar\(y_{0}=5 \mathrm{ft}, v_{0}=100 \mathrm{ft} / \mathrm{s},\) y\(a=-32 \mathrm{ft} / \mathrm{s}^{2}\), y luego usar una calculadora para obtener

\[\begin{aligned} t &=\frac{-100 \mathrm{ft} / \mathrm{s} \pm \sqrt{(100 \mathrm{ft} / \mathrm{s})^{2}-2\left(-32 \mathrm{ft} / \mathrm{s}^{2}\right)(5 \mathrm{ft})}}{-32 \mathrm{ft} / \mathrm{s}^{2}} \\ t & \approx-0.05,6.29 \mathrm{s} \end{aligned}\]

La respuesta negativa no aplica en esta situación, por lo que mantenemos la solución\(t \approx 6.29\) segundos. Observe cómo esto concuerda con la solución que se encuentra en la calculadora gráfica.

Nuevamente, es importante asegurarse de que las unidades verifiquen. Debajo del radical, ambos términos tienen unidades\(\mathrm{ft}^{2} / \mathrm{s}^{2}\). Cuando se toma la raíz cuadrada, estas unidades se convierten en ft/s. Así, ambos términos en el numerador están en ft/s, pero el denominador tiene unidades\(\mathrm{ft} / \mathrm{s}^{2}\). Al invertir y multiplicar, como vimos en Ejemplo\(\PageIndex{5}\), las unidades se simplifican a segundos.

Ejercicio

En los Ejercicios 1 - 12, anota la fórmula d = vt y resuelve por la cantidad desconocida en el problema. Una vez que se complete, sustituya las cantidades conocidas en el resultado y simplifique. Asegúrese de verificar que sus unidades cancelen y proporcione las unidades adecuadas para su solución.

Ejercicio\(\PageIndex{1}\)

Si Martha mantiene una velocidad constante de 30 millas por hora, ¿hasta dónde viajará en 5 horas?

Contestar

150 millas

Ejercicio\(\PageIndex{2}\)

Si Jamal mantiene una velocidad constante de 25 millas por hora, ¿hasta dónde viajará en 5 horas?

Ejercicio\(\PageIndex{3}\)

Si Arturo mantiene una velocidad constante de 30 millas por hora, ¿cuánto tiempo le llevará recorrer 120 millas?

Contestar

4 horas

Ejercicio\(\PageIndex{4}\)

Si Mei mantiene una velocidad constante de 25 millas por hora, ¿cuánto tiempo le llevará recorrer 150 millas?

Ejercicio\(\PageIndex{5}\)

Si Allen mantiene una velocidad constante y recorre 250 millas en 5 horas, ¿cuál es su velocidad constante?

Contestar

50 millas por hora

Ejercicio\(\PageIndex{6}\)

Si Jane mantiene una velocidad constante y recorre 300 millas en 6 horas, ¿cuál es su velocidad constante?

Ejercicio\(\PageIndex{7}\)

Si José mantiene una velocidad constante de 15 pies por segundo, ¿hasta dónde viajará en 5 minutos?

Contestar

4500 pies

Ejercicio\(\PageIndex{8}\)

Si Tami mantiene una velocidad constante de 1.5 pies por segundo, ¿hasta dónde viajará en 4 minutos?

Ejercicio\(\PageIndex{9}\)

Si Carmen mantiene una velocidad constante de 80 metros por minuto, ¿hasta dónde viajará en 600 segundos?

Contestar

800 metros

Ejercicio\(\PageIndex{10}\)

Si Alfonso mantiene una velocidad constante de 15 pies por segundo, ¿cuánto tiempo le llevará recorrer 1 milla? Nota: 1 milla equivale a 5280 pies.

Ejercicio\(\PageIndex{11}\)

Si Hoshi mantiene una velocidad constante de 200 centímetros por segundo, ¿cuánto tiempo le llevará recorrer 20 metros? Nota: 100 centímetros equivale a 1 metro.

Contestar

10 segundos

Ejercicio\(\PageIndex{12}\)

Si Maeko mantiene una velocidad constante y recorre 5 millas en 12 minutos, ¿cuál es su velocidad en millas por hora?

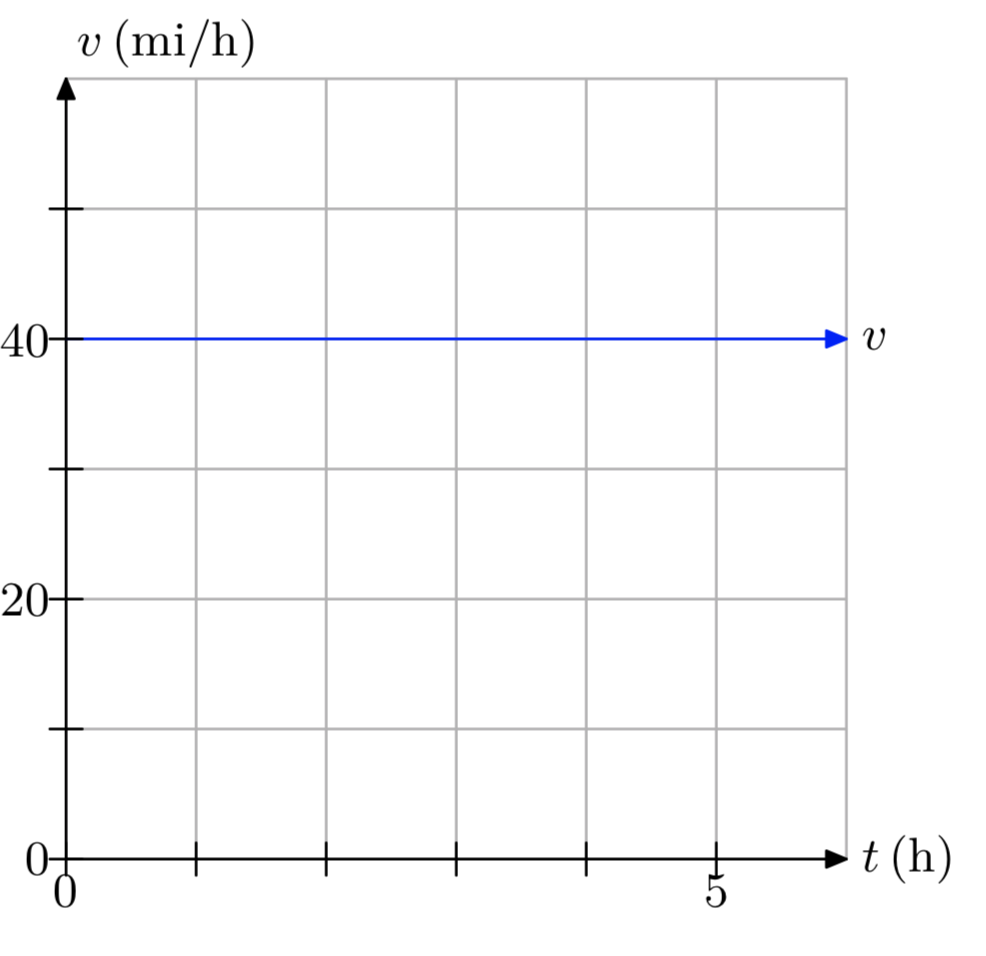
En los Ejercicios 13 - 18, se presenta una gráfica de velocidad v versus tiempo t.

1. Hacer una duplicación precisa de la trama en papel cuadriculado. Etiquetar y escalar cada eje. Marque las unidades en cada eje.
2. Utilice la gráfica para determinar la distancia recorrida durante el periodo de tiempo [0, 5], utilizando las unidades de tiempo dadas en la gráfica.

Ejercicio\(\PageIndex{13}\)

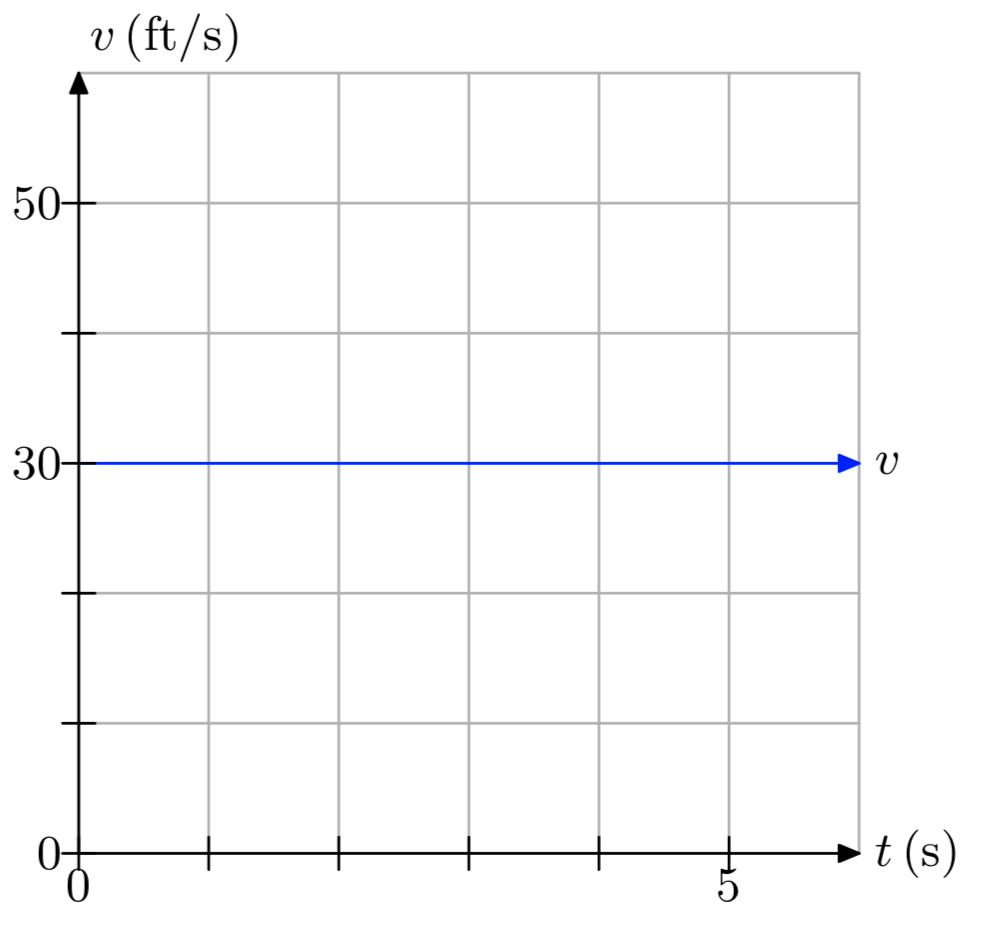
Contestar

La distancia recorrida es de 150 pies.

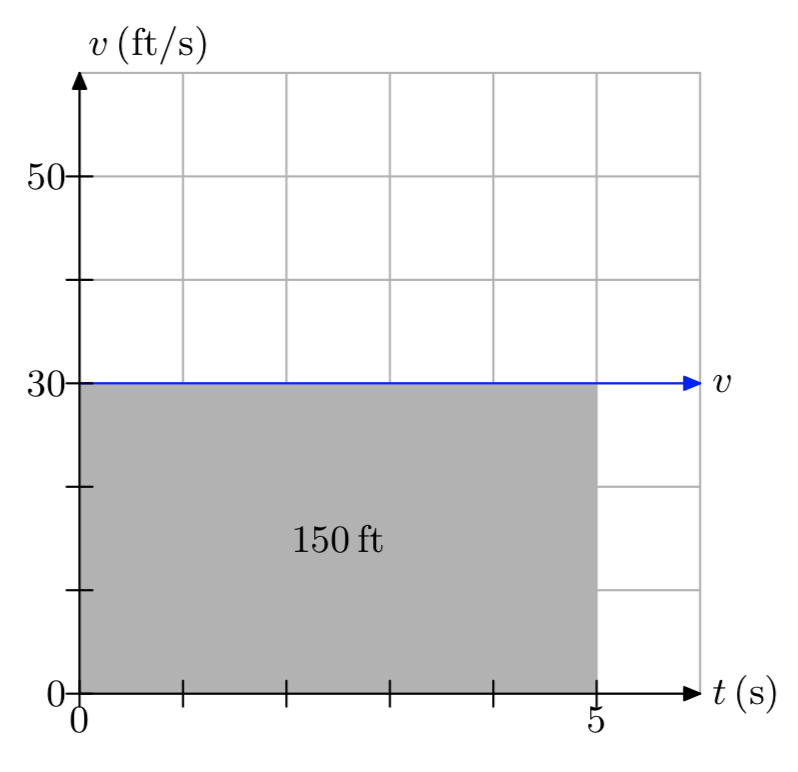
Ejercicio\(\PageIndex{14}\)

Ejercicio\(\PageIndex{15}\)

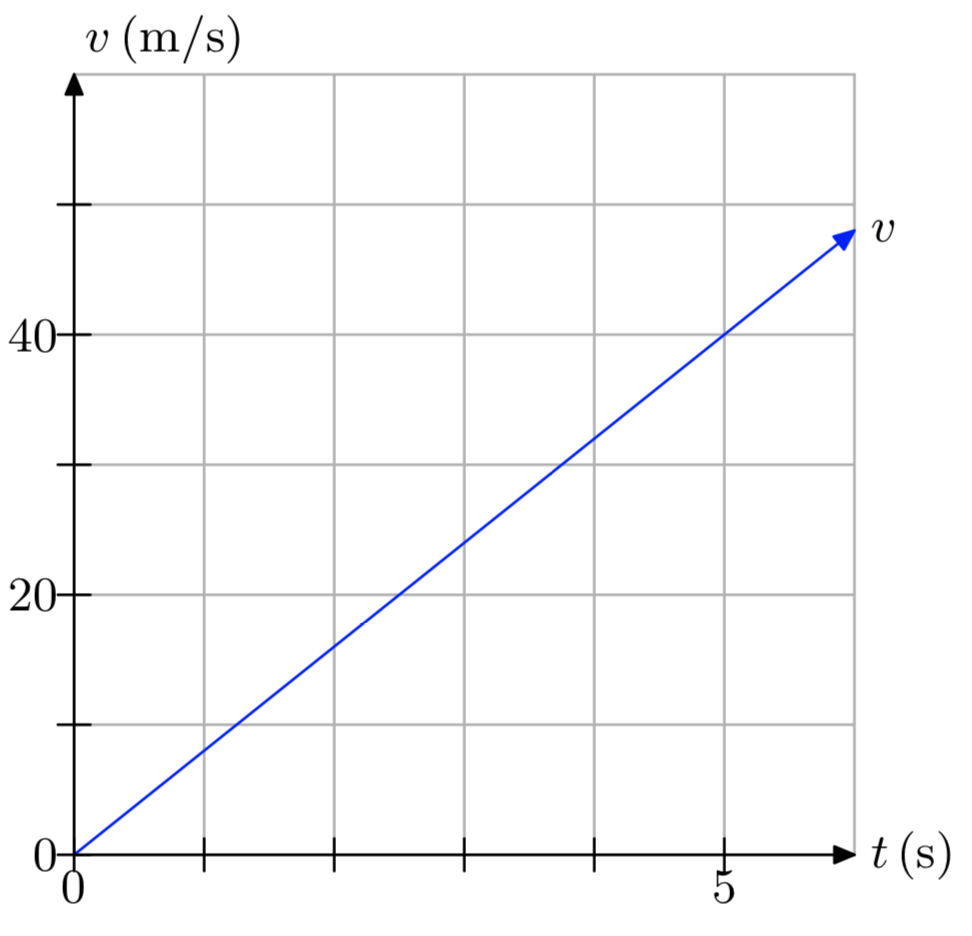
Contestar

La distancia recorrida es de 100 metros.

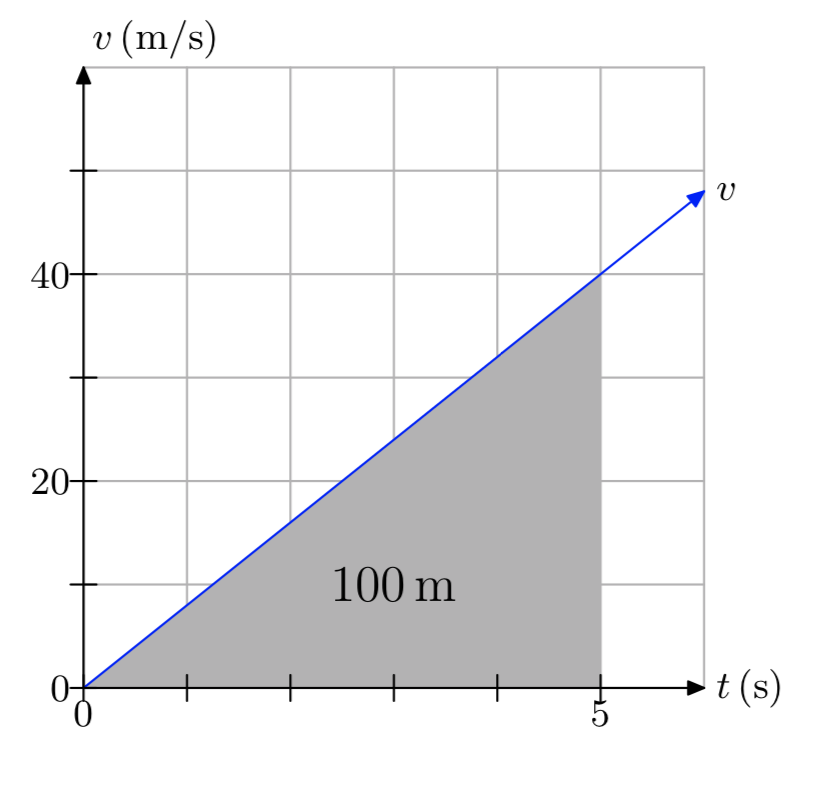
Ejercicio\(\PageIndex{16}\)

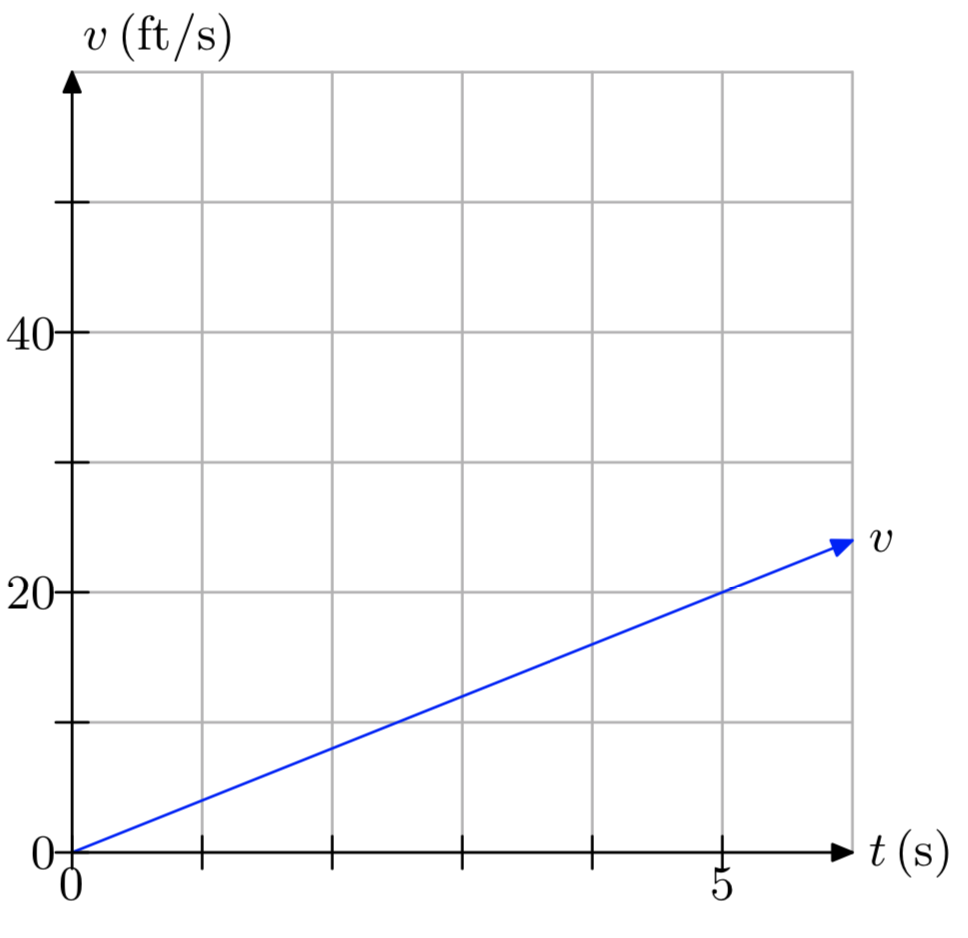
Ejercicio\(\PageIndex{17}\)

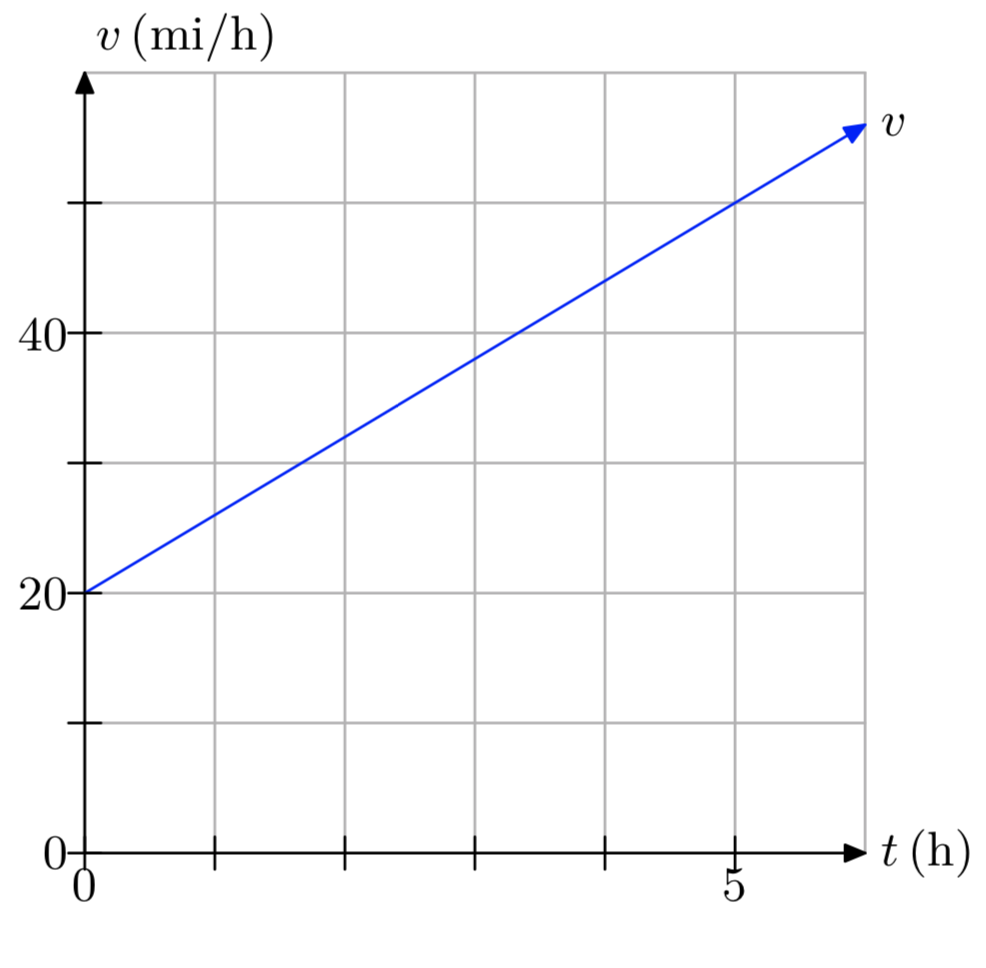
Contestar

La distancia recorrida es de 175 millas.

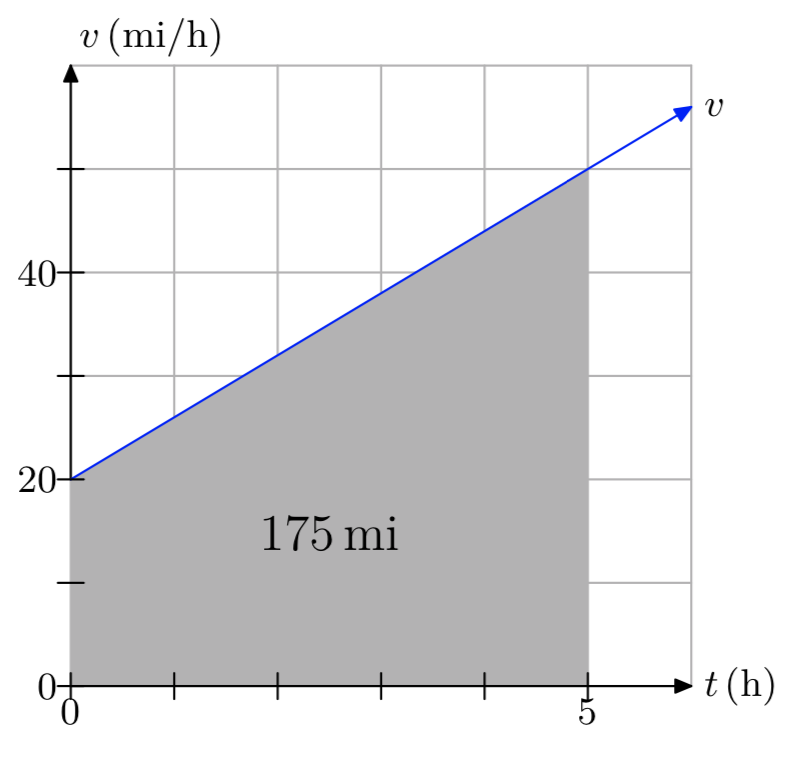
Ejercicio\(\PageIndex{18}\)

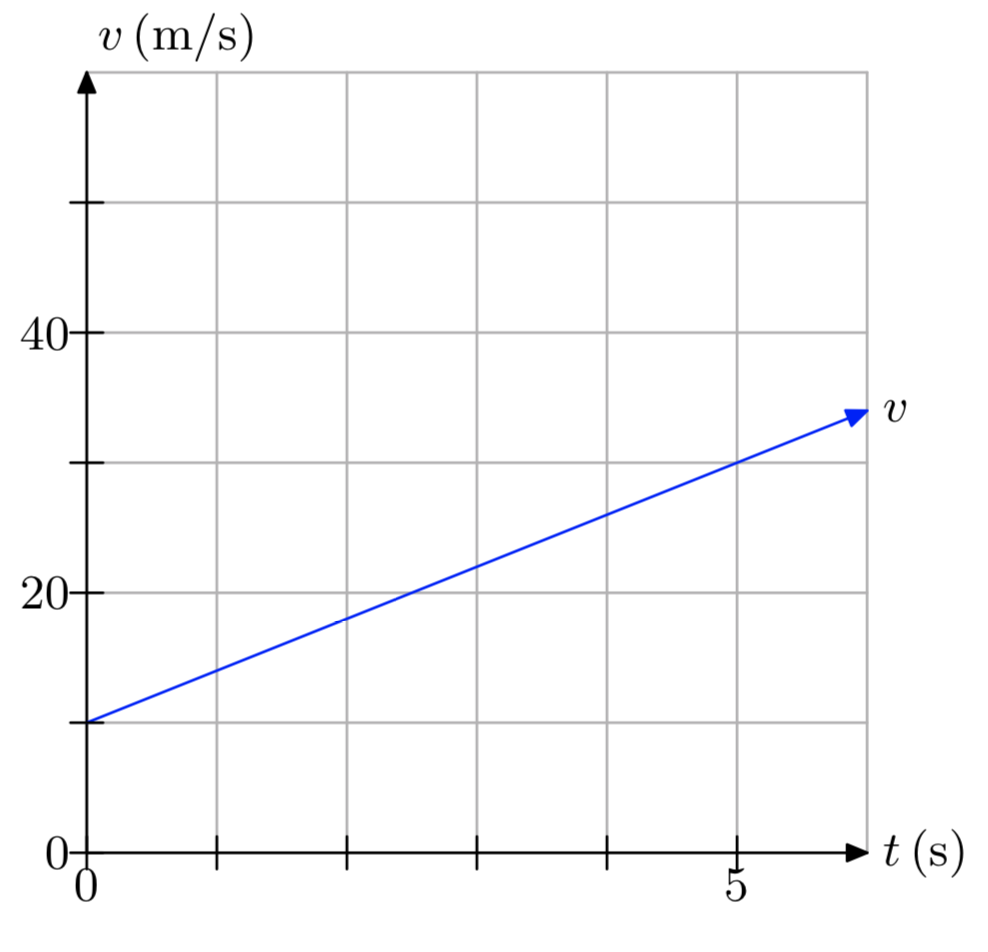
Ejercicio\(\PageIndex{19}\)

Te dicen que un auto se mueve con una aceleración constante de 7.5 pies/\(s^2\). En sus propias palabras, explique lo que esto significa.

Contestar

Significa que la velocidad del auto aumenta a una velocidad de 7.5 pies por segundo cada segundo.

Ejercicio\(\PageIndex{20}\)

Te dicen que un objeto caerá sobre un planeta distante con aceleración constante 6.5 m/\(s^2\). En sus propias palabras, explique lo que esto significa.

Ejercicio\(\PageIndex{21}\)

Te dicen que la aceleración de un auto es de −18 pies/\(s^2\). En sus propias palabras, explique lo que esto significa.

Contestar

Significa que la velocidad del automóvil está disminuyendo a una velocidad de 18 pies por segundo cada segundo.

Ejercicio\(\PageIndex{22}\)

Un observador en un planeta distante lanza un objeto al aire y a medida que se mueve hacia arriba informa que el objeto tiene una aceleración constante de −4.5 m/\(s^2\). En sus propias palabras, explique lo que esto significa.

En Ejercicios 23 - 28, realizar cada una de las siguientes tareas.

1. Resolver la ecuación\(v = v_{0} + at\) para la cantidad desconocida.
2. Sustituya las cantidades conocidas (por unidades) en su resultado, luego simplifique. Asegúrese de que las unidades cancelen y proporcione las unidades adecuadas para su solución.

Ejercicio\(\PageIndex{23}\)

Un cohete acelera desde el reposo con aceleración constante 15.8 m/\(s^2\). ¿Cuál será la velocidad del cohete después de 3 minutos?

Contestar

2, 844 m/s

Ejercicio\(\PageIndex{24}\)

Una piedra se deja caer del reposo sobre un planeta distante y acelera hacia el suelo con una aceleración constante 3.8ft/\(s^2\). ¿Cuál será la velocidad de la piedra después de 2 minutos?

Ejercicio\(\PageIndex{25}\)

Se lanza una piedra hacia abajo sobre un planeta distante con una velocidad inicial de 20 pies/s Si la piedra experimenta una aceleración constante de 32 pies/\(s^2\), ¿cuál será la velocidad de la piedra después de 1 minuto?

Contestar

1, 940 pies/s

Ejercicio\(\PageIndex{26}\)

Una pelota es arrojada hacia arriba con una velocidad inicial de 80m/s Si la pelota experimenta una aceleración constante de −9.8 m/\(s^2\), ¿cuál será la velocidad de la pelota al final de 5 segundos?

Ejercicio\(\PageIndex{27}\)

Un objeto es disparado al aire con una velocidad inicial de 100m/s Si el objeto experimenta una desaceleración constante de 9.8 m/\(s^2\), ¿cuánto tiempo tardará la pelota en alcanzar su altura máxima?

Contestar

Aproximadamente 10.2 segundos.

Ejercicio\(\PageIndex{28}\)

Un objeto se libera del reposo en un planeta distante y después de 5 segundos, su velocidad es de 98m/s Si el objeto cae con aceleración constante, determine la aceleración del objeto.

En los Ejercicios 29 - 42, utilizar la ecuación de movimiento apropiada, uno\(v = v_{0} + at\)\(x = x_{0}+v_{0}t+\frac{1}{2}at^2\) o ambos, para resolver la cuestión planteada en el ejercicio.

1. Seleccione la ecuación de movimiento apropiada y resuelva para la cantidad desconocida.
2. Sustituya las cantidades conocidas (con sus unidades) en su resultado y simplifique. Verifique que la cancelación de unidades proporcione unidades adecuadas para su solución.
3. Encuentra una aproximación decimal para tu respuesta.

Ejercicio\(\PageIndex{29}\)

Un cohete con velocidad inicial 30 m/s se mueve a lo largo de una línea recta con aceleración constante 2.5 m/\(s^2\). Encuentra la velocidad y la distancia recorrida por el cohete al cabo de 10 segundos.

Contestar

Velocidad = 55 m/s, Distancia recorrida = 425 m.

Ejercicio\(\PageIndex{30}\)

Un automóvil viaja a 88 pies/s cuando aplica los frenos y comienza a disminuir con una desaceleración constante de 5 pies/\(s^2\). ¿Cuál es su velocidad y hasta qué punto ha recorrido al final de 5 segundos?

Ejercicio\(\PageIndex{31}\)

Un automóvil viaja a 88 pies/s cuando aplica los frenos y se ralentiza a 58 pies/s en 10 segundos. Asumiendo una desaceleración constante, encuentra la desaceleración y la distancia recorrida por el automóvil en el intervalo de tiempo de 10 segundos. Pista: Calculo primero la desaceleración.

Contestar

Aceleración = −3 ft/\(s^2\), Distancia recorrida = 730 ft.

Ejercicio\(\PageIndex{32}\)

Una piedra es arrojada hacia abajo desde arriba de la superficie de un planeta distante con una velocidad inicial de 45 m/s. A continuación, al final de 10 segundos, la velocidad de la piedra es de 145 m/s. Suponiendo una aceleración constante, encuentra la aceleración de la piedra y la distancia recorrida en el periodo de tiempo de 10 segundos.

Ejercicio\(\PageIndex{33}\)

Un objeto es disparado al aire desde la superficie de la tierra con una velocidad inicial de 180 pies/s. Encuentra la altura máxima del objeto y el tiempo que tarda el objeto en alcanzar esa altura máxima.Pista: La aceleración debida a la gravedad cerca de la superficie de la tierra es bien conocida.

Contestar

Tiempo hasta la altura máxima = 5. 625 s, Altura máxima = 506. 25 pies

Ejercicio\(\PageIndex{34}\)

Un objeto es disparado al aire desde la superficie de un planeta distante con una velocidad inicial de 180 m/s. Encuentra la altura máxima del objeto y el tiempo que tarda el objeto en alcanzar esa altura máxima. Supongamos que la aceleración debida a la gravedad en este planeta distante es de 5.8 m/\(s^2\). Pista: Calcule primero el tiempo hasta la altura máxima.

Ejercicio\(\PageIndex{35}\)

Un automóvil viaja por el camino alto a 55 mi/h cuando el conductor ve un deslizamiento de rocas cubriendo la carretera y golpea los frenos, proporcionando una desaceleración constante de 12 pies/\(s^2\). ¿Cuánto tiempo tarda el auto en detenerse y qué tan lejos viaja durante este periodo de tiempo?

Contestar

Tiempo para parar\(\approx\) 6. 72 s, Distancia recorrida\(\approx\) 271 ft

Ejercicio\(\PageIndex{36}\)

Un automóvil viaja por la carretera en Alemania a 81 km/h cuando el conductor advierte que el tráfico se detiene en la carretera que tiene delante y golpea los frenos, proporcionando una desaceleración constante de 2.3 m/\(s^2\). ¿Cuánto tiempo tarda el auto en detenerse y qué tan lejos viaja durante este periodo de tiempo? Nota: 1 kilómetro equivale a 1000 metros.

Ejercicio\(\PageIndex{37}\)

Un objeto es liberado del reposo a cierta distancia sobre la superficie de la tierra. ¿Hasta dónde (en metros) caerá el objeto en 5 segundos y cuál será su velocidad al final de este periodo de tiempo de 5 segundos? Sugerencia: Debes conocer la aceleración debida a la gravedad cerca de la superficie de la tierra.

Contestar

Distancia = 122.5 m, Velocidad = −49 m/s.

Ejercicio\(\PageIndex{38}\)

Un objeto es liberado del reposo a cierta distancia sobre la superficie de un planeta distante. ¿Hasta dónde (en metros) caerá el objeto en 5 segundos y cuál será su velocidad al final de este periodo de tiempo de 5 segundos? Supongamos que la aceleración debida a la gravedad en el planeta distante es de 13.5 m/\(s^2\).

Ejercicio\(\PageIndex{39}\)

Un objeto es liberado del reposo a una distancia de 352 pies sobre la superficie de la tierra. ¿Cuánto tiempo tardará el objeto en impactar el suelo?

Contestar

Tiempo\(\approx\) 4.69 s

Ejercicio\(\PageIndex{40}\)

Un objeto es liberado del reposo a una distancia de 400 metros sobre la superficie de un planeta distante. ¿Cuánto tiempo tardará el objeto en impactar el suelo? Supongamos que la aceleración debida a la gravedad en el planeta distante es igual a 5.3 m/ (s^2\).

Ejercicio\(\PageIndex{41}\)

En la tierra, se lanza una pelota hacia arriba desde una altura inicial de 5 metros con una velocidad inicial de 100 m/s ¿Cuánto tiempo tardará la pelota en regresar al suelo?

Contestar

Tiempo\(\approx\) 20.5 s

Ejercicio\(\PageIndex{42}\)

En la tierra, se lanza una pelota hacia arriba desde una altura inicial de 5 pies con una velocidad inicial de 100 pies/s ¿Cuánto tiempo tardará la pelota en regresar al suelo?

Se lanza una pelota al aire cerca de la superficie de la tierra. En los Ejercicios 43 - 46 se da la altura inicial de la pelota y la velocidad inicial de la pelota. Completar las siguientes tareas.

1. Se usa\(y = y_{0} +v_{0}t+\frac{1}{2}at^2\) para configurar una fórmula para la altura y de la bola en función del tiempo t. Use la constante apropiada para la aceleración debida a la gravedad cerca de la superficie de la tierra.
2. Cargue la ecuación de la parte anterior en Y1 en su calculadora gráfica. Ajusta tu ventana de visualización para que sean visibles tanto el vértice como la hora en que la pelota regresa al suelo. Copia la imagen en tu papel de tarea. Etiquetar y escalar cada eje con xmin, xmax, ymin e ymax.
3. Usa la utilidad cero en el menú CALC de tu calculadora gráfica para determinar el momento en que la pelota regresa al suelo. Registre esta respuesta en la ubicación apropiada en su gráfica.
4. Usa la fórmula cuadrática para determinar el momento en que la pelota regresa al suelo. Usa tu calculadora para encontrar una aproximación decimal de tu solución. Debe estar de acuerdo con lo encontrado usando la utilidad cero en su calculadora gráfica. ¡Sé terco! Revisa tu trabajo hasta que las respuestas estén de acuerdo.

Ejercicio\(\PageIndex{43}\)

\(y_{0}\)= 50 pies,\(v_{0}\) = 120 pies/s.

Contestar

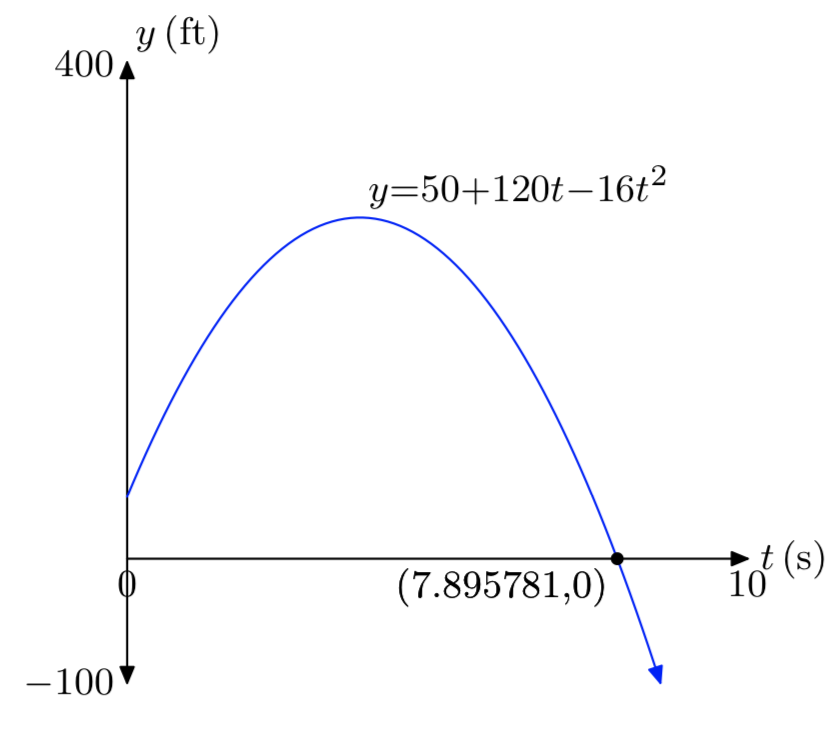
Ejercicio\(\PageIndex{44}\)

\(y_{0}\)= 30 m,\(v_{0}\) = 100 m/s.

Ejercicio\(\PageIndex{45}\)

\(y_{0}\)= 20m,\(v_{0}\) = 110m/s.

Contestar

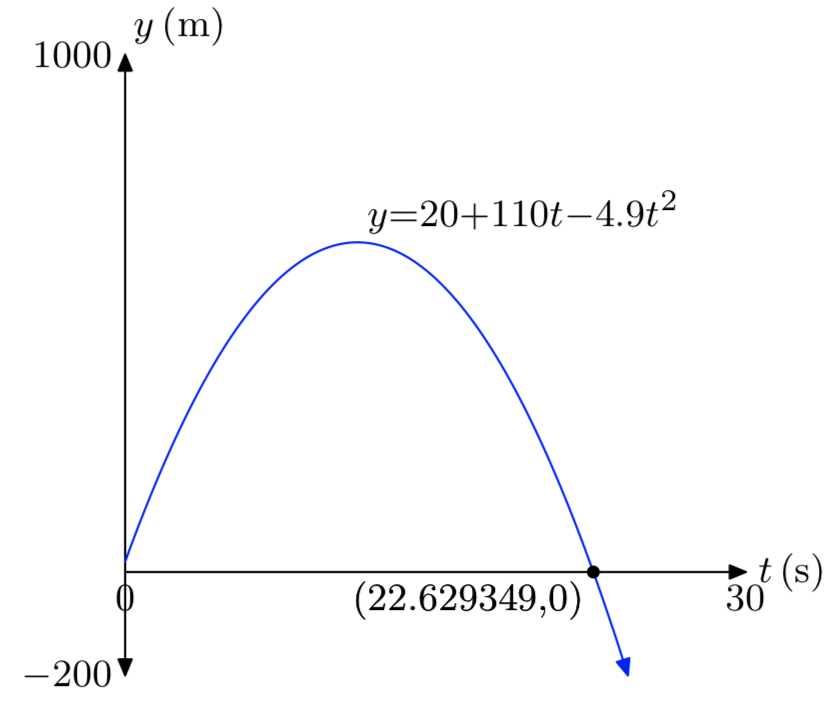
Ejercicio\(\PageIndex{46}\)

\(y_{0}\)= 100 pies,\(v_{0}\) = 200 pies/s.

Contestar

Agrega textos aquí. No elimine primero este texto.

Ejercicio\(\PageIndex{47}\)

Se lanza una roca hacia arriba a una velocidad inicial de 64 pies/s ¿Cuántos segundos le tomará a la roca elevarse 61 pies? Redondee su respuesta a la centésima de segundo más cercana.

Contestar

1. 57 segundos

Ejercicio\(\PageIndex{48}\)

Se lanza un centavo hacia abajo desde la cima de un árbol a una velocidad inicial de 28 pies/s ¿Cuántos segundos le tomará al centavo caer 289 pies? Redondee su respuesta a la centésima de segundo más cercana.

Ejercicio\(\PageIndex{49}\)

Un globo de agua se lanza hacia abajo desde el techo de un edificio a una velocidad inicial de 24 pies/s. el edificio mide 169 pies de altura. ¿Cuántos segundos tardará el globo de agua en chocar contra el suelo? Redondee su respuesta a la centésima de segundo más cercana.

Contestar

2. 59 segundos

Ejercicio\(\PageIndex{50}\)

Se lanza una roca hacia arriba a una velocidad inicial de 60 pies/s. ¿Cuántos segundos le tomará a la roca elevarse 51 pies? Redondee su respuesta a la centésima de segundo más cercana.

Ejercicio\(\PageIndex{51}\)

Se lanza una pelota hacia arriba desde una altura de 42 pies a una velocidad inicial de 63 pies/s ¿Cuántos segundos le llevará a la pelota golpear el suelo? Redondee su respuesta a la centésima de segundo más cercana.

Contestar

4. 52 segundos

Ejercicio\(\PageIndex{52}\)

Se lanza una roca hacia arriba desde una altura de 32 pies a una velocidad inicial de 25 pies/s. ¿Cuántos segundos le llevará a la roca chocar contra el suelo? Redondee su respuesta a la centésima de segundo más cercana.

Ejercicio\(\PageIndex{53}\)

Un centavo se lanza hacia abajo desde la parte superior de un árbol a una velocidad inicial de 16 pies/s El árbol mide 68 pies de altura. ¿Cuántos segundos tardará el centavo en chocar contra el suelo? Redondee su respuesta a la centésima de segundo más cercana.

Contestar

1. 62 segundos

Ejercicio\(\PageIndex{54}\)

Un centavo es arrojado hacia abajo desde el borde de un acantilado a una velocidad inicial de 32 pies/s ¿Cuántos segundos le tomará al centavo caer 210 pies? Redondee su respuesta a la centésima de segundo más cercana.