7.4: Productos y Cocientes de Funciones Racionales

En esta sección tratamos productos y cocientes de expresiones racionales. Antes de comenzar, tendremos que establecer algunas definiciones y técnicas fundamentales. Comenzamos con la definición del producto de dos números racionales.

Definición

Que a/b y c/d sean números racionales. El producto de estos números racionales se define por

\[\frac{a}{b} \times \frac{c}{d}=\frac{a \times c}{b \times d}, \quad \text { or more compactly, } \quad \frac{a}{b} \cdot \frac{c}{d}=\frac{a c}{b d}\]

La definición simplemente establece que se deben multiplicar los numeradores de cada número racional para obtener el numerador del producto, y también multiplicar los denominadores de cada número racional para obtener el denominador del producto. Por ejemplo,

\[\frac{2}{3} \cdot \frac{5}{7}=\frac{2 \cdot 5}{3 \cdot 7}=\frac{10}{21}\]

Por supuesto, también debes verificar para asegurarte de que tu respuesta final se reduzca a los términos más bajos.

Veamos un ejemplo.

Ejemplo\(\PageIndex{1}\)

Simplificar el producto de los números racionales\[\frac{6}{231} \cdot \frac{35}{10}\]

Solución

Primero, multiplique numeradores y denominadores juntos de la siguiente manera.

\[\frac{6}{231} \cdot \frac{35}{10}=\frac{6 \cdot 35}{231 \cdot 10}=\frac{210}{2310}\]

Sin embargo, la respuesta no se reduce a los términos más bajos. Podemos expresar el numerador como producto de primos.

\[210=21 \cdot 10=3 \cdot 7 \cdot 2 \cdot 5=2 \cdot 3 \cdot 5 \cdot 7\]

No es necesario organizar los factores en orden ascendente, pero cada poquito ayuda. El denominador también se puede expresar como un producto de primos.

\[2310=10 \cdot 231=2 \cdot 5 \cdot 7 \cdot 33=2 \cdot 3 \cdot 5 \cdot 7 \cdot 11\]

Ahora podemos cancelar factores comunes.

\[\frac{210}{2310}=\frac{2 \cdot 3 \cdot 5 \cdot 7}{2 \cdot 3 \cdot 5 \cdot 7 \cdot 11}=\frac{\not{2} \cdot \not{3} \cdot \not{5} \cdot \not{7}}{\not{2} \cdot \not{8} \cdot \not{5} \cdot \not{7} \cdot 11}=\frac{1}{11}\]

Sin embargo, este enfoque no es la forma más eficiente de proceder, ya que multiplicar numeradores y denominadores permite que los productos crezcan a números mayores, como en 210/2310. Entonces es un poco más difícil factorizar los números más grandes.

Un mejor enfoque es factorizar inmediatamente los numeradores y denominadores más pequeños, de la siguiente manera.

\[\frac{6}{231} \cdot \frac{35}{10}=\frac{2 \cdot 3}{3 \cdot 7 \cdot 11} \cdot \frac{5 \cdot 7}{2 \cdot 5}\]

Ahora podríamos multiplicar numeradores y denominadores, luego cancelar factores comunes, que coincidirían idénticamente con el último cálculo de la ecuación (5).

Sin embargo, también podemos emplear la siguiente regla de cancelación.

Regla de Cancelación

Al trabajar con el producto de dos o más expresiones racionales, factorizar todos los numeradores y denominadores, luego cancelar. La regla de cancelación es simple: cancelar un factor “en la parte superior” por un factor idéntico “en la parte inferior”. Hablando más técnicamente, cancelar cualquier factor en cualquier numerador por un factor idéntico en cualquier denominador.

Así, podemos terminar nuestro cálculo cancelando factores comunes, cancelando “algo en la parte superior por algo en la parte inferior”.

\[\frac{6}{231} \cdot \frac{35}{10}=\frac{2 \cdot 3}{3 \cdot 7 \cdot 11} \cdot \frac{5 \cdot 7}{2 \cdot 5}=\frac{\not{2} \cdot \not{8}}{\not{3} \cdot \not{7} \cdot 11} \cdot \frac{\not{5} \cdot \not{7}}{\not{2} \cdot \not{5}}=\frac{1}{11}\]

Tenga en cuenta que cancelamos un 2, 3, 5 y un 7 “en la parte superior” para un 2, 3, 5 y 7 “en la parte inferior”.

Así, tenemos dos opciones a la hora de multiplicar expresiones racionales:

• Multiplicar numeradores y denominadores, facturar, luego cancelar.
• Factorizar numeradores y denominadores, cancelar, luego multiplicar numeradores y denominadores.

Es este último enfoque el que vamos a utilizar en esta sección. Veamos otro ejemplo.

Ejemplo\(\PageIndex{2}\)

Simplificar la expresión Restricciones\[\frac{x^{2}-x-6}{x^{2}+2 x-15} \cdot \frac{x^{2}-x-30}{x^{2}-2 x-8}\] estatales.

Solución

Usa la prueba ac para factografiar cada numerador y denominador. Después cancela como se muestra.

\[\begin{aligned} \frac{x^{2}-x-6}{x^{2}+2 x-15} \cdot \frac{x^{2}-x-30}{x^{2}-2 x-8} &=\frac{(x+2)(x-3)}{(x-3)(x+5)} \cdot \frac{(x+5)(x-6)}{(x+2)(x-4)} \\ &=\frac{(x+2)(x-3)}{(x-3)(x+5)} \cdot \frac{(x+5)(x-4)}{(x+2)(x-4)} \\ &=\frac{x-6}{x-4} \end{aligned}\]

El denominador de la primera fracción tiene factores x − 3 y x + 5. De ahí que x = 3 o x = −5 hará que este denominador sea cero. Por lo tanto, el 3 y −5 son restricciones.

El denominador de la segunda fracción tiene factores x + 2 y x − 4. De ahí que x = −2 o x = 4 hará que este denominador sea cero.

Por lo tanto, −2 y 4 son restricciones. Por lo tanto, para todos los valores de x, excepto las restricciones −5, −2, 3 y 4, el lado izquierdo de\[\frac{x^{2}-x-6}{x^{2}+2 x-15} \cdot \frac{x^{2}-x-30}{x^{2}-2 x-8}=\frac{x-6}{x-4}\]

es idéntico a su lado derecho.

Es posible usar su calculadora gráfica para verificar sus resultados. Primero, cargue los lados izquierdo y derecho de la ecuación (8) en las calculadoras en Y1 e Y2 en el menú Y= de su calculadora gráfica, como se muestra en la Figura\(\PageIndex{1}\) (a). Presione 2do TBLSET y ajuste TBLStart = −6 y\(\Delta \mathrm{Tb} 1=1\), como se muestra en la Figura\(\PageIndex{1}\) (b). Asegúrese de que AUTO esté resaltado y seleccionado con la tecla ENTER tanto en las variables independientes como dependientes. Presione 2nd TABLE para producir la visualización tabular en la Figura\(\PageIndex{1}\) (c).

Figura\(\PageIndex{1}\). Usando las características de tabla de la calculadora gráfica para verificar el resultado en la ecuación (8).

Recuerde que los lados izquierdo y derecho de la ecuación (8) se cargan en Y1 e Y2, respectivamente.

• En la Figura\(\PageIndex{1}\) (c), anote el mensaje ERR (error) en los valores restringidos de x = −5 y x = −2. Sin embargo, aparte de estas dos restricciones, las funciones Y1 e Y2 coinciden en todos los demás valores de x en la Figura\(\PageIndex{1}\) (c).
• Utilice la flecha hacia abajo para desplazarse hacia abajo en la tabla para producir los resultados tabulares que se muestran en la Figura\(\PageIndex{1}\) (d). Anote el mensaje ERR (error) en los valores restringidos de x = 3 y x = 4. Sin embargo, aparte de estas dos restricciones, las funciones Y1 e Y2 coinciden en todos los demás valores de x en la Figura\(\PageIndex{1}\) (d).
• Si se desplaza hacia arriba o hacia abajo en la tabla, encontrará que las funciones Y1 e Y2 coinciden en todos los valores de x que no sean los valores restringidos −5, −2, 3 y 4.

Veamos otro ejemplo.

Ejemplo\(\PageIndex{3}\)

Simplificar\[\frac{9-x^{2}}{x^{2}+3 x} \cdot \frac{6 x-2 x^{2}}{x^{2}-6 x+9}\] Estado cualquier restricción.

Solución

El primer numerador se puede factorizar usando la diferencia de patrón de dos cuadrados.

\[9-x^{2}=(3+x)(3-x)\]

El segundo denominador es un trinomio cuadrado perfecto y se puede factorizar como el cuadrado de un binomio.

\[x^{2}-6 x+9=(x-3)^{2}\]

Querrás eliminar el mayor factor común del primer denominador y del segundo numerador.

\[x^{2}+3 x=x(x+3) \quad \text { and } \quad 6 x-2 x^{2}=2 x(3-x)\]

Por lo tanto,\[\frac{9-x^{2}}{x^{2}+3 x} \cdot \frac{6 x-2 x^{2}}{x^{2}-6 x+9} \cdot=\frac{(3+x)(3-x)}{x(x+3)} \cdot \frac{2 x(3-x)}{(x-3)^{2}}\]

Tendremos que ejecutar un cambio de signo o dos para crear factores comunes en los numeradores y denominadores. Entonces, tanto en el primer como en el segundo numerador, factorizar a −1 del factor 3 − x para obtener 3 − x = −1 (x − 3). Debido a que el orden de los factores en un producto no importa, deslizaremos el −1 al frente en cada caso.

\[\frac{9-x^{2}}{x^{2}+3 x} \cdot \frac{6 x-2 x^{2}}{x^{2}-6 x+9} \cdot=\frac{-(3+x)(x-3)}{x(x+3)} \cdot \frac{-2 x(x-3)}{(x-3)^{2}}\]

Ahora podemos cancelar factores comunes.

\[\begin{aligned} \frac{9-x^{2}}{x^{2}+3 x} \cdot \frac{6 x-2 x^{2}}{x^{2}-6 x+9} &=\frac{-(3+x)(x-3)}{x(x+3)} \cdot \frac{-2 x(x-3)}{(x-3)^{2}} \\ &=\frac{-(3+x)(x-3)}{x(x+3)} \cdot \frac{-2 x(x-3)}{(x-3)^{2}} \\ &=2 \end{aligned}\]

Algunas cosas para notar:

• Los factores 3 + x y x + 3 son idénticos, por lo que pueden ser cancelados, uno en la parte superior por uno en la parte inferior.
• Dos factores de x − 3 en la parte superior se cancelan para (x − 3) 2 (que es equivalente a (x − 3) (x − 3)) en la parte inferior.
• Una x en la parte superior cancela una x en la parte inferior.
• Nos quedamos con dos signos menos (dos −1's) y un 2. Entonces la solución es positiva 2.

Finalmente, el primer denominador tiene factores x y x + 3, por lo que x = 0 y x = −3 son restricciones (hacen que este denominador sea igual a cero). El segundo denominador tiene dos factores de x − 3, por lo que x = 3 es una restricción adicional.

Por lo tanto, para todos los valores de x, excepto los valores restringidos −3, 0 y 3, el lado izquierdo de\[\frac{9-x^{2}}{x^{2}+3 x} \cdot \frac{6 x-2 x^{2}}{x^{2}-6 x+9}=2\]

es idéntico al lado derecho. Nuevamente, esta afirmación se prueba fácilmente en la calculadora gráfica que se evidencia en la secuencia de capturas de pantalla en la Figura\(\PageIndex{2}\).

Figura\(\PageIndex{2}\). Usando las características de tabla de la calculadora gráfica para verificar el resultado en la ecuación (11).

Un enfoque alternativo al problema en la ecuación (10) es anotar diferentes órdenes en los numeradores y denominadores (potencias descendentes, ascendentes de x) y anticipar la necesidad de un cambio de signo. Es decir, haz que el signo cambie antes de factizar.

Por ejemplo, negar (multiplicar por −1) tanto el numerador como la barra de fracción de la primera fracción para obtener

\[\frac{9-x^{2}}{x^{2}+3 x}=-\frac{x^{2}-9}{x^{2}+3 x}\]

De acuerdo con nuestra regla de cambio de signo, la negación de dos partes cualesquiera de una fracción deja la fracción sin cambios.

Si realizamos un cambio de signo similar en la segunda fracción (numerador negativo y barra de fracción), entonces podemos factorizar y cancelar factores comunes.

\[\begin{aligned} \frac{9-x^{2}}{x^{2}+3 x} \cdot \frac{6 x-2 x^{2}}{x^{2}-6 x+9} &=-\frac{x^{2}-9}{x^{2}+3 x} \cdot-\frac{2 x^{2}-6 x}{x^{2}-6 x+9} \\ &=-\frac{(x+3)(x-3)}{x(x+3)} \cdot-\frac{2 x(x-3)^{2}}{(x-3)^{2}} \\ &=-\frac{(x+3)(x-3)}{x(x+3)} \cdot-\frac{2 x(x-3)}{(x-3)^{2}} \\ &=2 \end{aligned}\]

División de Expresiones Racionales

Una definición simple cambiará un problema que implica la división de dos expresiones racionales en una que implica la multiplicación de dos expresiones racionales. Entonces no queda nada que explicar, pues ya sabemos multiplicar dos expresiones racionales.

Entonces, motivemos nuestra definición de división. Supongamos que hacemos la pregunta, ¿cuántas mitades hay en un todo? La respuesta es fácil, ya que dos mitades hacen un todo. Así, cuando dividimos 1 por 1/2, deberíamos obtener 2. Hay dos mitades en un todo.

Vamos a subir un poco las apuestas y preguntarnos ¿cuántas mitades hay en seis? Para que el problema sea más preciso, imagina que has pedido 6 pizzas y cortas cada una por la mitad. ¿Cuántas mitades tienes? Nuevamente, esto es fácil cuando piensas en el problema de esta manera, la respuesta es 12. Por lo tanto,

\[6 \div \frac{1}{2}\]

(cuántas mitades hay en seis) es idéntico a

\[6 \cdot 2\]

que, por supuesto, es 12. Ojalá, gracias a esta motivación de apertura, la siguiente definición no parecerá demasiado extraña.

Definición

Para realizar la división\[\frac{a}{b} \div \frac{c}{d}\], invertir la segunda fracción y multiplicar, como en\[\frac{a}{b} \cdot \frac{d}{c}\]

Así, si queremos saber cuántas mitades hay en 12, cambiamos la división en multiplicación (“invertir y multiplicar”).

\[12 \div \frac{1}{2}=12 \cdot 2=24\]

Esto tiene sentido, ya que hay 24 “mitades” en 12. Veamos un ejemplo más duro.

Ejemplo\(\PageIndex{4}\)

Simplificar\[\frac{33}{15} \div \frac{14}{10}\]

Solución

Invertir la segunda fracción y multiplicar. Después de eso, todo lo que tenemos que hacer es factorizar numeradores y denominadores, luego cancelar los factores comunes.

\[\frac{33}{15} \div \frac{14}{10}=\frac{33}{15} \cdot \frac{10}{14}=\frac{3 \cdot 11}{3 \cdot 5} \cdot \frac{2 \cdot 5}{2 \cdot 7}=\frac{\not{8} \cdot 11}{\not{3} \cdot \not{5}} \cdot \frac{\not{2} \cdot \not{5}}{\not{2} \cdot 7}=\frac{11}{7}\]

Una forma interesante de verificar este resultado en su calculadora se muestra en la secuencia de pantallas de la Figura\(\PageIndex{3}\).

Figura\(\PageIndex{3}\). Usando la calculadora para verificar la división de fracciones.

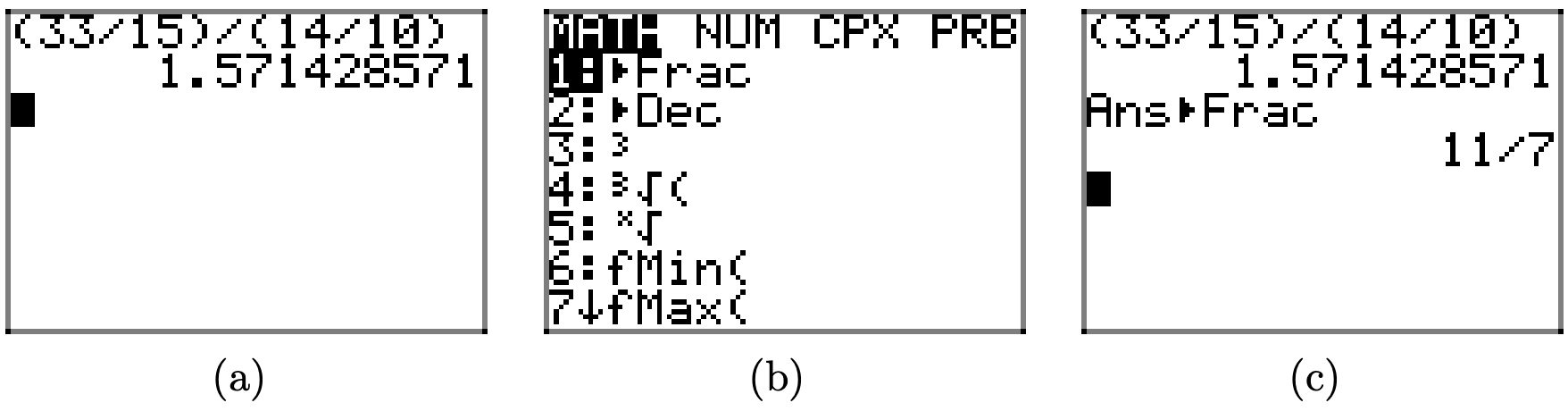
Después de ingresar el problema original en su calculadora, presione ENTRAR, luego presione el botón MATH, luego seleccione 1:I Frac en el menú y presione ENTRAR. El resultado se muestra en la Figura\(\PageIndex{3}\) (c), la cual concuerda con nuestro cálculo anterior.

Veamos otro ejemplo.

Ejemplo\(\PageIndex{5}\)

Simplificar\[\frac{9+3 x-2 x^{2}}{x^{2}-16} \div \frac{4 x^{3}-9 x}{2 x^{2}+5 x-12}\] Estado las restricciones.

Solución

Tenga en cuenta que el orden del primer numerador difiere del resto de numeradores y denominadores, por lo que “anticipamos” la necesidad de un cambio de signo, negando el numerador y la barra de fracción de la primera fracción. También invertimos la segunda fracción y cambiamos la división a multiplicación (“invertir y multiplicar”).

\[-\frac{2 x^{2}-3 x-9}{x^{2}-16} \cdot \frac{2 x^{2}+5 x-12}{4 x^{3}-9 x}\]

El numerador en la primera fracción de la ecuación (17) es un trinomio cuadrático, con ac = (2) (−9) = −18. El par entero 3 y −6 tiene el producto −18 y la suma −3. Por lo tanto,

\[\begin{aligned} 2 x^{2}-3 x-9 &=2 x^{2}+3 x-6 x-9 \\ &=x(2 x+3)-3(2 x+3) \\ &=(x-3)(2 x+3) \end{aligned}\]

El denominador de la primera fracción en la ecuación (17) factoriza fácilmente usando la diferencia del patrón de dos cuadrados.

\[x^{2}-16=(x+4)(x-4)\]

El numerador de la segunda fracción en la ecuación (17) es un trinomio cuadrático, con ac = (2) (−12) = −24. El par entero −3 y 8 tienen producto −24 y suma 5. Por lo tanto,

\[\begin{aligned} 2 x^{2}+5 x-12 &=2 x^{2}-3 x+8 x-12 \\ &=x(2 x-3)+4(2 x-3) \\ &=(x+4)(2 x-3) \end{aligned}\]

Para factorizar el denominador de la última fracción en la ecuación (17), primero tire del mayor factor común (en este caso x), luego complete la factorización usando el patrón de diferencia de dos cuadrados.

\[4 x^{3}-9 x=x\left(4 x^{2}-9\right)=x(2 x+3)(2 x-3)\]

Ahora podemos reemplazar cada numerador y denominador en la ecuación (17) con su factorización, luego cancelar factores comunes.

\[\begin{aligned}-\frac{2 x^{2}-3 x-9}{x^{2}-16} \cdot \frac{2 x^{2}+5 x-12}{4 x^{3}-9 x} &=-\frac{(x-3)(2 x+3)}{(x+4)(x-4)} \cdot \frac{(x+4)(2 x-3)}{x(2 x+3)(2 x-3)} \\ &=-\frac{(x-3)(2 x+3)}{(x+4)(x-4)} \cdot \frac{(x+4)(2 x-3)}{x(2 x+3)(2 x-3)} \\ &=-\frac{x-3}{x(x-4)} \end{aligned}\]

El último denominador tiene factores x y x − 4, por lo que x = 0 y x = 4 son restricciones. En el cuerpo de nuestro trabajo, el denominador de la primera fracción tiene factores x + 4 y x − 4. Ya hemos visto el factor x − 4, así que solo el factor x + 4 agrega una nueva restricción, x = −4. Nuevamente, en el cuerpo de nuestro trabajo, el denominador de la segunda fracción tiene factores x, 2x + 3, y 2x − 3, por lo que hemos agregado restricciones x = 0, x = −3/2, y x = 3/2.

Aquí hay un poco de engaños que se puede pasar por alto fácilmente. En el cuerpo de nuestro trabajo, el numerador de la segunda fracción era originalmente un denominador antes de invertir la fracción. Entonces, debemos considerar qué hace que este numerador sea cero también. Afortunadamente, los factores en este numerador son x + 4 y 2x − 3 y ya hemos considerado las restricciones que producen estos factores.

Por lo tanto, para todos los valores de x, excepto los valores restringidos −4, −3/2, 0, 3/2 y 4, el lado izquierdo de

\[\frac{9+3 x-2 x^{2}}{x^{2}-16} \div \frac{4 x^{3}-9 x}{2 x^{2}+5 x-12}=-\frac{x-3}{x(x-4)}\]

es idéntico al lado derecho.

Nuevamente, esta afirmación se verifica fácilmente mediante el uso de una calculadora gráfica, como se evidencia parcialmente (tendrás que desplazarte hacia abajo para ver la última restricción entrar a la vista) en la secuencia de capturas de pantalla en la Figura\(\PageIndex{4}\).

Figura\(\PageIndex{4}\). Usando la función de tabla de la calculadora para verificar el resultado en la ecuación (18).

Notación alternativa. Tenga en cuenta que la expresión fraccionaria a/b significa “a dividido por b”, por lo que podemos usar esta notación equivalente para\(a \div b\). Por ejemplo, la expresión

\[\frac{9+3 x-2 x^{2}}{x^{2}-16} \div \frac{4 x^{3}-9 x}{2 x^{2}+5 x-12}\]

es equivalente a la expresión

\[\frac{\frac{9+3 x-2 x^{2}}{x^{2}-16}}{\frac{4 x^{3}-9 x}{2 x^{2}+5 x-12}}\]

Veamos un ejemplo de esta notación en uso.

Ejemplo\(\PageIndex{6}\)

Dado eso\[f(x)=\frac{x}{x+3} \quad \text { and } \quad g(x)=\frac{x^{2}}{x+3}\], simplificar tanto f (x) g (x) como f (x) /g (x).

Solución

Primero, la multiplicación. No hay cancelación posible, así que simplemente multiplicamos numeradores y denominadores.

\[f(x) g(x)=\frac{x}{x+3} \cdot \frac{x^{2}}{x+3}=\frac{x^{3}}{(x+3)^{2}}\]

Este resultado es válido para todos los valores de x excepto −3.

Por otra parte,\[\frac{f(x)}{g(x)}=\frac{\frac{x}{x+3}}{\frac{x^{2}}{x+3}}=\frac{x}{x+3} \div \frac{x^{2}}{x+3}\]

Cuando “invertimos y multiplicamos”, luego cancelamos, obtenemos\[\frac{f(x)}{g(x)}=\frac{x}{x+3} \cdot \frac{x+3}{x^{2}}=\frac{1}{x}\]. Este resultado es válido para todos los valores de x excepto −3 y 0.

Ejercicio

En los Ejercicios 1 - 10, reducir el producto a una sola fracción en términos más bajos.

Ejercicio\(\PageIndex{1}\)

\(\frac{108}{14} \cdot \frac{6}{100}\)

Contestar

\(\frac{81}{175}\)

Ejercicio\(\PageIndex{2}\)

\(\frac{75}{63} \cdot \frac{18}{45}\)

Ejercicio\(\PageIndex{3}\)

\(\frac{189}{56} \cdot \frac{12}{27}\)

Contestar

\(\frac{3}{2}\)

Ejercicio\(\PageIndex{4}\)

\(\frac{45}{72} \cdot \frac{63}{64}\)

Ejercicio\(\PageIndex{5}\)

\(\frac{15}{36} \cdot \frac{28}{100}\)

Contestar

\(\frac{7}{60}\)

Ejercicio\(\PageIndex{6}\)

\(\frac{189}{49} \cdot \frac{32}{25}\)

EXERICSE\(\PageIndex{7}\)

\(\frac{21}{100} \cdot \frac{125}{16}\)

Contestar

\(\frac{105}{64}\)

Ejercicio\(\PageIndex{8}\)

\(\frac{21}{35} \cdot \frac{49}{45}\)

Ejercicio\(\PageIndex{9}\)

\(\frac{56}{20} \cdot \frac{98}{32}\)

Contestar

\(\frac{343}{40}\)

Ejercicio\(\PageIndex{10}\)

\(\frac{27}{125} \cdot \frac{4}{12}\)

En los Ejercicios 11 - 34, multiplique y simplifique. Estado todas las restricciones.

Ejercicio\(\PageIndex{11}\)

\(\frac{x+6}{x^2+16x+63} \cdot \frac{x^2+7x}{x+4}\)

Contestar

Proporcionado\(x \ne −9, −7, −4\),

\(\frac{x(x+6)}{(x+9)(x+4)}\)

Ejercicio\(\PageIndex{12}\)

\(\frac{x^2+9x}{x^2−25} \cdot \frac{x^2−x−20}{−18−11x−x^2}\)

Ejercicio\(\PageIndex{13}\)

\(\frac{x^2+7x+10}{x^2−1} \cdot \frac{−9+10x−x^2}{x^2+9x+20}\)

Contestar

Proporcionado\(x \ne 1, −1, −4, −5\),

\(−\frac{(x+2)(x−9)}{(x+1)(x+4)}\)

Ejercicio\(\PageIndex{14}\)

\(\frac{x^2+5x}{x−4}\ cdot \frac{x−2}{x^2+6x+5}\)

Ejercicio\(\PageIndex{15}\)

\(\frac{x^2−5x}{x^2+2x−48} \cdot \frac{x^2+11x+24}{x^2−x}\)

Contestar

Proporcionado\(x \ne −8, 6, 1, 0\),

\(\frac{(x−5)(x+3)}{(x−6)(x−1)}\)

Ejercicio\(\PageIndex{16}\)

\(\frac{x^2−6x−27}{x^2 +10x+24} \cdot \frac{x^2 +13x+42}{x^2−11x+18}\)

Ejercicio\(\PageIndex{17}\)

\(\frac{−x−x^2}{x^2−9x+8} \cdot \frac{x^2−4x+3}{x^2+4x+3}\)

Contestar

Proporcionado\(x \ne 1, 8, −3, −1\),

\(−\frac{x(x−3)}{(x−8)(x+3)}\)

Ejercicio\(\PageIndex{18}\)

\(\frac{x^2−12x+35}{x^2+2x−15} \cdot \frac{45+4x−x^2}{x^2+x−30}\)

Ejercicio\(\PageIndex{19}\)

\(\frac{x+2}{7−x} \cdot \frac{x^2+x−56}{x^2+7x+6}\)

Contestar

Proporcionado\(x \ne 7, −1, −6\),

\(−\frac{(x+2)(x+8)}{(x+1)(x+6)}\)

Ejercicio\(\PageIndex{20}\)

\(\frac{x^2−2x−15}{x^2 +x} \cdot \frac{x^2+7x}{x^2+12x+27}\)

Ejercicio\(\PageIndex{21}\)

\(\frac{x^2−9}{x^2−4x−45} \cdot \frac{x−6}{−3−x}\)

Contestar

Proporcionado\(x \ne −3, −5, 9\),

\(−\frac{(x−3)(x−6)}{(x−5)(x−3)}\)

Ejercicio\(\PageIndex{22}\)

\(\frac{x^2−12x+27}{x−5} \cdot \frac{x−4}{x^2−18x+8}\)

Ejercicio\(\PageIndex{23}\)

\(\frac{x+5}{x^2−2x−24} \cdot \frac{x^2+12x+32}{x+7}\)

Contestar

Proporcionado\(x \ne −8, −4, −7\),

\(\frac{(x+5)(x−6)}{(x+8)(x+7)}\)

Ejercicio\(\PageIndex{24}\)

\(\frac{x^2−36}{x^2+11x+24} \cdot \frac{−8−x}{x+4}\)

Ejercicio\(\PageIndex{25}\)

\(\frac{x−5}{x^2−8x+12} \cdot \frac{x^2−12x+36}{x−8}\)

Contestar

Proporcionado\(x \ne 2, 6, 8\),

\(\frac{(x−5)(x−6)}{(x−2)(x−8)}\)

Ejercicio\(\PageIndex{26}\)

\(\frac{x^2−5x−36}{x−1} \cdot \frac{x−5}{x^2−81}\)

Ejercicio\(\PageIndex{27}\)

\(\frac{x^2 +2x−15}{x^2−10x+16} \cdot \frac{x^2−7x+10}{3x^2+13x−10}\)

Contestar

Proporcionado\(x \ne 2, 8, \frac{2}{3}, −5\),

\(\frac{(x−3)(x−5)}{(3x−2)(x−8)}\)

Ejercicio\(\PageIndex{28}\)

\(\frac{5x^2+14x−3}{x+9} \cdot \frac{x−7}{x^2+10x+21}\)

Ejercicio\(\PageIndex{29}\)

\(\frac{x^2−4}{x^2+2x−63} \cdot \frac{x^2+6x−27}{x^2−6x−16}\)

Contestar

Proporcionado\(x \ne −9, 7, 8, −2\),

\(\frac{(x−2)(x−3)}{(x−7)(x−8)}\)

Ejercicio\(\PageIndex{30}\)

\(\frac{x^2+5x+6}{x^2−3x} \cdot \frac{x^2−5x}{x^2+9x+18}\)

Ejercicio\(\PageIndex{31}\)

\(\frac{x−1}{x^2+2x−63} \cdot \frac{x^2−81}{x+4}\)

Contestar

Proporcionado\(x \ne 7, −9, −4\),

\(\frac{(x−1)(x−9)}{(x−7)(x+4)}\)

Ejercicio\(\PageIndex{32}\)

\(\frac{x^2+9x}{x^2+7x+12} \cdot \frac{27+6x−x^2}{x^2−5x}\)

Ejercicio\(\PageIndex{33}\)

\(\frac{5−x}{x+3} \cdot \frac{x^2+3x−18}{2x^2−7x−15}\)

Contestar

Proporcionado\(x \ne −3, −\frac{3}{2}, 5\)

\(−\frac{(x+6)(x−3)}{(2x+3)(x+3)}\)

Ejercicio\(\PageIndex{34}\)

\(\frac{4x^2+21x+5}{18−7x−x^2} \cdot \frac{x^2+11x+18}{x^2−25}\)

En los Ejercicios 35 - 58, divide y simplifica. Estado todas las restricciones.

Ejercicio\(\PageIndex{35}\)

\(\frac{\frac{x^2−14x+48}{x^2+10x+16}}{\frac{−24+11x−x^2}{x^2−x−72}}\)

Contestar

Proporcionado\(x \ne −8, −2, 9, 3, 8\),

\(−\frac{(x−6)(x−9)}{(x+2)(x−3)}\)

Ejercicio\(\PageIndex{36}\)

\(\frac{x−1}{x^2−14x+48​} \div \frac{x+5}{x^2−3x−18}\)

Ejercicio\(\PageIndex{37}\)

\(\frac{x^2−1}{x^2−7x+12​} \div \frac{x^2+6x+5}{−24+10x−x^2}\)

Contestar

Proporcionado\(x \ne 4, 3, 6, −5, −1\),

\(−\frac{(x−1)(x−6)}{(x−3)(x+5)}\)

Ejercicio\(\PageIndex{38}\)

\(\frac{x^2−13x+42}{x^2−2x−63} \div \frac{x^2−x−42}{x^2+8x+7}\)

Ejercicio\(\PageIndex{39}\)

\(\frac{x^2−25}{x+1} \div \frac{5x^2+23x−10}{x−3}\)

Contestar

Proporcionado\(x \ne −1, \frac{2}{5}, −5, 3\),

\(\frac{(x−5)(x−3)​​​​​​}{(5x−2)(x+1)}\)

Ejercicio\(\PageIndex{40}\)

\(\frac{\frac{x^2−3x}{x^2−7x+6}}{\frac{x^2−4x}{3x^2−11x−42}}\)

Ejercicio\(\PageIndex{41}\)

\(\frac{\frac{x^2+10x+21}{x−4}}{\frac{x^2+3x}{x+8}}\)

Contestar

Proporcionado\(x \ne 4, 0, −3, −8\),

\(\frac{(x+7)(x+8)}{x(x−4)}\)

Ejercicio\(\PageIndex{42}\)

\(\frac{x^2+8x+15}{x^2−14x+45} \div \frac{x^2+11x+30}{−30+11x−x^2}\)

Ejercicio\(\PageIndex{43}\)

\(\frac{\frac{x^2−6x−16}{x^2+x−42}}{\frac{x^2−64}{x^2+12x+35}}\)

Contestar

Proporcionado\(x \ne −7, 6, −5, −8, 8\),

\(\frac{(x+2)(x+5)}{(x−6)(x+8)}\)

Ejercicio\(\PageIndex{44}\)

\(\frac{\frac{x^2+3x+2}{x^2−9x+18}}{\frac{x^2+7x+6}{x^2−6x}}\)

Ejercicio\(\PageIndex{45}\)

\(\frac{\frac{x^2+12x+35}{x+4}}{\frac{x^2+10x+25}{x+9}}\)

Contestar

Proporcionado\(x \ne −4, −5, −9\),

\(\frac{(x+7)(x+9)}{(x+4)(x+5)}\)

Ejercicio\(\PageIndex{46}\)

\(\frac{x^2−8x+7}{x^2+3x−18} \div \frac{x^2−7x}{x^2+6x−27}\)

Ejercicio\(\PageIndex{47}\)

\(\frac{x^2+x−30}{x^2+5x−36} \div \frac{−6−x}{x+8}\)

Contestar

Proporcionado\(x \ne 4, −9, −8, −6\),

\(−\frac{(x−5)(x+8)}{(x−4)(x+9)}\)

Ejercicio\(\PageIndex{48}\)

\(\frac{\frac{2x−x^2}{x^2−15x+54}}{\frac{x^2+x}{x^2−11x+30}}\)

Ejercicio\(\PageIndex{49}\)

\(\frac{\frac{x^2−9x+8}{x^2−9}}{\frac{x^2−8x−15}{−8x−x^2}}\)

Contestar

Proporcionado\(x \ne −3, 3, −5, 0, 8\),

\(−\frac{(x−1)(x+5)}{x(x−3)}\)

Ejercicio\(\PageIndex{50}\)

\(\frac{x+5}{x^2+2x+1} \div \frac{x−2}{x^2+10x+9}\)

Ejercicio\(\PageIndex{51}\)

\(\frac{\frac{x^2−4}{x+8}}{\frac{x^2−10x+16}{x+3}}\)

Contestar

Proporcionado\(x \ne −8, 8, 2, −3\),

\(\frac{(x+2)(x+3)}{(x+8)(x−8)}\)

Ejercicio\(\PageIndex{52}\)

\(\frac{27−6x−x^2}{x^2+9x+20} \div \frac{x^2−12x+27}{x^2+5x}\)

Ejercicio\(\PageIndex{53}\)

\(\frac{\frac{x^2+5x+6}{x^2 − 36}}{\frac{x−7}{−6−x}}\)

Contestar

Proporcionado\(x \ne 6, −6, 7\),

\(−\frac{(x+2)(x+3)}{(x−6)(x−7)}\)

Ejercicio\(\PageIndex{54}\)

\(\frac{2−x}{x−5} \div \frac{x^2+3x−10}{x^2−14x+48}\)

Ejercicio\(\PageIndex{55}\)

\(\frac{\frac{x+3}{x^2 +4x−12}}{\frac{x−4}{x^2−36}}\)

Contestar

Proporcionado\(x \ne 2, −6, 4, 6\),

\(\frac{(x+3)(x−6)}{(x−2)(x−4)}\)

Ejercicio\(\PageIndex{56}\)

\(\frac{x+3}{x^2−x−2​​​​​​} \div \frac{x}{x^2−3x−4}\)

Ejercicio\(\PageIndex{57}\)

\(\frac{x^2−11x+28}{x^2+5x+6} \div \frac{7x^2−30x+8}{x^2−x−6}\)

Contestar

Proporcionado\(x \ne −2, −3, 3, \frac{2}{7}, 4\),

\(\frac{(x−7)(x−3)}{(7x−2)(x+3)}\)

Ejercicio\(\PageIndex{58}\)

\(\frac{\frac{x−7}{3−x}}{\frac{2x^2+3x−5}{x^2−12x+27}}\)

Ejercicio\(\PageIndex{59}\)

Let

\(f(x) = \frac{x^2−7x+10}{x^2+4x−21}\)

y

\(g(x) = \frac{5x−x^2}{x^2+15x+56}\)

Calcula\(\frac{f(x)}{g(x)}\) y simplifica tu respuesta.

Contestar

Proporcionado\(x \ne −7, 3, −8, 0, 5\),

\(−\frac{(x−2)(x+8)}{x(x−3)}\)

Ejercicio\(\PageIndex{60}\)

Let

\(f(x) = \frac{x^2+15x+56}{x^2−x−20}\)

y

\(g(x) = \frac{−7−x}{x+1}\)

Calcula\(\frac{f(x)}{g(x)}\) y simplifica tu respuesta.

Ejercicio\(\PageIndex{61}\)

Let

\(f(x) = \frac{x^2+12x+35}{x^2+4x−32}\)

y

\(g(x) = \frac{x^2−2x−35}{x^2+8x}\)

Calcula\(\frac{f(x)}{g(x)}\) y simplifica tu respuesta.

Contestar

Proporcionado\(x \ne −8, 4, 0, 7, −5\),

\(\frac{x(x+7)}{(x−4)(x−7)}\)

Ejercicio\(\PageIndex{62}\)

Let

\(f(x) = \frac{x^2+4x+3}{x−1}\)

y

\(g(x) = \frac{x^2−4x−21}{x+5}\)

Calcula\(\frac{f(x)}{g(x)}\) y simplifica tu respuesta.

Ejercicio\(\PageIndex{63}\)

Let

\(f(x) = \frac{x^2+x−20}{x}\)

y

\(g(x) = \frac{x−1}{x^2−2x−35}\)

Calcula f (x) g (x) y simplifica tu respuesta.

Contestar

Proporcionado\(x \ne 0, 7, −5\),

\(\frac{(x−4)(x−1)}{x(x−7)}\)

Ejercicio\(\PageIndex{64}\)

Let

\(f(x) = \frac{x^2+10x+24}{x^2−13x+42}\)

y

\(g(x) = \frac{x^2−6x−7}{x^2+8x+12}\)

Calcula f (x) g (x) y simplifica tu respuesta.

Ejercicio\(\PageIndex{65}\)

Let
\(f(x) = \frac{x+5}{−6−x}\)

y

\(g(x) = \frac{x^2+8x+12}{x^2−49}\)

Calcula f (x) g (x) y simplifica tu respuesta.

Contestar

Proporcionado\(x \ne −6, −7, 7\),

\(−\frac{(x+5)(x+2)}{(x+7)(x−7)}\)

Ejercicio\(\PageIndex{66}\)

Let

\(f(x)= \frac{8−7x−x^2}{x^2−8x−9}\)

y

\(g(x) = \frac{x^2−6x−7}{x^2−6x+5}\)

Calcula f (x) g (x) y simplifica tu respuesta.