7.3: Graficar funciones racionales
- Page ID
- 110799
Hemos visto que nunca se permite que el denominador de una función racional sea igual a cero; la división por cero no está definida. Entonces, con las funciones racionales, hay valores especiales de la variable independiente que son de particular importancia. Ahora bien, no sorprende que cerca de valores que hacen que el denominador sea cero, las funciones racionales exhiben un comportamiento especial, pero aquí, también veremos que los valores que hacen que el numerador sea cero a veces crean un comportamiento especial adicional en las funciones racionales.
Comenzamos nuestra discusión enfocándonos en el dominio de una función racional.
El dominio de una función racional
Cuando se le presenta una función racional de la forma
\[f(x)=\frac{a_{0}+a_{1} x+a_{2} x^{2}+\cdots+a_{n} x^{n}}{b_{0}+b_{1} x+b_{2} x^{2}+\cdots+b_{m} x^{m}}\]
lo primero que debemos hacer es identificar el dominio. Equivalentemente, debemos identificar las restricciones, valores de la variable independiente (generalmente x) que no están en el dominio. Para facilitar la búsqueda de restricciones, debemos factorizar el denominador de la función racional (no va a doler factorizar también al numerador en este momento, como veremos pronto). Una vez que se establece el dominio y se identifican las restricciones, aquí están los hechos pertinentes.
Comportamiento de una función racional en sus restricciones
Una función racional solo puede exhibir uno de dos comportamientos en una restricción (un valor de la variable independiente que no está en el dominio de la función racional).
- La gráfica de la función racional tendrá una asíntota vertical en el valor restringido.
- La gráfica exhibirá un “agujero” en el valor restringido.
En los siguientes dos ejemplos, examinaremos cada uno de estos comportamientos. En este primer ejemplo, vemos una restricción que conduce a una asíntota vertical.
Ejemplo\(\PageIndex{1}\)
Esbozar el gráfico de\[f(x)=\frac{1}{x+2}\]
Solución
El primer paso es identificar el dominio. Tenga en cuenta que x = −2 hace que el denominador de f (x) = 1/ (x + 2) sea igual a cero. La división por cero no está definida. Por lo tanto, x = −2 no está en el dominio de f; es decir, x = −2 es una restricción. Equivalentemente, el dominio de f es\(\{x : x \neq-2\}\).
Ahora que hemos identificado la restricción, podemos usar la teoría de la Sección 7.1 para desplazar la gráfica de y = 1/x dos unidades hacia la izquierda para crear la gráfica de\(f(x) = 1/(x + 2)\), como se muestra en la Figura\(\PageIndex{1}\).
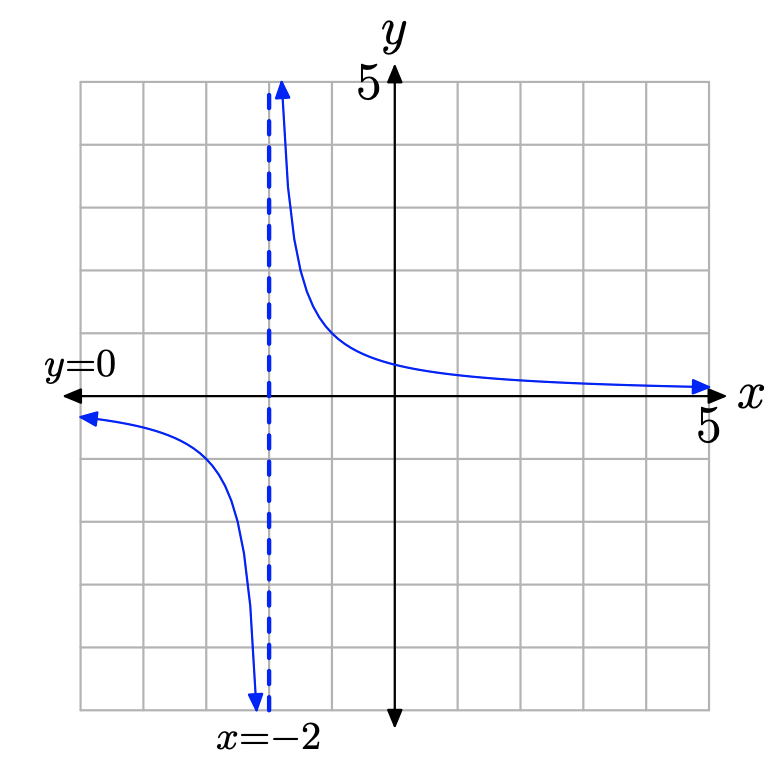
La función f (x) = 1/ (x + 2) tiene una restricción a x = −2 y la gráfica de f exhibe una asíntota vertical que tiene la ecuación x = −2.
Es importante señalar que aunque el valor restringido x = −2 hace que el denominador de f (x) = 1/ (x + 2) sea igual a cero, no hace que el numerador sea igual a cero. Pronto tendremos más que decir sobre esta observación.
Veamos un ejemplo de una función racional que exhibe un “agujero” en uno de sus valores restringidos.
Ejemplo\(\PageIndex{2}\)
Esbozar el gráfico de\[f(x)=\frac{x-2}{x^{2}-4}\]
Solución
Destacamos el primer paso.
Numeradores y denominadores factoriales
Al trabajar con funciones racionales, lo primero que debes hacer siempre es factorizar tanto el numerador como el denominador de la función racional.
Siguiendo este consejo, factorizamos tanto el numerador como el denominador de\(f(x) = (x − 2)/(x^2 − 4)\).
\[f(x)=\frac{x-2}{(x-2)(x+2)}\]
Es más fácil detectar las restricciones cuando el denominador de una función racional está en forma factorizada. Claramente, x = −2 y x = 2 harán que el denominador de f (x) = (x−2)/((x−2) (x+ 2)) sea igual a cero. De ahí que x = −2 y x = 2 son restricciones de la función racional f.
Ahora que se establecen las restricciones de la función racional f, se procede al segundo paso.
Reducir a los términos más bajos
Después de establecer las restricciones de la función racional, lo segundo que debes hacer es reducir la función racional a los términos más bajos.
Siguiendo este consejo, cancelamos factores comunes y reducimos la función racional f (x) = (x − 2)/((x − 2) (x + 2)) a términos más bajos, obteniendo una nueva función,
\[g(x)=\frac{1}{x+2}\]
Las funciones f (x) = (x − 2)/((x − 2) (x + 2)) y g (x) = 1/ (x + 2) no son funciones idénticas. Tienen diferentes dominios. El dominio de f es\(D_{f}=\{x : x \neq-2,2\}\), pero el dominio de g es\(D_{g}=\{x : x \neq-2\}\). De ahí que la única diferencia entre las dos funciones se produzca en x = 2. El número 2 está en el dominio de g, pero no en el dominio de f.
Sabemos cómo se ve la gráfica de la función g (x) = 1/ (x + 2). Dibujamos esta gráfica en Ejemplo\(\PageIndex{1}\) y la imaginamos de nuevo en Figura\(\PageIndex{2}\).
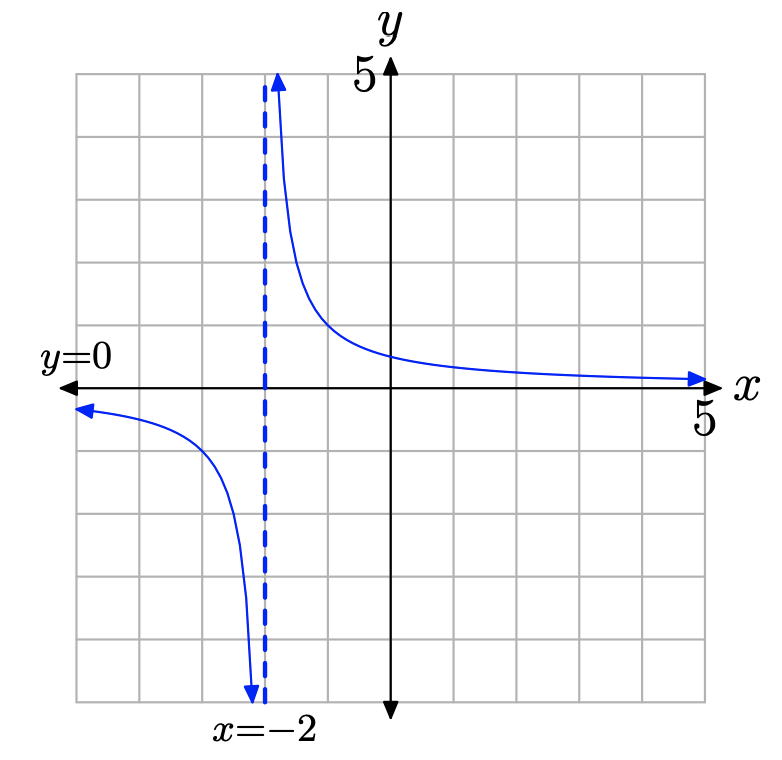
La dificultad que enfrentamos ahora es el hecho de que nos han pedido dibujar la gráfica de f, no la gráfica de g Sin embargo, sabemos que las funciones f y g coinciden en todos los valores de x excepto x = 2. Si eliminamos este valor de la gráfica de g, entonces tendremos la gráfica de f.
Entonces, ¿qué punto debemos eliminar de la gráfica de g? Deberíamos eliminar el punto que tiene un valor x igual a 2. Por lo tanto, evaluamos la función g (x) = 1/ (x + 2) en x = 2 y encontramos\[g(2)=\frac{1}{2+2}=\frac{1}{4}\]
Debido a que g (2) = 1/4, eliminamos el punto (2, 1/4) de la gráfica de g para producir la gráfica de f. el resultado se muestra en la Figura\(\PageIndex{3}\).
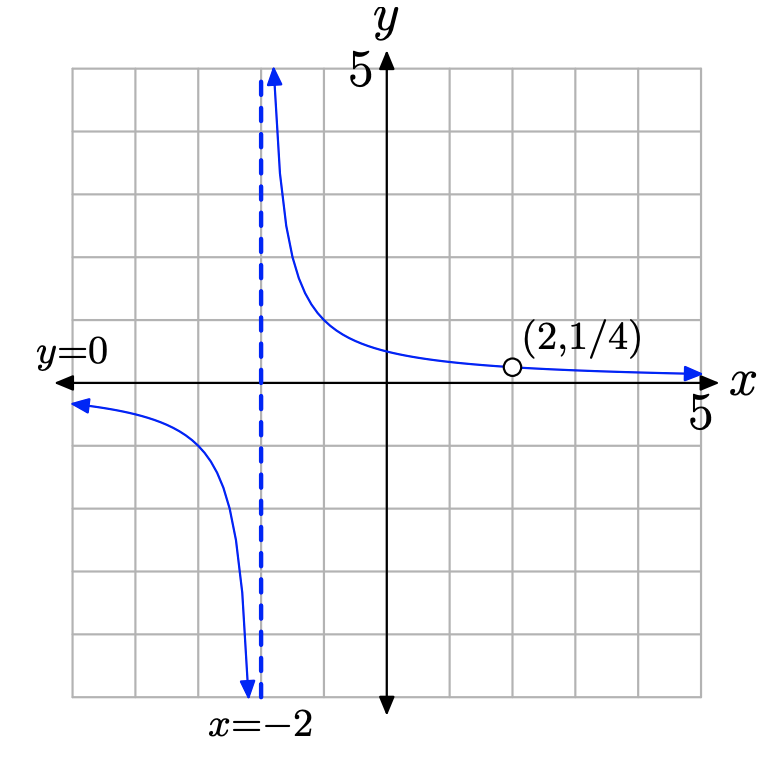
Hacemos una pausa para hacer una observación importante. En Ejemplo\(\PageIndex{2}\), empezamos con la función
\[f(x)=\frac{x-2}{(x-2)(x+2)}\]
que tenían restricciones en x = 2 y x = −2. Después de reducir, la función
\[g(x)=\frac{1}{x+2}\]
ya no tenía restricción a x = 2. La función g tuvo una restricción única a x = −2. El resultado, como se ve en la Figura\(\PageIndex{3}\), fue una asíntota vertical en la restricción restante, y un agujero en la restricción que “se fue” por cancelación. Esto nos lleva al siguiente procedimiento.
¿Asymptote o Hoyo?
Para determinar si la gráfica de una función racional tiene una asíntota vertical o un agujero en una restricción, proceda de la siguiente manera:
- Numerador factorial y denominador de la función racional original f. Identificar las restricciones de f.
- Reducir la función racional a los términos más bajos, nombrando la nueva función g. Identificar las restricciones de la función g.
- Aquellas restricciones de f que queden restricciones de la función g introducirán asíntotas verticales en la gráfica de f.
- Aquellas restricciones de f que ya no sean restricciones de la función g introducirán “agujeros” en la gráfica de f. para determinar las coordenadas de los agujeros, sustituya cada restricción de f que no sea una restricción de g en la función g para determinar el valor y del agujero.
Ahora volvemos nuestra atención a los ceros de una función racional.
Los ceros de una función racional
Hemos visto que la división por cero es indefinida. Es decir, si tenemos una fracción N/D, entonces D (el denominador) no debe ser igual a cero. Así, 5/0, −15/0 y 0/0 son todos indefinidos. Por otro lado, en la fracción N/D, si N = 0 y\(D \neq 0\), entonces la fracción es igual a cero. Por ejemplo, 0/5, 0/ (−15) y 0\(/ \pi\) son todos iguales a cero.
Por lo tanto, cuando se trabaja con una función racional arbitraria, como
\[f(x)=\frac{a_{0}+a_{1} x+a_{2} x^{2}+\cdots+a_{n} x^{n}}{b_{0}+b_{1} x+b_{2} x^{2}+\cdots+b_{m} x^{m}}\]
cualquiera que sea el valor de x que haga que el numerador sea cero sin hacer simultáneamente el denominador igual a cero será un cero de la función racional f.
Esta discusión lleva al siguiente procedimiento para identificar los ceros de una función racional.
Encontrar ceros de funciones racionales
Para determinar los ceros de una función racional, proceda de la siguiente manera.
- Factorizar tanto el numerador como el denominador de la función racional f.
- Identificar las restricciones de la función racional f.
- Identificar los valores de la variable independiente (generalmente x) que hacen que el numerador sea igual a cero.
- Los ceros de la función racional f serán aquellos valores de x que hacen cero al numerador pero no son restricciones de la función racional f.
Veamos un ejemplo.
Ejemplo\(\PageIndex{3}\)
Encuentra los ceros de la función racional definida por\[f(x)=\frac{x^{2}+3 x+2}{x^{2}-2 x-3}\]
Solución
Numerador factorial y denominador de la función racional f.
\[f(x)=\frac{(x+1)(x+2)}{(x+1)(x-3)}\]
Los valores x = −1 y x = 3 hacen que el denominador sea igual a cero y son restricciones.
A continuación, tenga en cuenta que x = −1 y x = −2 ambos hacen que el numerador sea igual a cero. Sin embargo, x = −1 también es una restricción de la función racional f, por lo que no será un cero de f Por otro lado, el valor x = −2 no es una restricción y será un cero de f.
Aunque hemos identificado correctamente los ceros de f, es instructivo verificar los valores de x que hacen que el numerador de f sea igual a cero. Si sustituimos x = −1 en la función original definida por la ecuación (6), encontramos que
\[f(-1)=\frac{(-1)^{2}+3(-1)+2}{(-1)^{2}-2(-1)-3}=\frac{0}{0}\]
está indefinido. Por lo tanto, x = −1 no es un cero de la función racional f. La dificultad en este caso es que x = −1 también hace que el denominador sea igual a cero.
Por otro lado, cuando sustituimos x = −2 en la función definida por la ecuación (6),
\[f(-2)=\frac{(-2)^{2}+3(-2)+2}{(-2)^{2}-2(-2)-3}=\frac{0}{5}=0\]
En este caso, x = −2 hace que el numerador sea igual a cero sin que el denominador sea igual a cero. Por lo tanto, x = −2 es un cero de la función racional f.
Es importante señalar que se debe trabajar con la función racional original, y no su forma reducida, al identificar los ceros de la función racional.
Ejemplo\(\PageIndex{4}\)
Identificar los ceros de la función racional\[f(x)=\frac{x^{2}-6 x+9}{x^{2}-9}\]
Solución
Facturar tanto el numerador como el denominador. \[f(x)=\frac{(x-3)^{2}}{(x+3)(x-3)}\]
Tenga en cuenta que x = −3 y x = 3 son restricciones. Además, el único valor de x que hará que el numerador sea igual a cero es x = 3. Sin embargo, esto también es una restricción. De ahí que la función f no tenga ceros.
El punto a hacer aquí es lo que sucedería si se trabaja con la forma reducida de la función racional al intentar encontrar sus ceros. La cancelación de factores similares conduce a una nueva función,
\[g(x)=\frac{x-3}{x+3}\]
Tenga en cuenta que g tiene solo una restricción, x = −3. Además, x = 3 hace que el numerador de g sea igual a cero y no es una restricción. De ahí que x = 3 es un cero de la función g, pero no es un cero de la función f.
Este ejemplo demuestra que debemos identificar los ceros de la función racional antes de cancelar los factores comunes.
Dibujando la Gráfica de una Función Racional
En esta sección utilizaremos los ceros y asíntotas de la función racional para ayudar a dibujar la gráfica de una función racional. También investigaremos el comportamiento final de las funciones racionales. Empecemos con un ejemplo.
Ejemplo\(\PageIndex{5}\)
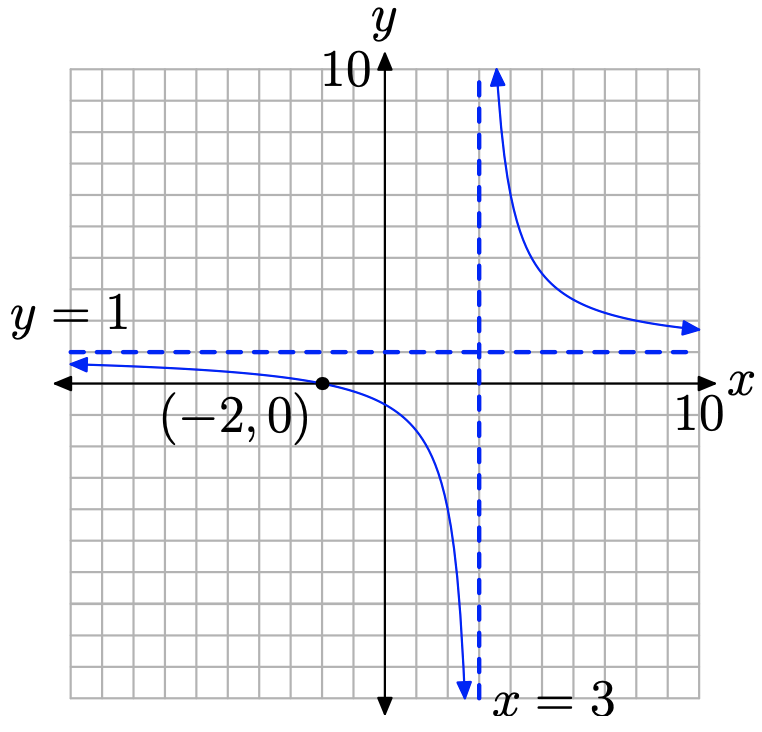
Esbozar el gráfico de la función racional\[f(x)=\frac{x+2}{x-3}\]
Solución
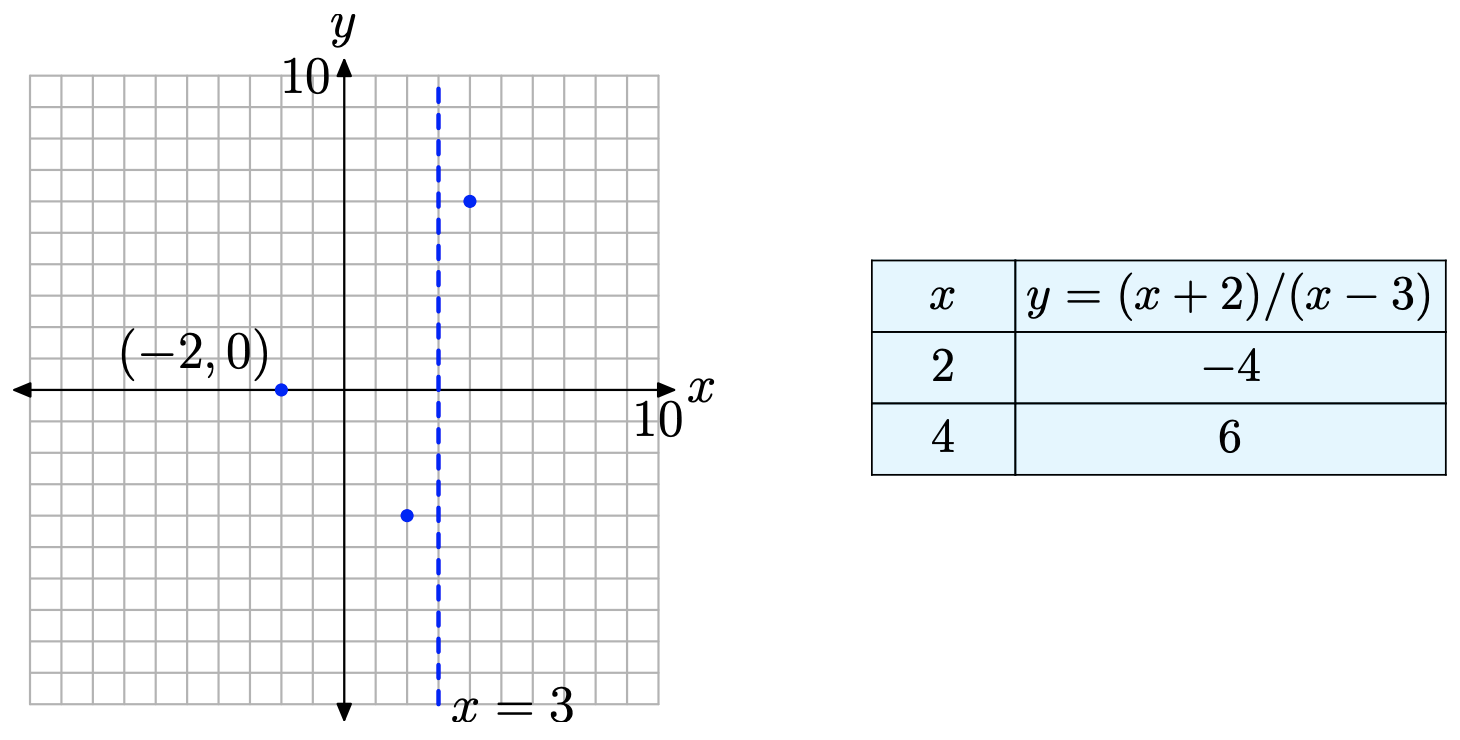
Primero, tenga en cuenta que tanto el numerador como el denominador ya están factorizados. La función tiene una restricción, x = 3. A continuación, tenga en cuenta que x = −2 hace que el numerador de la ecuación (9) sea cero y no sea una restricción. Por lo tanto, x = −2 es un cero de la función. Recordemos que una función es cero donde su gráfica cruza el eje horizontal. De ahí que la gráfica de f cruzará el eje x en (−2, 0), como se muestra en la Figura\(\PageIndex{4}\).
Obsérvese que la función racional (9) ya está reducida a los términos más bajos. De ahí que la restricción en x = 3 colocará una asíntota vertical en x = 3, la cual también se muestra en la Figura\(\PageIndex{4}\).
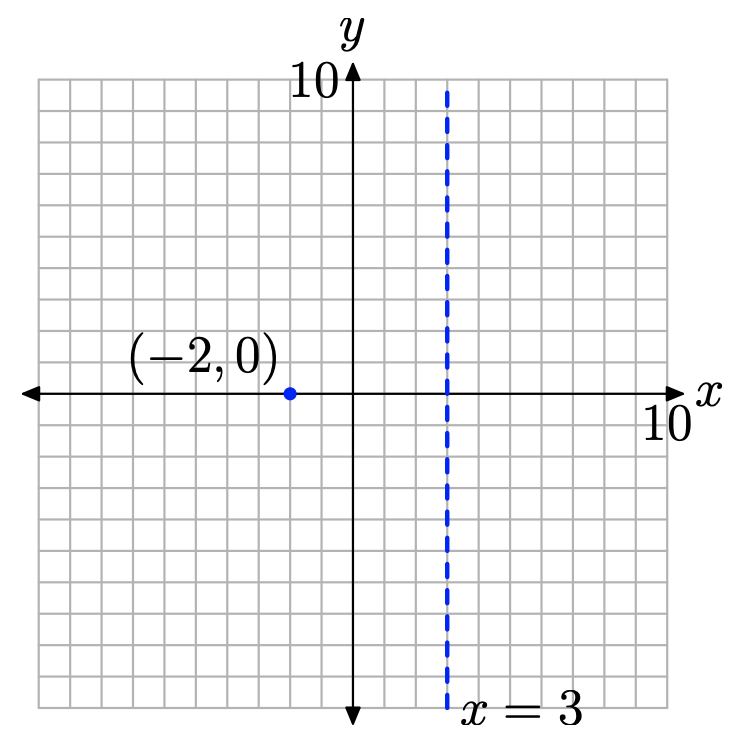
En este punto, sabemos dos cosas:
- La gráfica cruzará el eje x en (−2, 0).
- A cada lado de la asíntota vertical en x = 3, puede suceder una de dos cosas. O la gráfica se elevará al infinito positivo o la gráfica caerá al infinito negativo.
Para descubrir el comportamiento cerca de la asíntota vertical, trazemos un punto a cada lado de la asíntota vertical, como se muestra en la Figura\(\PageIndex{5}\).
Considera el lado derecho de la asíntota vertical y el punto trazado (4, 6) por el que debe pasar nuestra gráfica. A medida que la gráfica se acerca a la asíntota vertical en x = 3, solo puede suceder una de dos cosas. O la gráfica sube al infinito positivo o la gráfica cae al infinito negativo. No obstante, para que esto último suceda, la gráfica primero debe pasar por el punto (4, 6), luego cruzar el eje x entre x = 3 y x = 4 en su descenso a menos infinito. Pero ya sabemos que la única intercepción x está en el punto (2, 0), así que esto no puede suceder. De ahí que a la derecha, la gráfica debe pasar por el punto (4, 6), luego elevarse hasta el infinito positivo, como se muestra en la Figura\(\PageIndex{6}\).
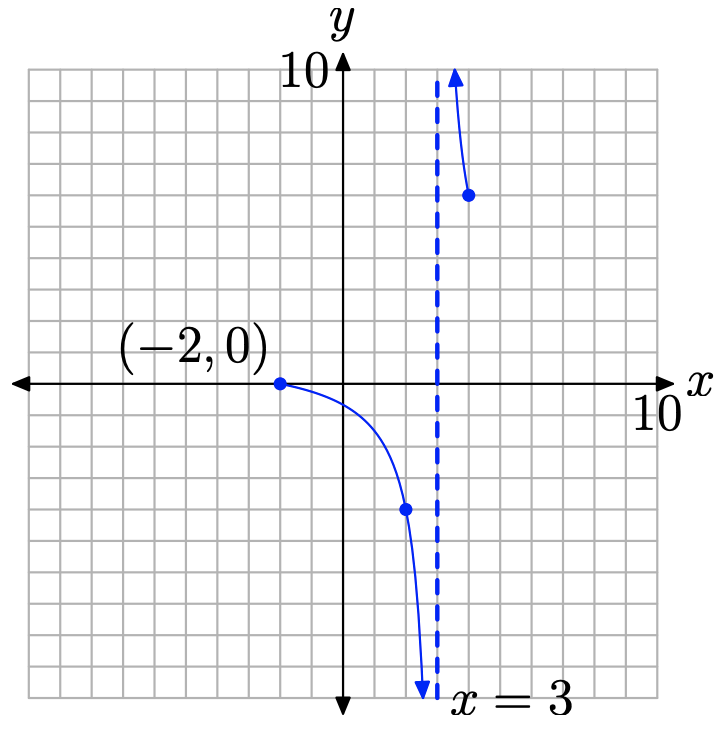
Un argumento similar se mantiene a la izquierda de la asíntota vertical en x = 3. La gráfica no puede pasar por el punto (2, −4) y elevarse al infinito positivo a medida que se acerca a la asíntota vertical, ya que para ello requeriría que cruzara el eje x entre x = 2 y x = 3. Sin embargo, no hay intercepción x en esta región disponible para este propósito. De ahí que a la izquierda, la gráfica debe pasar por el punto (2, −4) y caer al infinito negativo a medida que se acerca a la asíntota vertical en x = 3. Este comportamiento se muestra en la Figura\(\PageIndex{6}\).
Por último, ¿qué pasa con el comportamiento final de la función racional? ¿Qué pasa con la gráfica de la función racional a medida que x aumenta sin límite? ¿Qué sucede cuando x disminuye sin ataduras? Una forma sencilla de responder a estas preguntas es usar una tabla para investigar el comportamiento numéricamente. La calculadora gráfica facilita esta tarea.
Primero, ingrese su función como se muestra en la Figura\(\PageIndex{7}\) (a), luego presione 2nd TBLSET para abrir la ventana que se muestra en la Figura\(\PageIndex{7}\) (b). Por lo que estamos a punto de hacer, todos los ajustes en esta ventana son irrelevantes, guardar uno. Asegúrese de utilizar las teclas de flecha para resaltar ASK para la variable Indpnt (independiente) y presione ENTRAR para seleccionar esta opción. Finalmente, seleccione 2nd TABLE, luego ingrese los valores x 10, 100, 1000 y 10000, presionando ENTRAR después de cada uno.
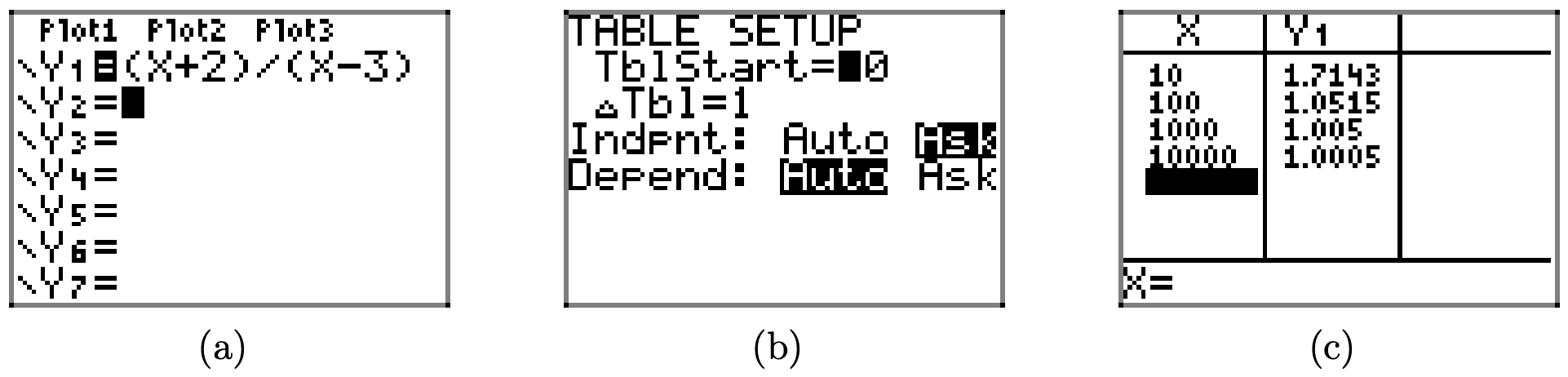
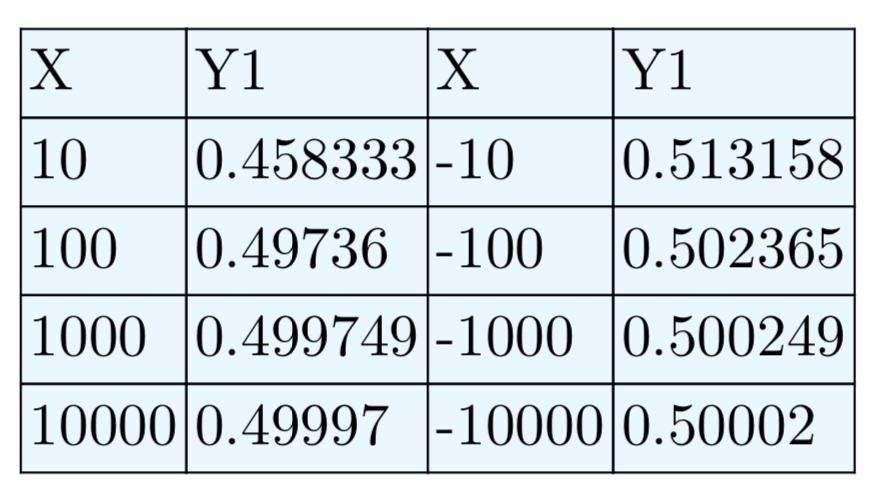
Anote los valores y resultantes en la segunda columna de la tabla (la columna Y1) en la Figura\(\PageIndex{7}\) (c). A medida que x está aumentando sin límite, los valores y son mayores que 1, sin embargo, parecen estar acercándose al número 1. Por lo tanto, a medida que nuestra gráfica se mueve hacia la extrema derecha, debe acercarse a la asíntota horizontal en y = 1, como se muestra en la Figura\(\PageIndex{9}\).
Un esfuerzo similar predice el comportamiento final ya que x disminuye sin límite, como se muestra en la secuencia de imágenes de la Figura\(\PageIndex{8}\). A medida que x disminuye sin límite, los valores y son menores que 1, pero de nuevo se acercan al número 1, como se muestra en la Figura\(\PageIndex{8}\) (c).
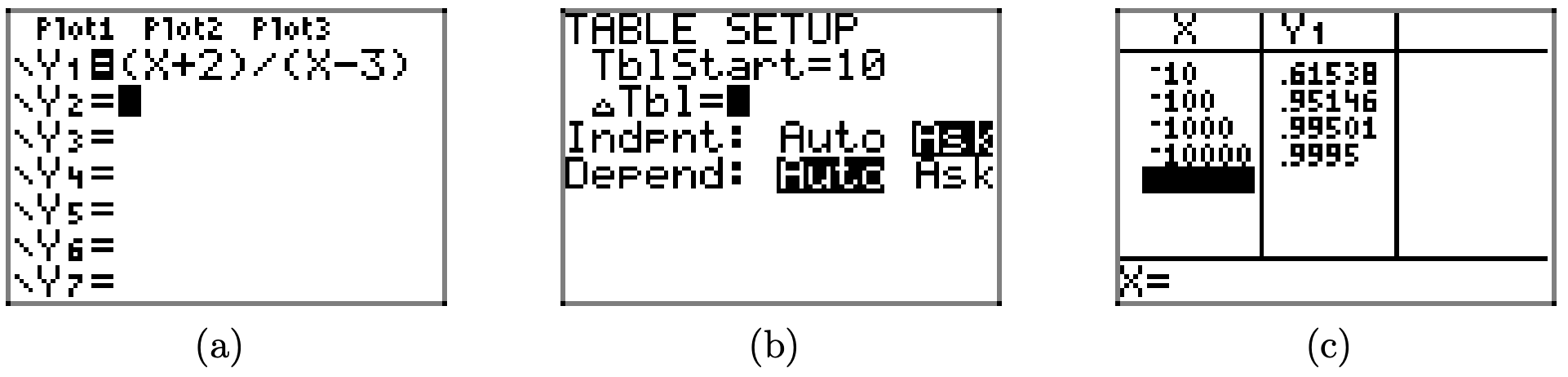
La evidencia en la Figura\(\PageIndex{8}\) (c) indica que a medida que nuestra gráfica se mueve hacia el extremo izquierdo, debe acercarse a la asíntota horizontal en y = 1, como se muestra en la Figura\(\PageIndex{9}\).
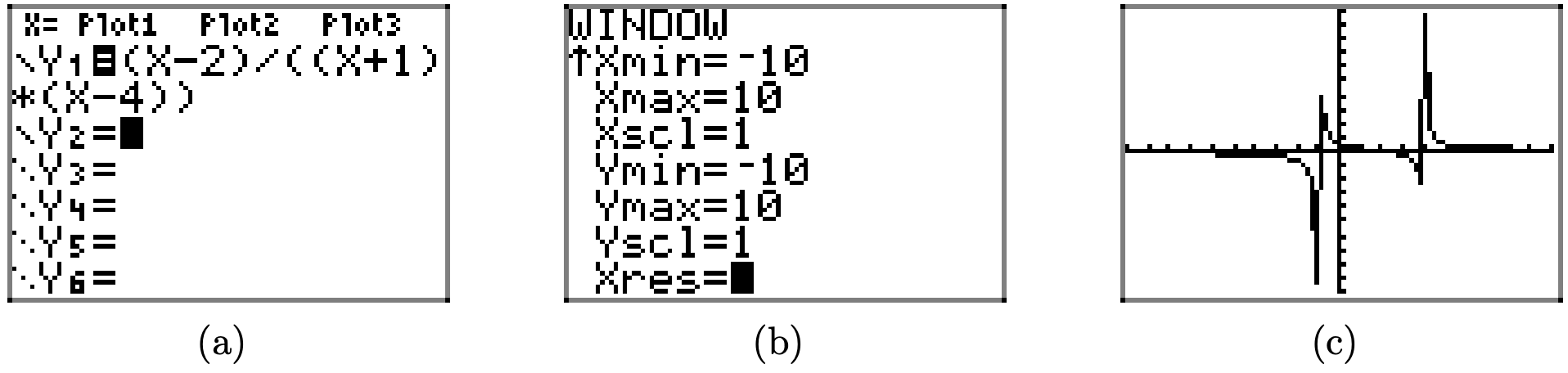
¿Qué tipo de trabajo hará la calculadora gráfica con la gráfica de esta función racional? En la Figura\(\PageIndex{10}\) (a), ingresamos a la función, ajustamos los parámetros de la ventana como se muestra en la Figura\(\PageIndex{10}\) (b), luego presionamos el botón GRAPH para producir el resultado en la Figura\(\PageIndex{10}\) (c).
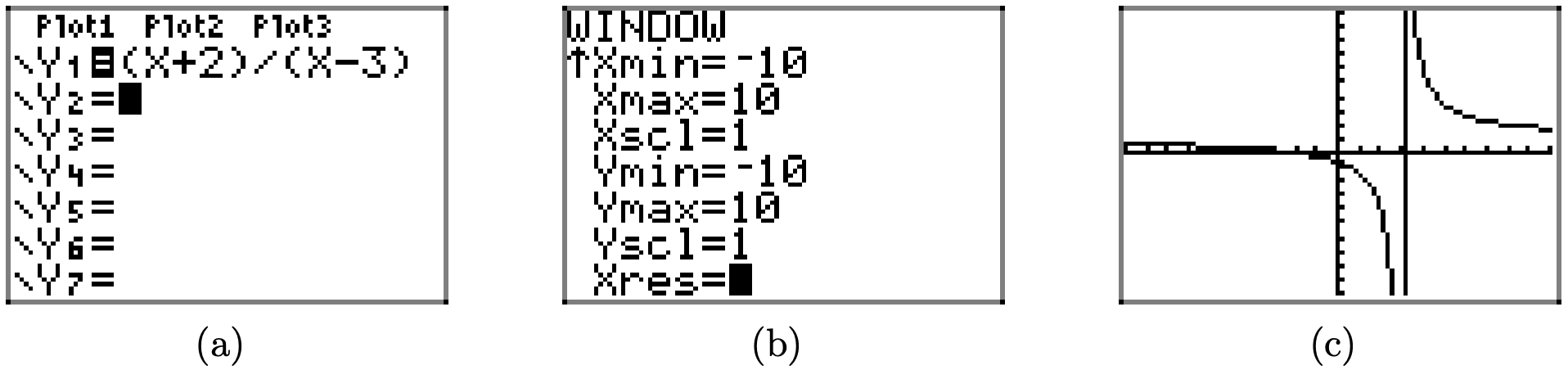
Como se discutió en la primera sección, la calculadora gráfica maneja extremadamente bien las gráficas de funciones “continuas”, pero tiene dificultades para dibujar gráficas con discontinuidades. En el caso de la presente función racional, la gráfica “salta” de negativo
infinito a infinito positivo a través de la asíntota vertical x = 3. La calculadora solo sabe una cosa: trazar un punto, luego conectarlo al punto previamente trazado con un segmento de línea. En consecuencia, hace lo que se le dice, y “conecta” infinidades cuando no debería.
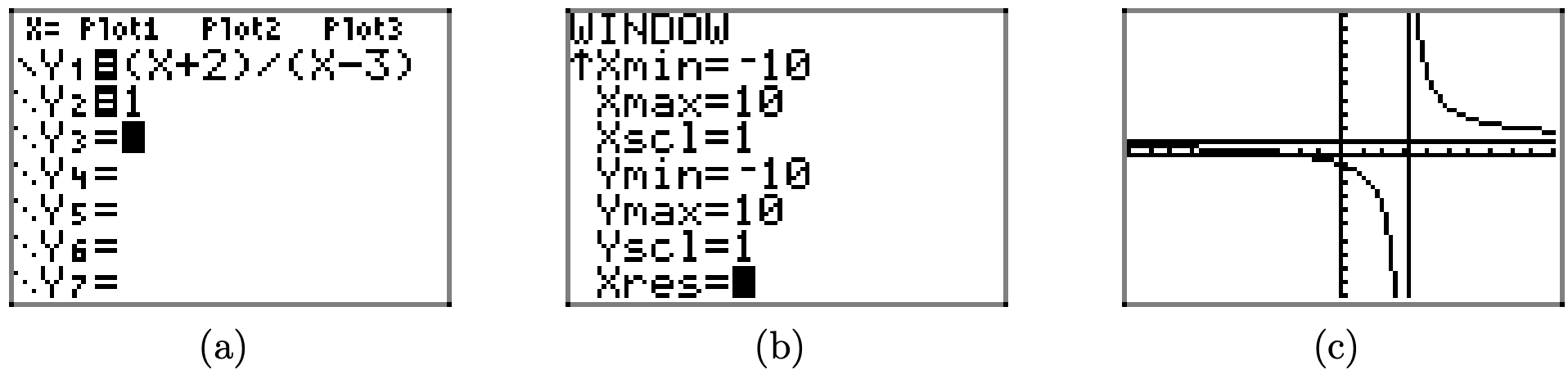
No obstante, si hemos preparado de antemano, identificando ceros y asíntotas verticales, entonces podemos interpretar lo que vemos en la pantalla en la Figura\(\PageIndex{10}\) (c), y utilizar esa información para producir la gráfica correcta que se muestra en la Figura\(\PageIndex{9}\). Incluso podemos agregar la asíntota horizontal a nuestra gráfica, como se muestra en la secuencia de la Figura\(\PageIndex{11}\).
Este es un punto apropiado para hacer una pausa y resumir los pasos requeridos para dibujar la gráfica de una función racional.
Procedimiento para Graficar Funciones Racionales
Considerar la función racional\[f(x)=\frac{a_{0}+a_{1} x+a_{2} x^{2}+\cdots+a_{n} x^{n}}{b_{0}+b_{1} x+b_{2} x^{2}+\cdots+b_{m} x^{m}}\]. Para dibujar la gráfica de esta función racional, proceda de la siguiente manera:
- Factorizar el numerador y denominador de la función racional f.
- Identificar el dominio de la función racional f enumerando cada restricción, valores de la variable independiente (generalmente x) que hacen que el denominador sea igual a cero.
- Identificar los valores de la variable independiente que hacen que el numerador de f sea igual a cero y no sean restricciones. Estos son los ceros de f y proporcionan las coordenadas x de las intercepciones x de la gráfica de la función racional. Trazar estas intercepciones en un sistema de coordenadas y etiquetarlas con sus coordenadas.
- Cancelar factores comunes para reducir la función racional a los términos más bajos. − Las restricciones de f que permanecen restricciones de esta forma reducida colocarán asíntotas verticales en la gráfica de f. Dibuja las asíntotas verticales en su sistema de coordenadas como líneas discontinuas y etiquetarlas con sus ecuaciones. − La restricciones de f que no sean restricciones de la forma reducida colocarán “agujeros” en la gráfica de f. Nos ocuparemos de los agujeros en el paso 8 de este procedimiento.
- Para determinar el comportamiento cerca de cada asíntota vertical, calcular y trazar un punto a cada lado de cada asíntota vertical.
- Para determinar el comportamiento final de la función racional dada, use la capacidad de tabla de su calculadora para determinar el límite de la función a medida que x se acerca al infinito positivo y/o negativo (como hicimos en las secuencias mostradas en Figura\(\PageIndex{7}\) y Figura\(\PageIndex{8}\)). Esto determina la asíntota horizontal. Dibuje la asíntota horizontal como una línea discontinua en su sistema de coordenadas y etiquételo con su ecuación.
- Dibuja la gráfica de la función racional.
- Si determinó que una restricción era un “agujero”, utilice la restricción y la forma reducida de la función racional para determinar el valor y del “agujero”. Dibuja un círculo abierto en esta posición para representar el “agujero” y etiquetar el “agujero” con sus coordenadas.
- Por último, usa tu calculadora para verificar la validez de tu resultado.
Veamos otro ejemplo.
Ejemplo\(\PageIndex{6}\)
Esbozar el gráfico de la función racional\[f(x)=\frac{x-2}{x^{2}-3 x-4}\]
Solución
Seguiremos el esquema presentado en el Procedimiento para Graficar Funciones Racionales.
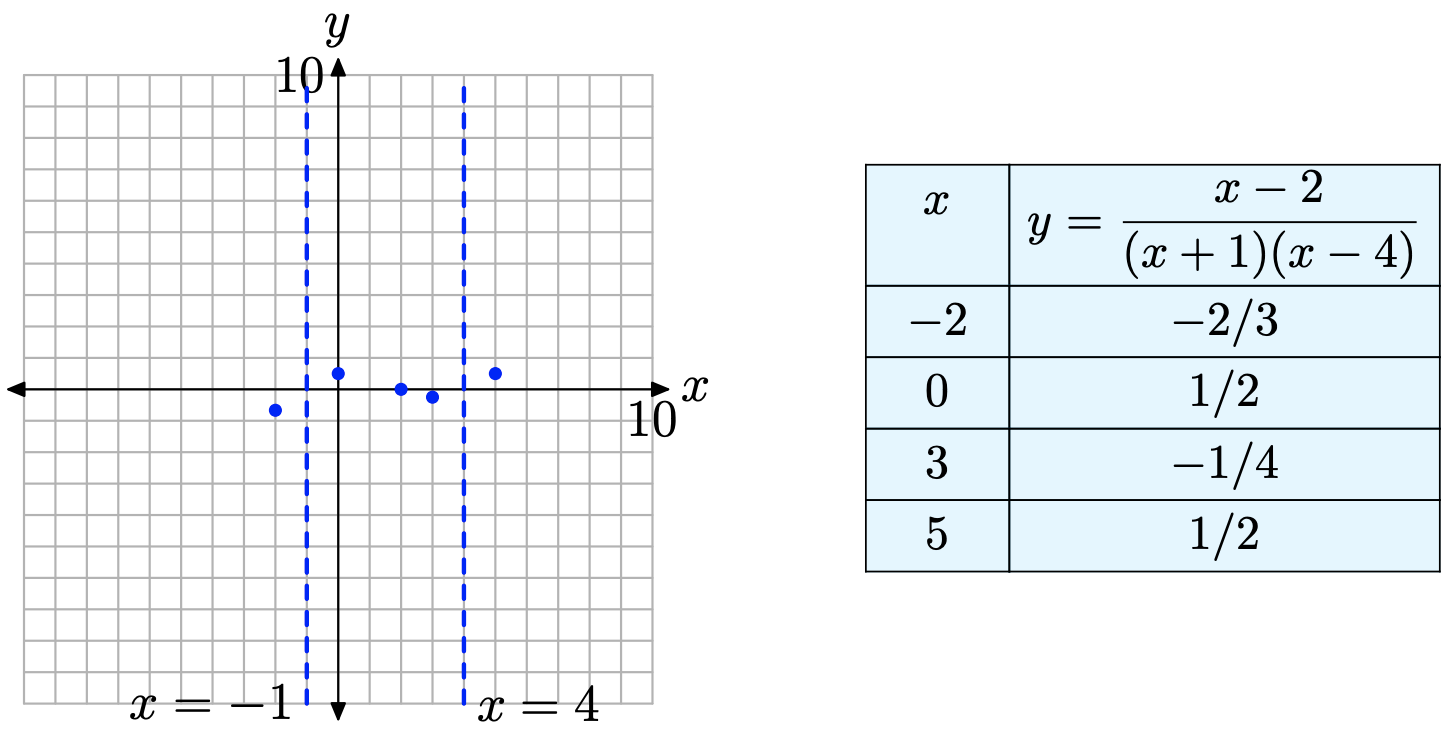
Paso 1: Primero, factorizar tanto el numerador como el denominador.
\[f(x)=\frac{x-2}{(x+1)(x-4)}\]
Paso 2: Así, f tiene dos restricciones, x = −1 y x = 4. Es decir, el dominio de f es\(D_{f}=\{s : x \neq-1,4\}\).
Paso 3: El numerador de la ecuación (12) es cero a x = 2 y este valor no es una restricción. Así, 2 es un cero de f y (2, 0) es una intercepción x de la gráfica de f, como se muestra en la Figura\(\PageIndex{12}\).
Paso 4: Tenga en cuenta que la función racional ya está reducida a los términos más bajos (si no lo fuera, reduciríamos en este punto). Tenga en cuenta que las restricciones x = −1 y x = 4 siguen siendo restricciones de la forma reducida. De ahí que estas sean las ubicaciones y ecuaciones de las asíntotas verticales, que también se muestran en la Figura\(\PageIndex{12}\).
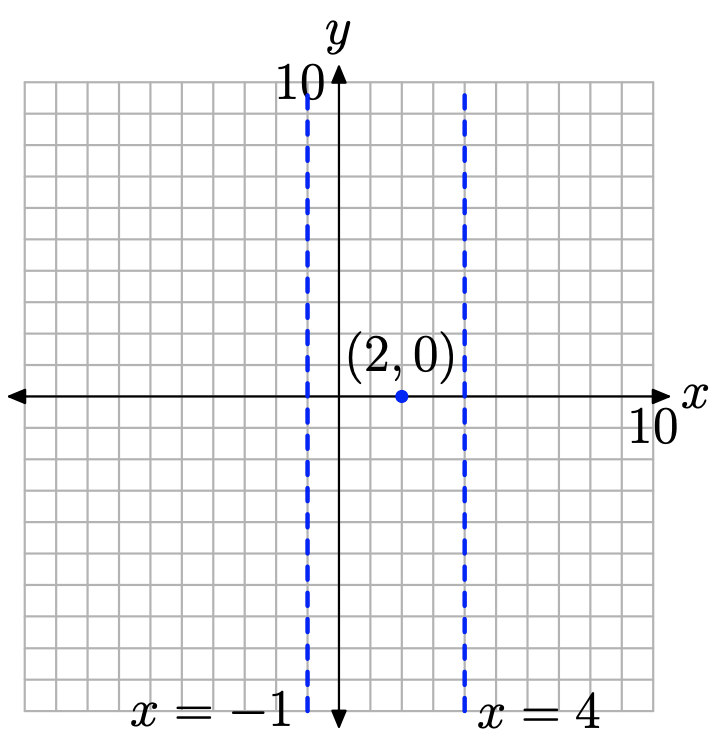
Todas las restricciones de la función original siguen siendo restricciones de la forma reducida. Por lo tanto, no habrá “agujeros” en la gráfica de f.
Paso 5: Trazar puntos a la derecha e izquierda inmediatas de cada asíntota, como se muestra en la Figura\(\PageIndex{13}\). Estos puntos adicionales determinan completamente el comportamiento de la gráfica cerca de cada asíntota vertical. Por ejemplo, considere el punto (5, 1/2) a la derecha inmediata de la asíntota vertical x = 4 en la Figura\(\PageIndex{13}\). Debido a que no hay intercepción x entre x = 4 y x = 5, y la gráfica ya está por encima del eje x en el punto (5, 1/2), la gráfica se ve obligada a aumentar hasta el infinito positivo a medida que se acerca a la asíntota vertical x = 4. Comentarios similares están en orden para el comportamiento en cada lado de cada asíntota vertical.
Paso 6: Utilice la utilidad de tabla en su calculadora para determinar el comportamiento final de la función racional a medida que x disminuye y/o aumenta sin límite. Para determinar el comportamiento final a medida que x va al infinito (aumenta sin límite), ingrese la ecuación en su calculadora, como se muestra en la Figura\(\PageIndex{14}\) (a). Seleccione 2do TBLSET y resalte ASK para la variable independiente. Seleccione 2da TABLA, luego ingrese 10, 100, 1000 y 10000, como se muestra en la Figura\(\PageIndex{14}\) (c).
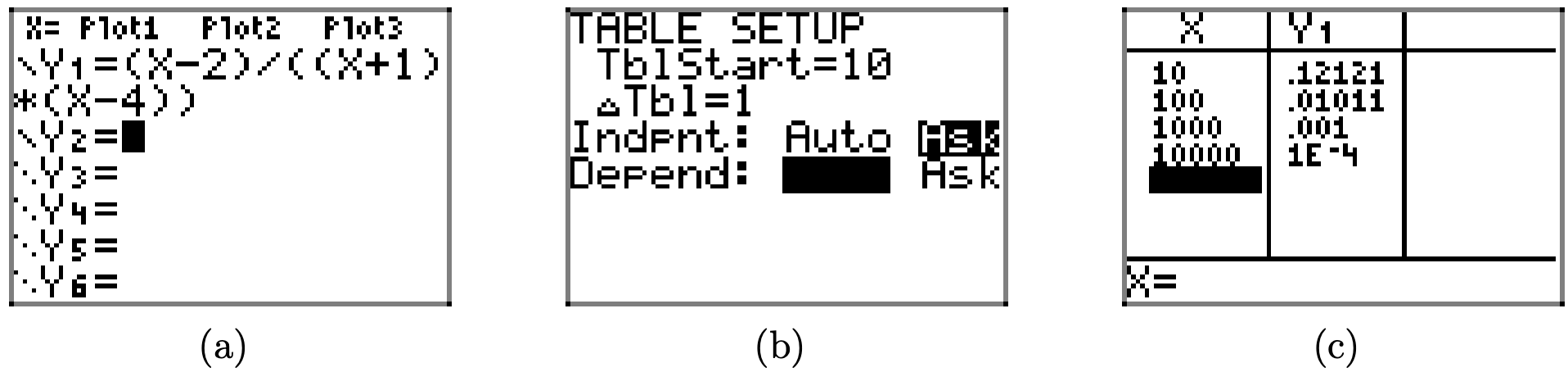
Si examina los valores y en la Figura\(\PageIndex{14}\) (c), verá que se dirigen hacia cero (medias 1e-4\(1 \times 10^{-4}\), lo que equivale a 0.0001). Esto implica que la línea y = 0 (el eje x) está actuando como una asíntota horizontal.
También puede determinar el comportamiento final a medida que x se acerca al infinito negativo (disminuye sin límite), como se muestra en la secuencia de la Figura\(\PageIndex{15}\). El resultado en la Figura\(\PageIndex{15}\) (c) proporciona evidencia clara de que los valores y se acercan a cero a medida que x va al infinito negativo. Nuevamente, esto hace que y = 0 sea una asíntota horizontal.
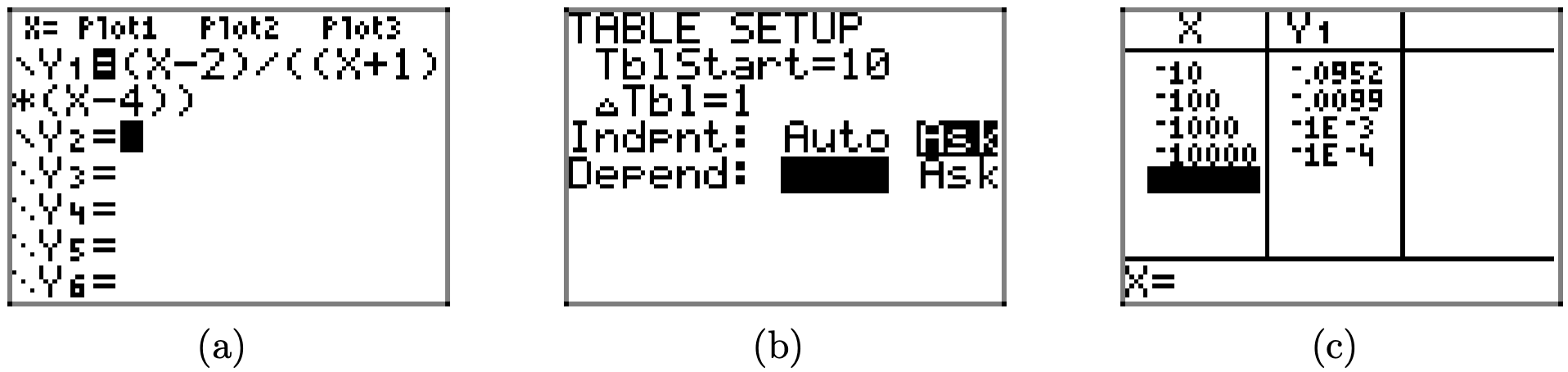
Agrega la asíntota horizontal y = 0 a la imagen de la Figura\(\PageIndex{13}\).
Paso 7: Podemos utilizar toda la información recopilada hasta la fecha para dibujar la imagen que se muestra en la Figura\(\PageIndex{16}\).
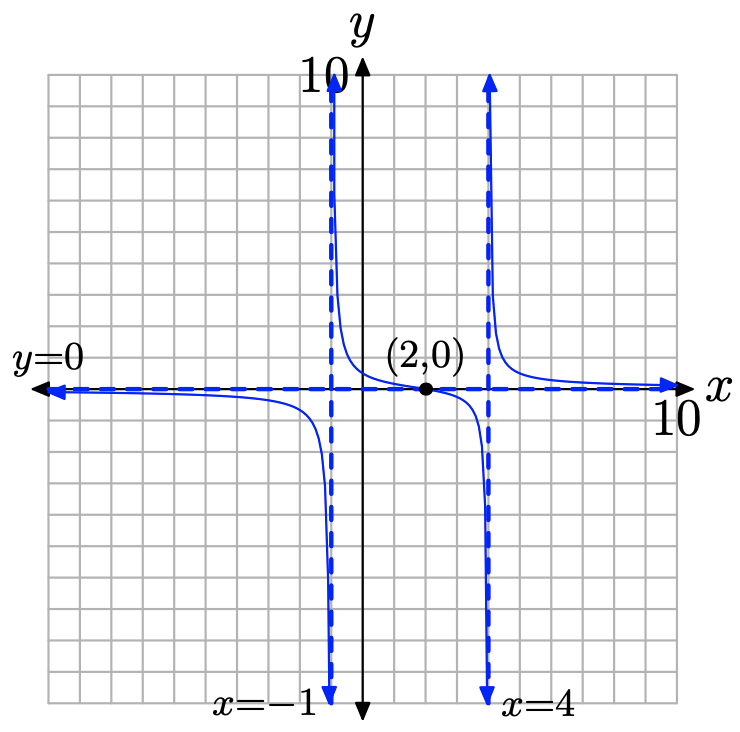
Paso 8: Como se indicó anteriormente, no hay “agujeros” en la gráfica de f.
Paso 9: Usa tu calculadora gráfica para verificar la validez de tu resultado. Observe cómo la calculadora gráfica maneja la gráfica de esta función racional en la secuencia de la Figura\(\PageIndex{17}\). La imagen en la Figura\(\PageIndex{17}\) (c) no está ni cerca de la calidad de la imagen que tenemos en la Figura\(\PageIndex{16}\), pero ahí hay suficiente para intuir la gráfica real si se prepara adecuadamente de antemano (ceros, asíntotas verticales, análisis de comportamiento final, etc.).
Ejercicio
Para funciones racionales Ejercicios 1 - 20, siga el Procedimiento para Graficar Funciones Racionales en la narrativa, realizando cada una de las siguientes tareas.
- Configure un sistema de coordenadas en papel cuadriculado. Etiquetar y escalar cada eje. Recuerda dibujar todas las líneas con una regla.
- Realizar cada uno de los nueve pasos enumerados en el Procedimiento para Graficar Funciones Racionales en la narrativa.
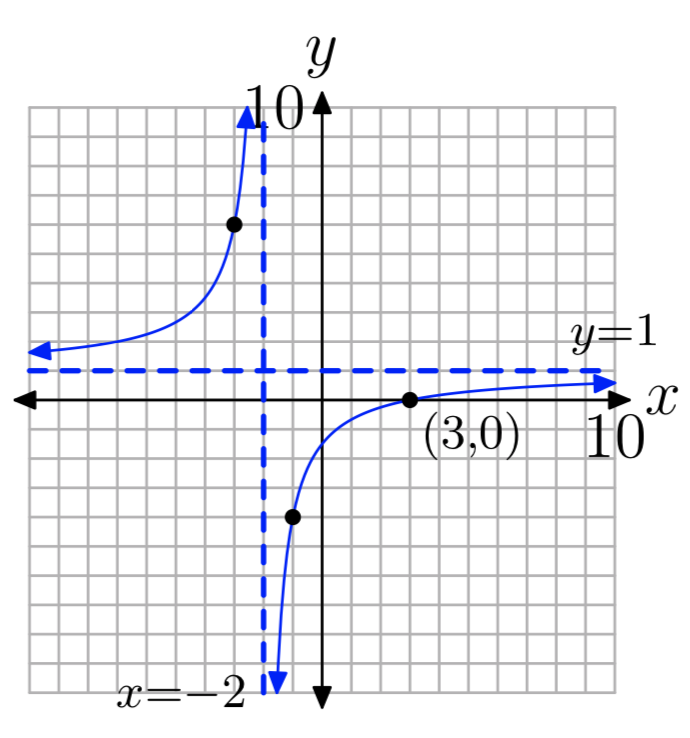
Ejercicio\(\PageIndex{1}\)
\(f(x) = \frac{x−3}{x+2}\)
- Contestar
-
Ejercicio\(\PageIndex{2}\)
\(f(x) = \frac{x+2}{x−4}\)
Ejercicio\(\PageIndex{3}\)
\(f(x) = \frac{5−x}{x+1}\)
- Contestar
-
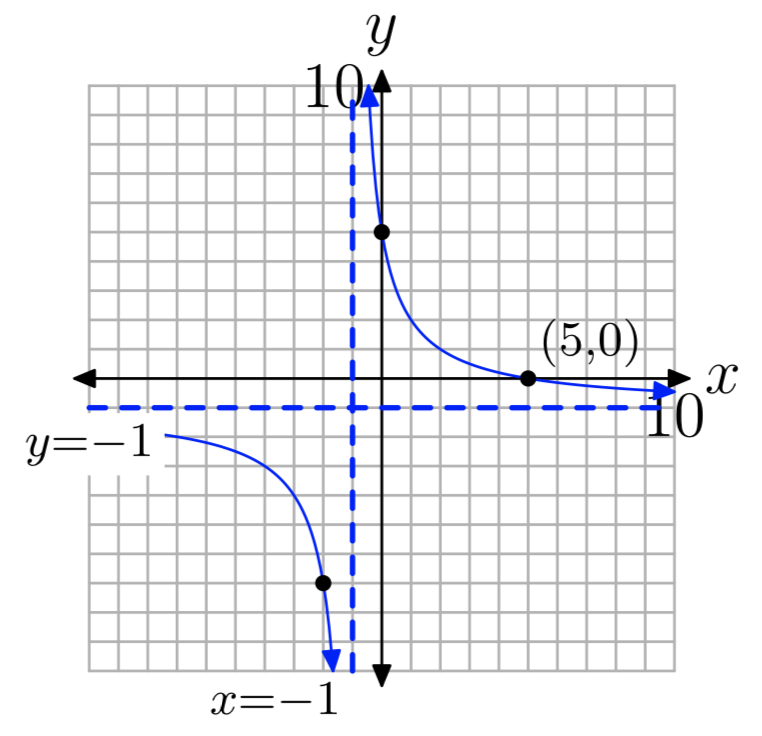
Ejercicio\(\PageIndex{4}\)
\(f(x) = \frac{x+2}{4−x}\)
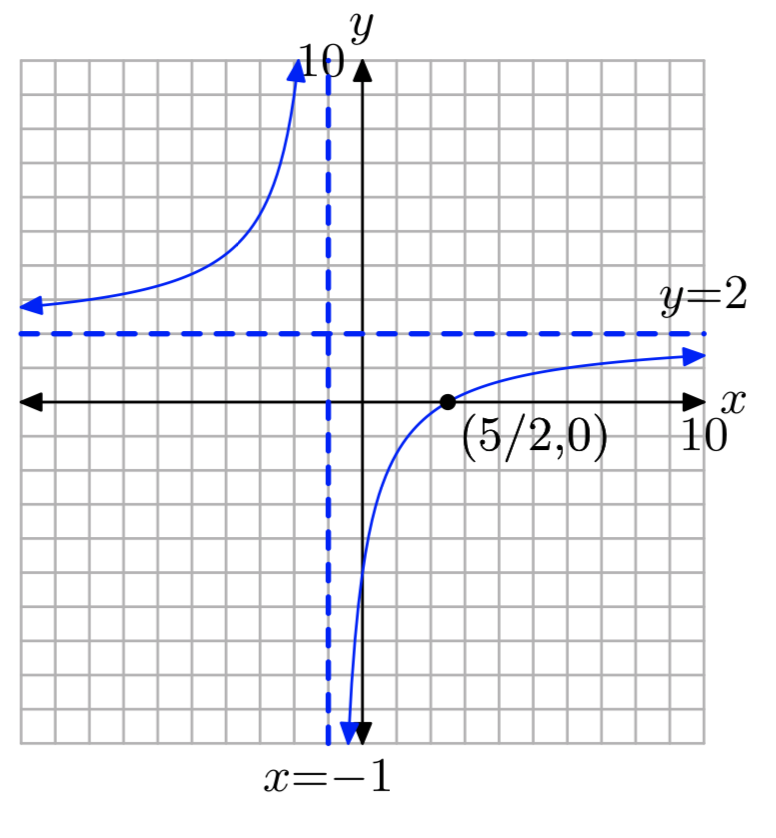
Ejercicio\(\PageIndex{5}\)
\(f(x) = \frac{2x−5}{x+1}\)
- Contestar
-
Ejercicio\(\PageIndex{6}\)
\(f(x) = \frac{2x+5}{3−x}\)
Ejercicio\(\PageIndex{7}\)
\(f(x) = \frac{x+2}{x^2−2x−3}\)
- Contestar
-
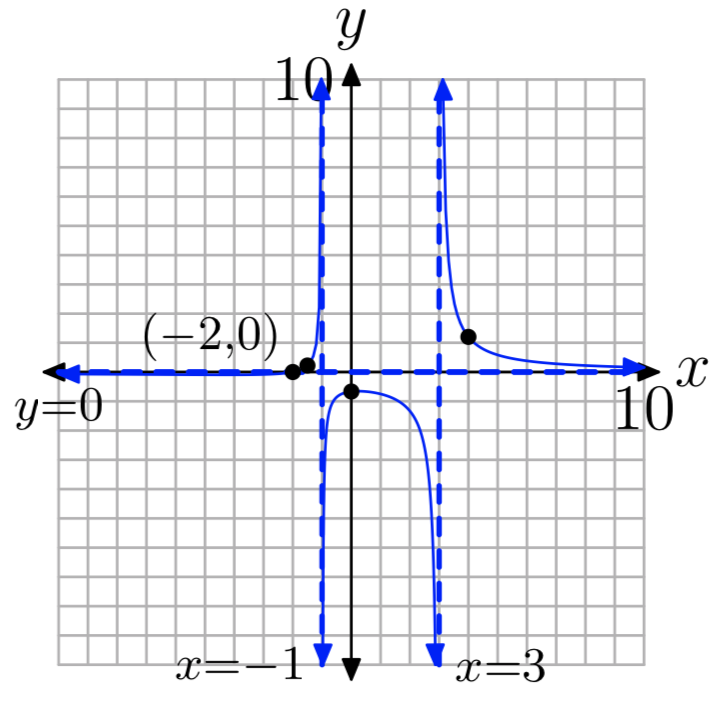
Ejercicio\(\PageIndex{8}\)
\(f(x) = \frac{x−3}{x^2−3x−4}\)
Ejercicio\(\PageIndex{9}\)
\(f(x) = \frac{x+1}{x^2+x−2}\)
- Contestar
-
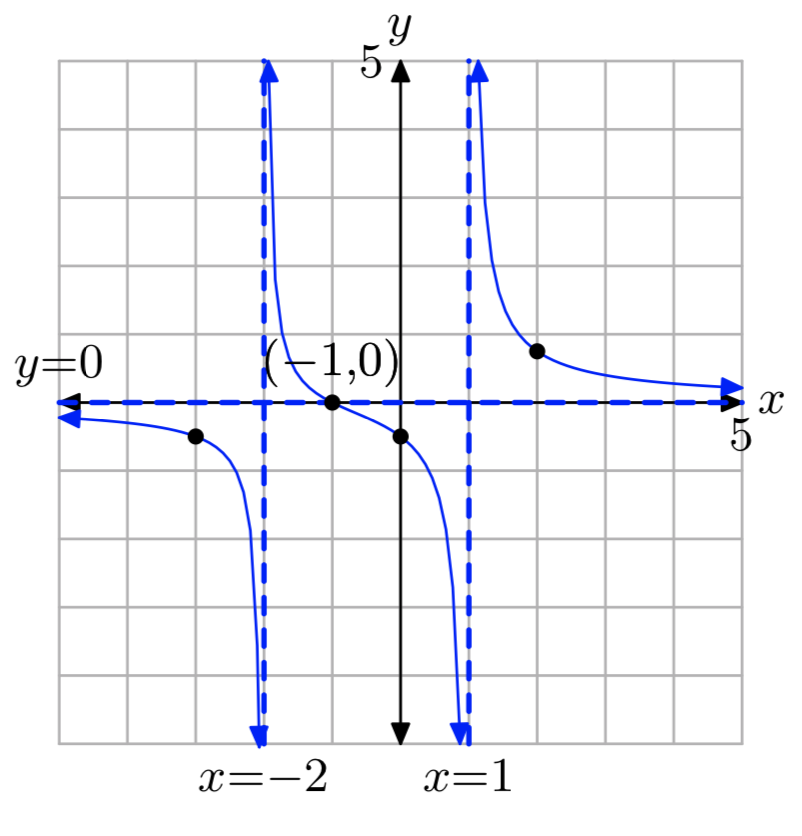
Ejercicio\(\PageIndex{10}\)
\(f(x) = \frac{x−1}{x^2−x−2}\)
Ejercicio\(\PageIndex{11}\)
\(f(x) = \frac{x^2−2x}{x^2+x−2}\)
- Contestar
-
Ejercicio\(\PageIndex{12}\)
\(f(x) = \frac{x^2−2x}{x^2−2x−8}\)
Ejercicio\(\PageIndex{13}\)
\(f(x) = \frac{2x^2−2x−4}{x^2−x−12}\)
- Contestar
-
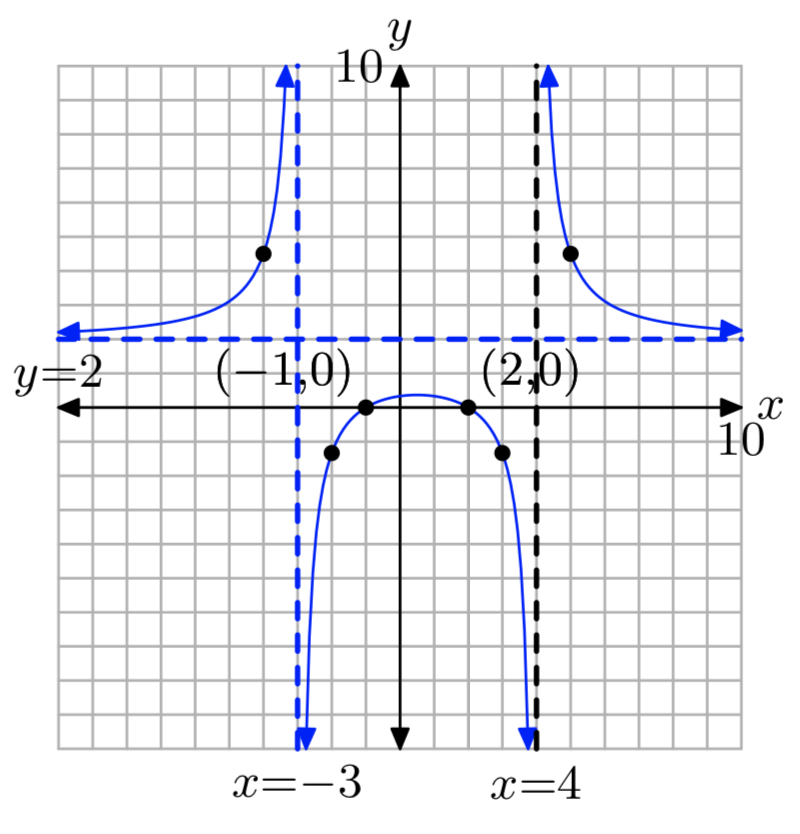
Ejercicio\(\PageIndex{14}\)
\(f(x) = \frac{8x−2x^2}{x^2−x−6}\)
Ejercicio\(\PageIndex{15}\)
\(f(x) = \frac{x−3}{x^2−5x+6}\)
- Contestar
-
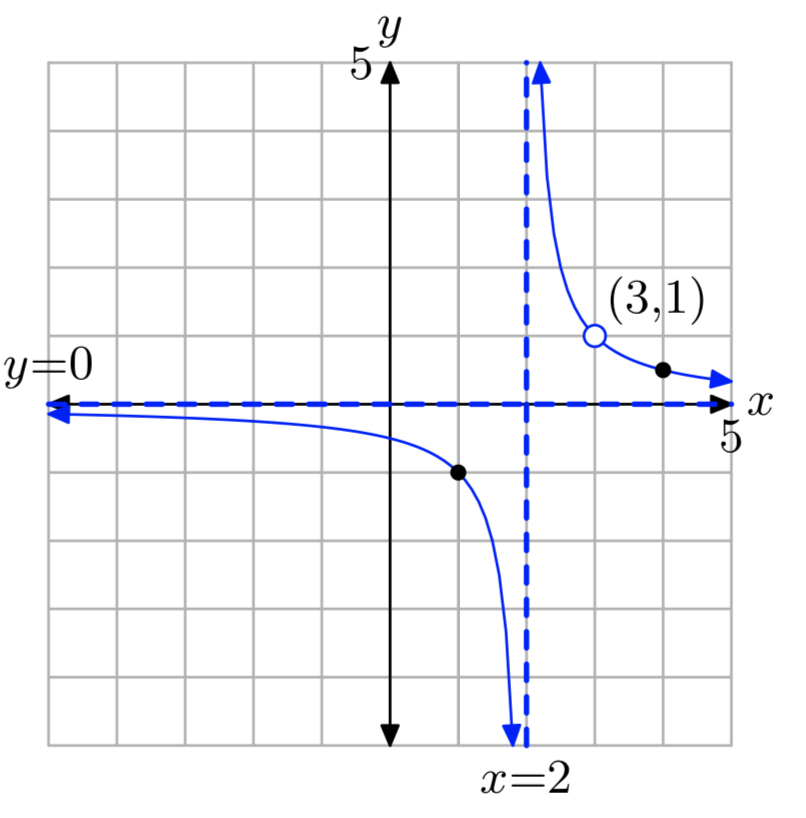
Ejercicio\(\PageIndex{16}\)
\(f(x) = \frac{2x−4}{x^2−x−2}\)
Ejercicio\(\PageIndex{17}\)
\(f(x) = \frac{2x^2−x−6}{x^2−2x}\)
- Contestar
-
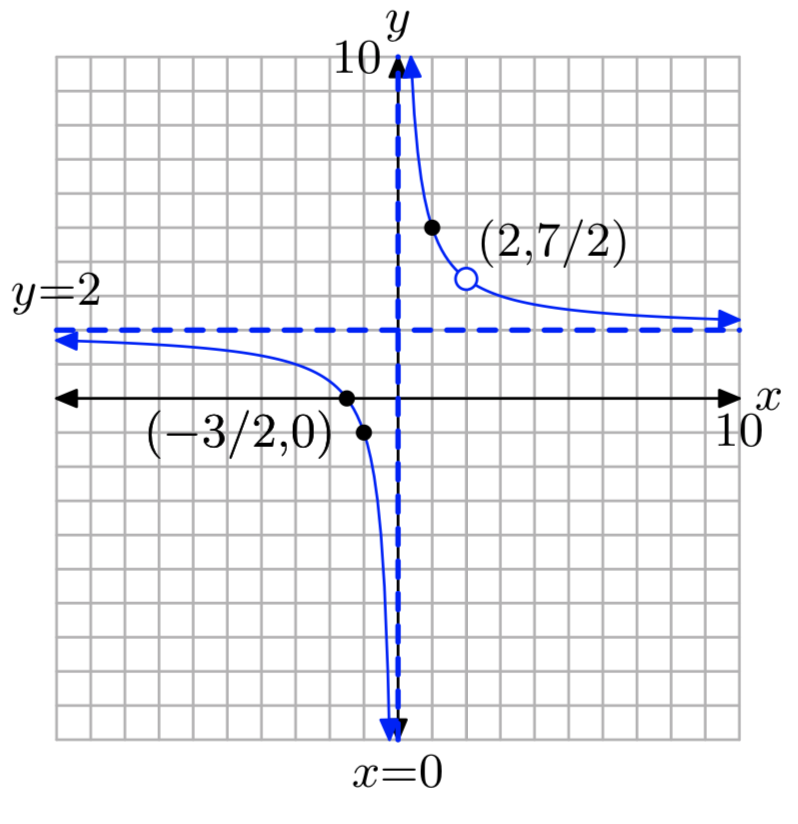
Ejercicio\(\PageIndex{18}\)
\(f(x) = \frac{2x^2−x−6}{x^2−2x}\)
Ejercicio\(\PageIndex{19}\)
\(f(x) = \frac{4+2x−2x^2}{x^2+4x+3}\)
- Contestar
-
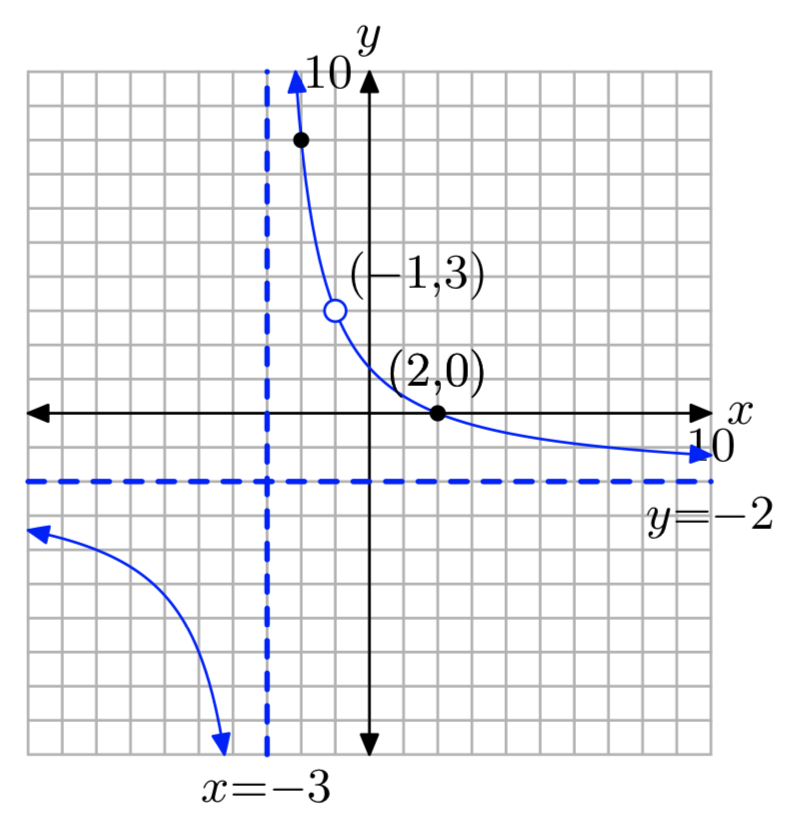
Ejercicio\(\PageIndex{20}\)
\(f(x) = \frac{3x^2−6x−9}{1−x^2}\)
En los Ejercicios 21 - 28, encuentra las coordenadas de la (s) intersección (s) x de la gráfica de la función racional dada.
Ejercicio\(\PageIndex{21}\)
\(f(x) = \frac{81−x^2}{x^2+10x+9}\)
- Contestar
-
(9, 0)
Ejercicio\(\PageIndex{22}\)
\(f(x) = \frac{x−x^2}{x^2+5x−6}\)
Ejercicio\(\PageIndex{23}\)
\(f(x) = \frac{x^2−x−12}{x^2+2x−3}\)
- Contestar
-
(4, 0)
Ejercicio\(\PageIndex{24}\)
\(f(x) = \frac{x^2−81}{x^2−4x−45}\)
Ejercicio\(\PageIndex{25}\)
\(f(x) = \frac{6x−18}{x^2−7x+12}\)
- Contestar
-
sin intercepciones x
Ejercicio\(\PageIndex{26}\)
\(f(x) = \frac{4x+36}{x^2+15x+54}\)
Ejercicio\(\PageIndex{27}\)
\(f(x) = \frac{x^2−9x+14}{x^2−2x}\)
- Contestar
-
(7, 0)
Ejercicio\(\PageIndex{28}\)
\(f(x) = \frac{x^2−5x−36}{x^2−9x+20}\)
En los Ejercicios 29 - 36, encuentra las ecuaciones de todas las asíntotas verticales.
Ejercicio\(\PageIndex{29}\)
\(f(x) = \frac{x^2−7x}{x^2−2x}\)
- Contestar
-
x = 2
Ejercicio\(\PageIndex{30}\)
\(f(x) = \frac{x^2+4x−45}{3x+27}\)
Ejercicio\(\PageIndex{31}\)
\(f(x) = \frac{x^2−6x+8}{x^2−16}\)
- Contestar
-
x = −4
Ejercicio\(\PageIndex{32}\)
\(f(x) = \frac{x^2−11x+18}{2x−x^2}\)
Ejercicio\(\PageIndex{33}\)
\(f(x) = \frac{x^2+x−12}{−4x+12}\)
- Contestar
-
sin asíntotas verticales
Ejercicio\(\PageIndex{34}\)
\(f(x) = \frac{x^2−3x−54}{9x−x^2}\)
Ejercicio\(\PageIndex{35}\)
\(f(x) = \frac{16−x^2}{x^2+7x+12}\)
- Contestar
-
x = −3
Ejercicio\(\PageIndex{36}\)
\(f(x) = \frac{x^2−11x+30}{−8x+48}\)
En los Ejercicios 37 - 42, utilice una calculadora gráfica para determinar el comportamiento de la función racional dada a medida que x se acerca al infinito tanto positivo como negativo realizando las siguientes tareas:
- Carga la función racional en el menú y=de tu calculadora.
- Utilice la función TABLE de su calculadora para determinar el valor de f (x) para x = 10, 100, 1000 y 10000. Registre estos resultados en su tarea en forma de tabla.
- Utilice la función TABLE de su calculadora para determinar el valor de f (x) para x = −10, −100, −1000 y −10000. Registre estos resultados en su casa- trabajo en forma de tabla.
- Usa los resultados de tu exploración tabular para determinar la ecuación de la asíntota horizontal.
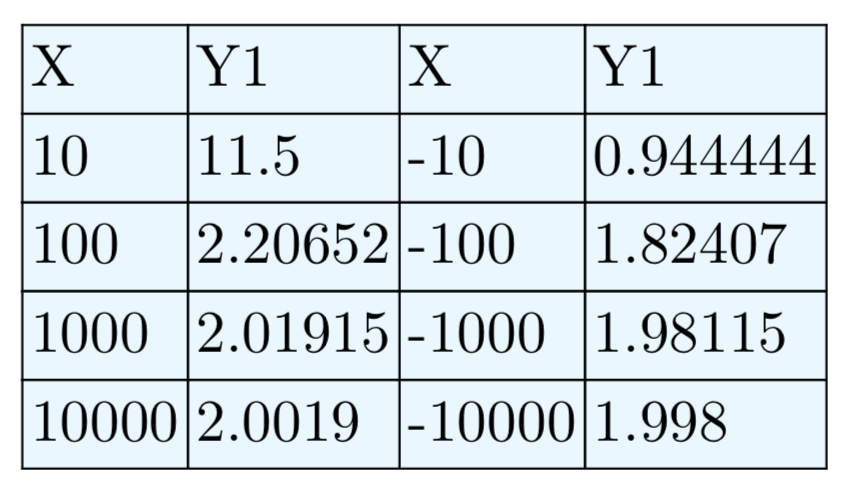
Ejercicio\(\PageIndex{37}\)
\(f(x) = \frac{2x+3}{x−8}\)
- Contestar
-
Asymptota horizontal a y = 2.
Ejercicio\(\PageIndex{38}\)
\(f(x) = \frac{4−3x}{x+2}\)
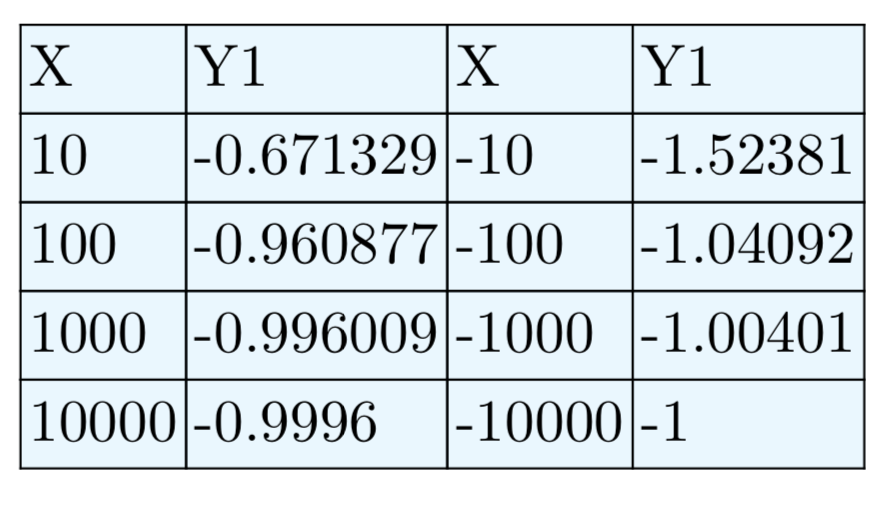
Ejercicio\(\PageIndex{39}\)
\(f(x) = \frac{4−x^2}{x^2+4x+3}\)
- Contestar
-
Asymptota horizontal en y = −1.
Ejercicio\(\PageIndex{40}\)
\(f(x) = \frac{10−2x^2}{x^2−4}\)
Ejercicio\(\PageIndex{41}\)
\(f(x) = \frac{x^2−2x−3}{2x^2−3x−2}\)
- Contestar
-
Asintota horizontal en\(y = \frac{1}{2}\).
Ejercicio\(\PageIndex{42}\)
\(f(x) = \frac{2x^2−3x−5}{x^2−x−6}\)
En los Ejercicios 43 - 48, utilizar un método puramente analítico para determinar el dominio de la función racional dada. Describir el dominio usando la notación set-builder.
Ejercicio\(\PageIndex{43}\)
\(f(x) = \frac{x^2−5x−6}{−9x−9}\)
- Contestar
-
Dominio = {x:\(x \ne −1\)}
Ejercicio\(\PageIndex{44}\)
\(f(x) = \frac{x^2+4x+3}{x^2−5x−6}\)
Ejercicio\(\PageIndex{45}\)
\(f(x) = \frac{x^2+5x−24}{x^2−3x}\)
- Contestar
-
Dominio = {x:\(x \ne 3, 0\)}
Ejercicio\(\PageIndex{46}\)
\(f(x) = \frac{x^2−3x−4}{x^2−5x−6}\)
Ejercicio\(\PageIndex{47}\)
\(f(x) = \frac{x^2−4x+3}{x−x^2}\)
- Contestar
-
Dominio = {x:\(x \ne 0, 1\)}
Ejercicio\(\PageIndex{48}\)
\(f(x) = \frac{x^2−4}{x^2−9x+14}\)