8.3: Aplicaciones de las Funciones Exponenciales

Última actualización
Guardar como PDF

Page ID: 110690

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

En el apartado anterior, se examinó un problema de crecimiento poblacional en el que la población creció en un porcentaje fijo cada año. En ese caso, encontramos que la población puede ser descrita por una función exponencial. Un análisis similar mostrará que cualquier proceso en el que una cantidad crezca en un porcentaje fijo cada año (o cada día, hora, etc.) puede ser modelado por una función exponencial. El interés compuesto es un buen ejemplo de tal proceso.

Interés Compuesto Discreto

Si pones dinero en una cuenta de ahorros, entonces el banco te pagará intereses (un porcentaje del saldo de tu cuenta) al final de cada periodo de tiempo, normalmente un mes o un día. Por ejemplo, si el periodo de tiempo es de un mes, este proceso se denomina composición mensual. El término capitalización se refiere al hecho de que los intereses se agregan a su cuenta cada mes y luego en los meses subsiguientes usted gana intereses sobre los intereses. Si el periodo de tiempo es de un día, se llama composición diaria.

Veamos la composición mensual con más detalle. Supongamos que depositas $100 en tu cuenta, y el banco paga intereses a una tasa anual del 5%. Deja que la función P (t) represente la cantidad de dinero que tienes en tu cuenta en el tiempo t, donde medimos t en años. Comenzaremos el tiempo en t = 0 cuando el monto inicial, llamado el principal, sea de $100. Es decir, P (0) = 100.

En la discusión que sigue, calcularemos el saldo de la cuenta al final de cada mes. Ya que un mes es$\frac{1}{12}$ de un año,$P(\frac{1}{12})$ representa el saldo al final del primer mes,$P(\frac{2}{12})$ representa el saldo al final del segundo mes, etc.

Al final del primer mes, se agregan intereses al saldo de la cuenta. Dado que la tasa de interés anual 5%, la tasa de interés mensual es$\frac{5%}{12}$, o$\frac{.05}{12}$ en forma decimal. Si bien podríamos aproximarnos$\frac{.05}{12}$ por un decimal, será más útil, además de más preciso, dejarla en esta forma. Por lo tanto, al cierre del primer mes, los intereses devengados serán$100(\frac{.05}{12})$, por lo que el monto total será

$P(\frac{1}{12}) = 100+100(\frac{.05}{12}) =100(1+\frac{.05}{12})$. (1)

Ahora al final del segundo mes, tendrás la cantidad con la que empezaste ese mes, es decir$P(\frac{1}{12})$, más otro mes de intereses sobre esa cantidad. Por lo tanto, el monto total será

$P(\frac{2}{12}) = P(\frac{1}{12})+P(\frac{1}{12})(\frac{.05}{12}) = P(\frac{1}{12})(1+\frac{.05}{12})$. (2)

Si reemplazamos$P(\frac{1}{12})$ en la ecuación (2) con el resultado que se encuentra en la ecuación (1), entonces

$P(\frac{2}{12})=100(1+\frac{.05}{12})(1+\frac{.05}{12}) = 100(1+ \frac{.05}{12})^2$. (3)

Vamos a iterar un mes más. Al finalizar el tercer mes, tendrás la cantidad con la que empezaste ese mes, es decir$P(\frac{2}{12})$, más otro mes de intereses sobre esa cantidad. Por lo tanto, el monto total será

$P(\frac{3}{12}) = P(\frac{2}{12}) + P(\frac{2}{12})(\frac{.05}{12}) = P(\frac{2}{12})(1+\frac{.05}{12})$. (4)

Sin embargo, si reemplazamos$P(\frac{2}{12})$ en la ecuación (4) con el resultado que se encuentra en la ecuación (3), entonces

$P(\frac{3}{12}) = 100(1+\frac{.05}{12})^2(1+\frac{.05}{12}) = 100(1+\frac{.05}{12})^3$. (5)

El patrón ahora debería ser claro. La cantidad de dinero que tendrá en la cuenta al final de m meses viene dada por la función

$P(\frac{m}{12}) = 100(1+\frac{.05}{12})^m$.

Podemos reescribir esta fórmula en términos de años t reemplazando$\frac{m}{12}$ por t. Luego m = 12t, por lo que la fórmula se convierte

$P(t) = 100(1+\frac{.05}{12})^{12t}$. (6)

¿Qué sería diferente si hubieras empezado con un director de 200? Al rastrear nuestros pasos anteriores, debería ser fácil ver que la nueva fórmula sería

$P(t) = 200(1+\frac{.05}{12})^{12t}$.

De igual manera, si la tasa de interés hubiera sido del 4% anual en lugar del 5%, entonces habríamos terminado con la fórmula

$P(t) = 100(1+\frac{.04}{12})^{12t}$.

Así, si dejamos$P_{0}$ representar el principal, y r representar la tasa de interés anual (en forma decimal), entonces podemos generalizar la fórmula para

$P(t) = P_{0}(1+\frac{r}{12})^{12t}$. (7)

Ejemplo$\PageIndex{8}$

Si el principal es de $100, la tasa de interés anual es del 5%, y el interés se compone mensualmente, ¿cuánto dinero tendrá después de diez años?

En la fórmula (7), let$P_{0} = 100$, r = .05, y t = 10:

$P(10) = 100(1+\frac{.05}{12})^{12 \cdot 10}$

Podemos utilizar nuestra calculadora gráfica para aproximar esta solución, como se muestra en la Figura 1.

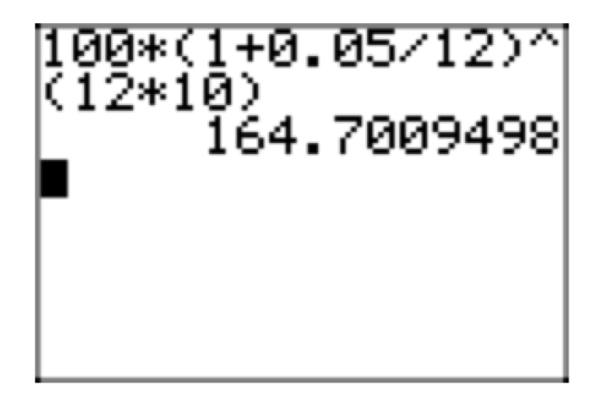
Screen Shot 2019-07-26 a las 4.43.50 PM.png — Figura 1. Computar el monto después de componer mensualmente por 10 años.

Así, tendrías $164.70 después de diez años.

Ejemplo$\PageIndex{9}$

Si el principal es de 10000 dólares, la tasa de interés anual es del 5%, y el interés se compone mensualmente, ¿cuánto dinero tendrá después de cuarenta años?

En la fórmula (7), let$P_{0} = 10000$, r =. 05, y t = 40:

$P(40) = 10000(1+\frac{.05}{12})^{12 \cdot 40} \approx 73584.17$

Así, tendrías $73,584.17 después de cuarenta años.

Estos ejemplos ilustran el “milagro del interés compuesto”. En el último ejemplo, tu cuenta es más de siete veces más grande que la original, y tu “ganancia” total (la cantidad de intereses que has recibido) es de 63584.17 dólares. Compare esto con la cantidad que habría recibido si hubiera retirado los intereses cada mes (es decir, sin capitalización). En ese caso, su “ganancia” solo sería de $20000:

$years \cdot \frac{months}{year} \cdot \frac{interest}{month} = 40 \cdot 12 \cdot [(10000)(\frac{.05}{12})] =20000$

La gran diferencia se puede atribuir a la forma de la gráfica de la función P (t). Recordemos de la sección anterior que esta es una función de crecimiento exponencial, por lo que a medida que t se agranda, la gráfica eventualmente subirá pronunciadamente. Así, si puedes dejar tu dinero en el banco el tiempo suficiente, eventualmente crecerá dramáticamente.

¿Qué pasa con la composición diaria? Analicemos nuevamente la situación en la que el principal es de $100 y la tasa de interés anual es del 5%. En este caso, el periodo de tiempo durante el cual se pagan los intereses es de un día, o$\frac{1}{365}$ de un año, y la tasa de interés diaria es$\frac{5%}{365}$, o$\frac{.05}{365}$ en forma decimal. Ya que estamos midiendo el tiempo en años,$P(\frac{1}{365})$ representa el saldo al final del primer día,$P(\frac{2}{365})$ representa el saldo al final del segundo día, etc. seguiremos los mismos pasos que en el análisis anterior para la capitalización mensual.

Al final del primer día, tendrás

$P(\frac{1}{365}) = 100+100(\frac{.05}{365}) = 100(1+\frac{.05}{365})$. (10)

Al finalizar el segundo día, tendrás la cantidad con la que empezaste ese día, es decir$P(\frac{1}{365})$, más el valor de otro día de interés sobre esa cantidad. Por lo tanto, el monto total será

$P(\frac{2}{365}) = P(\frac{1}{365})+P(\frac{1}{365})(\frac{.05}{365}) = P(\frac{1}{365})(1+\frac{.05}{365})$. (11)

Si reemplazamos$P(\frac{1}{365})$ en la ecuación (11) con el resultado que se encuentra en la ecuación (10), entonces

$P(\frac{2}{365})=100(1+\frac{.05}{365})(1+\frac{.05}{365}) = 100(1+\frac{.05}{365}^2$. (12)

Al finalizar el tercer día, tendrás la cantidad con la que empezaste ese día, es decir$P(\frac{2}{365})$, más el valor de otro día de interés sobre esa cantidad. Por lo tanto, el monto total será

$P(\frac{3}{365}) = P(\frac{2}{365})+P(\frac{2}{365})(\frac{.05}{365}) = P(\frac{2}{365})(1+\frac{.05}{365})$. (13)

Nuevamente, reemplazar$P(\frac{2}{365})$ en la ecuación (13) con el resultado encontrado en la ecuación (12) rinde

$P(\frac{3}{365})=100(1+\frac{.05}{365})^{2}(1+\frac{.05}{365}) = 100(1+\frac{.05}{365})^3$. (14)

Continuar con este patrón muestra que la cantidad de dinero que tendrá en la cuenta al final de d días viene dada por la función

$P(\frac{d}{365}) = 100(1+\frac{.05}{365})^d$.

Podemos reescribir esta fórmula en términos de años t reemplazando$\frac{d}{365}$ por t. Luego d = 365t, por lo que la fórmula se convierte

$P(t) = 100(1+\frac{.05}{365})^{365t}$. (15)

De manera más general, si hubieras comenzado con un principal de$P_{0}$ y una tasa de interés anual de r (en forma decimal), entonces la fórmula sería

$P(t) = P_{0}(1+\frac{r}{365})^{365t}$. (16)

Al comparar las fórmulas (7) y (16) para la composición mensual y diaria, debe ser evidente que la única diferencia es que el número 12 se usa en la fórmula de composición mensual y el número 365 se usa en la fórmula de composición diaria. Al observar el análisis respectivo se desprende que este número surge de la porción del año en que se pagan los intereses ($\frac{1}{12}$en el caso de la capitalización mensual, y$\frac{1}{365}$ en el caso de la capitalización diaria). Así, en cada caso, este número (12 o 365) también es igual al número de veces que el interés se compone por año. De ello se deduce que si el interés se compone trimestralmente (cada tres meses, o 4 veces al año), la fórmula sería

$P(t)=P_{0}(1+\frac{r}{4})^{4t}$.

Del mismo modo, si el interés se compone por hora (8760 veces al año), la fórmula sería

$P(t) = P_{0}(1+\frac{r}{8760})^{8760t}$.

Resumiendo, tenemos una generalización final:

Intereses compuestos discretos

Si$P_{0}$ es el principal, r es la tasa de interés anual, y n es el número de veces que se compone el interés por año, entonces el saldo a tiempo t años es

$P(t) = P_{0}(1+\frac{r}{n})^{nt}$. (17)

Ejemplo$\PageIndex{18}$

Si el principal es de $100, la tasa de interés anual es del 5%, y el interés se compone diariamente, ¿cuál será el saldo después de diez años?

En la fórmula (17), let$P_{0} = 100$, r = .05, n = 365, y t = 10:

$P(10) = 100(1+\frac{.05}{365})^{365 \cdot 10} \approx 164.87$

Así, tendrías $164.87 después de diez años.

Ejemplo$\PageIndex{19}$

Si el principal es de 10000 dólares, la tasa de interés anual es del 5%, y el interés se compone diariamente, ¿cuál será el saldo después de cuarenta años?

En la fórmula (17), vamos$P_{0} = 10000$, r = .05, n = 365, and t = 40:

$P(40) = 10000(1+\frac{.05}{365})^{365 \cdot 40} \approx 73880.44$

Así, tendrías $73880.44 después de cuarenta años.

Como puede ver al comparar los Ejemplos 8 y 18, y los Ejemplos 9 y 19, la diferencia entre la composición mensual y diaria es generalmente pequeña. Sin embargo, la diferencia puede ser sustancial para grandes principios y/o grandes periodos de tiempo.

Ejemplo$\PageIndex{20}$

Si el principal es de $500, la tasa de interés anual es de 8%, y el interés se compone trimestralmente, ¿cuál será el saldo después de 42 meses?

42 meses es 3.5 años, así que vamos$P_{0} = 500$, r =. 08, n = 4, y t = 3. 5 en la fórmula (17):

$P(3.5) = 500(1+\frac{.08}{4})^{4 \cdot 3.5} \approx 659.74$

Por lo tanto, tendrías $659.74 después de 42 meses.

Interés Compuesto Continuo y el Número e

Usando la fórmula (17), es una cuestión sencilla calcular la cantidad total para cualquier tipo de composición. Aunque la mayoría de los bancos componen el interés ya sea diario o mensual, podría hacerse cada hora, o cada minuto, o cada segundo, etc. ¿Qué sucede con el monto total a medida que se acorta el período de tiempo? Equivalentemente, ¿qué sucede a medida que n aumenta en la fórmula (17)? En el Cuadro 1 se muestra la cantidad después de un año con un principal de$P_{0} = 100$, r = .05, y diversos valores de n:

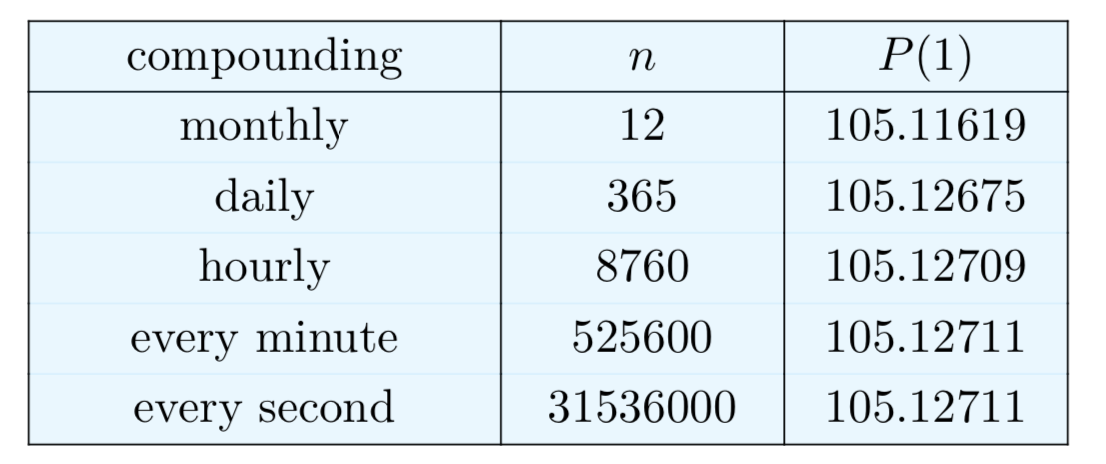
$Screen Shot 2019-07-28 at 11.03.45 PM.png$

Cuadro 1. Comparación de la composición discreta con$P_{0} = 100$, r = .05, y t = 1 año.

Aunque llevemos a cabo nuestros cómputos a ocho dígitos, parece que los montos en la columna derecha del Cuadro 1 se están estabilizando. De hecho, usando el cálculo, se puede demostrar que estas cantidades sí se acercan cada vez más a un número en particular, y podemos calcular ese número.

Comenzando con la fórmula (17), dejaremos que n se acerque$\infty$. En otras palabras, vamos a dejar que n se haga más grande y más grande sin ataduras, como empezamos a hacer en la Tabla 1. El primer paso es usar las Leyes de los Exponentes para escribir

$P_{0}(1+\frac{r}{n})^{nt} = P_{0}[(1+\frac{r}{n})^{\frac{n}{r}}]^{rt}$

En el siguiente paso, sustitúyase$frac{n}{r}$ por m. Ya que$\frac{n}{r} = m$, se deduce que$\frac{r}{n} = \frac{1}{m}$, y tenemos

$P_{0}[(1+\frac{r}{n})^{\frac{n}{r}}]^{rt} = P_{0}[(1+\frac{1}{m})^{m}]^{rt}$

Ahora vamos a acercarse n$\infty$. Dado que$m = \frac{n}{r}$ y r es fijo, se deduce que m también se acerca$\infty$. Podemos utilizar la característica TABLE de la calculadora gráfica para investigar la convergencia de la expresión entre paréntesis a medida que m se acerca al infinito.

Cargue$(1+\frac{1}{m})^m$ en el menú Y= de la calculadora gráfica, como se muestra en la Figura 2 (a). Por supuesto, debes usar x en lugar de m e ingresar (1+1/X) ^X.
Use TBLSET y establezca Indepnt en Preguntar, seleccione TABLE, luego ingrese los números 10, 100,1000, 10000, 100000 y 1000000 para producir el resultado que se muestra en la Figura 2 (b). Tenga en cuenta que (1+1/X) ^X parece converger al número 2.7183. Si mueve el cursor sobre el último resultado en la columna Y1, puede ver más precisión,2.71828046932.

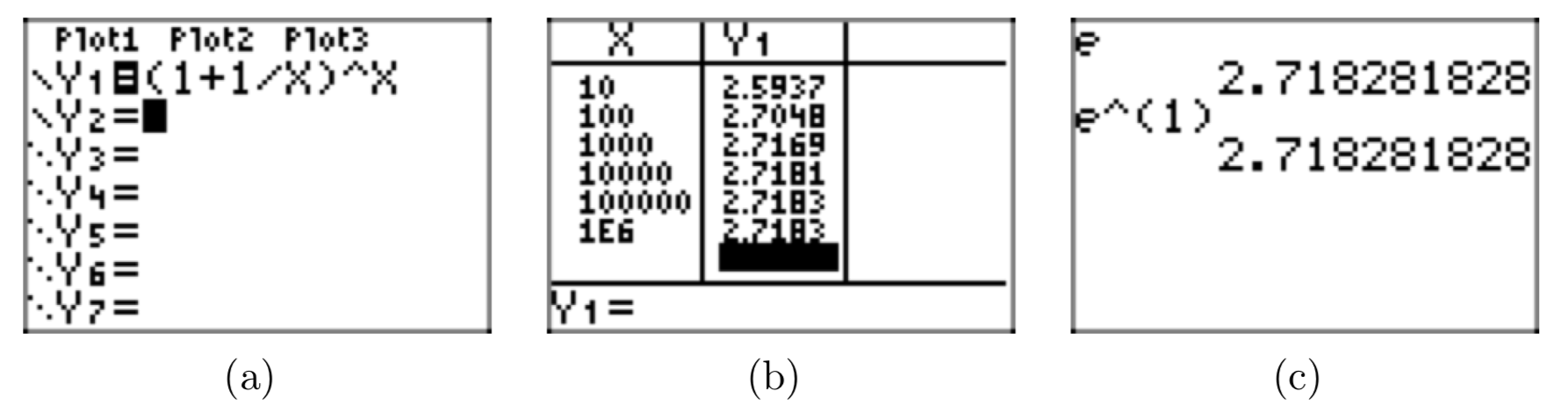
Screen Shot 2019-08-06 at 2.31.04 PM.png — Figura 2. Ilustración de la convergencia de$(1 + \frac{1}{m})^m$ a e a medida que m aumenta al infinito

Obsérvese que los números en la segunda columna de la Figura 2 (b) parecen estabilizarse. En efecto, se puede demostrar usando cálculo que la expresión entre paréntesis arriba se acerca cada vez más a un solo número, que se llama e. Para representar esta convergencia, escribimos

$1+\frac{1}{m})^m \rightarrow e$

e es un número irracional, aproximadamente 2.7183, como lo muestran los cálculos de la Figura 2 (b). De ello se deduce que

$P_{0}[(1+\frac{1}{m})^{m}]^{rt} \rightarrow P_{0}e^{rt}$

INTERÉS CONTINUO

Si$P_{0}$ es el principal, r es la tasa de interés anual, y el interés se compone continuamente, entonces el saldo a tiempo t años es

$P(t) = P_{0}e^{rt}$

Antes de trabajar los siguientes ejemplos, encuentra los botones en tu calculadora para el número e y para la función exponencial$e^x$. Al escribir e o e^ (1) (usando el$e^x$ botón) se obtendrá una aproximación al número e, como se muestra en la Figura 2 (c). Compare esta aproximación con la que obtuvo anteriormente en la Figura 2 (b).

Ejemplo$\PageIndex{23}$

Si el principal es de $100, la tasa de interés anual es del 5%, y el interés se compone continuamente, cuál será el saldo después de diez años?

En la fórmula (22), let$P_{0} = 100$, r = 0.05, y t = 10:

$P (10) = 100e^{(0.05)(10)}$

Usa tu calculadora para aproximar este resultado, como se muestra en la Figura 3.

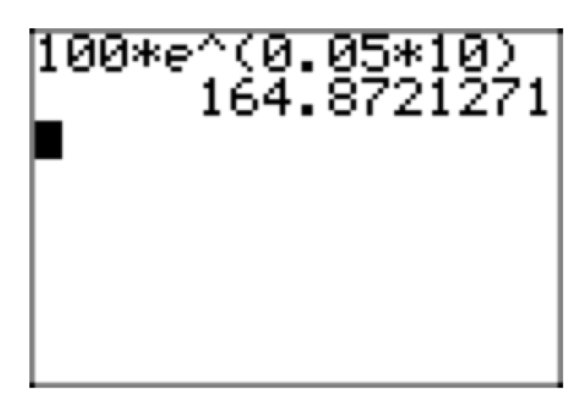
Screen Shot 2019-08-06 at 2.42.49 PM.png — Figura 3. Cálculo de la cantidad después de componer continuamente durante 10 años.

Así, tendrías $164.87 después de diez años.

Ejemplo$\PageIndex{24}$

Si el principal es de 10,000 dólares, la tasa de interés anual es del 5%, y el interés se compone continuamente, ¿cuál será el saldo después de cuarenta años?

En la fórmula (22), let$P_{0} = 10000$, r = 0.05, y t = 40:

$P (10) = 10000e^{(0.05)(40)} \approx 73 890.56$

Así, tendrías 73 890.56 dólares después de cuarenta años.

Observe que la fórmula de composición continua (22) es mucho más simple que la fórmula de composición discreta (17). A menos que el principal sea muy grande o el período de tiempo sea muy largo, los ejemplos anteriores muestran que la composición continua también es una aproximación cercana a la composición diaria. En el Ejemplo 23, la cantidad de $164.87 es la misma (redondeada al centavo más cercano) que la cantidad para la composición diaria que se encuentra en el Ejemplo 18. Con un principal mayor y un período de tiempo más largo, la cantidad de 73 890.56 dólares en el Ejemplo 24 usando composición continua sigue siendo solo alrededor de $10 más que la cantidad de 73 880.44 dólares para la composición diaria que se encuentra en el Ejemplo 19.

OBSERVACIÓN$\PageIndex{25}$

El número e puede parecerte como una mera curiosidad. Si es así, eso sería un gran error. El número e es en realidad uno de los números más importantes en matemáticas (es probablemente el segundo número más famoso, después de π), y surge naturalmente como el límite descrito en (21) anterior. Usando la notación del cálculo, escribimos

$lim_{m \rightarrow \infty} (1 +\frac{1}{m})^m = e \approx 2.71828$. (26)

Si bien en nuestra discusión anterior este límite surgió en un proceso hecho por el hombre, interés compuesto, se manifiesta de manera similar en estudios de muchos fenómenos naturales. Analizaremos algunas de estas aplicaciones más adelante en este capítulo.

2. Asimismo, la función exponencial ex es una de las funciones más importantes utilizadas en matemáticas, estadística y muchos campos de la ciencia. Por diversas razones, la base e resulta ser la base más natural para usar para una función exponencial. En consecuencia, la función$f(x) = e^x$ es conocida como la función exponencial natural.

Valor Futuro y Valor Presente

En esta sección hemos derivado dos fórmulas, una para interés compuesto discreto y otra para interés compuesto continuo. No obstante, en los ejemplos presentados hasta el momento, solo hemos utilizado estas fórmulas para calcular el valor futuro: dado un P0 principal y una tasa de interés r, ¿cuánto tendrá en su cuenta en t años?

Otro tipo de pregunta que podemos resolver se conoce como problema de valor presente: ¿cuánto dinero tendrías que invertir a interés r para tener Q dólares en t años? Aquí hay un par de ejemplos:

Ejemplo$\PageIndex{26}$

¿Cuánto dinero tendrías que invertir al 4% de interés compuesto diariamente para tener $8000 dólares en 6 años?

En este caso,$P_{0}$ se desconoce el principal, y sustituimos r = 0. 04, n = 365, y t = 6, en la fórmula de composición discreta (17). Desde P (6) = 8000, tenemos la ecuación

$8000 = P(6) = P_{0}(1+\frac{0.04}{365})^{(365)(5)}$

Esta ecuación se puede resolver por división:

$\frac{8000}{1+\frac{0.04}{365}} = P_{0}$

La Figura 4 muestra una aproximación de calculadora para este resultado.

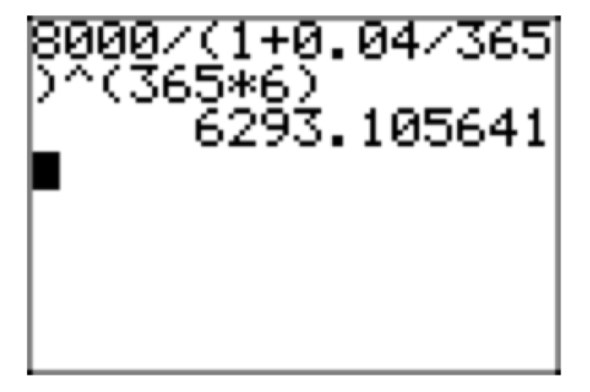
Screen Shot 2019-08-06 at 2.54.34 PM.png — Figura 4. El valor actual de $8000, compuesto diariamente por seis años.

Así, el valor presente es aproximadamente$P_{0} \approx $6293.11$. Si esta cantidad se invierte ahora en 4% compuesto diariamente, entonces su valor futuro en 6 años será de $8000.

Ejemplo$\PageIndex{27}$

¿Cuánto dinero tendrías que invertir al 7% de interés compuesto continuamente para tener 5000 dólares en 4 años?

Al igual que en el último ejemplo,$P_{0}$ se desconoce el principal, y esta vez r = 0.07 y t = 4 en la fórmula de composición continua (22). Entonces P (4) = 5000 produce la ecuación

$5000 = P(4) = P_{0}e^{(0.07)(4)}$.

Como en el último ejemplo, esta ecuación también se puede resolver por división:

$\frac{5000}{e^{(0.07)(4)}} = P_{0}$

En la Figura 5 se muestra una aproximación de calculadora para este resultado.

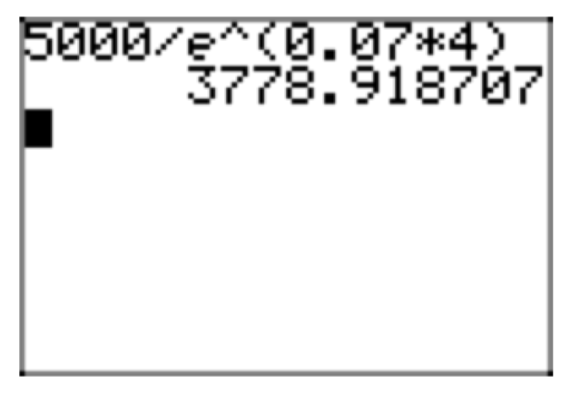
Screen Shot 2019-08-06 at 2.58.30 PM.png — Figura 5. El valor actual de 5000 dólares, se agravó continuamente por cuatro años.

Así, el valor presente es aproximadamente$P_{0} \approx $3778.92$. Si esta cantidad se invierte ahora en 7% compuesto continuamente, entonces su valor futuro en 4 años será de 5000 dólares.

Preguntas adicionales

En cuanto a las aplicaciones prácticas, también hay otro tipo de preguntas que sería interesante considerar. Aquí hay dos ejemplos:

Si depositas $1000 en una cuenta pagando 6% compuesto continuamente, ¿cuánto tiempo tardarás en tener 1500 dólares en tu cuenta?
Si depositas $1000 en una cuenta pagando 5% compuesto mensualmente, ¿cuánto tiempo tardará tu dinero en duplicarse?

Veamos la primera pregunta (la segunda es similar). En este caso,$P_{0} = 1000$ y r = 0.06. Insertando estos valores en la fórmula de composición continua (22), obtenemos

$P(t) = 1000e^{0.06t}$.

Ahora queremos que el valor futuro P (t) de la cuenta en algún momento t sea igual a 1500 dólares.

Por lo tanto, debemos resolver la ecuación

$1500 = 1000e^{0.06t}$.

No obstante, ahora tenemos un problema, porque la variable t se ubica en el exponente de la expresión en el lado derecho de la ecuación. Aunque podríamos aproximar una solución gráficamente, actualmente no tenemos un método algebraico para resolver una ecuación como esta, donde la variable está en el exponente (este tipo de ecuaciones se denominan ecuaciones exponenciales). En el transcurso de las siguientes secciones, definiremos otro tipo de función, la función logaritmo, que a su vez nos proporcionará un método para resolver ecuaciones exponenciales. Después volveremos a estas preguntas, y también discutiremos aplicaciones adicionales.

Ejercicio

Ejercicio$\PageIndex{1}$

Supongamos que inviertes $15,000 al 7% de interés compuesto mensualmente. ¿Cuánto dinero habrá en tu cuenta en 4 años? Redondee su respuesta al centavo más cercano.

Contestar: 19830 dólares. 81

Ejercicio$\PageIndex{2}$

Supongamos que inviertes $14,000 al 3% de interés compuesto mensualmente. ¿Cuánto dinero habrá en tu cuenta en 7 años? Redondee su respuesta al centavo más cercano.

Ejercicio$\PageIndex{3}$

Supongamos que inviertes $14,000 a 4% de interés compuesto diariamente. ¿Cuánto dinero habrá en tu cuenta en 6 años? Redondee su respuesta al centavo más cercano.

Contestar: 17797 dólares. 25

Ejercicio$\PageIndex{4}$

Supongamos que inviertes $15,000 al 8% de interés compuesto mensualmente. ¿Cuánto dinero habrá en tu cuenta en 8 años? Redondee su respuesta al centavo más cercano.

Ejercicio$\PageIndex{5}$

Supongamos que inviertes $4,000 al 3% de interés compuesto mensualmente. ¿Cuánto dinero habrá en tu cuenta en 7 años? Redondee su respuesta al centavo más cercano.

Contestar: 4933 dólares. 42

Ejercicio$\PageIndex{6}$

Supongamos que inviertes $3,000 al 5% de interés compuesto mensualmente. ¿Cuánto dinero habrá en tu cuenta en 4 años? Redondee su respuesta al centavo más cercano.

Ejercicio$\PageIndex{7}$

Supongamos que inviertes $1,000 al 3% de interés compuesto mensualmente. ¿Cuánto dinero habrá en tu cuenta en 4 años? Redondee su respuesta al centavo más cercano.

Contestar: 1127 dólares. 33

EXERICSE$\PageIndex{8}$

Supongamos que invierte $19,000 a 2% de interés compuesto diariamente. ¿Cuánto dinero habrá en tu cuenta en 9 años? Redondee su respuesta al centavo más cercano.

Ejercicio$\PageIndex{9}$

Supongamos que puedes invertir dinero al 4% de interés compuesto mensualmente. ¿Cuánto debes invertir para tener 20,000 dólares en 2 años? Redondee su respuesta al centavo más cercano.

Contestar: $18464. 78

Ejercicio$\PageIndex{10}$

Supongamos que se puede invertir dinero al 6% de interés compuesto diariamente. ¿Cuánto debes invertir para tener $1,000 en 2 años? Redondee su respuesta al centavo más cercano.

Ejercicio$\PageIndex{11}$

Supongamos que se puede invertir dinero al 3% de interés compuesto diariamente. ¿Cuánto debes invertir para tener 20,000 dólares en 3 años? Redondee su respuesta al centavo más cercano.

Contestar: $18278. 69

Ejercicio$\PageIndex{12}$

Supongamos que puedes invertir dinero al 3% de interés compuesto mensualmente. ¿Cuánto debes invertir para tener 10,000 dólares en 7 años? Redondee su respuesta al centavo más cercano.

Ejercicio$\PageIndex{13}$

Supongamos que se puede invertir dinero al 9% de interés compuesto diariamente. ¿Cuánto debes invertir para tener $4,000 en 9 años? Redondee su respuesta al centavo más cercano.

Contestar: 1779$. 61

Ejercicio$\PageIndex{14}$

Supongamos que se puede invertir dinero al 8% de interés compuesto diariamente. ¿Cuánto debes invertir para tener $18,000 en 6 años? Redondee su respuesta al centavo más cercano.

Ejercicio$\PageIndex{15}$

Supongamos que se puede invertir dinero al 8% de interés compuesto diariamente. ¿Cuánto debes invertir para tener $17,000 en 6 años? Redondee su respuesta al centavo más cercano.

Contestar: 10519 dólares. 87

Ejercicio$\PageIndex{16}$

Supongamos que se puede invertir dinero al 9% de interés compuesto diariamente. ¿Cuánto debes invertir para tener $5,000 en 7 años? Redondee su respuesta al centavo más cercano.

En Ejercicios 17 - 24, evaluar la función al valor dado p. Redondee su respuesta a la centésima más cercana.

Ejercicio$\PageIndex{17}$

$f(x) = e^x$; p = 1.57.

Contestar: 4. 81

Ejercicio$\PageIndex{18}$

$f(x) = e^x$; p = 2.61.

Ejercicio$\PageIndex{19}$

$f(x) = e^x$; p = 3.07.

Contestar: 21. 54

Ejercicio$\PageIndex{20}$

$f(x) = e^x$; p = −4.33.

Ejercicio$\PageIndex{21}$

$f(x) = e^x$; p = 1.42.

Contestar: 4. 14

Ejercicio$\PageIndex{22}$

$f(x) = e^x$; p = −0.8.

Ejercicio$\PageIndex{23}$

$f(x) = e^x$; p = 4.75

Contestar: 115. 58

Ejercicio$\PageIndex{24}$

$f(x) = e^x$; p = 3.60.

Ejercicio$\PageIndex{25}$

Supongamos que invierte $3,000 a 4% de interés compuesto continuamente. ¿Cuánto dinero habrá en tu cuenta en 9 años? Redondee su respuesta al centavo más cercano.

Contestar: $4299. 99

Ejercicio$\PageIndex{26}$

Supongamos que inviertes $8,000 a 8% de interés compuesto continuamente. ¿Cuánto dinero habrá en tu cuenta en 7 años? Redondee su respuesta al centavo más cercano.

Ejercicio$\PageIndex{27}$

Supongamos que invierte $1,000 al 2% de interés compuesto continuamente. ¿Cuánto dinero habrá en tu cuenta en 3 años? Redondee su respuesta al centavo más cercano.

Contestar: $1061. 84

Ejercicio$\PageIndex{28}$

Supongamos que invierte $3,000 a 8% de interés compuesto continuamente. ¿Cuánto dinero habrá en tu cuenta en 4 años? Redondee su respuesta al centavo más cercano.

Ejercicio$\PageIndex{29}$

Supongamos que invierte $15,000 a 2% de interés compuesto continuamente. ¿Cuánto dinero habrá en tu cuenta en 4 años? Redondee su respuesta al centavo más cercano.

Contestar: 16249$. 31

Ejercicio$\PageIndex{30}$

Supongamos que inviertes $8,000 a 2% de interés compuesto continuamente. ¿Cuánto dinero habrá en tu cuenta en 6 años? Redondee su respuesta al centavo más cercano.

Ejercicio$\PageIndex{31}$

Supongamos que invierte $13,000 al 9% de interés compuesto continuamente. ¿Cuánto dinero habrá en tu cuenta en 8 años? Redondee su respuesta al centavo más cercano.

Contestar: 26707 dólares. 63

Ejercicio$\PageIndex{32}$

Supongamos que invierte $16,000 a 4% de interés compuesto continuamente. ¿Cuánto dinero habrá en tu cuenta en 6 años? Redondee su respuesta al centavo más cercano.

Ejercicio$\PageIndex{33}$

Supongamos que se puede invertir dinero al 6% de interés compuesto continuamente. ¿Cuánto debes invertir para tener $17,000 en 9 años? Redondee su respuesta al centavo más cercano.

Contestar: $9906. 72

Ejercicio$\PageIndex{34}$

Supongamos que se puede invertir dinero al 8% de interés compuesto continuamente. ¿Cuánto debes invertir para tener $5,000 en 6 años? Redondee su respuesta al centavo más cercano.

Ejercicio$\PageIndex{35}$

Supongamos que se puede invertir dinero al 8% de interés compuesto continuamente. ¿Cuánto debes invertir para tener 10,000 dólares en 6 años? Redondee su respuesta al centavo más cercano.

Contestar: $6187. 83

Ejercicio$\PageIndex{36}$

Supongamos que se puede invertir dinero al 6% de interés compuesto continuamente. ¿Cuánto debes invertir para tener $17,000 en 13 años? Redondee su respuesta al centavo más cercano.

Ejercicio$\PageIndex{37}$

Supongamos que se puede invertir dinero al 2% de interés compuesto continuamente. ¿Cuánto debes invertir para tener $13,000 en 8 años? Redondee su respuesta al centavo más cercano.

Contestar: 11077 dólares. 87

Ejercicio$\PageIndex{38}$

Supongamos que se puede invertir dinero al 9% de interés compuesto continuamente. ¿Cuánto debes invertir para tener 10,000 dólares en 15 años? Redondee su respuesta al centavo más cercano.

Ejercicio$\PageIndex{39}$

Supongamos que se puede invertir dinero al 7% de interés compuesto continuamente. ¿Cuánto debes invertir para tener $18,000 en 10 años? Redondee su respuesta al centavo más cercano.

Contestar: 8938 dólares. 54

Ejercicio$\PageIndex{40}$

Supongamos que se puede invertir dinero al 9% de interés compuesto continuamente. ¿Cuánto debes invertir para tener $14,000 en 12 años? Redondee su respuesta al centavo más cercano.