8.2: Funciones exponenciales
- Page ID
- 110707
Supongamos que la población actual de la ciudad de Pleasantville es de 10000 y que la población está creciendo a una tasa de 2% anual. Para analizar el crecimiento poblacional a lo largo de un periodo de años, intentaremos desarrollar una fórmula para la población en función del tiempo, para luego graficar el resultado.
Primero, señalar que al cierre de un año, el incremento poblacional es de 2% de 10000, o 200 personas. Ahora tendríamos 10 mil 200 personas en Pleasantville. Al cierre del segundo año, tomar otro 2% de 10200, lo que supone un incremento de 204 personas, para un total de 10404. Debido a que el incremento cada año no es constante, la gráfica de población versus tiempo no puede ser una línea. De ahí que nuestra eventual función poblacional no sea lineal.
Para desarrollar nuestra fórmula poblacional, comenzamos dejando que la función P (t) represente la población de Pleasantville en el tiempo t, donde medimos t en años. Comenzaremos el tiempo en t = 0 cuando la población inicial de Pleasantville sea 10000. Es decir, P (0) = 10000. La clave para entender este ejemplo es que la población aumenta 2% cada año. Estamos haciendo una suposición aquí de que este crecimiento general da cuenta de nacimientos, muertes y personas que entran y salen de Pleasantville. Es decir, al cierre del primer año, la población de Pleasantville será del 102% de la población inicial. Por lo tanto,
\[P(1) = 1.02P(0) = 1.02(10000). \label{1}\]
Podríamos multiplicar el lado derecho de esta ecuación, pero en realidad será más útil dejarla en su forma actual.
Ahora cada año la población aumenta 2%. Por lo tanto, al cierre del segundo año, la población será del 102% de la población al cierre del primer año. En otras palabras,
\[P(2) = 1.02P(1). \label{2}\]
Si reemplazamos\(P(1)\) en la Ecuación\ ref {2} con el resultado que se encuentra en la Ecuación\ ref {1}, entonces
\[P(2) = (1.02)(1.02)(10000) = (1.02)^{2}(10000). \label{3}\]
Vamos a iterar un año más. Al cierre del tercer año, la población será del 102% de la población al cierre del segundo año, por lo que
\[P(3) = 1.02P(2). \label{4}\]
Sin embargo, si reemplazamos\(P(2)\) en la Ecuación\ ref {4} con el resultado encontrado en la Ecuación\ ref {3}, obtenemos
\[P(3) = (1.02)(1.02)^{2}(10000) = (1.02)^{3}(10000). \label{5}\]
El patrón ahora debería ser claro. La población al final de los\(t\) años viene dada por la función.
\[P(t) = (1.02)^{t}(10000)\]
Es tradicional en matemáticas y ciencias colocar a la población inicial al frente en esta fórmula, escribiendo en su lugar
\[P(t) = 10000(1.02)^{t}. \label{6}\]
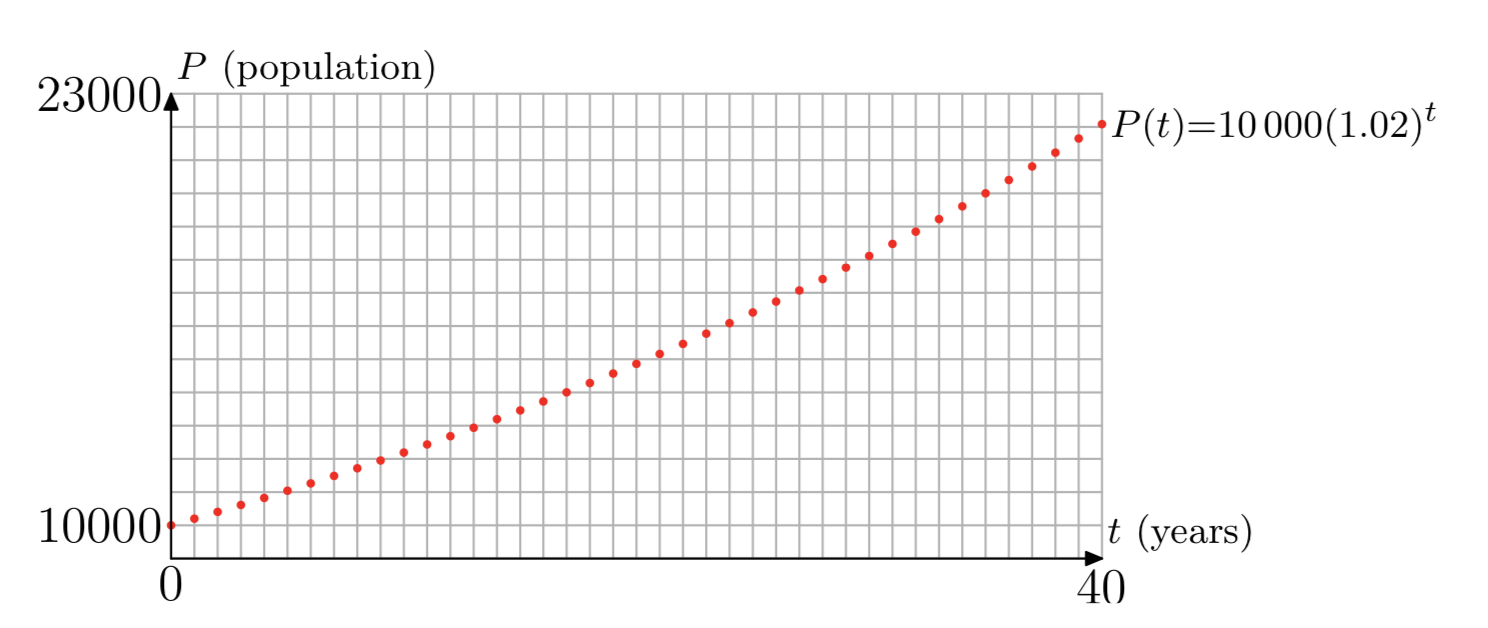
Nuestra función\(P(t)\) se define por la Ecuación\ ref {6} para todos los enteros positivos {1, 2, 3,.}, y\(P(0) = 10000\), la población inicial. La Figura 1 muestra una gráfica de nuestra función. Aunque los puntos se trazan solo a valores enteros de t de 0 a 40, eso es suficiente para mostrar la tendencia de la población a lo largo del tiempo. La población comienza en 10000, aumenta con el tiempo, y el incremento anual (la diferencia de población de un año a otro) también aumenta a medida que pasa el tiempo.
Ejercicio\(\PageIndex{7}\)
Ahora podemos usar la función P (t) para predecir la población en años posteriores. Suponiendo que la tasa de crecimiento del 2% continúe, ¿cuál será la población de Pleasantville después de 40 años? ¿Qué será después de 100 años?
Solución
\(t = 40\) and \(t = 100\) intoEcuación sustituta\ ref {6}. El pop ulation en 40 años será
\[P(40) = 10000(1.02)^{40} \approx 22080 \nonumber\]
y la población en 100 años será
\[P(100) = 10000(1.02)^{100} \approx 72446. \nonumber\]
¿Qué sería diferente si hubiéramos comenzado con una población de 12000? Al rastrear nuestros pasos anteriores, debería ser fácil ver que la nueva fórmula sería
\[P(t) = 12000(1.02)^{t}. \nonumber\]
De igual manera, si la tasa de crecimiento hubiera sido de 3% anual en lugar de 2%, entonces habríamos terminado con la fórmula
\[P(t) = 10000(1.03)^t. \nonumber\]
Así, dejando\(P_{0}\) representar la población inicial, y\(r\) representar la tasa de crecimiento (en forma decimal), podemos generalizar la fórmula para
\[P(t) = P_{0}(1+r)^{t}. \label{8)}\]
Tenga en cuenta que nuestra fórmula para la función\(P(t)\) es diferente de las funciones anteriores que hemos estudiado hasta ahora, en que la variable de entrada\(t\) es parte del exponente en la fórmula. Así, este es un nuevo tipo de función.
Ahora contrastemos la situación en Pleasantville con la dinámica poblacional de Ghosttown. Ghosttown también inicia con una población de 10000 habitantes, pero varias fábricas han cerrado, por lo que algunas personas se van por mejores oportunidades. En este caso, la población de Ghosttown está disminuyendo a una tasa de 2% anual. Nuevamente desarrollaremos una fórmula para la población en función del tiempo, y luego graficaremos el resultado.
En primer lugar, señalar que al cierre de un año, la disminución poblacional es de 2% de 10000, o 200 personas. Ahora nos quedarían 9800 personas en Ghosttown. Al cierre del segundo año, tomar otro 2% de 9800, lo que es una disminución de 196 personas, para un total de 9604. Como antes, debido a que la disminución de cada año no es constante, la gráfica de población versus tiempo no puede ser una línea, por lo que nuestra eventual función poblacional no será lineal.
Ahora que la función\(P(t)\) represente a la población de Ghosttown en el momento\(t\), donde medimos\(t\) en años. La población inicial de Ghosttown en\(t = 0\) es 10000, entonces\(P(0) = 10,000\). Dado que la población disminuye 2% cada año, al final del primer año la población de Ghosttown será 98% de la población inicial. Por lo tanto,
\[P(1) = 0.98P(0) = 0.98(10000). \label{9}\]
Cada año la población disminuye 2%. Por lo tanto, al cierre del segundo año, la población será 98% de la población al cierre del primer año. En otras palabras,
\[P(2) = 0.98P(1). \label{10}\]
Si reemplazamos\(P (1)\) en la Ecuación\ ref {10} con el resultado que se encuentra en la Ecuación\ ref {9}, entonces
\[P(2) = (0.98)(0.98)(10 000) = (0.98)^{2}(10000). \label{11}\]
Vamos a iterar un año más. Al cierre del tercer año, la población será 98% de la población al cierre del segundo año, por lo que
\[P(3) = 0.98P(2). \label{12}\]
Sin embargo, si reemplazamos\(P (2)\) en la Ecuación\ ref {12} con el resultado que se encuentra en la Ecuación\ label {11}, obtenemos
\[P(3) = (0.98)(0.98)^{2}(10000) = (0.98)^{3}(10000). \label{13}\]
El patrón ahora debería ser claro. La población al final de los\(t\) años viene dada por la función
\[P(t) = (0.98)^{t}(10000), \nonumber\]
O equivalentemente,
\[P(t) = 10000(0.98)^t\). \label{14}\]
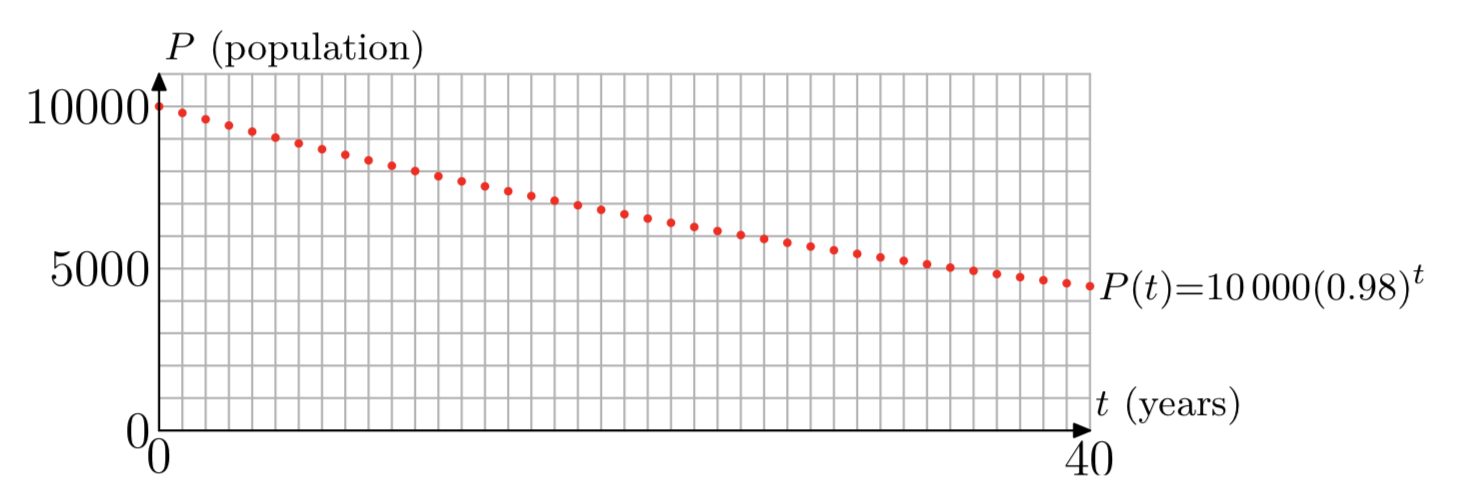
Nuestra función\(P(t)\) está definida por la Ecuación\ ref {14} para todos los enteros positivos {1, 2, 3,.}, y P (0) = 10000, la población inicial. La Figura 2 muestra una gráfica de nuestra función. Aunque los puntos se trazan solo a valores enteros de t de 0 a 40, eso es suficiente para mostrar la tendencia de la población a lo largo del tiempo. La población comienza en 10 000, disminuye con el tiempo, y la disminución anual (la diferencia de población de un año a otro) también disminuye a medida que pasa el tiempo.
Ejercicio\(\PageIndex{15}\)
Suponiendo que la tasa de disminución continúe en 2%, predecir la población de Ghosttown después de 40 años y después de 100 años.
Solución
Sustituir\(t = 40\) and \(t = 100\) in a la Ecuación\ ref {14}. La población en 40 años será
\(P(40) = 10000(0.98)^{40} \approx 4457\),
y la población en 100 años será
\(P(100) = 10000(0.98)^{100} \approx 1326\).
Tenga en cuenta que si en cambio hubiéramos comenzado con una población de 9000, por ejemplo, entonces la nueva fórmula sería
\(P(t) = 9000(0.98)^t\).
De igual manera, si la tasa de disminución hubiera sido de 5% anual en lugar de 2%, entonces habríamos terminado con la fórmula
\(P(t) = 10000(0.95)^t\).
Así, dejando\(P_{0}\) representar la población inicial, y\(r\) representar la tasa de crecimiento (en forma decimal), podemos generalizar la fórmula para
\[P(t) = P_{0}(1−r)^t. \label{16}\]
Definición
Como se señaló anteriormente, nuestras funciones\(P(t)\) en nuestros ejemplos de Pleasantville y Ghosttown son un nuevo tipo de función, porque la variable de entrada\(t\) es parte del exponente en la fórmula.
Definición\(\PageIndex{17}\): Exponential Function
Una función exponencial es una función de la forma
\(f(t) = b^t\)
donde b > 0 y\(b \ne 1\). \(b\)se llama la base de la función exponencial. De manera más general, una función de la forma
\(f(t) = Ab^t\),
donde b > 0\(b \ne 1\), y\(A \ne 0\), también se conoce como una función exponencial. En este caso, el valor de la función cuando t = 0 es f (0) = A, por lo que A es la cantidad inicial.
En las aplicaciones, casi siempre encontrarás funciones exponenciales en la forma más general\(Ab^t\). De hecho, tenga en cuenta que en los ejemplos poblacionales anteriores, la función P (t) tiene esta forma\(P(t) = Ab^t\), con\(A = P_{0}\),\(b = 1+r\) en Pleasantville, y\(b = 1−r\) en Ghosttown. En particular,\(A = P_{0}\) es la población inicial.
Dado que las funciones exponenciales se utilizan a menudo para modelar procesos que varían con el tiempo, generalmente usamos la variable de entrada\(t\) (aunque por supuesto se puede usar cualquier variable). También, puede que tengas curiosidad por qué dice la definición\(b \ne 1\), ya que\(1^t\) solo equivale a 1. Explicaremos esta curiosidad al final de esta sección.
Gráficas de Funciones Exponenciales
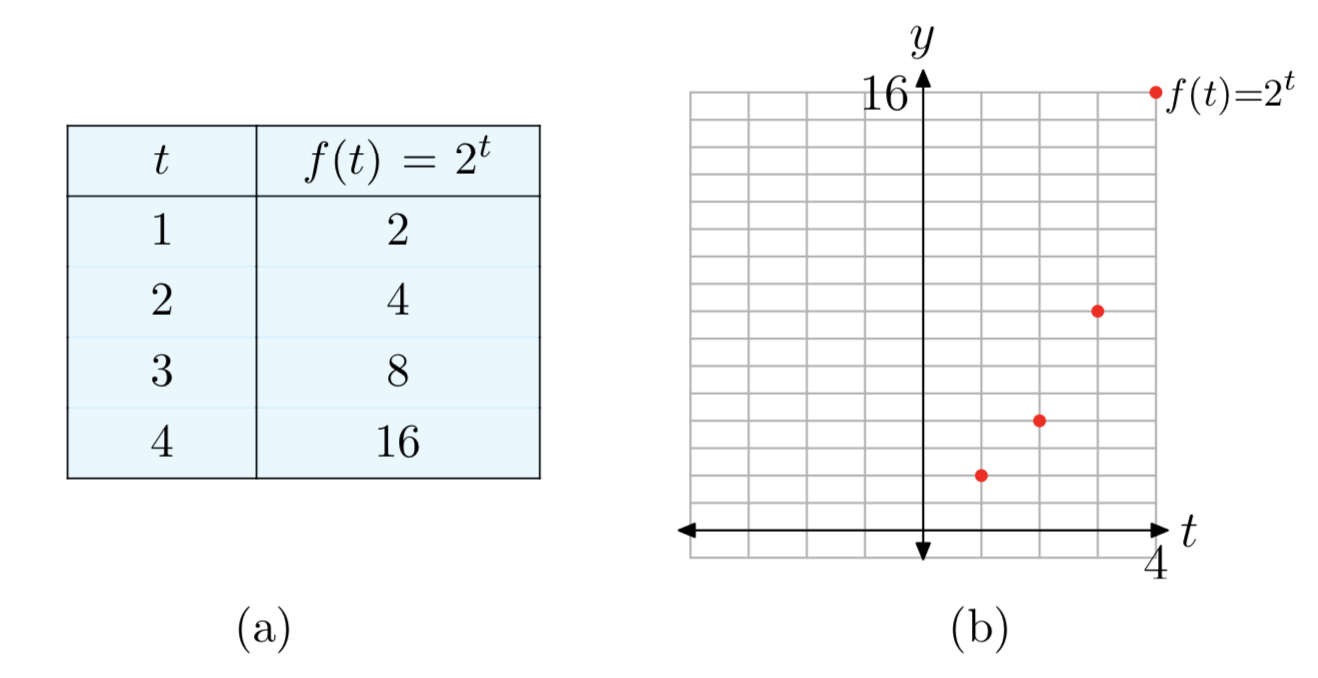
\(b^t\)Primero desarrollaremos las propiedades para la función exponencial básica, y luego anotaremos los cambios menores para la forma más general\(Ab^t\). Para un ejemplo de trabajo, usemos base b = 2, y calculemos algunos valores\(f(t) = 2^t\) y graficemos el resultado (Figura 3).
Recordemos de la sección anterior que 2t también se define para los exponentes negativos t y el exponente 0. Así, la función exponencial\(f(t) = 2^t\) se define para todos los enteros. La Figura 4 muestra una nueva tabla y gráfica con puntos añadidos a 0 y valores enteros negativos.
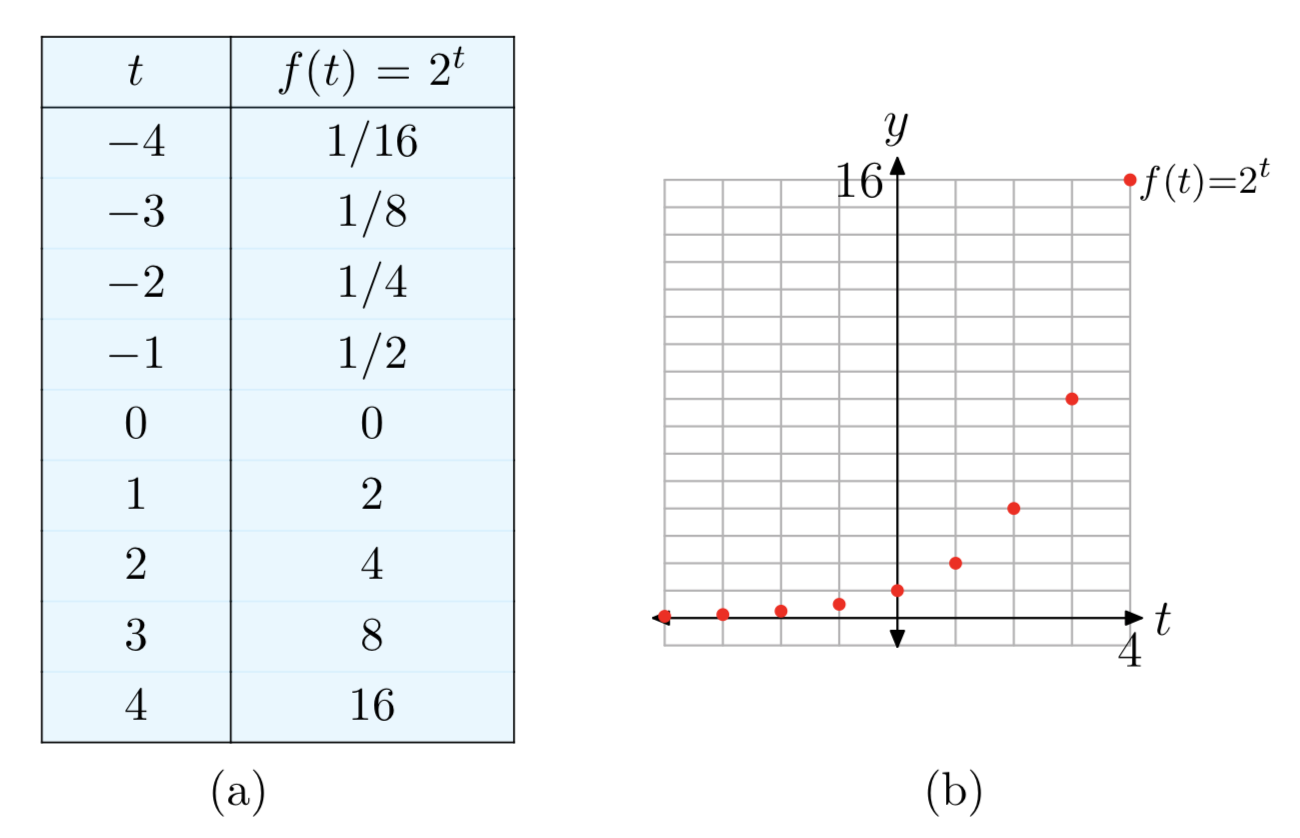
Sin embargo, la sección anterior mostró que también\(2^t\) se define para exponentes racionales e irracionales. Por lo tanto, el dominio de la función exponencial\(f(t) = 2^t\) es el conjunto de todos los números reales. Cuando sumamos los valores de la función en todos los valores racionales e irracionales de\(t\), obtenemos una curva continua final como se muestra en la Figura 5.
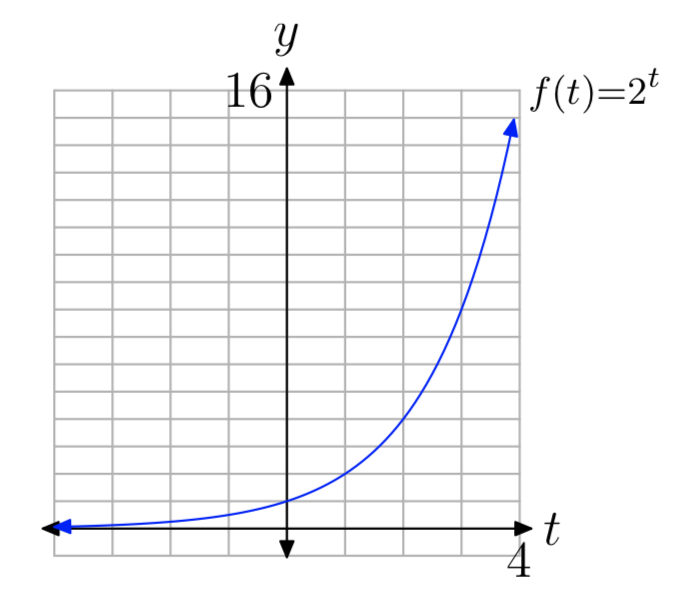
Obsérvese varias propiedades de la gráfica en la Figura 5:
- Al moverse de izquierda a derecha, la curva se eleva, lo que significa que la función aumenta a medida que t aumenta. De hecho, la función aumenta rápidamente para t positiva.
- La gráfica se encuentra por encima del eje t, por lo que los valores de la función son siempre positivos. Por lo tanto, el rango de la función es\((0, \infty)\).
- La gráfica tiene una asíntota horizontal y = 0 (el eje t) en el lado izquierdo. Esto significa que la función casi “se extingue” (los valores se acercan cada vez más a 0) a medida que t se acerca\(−\infty\).
¿Y las gráficas de otras funciones exponenciales con diferentes bases? Usaremos la calculadora para explorar varios de estos.
Primero, usa tu calculadora para comparar\(y_{1}(x) = 2^x\) y\(y_{2}(x) = 3^x\). Como puede verse en la Figura 6 (a), la gráfica de\(3^x\) se eleva más rápido que\(2^x\) para x > 0, y se extingue más rápido para x < 0.
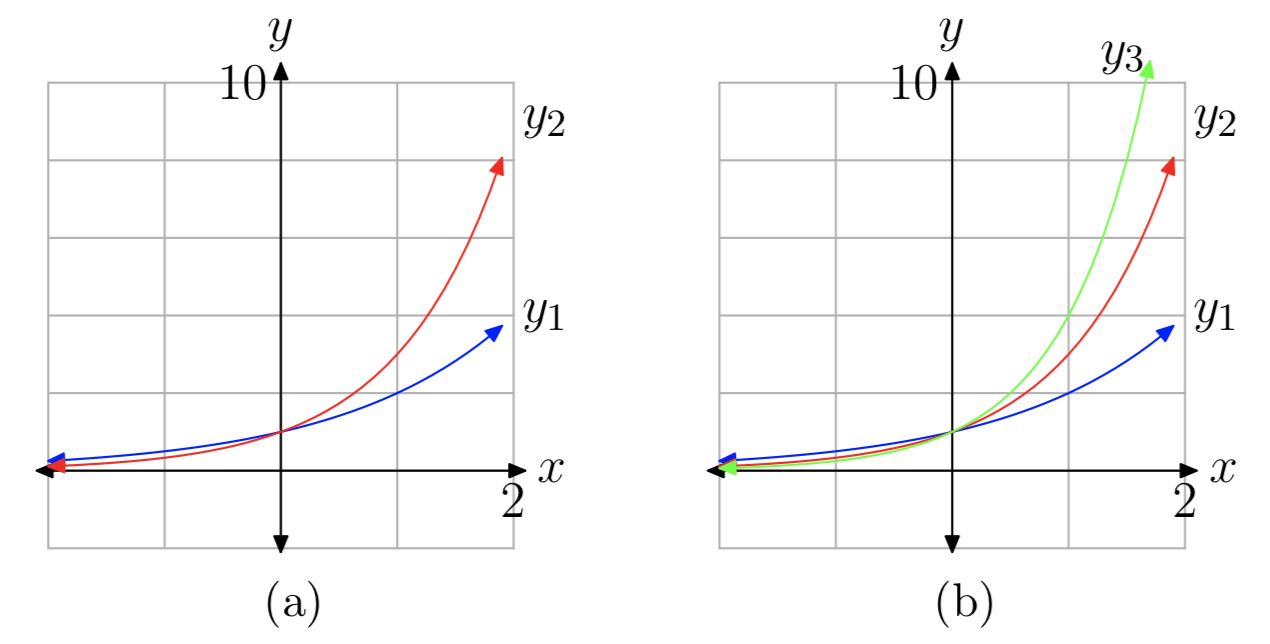
A continuación, agregue\(y_{3}(x) = 4^x\). El resultado se muestra en la Figura 6 (b). Nuevamente, aumentar el tamaño de la base a b = 4 da como resultado una función que se eleva aún más rápido a la derecha e igualmente muere más rápido a la izquierda. Si sigues aumentando el tamaño de la base b, verás que esta tendencia continúa. Eso no es terriblemente sorprendente porque, si calculamos el valor de estas funciones en una x positiva fija, por ejemplo en x = 2, entonces los valores aumentan:\(2^2 < 3^2 < 4^2 < ....\) De manera similar, en x = −2, los valores disminuyen:\(2^{−2} > 3^{−2} > 4^{−2} >....\)
Todas las funciones en nuestros experimentos hasta ahora comparten las propiedades enumeradas en (a) — (c) anterior: la función aumenta, el rango es\((0, \infty)\), y la gráfica tiene una asíntota horizontal y = 0 en el lado izquierdo. Ahora probemos valores más pequeños de la base b. Primero use la calculadora para trazar la gráfica de\(y_{1}(x) = (\frac{1}{2})^x\) (ver Figura 7 (a)).
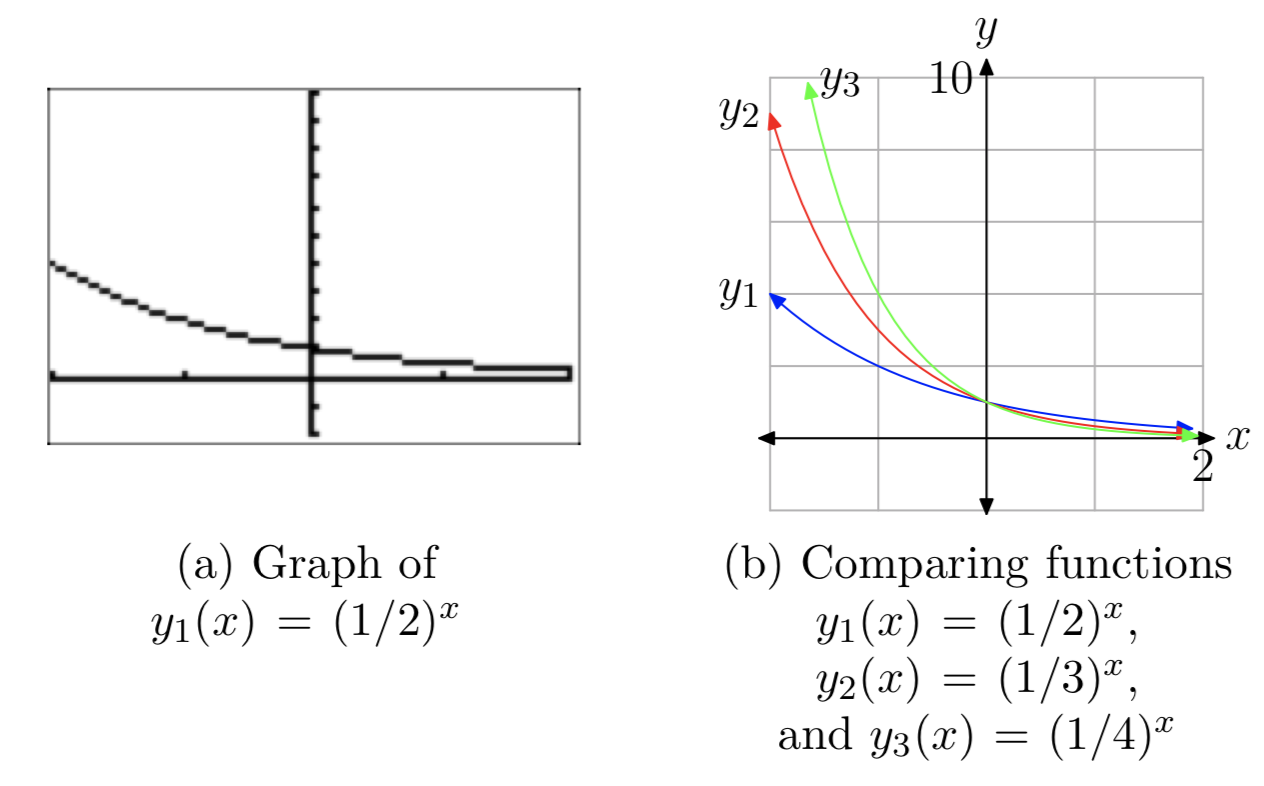
Esta gráfica es muy diferente. Se eleva rápidamente hacia la izquierda, y casi se extingue a la derecha. Compárelo con\(y_{2}(x) = (\frac{1}{3})^x\) y\(y_{3}(x) = (\frac{1}{4})^x\) (ver Figura 7 (b)). A medida que la base se hace más pequeña, la gráfica se eleva más rápido a la izquierda y se extingue más rápido a la derecha.
Usando las propiedades de reflexión, es fácil entender la apariencia de estas tres últimas gráficas. Tenga en cuenta que
\((\frac{1}{2})^x = (2^{−1})^x = 2^{−x}\)
por lo que se deduce que la gráfica de\((\frac{1}{2})^x\) es solo una reflexión en el eje y de la gráfica de\(2^x\) (ver Figura 8).
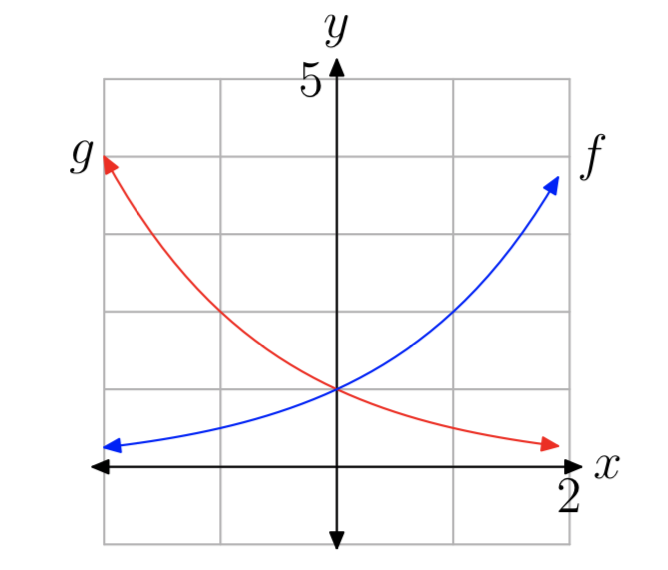
Así, parece que tenemos dos tipos diferentes de gráficas, y por lo tanto dos tipos de funciones exponenciales: un tipo va en aumento y el otro decreciente. Nuestros experimentos anteriores, junto con un poco más de experimentación, deberían convencerte de que\(b^x\) está aumentando para b > 1, y disminuyendo para 0 < b < 1. El primer tipo de funciones se denominan funciones de crecimiento exponencial, y el segundo tipo son funciones de decaimiento exponencial.
FUNCIONES DE CRECIMIENTO EXPONENCIAL:\(F(X) = B^X\) WITH B > 1
- El dominio es el conjunto de todos los números reales.
- Al moverse de izquierda a derecha, la gráfica se eleva, lo que significa que la función aumenta a medida que aumenta x. La función aumenta rápidamente para x positivo.
- La gráfica se encuentra por encima del eje x, por lo que los valores de la función son siempre positivos. Por lo tanto, el rango es\((0, \infty)\).
- La gráfica tiene una asíntota horizontal y = 0 (el eje x) en el lado izquierdo. Esto significa que la función casi “se extingue” (los valores se acercan cada vez más a 0) a medida que se acerca x\(−\infty\).
La segunda propiedad anterior merece alguna explicación adicional. Al observar la Figura 6 (b), parece que\(y_{2}\) y\(y_{3}\) aumenta rápidamente a medida que x aumenta, pero\(y_{1}\) parece aumentar lentamente. Sin embargo, esto se debe a que la gráfica de solo\(y_{1}(x) = 2^x\) se muestra en el intervalo [− 2, 2]. En la Figura 5, la misma función se grafica en el intervalo [− 4, 4], y ciertamente parece aumentar rápidamente en esa gráfica. El punto aquí es que las funciones de crecimiento exponencial eventualmente aumentan rápidamente a medida que x aumenta. Si graficas la función en un intervalo lo suficientemente grande, la función eventualmente se volverá muy empinada en el lado derecho de la gráfica. Esta es una propiedad importante de las funciones de crecimiento exponencial, y se explorará más a fondo en los ejercicios.
Propiedades de las funciones de decaimiento exponencial:\(F(X) = B^X\) WITH 0 < B < 1
- El dominio es el conjunto de todos los números reales.
- Al moverse de izquierda a derecha, la gráfica cae, lo que significa que la función se desarruga a medida que x aumenta. La función disminuye rápidamente para x negativo.
- La gráfica se encuentra por encima del eje x, por lo que los valores de la función son siempre positivos. Por lo tanto, el rango es\((0, \infty)\).
- La gráfica tiene una asíntota horizontal y = 0 (el eje x) en el lado derecho. Esto significa que la función casi “se extingue” (los valores se acercan cada vez más a 0) a medida que se acerca x\(\infty\).
¿Por qué nos abstenemos de usar la base b = 1? Después de todo, ciertamente\(1^x\) se define: tiene el valor 1 para todos x. Pero eso significa que\(f(x) = 1^x\) es solo una función lineal constante — su gráfica es una línea horizontal. Por lo tanto, esta función no comparte las mismas propiedades que las otras funciones exponenciales, y ya la hemos clasificado como una función lineal. Por lo tanto, no\(1^x\) se considera como una función exponencial.
Ejemplo\(\PageIndex{19}\)
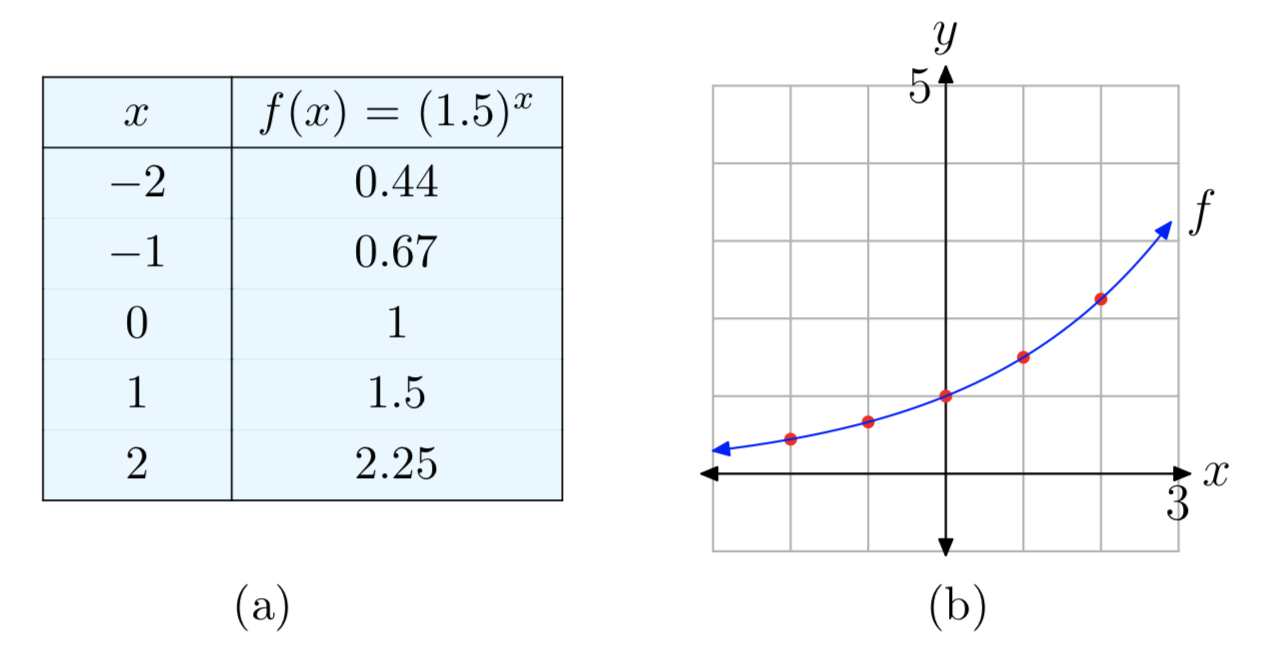
Trazar la gráfica de la función\(f(x) = (1.5)^x\). Identificar el rango de la función y la asíntota horizontal.
Solución
Dado que la base 1.5 es mayor que 1, esta es una función de crecimiento exponencial. Por lo tanto, su gráfica tendrá una forma similar a las gráficas de la Figura 6. La gráfica se eleva, habrá una asíntota horizontal y = 0 en el lado izquierdo, y el rango de la función es\((0, \infty)\). La gráfica se puede trazar a mano usando este conocimiento junto con valores aproximados en x = − 2, − 1, 0, 1, 2. Ver Figura 9.
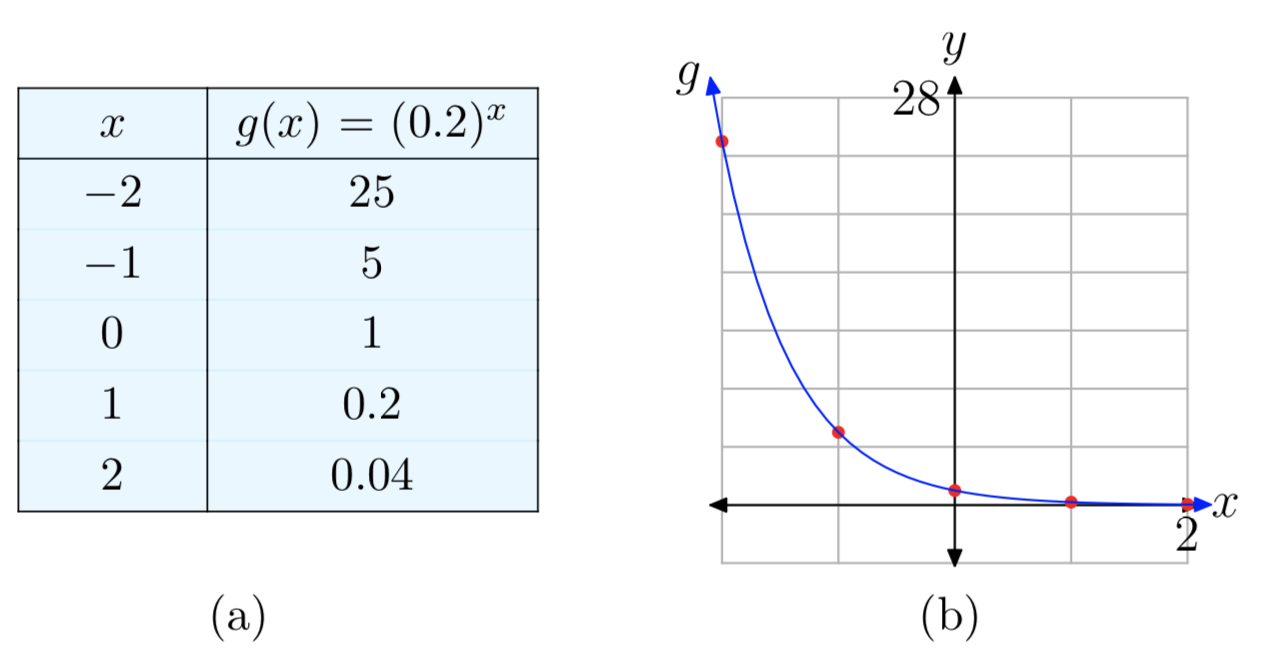
Ejemplo\(\PageIndex{20}\)
Trazar la gráfica de la función\(g(x) = (0.2)^x\). Identificar el rango de la función y la asíntota horizontal.
Solución
Dado que la base 0.2 es menor que 1, esta es una función de decaimiento exponencial. Por lo tanto, su gráfica tendrá una forma similar a las gráficas de la Figura 7. El gráfico cae, habrá una asíntota horizontal y = 0 en el lado derecho, y el rango de la función es\((0, \infty)\). The graph can then be plotted by hand by using this knowledge along with approximate values at x = − 2, − 1, 0, 1, 2. Ver Figura 10.
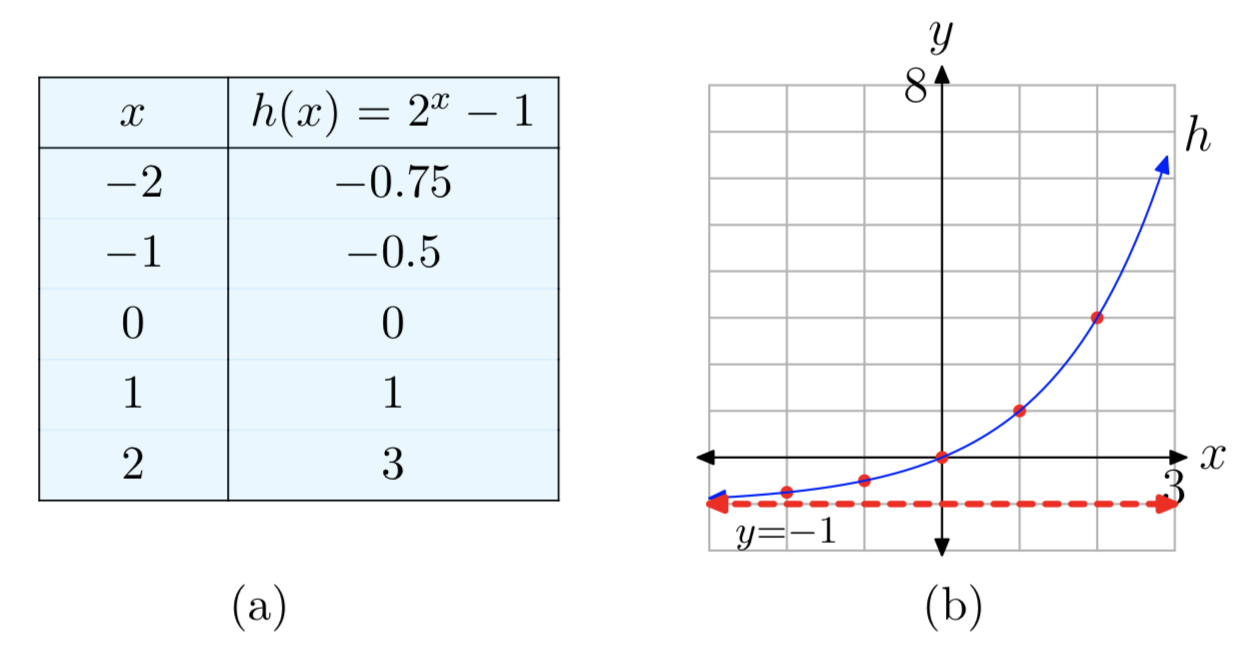
Ejemplo\(\PageIndex{21}\)
Trazar la gráfica de la función\(f(x) = 2^x−1\). Identificar el rango de la función y la asíntota horizontal.
Solución
La gráfica de h se puede obtener a partir de la gráfica de\(f(x) = 2^x\) (ver Figura 5) mediante un desplazamiento vertical hacia abajo 1 unidad. Por lo tanto, la asíntota horizontal y = 0 de la gráfica de f también se desplazará hacia abajo 1 unidad, por lo que la gráfica de h tiene una asíntota horizontal y = − 1. Del mismo modo, el rango de f se desplazará hacia abajo a\((−1, \infty)\) = Rango (h). La gráfica se puede trazar a mano usando este conocimiento junto con valores aproximados en x = − 2, − 1, 0, 1, 2. Ver Figura 11.
En secciones posteriores de este capítulo, también veremos funciones exponenciales más generales de la forma\(f(x) = Ab^x\) (de hecho, las funciones de Pleasantville y Ghosttown al inicio de esta sección son de esta forma). Si A es positivo, entonces las gráficas de estas funciones se pueden obtener de las gráficas exponenciales básicas mediante escalado vertical, por lo que las gráficas tendrán la misma forma general que ya sea las curvas de crecimiento exponencial (si b > 1) o las curvas de decaimiento exponencial (if\(0 < b < 1\)) que trazamos anteriormente.
Ejercicio
Ejercicio\(\PageIndex{1}\)
La población actual de Fortuna es de 10 mil almas abundantes. Se sabe que la población está creciendo a una tasa de 4% anual. Suponiendo que esta tasa se mantenga constante, realice cada una de las siguientes tareas.
- Establecer una ecuación que modele la población P (t) en función del tiempo t.
- Utilizar el modelo de la parte anterior para predecir la población dentro de 40 años.
- Usa tu calculadora para bosquejar la gráfica de la población durante los próximos 40 años.
- Responder
-
- \(P(t) = 10000(1.04)^t\)
- \(P(40) \approx 48101\)
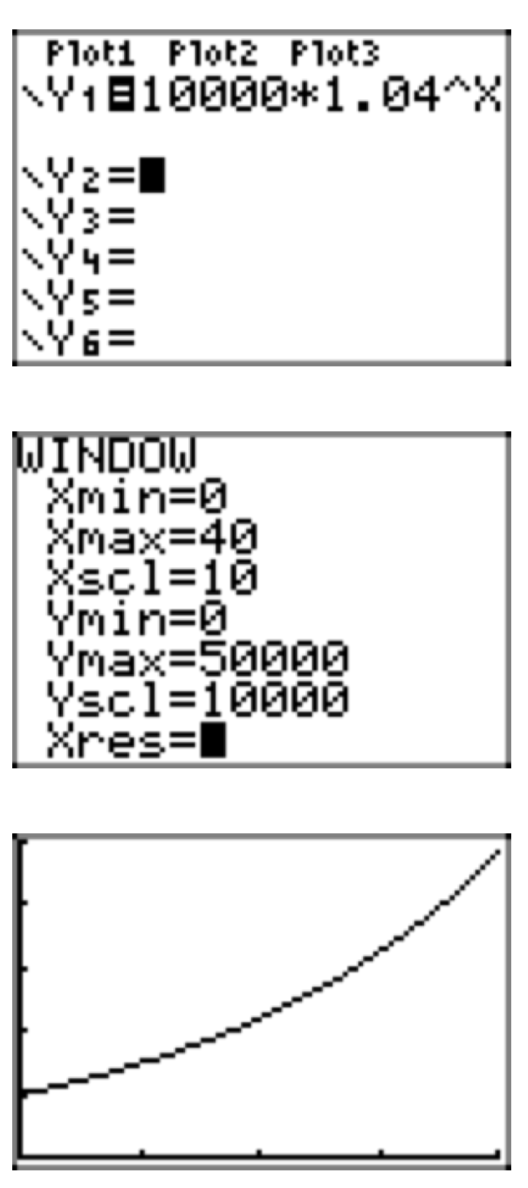
Ejercicio\(\PageIndex{2}\)
La población de la localidad de Imaginación cuenta actualmente con 12 mil personas. Se sabe que la población está creciendo a una tasa de 6% anual. Suponiendo que esta tasa se mantenga constante, realice cada una de las siguientes tareas.
- Establecer una ecuación que modele la población P (t) en función del tiempo t.
- Utilizar el modelo de la parte anterior para predecir la población dentro de 30 años.
- Usa tu calculadora para bosquejar la gráfica de la población durante los próximos 30 años.
Ejercicio\(\PageIndex{3}\)
La población de la localidad de Despairia cuenta actualmente con 15 mil individuos. Se sabe que la población está en descomposición a una tasa de 5% anual. Suponiendo que esta tasa se mantenga constante, realice cada una de las siguientes tareas.
- Establecer una ecuación que modele la población P (t) en función del tiempo t.
- Utilizar el modelo de la parte anterior para predecir la población dentro de 50 años.
- Usa tu calculadora para bosquejar la gráfica de la población durante los próximos 50 años.
- Responder
-
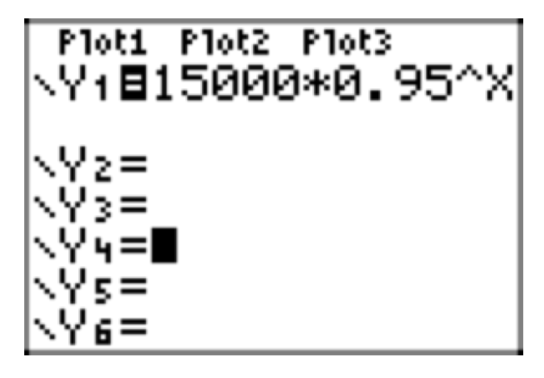
- \(p(t) = 15 000(0.95)^t\)
- \(P(50) \approx 1154\)
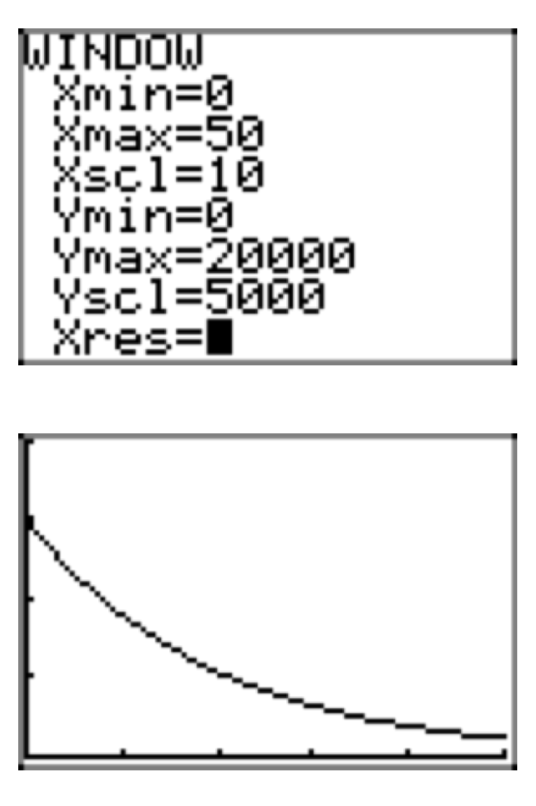
Ejercicio\(\PageIndex{4}\)
La población de la localidad de Hopeless cuenta actualmente con 25 mil individuos. Se sabe que la población está en descomposición a una tasa de 6% anual. Suponiendo que esta tasa se mantenga constante, realice cada una de las siguientes tareas.
- Establecer una ecuación que modele la población P (t) en función del tiempo t.
- Utilizar el modelo de la parte anterior para predecir la población dentro de 40 años.
- Usa tu calculadora para bosquejar la gráfica de la población durante los próximos 40 años.
En los Ejercicios 5 - 12, realice cada una de las siguientes tareas para la función dada.
- Encuentra la intercepción y de la gráfica de la función. Además, usa tu calculadora para encontrar dos puntos en la gráfica a la derecha del eje y, y dos puntos a la izquierda.
- Usando sus cinco puntos de (a) como guía, establezca un sistema de coordenadas en papel gráfico. Elija y etiquete las escalas apropiadas para cada eje. Traza los cinco puntos, y cualquier punto adicional que consideres necesario para discernir la forma de la gráfica.
- Dibuja la asíntota horizontal con una línea discontinua, y etiquételo con su ecuación.
- Croquis de la gráfica de la función.
- Utilice la notación de intervalos para describir tanto el dominio como el rango de la función.
Ejercicio\(\PageIndex{5}\)
\(f(x) = (2.5)^x\)
- Responder
-
- La intercepción y es (0, 1). Evaluar la función en x = 1, 2, −1, −2 para obtener los puntos (1, 2.5), (2, 6.25), (−1, 0.4), (−2, 0.16) (otras respuestas son posibles).
- Ver la gráfica en la parte (4).
- La asíntota horizontal es y = 0. Ver la gráfica en la parte (4).
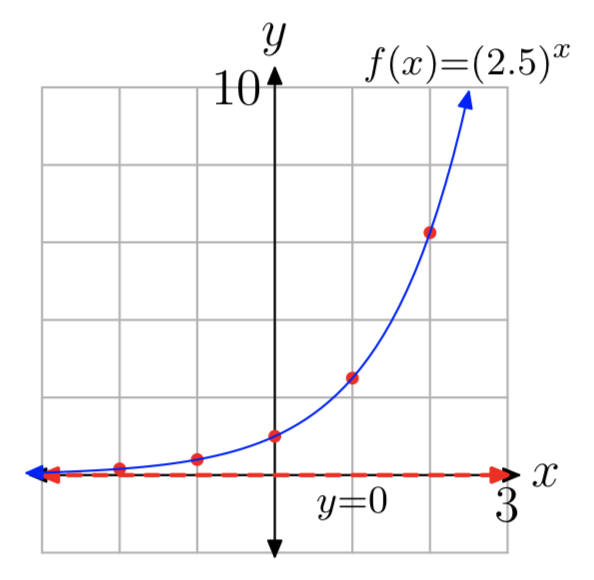
- Dominio =\((−\infty, \infty)\), Rango =\((0, \infty)\)
Ejercicio\(\PageIndex{6}\)
\(f(x) = (0.1)^x\)
Ejercicio\(\PageIndex{7}\)
\(f(x) = (0.75)^x\)
- Responder
-
- La intercepción y es (0, 1). Evaluar la función en x = 1, 2, −1, −2 para obtener los puntos (1, 0.75), (2, 0.56), (−1, 1.34), (−2, 1.78) (otras respuestas son posibles).
- Ver la gráfica en la parte (4).
- La asíntota horizontal es y = 0. Ver la gráfica en la parte (4).
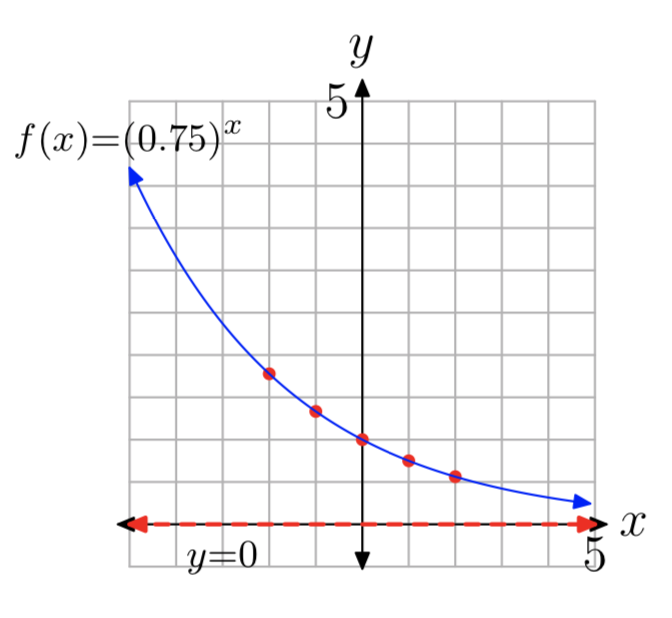
- Dominio =\((−\infty, \infty)\), Rango =\((0, \infty)\)
Ejercicio\(\PageIndex{8}\)
\(f(x) = (1.1)^x\)
Ejercicio\(\PageIndex{9}\)
\(f(x) = 3^x+1\)
- Contestar
-
- La intercepción y es (0, 2). Evaluar la función en x = 1, 2, −1, −2 para obtener los puntos (1, 4), (2, 10), (−1, 1.34), (−2, 1.11) (otras respuestas son posibles).
- Ver la gráfica en la parte (4).
- La asíntota horizontal es y = 1. Ver la gráfica en la parte (4).
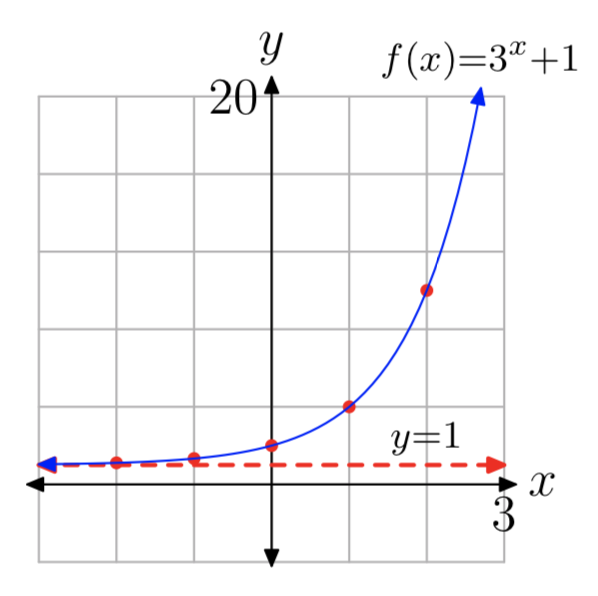
- Dominio =\((−\infty, \infty)\), Rango =\((1, \infty)\)
Ejercicio\(\PageIndex{10}\)
\(f(x) = 4^x−5\)
Ejercicio\(\PageIndex{11}\)
\(f(x) = 2^x−3\)
- Contestar
-
- La intercepción y es (0, −2). Evaluar la función en x = 1, 2, −1, −2 para obtener los puntos (1, −1), (2, 1), (−1, −2.5), (−2, −2.75) (otras respuestas son posibles).
- Ver la gráfica en la parte (4).
- La asíntota horizontal es y = −3. Ver la gráfica en la parte (4).
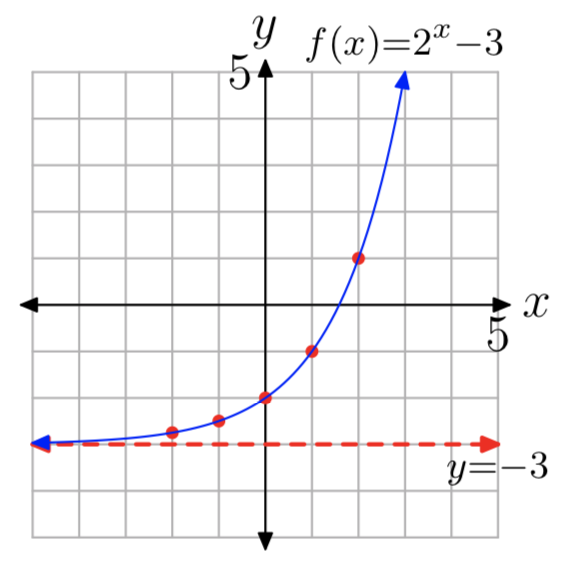
- Dominio =\((−\infty, \infty)\), Rango =\((−3, \infty)\)
Ejercicio\(\PageIndex{12}\)
\(f(x) = 5^x+2\)
En los Ejercicios 13 - 20 se muestra la gráfica de una función ex ponencial de\(f(x) = b^x+c\) la forma. La línea roja discontinua es una asíntota horizontal. Determinar el rango de la función. Exprese su un swer en notación de intervalos.
Ejercicio\(\PageIndex{13}\)
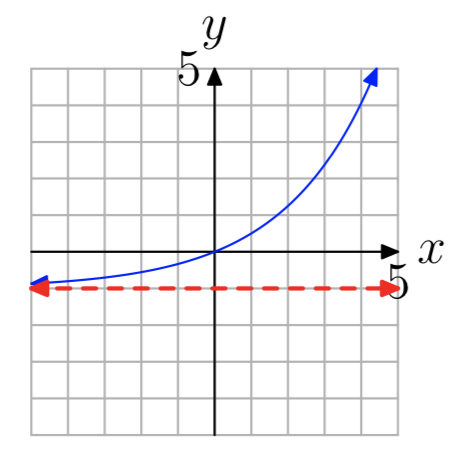
- Contestar
-
\((−1, \infty)\)
Ejercicio\(\PageIndex{14}\)
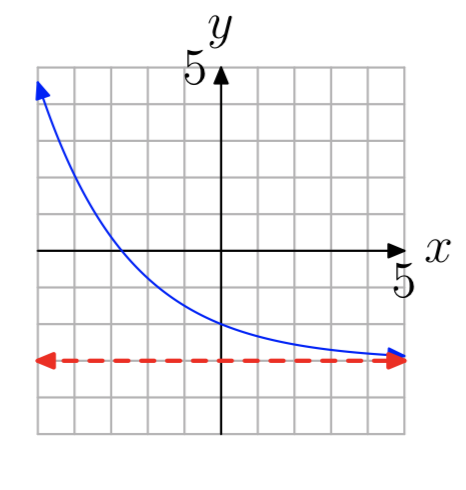
Ejercicio\(\PageIndex{15}\)
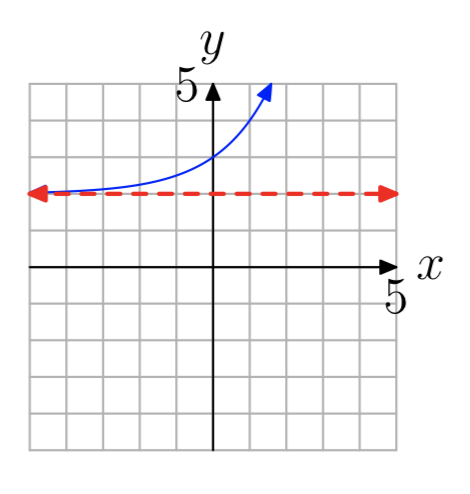
- Contestar
-
\((2, \infty)\)
Ejercicio\(\PageIndex{16}\)
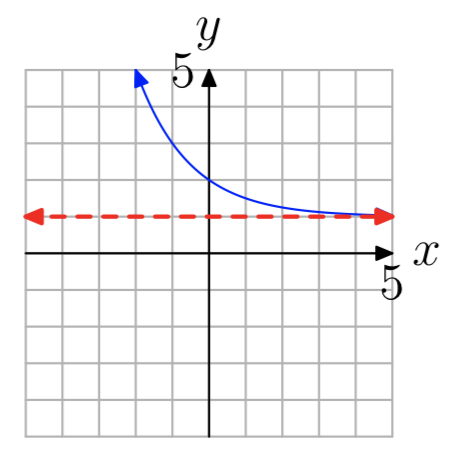
Ejercicio\(\PageIndex{17}\)
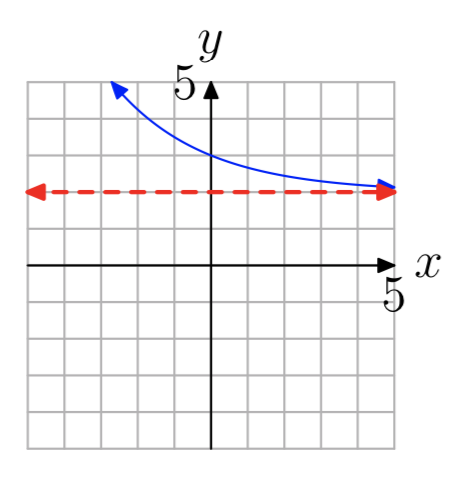
- Contestar
-
\((2, \infty)\)
Ejercicio\(\PageIndex{18}\)
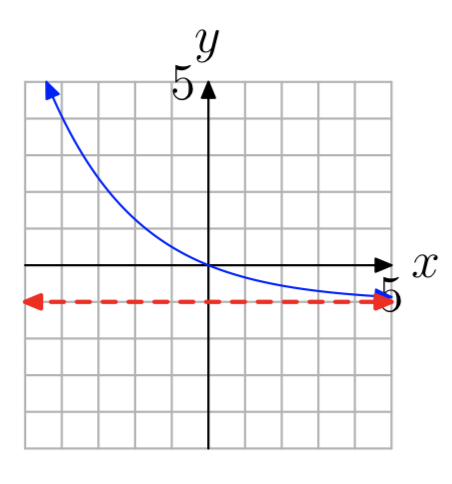
Ejercicio\(\PageIndex{19}\)
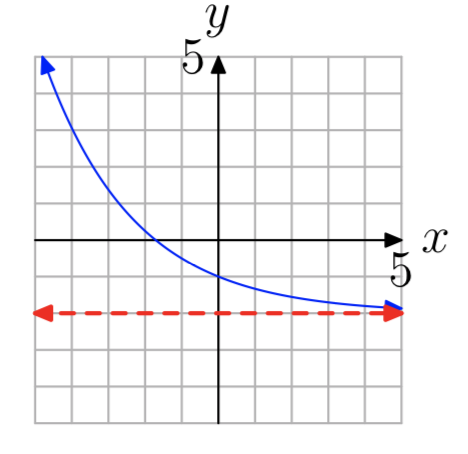
- Contestar
-
\((−2, \infty)\)
Ejercicio\(\PageIndex{20}\)
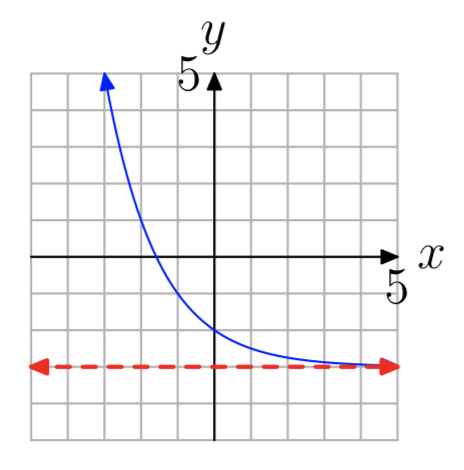
En Ejercicios 21 - 32, computar f (p) al valor dado p.
Ejercicio\(\PageIndex{21}\)
\(f(x) = (\frac{1}{3})^x\); p = −4
- Contestar
-
81
Ejercicio\(\PageIndex{22}\)
\(f(x) = (\frac{3}{4})^x\); p = 1
Ejercicio\(\PageIndex{23}\)
\(f(x) = 5^x\); p = 5
- Contestar
-
3125
Ejercicio\(\PageIndex{24}\)
\(f(x) = (\frac{1}{3})^x\); p = 4
Ejercicio\(\PageIndex{25}\)
\(f(x) = 4^x\); p = −4
- Contestar
-
\(\frac{1}{256}\)
Ejercicio\(\PageIndex{26}\)
\(f(x) = 5^x\); p = −3
Ejercicio\(\PageIndex{27}\)
\(f(x) = (\frac{5}{2})^x\); p = −3
- Contestar
-
\(\frac{8}{125}\)
Ejercicio\(\PageIndex{28}\)
\(f(x) = 9^x\); p = 3
Ejercicio\(\PageIndex{29}\)
\(f(x) = 5^x\); p = −4
- Contestar
-
\(\frac{1}{625}\)
Ejercicio\(\PageIndex{30}\)
\(f(x) = 9^x\); p = 0
Ejercicio\(\PageIndex{31}\)
\(f(x) = (\frac{6}{5})^x\); p = −4
- Contestar
-
\(\frac{625}{1296}\)
Ejercicio\(\PageIndex{32}\)
\(f(x) = (\frac{3}{5})^x\); p = 0
En Ejercicios 33 - 40, usa tu calculadora para evaluar la función al valor dado p. Redondea tu respuesta a la centésima más cercana.
Ejercicio\(\PageIndex{33}\)
\(f(x) = 10^x\); p = −0.7.
- Contestar
-
0.20
Ejercicio\(\PageIndex{34}\)
\(f(x) = 10^x\); p = −1.6.
Ejercicio\(\PageIndex{35}\)
\(f(x) = (\frac{2}{5})^x\); p = 3.67.
- Contestar
-
0.03
Ejercicio\(\PageIndex{36}\)
\(f(x) = 2^x\);\(p = −\frac{3}{4}\).
Ejercicio\(\PageIndex{37}\)
\(f(x) = 10^x\); p = 2.07.
- Contestar
-
117.49
Ejercicio\(\PageIndex{38}\)
\(f(x) = 7^x\);\(p = \frac{4}{3}\).
Ejercicio\(\PageIndex{39}\)
\(f(x) = 10^x\);\(p = −\frac{1}{5}\).
- Contestar
-
0.63
Ejercicio\(\PageIndex{40}\)
\(f(x) = (\frac{4}{3})^x\); p = 1.15
Ejercicio\(\PageIndex{41}\)
Este ejercicio explora la propiedad de que las funciones de crecimiento exponencial eventualmente aumentan rápidamente a medida que x aumenta. Vamos\(f(x) = 1.05^x\). Usa tu calculadora gráfica para graficar f en los intervalos
a) [0, 10] y b) [0, 100].
Para (a), use Ymin = 0 e Ymax = 10.
Para (b), use Ymin = 0 e Ymax = 100.
Haga copias precisas de las imágenes en su ventana de visualización en su papel de tarea. ¿Qué observas al comparar las dos gráficas?
- Contestar
-
(a) La gráfica sobre el intervalo [0, 10] aumenta muy lentamente. De hecho, la gráfica se ve casi lineal.
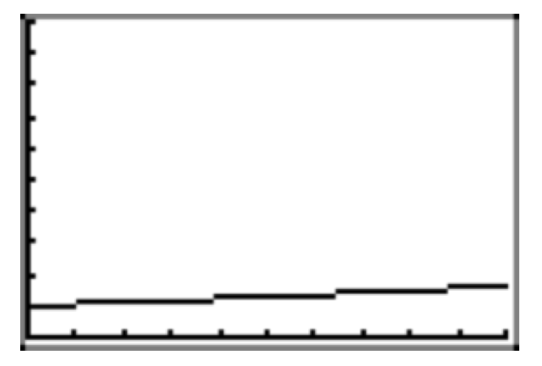
(b) La gráfica del intervalo [0, 100] aumenta lentamente al principio, pero luego aumenta muy rápidamente en la segunda mitad del intervalo.
