4.8: Graficando Sistemas de Desigualdades Lineales
- Page ID
- 112373
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Al final de esta sección, podrás:
- Determinar si un par ordenado es una solución de un sistema de desigualdades lineales
- Resolver un sistema de desigualdades lineales graficando
- Resolver aplicaciones de sistemas de desigualdades
Antes de comenzar, toma este cuestionario de preparación.
Determinar si un par ordenado es una solución de un sistema de desigualdades lineales
La definición de un sistema de desigualdades lineales es muy similar a la definición de un sistema de ecuaciones lineales.
Dos o más desigualdades lineales agrupadas forman un sistema de desigualdades lineales.
Un sistema de desigualdades lineales parece un sistema de ecuaciones lineales, pero tiene desigualdades en lugar de ecuaciones. Aquí se muestra un sistema de dos desigualdades lineales.
\[\left\{\begin{array} {l} x+4y\geq 10\\3x−2y<12\end{array}\right.\nonumber\]
Para resolver un sistema de desigualdades lineales, encontraremos valores de las variables que son soluciones a ambas desigualdades. Resolvemos el sistema usando las gráficas de cada desigualdad y mostramos la solución como gráfica. Encontraremos la región en el plano que contiene todos los pares ordenados\((x,y)\) que hacen que ambas desigualdades sean verdaderas.
Las soluciones de un sistema de desigualdades lineales son los valores de las variables que hacen verdaderas todas las desigualdades.
La solución de un sistema de desigualdades lineales se muestra como una región sombreada en el sistema\(xy\) de coordenadas que incluye todos los puntos cuyos pares ordenados hacen que las desigualdades sean verdaderas.
Para determinar si un par ordenado es una solución a un sistema de dos desigualdades, sustituimos los valores de las variables en cada desigualdad. Si el par ordenado hace que ambas desigualdades sean verdaderas, es una solución al sistema.
Determinar si el par ordenado es una solución para el sistema\(\left\{\begin{array} {l} x+4y\geq 10\\3x−2y<12\end{array}\right.\)
a.\((−2,4)\) b.\((3,1)\)
Solución:
a. ¿El par ordenado es\((−2,4)\) una solución?

El par ordenado\((−2,4)\) hizo que ambas desigualdades fueran ciertas. Por lo tanto,\((−2,4)\) es una solución a este sistema.
b. ¿El par ordenado es\((3,1)\) una solución?

El par ordenado\((3,1)\) hizo que una desigualdad fuera cierta, pero la otra falsa. Por lo tanto, no\((3,1)\) es una solución a este sistema.
Determine si el par ordenado es una solución para el sistema:\(\left\{ \begin{array} {l} x−5y>10\\2x+3y>−2 \end{array} \right.\)
a.\((3,−1)\) b.\((6,−3)\)
- Responder
-
a. no
b. si
Determine si el par ordenado es una solución para el sistema:\(\left\{ \begin{array} {l} y>4x−2\\4x−y<20 \end{array} \right.\)
a.\((−2,1)\) b.\((4,−1)\)
- Responder
-
a. si
b. no
Resolver un Sistema de Desigualdades Lineales Graficando
La solución a una sola desigualdad lineal es la región en un lado de la línea límite que contiene todos los puntos que hacen que la desigualdad sea verdadera. La solución a un sistema de dos desigualdades lineales es una región que contiene las soluciones a ambas desigualdades. Para encontrar esta región, graficaremos cada desigualdad por separado y luego ubicaremos la región donde ambas son verdaderas. La solución siempre se muestra como una gráfica.
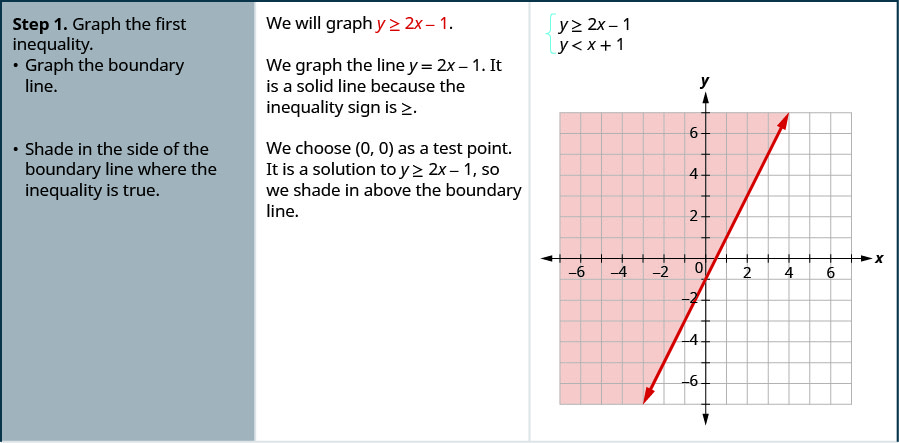
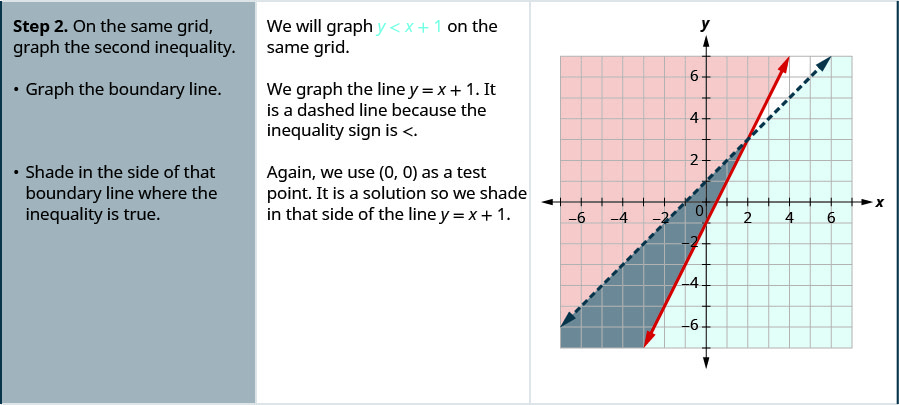
Resuelve el sistema graficando:\(\left\{\begin{array} {l} y\geq 2x−1 \\ y<x+1\end{array}\right.\)
Solución:


Resuelve el sistema graficando:\(\left\{\begin{array} {l} y<3x+2\\y>−x−1\end{array}\right.\)
- Responder
-
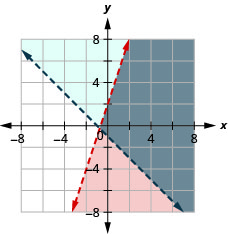
La solución es la región gris.
Resuelve el sistema graficando:\(\left\{\begin{array} {l} y<−12x+3 \\ y<3x−4\end{array}\right.\)
- Responder
-
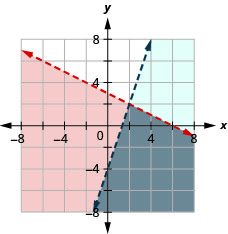
La solución es la región gris.
- Grafica la primera desigualdad.
- Grafica la línea límite.
- Sombra en el lado de la línea límite donde la desigualdad es verdadera.
- En la misma cuadrícula, grafica la segunda desigualdad.
- Grafica la línea límite.
- Sombra en el lado de esa línea límite donde la desigualdad es verdadera.
- La solución es la región donde se superpone el sombreado.
- Verifique eligiendo un punto de prueba.
Resuelve el sistema graficando:\(\left\{\begin{array} {l} x−y>3\\y<−15x+4\end{array}\right.\)
Solución:
| \(\left\{\begin{array} {l} x−y>3\\y<−15x+4\end{array}\right.\) | |
| Gráfica\(x - y > 3,\) graficando\(x - y = 3\) y probando un punto. Las intercepciones son\(x = 3\) y\(y = −3\) y la línea límite será discontinua. Prueba\((0, 0)\) que hace que la desigualdad sea falsa para sombrear (rojo) el lado que no contiene\((0, 0).\) |
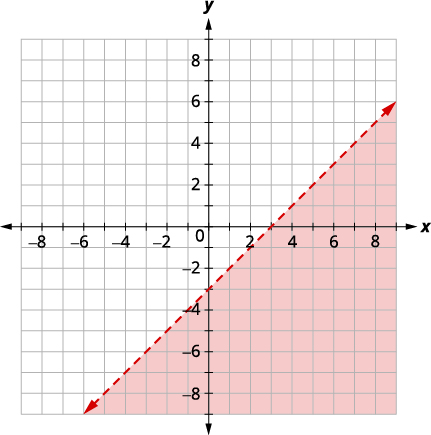 |
| Gráfica\(y<−15x+4\) graficando\(y=−15x+4\) usando la pendiente\(m=−15\) e\(y\) -intercepción\(b = 4.\) La línea límite será discontinua Prueba\((0, 0)\) que hace que la desigualdad sea verdadera, entonces sombrear (azul) el lado que contiene\((0, 0).\) Elija un punto de prueba en la solución y verifique que sea una solución a ambas desigualdades. |
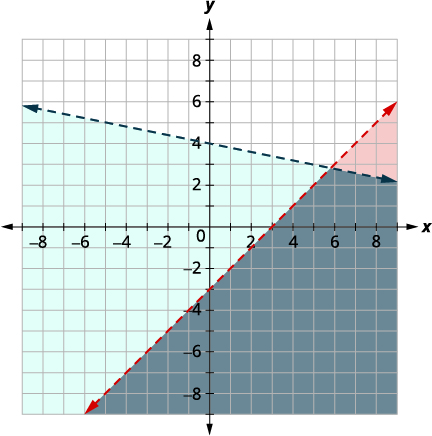 |
El punto de intersección de las dos líneas no se incluye ya que ambas líneas límite fueron discontinuas. La solución es el área sombreada dos veces, que aparece como la región sombreada más oscura.
Resuelve el sistema graficando:\(\left\{\begin{array} {l} x+y\leq 2 \\ y\geq \frac{2}{3}x−1\end{array}\right.\)
- Responder
-
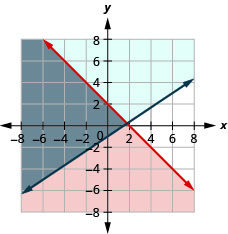
La solución es la región gris.
Resuelve el sistema graficando:\(\left\{\begin{array} {l} 3x−2y\leq 6\\y>−\frac{1}{4}x+5\end{array} \right.\)
- Responder
-
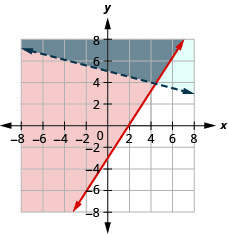
La solución es la región gris.
Resuelve el sistema graficando:\(\left\{\begin{array} {l} x−2y<5\\y>−4\end{array}\right.\)
Solución:
| \(\left\{\begin{array} {l} x−2y<5\\y>−4\end{array}\right.\) | |
| Gráfica\(x−2y<5\), graficando\(x−2y=5\) y probando un punto. Las intercepciones son\(x = 5\) y\(y = −2.5\) y la línea límite será discontinua. Prueba\((0, 0)\) que hace que la desigualdad sea verdadera, así que sombrea (rojo) el lado que contiene\((0, 0).\) |
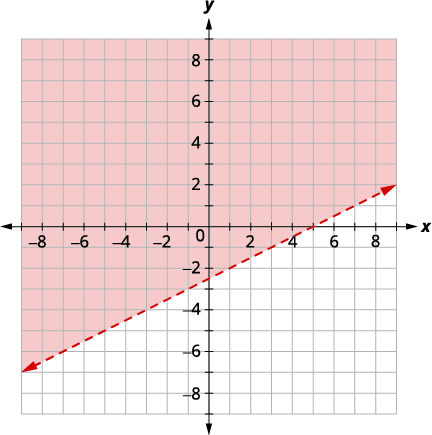 |
| Gráfica\(y>−4\), graficando\(y=−4\) y reconociendo que es una línea horizontal a través\(y=−4\). La línea límite será discontinua. Prueba\((0, 0)\) que hace que la desigualdad sea verdadera para sombrear (azul) el lado que contiene\((0, 0).\) |
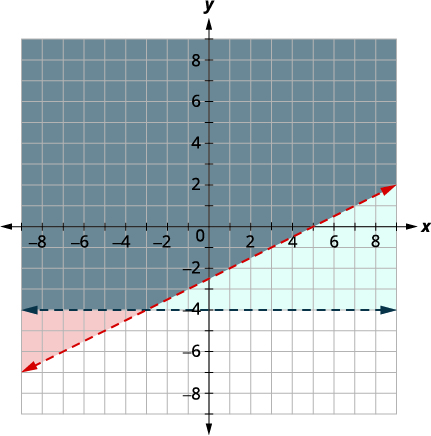 |
El punto\((0,0)\) está en la solución y ya hemos encontrado que es una solución de cada desigualdad. El punto de intersección de las dos líneas no se incluye ya que ambas líneas límite fueron discontinuas.
La solución es el área sombreada dos veces, que aparece como la región sombreada más oscura.
Resuelve el sistema graficando:\(\left\{\begin{array} {l} y\geq 3x−2 \\ y<−1\end{array}\right.\)
- Responder
-
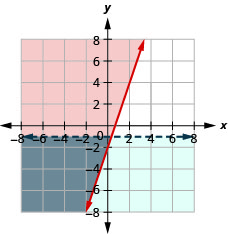
La solución es la región gris.
Resuelve el sistema graficando:\(\left\{\begin{array} {l} x>−4x−2 \\ y\geq −4 \end{array}\right.\)
- Responder
-
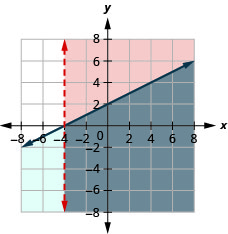
La solución es la región gris.
Los sistemas de desigualdades lineales donde las líneas limítrofes son paralelas podrían no tener solución. Esto lo veremos en el siguiente ejemplo.
Resuelve el sistema graficando:\(\left\{\begin{array} {l} 4x+3y\geq 12 \\ y<−\frac{4}{3}x+1\end{array}\right.\)
Solución:
| \(\left\{\begin{array} {l} 4x+3y\geq 12 \\ y<−\frac{4}{3}x+1\end{array}\right.\) | |
| Gráfica\(4x+3y\geq 12\), graficando\(4x+3y=12\) y probando un punto. Las intercepciones son\(x = 3\) y\(y = 4\) y la línea límite será sólida. Prueba\((0, 0)\) que hace falsa la desigualdad, así que sombrea (rojo) el lado que no contiene\((0, 0).\) |
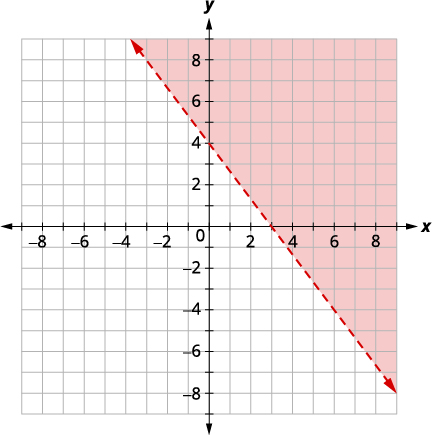 |
| Gráfica\(y<−\frac{4}{3}x+1\) graficando\(y=−\frac{4}{3}x+1\) usando la pendiente\(m=−\frac{4}{3}\) e\(y\) -intercepción\(b = 1.\) La línea límite será discontinua. Prueba\((0, 0)\) que hace que la desigualdad sea verdadera, así que sombrea (azul) el lado que contiene\((0, 0).\) |
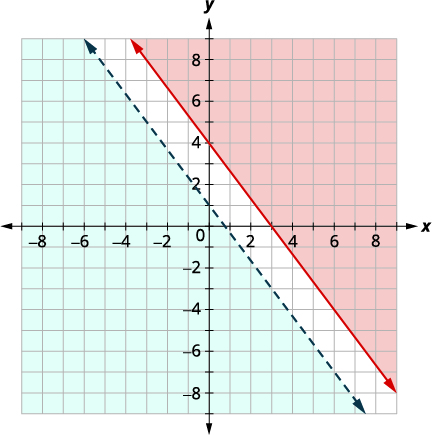 |
No tiene sentido en ambas regiones sombreadas, por lo que el sistema no tiene solución.
Resuelve el sistema graficando:\(\left\{\begin{array} {l} 3x−2y\geq 12 \\ y\geq \frac{3}{2}x+1\end{array}\right.\)
- Responder
-
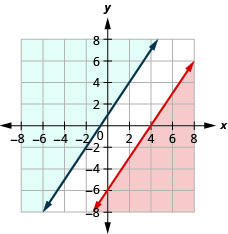
Sin solución.
Resuelve el sistema graficando:\(\left\{\begin{array} {l} x+3y>8\\y<−\frac{1}{3}x−2\end{array}\right.\)
- Responder
-
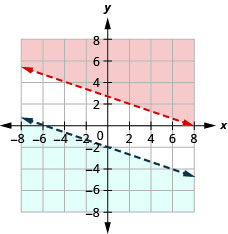
Sin solución.
Algunos sistemas de desigualdades lineales donde las líneas limítrofes son paralelas tendrán una solución. Esto lo veremos en el siguiente ejemplo.
Resuelve el sistema graficando:\(\left\{\begin{array} {l} y>\frac{1}{2}x−4\\x−2y<−4\end{array}\right.\)
Solución:
| \(\left\{\begin{array} {l} y>\frac{1}{2}x−4\\x−2y<−4\end{array}\right.\) | |
| Gráfica\(y>\frac{1}{2}x−4\) graficando\(y=\frac{1}{2}x−4\) usando la pendiente\(m=\frac{1}{2}\) y la intersección\(b = −4.\) La línea límite será discontinua. Prueba\((0, 0)\) que hace que la desigualdad sea verdadera, así que sombrea (rojo) el lado que contiene\((0, 0).\) |
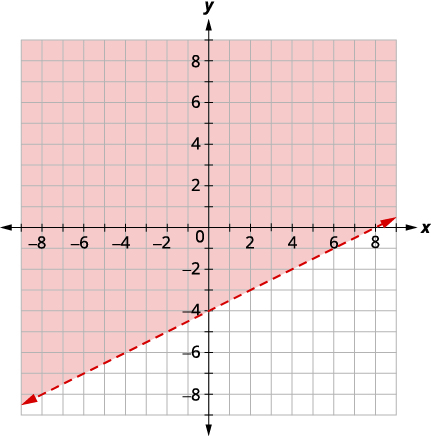 |
| Gráfica\(x−2y<−4\) graficando\(x−2y=−4\) y probando un punto. Las intercepciones son\(x = -4\) y\(y=2\) y la línea límite será discontinua. Elija un punto de prueba en la solución y verifique que sea una solución a ambas inqualidades. Prueba\((0, 0)\) que hace falsa la desigualdad, así que sombrea (azul) el lado que no contiene\((0, 0).\) |
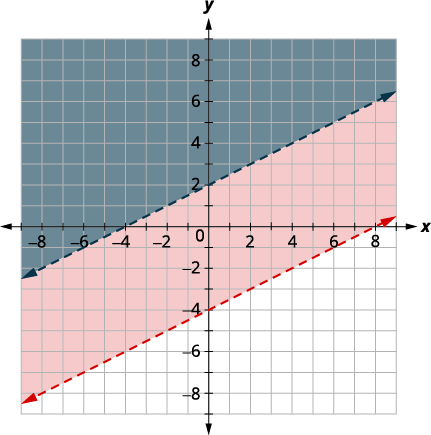 |
No se incluye ningún punto en las líneas de límite en la solución ya que ambas líneas están discontinuas.
La solución es la región que está sombreada dos veces que también es la solución a\(x−2y<−4\).
Resuelve el sistema graficando:\(\left\{\begin{array} {l} y\geq 3x+1 \\ −3x+y\geq −4\end{array}\right.\)
- Responder
-
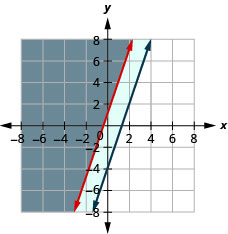
La solución es la región gris.
Resuelve el sistema graficando:\(\left\{\begin{array} {l} y\leq −\frac{1}{4}x+2\\x+4y\leq 4\end{array}\right.\)
- Responder
-
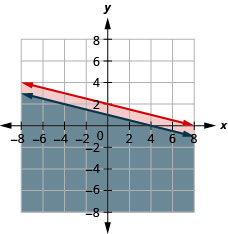
La solución es la región gris.
Resolver Aplicaciones de Sistemas de Desigualdades
Lo primero que tendremos que hacer para resolver aplicaciones de sistemas de desigualdades es traducir cada condición en una desigualdad. Después graficamos el sistema, como hicimos anteriormente, para ver la región que contiene las soluciones. Muchas situaciones serán realistas solo si ambas variables son positivas, por lo que agregamos desigualdades al sistema como requisitos adicionales.
Christy vende sus fotografías en una caseta en una feria callejera. Al inicio del día, quiere tener al menos 25 fotos para exhibir en su stand. Cada foto pequeña que muestra le cuesta $4 y cada foto grande le cuesta $10. Ella no quiere gastar más de 200 dólares en fotos para exhibir.
a. Escribir un sistema de desigualdades para modelar esta situación.
b. graficar el sistema.
c. ¿Podría exhibir 10 fotos pequeñas y 20 grandes?
d. ¿Podría exhibir 20 fotos grandes y 10 pequeñas?
Solución:
a.
\(\begin{array} {ll} \text{Let} &{x=\text{the number of small photos.}} \\ {} &{y=\text{the number of large photos}}\end{array}\)
Para encontrar el sistema de ecuaciones traducir la información.
\( \qquad \begin{array} {l} \\ \\ \text{She wants to have at least 25 photos.} \\ \text{The number of small plus the number of large should be at least }25. \\ \hspace{45mm} x+y\geq 25 \\ \\ \\ $4 \text{ for each small and }$10\text{ for each large must be no more than }$200 \\ \hspace{40mm} 4x+10y\leq 200 \\ \\ \\ \text{The number of small photos must be greater than or equal to }0. \\ \hspace{50mm} x\geq 0 \\ \\ \\ \text{The number of large photos must be greater than or equal to }0. \\ \hspace{50mm} y\geq 0 \end{array} \)
Tenemos nuestro sistema de ecuaciones.
\(\hspace{65mm} \left\{\begin{array} {l} x+y\geq 25 \\4x+10y\leq 200\\x\geq 0\\y\geq 0\end{array}\right.\)
b.
Dado que\(x\geq 0\) y\(y\geq 0\) (ambas son mayores o iguales a) todas las soluciones estarán en el primer cuadrante. Como resultado, nuestra gráfica muestra solo el cuadrante uno.
| Para graficar\(x+y\geq 25\), graficar\(x+y=25\) como una línea continua. Elija\((0, 0)\) como punto de prueba. Ya que no hace verdadera la desigualdad, sombrea (rojo) el lado que no incluye el punto\((0, 0).\) Para graficar\(4x+10y\leq 200\), graficar\(4x+10y=200\) como una línea continua. Elija\((0, 0)\) como punto de prueba. Ya que hace que la desigualdad sea cierta, sombree (azul) el lado que incluye el punto\((0, 0).\) |
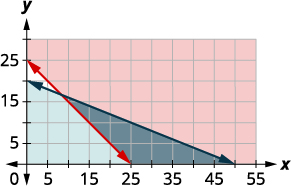 |
La solución del sistema es la región de la gráfica que está sombreada la más oscura. Las secciones de línea límite que bordean la sección sombreada oscura se incluyen en la solución al igual que los puntos en el\(x\) eje -desde\((25, 0)\) hasta\((55, 0).\)
c. Para determinar si funcionarían 10 fotos pequeñas y 20 grandes, miramos la gráfica para ver si el punto\((10, 20)\) está en la región de solución. También podríamos probar el punto para ver si es una solución de ambas ecuaciones.
No lo es, Christy no mostraría 10 fotos pequeñas y 20 grandes.
d. Para determinar si funcionarían 20 fotos pequeñas y 10 grandes, miramos la gráfica para ver si el punto\((20, 10)\) está en la región de solución. También podríamos probar el punto para ver si es una solución de ambas ecuaciones.
Lo es, así que Christy podría optar por mostrar 20 fotos pequeñas y 10 grandes.
Observe que también podríamos probar las posibles soluciones sustituyendo los valores en cada desigualdad.
Un remolque puede llevar un peso máximo de 160 libras y un volumen máximo de 15 pies cúbicos. Un horno microondas pesa 30 libras y tiene 2 pies cúbicos de volumen, mientras que una impresora pesa 20 libras y tiene 3 pies cúbicos de espacio.
a. Escribir un sistema de desigualdades para modelar esta situación.
b. graficar el sistema.
c. ¿Se podrían llevar 4 microondas y 2 impresoras en este tráiler?
d. ¿Se podrían llevar 7 microondas y 3 impresoras en este tráiler?
- Responder
-
a.\(\left\{\begin{array} {l} 30m+20p\leq 160\\2m+3p\leq 15\end{array}\right.\)
b.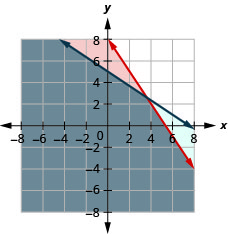
c. si
d. no
Mary necesita comprar suministros de hojas de respuestas y lápices para una prueba estandarizada que se le dará a los estudiantes de segundo año en su escuela secundaria. El número de las hojas de respuesta necesarias es al menos 5 más que el número de lápices. Los lápices cuestan $2 y las hojas de respuesta cuestan $1. El presupuesto de Mary para estos suministros permite un costo máximo de $400.
a. Escribir un sistema de desigualdades para modelar esta situación.
b. graficar el sistema.
c. ¿Podría Mary comprar 100 lápices y 100 hojas de respuesta?
d. ¿Podría Mary comprar 150 lápices y 150 hojas de respuesta?
- Responder
-
a.\(\left\{\begin{array} {l} a\geq p+5 \\ a+2p\leq 400\end{array}\right.\)
b.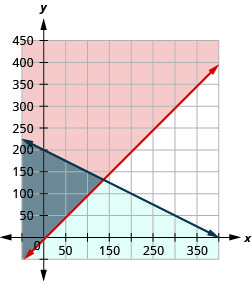
c. no
d. no
Cuando usamos variables distintas\(y\) a\(x\) y para definir una cantidad desconocida, también debemos cambiar los nombres de los ejes de la gráfica.
Omar necesita comer al menos 800 calorías antes de ir a la práctica de su equipo. Todo lo que quiere son hamburguesas y galletas, y no quiere gastar más de 5 dólares. En el restaurante de hamburguesas cerca de su universidad, cada hamburguesa tiene 240 calorías y cuesta $1.40. Cada cookie tiene 160 calorías y cuesta $0.50.
a. Escribir un sistema de desigualdades para modelar esta situación.
b. graficar el sistema.
c. ¿Podría comer 3 hamburguesas y 1 galleta?
d. ¿Podría comer 2 hamburguesas y 4 galletas?
Solución:
a.
\(\begin{array} {ll} \text{Let} & h=\text{the number of hamburgers.} \\ & c=\text{the number of cookies}\end{array}\)
Para encontrar el sistema de ecuaciones traducir la información.
Las calorías de las hamburguesas a 240 calorías cada una, más las calorías de las galletas a 160 calorías cada una deben ser más de 800.
\(\qquad \begin{array} {l} \hspace{40mm} 240h+160c\geq 800 \\ \\ \\ \text{The amount spent on hamburgers at }$1.40\text{ each, plus the amount spent on cookies}\\\text{at }$0.50\text{ each must be no more than }$5.00.\\ \hspace{40mm} 1.40h+0.50c\leq 5 \\ \\ \\ \text{The number of hamburgers must be greater than or equal to 0.} \\ \hspace{50mm} h\geq 0 \\ \text{The number of cookies must be greater than or equal to 0.}\\ \hspace{50mm} c\geq 0 \end{array} \)
\(\text{We have our system of equations.} \qquad \left\{ \begin{array} {l} 240h+160c\geq 800 \\ 1.40h+0.50c\leq 5 \\ h\geq 0 \\ c\geq 0\end{array} \right.\)
b.
Dado que\(h\geq 0\) y\(c\geq 0\) (ambas son mayores o iguales a) todas las soluciones estarán en el primer cuadrante. Como resultado, nuestra gráfica muestra solo el cuadrante uno.
| Para graficar\(240h+160c\geq 800\), graficar\(240h+160c=800\) como una línea continua. Elija\((0, 0)\) como punto de prueba. Ya que no hace verdadera la desigualdad, sombrea (rojo) el lado que no incluye el punto\((0, 0).\) |
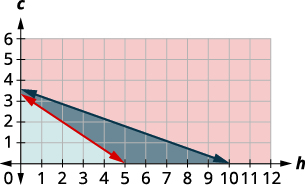 |
Gráfica\(1.40h+0.50c\leq 5\). La línea límite es\(1.40h+0.50c=5\). Probamos\((0, 0)\) y hace realidad la desigualdad. Sombreamos el lado de la línea que incluye\((0, 0).\)
La solución del sistema es la región de la gráfica que está sombreada la más oscura. Las secciones de línea límite que bordean la sección sombreada oscura se incluyen en la solución al igual que los puntos en el\(x\) eje -desde\((5, 0)\) hasta\((10, 0).\)
c. Para determinar si 3 hamburguesas y 2 galletas cumplirían con los criterios de Omar, vemos si el punto\((3, 2)\) está en la región de solución. Lo es, así que Omar podría optar por comer 3 hamburguesas y 2 galletas.
d. Para determinar si 2 hamburguesas y 4 galletas cumplirían con los criterios de Omar, vemos si el punto\((2, 4)\) está en la región de solución. Es, Omar podría optar por comer 2 hamburguesas y 4 galletas.
También podríamos probar las posibles soluciones sustituyendo los valores en cada desigualdad.
La tensión necesita comer al menos 1,000 calorías adicionales al día para prepararse para correr un maratón. Solo tiene 25 dólares para gastar en la comida extra que necesita y la gastará en donas de $0.75 que tienen 360 calorías cada una y $2 bebidas energéticas que tienen 110 calorías.
a. Escribir un sistema de desigualdades que modele esta situación.
b. graficar el sistema.
c. ¿Puede comprar 8 donas y 4 bebidas energéticas y satisfacer sus necesidades calóricas?
d. ¿Puede comprar 1 donut y 3 bebidas energéticas y satisfacer sus necesidades calóricas?
- Responder
-
a.\(\left\{\begin{array} {l} 0.75d+2e\leq 25\\360d+110e\geq 1000\end{array}\right.\)
b.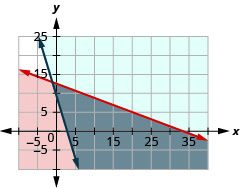
c. si
d. no
El médico de Philip le dice que debería agregar al menos 1,000 calorías más por día a su dieta habitual. Philip quiere comprar barras de proteína que cuesten $1.80 cada una y que tengan 140 calorías y jugo que cuesta $1.25 por botella y que tengan 125 calorías. No quiere gastar más de 12 dólares.
a. Escribir un sistema de desigualdades que modele esta situación.
b. graficar el sistema.
c. ¿Puede comprar 3 barras de proteína y 5 botellas de jugo?
d. ¿Puede comprar 5 barras de proteína y 3 botellas de jugo?
- Responder
-
a.\(\left\{\begin{array} {l} 140p+125j\geq 1000\\1.80p+1.25j\leq 12\end{array}\right.\)
b.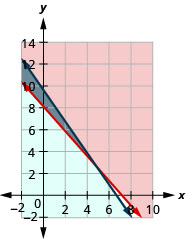
c. si
d. no
Acceda a estos recursos en línea para obtener instrucción y práctica adicionales con la resolución de sistemas de desigualdades lineales mediante gráficos.
- Resolver sistemas de desigualdades lineales mediante gráficos
- Sistemas de Desigualdades Lineales
Conceptos clave
- Soluciones de un Sistema de Desigualdades Lineales: Las soluciones de un sistema de desigualdades lineales son los valores de las variables que hacen verdaderas todas las desigualdades. La solución de un sistema de desigualdades lineales se muestra como una región sombreada en el sistema de\(xy\) coordenadas que incluye todos los puntos cuyos pares ordenados hacen verdaderas las desigualdades.
- Cómo resolver un sistema de desigualdades lineales mediante la gráfica.
- Grafica la primera desigualdad.
Grafica la línea límite.
Sombra en el lado de la línea límite donde la desigualdad es verdadera. - En la misma cuadrícula, grafica la segunda desigualdad.
Grafica la línea límite.
Sombra en el lado de esa línea límite donde la desigualdad es verdadera. - La solución es la región donde se superpone el sombreado.
- Verifique eligiendo un punto de prueba.
- Grafica la primera desigualdad.
Glosario
- sistema de desigualdades lineales
- Dos o más desigualdades lineales agrupadas forman un sistema de desigualdades lineales.


