Saltar al contenido principal
LibreTexts Español

8.3E: Ejercicios

  1. Última actualización
  2. Guardar como PDF
  • Page ID
    112494

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    La práctica hace la perfección

    Ejercicio SET A: utilizar la propiedad product para simplificar expresiones radicales

    En los siguientes ejercicios, utilice la Propiedad del Producto para simplificar expresiones radicales.

    1. \(\sqrt{27}\)
    2. \(\sqrt{80}\)
    3. \(\sqrt{125}\)
    4. \(\sqrt{96}\)
    5. \(\sqrt{147}\)
    6. \(\sqrt{450}\)
    7. \(\sqrt{800}\)
    8. \(\sqrt{675}\)
      1. \(\sqrt[4]{32}\)
      2. \(\sqrt[5]{64}\)
      1. \(\sqrt[3]{625}\)
      2. \(\sqrt[6]{128}\)
      1. \(\sqrt[5]{64}\)
      2. \(\sqrt[3]{256}\)
      1. \(\sqrt[4]{3125}\)
      2. \(\sqrt[3]{81}\)
    Contestar

    1. \(3\sqrt{3}\)

    3. \(5\sqrt{5}\)

    5. \(7\sqrt{3}\)

    7. \(20\sqrt{2}\)

    9.

    1. \(2 \sqrt[4]{2}\)
    2. \(2 \sqrt[5]{2}\)

    11.

    1. \(2 \sqrt[5]{2}\)
    2. \(4 \sqrt[3]{4}\)
    Ejercicio SET B: utilizar la propiedad product para simplificar expresiones radicales

    En los siguientes ejercicios, simplifique el uso de signos de valor absoluto según sea necesario.

      1. \(\sqrt{y^{11}}\)
      2. \(\sqrt[3]{r^{5}}\)
      3. \(\sqrt[4]{s^{10}}\)
      1. \(\sqrt{m^{13}}\)
      2. \(\sqrt[5]{u^{7}}\)
      3. \(\sqrt[6]{v^{11}}\)
      1. \(\sqrt{n^{21}}\)
      2. \(\sqrt[3]{q^{8}}\)
      3. \(\sqrt[8]{n^{10}}\)
      1. \(\sqrt{r^{25}}\)
      2. \(\sqrt[5]{p^{8}}\)
      3. \(\sqrt[4]{m^{5}}\)
      1. \(\sqrt{125 r^{13}}\)
      2. \(\sqrt[3]{108 x^{5}}\)
      3. \(\sqrt[4]{48 y^{6}}\)
      1. \(\sqrt{80 s^{15}}\)
      2. \(\sqrt[5]{96 a^{7}}\)
      3. \(\sqrt[6]{128 b^{7}}\)
      1. \(\sqrt{242 m^{23}}\)
      2. \(\sqrt[4]{405 m 10}\)
      3. \(\sqrt[5]{160 n^{8}}\)
      1. \(\sqrt{175 n^{13}}\)
      2. \(\sqrt[5]{512 p^{5}}\)
      3. \(\sqrt[4]{324 q^{7}}\)
      1. \(\sqrt{147 m^{7} n^{11}}\)
      2. \(\sqrt[3]{48 x^{6} y^{7}}\)
      3. \(\sqrt[4]{32 x^{5} y^{4}}\)
      1. \(\sqrt{96 r^{3} s^{3}}\)
      2. \(\sqrt[3]{80 x^{7} y^{6}}\)
      3. \(\sqrt[4]{80 x^{8} y^{9}}\)
      1. \(\sqrt{192 q^{3} r^{7}}\)
      2. \(\sqrt[3]{54 m^{9} n^{10}}\)
      3. \(\sqrt[4]{81 a^{9} b^{8}}\)
      1. \(\sqrt{150 m^{9} n^{3}}\)
      2. \(\sqrt[3]{81 p^{7} q^{8}}\)
      3. \(\sqrt[4]{162 c^{11} d^{12}}\)
      1. \(\sqrt[3]{-864}\)
      2. \(\sqrt[4]{-256}\)
      1. \(\sqrt[5]{-486}\)
      2. \(\sqrt[6]{-64}\)
      1. \(\sqrt[5]{-32}\)
      2. \(\sqrt[8]{-1}\)
      1. \(\sqrt[3]{-8}\)
      2. \(\sqrt[4]{-16}\)
      1. \(5+\sqrt{12}\)
      2. \(\dfrac{10-\sqrt{24}}{2}\)
      1. \(8+\sqrt{96}\)
      2. \(\dfrac{8-\sqrt{80}}{4}\)
      1. \(1+\sqrt{45}\)
      2. \(\dfrac{3+\sqrt{90}}{3}\)
      1. \(3+\sqrt{125}\)
      2. \(\dfrac{15+\sqrt{75}}{5}\)
    Contestar

    1.

    1. \(\left|y^{5}\right| \sqrt{y}\)
    2. \(r \sqrt[3]{r^{2}}\)
    3. \(s^{2} \sqrt[4]{s^{2}}\)

    3.

    1. \(n^{10} \sqrt{n}\)
    2. \(q^{2} \sqrt[3]{q^{2}}\)
    3. \(|n| \sqrt[8]{n^{2}}\)

    5.

    1. \(5 r^{6} \sqrt{5 r}\)
    2. \(3 x \sqrt[3]{4 x^{2}}\)
    3. \(2|y| \sqrt[4]{3 y^{2}}\)

    7.

    1. \(11\left|m^{11}\right| \sqrt{2 m}\)
    2. \(3 m^{2} \sqrt[4]{5 m^{2}}\)
    3. \(2 n \sqrt[5]{5 n^{3}}\)

    9.

    1. \(7\left|m^{3} n^{5}\right| \sqrt{3 m n}\)
    2. \(2 x^{2} y^{2} \sqrt[3]{6 y}\)
    3. \(2|x y| \sqrt[4]{2 x}\)

    11.

    1. \(8\left|q r^{3}\right| \sqrt{3 q r}\)
    2. \(3 m^{3} n^{3} \sqrt[3]{2 n}\)
    3. \(3 a^{2} b^{2} \sqrt[4]{a}\)

    13.

    1. \(-6 \sqrt[3]{4}\)
    2. no real

    15.

    1. \(-2\)
    2. no real

    17.

    1. \(5+2 \sqrt{3}\)
    2. \(5-\sqrt{6}\)

    19.

    1. \(1+3 \sqrt{5}\)
    2. \(1+\sqrt{10}\)
    Conjunto de ejercicios C: utilizar la propiedad cociente para simplificar expresiones radicales

    En los siguientes ejercicios, utilice la Propiedad Cociente para simplificar las raíces cuadradas.

      1. \(\sqrt{\dfrac{45}{80}}\)
      2. \(\sqrt[3]{\dfrac{8}{27}}\)
      3. \(\sqrt[4]{\dfrac{1}{81}}\)
      1. \(\sqrt{\dfrac{72}{98}}\)
      2. \(\sqrt[3]{\dfrac{24}{81}}\)
      3. \(\sqrt[4]{\dfrac{6}{96}}\)
      1. \(\sqrt{\dfrac{100}{36}}\)
      2. \(\sqrt[3]{\dfrac{81}{375}}\)
      3. \(\sqrt[4]{\dfrac{1}{256}}\)
      1. \(\sqrt{\dfrac{121}{16}}\)
      2. \(\sqrt[3]{\dfrac{16}{250}}\)
      3. \(\sqrt[4]{\dfrac{32}{162}}\)
      1. \(\sqrt{\dfrac{x^{10}}{x^{6}}}\)
      2. \(\sqrt[3]{\dfrac{p^{11}}{p^{2}}}\)
      3. \(\sqrt[4]{\dfrac{q^{17}}{q^{13}}}\)
      1. \(\sqrt{\dfrac{p^{20}}{p^{10}}}\)
      2. \(\sqrt[5]{\dfrac{d^{12}}{d^{7}}}\)
      3. \(\sqrt[8]{\dfrac{m^{12}}{m^{4}}}\)
      1. \(\sqrt{\dfrac{y^{4}}{y^{8}}}\)
      2. \(\sqrt[5]{\dfrac{u^{21}}{u^{11}}}\)
      3. \(\sqrt[6]{\dfrac{v^{30}}{v^{12}}}\)
      1. \(\sqrt{\dfrac{q^{8}}{q^{14}}}\)
      2. \(\sqrt[3]{\dfrac{r^{14}}{r^{5}}}\)
      3. \(\sqrt[4]{\dfrac{c^{21}}{c^{9}}}\)
    9. \(\sqrt{\dfrac{96 x^{7}}{121}}\)
    10. \(\sqrt{\dfrac{108 y^{4}}{49}}\)
    11. \(\sqrt{\dfrac{300 m^{5}}{64}}\)
    12. \(\sqrt{\dfrac{125 n^{7}}{169}}\)
    13. \(\sqrt{\dfrac{98 r^{5}}{100}}\)
    14. \(\sqrt{\dfrac{180 s^{10}}{144}}\)
    15. \(\sqrt{\dfrac{28 q^{6}}{225}}\)
    16. \(\sqrt{\dfrac{150 r^{3}}{256}}\)
      1. \(\sqrt{\dfrac{75 r^{9}}{s^{8}}}\)
      2. \(\sqrt[3]{\dfrac{54 a^{8}}{b^{3}}}\)
      3. \(\sqrt[4]{\dfrac{64 c^{5}}{d^{4}}}\)
      1. \(\sqrt{\dfrac{72 x^{5}}{y^{6}}}\)
      2. \(\sqrt[5]{\dfrac{96 r^{11}}{s^{5}}}\)
      3. \(\sqrt[6]{\dfrac{128 u^{7}}{v^{12}}}\)
      1. \(\sqrt{\dfrac{28 p^{7}}{q^{2}}}\)
      2. \(\sqrt[3]{\dfrac{81 s^{8}}{t^{3}}}\)
      3. \(\sqrt[4]{\dfrac{64 p^{15}}{q^{12}}}\)
      1. \(\sqrt{\dfrac{45 r^{3}}{s^{10}}}\)
      2. \(\sqrt[3]{\dfrac{625 u^{10}}{v^{3}}}\)
      3. \(\sqrt[4]{\dfrac{729 c^{21}}{d^{8}}}\)
      1. \(\sqrt{\dfrac{32 x^{5} y^{3}}{18 x^{3} y}}\)
      2. \(\sqrt[3]{\dfrac{5 x^{6} y^{9}}{40 x^{5} y^{3}}}\)
      3. \(\sqrt[4]{\dfrac{5 a^{8} b^{6}}{80 a^{3} b^{2}}}\)
      1. \(\sqrt{\dfrac{75 r^{6} s^{8}}{48 r s^{4}}}\)
      2. \(\sqrt[3]{\dfrac{24 x^{8} y^{4}}{81 x^{2} y}}\)
      3. \(\sqrt[4]{\dfrac{32 m^{9} n^{2}}{162 m n^{2}}}\)
      1. \(\sqrt{\dfrac{27 p^{2} q}{108 p^{4} q^{3}}}\)
      2. \(\sqrt[3]{\dfrac{16 c^{5} d^{7}}{250 c^{2} d^{2}}}\)
      3. \(\sqrt[6]{\dfrac{2 m^{9} n^{7}}{128 m^{3} n}}\)
      1. \(\sqrt{\dfrac{50 r^{5} s^{2}}{128 r^{2} s^{6}}}\)
      2. \(\sqrt[3]{\dfrac{24 m^{9} n^{7}}{375 m^{4} n}}\)
      3. \(\sqrt[4]{\dfrac{81 m^{2} n^{8}}{256 m^{1} n^{2}}}\)
      1. \(\dfrac{\sqrt{45 p^{9}}}{\sqrt{5 q^{2}}}\)
      2. \(\dfrac{\sqrt[4]{64}}{\sqrt[4]{2}}\)
      3. \(\dfrac{\sqrt[5]{128 x^{8}}}{\sqrt[5]{2 x^{2}}}\)
      1. \(\dfrac{\sqrt{80 q^{5}}}{\sqrt{5 q}}\)
      2. \(\dfrac{\sqrt[3]{-625}}{\sqrt[3]{5}}\)
      3. \(\dfrac{\sqrt[4]{80 m^{7}}}{\sqrt[4]{5 m}}\)
      1. \(\dfrac{\sqrt{50 m^{7}}}{\sqrt{2 m}}\)
      2. \(\sqrt[3]{\dfrac{1250}{2}}\)
      3. \(\sqrt[4]{\dfrac{486 y^{9}}{2 y^{3}}}\)
      1. \(\dfrac{\sqrt{72 n^{11}}}{\sqrt{2 n}}\)
      2. \(\sqrt[3]{\dfrac{162}{6}}\)
      3. \(\sqrt[4]{\dfrac{160 r^{10}}{5 r^{3}}}\)
    Contestar

    1.

    1. \(\dfrac{3}{4}\)
    2. \(\dfrac{2}{3}\)
    3. \(\dfrac{1}{3}\)

    3.

    1. \(\dfrac{5}{3}\)
    2. \(\dfrac{3}{5}\)
    3. \(\dfrac{1}{4}\)

    5.

    1. \(x^{2}\)
    2. \(p^{3}\)
    3. \(|q|\)

    7.

    1. \(\dfrac{1}{y^{2}}\)
    2. \(u^{2}\)
    3. \(|v^{3}|\)

    9. \(\dfrac{4\left|x^{3}\right| \sqrt{6 x}}{11}\)

    11. \(\dfrac{10 m^{2} \sqrt{3 m}}{8}\)

    13. \(\dfrac{7 r^{2} \sqrt{2 r}}{10}\)

    15. \(\dfrac{2\left|q^{3}\right| \sqrt{7}}{15}\)

    17.

    1. \(\dfrac{5 r^{4} \sqrt{3 r}}{s^{4}}\)
    2. \(\dfrac{3 a^{2} \sqrt[3]{2 a^{2}}}{|b|}\)
    3. \(\dfrac{2|c| \sqrt[4]{4 c}}{|d|}\)

    19.

    1. \(\dfrac{2\left|p^{3}\right| \sqrt{7 p}}{|q|}\)
    2. \(\dfrac{3 s^{2} \sqrt[3]{3 s^{2}}}{t}\)
    3. \(\dfrac{2\left|p^{3}\right| \sqrt[4]{4 p^{3}}}{\left|q^{3}\right|}\)

    21.

    1. \(\dfrac{4|x y|}{3}\)
    2. \(\dfrac{y^{2} \sqrt[3]{x}}{2}\)
    3. \(\dfrac{|a b| \sqrt[4]{a}}{4}\)

    23.

    1. \(\dfrac{1}{2|p q|}\)
    2. \(\dfrac{2 c d \sqrt[5]{2 d^{2}}}{5}\)
    3. \(\dfrac{|m n| \sqrt[6]{2}}{2}\)

    25.

    1. \(\dfrac{3 p^{4} \sqrt{p}}{|q|}\)
    2. \(2 \sqrt[4]{2}\)
    3. \(2 x \sqrt[5]{2 x}\)

    27.

    1. \(5\left|m^{3}\right|\)
    2. \(5 \sqrt[3]{5}\)
    3. \(3|y| \sqrt[4]{3 y^{2}}\)
    Ejercicio SET D: ejercicios de escritura
    1. Explique por qué\(\sqrt{x^{4}}=x^{2}\). Entonces explica por qué\(\sqrt{x^{16}}=x^{8}\).
    2. \(7+\sqrt{9}\)Explique por qué no es igual a\(\sqrt{7+9}\).
    3. Explica cómo lo sabes\(\sqrt[5]{x^{10}}=x^{2}\).
    4. \(\sqrt[4]{-64}\)Explique por qué no es un número real sino\(\sqrt[3]{-64}\) que sí.
    Contestar

    1. Las respuestas pueden variar

    3. Las respuestas pueden variar

    Autocomprobación

    a. después de completar los ejercicios, utilice esta lista de verificación para evaluar su dominio de los objetivos de esta sección.

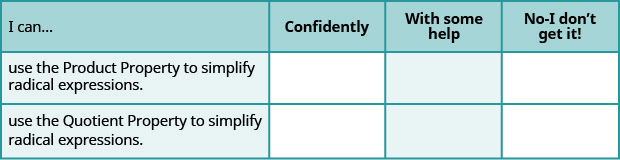
    Esta tabla tiene 3 filas y 4 columnas. La primera fila es una fila de encabezado y etiqueta cada columna. El encabezado de la primera columna es “I can…â€, el segundo es “confiadamente, el tercero es “con algo de ayudaâ €, y el cuarto es †œno, I donâ €™ t get itâ €. Bajo la primera columna están las frases “use la propiedad del producto para simplificar las expresiones radicales†y “use la propiedad del cociente para simplificar las expresiones radicalesâ €. Las otras columnas se dejan en blanco para que el alumno pueda indicar su nivel de dominio para cada tema.
    Figura 8.2.1

    b. Después de revisar esta lista de verificación, ¿qué harás para tener confianza en todos los objetivos?

    This page titled 8.3E: Ejercicios is shared under a CC BY 4.0 license and was authored, remixed, and/or curated by OpenStax via source content that was edited to the style and standards of the LibreTexts platform; a detailed edit history is available upon request.