8.8: Usar radicales en las funciones
- Page ID
- 112485
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Al final de esta sección, podrás:
- Evaluar una función radical
- Encontrar el dominio de una función radical
- Funciones radicales gráficas
Antes de comenzar, toma este cuestionario de preparación.
- Resolver:\(1−2x≥0\).
Si te perdiste este problema, revisa el Ejemplo 2.50. - Para\(f(x)=3x−4\), evaluar\(f(2),f(−1),f(0)\).
Si te perdiste este problema, revisa el Ejemplo 3.48. - Gráfica\(f(x)=\sqrt{x}\). Indicar el dominio y el rango de la función en notación de intervalos.
Si te perdiste este problema, revisa el Ejemplo 3.56.
Evaluar una función radical
En esta sección ampliaremos nuestro trabajo previo con funciones para incluir radicales. Si una función es definida por una expresión radical, la llamamos función radical.
- La función de raíz cuadrada es\(f(x)=\sqrt{x}\).
- La función de raíz cubo es\(f(x)=\sqrt[3]{x}\).
Una función radical es una función que se define por una expresión radical.
Para evaluar una función radical, encontramos el valor de\(f(x)\) para un valor dado de\(x\) tal como lo hicimos en nuestro trabajo anterior con funciones.
Para la función\(f(x)=\sqrt{2 x-1}\), encontrar
- \(f(5)\)
- \(f(-2)\)
Solución:
a.
\(f(x)=\sqrt{2 x-1}\)
Evaluar\(f(5)\),\(5\) sustituir\(x\).
\(f(5)=\sqrt{2 \cdot 5-1}\)
Simplificar.
\(f(5)=\sqrt{9}\)
Toma la raíz cuadrada.
\(f(5)=3\)
b.
\(f(x)=\sqrt{2 x-1}\)
Evaluar\(f(-2)\),\(-2\) sustituir\(x\).
\(f(-2)=\sqrt{2(-2)-1}\)
Simplificar.
\(f(-2)=\sqrt{-5}\)
Dado que la raíz cuadrada de un número negativo no es un número real, la función no tiene un valor at\(x=-2\).
Para la función\(f(x)=\sqrt{3 x-2}\), encontrar
- \(f(6)\)
- \(f(0)\)
- Contestar
-
- \(f(6)=4\)
- sin valor en\(x=0\)
Para la función\(g(x)=\sqrt{5x+5}\), encontrar
- \(g(4)\)
- \(g(-3)\)
- Contestar
-
- \(g(4)=5\)
- sin valor en\(f(-3)\)
Seguimos el mismo procedimiento para evaluar las raíces cubicas.
Para la función\(g(x)=\sqrt[3]{x-6}\), encontrar
- \(g(14)\)
- \(g(-2)\)
Solución:
a.
\(g(x)=\sqrt[3]{x-6}\)
Evaluar\(g(14)\),\(14\) sustituir\(x\).
\(g(14)=\sqrt[3]{14-6}\)
Simplificar.
\(g(14)=\sqrt[3]{8}\)
Toma la raíz cubicada.
\(g(14)=2\)
b.
\(g(x)=\sqrt[3]{x-6}\)
Evaluar\(g(-2)\),\(-2\) sustituir\(x\).
\(g(-2)=\sqrt[3]{-2-6}\)
Simplificar.
\(g(-2)=\sqrt[3]{-8}\)
Toma la raíz cubicada.
\(g(-2)=-2\)
Para la función\(g(x)=\sqrt[3]{3 x-4}\), encontrar
- \(g(4)\)
- \(g(1)\)
- Contestar
-
- \(g(4)=2\)
- \(g(1)=-1\)
Para la función\(h(x)=\sqrt[3]{5 x-2}\), encontrar
- \(h(2)\)
- \(h(-5)\)
- Contestar
-
- \(h(2)=2\)
- \(h(-5)=-3\)
El siguiente ejemplo tiene cuartas raíces.
Para la función\(f(x)=\sqrt[4]{5 x-4}\), encontrar
- \(f(4)\)
- \(f(-12)\)
Solución:
a.
\(f(x)=\sqrt[4]{5 x-4}\)
Evaluar\(f(4)\),\(4\) sustituir\(x\).
\(f(4)=\sqrt[4]{5 \cdot 4-4}\)
Simplificar.
\(f(4)=\sqrt[4]{16}\)
Toma la cuarta raíz.
\(f(4)=2\)
b.
\(f(x)=\sqrt[4]{5 x-4}\)
Evaluar\(f(-12)\),\(-12\) sustituir\(x\).
\(f(-12)=\sqrt[4]{5(-12)-4}\)
Simplificar.
\(f(-12)=\sqrt[4]{-64}\)
Dado que la cuarta raíz de un número negativo no es un número real, la función no tiene un valor at\(x=-12\).
Para la función\(f(x)=\sqrt[4]{3 x+4}\), encontrar
- \(f(4)\)
- \(f(-1)\)
- Contestar
-
- \(f(4)=2\)
- \(f(-1)=1\)
Para la función\(g(x)=\sqrt[4]{5 x+1}\), encontrar
- \(g(16)\)
- \(g(3)\)
- Contestar
-
- \(g(16)=3\)
- \(g(3)=2\)
Encontrar el dominio de una función radical
Para encontrar el dominio y rango de funciones radicales, utilizamos nuestras propiedades de radicales. Para un radical con un índice par, dijimos que el radicando tenía que ser mayor o igual a cero ya que las raíces pares de números negativos no son números reales. Para un índice impar, el radicando puede ser cualquier número real. Reformulamos las propiedades aquí para referencia.
Propiedades de\(\sqrt[n]{a}\)
Cuando\(n\) es un número par y:
- \(a \geq 0\), entonces\(\sqrt[n]{a}\) es un número real.
- \(a<0\), entonces no\(\sqrt[n]{a}\) es un número real.
Cuando\(n\) es un número impar,\(\sqrt[n]{a}\) es un número real para todos los valores de\(a\).
Entonces, para encontrar el dominio de una función radical con índice par, establecemos que el radicando sea mayor o igual a cero. Para un radical índice impar, el radicando puede ser cualquier número real.
Dominio de una función radical
Cuando el índice del radical es par, el radicando debe ser mayor o igual a cero.
Cuando el índice del radical es impar, el radicando puede ser cualquier número real.
Encuentra el dominio de la función,\(f(x)=\sqrt{3 x-4}\). Escribe el dominio en notación de intervalos.
Solución:
Ya que la función,\(f(x)=\sqrt{3 x-4}\) tiene un radical con un índice de\(2\), que es par, sabemos que el radicando debe ser mayor o igual a\(0\). Establecimos que el radicando sea mayor o igual a\(0\) y luego resolvemos encontrar el dominio.
Resolver.
\(\begin{aligned} 3 x-4 & \geq 0 \\ 3 x & \geq 4 \\ x & \geq \frac{4}{3} \end{aligned}\)
El dominio de\(f(x)=\sqrt{3 x-4}\) es todos los valores\(x \geq \frac{4}{3}\) y lo escribimos en notación de intervalos como\(\left[\frac{4}{3}, \infty\right)\).
Encuentra el dominio de la función,\(f(x)=\sqrt{6 x-5}\). Escribe el dominio en notación de intervalos.
- Contestar
-
\(\left[\frac{5}{6}, \infty\right)\)
Encuentra el dominio de la función,\(f(x)=\sqrt{4-5 x}\). Escribe el dominio en notación de intervalos.
- Contestar
-
\(\left(-\infty, \frac{4}{5}\right]\)
Encuentra el dominio de la función,\(g(x)=\sqrt{\frac{6}{x-1}}\). Escribe el dominio en notación de intervalos.
Solución:
Resolver la función,\(g(x)=\sqrt{\frac{6}{x-1}}\) tiene un radical con un índice de\(2\), que es par, sabemos que el radicando debe ser mayor o igual a\(0\).
El radicando no puede ser cero ya que el numerador no es cero.
\(\frac{6}{x-1}\)Para ser mayor que cero, el denominador debe ser positivo ya que el numerador es positivo. Sabemos que un positivo dividido por un positivo es positivo.
Establecimos\(x-1>0\) y resolvemos.
\(x-1>0\)
Resolver.
\(x>1\)
También, como el radicando es una fracción, debemos darnos cuenta de que el denominador no puede ser cero.
Resolvemos\(x-1=0\) encontrar el valor que se debe eliminar del dominio.
\(x-1=0\)
Resolver.
\(x=1\)así\(x/neq 1\) en el dominio.
Armando esto obtenemos el dominio es\(x>1\) y lo escribimos como\((1, \infty)\).
Encuentra el dominio de la función,\(f(x)=\sqrt{\frac{4}{x+3}}\). Escribe el dominio en notación de intervalos.
- Contestar
-
\((-3, \infty)\)
Encuentra el dominio de la función,\(h(x)=\sqrt{\frac{9}{x-5}}\). Escribe el dominio en notación de intervalos.
- Contestar
-
\((5, \infty)\)
El siguiente ejemplo involucra una raíz cubo y por lo tanto requerirá un pensamiento diferente.
Encuentra el dominio de la función,\(f(x)=\sqrt[3]{2 x^{2}+3}\). Escribe el dominio en notación de intervalos.
Solución:
Dado que la función,\(f(x)=\sqrt[3]{2 x^{2}+3}\) tiene un radical con un índice de\(3\), que es impar, sabemos que el radicando puede ser cualquier número real. Esto nos dice que el dominio es cualquier número real. En notación de intervalos, escribimos\((-\infty, \infty)\).
El dominio de\(f(x)=\sqrt[3]{2 x^{2}+3}\) es todo números reales y lo escribimos en notación de intervalos como\((-\infty, \infty)\).
Encuentra el dominio de la función,\(f(x)=\sqrt[3]{3 x^{2}-1}\). Escribe el dominio en notación de intervalos.
- Contestar
-
\((-\infty, \infty)\)
Encuentra el dominio de la función,\(g(x)=\sqrt[3]{5 x-4}\). Escribe el dominio en notación de intervalos.
- Contestar
-
\((-\infty, \infty)\)
Funciones de Radical Gráfica
Antes de graficar cualquier función radical, primero encontramos el dominio de la función. Para la función,\(f(x)=\sqrt{x}\), el índice es parejo, y así el radicando debe ser mayor o igual a\(0\).
Esto nos dice que el dominio es\(x≥0\) y lo escribimos en notación de intervalos como\([0,∞)\).
Anteriormente se utilizó la gráfica de puntos para graficar la función,\(f(x)=\sqrt{x}\). Elegimos\(x\) -valores, los sustituimos y luego creamos un gráfico. Observe que elegimos puntos que son cuadrados perfectos para facilitar la toma de la raíz cuadrada.
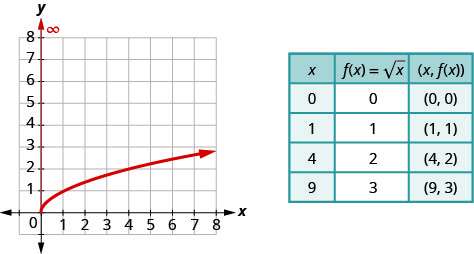
Una vez que vemos la gráfica, podemos encontrar el rango de la función. Los\(y\) -valores de la función son mayores o iguales a cero. El rango entonces es\([0,∞)\).
Para la función\(f(x)=\sqrt{x+3}\),
- encontrar el dominio
- graficar la función
- usar la gráfica para determinar el rango
Solución:
- Dado que el radical tiene índice\(2\), sabemos que el radicando debe ser mayor o igual a cero. Si\(x+3 \geq 0\), entonces\(x \geq-3\). Esto nos dice que el dominio es todos los valores\(x \geq-3\) y escrito en notación de intervalo como\([-3, \infty)\).
- Para graficar la función, elegimos puntos en el intervalo\([-3, \infty)\) que también nos darán un radicando el cual será fácil tomar la raíz cuadrada.
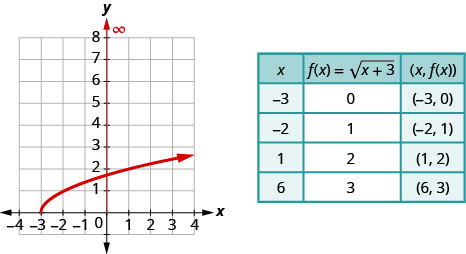
c. Al mirar la gráfica, vemos que los\(y\) -valores de la función son mayores o iguales a cero. El rango entonces es\([0, \infty)\).
Para la función\(f(x)=\sqrt{x+2}\),
- encontrar el dominio
- graficar la función
- usar la gráfica para determinar el rango
- Contestar
-
- dominio:\([-2, \infty)\)
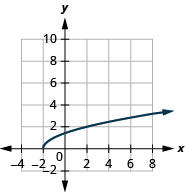
Figura 8.7.3- rango:\([0, \infty)\)
Para la función\(f(x)=\sqrt{x-2}\),
- encontrar el dominio
- graficar la función
- usar la gráfica para determinar el rango
- Contestar
-
- dominio:\([2, \infty)\)
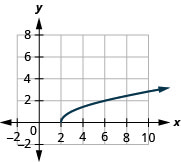
Figura 8.7.4- rango:\([0, \infty)\)
En nuestro trabajo anterior graficamos funciones, graficamos\(f(x)=x^{3}\) pero no graficamos la función\(f(x)=\sqrt[3]{x}\). Esto lo haremos ahora en el siguiente ejemplo.
Para la función\(f(x)=\sqrt[3]{x}\),
- encontrar el dominio
- graficar la función
- usar la gráfica para determinar el rango
Solución:
a. como el radical tiene índice\(3\), sabemos que el radicando puede ser cualquier número real. Esto nos dice que el dominio es todo números reales y escrito en notación de intervalos como\((-\infty, \infty)\)
b. Para graficar la función, elegimos puntos en el intervalo\((-\infty, \infty)\) que también nos darán un radicand que será fácil de tomar la raíz cubo.

c. Al mirar la gráfica, vemos que los\(y\) -valores de la función son todos números reales. El rango entonces es\((-\infty, \infty)\).
Para la función\(f(x)=-\sqrt[3]{x}\),
- encontrar el dominio
- graficar la función
- usar la gráfica para determinar el rango
- Contestar
-
- dominio:\((-\infty, \infty)\)
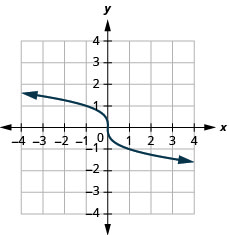
Figura 8.7.6- rango:\((-\infty, \infty)\)
Para la función\(f(x)=\sqrt[3]{x-2}\),
- encontrar el dominio
- graficar la función
- usar la gráfica para determinar el rango
- Contestar
-
- dominio:\((-\infty, \infty)\)
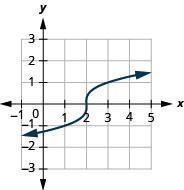
Figura 8.7.7- rango:\((-\infty, \infty)\)
Acceda a estos recursos en línea para obtener instrucción adicional y práctica con funciones radicales.
- Dominio de una función radical
- Dominio de una función radical 2
- Encontrar el dominio de una función radical
Conceptos clave
- Propiedades de\(\sqrt[n]{a}\)
- Cuando\(n\) es un número par y:
\(a≥0\), entonces\(\sqrt[n]{a}\) es un número real.
\(a<0\), entonces no\(\sqrt[n]{a}\) es un número real. - Cuando\(n\) es un número impar,\(\sqrt[n]{a}\) es un número real para todos los valores de\(a\).
- Cuando\(n\) es un número par y:
- Dominio de una función radical
- Cuando el índice del radical es par, el radicando debe ser mayor o igual a cero.
- Cuando el índice del radical es impar, el radicando puede ser cualquier número real.
Glosario
- función radical
- Una función radical es una función que se define por una expresión radical.


