8.8E: Ejercicios

Última actualización
Guardar como PDF

Page ID: 112495

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

La práctica hace la perfección

Ejercicio$\PageIndex{17}$ Evaluate a Radical Function

En los siguientes ejercicios, evalúe cada función.

$f(x)=\sqrt{4 x-4}$, encuentra
1. $f(5)$
2. $f(0)$
$f(x)=\sqrt{6 x-5}$, encuentra
1. $f(5)$
2. $f(-1)$
$g(x)=\sqrt{6 x+1}$, encuentra
1. $g(4)$
2. $g(8)$
$g(x)=\sqrt{3 x+1}$, encuentra
1. $g(8)$
2. $g(5)$
$F(x)=\sqrt{3-2 x}$, encuentra
1. $F(1)$
2. $F(-11)$
$F(x)=\sqrt{8-4 x}$, encuentra
1. $F(1)$
2. $F(-2)$
$G(x)=\sqrt{5 x-1}$, encuentra
1. $G(5)$
2. $G(2)$
$G(x)=\sqrt{4 x+1}$, encuentra
1. $G(11)$
2. $G(2)$
$g(x)=\sqrt[3]{2 x-4}$, encuentra
1. $g(6)$
2. $g(-2)$
$g(x)=\sqrt[3]{7 x-1}$, encuentra
1. $g(4)$
2. $g(-1)$
$h(x)=\sqrt[3]{x^{2}-4}$, encuentra
1. $h(-2)$
2. $h(6)$
$h(x)=\sqrt[3]{x^{2}+4}$, encuentra
1. $h(-2)$
2. $h(6)$
Para la función$f(x)=\sqrt[4]{2 x^{3}}$, encontrar
1. $f(0)$
2. $f(2)$
Para la función$f(x)=\sqrt[4]{3 x^{3}}$, encontrar
1. $f(0)$
2. $f(3)$
Para la función$g(x)=\sqrt[4]{4-4 x}$, encontrar
1. $g(1)$
2. $g(-3)$
Para la función$g(x)=\sqrt[4]{8-4 x}$, encontrar
1. $g(-6)$
2. $g(2)$

Contestar

$f(5)=4$
sin valor en$x=0$

$g(4)=5$
$g(8)=7$

$F(1)=1$
$F(-11)=5$

$G(5)=2 \sqrt{6}$
$G(2)=3$

$g(6)=2$
$g(-2)=-2$

11.

$h(-2)=0$
$h(6)=2 \sqrt[3]{4}$

13.

$f(0)=0$
$f(2)=2$

15.

$g(1)=0$
$g(-3)=2$

Ejercicio$\PageIndex{18}$ Find the Domain of a Radical Function

En los siguientes ejercicios, encuentra el dominio de la función y escribe el dominio en notación de intervalos.

$f(x)=\sqrt{3 x-1}$
$f(x)=\sqrt{4 x-2}$
$g(x)=\sqrt{2-3 x}$
$g(x)=\sqrt{8-x}$
$h(x)=\sqrt{\frac{5}{x-2}}$
$h(x)=\sqrt{\frac{6}{x+3}}$
$f(x)=\sqrt{\frac{x+3}{x-2}}$
$f(x)=\sqrt{\frac{x-1}{x+4}}$
$g(x)=\sqrt[3]{8 x-1}$
$g(x)=\sqrt[3]{6 x+5}$
$f(x)=\sqrt[3]{4 x^{2}-16}$
$f(x)=\sqrt[3]{6 x^{2}-25}$
$F(x)=\sqrt[4]{8 x+3}$
$F(x)=\sqrt[4]{10-7 x}$
$G(x)=\sqrt[5]{2 x-1}$
$G(x)=\sqrt[5]{6 x-3}$

Contestar

1. $\left[\frac{1}{3}, \infty\right)$

3. $\left(-\infty, \frac{2}{3}\right]$

5. $(2, \infty)$

7. $(-\infty,-3] \cup(2, \infty)$

9. $(-\infty, \infty)$

11. $(-\infty, \infty)$

13. $\left[-\frac{3}{8}, \infty\right)$

15. $(-\infty, \infty)$

Ejercicio$\PageIndex{19}$ graph radical functions

En los siguientes ejercicios,

encontrar el dominio de la función
graficar la función
usar la gráfica para determinar el rango
1. $f(x)=\sqrt{x+1}$
2. $f(x)=\sqrt{x-1}$
3. $g(x)=\sqrt{x+4}$
4. $g(x)=\sqrt{x-4}$
5. $f(x)=\sqrt{x}+2$
6. $f(x)=\sqrt{x}-2$
7. $g(x)=2 \sqrt{x}$
8. $g(x)=3 \sqrt{x}$
9. $f(x)=\sqrt{3-x}$
10. $f(x)=\sqrt{4-x}$
11. $g(x)=-\sqrt{x}$
12. $g(x)=-\sqrt{x}+1$
13. $f(x)=\sqrt[3]{x+1}$
14. $f(x)=\sqrt[3]{x-1}$
15. $g(x)=\sqrt[3]{x+2}$
16. $g(x)=\sqrt[3]{x-2}$
17. $f(x)=\sqrt[3]{x}+3$
18. $f(x)=\sqrt[3]{x}-3$
19. $g(x)=\sqrt[3]{x}$
20. $g(x)=-\sqrt[3]{x}$
21. $f(x)=2 \sqrt[3]{x}$
22. $f(x)=-2 \sqrt[3]{x}$

Contestar

dominio:$[-1, \infty)$
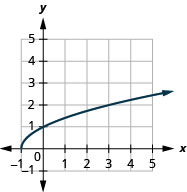
$La figura muestra una gráfica de función de raíz cuadrada en el plano de coordenadas x y. El eje x del plano va de negativo 1 a 7. El eje y va de 2 a 10 negativos. La función tiene un punto de partida en (negativo 1, 0) y pasa por los puntos (0, 1) y (3, 2).$
Figura 8.7.8
$[0, \infty)$

dominio:$[-4, \infty)$
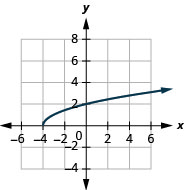
$La figura muestra una gráfica de función de raíz cuadrada en el plano de coordenadas x y. El eje x del plano va de negativo 4 a 4. El eje y va de 2 a 6 negativos. La función tiene un punto de partida en (negativo 4, 0) y pasa por los puntos (negativo 3, 1) y (0, 2).$
Figura 8.7.9
$[0, \infty)$

dominio:$[0, \infty)$
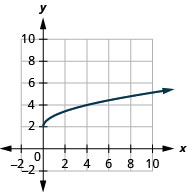
$La figura muestra una gráfica de función de raíz cuadrada en el plano de coordenadas x y. El eje x del plano va de 0 a 8. El eje y va de 0 a 8. La función tiene un punto de partida en (0, 2) y pasa por los puntos (1, 3) y (4, 4).$
Figura 8.7.10
$[2, \infty)$

dominio:$[0, \infty)$
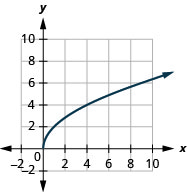
$La figura muestra una gráfica de función de raíz cuadrada en el plano de coordenadas x y. El eje x del plano va de 0 a 8. El eje y va de 0 a 8. La función tiene un punto de partida en (0, 0) y pasa por los puntos (1, 2) y (4, 4).$
Figura 8.7.11
$[0, \infty)$

dominio:$(-\infty, 3]$
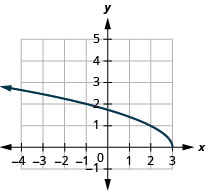
$La figura muestra una gráfica de función de raíz cuadrada en el plano de coordenadas x y. El eje x del plano va de negativo 6 a 4. El eje y va de 0 a 8. La función tiene un punto de partida en (3, 0) y pasa por los puntos (2, 1), (negativo 1, 2) y (negativo 6, 3).$
Figura 8.7.12
$[0, \infty)$

11.

dominio:$[0, \infty)$
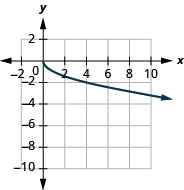
$La figura muestra una gráfica de función de raíz cuadrada en el plano de coordenadas x y. El eje x del plano va de 0 a 8. El eje y va de negativo 8 a 0. La función tiene un punto de partida en (0, 0) y pasa por los puntos (1, negativo 1) y (4, negativo 2).$
Figura 8.7.13
$(-\infty, 0]$

13.

dominio:$(-\infty, \infty)$
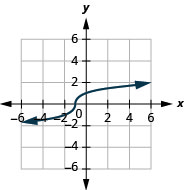
$La figura muestra una gráfica de función de raíz cubo en el plano de coordenadas x y. El eje x del plano va de negativo 4 a 4. El eje y va de negativo 4 a 4. La función tiene un punto central en (negativo 1, 0) y pasa por los puntos (negativo 2, negativo 1) y (0, 1).$
Figura 8.7.14
$(-\infty, \infty)$

15.

dominio:$(-\infty, \infty)$
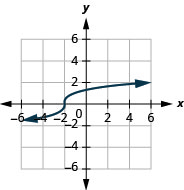
$La figura muestra una gráfica de función de raíz cubo en el plano de coordenadas x y. El eje x del plano va de negativo 4 a 4. El eje y va de negativo 4 a 4. La función tiene un punto central en (negativo 4, 0) y pasa por los puntos (negativo 3, negativo 1) y (negativo 1, 1).$
Figura 8.7.15
$(-\infty, \infty)$

17.

dominio:$(-\infty, \infty)$
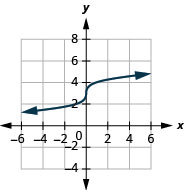
$La figura muestra una gráfica de función de raíz cubo en el plano de coordenadas x y. El eje x del plano va de negativo 4 a 4. El eje y va de 2 a 6 negativos. La función tiene un punto central en (0, 3) y pasa por los puntos (negativo 1, 2) y (1, 4).$
Figura 8.7.16
$(-\infty, \infty)$

19.

dominio:$(-\infty, \infty)$
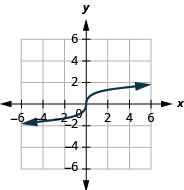
$La figura muestra una gráfica de función de raíz cubo en el plano de coordenadas x y. El eje x del plano va de negativo 4 a 4. El eje y va de negativo 4 a 4. La función tiene un punto central en (0, 0) y pasa por los puntos (1, 1) y (negativo 1, negativo 1).$
Figura 8.7.17
$(-\infty, \infty)$

21.

dominio:$(-\infty, \infty)$
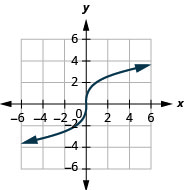
$La figura muestra una gráfica de función de raíz cubo en el plano de coordenadas x y. El eje x del plano va de negativo 4 a 4. El eje y va de negativo 4 a 4. La función tiene un punto central en (0, 0) y pasa por los puntos (1, 2) y (negativo 1, negativo 2).$
Figura 8.7.18
$(-\infty, \infty)$

Ejercicio$\PageIndex{20}$ writing exercises

Explicar cómo encontrar el dominio de una cuarta función raíz.
Explicar cómo encontrar el dominio de una quinta función raíz.
Explique por qué$y=\sqrt[3]{x}$ es una función.
Explicar por qué el proceso de encontrar el dominio de una función radical con un índice par es diferente del proceso cuando el índice es impar.

Contestar

1. Las respuestas pueden variar

3. Las respuestas pueden variar

Autocomprobación

a. después de completar los ejercicios, utilice esta lista de verificación para evaluar su dominio de los objetivos de esta sección.

La tabla tiene 4 columnas y 4 filas. La primera fila es una fila de encabezado con las cabeceras â€œI canâ €, â € œœconfiadamente â€, â€œCon algo de ayuda.â€, y â€ œNo â€ “I donâ €™ t get it! â€. La primera columna contiene las frases “evaluar una función radical”, “encontrar el dominio de una función radical” y “graficar una función radical”. Las otras columnas se dejan en blanco para que el alumno pueda indicar su nivel de comprensión. — Figura 8.7.19

b. ¿Qué te dice esta lista de verificación sobre tu dominio de esta sección? ¿Qué pasos tomarás para mejorar?

Search

Text Color

Text Size

Margin Size

Font Type

Ejercicio\(\PageIndex{17}\) Evaluate a Radical Function

Ejercicio\(\PageIndex{18}\) Find the Domain of a Radical Function

Ejercicio\(\PageIndex{19}\) graph radical functions

Ejercicio\(\PageIndex{20}\) writing exercises