9.3: Resolver ecuaciones cuadráticas completando el cuadrado
- Page ID
- 112676
Al final de esta sección, podrás:
- Completar el cuadrado de una expresión binomial
- Resolver ecuaciones cuadráticas de la forma\(x^{2}+bx+c=0\) completando el cuadrado
- Resolver ecuaciones cuadráticas de la forma\(ax^{2}+bx+c=0\) completando el cuadrado
Antes de comenzar, toma este cuestionario de preparación.
- Ampliar:\((x+9)^{2}\).
Si te perdiste este problema, revisa el Ejemplo 5.32. - Factor\(y^{2}-14 y+49\).
Si te perdiste este problema, revisa el Ejemplo 6.9. - Factor\(5 n^{2}+40 n+80\).
Si te perdiste este problema, revisa el Ejemplo 6.14.
Hasta el momento hemos resuelto ecuaciones cuadráticas factorizando y usando la Propiedad Raíz Cuadrada. En esta sección, resolveremos ecuaciones cuadráticas mediante un proceso llamado completar el cuadrado, lo cual es importante para nuestro trabajo sobre cónicas posteriormente.
Completa el cuadrado de una expresión binomial
En la última sección, pudimos usar la Propiedad Raíz Cuadrada para resolver la ecuación\((y-7)^{2}=12\) porque el lado izquierdo era un cuadrado perfecto.
\(\begin{aligned}(y-7)^{2} &=12 \\ y-7 &=\pm \sqrt{12} \\ y-7 &=\pm 2 \sqrt{3} \\ y &=7 \pm 2 \sqrt{3} \end{aligned}\)
También resolvimos una ecuación en la que el lado izquierdo era un trinomio cuadrado perfecto, pero tuvimos que reescribirlo el formulario\((x−k)^{2}\) para poder usar la Propiedad Raíz Cuadrada.
\(\begin{aligned} x^{2}-10 x+25 &=18 \\(x-5)^{2} &=18 \end{aligned}\)
¿Qué pasa si la variable no forma parte de un cuadrado perfecto? ¿Podemos usar álgebra para hacer un cuadrado perfecto?
Veamos dos ejemplos para ayudarnos a reconocer los patrones.
\(\begin{array}{cc}{(x+9)^{2}} & {(y-7)^{2}} \\ {(x+9 )(x+9)} & {(y-7)(y-7)} \\ {x^{2}+9 x+9 x+81} & {y^{2}-7 y-7 y+49} \\ {x^{2}+18 x+81} & {y^{2}-14 y+49}\end{array}\)
Reafirmamos los patrones aquí para referencia.
Si\(a\) y\(b\) son números reales,
Podemos usar este patrón para “hacer” un cuadrado perfecto.
Empezaremos con la expresión\(x^{2}+6 x\). Ya que hay un signo más entre los dos términos, usaremos el\((a+b)^{2}\) patrón,\(a^{2}+2 a b+b^{2}=(a+b)^{2}\).
En última instancia, necesitamos encontrar el último término de este trinomio que lo convierta en un trinomio cuadrado perfecto. Para ello tendremos que encontrar\(b\). Pero primero empezamos por determinar\(a\). Observe que el primer término de\(x^{2}+6x\) es un cuadrado,\(x^{2}\). Esto nos dice eso\(a=x\).
¿Qué número,\(b\), cuando se multiplica por\(2x\) da\(6x\)? Tendría que serlo\(3\), que es\(\frac{1}{2}(6)\). Entonces\(b=3\).
Ahora para completar el trinomio cuadrado perfecto, encontraremos el último término por cuadratura\(b\), que es\(3^{2}=9\).
Ahora podemos factorial.
Entonces encontramos que sumando\(9\) a\(x^{2}+6 x\) 'completa el cuadrado', y lo escribimos como\((x+3)^{2}\).
- Identificar\(b\), el coeficiente de\(x\).
- Encuentra\(\left(\frac{1}{2} b\right)^{2}\), el número para completar la plaza.
- Agregar el\(\left(\frac{1}{2} b\right)^{2}\) a\(x^{2}+bx\).
- Factorizar el trinomio cuadrado perfecto, escribiéndolo como un binomio cuadrado.
Completa el cuadrado para hacer un trinomio cuadrado perfecto. Después escribe el resultado como un binomio al cuadrado.
- \(x^{2}-26 x\)
- \(y^{2}-9 y\)
- \(n^{2}+\frac{1}{2} n\)
Solución:
a.
 |
|
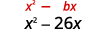| El coeficiente de\(x\) es -26. | |
|
Encuentra\(\left(\frac{1}{2} b\right)^{2}\). \(\left(\frac{1}{2} \cdot(-26)\right)^{2}\) |
|
| Agregar\(169\) al binomio para completar el cuadrado. |
\(x^{2}-26 x+169\) |
| Factorizar el trinomio cuadrado perfecto, escribiéndolo como un binomio cuadrado. |
\((x-13)^{2}\) |
b.
 |
|
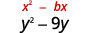| El coeficiente de\(y\) es\(-9\). | |
|
Encuentra\(\left(\frac{1}{2} b\right)^{2}\). \(\left(\frac{1}{2} \cdot(-9)\right)^{2}\) |
|
| Agregar\(\frac{81}{4}\) al binomio para completar el cuadrado. |
\(y^{2}-9 y+\frac{81}{4}\) |
| Factorizar el trinomio cuadrado perfecto, escribiéndolo como un binomio cuadrado. |
\(\left(y-\frac{9}{2}\right)^{2}\) |
c.
 |
|
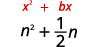| El coeficiente de\(n\) es\(\frac{1}{2}\). | |
|
Encuentra\(\left(\frac{1}{2} b\right)^{2}\). \(\left(\frac{1}{2} \cdot \frac{1}{2}\right)^{2}\) |
|
| Agregar\(\frac{1}{16}\) al binomio para completar el cuadrado. | \(n^{2}+\frac{1}{2} n+\frac{1}{16}\) |
| Reescribir como un cuadrado binomial. | \(\left(n+\frac{1}{4}\right)^{2}\) |
Completa el cuadrado para hacer un trinomio cuadrado perfecto. Después escribe el resultado como un binomio al cuadrado.
- \(a^{2}-20 a\)
- \(m^{2}-5 m\)
- \(p^{2}+\frac{1}{4} p\)
- Contestar
-
- \((a-10)^{2}\)
- \(\left(b-\frac{5}{2}\right)^{2}\)
- \(\left(p+\frac{1}{8}\right)^{2}\)
Completa el cuadrado para hacer un trinomio cuadrado perfecto. Después escribe el resultado como un binomio al cuadrado.
- \(b^{2}-4 b\)
- \(n^{2}+13 n\)
- \(q^{2}-\frac{2}{3} q\)
- Contestar
-
- \((b-2)^{2}\)
- \(\left(n+\frac{13}{2}\right)^{2}\)
- \(\left(q-\frac{1}{3}\right)^{2}\)
Resolver ecuaciones cuadráticas de la forma\(x^{2}+bx+c=0\) completando el cuadrado
Al resolver ecuaciones, siempre debemos hacer lo mismo a ambos lados de la ecuación. Esto es cierto, por supuesto, cuando resolvemos una ecuación cuadrática completando también el cuadrado. Cuando agregamos un término a un lado de la ecuación para hacer un trinomio cuadrado perfecto, también debemos agregar el mismo término al otro lado de la ecuación.
Por ejemplo, si empezamos con la ecuación\(x^{2}+6x=40\), y queremos completar el cuadrado de la izquierda, agregaremos 9 a ambos lados de la ecuación.
 |
|
 |
|
 |
|
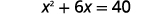| Agrega\(9\) a ambos lados para completar el cuadrado. |  |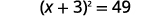
Ahora la ecuación está en la forma de resolver usando la Propiedad Raíz Cuadrada! Completar el cuadrado es una forma de transformar una ecuación en la forma que necesitamos para poder usar la Propiedad Raíz Cuadrada.
Resuelve completando la plaza:\(x^{2}+8x=48\).
Solución:
| Paso 1: Aísle los términos variables por un lado y los términos constantes por el otro. | Esta ecuación tiene todas las variables a la izquierda. | \(\begin{array}{l}{\color{red}{x^{2}+b x\quad\:\:\: c }} \\ {x^{2}+8 x=48}\end{array}\) |
| Paso 2: Encuentra\(\left(\frac{1}{2} \cdot b\right)^{2}\), el número para completar el cuadrado. Agrégalo a ambos lados de la ecuación. |
Toma la mitad\(8\) y cuadrázala. \(4^{2}=16\) Agregar\(16\) a AMBOS lados de la ecuación. |
\(x^{2}+8 x+\frac{}{\color{red}{\left(\frac{1}{2} \cdot 8\right)^{2}}}\color{black}{=}48 \) \(x^{2}+8 x\color{red}{+16}\color{black}{=}48\color{red}{+16}\) |
| Paso 3: Factorizar el trinomio cuadrado perfecto como un cuadrado binomial. |
\(x^{2}+8 x+16=(x+4)^{2}\) Agrega los términos a la derecha. |
\((x+4)^{2}=64\) |
| Paso 4: Utilice la Propiedad Raíz Cuadrada. | \(x+4=\pm \sqrt{64}\) | |
| Paso 5: Simplifica el radical y luego resuelve las dos ecuaciones resultantes. |
\(x+4=\pm 8\) \(\begin{aligned} x+4 &=8 \quad x+4=-8 \\ x &=4 \quad\quad\:\:\: x=-12 \end{aligned}\) |
|
| Paso 6: Consulta las soluciones. | Pon cada respuesta en la ecuación original para verificar. Sustituto\(x=4\) y\(x=-12\). |
\(\begin{array}{r}{x^{2}+8 x=48} \\ {(\color{red}{4}\color{black}{)}^{2}+8(\color{red}{4}\color{black}{)} \stackrel{?}{=} 48} \\ {16+32\stackrel{?}{=}48} \\ {48=48}\end{array}\) \(\begin{array}{r}{x^{2}+8 x=48} \\ {(\color{red}{-12}\color{black}{)}^{2}+8(\color{red}{-12}\color{black}{)}\stackrel{?}{=} 48} \\ {144-96 \stackrel{?}{=} 48} \\ {48=48}\end{array}\) |
Resuelve completando la plaza:\(x^{2}+4 x=5\).
- Contestar
-
\(x=-5, x=-1\)
Resuelve completando la plaza:\(y^{2}−10y=−9\).
- Contestar
-
\(y=1, y=9\)
Aquí se enumeran los pasos para resolver una ecuación cuadrática completando el cuadrado.
Resolver una ecuación cuadrática de la forma\(x^{2}+bx+c=0\) completando el cuadrado
- Aísle los términos variables por un lado y los términos constantes por el otro.
- Encuentra\(\left(\frac{1}{2} \cdot b\right)^{2}\), el número necesario para completar la plaza. Agrégalo a ambos lados de la ecuación.
- Factorizar el trinomio cuadrado perfecto, escribirlo como un binomio cuadrado a la izquierda y simplificar agregando los términos a la derecha
- Utilice la Propiedad Raíz Cuadrada.
- Simplifica el radical y luego resuelve las dos ecuaciones resultantes.
- Consulta las soluciones.
Cuando resolvemos una ecuación completando el cuadrado, las respuestas no siempre serán números enteros.
Resuelve completando la plaza:\(x^{2}+4 x=-21\).
Solución:
 |
|
|
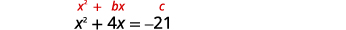Los términos variables están en el lado izquierdo. Toma la mitad\(4\) y cuadrázala. |
 |
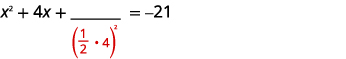| \(\left(\frac{1}{2}(4)\right)^{2}=4\) | |
| Añadir\(4\) a ambos lados. |  |
| Factorizar el trinomio cuadrado perfecto, escribiéndolo como un binomio cuadrado. |  |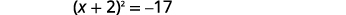
| Utilice la Propiedad Raíz Cuadrada. |  |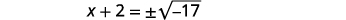
| Simplificando el uso de números complejos. |  |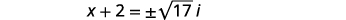
| Restar\(2\) de cada lado. |  |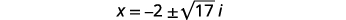
| Reescribe para mostrar dos soluciones. |  |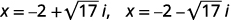
| Te dejamos el cheque a ti. |
Resuelve completando la plaza:\(y^{2}-10 y=-35\).
- Contestar
-
\(y=5+\sqrt{15} i, y=5-\sqrt{15 i}\)
Resuelve completando la plaza:\(z^{2}+8 z=-19\).
- Contestar
-
\(z=-4+\sqrt{3} i, z=-4-\sqrt{3} i\)
En el ejemplo anterior, nuestras soluciones eran números complejos. En el siguiente ejemplo, las soluciones serán números irracionales.
Resuelve completando la plaza:\(y^{2}-18 y=-6\).
Solución:
 |
|
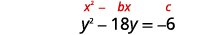| Los términos variables están en el lado izquierdo. Toma la mitad\(-18\) y cuadrázala. | |
| \(\left(\frac{1}{2}(-18)\right)^{2}=81\) |  |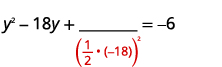
| Añadir\(81\) a ambos lados. |  |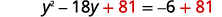
| Factorizar el trinomio cuadrado perfecto, escribiéndolo como un binomio cuadrado. |  |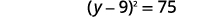
| Utilice la Propiedad Raíz Cuadrada. |  |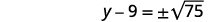
| Simplifica lo radical. |  |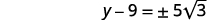
| Resolver para\(y\). |  |
|
Cheque.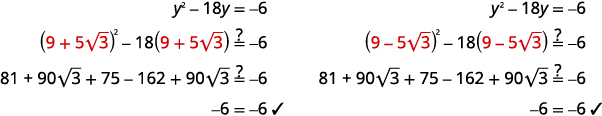 
|
|
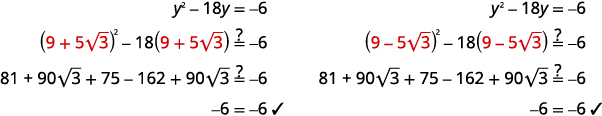Otra forma de verificar esto sería usar una calculadora. Evaluar\(y^{2}−18y\) para ambas soluciones. La respuesta debería ser\(−6\).
Resuelve completando la plaza:\(x^{2}-16 x=-16\).
- Responder
-
\(x=8+4 \sqrt{3}, x=8-4 \sqrt{3}\)
Resuelve completando la plaza:\(y^{2}+8 y=11\).
- Responder
-
\(y=-4+3 \sqrt{3}, y=-4-3 \sqrt{3}\)
Comenzaremos el siguiente ejemplo aislando los términos variables en el lado izquierdo de la ecuación.
Resuelve completando la plaza:\(x^{2}+10 x+4=15\).
Solución:
 |
|
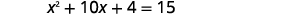| Aísle los términos variables en el lado izquierdo. Restar\(4\) para obtener los términos constantes en el lado derecho. |  |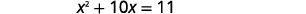
| Toma la mitad\(10\) y cuadrázala. | |
| \(\left(\frac{1}{2}(10)\right)^{2}=25\) |  |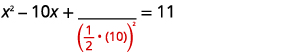
| Añadir\(25\) a ambos lados. |  |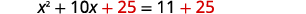
| Factorizar el trinomio cuadrado perfecto, escribiéndolo como un binomio cuadrado. |  |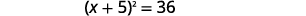
| Utilice la Propiedad Raíz Cuadrada. |  |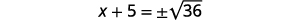
| Simplifica lo radical. |  |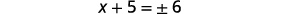
| Resolver para\(x\). |  |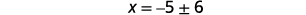
| Reescribe para mostrar dos soluciones. |  |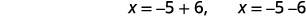
| Resuelve las ecuaciones. |  |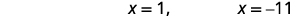
|
Comprobar: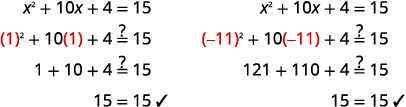 
|
Resuelve completando la plaza:\(a^{2}+4 a+9=30\).
- Responder
-
\(a=-7, a=3\)
Resuelve completando la plaza:\(b^{2}+8 b-4=16\).
- Responder
-
\(b=-10, b=2\)
Para resolver la siguiente ecuación, primero debemos recopilar todos los términos variables en el lado izquierdo de la ecuación. Después procedemos como hicimos en los ejemplos anteriores.
Resuelve completando la plaza:\(n^{2}=3 n+11\).
Solución:
 |
|
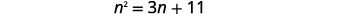| Restar\(3n\) para obtener los términos variables en el lado izquierdo. |  |
| Toma la mitad\(-3\) y cuadrázala. | |
| \(\left(\frac{1}{2}(-3)\right)^{2}=\frac{9}{4}\) |  |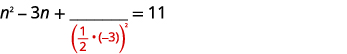
| Añadir\(\frac{9}{4}\) a ambos lados. |  |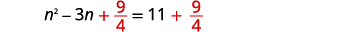
| Factorizar el trinomio cuadrado perfecto, escribiéndolo como un binomio cuadrado. |  |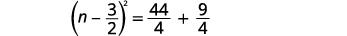
| Agrega las fracciones en el lado derecho. |  |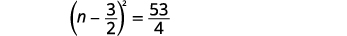
| Utilice la Propiedad Raíz Cuadrada. |  |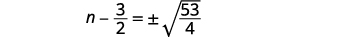
| Simplifica lo radical. |  |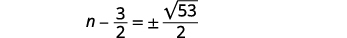
| Resolver para\(n\). |  |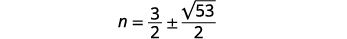
| Reescribe para mostrar dos soluciones. |  |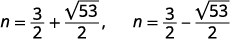
|
Comprobar: ¡Te dejamos el cheque! |
Resuelve completando la plaza:\(p^{2}=5 p+9\).
- Responder
-
\(p=\frac{5}{2}+\frac{\sqrt{61}}{2}, p=\frac{5}{2}-\frac{\sqrt{61}}{2}\)
Resuelve completando la plaza:\(q^{2}=7 q-3\).
- Responder
-
\(q=\frac{7}{2}+\frac{\sqrt{37}}{2}, q=\frac{7}{2}-\frac{\sqrt{37}}{2}\)
Observe que el lado izquierdo de la siguiente ecuación está en forma factorizada. Pero el lado derecho no es cero. Entonces, no podemos usar la Propiedad Zero Product ya que dice “Si\(a⋅b=0\), entonces\(a=0\) o”\(b=0\). En cambio, multiplicamos los factores y luego ponemos la ecuación en forma estándar para resolverla completando el cuadrado.
Resuelve completando la plaza:\((x-3)(x+5)=9\).
Solución:
 |
|
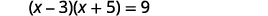| Multiplamos los binomios a la izquierda. |  |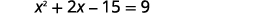
| Agregar\(15\) para aislar los términos constantes a la derecha. |  |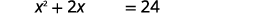
| Toma la mitad\(2\) y cuadrázala. | |
| \(\left(\frac{1}{2} \cdot(2)\right)^{2}=1\) |  |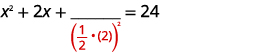
| Añadir\(1\) a ambos lados. |  |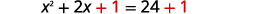
| Factorizar el trinomio cuadrado perfecto, escribiéndolo como un binomio cuadrado. |  |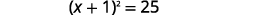
| Utilice la Propiedad Raíz Cuadrada. |  |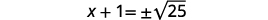
| Resolver para\(x\). |  |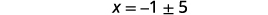
| Reescribe para mostrar dos soluciones. |  |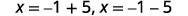
| Simplificar. |  |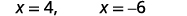
|
Comprobar: ¡Te dejamos el cheque! |
Resuelve completando la plaza:\((c-2)(c+8)=11\).
- Responder
-
\(c=-9, c=3\)
Resuelve completando la plaza:\((d-7)(d+3)=56\).
- Responder
-
\(d=11, d=-7\)
Resolver ecuaciones cuadráticas de la forma\(ax^{2}+bx+c=0\) completando el cuadrado
El proceso de completar el cuadrado funciona mejor cuando el coeficiente de\(x^{2}\) es\(1\), por lo que el lado izquierdo de la ecuación es de la forma\(x^{2}+bx+c\). Si el\(x^{2}\) término tiene un coeficiente distinto al\(1\), tomamos algunos pasos preliminares para que el coeficiente sea igual a\(1\).
A veces el coeficiente puede ser factorizado a partir de los tres términos del trinomio. Esta será nuestra estrategia en el siguiente ejemplo.
Resuelve completando la plaza:\(3 x^{2}-12 x-15=0\).
Solución:
Para completar el cuadrado, necesitamos el coeficiente de\(x^{2}\) ser uno. Si factorizamos el coeficiente de\(x^{2}\) como factor común, podemos continuar resolviendo la ecuación completando el cuadrado.
 |
|
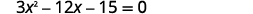| Facturar el mayor factor común. |  |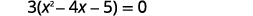
| Dividir ambos lados por\(3\) para aislar el trinomio con coeficiente\(1\). |  |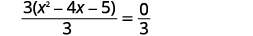
| Simplificar. |  |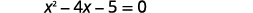
| Agrega\(5\) para obtener los términos constantes en el lado derecho. |  |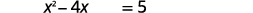
| Toma la mitad\(4\) y cuadrázala. | |
| \(\left(\frac{1}{2}(-4)\right)^{2}=4\) |  |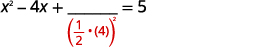
| Añadir\(4\) a ambos lados. |  |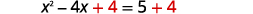
| Factorizar el trinomio cuadrado perfecto, escribiéndolo como un binomio cuadrado. |  |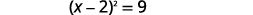
| Utilice la Propiedad Raíz Cuadrada. |  |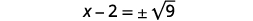
| Resolver para\(x\). |  |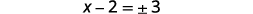
| Reescribe para mostrar dos soluciones. |  |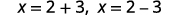
| Simplificar. |  |
|
Comprobar: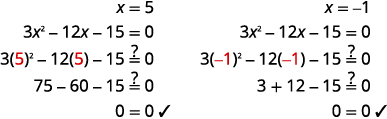 
|
Resuelve completando la plaza:\(2 m^{2}+16 m+14=0\).
- Responder
-
\(m=-7, m=-1\)
Resuelve completando la plaza:\(4 n^{2}-24 n-56=8\).
- Responder
-
\(n=-2, n=8\)
Para completar el cuadrado, el coeficiente del\(x^{2}\) debe ser\(1\). Cuando el coeficiente principal no sea un factor de todos los términos, ¡dividiremos ambos lados de la ecuación por el coeficiente principal! Esto nos dará una fracción para el segundo coeficiente. Ya hemos visto cómo completar el cuadrado con fracciones en esta sección.
Resuelve completando la plaza:\(2 x^{2}-3 x=20\).
Solución:
Para completar el cuadrado necesitamos el coeficiente de\(x^{2}\) ser uno. Dividiremos ambos lados de la ecuación por el coeficiente de\(x^{2}\). Entonces podemos seguir resolviendo la ecuación completando el cuadrado.
 |
|
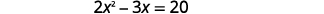| Dividir ambos lados por\(2\) para obtener el coeficiente\(x^{2}\) de ser\(1\). |  |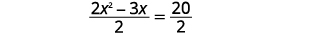
| Simplificar. |  |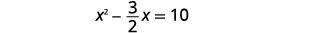
| Toma la mitad\(-\frac{3}{2}\) y cuadrázala. | |
| \(\left(\frac{1}{2}\left(-\frac{3}{2}\right)\right)^{2}=\frac{9}{16}\) |  |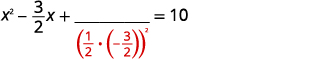
| Añadir\(\frac{9}{16}\) a ambos lados. |  |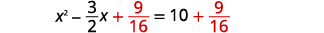
| Factorizar el trinomio cuadrado perfecto, escribiéndolo como un binomio cuadrado. |  |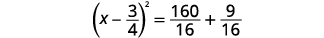
| Agrega las fracciones en el lado derecho. |  |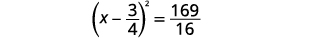
| Utilice la Propiedad Raíz Cuadrada. |  |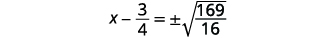
| Simplifica lo radical. |  |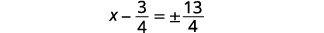
| Resolver para\(x\). |  |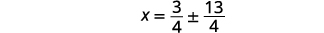
| Reescribe para mostrar dos soluciones. |  |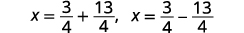
| Simplificar. |  |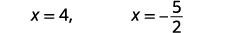
|
Comprobar: ¡Te dejamos el cheque! |
Resuelve completando la plaza:\(3 r^{2}-2 r=21\).
- Responder
-
\(r=-\frac{7}{3}, r=3\)
Resuelve completando la plaza:\(4 t^{2}+2 t=20\).
- Responder
-
\(t=-\frac{5}{2}, t=2\)
Ahora que hemos visto que el coeficiente de\(x^{2}\) debe ser\(1\) para que completemos el cuadrado, actualizamos nuestro procedimiento para resolver una ecuación cuadrática completando el cuadrado para incluir ecuaciones de la forma\(a x^{2}+b x+c=0\).
- Dividir por aa para hacer el coeficiente de\(x^{2}\) término\(1\).
- Aísle los términos variables por un lado y los términos constantes por el otro.
- Encuentra\(\left(\frac{1}{2} \cdot b\right)^{2}\), el número necesario para completar la plaza. Agrégalo a ambos lados de la ecuación.
- Factorizar el trinomio cuadrado perfecto, escribirlo como un binomio cuadrado a la izquierda y simplificar agregando los términos a la derecha
- Utilice la Propiedad Raíz Cuadrada.
- Simplifica el radical y luego resuelve las dos ecuaciones resultantes.
- Consulta las soluciones.
Resuelve completando la plaza:\(3 x^{2}+2 x=4\).
Solución:
Nuevamente, nuestro primer paso será hacer el coeficiente de\(x^{2}\) uno. Al dividir ambos lados de la ecuación por el coeficiente de\(x^{2}\), entonces podemos continuar resolviendo la ecuación completando el cuadrado.
 |
|
| Dividir ambos lados por\(3\) para hacer el coeficiente de\(x^{2}\) igual\(1\). |  |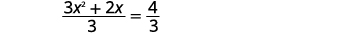
| Simplificar. |  |
| Toma la mitad\(\frac{2}{3}\) y cuadrázala. | |
| \(\left(\frac{1}{2} \cdot \frac{2}{3}\right)^{2}=\frac{1}{9}\) |  |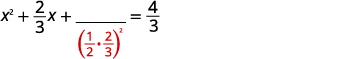
| Añadir\(\frac{1}{9}\) a ambos lados. |  |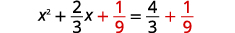
| Factorizar el trinomio cuadrado perfecto, escribiéndolo como un binomio cuadrado. |  |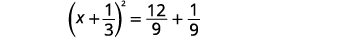
| Utilice la Propiedad Raíz Cuadrada. |  |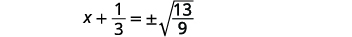
| Simplifica lo radical. |  |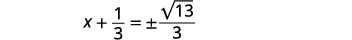
| Resolver para\(x\). |  |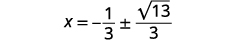
| Reescribe para mostrar dos soluciones. |  |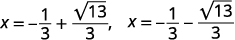
|
Comprobar: ¡Te dejamos el cheque! |
Resuelve completando la plaza:\(4 x^{2}+3 x=2\).
- Responder
-
\(x=-\frac{3}{8}+\frac{\sqrt{41}}{8}, x=-\frac{3}{8}-\frac{\sqrt{41}}{8}\)
Resuelve completando la plaza:\(3 y^{2}-10 y=-5\).
- Responder
-
\(y=\frac{5}{3}+\frac{\sqrt{10}}{3}, y=\frac{5}{3}-\frac{\sqrt{10}}{3}\)
Acceda a estos recursos en línea para obtener instrucción adicional y práctica al completar la plaza.
Conceptos clave
- Patrón Cuadrados Binomiales
Si\(a\) y\(b\) son números reales,
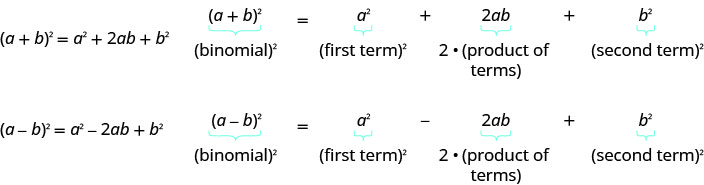
- Cómo Completar un Cuadrado
- Identificar\(b\), el coeficiente de\(x\).
- Encuentra\(\left(\frac{1}{2} b\right)^{2}\), el número para completar la plaza.
- Agregar el\(\left(\frac{1}{2} b\right)^{2}\) a\(x^{2}+bx\)
- Reescribir el trinomio como un cuadrado binomial
- Cómo resolver una ecuación cuadrática de la forma \(a x^{2}+b x+c=0\)completando el cuadrado.
- Dividir por\(a\) para hacer el coeficiente de\(x^{2}\) término\(1\).
- Aísle los términos variables por un lado y los términos constantes por el otro.
- Encuentra\(\left(\frac{1}{2} \cdot b\right)^{2}\), el número necesario para completar la plaza. Agrégalo a ambos lados de la ecuación.
- Factorizar el trinomio cuadrado perfecto, escribiéndolo como un binomio cuadrado a la izquierda y simplificarlo agregando los términos a la derecha.
- Utilice la Propiedad Raíz Cuadrada.
- Simplifica el radical y luego resuelve las dos ecuaciones resultantes.
- Consulta las soluciones.