12.3E: Ejercicios

Última actualización

30 oct 2022
Guardar como PDF
- 12.3: Secuencias Aritméticas
- 12.4: Secuencias geométricas y series

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\id}{\mathrm{id}}$ $\newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$ $\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$ $\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$ $\newcommand{\AA}{\unicode[.8,0]{x212B}}$

$\newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$\newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$\newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vectorC}[1]{\textbf{#1}}$

$\newcommand{\vectorD}[1]{\overrightarrow{#1}}$

$\newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}}$

$\newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}}$

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\avec}{\mathbf a}$

$\newcommand{\bvec}{\mathbf b}$

$\newcommand{\cvec}{\mathbf c}$

$\newcommand{\dvec}{\mathbf d}$

$\newcommand{\dtil}{\widetilde{\mathbf d}}$

$\newcommand{\evec}{\mathbf e}$

$\newcommand{\fvec}{\mathbf f}$

$\newcommand{\nvec}{\mathbf n}$

$\newcommand{\pvec}{\mathbf p}$

$\newcommand{\qvec}{\mathbf q}$

$\newcommand{\svec}{\mathbf s}$

$\newcommand{\tvec}{\mathbf t}$

$\newcommand{\uvec}{\mathbf u}$

$\newcommand{\vvec}{\mathbf v}$

$\newcommand{\wvec}{\mathbf w}$

$\newcommand{\xvec}{\mathbf x}$

$\newcommand{\yvec}{\mathbf y}$

$\newcommand{\zvec}{\mathbf z}$

$\newcommand{\rvec}{\mathbf r}$

$\newcommand{\mvec}{\mathbf m}$

$\newcommand{\zerovec}{\mathbf 0}$

$\newcommand{\onevec}{\mathbf 1}$

$\newcommand{\real}{\mathbb R}$

$\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$

$\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$

$\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$

$\newcommand{\laspan}[1]{\text{Span}\{#1\}}$

$\newcommand{\bcal}{\cal B}$

$\newcommand{\ccal}{\cal C}$

$\newcommand{\scal}{\cal S}$

$\newcommand{\wcal}{\cal W}$

$\newcommand{\ecal}{\cal E}$

$\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$

$\newcommand{\gray}[1]{\color{gray}{#1}}$

$\newcommand{\lgray}[1]{\color{lightgray}{#1}}$

$\newcommand{\rank}{\operatorname{rank}}$

$\newcommand{\row}{\text{Row}}$

$\newcommand{\col}{\text{Col}}$

$\renewcommand{\row}{\text{Row}}$

$\newcommand{\nul}{\text{Nul}}$

$\newcommand{\var}{\text{Var}}$

$\newcommand{\corr}{\text{corr}}$

$\newcommand{\len}[1]{\left|#1\right|}$

$\newcommand{\bbar}{\overline{\bvec}}$

$\newcommand{\bhat}{\widehat{\bvec}}$

$\newcommand{\bperp}{\bvec^\perp}$

$\newcommand{\xhat}{\widehat{\xvec}}$

$\newcommand{\vhat}{\widehat{\vvec}}$

$\newcommand{\uhat}{\widehat{\uvec}}$

$\newcommand{\what}{\widehat{\wvec}}$

$\newcommand{\Sighat}{\widehat{\Sigma}}$

$\newcommand{\lt}{<}$

$\newcommand{\gt}{>}$

$\newcommand{\amp}{&}$

$\definecolor{fillinmathshade}{gray}{0.9}$

La práctica hace la perfección

Ejercicio $\PageIndex{17}$ Determine if a Sequence is Arithmetic

En los siguientes ejercicios, determinar si cada secuencia es aritmética, y de ser así, indicar la diferencia común.

$4,12,20,28,36,44, \dots$
$-7,-2,3,8,13,18, \dots$
$-15,-16,3,12,21,30, \dots$
$11,5,-1,-7-13,-19, \dots$
$8,5,2,-1,-4,-7, \dots$
$15,5,-5,-15,-25,-35, \dots$

Responder

1. La secuencia es aritmética con diferencia común $d=8$ .

3. La secuencia no es aritmética.

5. La secuencia es aritmética con diferencia común $d=−3$ .

Ejercicio $\PageIndex{18}$ Determine if a Sequence is Arithmetic

En los siguientes ejercicios, escribir los primeros cinco términos de cada secuencia con el primer término dado y diferencia común.

$a_{1}=11$ y $d=7$
$a_{1}=18$ y $d=9$
$a_{1}=-7$ y $d=4$
$a_{1}=-8$ y $d=5$
$a_{1}=14$ y $d=-9$
$a_{1}=-3$ y $d=-3$

Responder

1. $11,18,25,32,39$

3. $-7,-3,1,5,9$

5. $14,5,-4,-13,-22$

Ejercicio $\PageIndex{19}$ Find the General Term ( $n$ the Term) of an Arithmetic Sequence

En los siguientes ejercicios, encuentra el término descrito utilizando la información proporcionada.

Encuentra el vigésimo primer término de una secuencia donde el primer término es tres y la diferencia común es ocho.
Encuentra el vigésimo tercer término de una secuencia donde el primer término es seis y la diferencia común es cuatro.
Encuentra el trigésimo término de una secuencia donde está el primer término $−14$ y la diferencia común es cinco.
Encuentra el cuadragésimo término de una secuencia donde está el primer término $−19$ y la diferencia común es siete.
Encuentra el decimosexto término de una secuencia donde está el primer término $11$ y la diferencia común es $−6$ .
Encuentra el decimocuarto término de una secuencia donde el primer término es ocho y la diferencia común es $−3$ .
Encuentra el vigésimo término de una secuencia donde está el quinto término $−4$ y la diferencia común es $−2$ . Dar la fórmula para el término general.
Encuentra el decimotercer término de una secuencia donde está el sexto término $−1$ y la diferencia común es $−4$ . Dar la fórmula para el término general.
Encuentra el undécimo término de una secuencia donde está el tercer término $19$ y la diferencia común es cinco. Dar la fórmula para el término general.
Encuentra el decimoquinto término de una secuencia donde está el décimo término $17$ y la diferencia común es siete. Dar la fórmula para el término general.
Encuentra el octavo término de una secuencia donde está el séptimo término $−8$ y la diferencia común es $−5$ . Dar la fórmula para el término general.
Encuentra el decimoquinto término de una secuencia donde está el décimo término $−11$ y la diferencia común es $−3$ . Dar la fórmula para el término general.

Responder

1. $163$

3. $131$

5. $-79$

7. $a_{20}=-34 .$ El término general es $a_{n}=-2 n+6$ .

9. $a_{11}=59 .$ El término general es $a_{n}=5 n+4$ .

11. $a_{8}=-13 .$ El término general es $a_{n}=-5 n+27$ .

Ejercicio $\PageIndex{20}$ Find the General Term ( $n$ the Term) of an Arithmetic Sequence

En los siguientes ejercicios, encuentra el primer término y diferencia común de la secuencia con los términos dados. Dar la fórmula para el término general.

El segundo término es $14$ y el decimotercer término es $47$ .
El tercer término es $18$ y el decimocuarto término es $73$ .
El segundo término es $13$ y el décimo término es $−51$ .
El tercer término es cuatro y el décimo término es $−38$ .
El cuarto término es $−6$ y el decimoquinto término es $27$ .
El tercer término es $−13$ y el decimoséptimo término es $15$ .

Responder

1. $a_{1}=11, d=3 .$ El término general es $a_{n}=3 n+8$ .

3. $a_{1}=21, d=-8 .$ El término general es $a_{n}=-8 n+29$

5. $a_{1}=-15, d=3 .$ El término general es $a_{n}=3 n-18$ .

Ejercicio $\PageIndex{21}$ Find the Sum of the First $n$ Terms of an Arithmetic Sequence

En los siguientes ejercicios, encuentra la suma de los primeros $30$ términos de cada secuencia aritmética.

$11,14,17,20,23, \dots$
$12,18,24,30,36, \dots$
$8,5,2,-1,-4, \dots$
$16,10,4,-2,-8, \dots$
$-17,-15,-13,-11,-9, \dots$
$-15,-12,-9,-6,-3, \dots$

Responder

1. $1,635$

3. $-1,065$

5. $360$

Ejercicio $\PageIndex{22}$ Find the Sum of the First $n$ Terms of an Arithmetic Sequence

En los siguientes ejercicios, encuentra la suma de los primeros $50$ términos de la secuencia aritmética cuyo término general se da.

$a_{n}=5 n-1$
$a_{n}=2 n+7$
$a_{n}=-3 n+5$
$a_{n}=-4 n+3$

Responder

1. $6,325$

3. $-3,575$

Ejercicio $\PageIndex{23}$ Find the Sum of the First $n$ Terms of an Arithmetic Sequence

En los siguientes ejercicios, encuentra cada suma.

$\sum_{i=1}^{40}(8 i-7)$
$\sum_{i=1}^{45}(7 i-5)$
$\sum_{i=1}^{50}(3 i+6)$
$\sum_{i=1}^{25}(4 i+3)$
$\sum_{i=1}^{35}(-6 i-2)$
$\sum_{i=1}^{30}(-5 i+1)$

Responder

1. $6,280$

3. $4,125$

5. $-3,580$

Ejercicio $\PageIndex{24}$ Writing Exercises

En sus propias palabras, explique cómo determinar si una secuencia es aritmética.
En sus propias palabras, explique cómo se utilizan los dos primeros términos para encontrar el décimo término. Muestra un ejemplo para ilustrar tu explicación.
En sus propias palabras, explique cómo encontrar el término general de una secuencia aritmética.
En sus propias palabras, explique cómo encontrar la suma de los primeros $n$ términos de una secuencia aritmética sin agregar todos los términos.

Responder

1. La respuesta puede variar

3. La respuesta puede variar

Autocomprobación

a. después de completar los ejercicios, utilice esta lista de verificación para evaluar su dominio de los objetivos de esta sección.

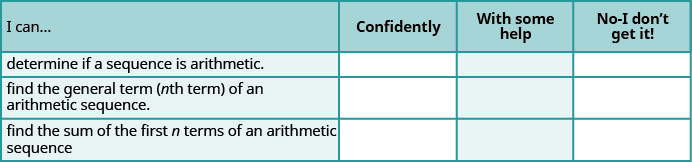
Esta figura muestra un gráfico con cuatro filas y cuatro columnas. La primera fila es la fila de encabezado y dice: “Puedo”, “Confiadamente”, “Con algo de ayuda”, y “¡No, no lo consigo!” La columna, comenzando con la segunda fila dice 1. Determinar si una Secuencia es Aritmética, 2. Encuentra el Término General (enésimo término) de Secuencia Aritmética, y 3. Encuentra la suma de los primeros Términos de una Secuencia Aritmética”. Las columnas restantes están en blanco. — Figura 12.2.29

b. Después de revisar esta lista de verificación, ¿qué harás para tener confianza en todos los objetivos?

Search

Text Color

Text Size

Margin Size

Font Type

Ejercicio $\PageIndex{17}$ Determine if a Sequence is Arithmetic

Ejercicio $\PageIndex{18}$ Determine if a Sequence is Arithmetic

Ejercicio $\PageIndex{19}$ Find the General Term ( $n$ the Term) of an Arithmetic Sequence

Ejercicio $\PageIndex{20}$ Find the General Term ( $n$ the Term) of an Arithmetic Sequence

Ejercicio $\PageIndex{21}$ Find the Sum of the First $n$ Terms of an Arithmetic Sequence

Ejercicio $\PageIndex{22}$ Find the Sum of the First $n$ Terms of an Arithmetic Sequence

Ejercicio $\PageIndex{23}$ Find the Sum of the First $n$ Terms of an Arithmetic Sequence

Ejercicio $\PageIndex{24}$ Writing Exercises

La práctica hace la perfección

Ejercicio12.3E.17\PageIndex{17} Determine if a Sequence is Arithmetic

Ejercicio12.3E.18\PageIndex{18} Determine if a Sequence is Arithmetic

Ejercicio12.3E.19\PageIndex{19} Find the General Term (nnthe Term) of an Arithmetic Sequence

Ejercicio12.3E.20\PageIndex{20} Find the General Term (nnthe Term) of an Arithmetic Sequence

Ejercicio12.3E.21\PageIndex{21} Find the Sum of the First nn Terms of an Arithmetic Sequence

Ejercicio12.3E.22\PageIndex{22} Find the Sum of the First nn Terms of an Arithmetic Sequence

Ejercicio12.3E.23\PageIndex{23} Find the Sum of the First nn Terms of an Arithmetic Sequence

Ejercicio12.3E.24\PageIndex{24} Writing Exercises

Autocomprobación

Support Center

How can we help?

Ejercicio $\PageIndex{17}$ Determine if a Sequence is Arithmetic

Ejercicio $\PageIndex{18}$ Determine if a Sequence is Arithmetic

Ejercicio $\PageIndex{19}$ Find the General Term ( $n$ the Term) of an Arithmetic Sequence

Ejercicio $\PageIndex{20}$ Find the General Term ( $n$ the Term) of an Arithmetic Sequence

Ejercicio $\PageIndex{21}$ Find the Sum of the First $n$ Terms of an Arithmetic Sequence

Ejercicio $\PageIndex{22}$ Find the Sum of the First $n$ Terms of an Arithmetic Sequence

Ejercicio $\PageIndex{23}$ Find the Sum of the First $n$ Terms of an Arithmetic Sequence

Ejercicio $\PageIndex{24}$ Writing Exercises