12.2: Secuencias
- Page ID
- 112253
Al final de esta sección, podrás:
- Escribe los primeros términos de una secuencia
- Encontrar una fórmula para el término general (enésimo término) de una secuencia
- Usar notación factorial
- Encuentra la suma parcial
- Usar notación de suma para escribir una suma
Antes de comenzar, toma este cuestionario de preparación.
- Evaluar\(2n+3\) para los enteros\(1, 2, 3\), y\(4\).
Si te perdiste este problema, revisa el Ejemplo 1.6. - Evaluar\((−1)^{n}\) para los enteros\(1, 2, 3\), y\(4\).
Si te perdiste este problema, revisa el Ejemplo 1.19. - Si\(f(n)=n^{2}+2\), encuentra\(f(1)+f(2)+f(3)\).
Si te perdiste este problema, revisa el Ejemplo 3.49.
Escribe los primeros términos de una secuencia
Veamos la función\(f(x)=2x\) y evaluarla solo para los números de conteo.
| \(f(x)=2x\) | |
| \(x\) | \(2x\) |
| \(1\) | \(2\) |
| \(2\) | \(4\) |
| \(3\) | \(6\) |
| \(4\) | \(8\) |
| \(5\) | \(10\) |
| \(...\) | \(...\) |
Si enumeramos los valores de la función en orden como\(2, 4, 6, 8\)\(10\), y,... tenemos una secuencia. Una secuencia es una función cuyo dominio son los números de conteo.
Una secuencia es una función cuyo dominio son los números de conteo.
Una secuencia también puede verse como una lista ordenada de números y cada número de la lista es un término. Una secuencia puede tener un número infinito de términos o un número finito de términos. Nuestra secuencia tiene tres puntos (puntos suspensivos) al final lo que indica que la lista nunca termina. Si el dominio es el conjunto de todos los números de conteo, entonces la secuencia es una secuencia infinita. Su dominio es todo contar números y hay un número infinito de números de conteo.
\(2,4,6,8,10, \dots\)
Si limitamos el dominio a un número finito de números de conteo, entonces la secuencia es una secuencia finita. Si usamos solo los primeros cuatro números de conteo,\(1, 2, 3, 4\) nuestra secuencia sería la secuencia finita,
\(2,4,6,8\)
Muchas veces al trabajar con secuencias no queremos escribir todos los términos. Queremos una forma más compacta de mostrar cómo se define cada término. Cuando trabajamos con funciones, escribimos\(f(x)=2x\) y dijimos que la expresión\(2x\) era la regla que definía valores en el rango. Si bien una secuencia es una función, no utilizamos la notación de función habitual. En lugar de escribir la función como\(f(x)=2x\), la escribiríamos como\(a_{n}=2n\). El\(a_{n}\) es el término\(n\) th de la secuencia, el término en la posición\(n\) th donde\(n\) es un valor en el dominio. La fórmula para escribir el término\(n\) th de la secuencia se llama término general o fórmula de la secuencia.
El término general de la secuencia se encuentra a partir de la fórmula para escribir el término\(n\) th de la secuencia. El término\(n\) th de la secuencia,\(a_{n}\), es el término en la posición\(n\) th donde\(n\) es un valor en el dominio.
Cuando se nos da el término general de la secuencia, podemos encontrar los términos\(n\) reemplazando por los números de conteo en orden. Para\(a_{n}=2 n\),
| \(n\) | \(1\) | \(2\) | \(3\) | \(4\) | \(5\) | \(6\) |
| \(a_{n}\) | 2\(\cdot 1\) | 2\(\cdot 2\) | 2\(\cdot 3\) | 2\(\cdot 4\) | 2\(\cdot 5\) | 2\(\cdot 6\) |
| \(2\) | \(4\) | \(6\) | \(8\) | \(10\) |
\(a_{1}, \quad a_{2}, \quad a_{3}, \quad a_{4}, \quad a_{5}, \ldots, \quad a_{n}, \dots\)
\(2, \quad 4, \quad 6, \quad 8, \quad10, \dots\)
Para encontrar los valores de una secuencia, sustituimos en los números de conteo en orden en el término general de la secuencia.
Escribir los primeros cinco términos de la secuencia cuyo término general es\(a_{n}=4 n-3\).
Solución:
Sustituimos los valores\(1, 2, 3, 4\), y\(5\) en la fórmula,\(a_{n}=4n−3\), en orden.
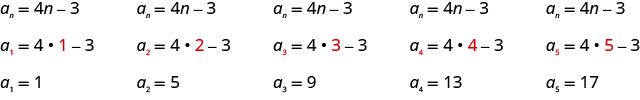
Respuesta:
Los primeros cinco términos de la secuencia son\(1, 5, 9, 13\), y\(17\).
Escribir los primeros cinco términos de la secuencia cuyo término general es\(a_{n}=3n-4\).
- Contestar
-
\(-1,2,5,8,11\)
Escribir los primeros cinco términos de la secuencia cuyo término general es\(a_{n}=2n-5\).
- Contestar
-
\(-3,-1,1,3,5\)
Para algunas secuencias, la variable es un exponente.
Escribir los primeros cinco términos de la secuencia cuyo término general es\(a_{n}=2^{n}+1\).
Solución:
Sustituimos los valores\(1, 2, 3, 4\), y\(5\) en la fórmula,\(a_{n}=2^{n}+1\), en orden.
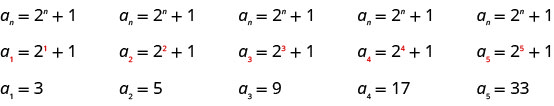
Respuesta:
Los primeros cinco términos de la secuencia son\(3, 5, 9, 17\), y\(33\).
Escribir los primeros cinco términos de la secuencia cuyo término general es\(a_{n}=3^{n}+4\).
- Contestar
-
\(7,13,31,85,247\)
Escribir los primeros cinco términos de la secuencia cuyo término general es\(a_{n}=2^{n}-5\).
- Contestar
-
\(-3,-1,3,11,27\)
No es raro ver las expresiones\((−1)^{n}\) o\((−1)^{n+1}\) en el término general para una secuencia. Si evaluamos cada una de estas expresiones para unos pocos valores, vemos que esta expresión alterna el signo para los términos.
| \(n\) | \(1\) | \(2\) | \(3\) | \(4\) | \(5\) |
|---|---|---|---|---|---|
| \ (n\) ">\((-1)^{n}\) | \ (1\) ">\((-1)^{1}\) \(-1\) |
\ (2\) ">\((-1)^{2}\) 1 |
\ (3\) ">\((-1)^{3}\) \(-1\) |
\ (4\) ">\((-1)^{4}\) \(1\) |
\ (5\) ">\((-1)^{5}\) \(-1\) |
| \ (n\) ">\((-1)^{n+1}\) | \ (1\) ">\((-1)^{1+1}\) 1 |
\ (2\) ">\((-1)^{2+1}\) \(-1\) |
\ (3\) ">\((-1)^{3+1}\) 1 |
\ (4\) ">\((-1)^{4+1}\) \(-1\) |
\ (5\) ">\((-1)^{5+1}\) 1 |
\(a_{1}, \quad a_{2}, \quad a_{3}, \quad a_{4}, \quad a_{5}, \dots, \quad a_{n}, \dots\)
\(\begin{array}{rrrr}{-1,} & {1,} & {-1,} & {1,} & {-1 \ldots} \\ {1,} & {-1,} & {1,} & {-1,} & {1 \ldots}\end{array}\)
Escribir los primeros cinco términos de la secuencia cuyo término general es\(a_{n}=(-1)^{n} n^{3}\).
Solución:
Sustituimos los valores\(1, 2, 3, 4\), y\(5\) en la fórmula,\(a_{n}=(-1)^{n} n^{3}\), en orden.
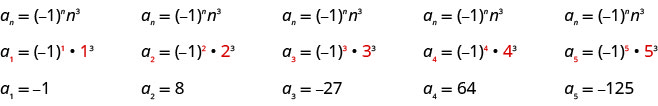
Respuesta:
Los primeros cinco términos de la secuencia son\(−1, 8, −27, 64, −1, 8, −27, 64\), y\(−125\).
Escribir los primeros cinco términos de la secuencia cuyo término general es\(a_{n}=(-1)^{n} n^{2}\).
- Contestar
-
\(-1,4,-9,16,-25\)
Escribir los primeros cinco términos de la secuencia cuyo término general es\(a_{n}=(-1)^{n+1} n^{3}\).
- Contestar
-
\(1,-8,27,-64,125\)
Encuentre una Fórmula para el Término General (\(n\)Término) de una Secuencia
A veces tenemos algunos términos de una secuencia y sería útil conocer el término general o el término\(n\) th. Para encontrar el término general, buscamos patrones en los términos. A menudo los patrones involucran múltiplos o poderes. También buscamos un patrón en los signos de los términos.
Encuentra un término general para la secuencia cuyos primeros cinco términos se muestran. \(4,8,12,16,20, \dots\)
Solución:
-
Buscamos un patrón en los términos.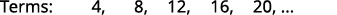 
Los números son todos múltiplos de\(4\).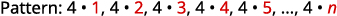 
El término general de la secuencia es\(a_{n}=4n\). Cuadro 12.1.4 Respuesta:
El término general de la secuencia es\(a_{n}=4n\).
Encuentra un término general para la secuencia cuyos primeros cinco términos se muestran.
\(3,6,9,12,15, \dots\)
- Contestar
-
\(a_{n}=3 n\)
Encuentra un término general para la secuencia cuyos primeros cinco términos se muestran.
\(5,10,15,20,25, \dots\)
- Contestar
-
\(a_{n}=5 n\)
Encuentra un término general para la secuencia cuyos primeros cinco términos se muestran. \(2,-4,8,-16,32, \dots\)
Solución:
-
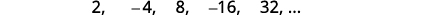
Figura 12.1.8 
Figura 12.1.9 Buscamos un patrón en los términos.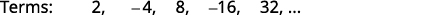 
Figura 12.1.10 Los números son poderes de\(2\). Los signos son alternantes, con incluso\(n\) negativos.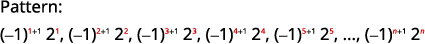 
Figura 12.1.11 El término general de la secuencia es\(a_{n}=(-1)^{n+1} 2^{n}\) Cuadro 12.1.5 Respuesta:
El término general de la secuencia es\(a_{n}=(-1)^{n+1}2^{n}\).
Encuentra un término general para la secuencia cuyos primeros cinco términos se muestran.
\(-3,9,-27,81,-243, \dots\)
- Contestar
-
\(a_{n}=(-1)^{n} 3^{n}\)
Buscar un término general para la secuencia cuyos primeros cinco términos se muestran
\(1,-4,9,-16,25, \dots\)
- Contestar
-
\(a_{n}=(-1)^{n+1} n^{2}\)
Encuentra un término general para la secuencia cuyos primeros cinco términos se muestran. \(\frac{1}{3}, \frac{1}{9}, \frac{1}{27}, \frac{1}{81}, \frac{1}{243}, \dots\)
Solución:
-
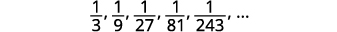
Figura 12.1.12 
Figura 12.1.13 Buscamos un patrón en los términos.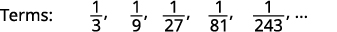 
Figura 12.1.14 Los numeradores son todos\(1\).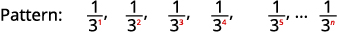 
Figura 12.1.15 Los denominadores son poderes de\(3\). El término general de la secuencia es\(a_{n}=\frac{1}{3^{n}}\). Cuadro 12.1.6 Respuesta:
El término general de la secuencia es\(a_{n}=\frac{1}{3^{n}}\).
Encuentra un término general para la secuencia cuyos primeros cinco términos se muestran.
\(\frac{1}{2}, \frac{1}{4}, \frac{1}{8}, \frac{1}{16}, \frac{1}{32}, \dots\)
- Contestar
-
\(a_{n}=\frac{1}{2^{n}}\)
Encuentra un término general para la secuencia cuyos primeros cinco términos se muestran.
\(\frac{1}{1}, \frac{1}{4}, \frac{1}{9}, \frac{1}{16}, \frac{1}{25}, \dots\)
- Contestar
-
\(a_{n}=\frac{1}{n^{2}}\)
Usar notación factorial
Las secuencias suelen tener términos que son productos de enteros consecutivos. Indicamos estos productos con una notación especial llamada notación factorial. Por ejemplo,\(5!\), leer\(5\) factorial, significa\(5⋅4⋅3⋅2⋅1\). El signo de exclamación no es puntuación aquí; indica la notación factorial.
Si\(n\) es un entero positivo, entonces\(n!\) es
\(n !=n(n-1)(n-2) \dots\)
Definimos\(0!\) como\(1\), así\(0!=1\).
Se muestran los valores de\(n!\) para los primeros enteros\(5\) positivos.
\(\begin{array}{ccccc}{1 !} & {2 !} & {3 !} & {4 !} & {5 !} \\ {1} & \quad{2 \cdot 1} & \quad {3 \cdot 2 \cdot 1} & \quad{4 \cdot 3 \cdot 2 \cdot 1} & \quad {5 \cdot 4 \cdot 3 \cdot 2 \cdot 1} \\ {1} & {2} & {6} & {24} & {120}\end{array}\)
Escribir los primeros cinco términos de la secuencia cuyo término general es\(a_{n}=\frac{1}{n !}\).
Solución:
Sustituimos los valores\(1, 2, 3, 4, 5\) en la fórmula,\(a_{n}=\frac{1}{n !}\), en orden.
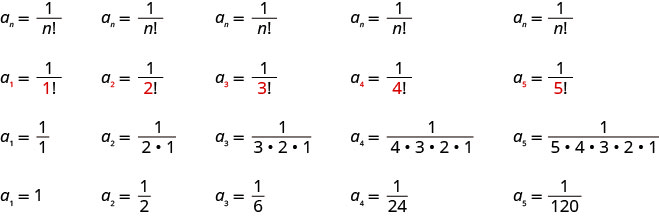
Respuesta:
Los primeros cinco términos de la secuencia son\(1, \frac{1}{2}, \frac{1}{6}, \frac{1}{24}, \frac{1}{120}\).
Escribir los primeros cinco términos de la secuencia cuyo término general es\(a_{n}=\frac{2}{n !}\).
- Contestar
-
\(2,1, \frac{1}{3}, \frac{1}{12}, \frac{1}{60}\)
Escribir los primeros cinco términos de la secuencia cuyo término general es\(a_{n}=\frac{3}{n !}\).
- Contestar
-
\(3, \frac{3}{2}, \frac{1}{2}, \frac{1}{8}, \frac{1}{40}\)
Cuando hay una fracción con factoriales en el numerador y denominador, alineamos los factores verticalmente para facilitar nuestros cálculos.
Escribir los primeros cinco términos de la secuencia cuyo término general es\(a_{n}=\frac{(n+1) !}{(n-1) !}\).
Solución:
Sustituimos los valores\(1, 2, 3, 4, 5\) en la fórmula,\(a_{n}=\frac{(n+1) !}{(n-1) !}\), en orden.
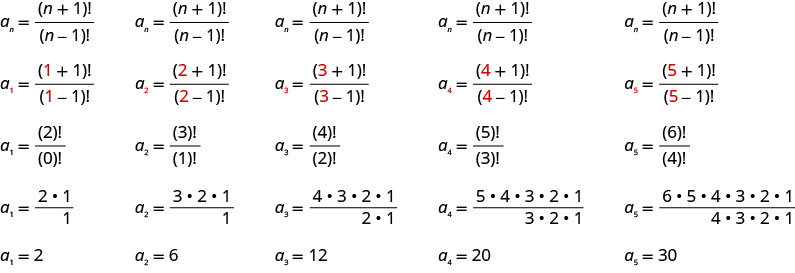
Respuesta:
Los primeros cinco términos de la secuencia son\(2, 6, 12, 20\), y\(30\).
Escribe los primeros cinco términos de la secuencia cuyo término general es\(a_{n}=\frac{(n-1) !}{(n+1) !}\)
- Contestar
-
\(\frac{1}{2}, \frac{1}{6}, \frac{1}{12}, \frac{1}{20}, \frac{1}{30}\)
Escribir los primeros cinco términos de la secuencia cuyo término general es\(a_{n}=\frac{n !}{(n+1) !}\).
- Contestar
-
\(\frac{1}{2}, \frac{1}{3}, \frac{1}{4}, \frac{1}{5}, \frac{1}{6}\)
Encuentra la suma parcial
A veces en las aplicaciones, en lugar de solo enumerar los términos, es importante para nosotros agregar los términos de una secuencia. En lugar de simplemente conectar los términos con signos más, podemos usar notación de suma.
Por ejemplo, se\(a_{1}+a_{2}+a_{3}+a_{4}+a_{5}\) puede escribir como\(\sum_{i=1}^{5} a_{i}\). Leemos esto como “la suma de\(a\) sub\(i\) de\(i\) igual a uno a cinco”. El símbolo\(∑\) significa sumar y el\(i\) es el índice de suma. El nos\(1\) dice por dónde empezar (valor inicial) y el nos\(5\) dice dónde terminar (valor terminal).
La suma de los primeros\(n\) términos de una secuencia cuyo término\(n\) th\(a_{n}\) está escrito en notación sumatoria como:
\(\sum_{i=1}^{n} a_{i}=a_{1}+a_{2}+a_{3}+a_{4}+a_{5}+\ldots+a_{n}\)
El\(i\) es el índice de suma y el nos\(1\) dice por dónde empezar y el nos\(n\) dice por dónde terminar.
Cuando agregamos un número finito de términos, llamamos a la suma una suma parcial.
Expandir la suma parcial y encontrar su valor:\(\sum_{i=1}^{5} 2 i\).
Solución:
-
\(\sum_{i=1}^{5} 2 i\) Sustituimos los valores\(1, 2, 3, 4, 5\) en orden. \(2 \cdot 1+2 \cdot 2+2 \cdot 3+2 \cdot 4 + 2 \cdot 5\) Simplificar. \(2+4+6+8+10\) Agregar. \(\begin{array} {c} 30\\ \sum_{i=1}^{5} 2 i=30 \end{array}\) Cuadro 12.1.7 Respuesta:
\(\begin{array} {c} 30\\ \sum_{i=1}^{5} 2 i=30 \end{array}\)
Expandir la suma parcial y encontrar su valor:\(\sum_{i=1}^{5} 3 i\).
- Contestar
-
\(45\)
Expandir la suma parcial y encontrar su valor:\(\sum_{i=1}^{5} 4 i\).
- Contestar
-
\(60\)
El índice no siempre tiene que ser\(i\) podemos usar cualquier letra, pero\(i\) y\(k\) son de uso común. El índice no tiene que comenzar con\(1\) ninguno, puede comenzar y terminar con cualquier entero positivo.
Expandir la suma parcial y encontrar su valor:\(\sum_{k=0}^{3} \frac{1}{k !}\).
Solución:
\(\begin{array}{c c} {}&{\sum_{k=0}^{3} \frac{1}{k !}} \\ {We\:substitute\:the\:values\:0,1,2,3\:in\:order.}&{\frac{1}{1}+\frac{1}{1 !}+\frac{1}{2 !}+\frac{1}{3 !}} \\ {Evaluate\:the\:factorials.}& {\frac{1}{1}+\frac{1}{1}+\frac{1}{2 !}+\frac{1}{6}} \\ {Simplify.}&{1+1+\frac{3}{6}+\frac{1}{6}} \\{Simplify.}& {\frac{16}{6}} \\ {Simplify.}&{\frac{8}{3}} \\{}& {\sum_{k=0}^{3} \frac{1}{k !}=\frac{8}{3}}\end{array}\)
Expandir la suma parcial y encontrar su valor:\(\sum_{k=0}^{3} \frac{2}{k !}\).
- Contestar
-
\(\frac{16}{3}\)
Expandir la suma parcial y encontrar su valor:\(\sum_{k=0}^{3} \frac{3}{k !}\).
- Contestar
-
\(8\)
Usar notación de suma para escribir una suma
En los dos últimos ejemplos, pasamos de la notación de suma a escribir la suma. Ahora comenzaremos con una suma y la cambiaremos a notación de suma. Esto es muy similar a encontrar el término general de una secuencia. Tendremos que mirar los términos y encontrar un patrón. A menudo los patrones involucran múltiplos o poderes.
Escribe la suma usando notación de suma:\(1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\frac{1}{5}\).
Solución:
\(\begin{array} {}&{ 1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\frac{1}{5}} \\ {}&{n : 1,2,3,4,5} \\ {\text{We look for a pattern in the terms.}}&{\text { Terms: } 1, \frac{1}{2}, \frac{1}{3}, \frac{1}{4}, \frac{1}{5}} \\ {\text{The numerators are all one.}}&{\text { Pattern: } \frac{1}{1}, \frac{1}{2}, \frac{1}{3}, \frac{1}{4}, \frac{1}{5}, \ldots \frac{1}{n}} \\ {\text{The denominators are the counting numbers from one to five.}}&{\text{The sum written in summation notation}} \\ {}&{1 + \frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\frac{1}{5}=\sum^{5}_{n=1} \frac{1}{n}.} \end{array}\)
Escribe la suma usando notación de suma:\(\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}\).
- Contestar
-
\(\sum_{n=1}^{5} \frac{1}{2^{n}}\)
Escribe la suma usando notación de suma:\(1+\frac{1}{4}+\frac{1}{9}+\frac{1}{16}+\frac{1}{25}\)
- Contestar
-
\(\sum_{n=1}^{5} \frac{1}{n^{2}}\)
Cuando los términos de una suma tienen coeficientes negativos, debemos analizar cuidadosamente el patrón de los signos.
Escribe la suma usando notación de suma:\(-1+8-27+64-125\).
Solución:
-
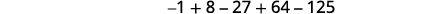
Figura 12.1.18 
Figura 12.1.19 Buscamos un patrón en los términos. 
Figura 12.1.20 Los signos de los términos se alternan,
y los términos impares son negativos.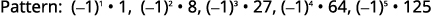
Figura 12.1.21 Los números son los cubos de los números de
conteo del uno al cinco.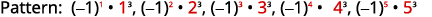
Figura 12.1.22 
Figura 12.1.23 La suma escrita en notación de suma es \(-1+8-27+64-125=\sum_{n=1}^{5}(-1)^{n} \cdot n^{3}\) Cuadro 12.1.8
Escribe cada suma usando notación de suma:\(1-4+9-16+25\).
- Contestar
-
\(\sum_{n=1}^{5}(-1)^{n+1} n^{2}\)
Escribe cada suma usando notación de suma:\(-2+4-6+8-10\).
- Contestar
-
\(\sum_{n=1}^{5}(-1)^{n} 2 n\)
Acceda a este recurso en línea para obtener instrucción adicional y práctica con secuencias.
Conceptos clave
- Notación factorial
Si\(n\) es un entero positivo, entonces\(n!\) es
\(n !=n(n-1)(n-2) \ldots(3)(2)(1)\)
Definimos\(0!\) como\(1\), así\(0!=1\)
- Notación de suma
La suma de los primeros\(n\) términos de una secuencia cuyo término\(n\) th\(a_{n}\) está escrito en notación de suma como:
\(\sum_{i=1}^{n} a_{i}=a_{1}+a_{2}+a_{3}+a_{4}+a_{5}+\ldots+a_{n}\)
El\(i\) es el índice de suma y el nos\(1\) dice por dónde empezar y el nos\(n\) dice por dónde terminar.
Glosario
- secuencia finita
- Una secuencia con un dominio que se limita a un número finito de números de conteo.
- término general de una secuencia
- El término general de la secuencia es la fórmula para escribir el término\(n\) th de la secuencia. El término\(n\) th de la secuencia,\(a_{n}\), es el término en la posición\(n\) th donde\(n\) es un valor en el dominio.
- secuencia infinita
- Una secuencia cuyo dominio es todo contar números y hay un número infinito de números de conteo.
- suma parcial
- Cuando agregamos un número finito de términos de una secuencia, llamamos a la suma una suma parcial.
- secuencia
- Una secuencia es una función cuyo dominio son los números de conteo.