12.4: Secuencias geométricas y series
- Page ID
- 112254
Al final de esta sección, podrás:
- Determinar si una secuencia es geométrica
- Encontrar el término general (término\(n\) th) de una secuencia geométrica
- Encuentra la suma de los primeros\(n\) términos de una secuencia geométrica
- Encuentra la suma de una serie geométrica infinita
- Aplicar secuencias geométricas y series en el mundo real
Antes de comenzar, toma este cuestionario de preparación.
- Simplificar:\(\frac{24}{32}\).
Si te perdiste este problema, revisa el Ejemplo 1.24. - Evaluar: a.\(3^{4}\) b\(\left(\frac{1}{2}\right)^{4}\).
Si te perdiste este problema, revisa el Ejemplo 1.19. - Si\(f(x)=4 \cdot 3^{x}\), encontrar a.\(f(1)\) b.\(f(2)\)\(f(3)\) c.
Si te perdiste este problema, revisa el Ejemplo 3.49.
Determinar si una secuencia es geométrica
Ahora estamos listos para mirar el segundo tipo especial de secuencia, la secuencia geométrica.
Una secuencia se denomina secuencia geométrica si la relación entre términos consecutivos es siempre la misma. La relación entre términos consecutivos en una secuencia geométrica es\(r\), la relación común, donde\(n\) es mayor o igual a dos.
Una secuencia geométrica es una secuencia donde la relación entre términos consecutivos es siempre la misma.
La relación entre términos consecutivos,\(\frac{a_{n}}{a_{n-1}}\), es\(r\), la relación común. \(n\)es mayor o igual a dos.
Considera estas secuencias.
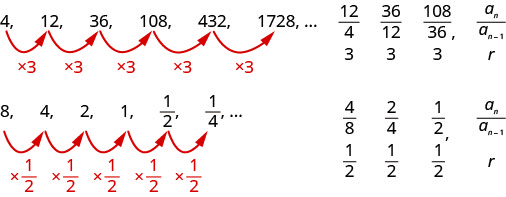
Determinar si cada secuencia es geométrica. Si es así, indicar la relación común.
- \(4,8,16,32,64,128, \dots\)
- \(-2,6,-12,36,-72,216, \dots\)
- \(27,9,3,1, \frac{1}{3}, \frac{1}{9}, \ldots\)
Solución:
Para determinar si la secuencia es geométrica, encontramos la relación de los términos consecutivos mostrados.
a. Encontrar la proporción de los términos consecutivos
\(\begin{aligned} 4, \quad& \:8, \quad 16, \quad 32, \quad 64, \quad 128, \dots \\ &\frac{8}{4} \quad\frac{16}{8}\quad\frac{32}{16}\quad\frac{64}{32}\quad\frac{128}{64} \\ &\:2 \quad\:\:\: 2 \quad\quad2\quad\quad2\quad\quad2 \end{aligned}\)
La secuencia es geométrica. La ración común es\(r=2\).
b. Encontrar la relación de los términos consecutivos
\(\begin{aligned}-\:2,\quad &\:\:\:6,\quad -12,\quad 36,\quad \:-72\quad \:\:216,\dots \\ & \frac{6}{-2}\quad\frac{-12}{6}\quad\frac{36}{-12}\quad\frac{-72}{36}\quad\frac{216}{-72} \\ & -3\quad -2\quad\:\: -3\quad \:\:\:-2\quad \:\:-3 \end{aligned}\)
La secuencia no es geométrica. No hay una relación común.
c. Encontrar la proporción de los términos consecutivos
\(\begin{aligned}27,\quad &\:\:9,\quad 3,\quad 1,\quad \frac{1}{3},\quad \frac{1}{9}, \ldots\\ & \frac{9}{27}\quad\frac{3}{9}\quad\frac{1}{3}\quad\frac{\frac{1}{3}}{1}\quad\frac{\frac{1}{9}}{\frac{1}{3}}\\ &\frac{1}{3}\quad\;\:\frac{1}{3}\quad\frac{1}{3}\quad\:\frac{1}{3}\quad\:\frac{1}{3}\end{aligned}\)
La secuencia es geométrica. La proporción común es\(r=\frac{1}{3}\).
Determinar si cada secuencia es geométrica. Si es así indicar la relación común.
- \(7,21,63,189,567,1,701, \dots\)
- \(64,16,4,1, \frac{1}{4}, \frac{1}{16}, \dots\)
- \(2,4,12,48,240,1,440, \dots\)
- Responder
-
- La secuencia es geométrica con relación común\(r=3\).
- La secuencia es geométrica con relación común\(d=\frac{1}{4}\).
- La secuencia no es geométrica. No hay una relación común.
Determinar si cada secuencia es geométrica. Si es así indicar la relación común.
- \(-150,-30,-15,-5,-\frac{5}{2}, 0, \dots\)
- \(5,10,20,40,80,160, \dots\)
- \(8,4,2,1, \frac{1}{2}, \frac{1}{4}, \ldots\)
- Responder
-
- La secuencia no es geométrica. No hay una relación común.
- La secuencia es geométrica con relación común\(r=2\).
- La secuencia es geométrica con relación común\(r=\frac{1}{2}\).
Si conocemos el primer término,\(a_{1}\), y la relación común,\(r\), podemos enumerar un número finito de términos de la secuencia.
Escribe los primeros cinco términos de la secuencia donde está el primer término\(3\) y la proporción común es\(r=−2\).
Solución:
Comenzamos con el primer término y lo multiplicamos por la proporción común. Entonces multiplicamos ese resultado por la proporción común para obtener el siguiente término, y así sucesivamente.
\(\begin{array}{cccc}{a_{1}} & {a_{2}} & {a_{3}} & {a_{4}} & {a_{5}} \\ {3} & {3 \cdot(-2)} & {-6 \cdot(-2)} & {12 \cdot(-2)} & {-24 \cdot(-2)} \\& {-6} & {12} & {-24} & {48}\end{array}\)
Respuesta:
La secuencia es\(3,-6,12,-24,48, \dots\)
Escribe los primeros cinco términos de la secuencia donde está el primer término\(7\) y la proporción común es\(r=−3\).
- Responder
-
\(7,-21,63,-189,567\)
Escribe los primeros cinco términos de la secuencia donde está el primer término\(6\) y la proporción común es\(r=−4\).
- Responder
-
\(6,-24,96,-384,1536\)
Encuentra el Término General (\(n\)Término) de una Secuencia Geométrica
Así como encontramos una fórmula para el término general de una secuencia y una secuencia aritmética, también podemos encontrar una fórmula para el término general de una secuencia geométrica.
Escribamos los primeros términos de la secuencia donde está el primer término\(a_{1}\) y la proporción común es\(r\). Entonces buscaremos un patrón.
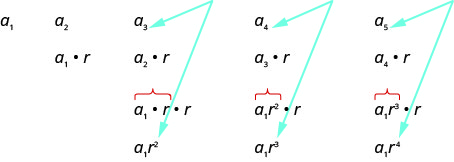
Al buscar un patrón en los cinco términos anteriores, vemos que cada uno de los términos comienza con\(a_{1}\).
El primer término,\(a_{1}\), no se multiplica por ninguno\(r\). En el segundo término, el\(a_{1}\) se multiplica por\(r\). En el tercer término, el\(a_{1}\) se multiplica por\(r\) dos veces (\(r⋅r\)o\(r^{2}\)). En el cuarto término, el\(a_{1}\) se multiplica por\(r\) tres veces (\(r⋅r⋅r\)o\(r^{3}\)) y en el quinto término, el\(a_{1}\) se multiplica por\(r\) cuatro veces. En cada término, el número de veces que\(a_{1}\) se multiplica por\(r\) es uno menos que el número del término. Esto nos lleva a lo siguiente
\(a_{n}=a_{1} r^{n-1}\)
El término general de una secuencia geométrica con primer término\(a_{1}\) y la relación común\(r\) es
\(a_{n}=a_{1} r^{n-1}\)
Utilizaremos esta fórmula en el siguiente ejemplo para encontrar el decimocuarto término de una secuencia.
Encuentra el decimocuarto término de una secuencia donde está el primer término\(64\) y la proporción común es\(r=\frac{1}{2}\).
Solución:
\(a_{n}=a_{1} r^{n-1}\)
Para encontrar el decimocuarto término,\(a_{14}\), usa la fórmula con\(a_{1}=64\) y\(r=\frac{1}{2}\).
\(a_{14}=64\left(\frac{1}{2}\right)^{14-1}\)
Sustituto en los valores.
\(a_{14}=64\left(\frac{1}{2}\right)^{13}\)
Simplificar.
\(a_{14}=\frac{1}{128}\)
Encuentra el decimotercer término de una secuencia donde está el primer término\(81\) y la proporción común es\(r=\frac{1}{3}\).
- Responder
-
\(\frac{1}{6,561}\)
Encuentra el duodécimo término de una secuencia donde está el primer término\(256\) y la proporción común es\(r=\frac{1}{4}\).
- Responder
-
\(\frac{1}{16,384}\)
En ocasiones desconocemos la proporción común y debemos usar la información dada para encontrarla antes de encontrar el término solicitado.
Encuentra el duodécimo término de la secuencia\(3, 6, 12, 24, 48, 96, …\) Encuentra el término general para la secuencia.
Solución:
Para encontrar el duodécimo término, usamos la fórmula\(a_{n}=a_{1} r^{n-1}\),, y así tenemos que determinar primero\(a_{1}\) y la relación común\(r\).
El primer término es de tres.
\(3,6,12,24,48,96, \dots\)
\(a_{1}=3\)
Encuentra la proporción común.
\(\begin{array}{l}{\frac{6}{3} \quad \frac{12}{6} \quad \frac{24}{12} \quad \frac{48}{24} \quad \frac{96}{48}} \\ {2 \:\:\:\quad 2 \quad \:\:2 \quad\:\:\: 2 \:\:\quad \:2} \\ {\text { The common ratio is } r=2}\end{array}\)
Para encontrar el duodécimo término\(a_{12}\),, usa la fórmula con\(a_{1}=3\) y\(r=2\).
\(a_{n}=a_{1} r^{n-1}\)
Sustituto en los valores.
\(a_{12}=3 \cdot 2^{12-1}\)
Simplificar.
\(a_{12}=3 \cdot 2^{11}\)
\(a_{12}=6,144\)
Encuentra el término general. Utilizamos la fórmula con\(a_{1}=3\) y\(r=2\).
\(a_{n}=a_{1} r^{n-1}\)
\(a_{n}=3(2)^{n-1}\)
Encuentra el noveno término de la secuencia\(6, 18, 54, 162, 486, 1,458, … \) Luego encuentra el término general para la secuencia.
- Responder
-
\(a_{9}=39,366 .\)El término general es\(a_{n}=6(3)^{n-1}\).
Encuentra el undécimo término de la secuencia\(7, 14, 28, 56, 112, 224, …\) Luego encuentra el término general para la secuencia.
- Responder
-
\(a_{11}=7,168 .\)El término general es\(a_{n}=7(2)^{n-1}\).
Encuentra la suma de los primeros\(n\) términos de una secuencia geométrica
Encontramos la suma tanto de secuencias generales como de secuencia aritmética. Ahora haremos lo mismo para las secuencias geométricas. La suma,\(S_{n}\), de los primeros\(n\) términos de una secuencia geométrica se escribe como\(S_{n}=a_{1}+a_{2}+a_{3}+\ldots+a_{n}\). Podemos escribir esta suma comenzando por el primer término,\(a_{1}\), y seguir multiplicando por\(r\) para obtener el siguiente término como:
\(S_{n}=a_{1}+a_{1} r+a_{1} r^{2}+\ldots+a_{1} r^{n-1}\)
Multipliquemos también ambos lados de la ecuación por\(r\).
\(r S_{n}=a_{1} r+a_{1} r^{2}+a_{1} r^{3}+\ldots+a_{1} r^{n}\)
A continuación, restamos estas ecuaciones. Veremos que cuando restemos, todos menos el primer término de la ecuación superior y el último término de la ecuación inferior restan a cero.
\(\begin{aligned} S_{n}&= a_{1}+a_{1} r+a_{1} r^{2}+a_{1} r^{3}+\ldots+a_{1} r^{n-1} \\ r S_{n} &= a_{1} r+a_{1} r^{2}+a_{1} r^{3}+\ldots+a_{1} r^{n-1}+a_{1} r^{n}\\\hline S_{n}-r S_{n} &= a_{1} -a_{1}r^{n} \end{aligned}\)
Tenemos en cuenta ambos lados.
\(S_{n}(1-r)=a_{1}\left(1-r^{n}\right)\)
Para obtener la fórmula para\(S_{n}\), dividir ambos lados por\((1-r)\).
\(S_{n}=\frac{a_{1}\left(1-r^{n}\right)}{1-r}\)
La suma,\(S_{n}\), de los primeros\(n\) términos de una secuencia geométrica es
\(S_{n}=\frac{a_{1}\left(1-r^{n}\right)}{1-r}\)
donde\(a_{1}\) es el primer término y\(r\) es la proporción común, y no\(r\) es igual a uno.
Aplicamos esta fórmula en el siguiente ejemplo donde se dan los primeros términos de la secuencia. Observe que la suma de una secuencia geométrica suele ser muy grande cuando la proporción común es mayor que uno.
Encuentra la suma de los primeros\(20\) términos de la secuencia geométrica\(7, 14, 28, 56, 112, 224, …\)
Solución:
Para encontrar la suma, usaremos la fórmula\(S_{n}=\frac{a_{1}\left(1-r^{n}\right)}{1-r}\). Sabemos\(a_{1}=7\),\(r=2\), y\(n=20\),
Saber\(a_{1}=7, r=2\), y\(n=20\), usar la fórmula de suma.
\(S_{n}=\frac{a_{1}\left(1-r^{n}\right)}{1-r}\)
Sustituto en los valores.
\(S_{20}=\frac{7\left(1-2^{20}\right)}{1-2}\)
Simplificar.
\(S_{20}=7,340,025\)
Encuentra la suma de los primeros\(20\) términos de la secuencia geométrica\(3, 6, 12, 24, 48, 96, …\)
- Responder
-
\(3,145,725\)
Encuentra la suma de los primeros\(20\) términos de la secuencia geométrica\(6, 18, 54, 162, 486, 1,458, …\)
- Responder
-
\(10,460,353,200\)
En el siguiente ejemplo, se nos da la suma en notación de suma. Si bien podría ser posible agregar todos los términos, la mayoría de las veces es más fácil usar la fórmula para encontrar la suma de los primeros\(n\) términos.
Para usar la fórmula, necesitamos\(r\). Podemos encontrarlo escribiendo los primeros términos de la secuencia y encontrar su proporción. Otra opción es darse cuenta de que en notación sumatoria, se escribe una secuencia en la forma\(\sum_{i=1}^{k} a(r)^{i}\), donde\(r\) está la relación común.
Encuentra la suma:\(\sum_{i=1}^{15} 2(3)^{i}\).
Solución:
Para encontrar la suma, usaremos la fórmula\(S_{n}=\frac{a_{1}\left(1-r^{n}\right)}{1-r}\), que requiere\(a_{1}\) y\(r\). Escribiremos algunos de los términos, para que podamos obtener la información necesaria.
 |
|
| Escribe los primeros términos. |  |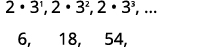
| Identificar\(a_{1}\). |  |
| Encuentra la proporción común. |  |
| Saber\(a_{1}=6\),\(r=3\), y\(n=15\), usar la fórmula de suma. |  |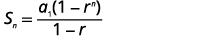
| Sustituto en los valores. |  |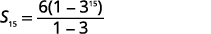
| Simplificar. |  |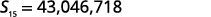
Encuentra la suma:\(\sum_{i=1}^{15} 6(2)^{i}\).
- Responder
-
\(393,204\)
Encuentra la suma:\(\sum_{i=1}^{10} 5(2)^{i}\).
- Responder
-
\(10,230\)
Encuentra la suma de una serie geométrica infinita
Si tomamos una secuencia geométrica y agregamos los términos, tenemos una suma que se llama serie geométrica. Una serie geométrica infinita es una suma infinita cuyo primer término es\(a_{1}\) y la relación común es\(r\) y está escrita
\(a_{1}+a_{1} r+a_{1} r^{2}+\ldots+a_{1} r^{n-1}+\ldots\)
Una serie geométrica infinita es una suma infinita cuyo primer término es\(a_{1}\) y la relación común es\(r\) y está escrita
\(a_{1}+a_{1} r+a_{1} r^{2}+\ldots+a_{1} r^{n-1}+\dots\)
Sabemos encontrar la suma de los primeros\(n\) términos de una serie geométrica usando la fórmula,\(S_{n}=\frac{a_{1}\left(1-r^{n}\right)}{1-r}\). Pero, ¿cómo encontramos la suma de una suma infinita?
Veamos la serie geométrica infinita\(3+6+12+24+48+96+….\). Cada término se hace cada vez más grande por lo que tiene sentido que la suma del número infinito de términos se haga más grande. Veamos algunas sumas parciales para esta serie. Vemos\(a_{1}=3\) y\(r=2\)
\(\begin{array}{lll}{S_{n}=\frac{a_{1}\left(1-r^{n}\right)}{1-r}} & {S_{n}=\frac{a_{1}\left(1-r^{n}\right)}{1-r}} & {S_{n}=\frac{a_{1}(1-r^{n})}{1-r}}\\ {S_{10}=\frac{3\left(1-2^{10}\right)}{1-2}} & {S_{30}=\frac{3\left(1-2^{30}\right)}{1-2}} & {S_{50}=\frac{3\left(1-2^{50}\right)}{1-2}} \\ {S_{10}=3,069} & {S_{30}=3,221,225,469} & {S_{50}\approx 3.38 \times 10^{15}}\end{array}\)
A medida que\(n\) se hace cada vez más grande, la suma se hace cada vez más grande. Esto es cierto cuando\(|r|≥1\) y llamamos a la serie divergente. No podemos encontrar una suma de una serie geométrica infinita cuando\(|r|≥1\).
Veamos una serie geométrica infinita cuya relación común es una fracción menor que uno,
\(\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}+\frac{1}{64}+\ldots\). Aquí los términos se hacen cada vez más pequeños a medida que\(n\) se hace más grande. Veamos algunas sumas finitas para esta serie. Vemos\(a_{1}=\frac{1}{2}\) y\(r=\frac{1}{2}\).
\(\begin{array}{lll}{S_{n}=\frac{a_{1}\left(1-r^{n}\right)}{1-r}} & {S_{n}=\frac{a_{1}\left(1-r^{n}\right)}{1-r}} & {S_{n}=\frac{a_{1}(1-r^{n})}{1-r}}\\ {S_{10}=\frac{\frac{1}{2}\left(1-\frac{1}{2}^{10}\right)}{1-\frac{1}{2}}} & {S_{20}=\frac{\frac{1}{2}\left(1-\frac{1}{2}^{20}\right)}{1-\frac{1}{2}}} & {S_{30}=\frac{\frac{1}{2}\left(1-\frac{1}{2}^{30}\right)}{1-\frac{1}{2}}} \\ {S_{10}\approx 0.9990234375} & {S_{20}\approx 0.9999990463} & {S_{30}\approx 0.9999999991}\end{array}\)
Observe que la suma se hace cada vez más grande pero también se acerca cada vez más a una. Cuando\(|r|<1\), la expresión\(r^{n}\) se hace cada vez más pequeña. En este caso, llamamos a la serie convergente. A medida que se\(n\) acerca al infinito, (se vuelve infinitamente grande),\(r^{n}\) se acerca cada vez más a cero. En nuestra fórmula de suma, podemos reemplazar el\(r^{n}\) por cero y luego obtenemos una fórmula para la suma,\(S\), para una serie geométrica infinita cuando\(|r|<1\).
\(\begin{aligned} S_{n} &=\frac{a_{1}\left(1-r^{n}\right)}{1-r} \\ S &=\frac{a_{1}(1-0)}{1-r} \\ S &=\frac{a_{1}}{1-r} \end{aligned}\)
Esta fórmula nos da la suma de la secuencia geométrica infinita. Observe el\(S\) no tiene el subíndice\(n\)\(S_{n}\) como en ya que no estamos agregando un número finito de términos.
Para una serie geométrica infinita cuyo primer término es\(a_{1}\) y proporción común\(r\),
Si\(|r|<1\), la suma es
\(S=\frac{a_{1}}{1-r}\)
Si\(|r|≥1\), la serie geométrica infinita no tiene suma. Decimos que la serie diverge.
Encuentra la suma de la serie geométrica infinita\(54+18+6+2+\frac{2}{3}+\frac{2}{9}+\ldots\)
Solución:
Para encontrar la suma, primero tenemos que verificar que la proporción común\(|r|<1\) y luego podemos usar la fórmula de suma\(S=\frac{a_{1}}{1-r}\).
Encuentra la proporción común.
\(\begin{array}{ll}{r=\frac{18}{54}} & {r=\frac{6}{18} \dots} \\ {r=\frac{1}{3}} & {r=\frac{1}{3} \quad|r|<1}\end{array}\)
Identificar\(a_{1}\).
\(a_{1}=54\)
Sabiendo\(a_{1}=54, r=\frac{1}{3}\), usa la fórmula de suma.
\(S=\frac{a_{1}}{1-r}\)
Sustituto en los valores.
\(S=\frac{54}{1-\frac{1}{3}}\)
Simplificar.
\(S=81\)
Respuesta:
\(S=80\)
Encuentra la suma de la serie geométrica infinita\(48+24+12+6+3+\frac{3}{2}+\dots\)
- Responder
-
\(96\)
Encuentra la suma de la serie geométrica infinita\(64+16+4+1+\frac{1}{4}+\frac{1}{16}+\dots\)
- Responder
-
\(\frac{256}{3}\)
Un uso interesante de las series geométricas infinitas es escribir un decimal repetido como fracción.
Escribe el decimal repetido\(0.5\) como una fracción.
Solución:
Reescribe la\(0.5\) presentación de los cinco repetidos. Utilice el valor posicional para reescribir esto como una suma. Se trata de una serie geométrica infinita.
0.55555555555\(\ldots\)
\(0.5+0.05+0.005+0.0005+\dots\)
Encuentra la proporción común.
\(\begin{array}{ll}{r=\frac{0.05}{0.5}} & {r=\frac{0.005}{0.05} \dots} \\ {r=0.1} & {r=0.1 \quad|r|<1}\end{array}\)
Identificar\(a_{1}\)
\(a_{1}=0.5\)
Sabiendo\(a_{1}=0.5 ,r=0.1\), usa la fórmula de suma.
\(S=\frac{a_{1}}{1-r}\)
Sustituto en los valores.
\(S=\frac{0.5}{1-0.1}\)
Simplificar.
\(S=\frac{0.5}{0.9}\)
Multiplica el numerador y el denominador por\(10\).
\(S=\frac{5}{9}\)
Se nos pide encontrar la forma de fracción.
\(0.5 = \frac{5}{9}\)
Escribe el decimal repetido\(0.4\) como una fracción.
- Responder
-
\(\frac{4}{9}\)
Escribe el decimal repetido\(0.8\) como una fracción.
- Responder
-
\(\frac{8}{9}\)
Aplicar secuencias geométricas y series en el mundo real
Una aplicación de secuencias geométricas tiene que ver con el gasto del consumidor. Si se da un reembolso fiscal a cada hogar, el efecto en la economía es muchas veces el monto del reembolso individual.
El gobierno ha decidido dar un reembolso\(1,000\) fiscal de $ a cada hogar para estimular la economía. Las estadísticas gubernamentales dicen que cada hogar gastará\(80\)% de la rebaja en bienes y servicios. Los negocios y las personas que se beneficiaron de ese\(80\)% gastarán entonces\(80\)% de lo que recibieron y así sucesivamente. El resultado se llama efecto multiplicador. ¿Cuál es el efecto total de la rebaja en la economía?
Solución:
Cada vez que el dinero entra en la economía,\(80\)% de él se gasta y luego está en la economía para ser gastado. Nuevamente,\(80\)% de este dinero se gasta nuevamente en la economía. Esta situación continúa y así nos lleva a una serie geométrica infinita.
\(1000+1000(0.8)+1000(0.8)^{2}+\ldots\)
Aquí es el primer término\(1,000, a_{1}=1000\). La proporción común es\(0.8, r=0.8\). Podemos evaluar esta suma desde entonces\(0.8<1\). Utilizamos la fórmula para la suma en una serie geométrica infinita.
\(S=\frac{a_{1}}{1-r}\)
Sustituir en los valores,\(a_{1}=1,000\) y\(r=0.8\).
\(S=\frac{1,000}{1-0.8}\)
Evaluar.
\(S=5,000\)
Respuesta:
El efecto total de los $\(1,000\) recibidos por cada hogar será un\(5,000\) crecimiento de $ en la economía.
¿Cuál es el efecto total en la economía de una rebaja fiscal gubernamental de $\(1,000\) a cada hogar para estimular la economía si cada hogar gastará\(90\)% de la rebaja en bienes y servicios?
- Responder
-
$\(10,000\)
¿Cuál es el efecto total en la economía de una rebaja fiscal gubernamental de $\(500\) a cada hogar para estimular la economía si cada hogar gastará\(85\)% de la rebaja en bienes y servicios?
- Responder
-
$\(3,333.33\)
Hemos visto una fórmula de interés compuesto donde un principal,\(P\), se invierte a una tasa de interés,\(r\), durante\(t\) años. El nuevo saldo,\(A\), es\(A=P\left(1+\frac{r}{n}\right)^{n t}\) cuando el interés se agrava\(n\) veces al año. Esta fórmula se aplica cuando se invirtió una suma global por adelantado y nos dice el valor después de cierto período de tiempo.
Una anualidad es una inversión que es una secuencia de depósitos periódicos iguales. Estaremos viendo anualidades que paguen los intereses al momento de los depósitos. A medida que desarrollemos la fórmula para el valor de una anualidad, vamos a dejar\(n=1\). Eso significa que hay un depósito por año.
\(\begin{aligned} &A =P\left(1+\frac{r}{n}\right)^{n t} \\ \text { Let } n=1 .\quad & A=P\left(1+\frac{r}{1}\right)^{1 t} \\ \text { Simplify. }\quad & A=P(1+r)^{t} \end{aligned}\)
Supongamos que los\(P\) dólares se invierten al final de cada año. Un año después ese depósito vale\(P(1+r)^{1}\) dólares, y otro año después vale\(P(1+r)^{2}\) dólares. Después de\(t\) años, valdrá\(P(1+r)^{t}\) dólares.
| Fin de año\(1\) | Fin de año\(2\) | Fin de año\(3\) | |
|---|---|---|---|
| Primer Depósito\(P\) @ fin de año\(1\) | \ (1\) ">\(P\) | \ (2\) ">Monto\(1\) año después\(P(1+r)^{1}\) | \ (3\) ">Cantidad\(2\) años después\(P(1+r)^{2}\) |
| \(2\)nd Depósito\(P\) @ fin de año\(2\) | \ (1\) "> | \ (2\) ">\(P\) | \ (3\) ">Monto\(1\) año después\(P(1+r)^{1}\) |
| \(3\)rd Depósito\(P\) @ fin de año\(3\) | \ (1\) "> | \ (2\) "> | \ (3\) ">\(P\) |
Después de tres años, el valor de la anualidad es
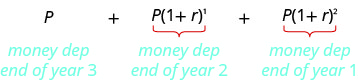
Esto es una suma de los términos de una secuencia geométrica donde está el primer término\(P\) y la relación común es\(1+r\). Sustituimos estos valores en la fórmula de suma. Ten cuidado, tenemos dos usos diferentes de\(r\). La fórmula\(r\) en la suma es la relación común de la secuencia. En este caso, ahí es\(1+r\) donde\(r\) está la tasa de interés.
\(\begin{aligned} &S_{t} =\frac{a_{1}\left(1-r^{t}\right)}{1-r} \\ \text { Substitute in the values. }\quad & S_{t}=\frac{P\left(1-(1+r)^{t}\right)}{1-(1+r)} \\ \text { Simplify. }\quad & S_{t} =\frac{P\left(1-(1+r)^{t}\right)}{-r} \\ &S_{t} =\frac{P\left((1+r)^{t}-1\right)}{r} \end{aligned}\)
Recuerda que nuestra premisa era que se hacía un depósito al final de cada año.
Podemos adaptar esta fórmula para\(n\) los depósitos realizados al año y el interés se compone\(n\) veces al año.
Para un principal,\(P\), invertido al término de un periodo compuesto, con una tasa de interés\(r\), que se compone\(n\) veces al año, el nuevo saldo\(A\), después de\(t\) años, es
\(A_{t}=\frac{P\left(\left(1+\frac{r}{n}\right)^{n t}-1\right)}{\frac{r}{n}}\)
Los nuevos padres deciden invertir $\(100\) mensuales en una anualidad para su hija pequeña. La cuenta pagará\(5\)% de interés anual el cual se compone mensualmente. ¿Cuánto habrá en la cuenta de la niña al cumplir dieciocho años?
Solución:
Para encontrar la fórmula de Anualidad\(A_{t}=\frac{P\left(\left(1+\frac{r}{n}\right)^{n t}-1\right)}{\frac{r}{n}}\),, necesitamos identificar\(P, r, n\), y\(t\).
Identificar\(P\), la cantidad invertida cada mes.
\(P=100\)
Identificar\(r\), la tasa de interés anual, en forma decimal.
\(r=0.05\)
Identificar\(n\), el número de veces que se realizará el depósito y los intereses compuestos cada año.
\(n=12\)
Identificar\(t\), el número de años.
\(t=18\)
Conocer\(P=100, r=0.05, n=12\) y\(t=18\), utilizar la fórmula de suma.
\(A_{t}=\frac{P\left(\left(1+\frac{r}{n}\right)^{n t}-1\right)}{\frac{r}{n}}\)
Sustituto en los valores.
\(A_{t}=\frac{100\left(\left(1+\frac{0.05}{12}\right)^{12.18}-1\right)}{\frac{0.05}{12}}\)
Utilice la calculadora para evaluar. Asegúrese de usar paréntesis según sea necesario.
\(A_{t}=34.920 .20\)
Respuesta:
El niño tendrá $\(34,920.20\)
Los abuelos nuevos deciden invertir $\(200\) mensuales en una anualidad para su nieto. La cuenta pagará\(5\)% de interés anual el cual se compone mensualmente. ¿Cuánto habrá en la cuenta del niño al cumplir 21 años?
- Responder
-
$\(88,868.36\)
Arturo acaba de obtener su primer trabajo de tiempo completo después de graduarse de la universidad a la edad\(27\). Decidió invertir $\(200\) mensuales en una IRA (una anualidad). El interés sobre la anualidad es\(8\)%, que se compone mensualmente. ¿Cuánto habrá en la cuenta de Arturo cuando se jubile al cumplir sesenta y siete años?
- Responder
-
$\(698,201.57\)
Acceda a estos recursos en línea para obtener instrucción adicional y práctica con secuencias.
Conceptos clave
- Término general (término\(n\) th) de una Secuencia Geométrica: El término general de una secuencia geométrica con primer término\(a_{1}\) y la relación común\(r\) es
\(a_{n}=a_{1} r^{n-1}\)
- Suma de los primeros\(n\) términos de una serie geométrica: La suma,\(S_{n}\), de los\(n\) términos de una secuencia geométrica es
\(S_{n}=\frac{a_{1}\left(1-r^{n}\right)}{1-r}\)
donde\(a_{1}\) es el primer término y\(r\) es la proporción común. Serie geométrica infinita: Una serie geométrica infinita es una suma infinita cuyo primer término es\(a_{1}\) y la relación común es\(r\) y está escrita\(a_{1}+a_{1} r+a_{1} r^{2}+\ldots+a_{1} r^{n-1}+\ldots\)
- Suma de una Serie Geométrica Infinita: Para una serie geométrica infinita cuyo primer término es\(a_{1}\) y proporción común\(r\),
Si\(|r|<1\), la suma es
\(S=\frac{a_{1}}{1-r}\)
Nosotros decimos que la serie converge.
Si\(|r|≥1\), la serie geométrica infinita no tiene suma. Decimos que la serie diverge.
- Valor de una anualidad con intereses compuestos \(n\)veces al año: Para un principal,\(P\), invertido al final de un período compuesto, con una tasa de interés,\(r\), que se compone\(n\) veces al año, el nuevo saldo,\(A\), después \(t\)años, es
\(A_{t}=\frac{P\left(\left(1+\frac{r}{n}\right)^{n t}-1\right)}{\frac{r}{n}}\)
Glosario
- anualidad
- Una anualidad es una inversión que es una secuencia de depósitos periódicos iguales.
- relación común
- La relación entre términos consecutivos en una secuencia geométrica\(\frac{a_{n}}{a_{n-1}}\),\(r\), es, la relación común, donde\(r\) mayor o igual a dos.
- secuencia geométrica
- Una secuencia geométrica es una secuencia donde la relación entre términos consecutivos es siempre la misma
- serie geométrica infinita
- Una serie geométrica infinita es una secuencia geométrica infinita de suma infinita.