3.1: Desigualdades lineales
- Page ID
- 117535
Cuando hay una solución a una ecuación como\(x = 4\), esta solución es única y es la única solución que hace que la afirmación sea cierta. Sin embargo, con las desigualdades, la solución es un intervalo de números en el que hacen realidad la desigualdad.
Una desigualdad es una relación entre dos números o dos conjuntos de números (o elementos) en los que no son estrictamente iguales, sino mayores que (o iguales a) o menores que (o iguales a).
\[\begin{array}{ll} >&\text{greater than} \\ \geq&\text{greater than or equal to} \\ <&\text{less than} \\ \leq&\text{less than or equal to}\end{array}\nonumber\]
El matemático inglés Thomas Harriot utilizó por primera vez los símbolos de desigualdad en 1631. Sin embargo, no fueron inmediatamente aceptados, donde símbolos\(\sqsubset\) y ya\(\sqsupset\) fueron acuñados por otro matemático inglés, William Oughtred.
Graficando Desigualdades Lineales
Si tenemos una declaración como\(x < 4\), esto significa que una solución puede ser cualquier número menor que\(4\) tal como\(−2,\: 0,\: 3,\: 3.9\) o incluso\(3.999999999\) siempre y cuando sea menor que\(4\). Si tenemos una declaración como\(x\geq −2\), esto significa que una solución puede ser cualquier número mayor o igual a\(−2\), tal como\(5,\: 0,\: −1,\: −1.9999,\) o incluso\(−2\). Debido a que no tenemos un valor como solución, a menudo es útil dibujar una imagen de las soluciones a la desigualdad en una recta numérica.
Una desigualdad lineal en una variable es una desigualdad de la forma\[ax + b < c,\nonumber\] donde se escribe la desigualdad en la misma forma para\(>,\: ≤,\: ≥\).
Reescribimos los\(>,\: <,\: \leq ,\: \geq\) símbolos como paréntesis y corchetes, es decir,\((,\: ),\: ],\: [,\) respectivamente, cuando escribimos la desigualdad en la notación de intervalos.
- Caso 1. Si\(x< a\), entonces el conjunto equivalente de números en notación de intervalo es\((-\infty, a)\); de manera similar, Si\(x\leq a\), entonces el conjunto equivalente de números en notación de intervalo es\((-\infty ,a]\).
- Caso 2. Si\(x>a\), entonces el conjunto equivalente de números en notación de intervalo es\((a, ∞)\); de manera similar, Si\(x ≥ a\), entonces el conjunto equivalente de números en notación de intervalo es\([a, ∞)\).
Grafica la desigualdad y reescribe la desigualdad en notación de intervalos:\(x < 2\)
Solución
Completaremos este ejemplo en pasos y usaremos este método para los ejemplos futuros restantes que involucren desigualdades.
Paso 1. Dibuja una recta numérica y marca el número en la desigualdad en la línea.

Paso 2. Escriba un paréntesis o corchete, dependiendo del signo de desigualdad, sobre el número en la recta numérica. Tenga en cuenta, podemos usar fácilmente\(•\) para\(≤\) y\(≥\), y\(◦\) para\(<\) y\(>\). Como tenemos\(x < 2\), entonces usamos\(◦\) o) en la recta numérica:

Paso 3. Dibuja una línea que conecte el\(]\) o\(◦\) en la dirección donde yace la solución. Desde\(x < 2\) entonces queremos que todos los números sean menores que\(2\); por lo tanto, dibujamos la línea a la izquierda para representar todos los números menores que\(2\):
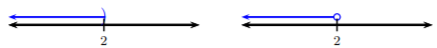
A pesar de que hay dos gráficas, una será suficiente. A discreción del instructor, se utilizarán corchetes y paréntesis, o círculos cerrados y abiertos al graficar las desigualdades.
Paso 4. Reescribir la desigualdad en la notación de intervalos. Ya que\(x < 2\), podemos ver que este es el caso 1 y así es el intervalo\((−∞, 2)\). Usamos un paréntesis en el\(2\) ya que es\(<\).
En Ejemplo\(\PageIndex{1}\), usamos un paréntesis en\(−∞\) porque no\(±∞\) son números reales y simboliza “algún número grande (positivo o negativo) más allá de cualquier número real”. Es una práctica común usar siempre paréntesis en infinidades para intervalos.
El símbolo del infinito fue utilizado por primera vez por los romanos a pesar de que, en su momento, se utilizó el número para\(1,000\). Los griegos también usaron el símbolo para\(10,000\).
Grafica la desigualdad y reescribe la desigualdad en notación de intervalos:\(y ≥ −1\)
Solución
Empezamos etiquetando la línea numérica con\(−1\). Luego dibuja una línea hacia la derecha ya que todos los números mayores que (o iguales a)\(−1\) están a la derecha:
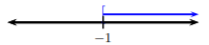
A continuación, escribimos\(y ≥ −1\) en notación de intervalos. Este es el caso 2 y el intervalo es\([−1, ∞)\); usamos un corchete debido a\(≥\).
Dada la gráfica, escriba la desigualdad equivalente y la notación de intervalo:
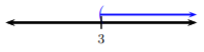
Solución
Dado que la gráfica muestra todos los números (estrictamente) mayores que\(3\), entonces la desigualdad es\(x > 3\); usamos\(>\) debido a la\((\) en la recta numérica. El intervalo equivalente sería, usando el caso 2,\((3, ∞)\).
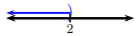
Dada la gráfica, escriba la desigualdad equivalente y la notación de intervalo:
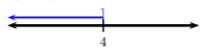
Solución
Dado que la gráfica muestra todos los números menores que (o iguales a)\(4\), entonces la desigualdad es\(x ≤ 4\); usamos\(≤\) debido a la\(]\) en la recta numérica. El intervalo equivalente sería, usando el caso 1,\((−∞, 4]\).
Resolver desigualdades lineales
Hay dos propiedades que se utilizan con desigualdades:
Propiedad 1. Adición Propiedad de Desigualdades: Para números\(a,\: b,\: c,\)\[a < b\text{ is equivalent to }a + c < b + c,\nonumber\] donde la forma es la misma para\(>,\: ≤,\: ≥\). Es decir, puede agregar un número a un lado de la desigualdad siempre y cuando agregue el mismo número al otro lado. (Esto debería recordarle la propiedad de suma para ecuaciones).
Propiedad 2. Multiplicación Propiedad de las Desigualdades: Para números\(a,\: b,\: c\) y\(c\neq 0\),\[a < b\text{ is equivalent to }a · c < b · c,\nonumber\] donde la forma es la misma para\(>,\: ≤,\: ≥\). Es decir, puedes multiplicar un número distinto de cero a un lado de la desigualdad siempre y cuando multipliques el mismo número distinto de cero al otro lado.
No obstante, si\(c < 0\), entonces la desigualdad se invierte, es decir, si multiplicas o divides por un negativo, entonces invierte el símbolo de desigualdad.
Resolver la desigualdad. Grafica la solución y escribe la solución en notación de intervalos.
\[5-2x\geq 11\nonumber\]
Solución
\[\begin{array}{rl}5-2x\geq 11&\text{Add the opposite of }5\text{ to each side} \\ 5-2x+\color{blue}{(-5)}\color{black}{}\geq 11+\color{blue}{(-5)}&\text{Simplify} \\ -2x\geq 6&\text{Multiply by the reciprocal of }-2 \\ \color{blue}{\left(-\frac{1}{2}\right)}\color{black}{}\cdot -2x\leq 6\cdot\color{blue}{\left(-\frac{1}{2}\right)}\color{black}{}&\text{Simplify and reverse the inequality sign} \\ x\color{blue}{\leq}\color{black}{}-3&\text{Solution}\end{array}\nonumber\]
Vamos a graficar la solución\(x ≤ −3\):
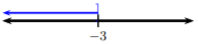
A continuación, escribimos\(x ≤ −3\) en notación de intervalos. Este es el caso 1 y el intervalo es\((−∞, −3]\); usamos un corchete debido a\(≤\).
Resolver la desigualdad. Grafica la solución y escribe la solución en notación de intervalos.
\[3(2x-4)+4x<4(3x-7)+8\nonumber\]
Solución
\[\begin{array}{rl}3(2x-4)+4x<4(3x-7)+8&\text{Distribute} \\ 6x-12+4x<12x-28+8&\text{Combine like terms} \\ 10x-12<12x-20&\text{Isolate the variable term} \\ 10x-12+\color{blue}{(-10x)}\color{black}{}<12x-20+\color{blue}{(-10x)}\color{black}{}&\text{Simplify} \\ -12<2x-20&\text{Add the opposite of }-20\text{ to each side} \\ -12+\color{blue}{20}\color{black}{}<2x-20+\color{blue}{20}\color{black}{}&\text{Simplify} \\ 8<2x&\text{Multiply by the reciprocal of }2 \\ \color{blue}{\frac{1}{2}}\color{black}{}\cdot 8<2x\cdot\color{blue}{\frac{1}{2}}&\text{Simplify} \\ 4<x&\text{Rewrite the inequality with }x\text{ on the left side} \\ x>4&\text{Solution}\end{array}\nonumber\]
Vamos a graficar la solución\(x>4\):
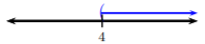
A continuación, escribimos\(x > 4\) en notación de intervalos. Este es el caso 2 y el intervalo es\((4, ∞)\); usamos un paréntesis debido a\(>\).
Es importante tener cuidado cuando la solución a la desigualdad tiene la variable aislada en el lado derecho como en Ejemplo\(\PageIndex{6}\), es decir,\(4 < x\) más que\(x > 4\). Es la mejor práctica escribir la variable en el lado izquierdo después de aislar la variable. Esto minimizará la confusión al graficar la solución y escribir la solución en notación de intervalos.
Desigualdades tripartitas
Un tipo especial de desigualdad compuesta se denomina desigualdad tripartita, cuando la variable (o expresión que contiene la variable) se encuentra entre dos números. Al resolver este tipo de desigualdades con tres partes, aplicaremos las propiedades de las desigualdades a las tres partes (en lugar de a dos lados) para aislar la variable en el medio.
Caso 1. Si\(a < x < b\), entonces el conjunto equivalente de números en notación de intervalo es\((a, b)\); de manera similar, Si\(a ≤ x ≤ b\), entonces el conjunto equivalente de números en notación de intervalo es\([a, b]\).
Caso 2. Si\(a < x ≤ b\), entonces el conjunto equivalente de números en notación de intervalo es\((a, b]\); de manera similar, Si\(a ≤ x < b\), entonces el conjunto equivalente de números en notación de intervalo es\([a, b)\).
Resolver la desigualdad. Grafica la solución y escribe la solución en notación de intervalos.
\[-6\leq -4x+2<2\nonumber\]
Solución
Resuelve la desigualdad, grafica la solución y da notación de intervalo.
\[\begin{array}{rl}-6\leq -4x+2<2&\text{Add the opposite of }2\text{ to each part of the inequality} \\ -6+\color{blue}{(-2)}\color{black}{}\leq -4x+2+\color{blue}{(-2)}\color{black}{}<2+\color{blue}{(-2)}\color{black}{}&\text{Simplify} \\ -8\leq -4x<0&\text{Multiply by the reciprocal of }-4 \\ \color{blue}{-\frac{1}{4}}\color{black}{}\cdot -8\geq \color{blue}{-\frac{1}{4}}\color{black}{}\cdot -4x>\color{blue}{-\frac{1}{4}}\color{black}{}\cdot 0&\text{Simplify} \\ 2\color{blue}{\geq}\color{black}{}x\color{blue}{>}\color{black}{}0&\text{Rewrite with }\geq,\: >\text{ signs} \\ 0<x\leq 2&\text{Solution}\end{array}\nonumber\]
Vamos a graficar la solución\(0<x\leq 2\):

A continuación, escribimos\(0 < x ≤ 2\) en notación de intervalos. Este es el caso 2 y el intervalo es\((0, 2]\).
Tareas Lineales Desigualdades
Grafica las desigualdades y reescribe las desigualdades en notación de intervalos.
\(n>-5\)
\(-2\geq k\)
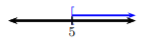
\(5\geq x\)
\(n>4\)
\(1\geq k\)
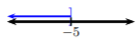
\(-5<x\)
Dada la gráfica, escribir la desigualdad equivalente y notación de intervalo.
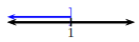
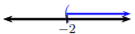
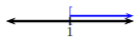
Resolver la desigualdad. Grafica la solución y escribe la solución en notación de intervalos.
\(\frac{x}{11}\geq 10\)
\(2+r<3\)
\(8+\frac{n}{3}\geq 6\)
\(2>\frac{a-2}{5}\)
\(−47 ≥ 8 − 5x\)
\(−2(3 + k) < −44\)
\(18 < −2(−8 + p)\)
\(24 ≥ −6(m − 6)\)
\(−r − 5(r − 6) < −18\)
\(24 + 4b < 4(1 + 6b)\)
\(−5v − 5 < −5(4v + 1)\)
\(4 + 2(a + 5) < −2(−a − 4)\)
\(−(k − 2) > −k − 20\)
\(−2 ≤ \frac{n}{13}\)
\(\frac{m}{5}\leq -\frac{6}{5}\)
\(11>8+\frac{x}{2}\)
\(\frac{v-9}{-4}\leq 2\)
\(\frac{6+x}{12}\leq -1\)
\(−7n − 10 ≥ 60\)
\(5\geq\frac{x}{5}+1\)
\(−8(n − 5) ≥ 0\)
\(−60 ≥ −4(−6x − 3)\)
\(−8(2 − 2n) ≥ −16 + n\)
\(−36 + 6x > −8(x + 2) + 4x\)
\(3(n + 3) + 7(8 − 8n) < 5n + 5 + 2\)
\(−(4 − 5p) + 3 ≥ −2(8 − 5p)\)
\(3 ≤ 9 + x ≤ 7\)
\(11 < 8 + k ≤ 12\)
\(−3 < x − 1 < 1\)
\(−4 < 8 − 3m ≤ 11\)
\(−16 ≤ 2n − 10 ≤ −22\)
\(0\geq\frac{x}{9}\geq -1\)
\(-11\leq n-9\leq -5\)
\(1\leq\frac{p}{8}\leq 0\)


