3.2: Desigualdades compuestas
- Page ID
- 117534
Varias desigualdades se combinan para formar desigualdades compuestas. Hay tres tipos de desigualdades compuestas que vamos a investigar en esta sección: y, o, y tripartita.
Dejar\(A\) y\(B\) ser conjuntos.
- La unión de dos conjuntos contiene todos los elementos contenidos en cualquiera de los conjuntos (o ambos conjuntos). Se denota el sindicato\(A ∪ B\).
- La intersección de dos conjuntos contiene sólo los elementos que están en ambos conjuntos. Se denota la intersección\(A ∩ B\).
Desigualdades compuestas con o
Para o las desigualdades compuestas, la solución es una verdadera afirmación de una desigualdad, de la otra desigualdad, o de ambas. Esto debería recordarle la unión de dos conjuntos excepto, en este caso, vamos a determinar la solución graficando cada desigualdad, y escribir la solución en notación de intervalos. Pista: Usaremos el símbolo de unión,\(∪\), en la solución.
Resolver la desigualdad compuesta. Grafica la solución y escribe la solución en notación de intervalos.
\[2x-5>3\quad\text{or}\quad 4-x\geq 6\nonumber\]
Solución
Comenzamos la solución resolviendo para cada desigualdad.
\[\begin{array}{rl}2x-5>3\quad\text{or}\quad 4-x\geq 6&\text{Solve each inequality} \\ 2x>8\quad\text{or}\quad -x\geq 2&\text{Divide by the coefficient of }x \\ x>4\quad\text{or}\quad x\leq -2&\text{Solution in inequality notation}\end{array}\nonumber\]
Vamos a graficar cada una de estas desigualdades para determinar la unión de los dos conjuntos.

Buscando la unión de estos dos conjuntos, vemos que la solución son todos los números a la izquierda de\(−2\) (inclusive), o a la derecha de\(4\), o en ambos. Por lo tanto, en notación de intervalos, la solución es\[(-\infty ,-2]\cup (4,\infty )\nonumber\]
El símbolo del infinito fue utilizado por primera vez por los romanos, aunque, en su momento, se utilizó el número para\(1,000\). Los griegos también usaron el símbolo para\(10,000\).
Hay casos especiales con las desigualdades o compuestas a la hora de obtener una solución.
Caso 1. Como una gráfica contenida en la otra, la unión de los dos conjuntos será el conjunto más grande.
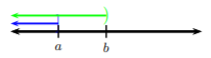
De ahí que en este caso, la solución sea\((-\infty , b)\).

De ahí que en este caso, la solución sea\((−∞, ∞)\).
Desigualdades compuestas con y
Para y las desigualdades compuestas, la solución es una verdadera declaración de ambas desigualdades. Esto debería recordarte la intersección de dos conjuntos excepto, en este caso, vamos a determinar la solución graficando cada desigualdad, y escribiremos la solución en notación de intervalos. Pista: La solución es un intervalo, y no se utilizan símbolos establecidos con y problemas.
Resolver la desigualdad compuesta. Grafica la solución y escribe la solución en notación de intervalos.
\[2x+8\geq 5x-7\quad\text{and}\quad 5x-3>3x+1\nonumber\]
Solución
Comenzamos la solución resolviendo para cada desigualdad.
\[\begin{array}{rl}2x+8\geq 5x-7\quad\text{and}\quad 5x-3>3x+1&\text{Solve each inequality} \\ 8\geq 3x-7\quad\text{and}\quad 2x-3>1 &\text{Isolate the variable term} \\ 15\geq 3x\quad\text{and}\quad 2x>4&\text{Divide by the coefficient of }x \\ 5\geq x\quad\text{and}\quad x>2&\text{Solution in inequality notation}\end{array}\nonumber\]
Vamos a graficar cada una de estas desigualdades para determinar la intersección de los dos conjuntos.
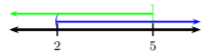
Buscando la intersección de estos dos conjuntos, vemos que la solución son todos los números entre 2 y 5 (inclusive). De ahí que en notación de intervalos, la solución es\((2, 5]\).
Hay casos especiales con las desigualdades y compuestas a la hora de obtener una solución.
Caso 1. Como una gráfica contenida en la otra, la intersección de los dos conjuntos será el conjunto más pequeño.
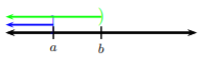
De ahí que en este caso, la solución sea\((−∞, a)\).
Caso 2. Como las gráficas no se cruzan, donde hay un hueco entre conjuntos, entonces no hay solución, es decir,\(∅\).

De ahí que en este caso, la solución no sea ninguna solución o\(\emptyset\).
Recordemos, 3.1.3 del apartado anterior. Las desigualdades tripartitas son y las desigualdades compuestas, donde estamos encontramos la intersección de los dos conjuntos. Observe que las soluciones en 3.1.3 fueron un intervalo como con y desigualdades compuestas.
Resolver la desigualdad compuesta. Grafica la solución y escribe la solución en notación de intervalos.
\[-6\leq -4x+2<2\nonumber\]
Solución
Comenzamos la solución aplicando las propiedades de las desigualdades a cada lado de la desigualdad.
\[\begin{array}{rl} -6\leq -4x+2<2&\text{Subtract }2\text{ from all three parts} \\ -8\leq -4x<0&\text{Divide all three parts by }-4 \\ 2\geq x>0&\text{Flip entire statement so values increase from left to right} \\ 0<x\leq 2&\text{Solution in inequality notation}\end{array}\nonumber\]
Vamos a graficar esta desigualdad para determinar la intersección de los dos conjuntos.

Podemos ver que la intersección es todos los números intermedios\(0\) y\(2\) (inclusive). De ahí que en notación de intervalos, la solución es\((0, 2]\).
Tareas Compuestas Desigualdades
Resolver las desigualdades compuestas. Grafica la solución y escribe la solución en notación de intervalos.
\(\frac{n}{3}\leq -3\)o\(-5n\leq -10\)
\(x + 7 ≥ 12\)o\(9x < −45\)
\(x − 6 < −13\)o\(6x ≤ −60\)
\(\frac{v}{8} > −1\)y\(v − 2 < 1\)
\(−8 + b < −3\)y\(4b < 20\)
\(a + 10 ≥ 3\)y\(8a ≤ 48\)
\(3 ≤ 9 + x ≤ 7\)
\(11 < 8 + k ≤ 12\)
\(−3 < x − 1 < 1\)
\(−4 < 8 − 3m ≤ 11\)
\(−16 ≤ 2n − 10 ≤ −22\)
\(−5b + 10 ≤ 30\)y\(7b + 2 ≤ −40\)
\(3x − 9 < 2x + 10\)y\(5 + 7x ≤ 10x − 10\)
\(−8 − 6v ≤ 8 − 8v\)y\(7v + 9 ≤ 6 + 10v\)
\(1 + 5k ≤ 7k − 3\)o\(k − 10 > 2k + 10\)
\(2x + 9 ≥ 10x + 1\)y\(3x − 2 < 7x + 2\)
\(6m ≥ −24\)o\(m − 7 < −12\)
\(10r > 0\)o\(r − 5 < −12\)
\(9 + n < 2\)o\(5n > 40\)
\(−9x < 63\)y\(\frac{x}{4} < 1\)
\(−6n ≤ 12\)y\(\frac{n}{3}≤ 2\)
\(−6 + v ≥ 0\)y\(2v > 4\)
\(0 ≥ \frac{x}{9} ≥ −1\)
\(−11 ≤ n − 9 ≤ −5\)
\(1 ≤ \frac{p}{8} ≤ 0\)
\(3 + 7r > 59\)o\(−6r − 3 > 33\)
\(−6 − 8x ≥ −6\)o\(2 + 10x > 82\)
\(n + 10 ≥ 15\)o\(4n − 5 < −1\)
\(4n + 8 < 3n − 6\)o\(10n − 8 ≥ 9 + 9n\)
\(5 − 2a ≥ 2a + 1\)o\(10a − 10 ≥ 9a + 9\)
\(8 − 10r ≤ 8 + 4r\)o\(−6 + 8r < 2 + 8r\)
\(−9m + 2 < −10 − 6m\)o\(−m + 5 ≥ 10 + 4m\)


