3.3: Desigualdades de valor absoluto
- Page ID
- 117542
Cuando una desigualdad contiene valor absoluto, necesitamos reescribir la desigualdad sin el valor absoluto para resolver la desigualdad. Consideremos\(|x| < 2\). Recordemos, el valor absoluto se define como la distancia desde cero. La idea detrás de la resolución\(|x| < 2\) es encontrar todos los números que tengan una distancia de cero que sea menor que\(2\). Echemos un vistazo a esto gráficamente.
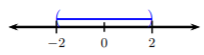
Esta gráfica debería recordarnos las desigualdades tripartitas (y) compuestas ¡y lo es! Ahora consideremos\(|x| > 2\). La idea detrás de la resolución\(|x| > 2\) es encontrar todos los números que tengan una distancia de cero que sea más que\(2\). Echemos un vistazo a esto gráficamente.
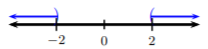
Esta gráfica debería recordarnos o agrandar desigualdades y lo es! Las desigualdades absolutas nos recordarán los conceptos a partir de las desigualdades compuestas.
A continuación se presentan los casos de valor absoluto para las desigualdades en una variable, donde\(a\) es un número real.
Caso 1. Si\(|x| < a\), entonces\(−a < x < a\).
Caso 2. Si\(|x| > a\), entonces\(x < −a\) o\(x > a\). Casos similares para\(≤\) y\(≥\), respectivamente.
La frase “valor absoluto” proviene del matemático alemán Karl Weierstrass en 1876, aunque utilizó el símbolo de valor absoluto para números complejos. El primer uso conocido del símbolo para enteros proviene de una edición de 1939 de un libro de texto de álgebra universitaria.
Resolver la desigualdad de valor absoluto. Grafica la solución y escribe la solución en notación de intervalos.
\[|4x-5|\geq 6\nonumber\]
Solución
Comenzamos la solución reescribiendo la desigualdad de valor absoluto utilizando los casos de la definición.
\[\begin{array}{rl} |4x-5|\geq 6&\text{Case 2. Rewrite as two inequalities using or} \\ 4x-5\geq 6\quad\text{or}\quad 4x-5\leq -6 &\text{Solve each inequality} \\ 4x\geq 11\quad\text{or}\quad 4x\leq -1&\text{Divide by the coefficient of }x \\ x\geq\frac{11}{4}\quad\text{or}\quad x\leq -\frac{1}{4}&\text{Solution in inequality notation}\end{array}\nonumber\]
Vamos a graficar cada una de estas desigualdades para determinar la unión de los dos conjuntos.
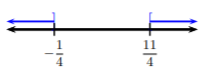
Buscando la unión de estos dos conjuntos, vemos que la solución son todos los números a la izquierda de\(−\frac{1}{4}\) (inclusive), o a la derecha de\(\frac{11}{4}\) (inclusive), o en ambos. Por lo tanto, en notación de intervalos, la solución es\[\left(-\infty ,-\frac{1}{4}\right]\cup\left[\frac{11}{4},\infty\right)\nonumber\]
Aislar el valor absoluto
Recordar. En el capítulo anterior, al resolver ecuaciones de valor absoluto, se requería aislar el término de valor absoluto antes de aplicar la definición. En esta sección, haremos el mismo método porque los métodos nunca cambian, solo problemas.
Resolver la desigualdad de valor absoluto. Grafica la solución y escribe la solución en notación de intervalos.
\[-4-3|x|\leq -16\nonumber\]
Solución
Comenzamos la solución reescribiendo la desigualdad de valor absoluto donde el término de valor absoluto se aísla en el lado izquierdo. Entonces podemos aplicar los casos en la definición.
\[\begin{array}{rl}-4-3|x|\leq -16&\text{Isolate the absolute value term} \\ -3|x|\leq -12&\text{Divide both sides by }-3 \\ |x|\color{blue}{\geq}\color{black}{}4&\text{Case 2. Rewrite as two inequalities using or} \\ x\geq 4\quad\text{or}\quad x\leq -4&\text{Solution in inequality notation}\end{array}\nonumber\]
Vamos a graficar cada una de estas desigualdades para determinar la unión de los dos conjuntos.

Buscando la unión de estos dos conjuntos, vemos que la solución son todos los números a la izquierda de\(−4\) (inclusive), o a la derecha de\(4\) (inclusive), o en ambos. Por lo tanto, en notación de intervalos, la solución es\[(-\infty , -4)\cup [4,\infty )\nonumber\]
Resolver la desigualdad de valor absoluto. Grafica la solución y escribe la solución en notación de intervalos.
\[9-2|4x+1|>3\nonumber\]
Solución
Comenzamos la solución reescribiendo la desigualdad de valor absoluto donde el término de valor absoluto se aísla en el lado izquierdo. Entonces podemos aplicar los casos en la definición.
\[\begin{array}{rl}9-2|4x+1|>3&\text{Isolate the absolute value term} \\ -2|4x+1|>-6&\text{Divide both sides by }-2 \\ |4x+1|\color{blue}{<}\color{black}{}3&\text{Case 1. Rewrite as a tripartite inequality} \\ -3<4x+1<3&\text{Solve, start by subtracting 1 from all three parts} \\ -4<4x<2&\text{Divide by the coefficient of }x \\ -1<x<\frac{1}{2}&\text{Solution in inequality notation}\end{array}\nonumber\]
Vamos a graficar esta desigualdad para determinar la intersección de los dos conjuntos.
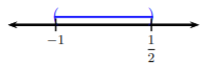
Podemos ver que la intersección es todos los números intermedios\(−1\) y\(\frac{1}{2}\). De ahí que en la notación de intervalos, la solución es\(\left(-1,\frac{1}{2}\right)\).
Casos Especiales con Desigualdades de Valor Absoluto
Hay casos especiales con las desigualdades de valor absoluto a la hora de obtener una solución. Recordamos que después de evaluar el valor absoluto de una expresión, el resultado es positivo. De ahí que si fuéramos a aislar el valor absoluto del lado izquierdo de la desigualdad, entonces ese resultado siempre es positivo, es decir\(|x|\geq 0\), sin importar el caso.
Resolver la desigualdad de valor absoluto. Grafica la solución y escribe la solución en notación de intervalos.
\[12+4|6x-1|<4\nonumber\]
Solución
Comenzamos la solución reescribiendo la desigualdad de valor absoluto donde el término de valor absoluto se aísla en el lado izquierdo. Entonces podemos aplicar los casos en la definición.
\[\begin{array}{rl}12+4|6x-1|<4&\text{Isolate the absolute value term} \\ 4|6x-1|<-8&\text{Divide by the coefficient }4 \\ |6x-1|<-2&\text{STOP The absolute value is always non-negative}\end{array}\nonumber\]
Por definición de valor absoluto,\(|6x − 1| ≥ 0\). De ahí, nunca\(|6x − 1|\) podría ser menor que cero, y mucho menos que\(−2\). Por lo tanto, esta desigualdad no tiene solución ni solución\(∅\). Para graficar una\(∅\) solución, dejamos una recta numérica vacía:
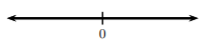
\(\PageIndex{4}\)Digamos, en Ejemplo no reconocemos que\(|6x − 1|\) era menor que un número negativo y lo resolvimos como de costumbre. Después de aplicar el Caso 1. en la definición, obtendríamos una declaración falsa. En Ejemplo\(\PageIndex{4}\), habríamos obtenido\[2 < 6x − 1 < −2,\nonumber\] pero\(2\) no es menor que\(−2 (2\cancel{<} −2)\). De ahí, una declaración falsa. En este punto, veríamos que la desigualdad no\(|6x − 1| < −2\) tiene solución.
Resolver la desigualdad de valor absoluto. Grafica la solución y escribe la solución en notación de intervalos.
\[5-6|x+7|\leq 17\nonumber\]
Solución
Comenzamos la solución reescribiendo la desigualdad de valor absoluto donde el término de valor absoluto se aísla en el lado izquierdo. Entonces podemos aplicar los casos en la definición.
\[\begin{array}{rl} 5-6|x+7|\leq 17&\text{Isolate the absolute value term} \\ -6|x+7|\leq 12&\text{Divide by the coefficient }-6 \\ |x+7|\color{blue}{\geq}\color{black}{}-2&\text{STOP The absolute value is always non-negative}\end{array}\nonumber\]
Por definición de valor absoluto,\(|x + 7| ≥ 0\). De ahí, siempre\(|x + 7|\) es mayor que\(−2\). Así, esta desigualdad tiene cada número real como solución y la solución es toda números reales o\((−∞, ∞)\). Para graficar una\((−∞, ∞)\) solución, trazamos una línea que incluye toda la línea numérica:
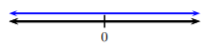
\(\PageIndex{5}\)Digamos, en Ejemplo no reconocemos que siempre\(|x + 7|\) fue mayor que un número negativo y lo resolvimos como de costumbre. Después de aplicar el Caso 2. en la definición, obtendríamos el mismo resultado. En Ejemplo\(\PageIndex{5}\), habríamos obtenido\[x+7\geq -2\quad\text{or}\quad x+7\leq 2,\nonumber\] qué resultados en, después de resolver,\[x\geq -9\quad\text{or}\quad x\leq -5\nonumber\]
Graficando cada desigualdad, obtenemos
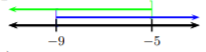
De ahí que la solución sea\((-\infty ,\infty )\).
Valores absolutos Desigualdades Tareas
Resolver las desigualdades de valor absoluto. Grafica la solución y escribe la solución en notación de intervalos.
\(|x| < 3\)
\(|2x| < 6\)
\(|x − 2| < 6\)
\(|x − 7| < 3\)
\(|3x − 2| < 9\)
\(1 + 2|x − 1| ≤ 9\)
\(6 − |2x − 5| ≥ 3\)
\(|3x| > 5\)
\(|x − 3| ≥ 3\)
\(|3x − 5| > 3\)
\(4 + 3|x − 1| ≥ 10\)
\(3 − 2|x − 5| ≤ −15\)
\(−2 − 3|4 − 2x| ≥ −8\)
\(4 − 5| − 2x − 7| < −1\)
\(3 − 2|4x − 5| ≥ 1\)
\(−5 − 2|3x − 6| < −8\)
\(4 − 4| − 2x + 6| > −4\)
\(| − 10 + x| ≥ 8\)
\(|x| ≤ 8\)
\(|x + 3| < 4\)
\(|x − 8| < 12\)
\(|x + 3| ≤ 4\)
\(|2x + 5| < 9\)
\(10 − 3|x − 2| ≥ 4\)
\(|x| > 5\)
\(|x − 4| > 5\)
\(|2x − 4| > 6\)
\(3 − |2 − x| < 1\)
\(3 − 2|3x − 1| ≥ −7\)
\(4 − 6| − 6 − 3x| ≤ −5\)
\(−3 − 2|4x − 5| ≥ 1\)
\(−2 + 3|5 − x| ≤ 4\)
\(−2 − 3| − 3x − 5 ≥ −5\)
\(6 − 3|1 − 4x| < −3\)
\(−3 − 4| − 2x − 5| ≥ −7\)


