3.4: Desigualdades lineales en dos variables

Última actualización
Guardar como PDF

Page ID: 117528

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Anteriormente, representamos desigualdades en una variable, pero ahora aprendemos a graficar las desigualdades en dos variables. Aunque esta sección puede parecer similar a las ecuaciones lineales en dos variables, las desigualdades lineales en dos variables tienen muchas aplicaciones. Por ejemplo, los dueños de negocios quieren saber cuándo los ingresos son mayores que el costo para que su negocio obtenga ganancias, por ejemplo,\(>\) costo de ingresos.

Definición: Desigualdad lineal

Una desigualdad lineal en dos variables es una desigualdad de la forma\[ax + by < c,\nonumber\] donde la desigualdad se escribe en la misma forma para\(>,\: ≤,\: ≥\) y\(a,\: b\neq 0\).

Recordar. La solución a una desigualdad lineal en una variable es un intervalo de números, e.g.\((−∞, ∞),\: [−2, 3),\: (1, 9),\: [−7, −3]\), etc.

Verificación de Soluciones

Solución a una desigualdad lineal en dos variables

Un par ordenado\((x, y)\) es una solución a una desigualdad lineal en dos variables,\(ax + by < c\), si el par ordenado\((x, y)\) hace que la desigualdad sea verdadera, donde lo mismo es para\(>,\: ≤,\: ≥\) y\(a,\: b\neq 0\).

Ejemplo \(\PageIndex{1}\)

Verificar si cada par ordenado es una solución a la desigualdad\(y > x + 4\).

\((0,0)\)
\((1,6)\)

Solución

Sustituimos los pares ordenados en la desigualdad y determinamos si los resultados son ciertos.

Sustituyamos\((0, 0)\) en la desigualdad y determinemos si el lado izquierdo es mayor que el lado derecho. \[\begin{array}{rl}y\stackrel{?}{>}x+4&\text{Substitute }x=0\text{ and }y=0 \\ 0\stackrel{?}{>}0+4&\text{Simplify} \\ 0\cancel{>}4&X\text{ False}\end{array}\nonumber\]De ahí\((0,0)\) que no sea una solución a la desigualdad\(y>x+4\).
Sustituyamos\((1, 6)\) en la desigualdad y determinemos si el lado izquierdo es mayor que el lado derecho. \[\begin{array}{rl}y\stackrel{?}{>}x+4&\text{Substitute }x=1\text{ and }y=6 \\ 6\stackrel{?}{>}1+4&\text{Simplify} \\ 6>5&\checkmark\text{ True}\end{array}\nonumber\]De ahí\((1,6)\) que sea una solución a la desigualdad\(y>x+4\).

Líneas de límite

Si se nos da una desigualdad lineal,\(ax + by < c\), podríamos ver en Ejemplo\(\PageIndex{1}\) que no todos los pares ordenados son una solución, sólo algunos. ¿Por qué? Bueno, fíjate que\((0, 0)\) está por debajo de la línea\(y = x + 4\) y\((1, 6)\) está por encima de la línea\(y = x + 4\). Esto implica que los pares ordenados en ciertas regiones son soluciones a la desigualdad\(y > x + 4\). De ahí que la línea\(y = x + 4\) sea crítica a la hora de encontrar soluciones a la desigualdad. Llamamos a la línea\(y = x + 4\) línea límite, una línea que separa los pares ordenados que son soluciones y los pares ordenados que no son soluciones de la desigualdad lineal en dos variables\(y > x + 4\).

Definición: Línea límite

Una ecuación lineal en dos variables\(ax + by = c\) se llama la línea límite, la línea que separa la región donde\(ax + by > c\) y de la región donde\(ax + by < c\).

Nota

Ya que hay cuatro símbolos de desigualdad:\(>,\: <,\: \geq ,\: \leq\), entonces tenemos desigualdades lineales en dos variables que incluyen el límite, por ejemplo, desigualdades con\(\leq\) y\(\geq\), y desigualdades lineales en dos variables que excluyen el límite, por ejemplo, desigualdades con\(<\) y\(>\).

Podemos usar la siguiente tabla para ayudar a identificar la línea de límite, determinar si incluir la línea límite y la forma en que la línea límite se ve gráficamente.

Mesa\(\PageIndex{1}\)

Caso 1.	Caso 2.
\(ax+by<c\)	\(ax+by\leq c\)
\(ax+by>c\)	\(ax+by\geq c\)
Línea límite:\(ax+by=c\)	Línea límite:\(ax+by=c\)
La línea límite está excluida en la solución	La línea límite está incluida en la solución
La línea límite está discontinua	La línea límite es sólida

Ejemplo\(\PageIndex{2}\)

Revisemos Ejemplo\(\PageIndex{1}\) y graficemos la línea límite y los puntos\((0, 0)\) y\((1, 6)\).

Solución

Ya que tenemos\(y > x + 4\), podemos ver en la tabla anterior tenemos Caso 1. y la línea límite está excluida. Representamos esto graficando la línea\(y = x + 4\) como una línea discontinua.

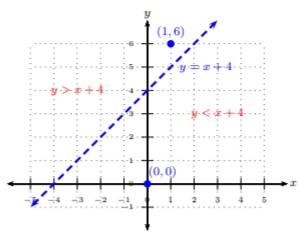
Podemos ver en la gráfica que el punto\((0, 0)\) se encuentra por debajo de la línea de límite\(y = x + 4\) y el punto\((1, 6)\) se encuentra por encima de la línea límite. Recordemos, el punto\((1, 6)\) se verificó como una solución de\(y > x + 4\) en Ejemplo\(\PageIndex{1}\). Además, cualquier par ordenado que se encuentre arriba\(y = x+ 4\) se verificará como solución, es decir, haciendo verdadera la desigualdad. Por lo general, representamos esta área sombreando la región donde el conjunto de pares ordenados hacen que la desigualdad sea cierta.

Graficando Desigualdades Lineales

Ejemplo\(\PageIndex{3}\)

Grafica la desigualdad a partir de Ejemplo\(\PageIndex{1}\).

Solución

Como sabemos que\((1, 6)\) es una solución a la desigualdad, entonces sombreamos por encima de la línea límite discontinua:

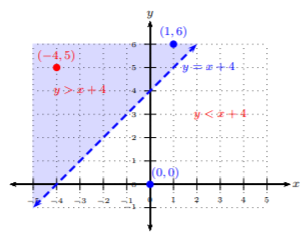
Vemos que cualquier par ordenado en la región sombreada es una solución a la desigualdad. Por ejemplo, escojamos\((−4, 5)\) y verifiquemos que esta es una solución:\[\begin{array}{rl}y\stackrel{?}{>}x+4&\text{Substitute }x=-4\text{ and }y=5 \\ 5\stackrel{?}{>}-4+4&\text{Simplify} 5>0&\checkmark\text{ True}\end{array}\nonumber\]

De ahí\((−4, 5)\) que sea una solución a la desigualdad\(y > x + 4\).

Pasos para Graficar Desigualdades Lineales en Dos Variables

Dada una desigualdad lineal en dos variables,\(ax + by < c\), utilizamos los pasos a continuación para graficar\(ax + by < c\), donde se aplica el mismo proceso para\(>,\: ≤,\: ≥\) y\(a,\: b\neq 0\).

Paso 1. Reescribir la desigualdad en forma de pendiente-intercepción, es decir,\(y = mx + b\).

Paso 2. Grafique la línea límite de acuerdo a los dos casos:

Caso 1. Si la desigualdad es\(<\) o\(>\), entonces la línea límite es discontinua.

Caso 2. Si la desigualdad es\(≥\) o\(≤\), entonces la línea límite es sólida.

Paso 3. Seleccione un punto de prueba que no esté en la línea de contorno. Pregunta: ¿Este par ordenado hace que la desigualdad sea cierta?

Paso 4. Si el par ordenado es

una solución a la desigualdad, es decir, hace que la desigualdad sea cierta, luego sombrear el lado que incluye al par ordenado.
no es una solución, luego sombrear el lado opuesto de la línea límite.

Nota

Si elegimos un punto de prueba en la línea límite, obtendremos una identidad, donde ambos lados del símbolo de desigualdad son el mismo número. De ahí que sea crítico elegir un punto que no esté en la línea limítrofe.

Ejemplo\(\PageIndex{4}\)

Grafica la desigualdad:\[2x − y > 3\nonumber .\]

Solución

Sigamos los pasos dados anteriormente para graficar la desigualdad.

Paso 1. Reescribir la desigualdad en forma de pendiente-intercepción, es decir,\(y = mx + b\). \[\begin{aligned} 2x-y&>3 \\ -y&>-2x+3 \\ y&<2x-3\end{aligned}\]

Paso 2. Grafique la línea límite de acuerdo a los dos casos. Ya que la desigualdad dada es\(<\), entonces tenemos el Caso 1.

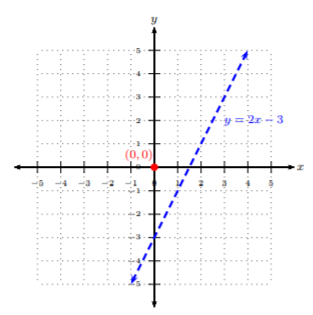
Paso 3. Seleccione un punto de prueba que no esté en la línea de contorno. Pregunta: ¿Este par ordenado hace que la desigualdad sea cierta?
¡Escojamos el punto de prueba\(\color{red}{(0, 0)}\) ya que es una gran elección! \[\begin{aligned} y&\stackrel{?}{<}2x-3 \\ 0&\stackrel{?}{<}2(0)-3 \\ 0&\cancel{\leq}-3\end{aligned}\]De ahí\((0,0)\) que, no haga realidad la desigualdad.

Paso 4. Si el par ordenado es

una solución a la desigualdad, es decir, hace que la desigualdad sea cierta, luego sombrear el lado que incluye al par ordenado.
no es una solución, luego sombrear el lado opuesto de la línea límite.

Dado que el par ordenado no\((0, 0)\) es una solución a la desigualdad, entonces sombreamos en el lado opuesto de la línea límite desde la ubicación del par ordenado.

Nota

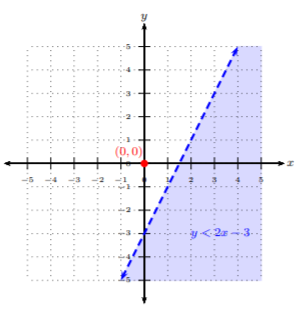
Otra forma de graficar las desigualdades lineales en dos variables es completar el Paso 1. y Paso 2. , pero en lugar de tomar un punto de prueba en el Paso 3. , podemos observar los símbolos de desigualdad. Si la desigualdad tiene\(<\) o\(≤\), entonces fácilmente sombreamos por debajo de la línea límite, es decir, por debajo de la\(y\) -intercepción. Del mismo modo, si la desigualdad tiene\(>\) o\(≥\), entonces fácilmente sombreamos por encima de la línea límite, es decir, por encima de la\(y\) -intercepción.

Ejemplo\(\PageIndex{5}\)

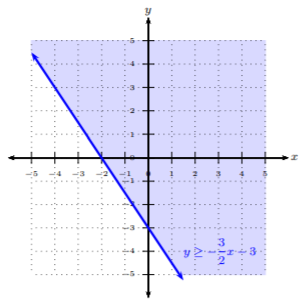
Grafica la desigualdad:\[3x + 2y ≥ −6.\nonumber\]

Solución

Sigamos los pasos dados anteriormente para graficar la desigualdad, pero intenta saltarte el Paso 3. y Paso 4.

Paso 1. Reescribir la desigualdad en forma de pendiente-intercepción, es decir,\(y = mx + b\). \[\begin{aligned}3x+2y&\geq -6 \\ 2y&\geq -3x-6 \\ y&\geq -\frac{3}{2}x-3\end{aligned}\]

Paso 2. Grafique la línea límite de acuerdo a los dos casos. Ya que la desigualdad dada es\(≥\), entonces tenemos el Caso 2.

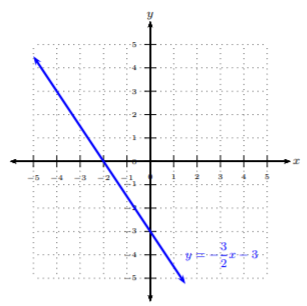
Dado que esta desigualdad es\(≥\), donde todos los pares ordenados por encima de la línea límite son soluciones a la desigualdad, podemos sombrear fácilmente por encima de la\(y\) -intercepción:

Desigualdades lineales en dos variables

Determinar si los pares ordenados dados son soluciones a la desigualdad.

Ejercicio\(\PageIndex{1}\)

\(x + 2y ≥ −4;\: (0, −4);\: (1, 1)\)

Ejercicio\(\PageIndex{2}\)

\(2x − y ≤ 2;\: (1, 5);\: (3, 1)\)

Grafica las siguientes desigualdades.

Ejercicio\(\PageIndex{3}\)

\(2x − y ≤ 2\)

Ejercicio\(\PageIndex{4}\)

\(x > 4y − 8\)

Ejercicio\(\PageIndex{5}\)

\(x + 2y ≥ −4\)

Ejercicio\(\PageIndex{6}\)

\(3x + 4y < 12\)

Ejercicio\(\PageIndex{7}\)

\(6x + 8y ≤ 24\)

Ejercicio\(\PageIndex{8}\)

\(5x + 3y ≤ 15\)

Ejercicio\(\PageIndex{9}\)

\(y > 3x + 1\)

Ejercicio\(\PageIndex{10}\)

\(3x + 2y ≤ 12\)

Ejercicio\(\PageIndex{11}\)

\(5x − 2y < 10\)

Ejercicio\(\PageIndex{12}\)

\(3x + 4y ≥ 24\)

Ejercicio\(\PageIndex{13}\)

\(y ≤ 3x − 4\)