9.2: Desigualdades racionales

Última actualización
Guardar como PDF

Page ID: 117519

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

En capítulos anteriores, discutimos muchos tipos de desigualdades, y una de las partes más críticas de las desigualdades es que sabemos que las soluciones son siempre intervalos de números. De ahí que ahora discutamos las desigualdades racionales donde las soluciones son intervalos, pero tomamos en cuenta un detalle crítico. Dado que las desigualdades racionales y las ecuaciones contienen valores excluidos, debemos tomarlo en consideración a la hora de obtener la solución. De hecho, utilizamos los valores excluidos y\(x\) -intercepta, si los hubiere, para determinar los intervalos en los que hacen verdadera la desigualdad. Nuevamente, con las desigualdades, estamos tratando de encontrar intervalos de números en los que las afirmaciones sean verdaderas.

Pasos para resolver desigualdades racionales

Paso 1. Reescribe la desigualdad para que solo el cero quede en el lado derecho.

Paso 2. Determinar dónde la expresión racional es indefinida o es igual a cero.

Paso 3. Grafique los valores encontrados en el Paso 2. en una recta numérico en dividir en intervalos.

Paso 4. Toma un punto de prueba dentro de cada intervalo y determina el signo del resultado.

Paso 5. Determinar la solución, donde la solución es el intervalo en el que hace verdadera la desigualdad.

Nota

Tenga cuidado a la hora de determinar los intervalos. Recordemos, donde la expresión es indefinida no se incluye en el intervalo, es decir, usar siempre paréntesis para los valores en los que la expresión es indefinida.

Ejemplo 9.2.1

Resolver\(\dfrac{x-3}{x+1}>0\).

Solución

Paso 1. Reescribe la desigualdad para que solo el cero quede en el lado derecho.
Como\(\dfrac{x-3}{x+1}>0\) ya tiene cero en el lado derecho, este paso está hecho.

Paso 2. Determinar dónde la expresión racional es indefinida o es igual a cero.
Para obtener donde la expresión racional es igual a cero, establecemos el numerador igual a cero:\[\begin{aligned} x − 3 &= 0\\ x &= 3\end{aligned}\] Para obtener donde la expresión está indefinida, encontramos su (los) valor (s) excluido (s) estableciendo el denominador igual a cero:\[\begin{aligned}x + 1 &= 0\\ x &= −1\end{aligned}\]

Paso 3. Grafique los valores encontrados en el Paso 2. en una recta numérica en dividir en intervalos.
Etiqueta\(-1\) y\(3\) en una línea numérica real en blanco:

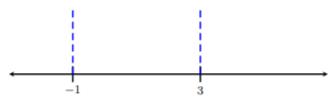
Paso 4. Toma un punto de prueba dentro de cada intervalo y determina el signo del resultado.
Tomamos valores de prueba en cada lado de\(−1\) y\(3\). Vamos a elegir números bastante fáciles como\(−2,\: 0,\) y\(4\). Conectamos estos números\(\dfrac{x − 3}{x + 1}\) y determinamos si el valor es positivo o negativo:

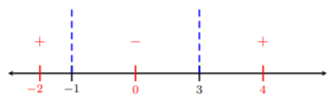
\[\begin{array}{rl} \text{letting }x=-2\Longrightarrow &\dfrac{-2-3}{-2+1}=5>0 \\ \text{letting }x=0\Longrightarrow &\dfrac{0-3}{0+1}=-3<0 \\ \text{letting }x=4\Longrightarrow &\dfrac{4-3}{4+1}=0.2>0\end{array}\nonumber\]

Paso 5. Determinar la solución, donde la solución es el intervalo en el que hace verdadera la desigualdad.
Desde\(\dfrac{x − 3}{x + 1} > 0\) (del Paso 1. ), entonces estamos buscando donde los valores de la prueba sean positivos. Mirando la recta numérica anterior, vemos que estos son los valores a la izquierda\(−1\) y a la derecha de\(3\). Así, la solución es\((−∞, −1) ∪ (3, ∞)\).

Nota

Siempre usamos un paréntesis para el valor que se excluye ya que este valor hace que la expresión racional sea indefinida. El uso de un paréntesis o paréntesis para donde la expresión es igual a cero se determina por el signo de desigualdad original, por ejemplo,\(<, >\) usar paréntesis y\(≥, ≤\) usar corchetes.

Ejemplo 9.2.2

Resolver\(\dfrac{2x+3}{x-2}\leq 1\).

Solución

Paso 1. Reescribe la desigualdad para que solo el cero quede en el lado derecho.
Reescribimos\(\dfrac{2x+3}{x-2}\leq 1\) para que haya cero en el lado derecho, y como una fracción:\[\begin{array}{rl}\dfrac{2x+3}{x-2}\leq 1&\text{Subtract }1\text{ from each side} \\ \dfrac{2x+3}{x-2}-1\leq 0&\text{Rewrite as one fraction where LCD: }(x-2) \\ \dfrac{2x+3}{x-2}-\dfrac{x-2}{x-2}\leq 0&\text{Subtract across numerators} \\ \dfrac{2x+3-x+2}{x-2}\leq 0&\text{Simplify} \\ \dfrac{x+5}{x-2}\leq 0&\text{We use this inequality to obtain the solution} \end{array}\nonumber\]

Paso 2. Determinar dónde la expresión racional es indefinida o es igual a cero.
Para obtener donde la expresión racional es igual a cero, establecemos el numerador igual a cero:\[\begin{aligned} x + 5 &= 0\\ x &= −5\end{aligned}\] Para obtener los valores excluidos, establecemos el denominador igual a cero:\[\begin{aligned}x − 2 &= 0 \\x &= 2\end{aligned}\]

Paso 3. Grafique los valores encontrados en el Paso 2. en una recta numérica en dividir en intervalos.
Etiqueta\(−5\) y\(2\) en una línea numérica en blanco:

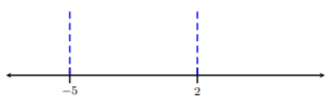
Paso 4. Toma un punto de prueba dentro de cada intervalo y determina el signo del resultado.
Tomamos valores de prueba en cada lado de\(−5\) y\(2\). Vamos a elegir números bastante fáciles como\(−6,\: 0,\) y\(3\). Conectamos estos números\(\dfrac{x + 5}{x − 2}\) y determinamos si el valor es positivo o negativo:

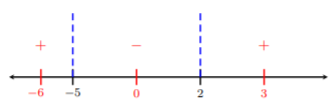
\[\begin{array}{rl} \text{letting }x=-6\Longrightarrow &\dfrac{-6+5}{-6-2}=\dfrac{1}{8}>0 \\ \text{letting }x=0\Longrightarrow &\dfrac{0+5}{0-2}=-\dfrac{5}{2}<0 \\ \text{letting }x=3\Longrightarrow &\dfrac{3+5}{3-2}=8>0\end{array}\nonumber\]

Paso 5. Determinar la solución, donde la solución es el intervalo en el que hace verdadera la desigualdad.
Desde\(\dfrac{x + 5}{x − 2} ≤ 0\) (del Paso 1. ), entonces estamos buscando donde los valores de prueba sean negativos o iguales a cero. Mirando la recta numérica anterior, vemos que estos son los valores entre\(−5\) y\(2\). Así, la solución es\([−5, 2)\).

Se utilizó un paréntesis\(−5\) puesto que la desigualdad original era\(≤\) y un paréntesis en\(2\) ya que\(2\) era un valor excluido.

Tareas Racionales Desigualdades

Resolver las desigualdades racionales. Escribe la solución en notación de intervalos.

Ejercicio 9.2.1

\(\dfrac{x-3}{x+1}<0\)

Ejercicio 9.2.2

\(\dfrac{x-7}{x+6}>0\)

Ejercicio 9.2.3

\(\dfrac{x-3}{x+1}<1\)

Ejercicio 9.2.4

\(\dfrac{x+27}{x+4}<9\)

Ejercicio 9.2.5

\(x+\dfrac{45}{x}<14\)

Ejercicio 9.2.6

\(\dfrac{(x-9)(x+9)}{x}\geq 0\)

Ejercicio 9.2.7

\(\dfrac{(x+12)(x-4)}{x-1}\geq 0\)

Ejercicio 9.2.8

\(\dfrac{3x}{7-x}<x\)

Ejercicio 9.2.9

\(\dfrac{4x}{3-x}\geq 4x\)

Ejercicio 9.2.10

\(\dfrac{8}{x-3}>\dfrac{6}{x-1}\)

Encuentra los valores de\(x\) que satisfagan la condición dada para la función.

Ejercicio 9.2.11

Resolver\(R(x)\geq 0\) si\(R(x)=\dfrac{x+6}{x-4}\).

Ejercicio 9.2.12

Resolver\(R(x)\leq 0\) si\(R(x)=\dfrac{x-4}{x+8}\).