12.3: Funciones logarítmicas
- Page ID
- 117511
Las funciones inversas de las funciones exponenciales son funciones logarítmicas, es decir, si tuviéramos que componer una función logarítmica con una función exponencial (o viceversa) y el resultado es\(x((f\circ g)(x)=x\), entonces las funciones logarítmica y exponencial son inversas entre sí. El estudio de logaritmos es particularmente interesante en muchos aspectos del álgebra, e incluso en álgebra avanzada, porque son una de las funciones más útiles. En esta sección, introducimos logaritmos.
La función logarítmica se denota por
\[y = \log_{a} x\text{ which is equivalent to }x = a^y,\nonumber\]
dónde\(a > 0\) y\(a\neq 1\). La base es\(a,\: y\) es el exponente, y\(x\) es el valor.
La ecuación\(y = \log_a x\) se llama la forma logarítmica y\(x = a^y\) se llama la forma exponencial.
Cuando reescribimos ecuaciones en forma logarítmica y exponencial, podemos mirar las ecuaciones de una manera más general para que sea obvio dónde colocamos los parámetros:
\[\color{blue}{\text{exponent}}\color{black}{=}\log_{\color{red}{\text{base}}}\color{GreenYellow}{\text{value}}\color{black}{\quad}which\: is\: equivalent\: to\quad\color{GreenYellow}{\text{value}}\color{black}{=}\color{red}{\text{base}}^{\color{blue}{\text{exponent}}}\nonumber\]
Escribir en forma logarítmica y exponencial
Escribe cada ecuación exponencial en su forma logarítmica equivalente.
- \(m^3=5\)
- \(7^2=b\)
- \(\left(\dfrac{2}{3}\right)^4=\dfrac{16}{81}\)
Solución
Primero comenzamos a identificar la base, exponente y valor. Después reescribimos la ecuación en forma logarítmica.
- En la ecuación\(m^3 = 5\), identificamos\(m\) es la base,\(3\) es el exponente, y\(5\) es el valor.
\[\color{blue}{3}\color{black}{=}\log_{\color{red}{m}}\color{GreenYellow}{5}\color{black}{\quad} which\: is\: equivalent\: to\quad\color{GreenYellow}{5}\color{black}{=}\color{red}{m}^{\color{blue}{3}}\nonumber\] - En la ecuación\(7^2 = b\), identificamos\(7\) es la base,\(2\) es el exponente, y\(b\) es el valor.
\[\color{blue}{2}\color{black}{=}\log_{\color{red}{7}}\color{GreenYellow}{b}\color{black}{\quad} which\: is\: equivalent\: to\quad\color{GreenYellow}{b}\color{black}{=}\color{red}{7}^{\color{blue}{2}}\nonumber\] - En la ecuación\(\left(\dfrac{2}{3}\right)^4=\dfrac{16}{81}\), identificamos\(\dfrac{2}{3}\) es la base,\(4\) es el exponente, y\(\dfrac{16}{81}\) es el valor.
\[\color{blue}{4}\color{black}{=}\log_{\color{red}{\dfrac{2}{3}}}\color{GreenYellow}{\dfrac{16}{81}}\color{black}{\quad} which\: is\: equivalent\: to\quad\color{GreenYellow}{\dfrac{16}{81}}\color{black}{=}\color{red}{\left(\dfrac{2}{3}\right)}^{\color{blue}{4}}\nonumber\]
Escribe cada ecuación logarítmica en su forma exponencial equivalente
- \(\log_x 16=2\)
- \(\log_3 x=7\)
- \(\log_9 3=x\)
Solución
Primero comenzamos a identificar la base, exponente y valor. Después reescribimos la ecuación en forma exponencial.
- En la ecuación\(\log_x 16 = 2\), identificamos\(x\) es la base,\(2\) es el exponente, y\(16\) es el valor.
\[\color{GreenYellow}{16}\color{black}{=}\color{red}{x}^{\color{blue}{2}}\color{black}{\quad}which\: is\: equivalent\: to\quad\color{blue}{2}\color{black}{=}\log_{\color{red}{x}}\color{GreenYellow}{16}\nonumber\] - En la ecuación\(\log_3 x = 7\), identificamos\(3\) es la base,\(7\) es el exponente, y\(x\) es el valor.
\[\color{GreenYellow}{x}\color{black}{=}\color{red}{3}^{\color{blue}{7}}\color{black}{\quad}which\: is\: equivalent\: to\quad\color{blue}{7}\color{black}{=}\log_{\color{red}{3}}\color{GreenYellow}{x}\nonumber\] - En la ecuación\(\log_9 3 = x\), identificamos\(9\) es la base,\(x\) es el exponente, y\(3\) es el valor.
\[\color{GreenYellow}{3}\color{black}{=}\color{red}{9}^{\color{blue}{x}}\color{black}{\quad}which\: is\: equivalent\: to\quad\color{blue}{x}\color{black}{=}\log_{\color{red}{9}}\color{GreenYellow}{3}\nonumber\]
Evaluar funciones logarítmicas
Dado que los logaritmos son solo exponentes, entonces podemos usar logaritmos para encontrar al exponente, o uno de los otros parámetros, la base o el valor.
Encuentra el valor exacto:\(\log_5 125\)
Solución
Para encontrar el valor exacto, nos abstenemos de utilizar cualquier tecnología para obtener la respuesta y solo usamos la definición de una función logarítmica. De ahí que cuando vemos la expresión\(\log_5 125\), preguntamos, “¿\(5\)a qué es el poder\(125\)?” porque, recordemos, los logaritmos son solo exponentes. Algunos ya pueden ver que la respuesta es\(3\), pero usemos la definición para presentar un método para evaluar logaritmos. Vamos\(\log_5 125 = x\).
\[\begin{array}{rl} \log_5 125=x & \text{Rewrite in exponential form} \\ 5^x=125 & \text{Rewrite using common base }5 \\ 5^x=5^3 & \text{Common base, equate exponents} \\ x=3 & \text{Solution}\end{array}\nonumber\]
Tenemos que tener cuidado porque introdujimos\(x\), pero nunca\(x\) formamos parte del problema original. Así, escribamos la respuesta correctamente.
\[\log_5 125=3\nonumber\]
Encuentra el valor exacto:\(\log_3 \dfrac{1}{27}\)
Solución
Para encontrar el valor exacto, nos abstenemos de utilizar cualquier tecnología para obtener la respuesta y solo usamos la definición de una función logarítmica. De ahí que cuando vemos la expresión\(\log_3 \dfrac{1}{27}\), preguntamos, “¿\(3\)a qué es el poder\(\dfrac{1}{27}\)?” porque, recordemos, los logaritmos son solo exponentes. Vamos\(\log_3 \dfrac{1}{27}=x\).
\[\begin{array}{rl} \log_3\dfrac{1}{27}=x & \text{Rewrite in exponential form} \\ 3^x=\dfrac{1}{27} & \text{Rewrite using common base }3 \\ 3^x=\dfrac{1}{3^3} & \text{Rewrite using negative exponent }-3 \\ 3^x=3^{-3} & \text{Common base, equate exponents} \\ x=-3 & \text{Solution}\end{array}\nonumber\]
Tenemos que tener cuidado porque introdujimos\(x\), pero nunca\(x\) formamos parte del problema original. Así, escribamos la respuesta correctamente.
\[\log_3\dfrac{1}{27}=-3\nonumber\]
Dominio de funciones logarítmicas
Recordar. El dominio de una función es el intervalo de valores independientes definidos para esa función.
De ahí que tenga sentido discutir el dominio de las funciones logarítmicas. Con funciones exponenciales, el dominio es todo números reales, pero veamos en qué forma se diferencia del dominio de una función logarítmica.
El dominio de la función logarítmica es\(\{x|x > 0\}\) o\((0, ∞)\), es decir, el valor (o argumento) del logaritmo es siempre positivo.
Dada la función logarítmica\(f(x) = \log_a x\), podemos seguir los pasos a continuación para obtener el dominio.
Paso 1. Identificar el valor del logaritmo,\(x\). El valor diferirá a\(x\) medida que cambien los problemas.
Paso 2. Establecer el valor mayor que cero, es decir,\(x > 0\).
Paso 3. Resolver la desigualdad como de costumbre.
Paso 4. Reescribir la desigualdad en la notación de intervalos, si es necesario.
Encuentra el dominio de\(f(x)=\log_5 (2x+3)\).
Solución
Podemos seguir los pasos para obtener el dominio de\(f(x)\).
Paso 1. El valor del logaritmo dado es\((2x + 3)\).
Paso 2. Estableciendo el valor mayor que cero, obtenemos\(2x + 3 > 0\).
Paso 3. Resolviendo la desigualdad como de costumbre,
\[\begin{aligned}2x+3&>0 \\ 2x&>-3 \\ x&>-\dfrac{3}{2}\end{aligned}\]
Esto significa que\(x\) se requiere que todos los valores para sean estrictamente mayores que\(-\dfrac{3}{2}\)\(f(x)\) para ser definidos.
Paso 4. Reescribiendo\(-\dfrac{3}{2}\) en notación de intervalos, obtenemos\(\left(-\dfrac{3}{2},\infty\right)\).
Así, el dominio de\(f(x)\) es\(\left\{x\mid x>-\dfrac{3}{2}\right\}\) o, equivalentemente,\(\left(-\dfrac{3}{2},\infty\right)\).
Funciones logarítmicas de la gráfica
Empecemos a echar un vistazo a las funciones logarítmicas mirando sus gráficas. Recall, las funciones logarítmicas y exponenciales son inversas entre sí. De ahí que veamos que sus propiedades también se invirten, es decir,\(x\) y\(y\) las coordenadas cambian.
Trazar\(f(x) = \log_3 x\) por puntos de trazado. A partir de la gráfica, determinar el dominio de la función.
Solución
Vamos a reescribir la función como\(y = \log_3 x\), y luego en su forma exponencial equivalente:\(3^y = x\). Mirando la forma exponencial de\(f(x)\), elegimos escoger\(y\) -coordenadas, y encontrar\(x\) -valores correspondientes. Al elegir\(y\) coordenadas, podemos evaluar la forma exponencial fácilmente.
| \(y\) | \(3^y=x\) | \((x,f(x))\) |
|---|---|---|
| \ (y\) ">\(-2\) | \ (3^y=x\) ">\(3^{\color{blue}{-2}}\color{black}{=}\dfrac{1}{9}\) | \ ((x, f (x))\) ">\(\left(\dfrac{1}{9},-2\right)\) |
| \ (y\) ">\(-1\) | \ (3^y=x\) ">\(3^{\color{blue}{-1}}\color{black}{=}\dfrac{1}{3}\) | \ ((x, f (x))\) ">\(\left(\dfrac{1}{3},-1\right)\) |
| \ (y\) ">\(0\) | \ (3^y=x\) ">\(3^{\color{blue}{0}}\color{black}{=}1\) | \ ((x, f (x))\) ">\((1,0)\) |
| \ (y\) ">\(1\) | \ (3^y=x\) ">\(3^{\color{blue}{1}}\color{black}{=}3\) | \ ((x, f (x))\) ">\((3,1)\) |
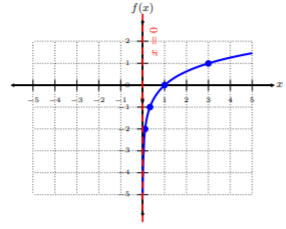
Trazar los cinco pares ordenados de la tabla. Para conectar los puntos, asegúrese de conectarlos desde el valor más pequeño hasta\(x\) el valor más grande\(x\), es decir, de izquierda a derecha. Observe que esta gráfica se eleva de izquierda a derecha, pero, a medida que la gráfica dispara hacia\(0\), nunca toca el\(y\) eje -ni lo cruza, resultando en una asíntota vertical,\(x = 0\). Ya que vemos que hay una restricción a la gráfica, el dominio es todo números reales mayores a cero o\((0, ∞)\).
Propiedad 1. El dominio de una función logarítmica es todos los números reales mayores que cero, es decir,\((0, ∞)\).
Propiedad 2. No hay\(y\) -intercepciones; la\(x\) -intercepción está en\((1, 0)\).
Propiedad 3. Si\(a > 1\), entonces la función es una función creciente. Si\(0 < a < 1\), entonces la función es una función decreciente.
Propiedad 4. Hay una asíntota vertical en\(x = 0\), a menos que haya un desplazamiento horizontal.
Una función logarítmica nunca cruza el\(y\) eje. De hecho, la función logarítmica general no se define en\(x = 0\). Eche un vistazo. Si\(x = 0\), entonces\(f(0) = \log_a 0\). Pregunte, “¿\(a\)a qué poder es cero?” No existe tal poder. No podemos elevar un número real positivo a una potencia y el resultado sea cero. En el caso de que una función logarítmica cruce el\(y\) eje -eje, entonces eso significa que hubo una transformación a la función logarítmica general.
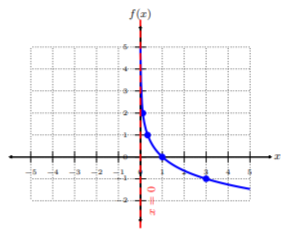
Trazar\(f(x) = \log_{1/3} x\) por puntos de trazado. A partir de la gráfica, determinar el dominio de la función.
Solución
Vamos a reescribir la función como\(y = \log_{1/3} x\), y luego en su forma exponencial equivalente:\(\left(\dfrac{1}{3}\right)^{y}=x\). Mirando la forma exponencial de\(f(x)\), elegimos escoger\(y\) -coordenadas, y encontrar\(x\) -valores correspondientes. Al elegir\(y\) coordenadas, podemos evaluar la forma exponencial fácilmente.
| \(x\) | \(\dfrac{1}{3}^y=x\) | \((x,f(x))\) |
|---|---|---|
| \ (x\) ">\(-1\) | \ (\ dfrac {1} {3} ^y=x\) ">\(\left(\dfrac{1}{3}\right)^{\color{blue}{-1}}\color{black}{=}3\) | \ ((x, f (x))\) ">\((3,-1)\) |
| \ (x\) ">\(0\) | \ (\ dfrac {1} {3} ^y=x\) ">\(\left(\dfrac{1}{3}\right)^{\color{blue}{0}}\color{black}{=}1\) | \ ((x, f (x))\) ">\((1,0)\) |
| \ (x\) ">\(1\) | \ (\ dfrac {1} {3} ^y=x\) ">\(\left(\dfrac{1}{3}\right)^{\color{blue}{1}}\color{black}{=}\dfrac{1}{3}\) | \ ((x, f (x))\) ">\(\left(\dfrac{1}{3},1\right)\) |
| \ (x\) ">\(2\) | \ (\ dfrac {1} {3} ^y=x\) ">\(\left(\dfrac{1}{3}\right)^{\color{blue}{2}}\color{black}{=}\dfrac{1}{9}\) | \ ((x, f (x))\) ">\(\left(\dfrac{1}{9},2\right)\) |
Trazar los cinco pares ordenados de la tabla. Para conectar los puntos, asegúrese de conectarlos desde el valor más pequeño hasta\(x\) el valor más grande\(x\), es decir, de izquierda a derecha. Observe que esta gráfica está cayendo de izquierda a derecha, pero, a medida que la gráfica dispara hacia\(0\), nunca toca el\(y\) eje -ni lo cruza, resultando en una asíntota horizontal en\(x = 0\). Ya que vemos que hay una restricción a la gráfica, el dominio es todo números reales mayores a cero o\((0, ∞)\).
Este es un buen momento para mencionar dos logaritmos muy importantes: el logaritmo natural y el común.
- El logaritmo natural viene dado por
\[y = \log_e x = \ln x\text{ if and only if }x = e^y\nonumber\]
donde\(e\) está el número irracional constante de Euler,\(e\approx 2.71828182\cdots\) Observe que\(\log_e\) se sustituye por\(\ln\), y esa es la única diferencia. - El logaritmo común viene dado por
\[y = \log_{10} x = \log x\text{ if and only if }x = 10^y\nonumber\]
Aviso el\(\log_{10}\) se sustituye por\(\log\), y esa es la única diferencia. Cuando no hay una base escrita en el logaritmo, entonces se asume que es el logaritmo común (a menos que lo sea\(\ln\)).
El matemático holandés Adriaan Vlacq publicó un libro de texto en 1628 que enumeraba logaritmos calculados\(1\) a partir de a\(100,000\).
Resolver ecuaciones logarítmicas
Resolver ecuaciones con logaritmos tiene técnicas que son similares a la hora de resolver ecuaciones exponenciales. Podemos reescribir la ecuación logarítmica en su forma exponencial equivalente y resolverla.
Resolver para\(x:\:\log_5 x=2\)
Solución
Resolvemos la ecuación reescribiendo la ecuación en su forma exponencial equivalente y resolvemos.
\[\begin{aligned}\log_5 x&=2\quad\text{Rewrite in exponential form} \\ 5^2&=x\quad\text{Simplify} \\ 25&=x\quad\text{Solution}\end{aligned}\]
Resolver para\(n:\:\log_2(3n+5)=4\)
Solución
Resolvemos la ecuación reescribiendo la ecuación en su forma exponencial equivalente y resolvemos.
\[\begin{array}{rl}\log_2(3n+5)=4 & \text{Rewrite in exponential form} \\ 2^4=3n+5 & \text{Simplify }2^4 \\ 16=3n+5 & \text{Isolate the variable term} \\ 11=3n & \text{Isolate }n \\ \dfrac{11}{3}=n & \text{Solution}\end{array}\nonumber\]
Podemos ver que la técnica es, una vez aislado el logaritmo en un lado de la ecuación, podemos reescribir la ecuación en su forma exponencial equivalente y resolverla.
Resolver para\(t:\: \log(2t-3)=-1\)
Solución
Resolvemos la ecuación reescribiendo la ecuación en su forma exponencial equivalente y resolvemos. Primero, vemos que no hay una base escrita en el logaritmo. De ahí que supongamos que se trata de un logaritmo común y la base es diez.
\[\begin{array}{rl} \log(2t-3)=-1 & \text{Write the common logarithm with a base }10 \\ \log_{10}(2t-3)=-1 & \text{Rewrite in exponential form} \\ 10^{-1}=2t-3 & \text{Simplify }10^{-1} \\ \dfrac{1}{10}=2t-3 & \text{Isolate the variable term} \\ \dfrac{31}{10}=2t & \text{Isolate }t \\ \dfrac{1}{2}\cdot\dfrac{31}{10}=t & \text{Simplify the left side} \\ \dfrac{31}{20}=t & \text{Solution}\end{array}\nonumber\]
Resolver para\(a:\:\ln a=4\)
Solución
Resolvemos la ecuación reescribiendo la ecuación en su forma exponencial equivalente y resolvemos. Primero, vemos ln y asumimos que este es un logaritmo natural y la base es\(e\).
\[\begin{array}{rl} \ln a=4 &\text{Write the natural logarithm with a base }e \\ \log_e a=4 &\text{Rewrite in exponential form} \\ e^4=a &\text{Solution} \\ 54.598\approx a &\text{Approximate solution for }a\end{array}\nonumber\]
Funciones logarítmicas Tareas
Reescribe cada ecuación en forma exponencial.
\(\log_9 81=2\)
\(\log_7\dfrac{1}{49}=-2\)
\(\log_{13}169=2\)
\(\log_b a=-16\)
\(\log_{16}256 =2\)
\(\log_{11}1=0\)
Reescribe cada ecuación en forma logarítmica.
\(8^0=1\)
\(15^2=225\)
\(64^{1/6}=2\)
\(17^{-2}=\dfrac{1}{289}\)
\(144^{1/2}=12\)
\(19^2=361\)
Encuentra el valor exacto para cada expresión.
\(\log_{125}5\)
\(\log_{343}\dfrac{1}{7}\)
\(\log_{4}16\)
\(\log_{6}36\)
\(\log_{2}64\)
\(\log_{5}125\)
\(\log_{7}1\)
\(\log_{4}\dfrac{1}{64}\)
\(\log_{36}6\)
\(\log_{3}243\)
Encuentra el dominio de cada función logarítmica.
\(g(x)=\log_{4}(7x+10)\)
\(h(x)=\log_{3}(3x+7)\)
\(h(x)=\log_{4}(7-8x)\)
\(g(x)=\log_{5}(4-8x)\)
Grafica cada función logarítmica.
\(f(x)=\log_{4}x\)
\(g(x)=\log_{1/4}x\)
\(q(n)=-\log_{2}n\)
\(h(t)=\log_{1/2}t\)
\(x(t)=-\log t\)
\(w(x)=\ln x\)
Resuelve cada ecuación.
\(\log_{5}x=1\)
\(\log_{2}x=-2\)
\(\log_{11}k=2\)
\(\log_{9}(n+9)=4\)
\(\log_{5}(-3m)=3\)
\(\log_{11}(x+5)=-1\)
\(\log_{4}(6b+4)=0\)
\(\log_{5}(-10x+4)=4\)
\(\log_{2}(10-5a)=3\)
\(\log_{8}k=3\)
\(\log n=3\)
\(\log_{4}p=4\)
\(\log_{11}(x-4)=-1\)
\(\log_{2}(-8r)=1\)
\(\ln (-3n)=4\)
\(\log_{11}(10v+1)=-1\)
\(\log_{9}(7-6x)=-2\)
\(\log_{8}(3k-1)=1\)


