13.3: Parábolas
- Page ID
- 117383
Recordar. La gráfica de una función cuadrática,\(f(x)=ax^2+bx+c\), es una parábola.
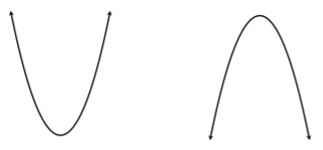
Como podemos ver, o bien teníamos una parábola ascendente o descendente dependiendo del coeficiente principal,\(a\).
No obstante, en esta sección, miramos una parábola en cuanto a su dirección. Ya discutimos la parábola que se abre hacia arriba o hacia abajo, pero, ahora, veamos una parábola que se abre a la izquierda o a la derecha:
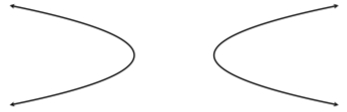
¿Cómo obtenemos este tipo de parábolas? Empecemos por mirar una parábola básica hacia arriba.
Hay un punto por encima del vértice llamado foco. La distancia desde este punto a la gráfica es la misma que la distancia desde una línea llamada directriz hasta el mismo punto. En la siguiente figura, las distancias\(d_1\) y\(d_2\) son las mismas, es decir,\(d_1 = d_2\).
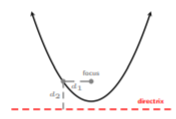
Dado que el foco y el vértice comparten la misma\(x\) coordenada, vamos a nombrar el punto de enfoque\((h, k + p)\), donde\(h\) está la\(x\) coordenada del vértice y\(k + p\) es la\(y\) coordenada del foco. Si la distancia vertical desde el vértice hasta el foco es\(p\), entonces la directriz es\(k − p\), donde\(k\) está la\(y\) coordenada del vértice.
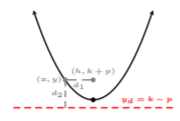
Ahora, podemos encontrar la distancia desde el foco hasta cualquier punto de la parábola\((x, y)\) usando la fórmula de distancia para calcular la distancia entre puntos\((x, y)\) a\((h, k + p)\).
Encuentra la distancia desde un punto en una parábola\((x, y)\) hasta su enfoque\((0, p)\) con vértice en\((0, 0)\) y directriz en\(y_d = −p\).
Solución
Sustituyendo directamente los dos puntos en la fórmula de distancia, obtenemos
\[d=\sqrt{(x-0)^2+(y-p)^2}\nonumber\]
Recordemos, la distancia desde el foco a cualquier punto de la parábola es la misma distancia del punto a la directriz. De ahí que la distancia del punto\((x, y)\) a la directriz sea\(y−(−p) = y+p\). Sustituyamos esto en la fórmula de distancia y reescribamos la ecuación en forma estándar para una parábola vertical:
\[\begin{aligned} y+p&=\sqrt{x^2+(y-p)^2} \\ (y+p)^2&=x^2+(y-p)^2 \\ y^2+2py+p^2&=x^2+y^2-2yp+p^2 \\ 4yp&=x^2\end{aligned}\]
Esta la ecuación resultante es una ecuación estándar de una parábola vertical con vértice en\((0, 0)\).
Generalizando la ecuación en Ejemplo 13.3.1 a cualquier punto de una parábola vertical con vértice\((h, k)\), obtenemos la ecuación estándar de cualquier parábola vertical con vértice\((h, k)\).
La ecuación estándar de una parábola vertical con vértice\((h, k)\) es
\[(x-h)^2=4p(y-k)\nonumber\]
Continuando, si aplicamos la misma idea a una parábola horizontal, donde la directriz es una línea vertical y el foco está a la izquierda o derecha del vértice, obtenemos
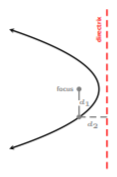
En la figura anterior, las distancias\(d_1\) y\(d_2\) son las mismas, es decir\(d_1 = d_2\), como lo es con una parábola ascendente. Y así, generalizando una ecuación para una parábola horizontal con vértice\((h, k)\), obtenemos la ecuación estándar de cualquier parábola horizontal con vértice\((h, k)\).
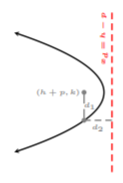
La ecuación estándar de una parábola horizontal con vértice\((h, k)\) es
\[(y-k)^2=4p(x-h)\nonumber\]
Graficar una parábola en forma de ecuación estándar
En general, la dirección de una parábola depende de la ubicación de la directriz y el foco. Armando todo esto con graficar funciones cuadráticas, obtenemos las propiedades de una parábola.
Para graficar una parábola, podemos usar la tabla para determinar la dirección y todas las demás propiedades.
| Ecuación | Dirección | Enfoque | Directrix | Eje de simetría |
|---|---|---|---|---|
| \((x-h)^2=4p(y-k)\) | Hacia arriba\((p>0)\) o hacia abajo\((p<0)\) | \((h,k+p)\) | \(y=k-p\) | \(x=h\) |
| \((y-k)^2=4p(x-h)\) | Izquierda\((p<0)\) o derecha\((p>0)\) | \((h+p,k)\) | \(x=h-p\) | \(y=k\) |
Grafica la parábola\((x + 1)^2 = −8(y − 3)\). Identificar y etiquetar el vértice, el enfoque, la directriz y el eje de simetría.
Solución
Para comenzar, podemos identificar las propiedades, luego graficar. Enseguida, vemos que el vértice es\((−1, 3)\) y el eje de simetría lo es\(x = −1\). Dado que el factor cuadrado contiene\(x\), sabemos que esta parábola se abre hacia arriba o hacia abajo. Busquemos\(p\) para determinar la dirección particular.
\[\begin{aligned}(x-h)^2&=\color{blue}{4p}\color{black}{(}y-k) \\ (x+1)^2&=\color{blue}{-8}\color{black}{(}y-3)\end{aligned}\]
Podemos ver a partir de la ecuación dada y la ecuación estándar,\(4p = −8\). Esto implica que\(p = −2\). Ya que\(p = −2 < 0\), la parábola se abrirá hacia abajo. Desde el conocimiento\(p = −2\), podemos encontrar el foco y directrix:
Enfoque:
\[\begin{array}{r}(h,k+p) \\ (-1,3+(-2)) \\ (-1,1)\end{array}\nonumber\]
El punto de enfoque es\((−1, 1)\).
Directrix:
\[\begin{aligned}y&=k-p \\ y&=3-(-2) \\ y&=5\end{aligned}\]
La directrix es la línea\(y = 5\). Ahora estamos listos para graficar la parábola con el vértice en\((−1, 3)\), el eje de simetría\(x = −1\), el punto de enfoque en\((−1, 1)\) y la directriz\(y = 5\).
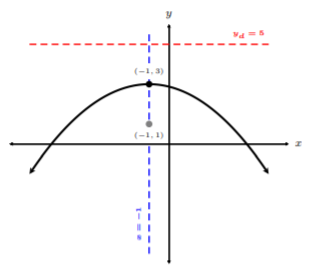
Reescribir una ecuación de una parábola en la forma de ecuación estándar
A veces no se nos da una parábola en su forma de ecuación estándar. De ahí que tengamos que reescribir la ecuación para que la ecuación de la parábola esté en la ecuación estándar. Esto lo podemos hacer completando la plaza en el término que es cuadrado.
Recordar. Para completar el cuadrado de una ecuación trinomial de la forma\(x^2 + bx + c = 0\), podemos agregar\(\left(\dfrac{b}{2}\right)^2\) a cada lado de la ecuación.
Paso 1. Agrupe la variable que está cuadrada en un lado de la ecuación y posicione la variable no cuadrada y la constante en el otro lado.
Paso 2. Completar el cuadrado, si es necesario, y dividir por el coeficiente del cuadrado perfecto, es decir, el término cuadrado debería gustar\((x − h)^2\) o\((y − k)^2\).
Paso 3. Factorizar el coeficiente de la variable no cuadrada y la constante.
Considera la ecuación de la parábola\(y^2 + 4y + 8x = 4\). Reescribe esta ecuación en la forma de ecuación estándar y grafica la parábola. Encuentre y etiquete el vértice, el enfoque, la directriz y el eje de simetría.
Solución
Para encontrar las propiedades de la parábola, necesitamos reescribir\(y^2 + 4y + 8x = 4\) en la forma de la ecuación estándar. Sigamos los pasos para obtener la forma de ecuación estándar de la ecuación dada de la parábola.
Paso 1. Agrupe la variable que está cuadrada en un lado de la ecuación y posicione la variable no cuadrada y la constante en el otro lado.
Notamos el término\(y^2\). Ya que el\(y\) es el término cuadrado, entonces sabemos que esta parábola se abre a la izquierda o a la derecha.
\[\begin{aligned}y^2+4y+8x&=4 \\ y^2+4y&=-8x+4\end{aligned}\]
Paso 2. Completa el cuadrado, si es necesario, y divide por el coeficiente del cuadrado perfecto.
\[\begin{aligned} y^2+4y&=-8x+4 \\ y^2+4y\color{blue}{+4}&\color{black}{=}-8x+4\color{blue}{+4} \\ y^2+4y+4&=-8x+8 \\ (y+2)^2&=-8x+8\end{aligned}\]
Paso 3. Factorizar el coeficiente de la variable no cuadrada y la constante.
\[\begin{aligned} (y+2)^2&=-8x+8 \\ (y+2)^2&=-8(x-1)\end{aligned}\]
De ahí que la parábola\(y^2 + 4y + 8x = 4\) en su ecuación estándar sea\((y + 2)^2 = −8(x−1)\). A continuación, identifiquemos todas las propiedades para graficar. Podemos ver fácilmente que el vértice es\((1, −2)\) y el eje de simetría lo es\(y = −2\). Necesitamos encontrar para\(p\) obtener el enfoque y la directrix. Podemos ver a partir de la ecuación dada y la ecuación estándar,\(4p = −8\). Esto implica que\(p = −2\). Ya que\(p = −2 < 0\), la parábola se abrirá a la izquierda. Desde el conocimiento\(p = −2\), podemos encontrar el foco y directrix:
Enfoque:
\[\begin{array}{r}(h+p,k) \\ (1+(-2),-2) \\ (-1,-2) \end{array}\nonumber\]
El punto de enfoque es\((-1,-2)\).
Directrix:
\[\begin{aligned} x&=h-p \\ x&=1-(-2) \\ x&=3\end{aligned}\]
La directrix es la línea\(x = 3\). Ahora estamos listos para graficar la parábola con el vértice en\((1, −2)\), el eje de simetría\(y = −2\), el punto de enfoque en\((−1, −2)\) y la directriz\(x = 3\).
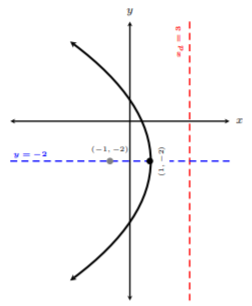
Así, la gráfica anterior es la gráfica de\((y + 2)^2 = −8(x − 1)\).
Tera de Parabolas
Esboza la gráfica de cada parábola. Encuentra el vértice, el enfoque, la directriz y el eje de simetría.
\((x-3)^2=-16y\)
\(\left(x+\dfrac{7}{3}\right)^2=2\left(y+\dfrac{5}{2}\right)\)
\((y-2)^2=-12(x+3)\)
\((y+4)^2=4x\)
\((x-1)^2=4(y+3)\)
\((x+2)^2=-20(y-5)\)
\((y-4)^2=18(x-2)\)
\(\left(y+\dfrac{3}{2}\right)^2=-7\left(x+\dfrac{9}{2}\right)\)
Reescriba la ecuación de la parábola en su forma de ecuación estándar e identifique el vértice, el foco, la directriz y el eje de simetría. Después bosquejar la gráfica.
\(x^2+2x-8y+49=0\)
\(3y^2-27y+4x+\dfrac{211}{4}=0\)
\(2y^2+4y+x-8=0\)
\(x^2-10x+12y+1=0\)


