7.10: Suplemento de ejercicio
( \newcommand{\kernel}{\mathrm{null}\,}\)
Suplemento de ejercicio
Graficando Ecuaciones Lineales y Desigualdades en una Variable
Para los siguientes problemas, graficar las ecuaciones y desigualdades.
6x−18=6

- Responder
-
x=4
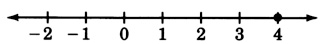
4x−3=−7

5x−1=2

- Responder
-
x=35
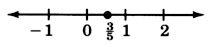
10x−16<4

−2y+1≤5

- Responder
-
y≥−2
−7a12≥2

3x+4≤12

- Responder
-
x≤83
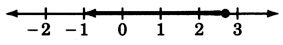
−16≤5x−1≤−11

0<−3y+9≤9

- Responder
-
0≤y<3
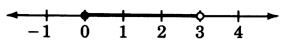
−5c2+1=7

Ploteo de puntos en el plano
Dibuja un sistema de coordenadas y traza los siguientes pares ordenados.
(3,1),(4,−2),(−1,−3),(0,3),(3,0),(5,−23)
- Responder
-
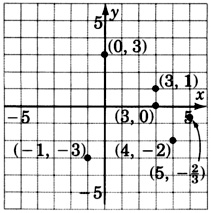
Con la mayor precisión posible, declarar las coordenadas de los puntos que se han trazado en la gráfica.
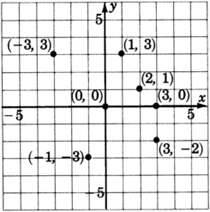
Graficando Ecuaciones Lineales en Dos Variables
¿Cuál es la estructura geométrica de la gráfica de todas las soluciones a la ecuación linealy=4x−9?
- Responder
-
una línea recta
Graficar ecuaciones lineales en dos variables - Graficar ecuaciones en forma de pendiente-intercepción
Para los siguientes problemas, grafica las ecuaciones.
y−x=2
y+x−3=0
- Responder
-
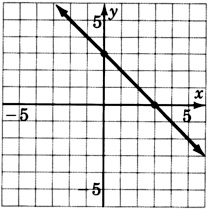
−2x+3y=−6
2y+x−8=0
- Responder
-
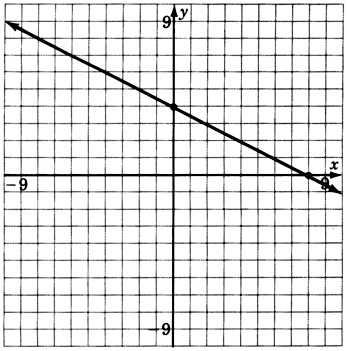
4(x−y)=12
3y−4x+12=0
- Responder
-
y=−3
y−2=0
- Responder
-
x=4
x+1=0
- Responder
-
x=0
y=0
- Responder
-
La forma de pendiente-interceptación de una línea
Escribe la forma pendiente-intercepción de una línea recta.
La pendiente de una línea recta es un ____ de la inclinación de la línea.
- Responder
-
medir
Escribe la fórmula para la pendiente de una línea que pasa por los puntos(x1,y1) y(x2,y2).
Para los siguientes problemas, determinar la pendiente y la intercepción y de las líneas.
y=4x+10
- Responder
-
pendiente:4
y-interceptar:(0,10)
y=3x−11
y=9x−1
- Responder
-
pendiente:9
y-interceptar:(0,−1)
y=−x+2
y=−5x−4
- Responder
-
pendiente:−5
y-interceptar:(0,−4)
y=x
y=−6x
- Responder
-
pendiente:−6
y-interceptar:(0,0)
3y=4x+9
4y=5x+1
- Responder
-
pendiente:54
y-interceptar:(0,14)
2y=9x
5y+4x=6
- Responder
-
pendiente:−45
y-interceptar:(0,65)
7y+3x=10
6y−12x=24
- Responder
-
pendiente:2
y-interceptar:(0,4)
5y−10x−15=0
3y+3x=1
- Responder
-
pendiente:−1
y-interceptar:(0,13)
7y+2x=0
y=4
- Responder
-
pendiente:0
y-interceptar:(0,4)
Para los siguientes problemas, encuentra la pendiente, si existe, de la línea a través de los pares de puntos dados.
(5,2),(6,3)
(8,−2),(10,−6)
- Responder
-
pendiente:−2
(0,5),(3,4)
(1,−4),(3,3)
- Responder
-
pendiente:72
(0,0),(−8,−5)
(−6,1),(−2,7)
- Responder
-
pendiente:32
(−3,−2),(−4,−5)
(4,7),(4,−2)
- Responder
-
Sin Talud
(−3,1),(4,1)
(13,34),(29,−56)
- Responder
-
pendiente:574
Moviéndose de izquierda a derecha, las líneas con pendiente suben mientras que las líneas con pendiente disminuyen.
Compara las pendientes de las líneas paralelas.
- Responder
-
Las pendientes de las líneas paralelas son iguales.
Encontrar la ecuación de una línea
Para los siguientes problemas, escriba la ecuación de la línea utilizando la información dada. Escribe la ecuación en forma de pendiente-intercepción.
Slope=4,y -intercept=5
Slope=3,y -intercept=−6
- Responder
-
y=3x−6
Slope=1,y -intercept=8
Slope=1,y -intercept=−2
- Responder
-
y=x−2
Slope=−5,y -intercept=1
Slope=−11,y -intercept=−4
- Responder
-
y=−11x−4
Slope=2,y -intercept=0
Slope=−1,y -intercept=0
- Responder
-
y=−x
m=3,(4,1)
m=2,(1,5)
- Responder
-
y=2x+3
m=6,(5,−2)
m=−5,(2,−3)
- Responder
-
y=−5x+7
m=−9,(−4,−7)
m=−2,(0,2)
- Contestar
-
y=−2x+2
m=−1,(2,0)
(2,3),(3,5)
- Contestar
-
y=2x−1
(4,4),(5,1)
(6,1),(5,3)
- Contestar
-
y=−2x+13
(8,6),(7,2)
(−3,1),(2,3)
- Contestar
-
y=25x+115
(−1,4),(−2,−4)
(0,−5),(6,−1)
- Contestar
-
y=23x−5
(2,1),(6,1)
(−5,7),(−2,7)
- Contestar
-
y=7(pendiente cero)
(4,1),(4,3)
(−1,−1),(−1,5)
- Contestar
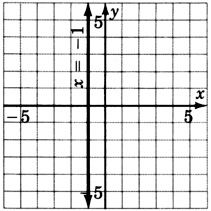
-
x=−1(sin pendiente)
(0,4),(0,−3)
(0,2),(1,0)
- Contestar
-
y=−2x+2
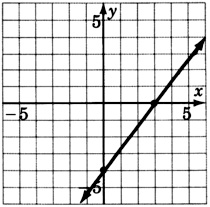
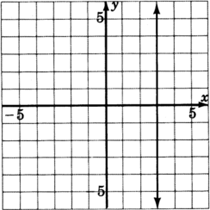
Para los siguientes problemas, leyendo sólo de la gráfica, determinar la ecuación de la línea.
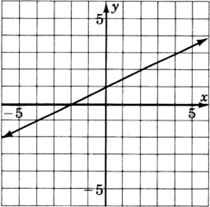
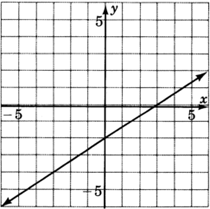
- Contestar
-
y=23x−2
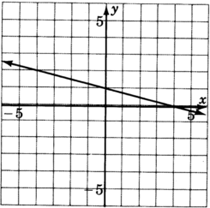
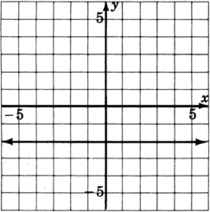
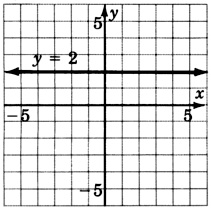
- Contestar
-
y=−2
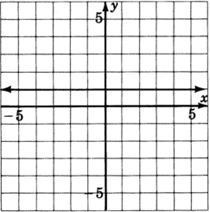
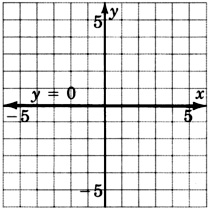
- Contestar
-
y=1
Graficando Desigualdades Lineales en Dos Variables
Para los siguientes problemas, grafica las desigualdades.
y≤x+2
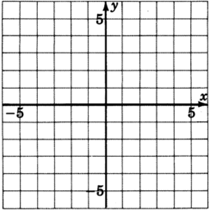
y<−12+3

- Contestar
-
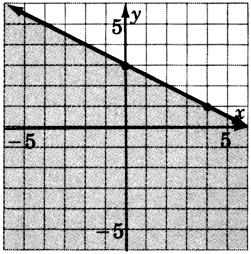
y>13x−3

−2x+3y≤−6

- Contestar
-
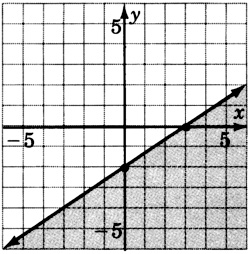
2x+5y≥20

4x−y+12>0

- Contestar
-
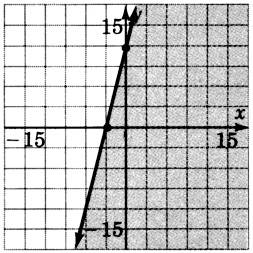
y≥−2

x<3

- Contestar
-
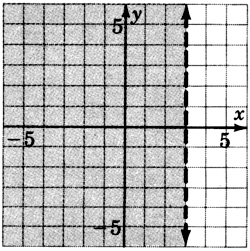
y≤0



