7.11: Examen de Aptitud

Última actualización
Guardar como PDF

Page ID: 112269

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Examen de competencia

Para los siguientes problemas, construir un sistema de coordenadas y graficar la desigualdad.

Ejercicio$\PageIndex{1}$

$−6x+4>−14$

Contestar

$x<3$

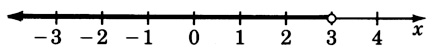
$Una línea numérica etiquetada con x con flechas en cada extremo, etiquetada de tres a cuatro negativos, en incrementos de uno. Hay un círculo abierto a las tres. Una línea oscura se origina desde este círculo y se dirige hacia la izquierda de tres.$

Ejercicio$\PageIndex{2}$

$−8<x+6≤−4$

Contestar

$−14<x≤−10$

$Una línea numérica etiquetada con x con flechas en cada extremo, etiquetada en negativo catorce y negativo diez. Hay un círculo cerrado en negativo diez y un círculo abierto en negativo catorce. Estos círculos están conectados por una línea negra$

Ejercicio$\PageIndex{3}$

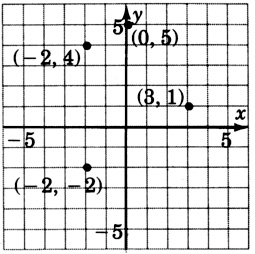
Trazar los pares ordenados$(3, 1),(−2, 4),(0, 5),(−2, −2)$.

$Un plano xy con líneas de cuadrícula, etiquetado negativo cinco y cinco en ambos ejes.$

Contestar: $Total de cuatro puntos trazados en un plano de coordenadas xy. Las coordenadas de estos puntos son negativas dos, negativas dos; negativas dos, cuatro; cero, cinco y tres, uno.$

Ejercicio$\PageIndex{4}$

Con la mayor precisión posible, etiquetar las coordenadas de los puntos que se hayan trazado en la gráfica.

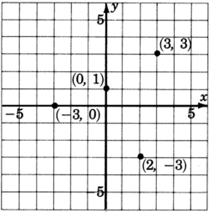
$Total de cuatro puntos trazados en un plano xy. Las coordenadas de estos puntos son negativas tres, cero; cero, uno; tres, tres y dos, negativas tres.$

Contestar: $(0,1),(3,3),(−3,0),(2,−3)$

Ejercicio$\PageIndex{5}$

¿Cuál es la estructura geométrica de la gráfica de todas las soluciones a la ecuación$2y+3x=−4$?

Contestar: línea recta

Ejercicio$\PageIndex{6}$

¿En qué forma se encuentra la ecuación lineal en dos variables$ax+by=c$?

Contestar: forma general

Ejercicio$\PageIndex{7}$

¿En qué forma se encuentra la ecuación lineal en dos variables$y=mx+b$?

Contestar: pendiente-intercepción

Ejercicio$\PageIndex{8}$

Si un par ordenado es una solución a una ecuación lineal en dos variables, ¿dónde se encuentra geométricamente?

Contestar: Se encuentra en la línea.

Ejercicio$\PageIndex{9}$

Considera la gráfica de$y=\dfrac{2}{7}x+16$. Si tuviéramos que colocar nuestro lápiz en algún punto de la línea y luego moverlo horizontalmente$7$ unidades hacia la derecha, ¿cuántas unidades y en qué dirección tendríamos que mover nuestro lápiz para volver a la línea?

Contestar: $2$unidades arriba

Para los siguientes problemas, encuentre la pendiente, si existe, de la línea que contiene los siguientes puntos.

Ejercicio$\PageIndex{10}$

(−6, −1) y (0, 8)

Contestar: $\dfrac{3}{2}$

Ejercicio$\PageIndex{11}$

(−2, −8) y (−2, 10)

Contestar: sin pendiente; línea vertical en$x=−2$

Ejercicio$\PageIndex{12}$

Determinar la pendiente y$y$ −intercept de la línea$3y+2x+1=0$.

Contestar: pendiente =$-\dfrac{2}{3}$,$y$ -intercepción es$(0, -\dfrac{1}{3})$

Ejercicio$\PageIndex{13}$

Al mirar una gráfica de izquierda a derecha, ¿suben o bajan las líneas con pendiente positiva?

Contestar: subir

Para los siguientes problemas, encuentre la ecuación de la línea utilizando la información proporcionada. Escribe la ecuación en forma de pendiente-intercepción

Ejercicio$\PageIndex{14}$

Pendiente =$4$,$y$ -intercepción =$−3$.

Contestar: $y=4x−3$

Ejercicio$\PageIndex{15}$

Pendiente =$-\dfrac{3}{2}$,$y$ -intercepción =$\dfrac{4}{3}$.

Contestar: $y = -\dfrac{3}{2}x + \dfrac{4}{3}$

Ejercicio$\PageIndex{16}$

Pendiente =$\dfrac{2}{3}$, pasa a través$(-1, 2)$

Contestar: $y = \dfrac{2}{3}x + \dfrac{8}{3}$

Ejercicio$\PageIndex{17}$

Pendiente =$7$, pasa a través$(0, 0)$

Contestar: $y=7x$

Ejercicio$\PageIndex{18}$

Pasa por los puntos$(5, 2)$ y$(2, 1)$.

Contestar: $y = \dfrac{1}{3}x + \dfrac{1}{3}$

Para los siguientes problemas, graficar la ecuación de desigualdad.

Ejercicio$\PageIndex{19}$

$y = \dfrac{1}{3}x - 2$

$Un plano xy con líneas de cuadrícula, etiquetado negativo cinco y cinco en ambos ejes.$

Contestar

$y = \dfrac{1}{3}x - 2$

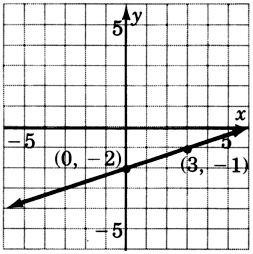
$Una gráfica de una línea que pasa por dos puntos con coordenadas cero, negativo dos y tres, negativo uno.$

Ejercicio$\PageIndex{20}$

$5y−2x+15=0$

$Un plano xy con líneas de cuadrícula, etiquetado negativo cinco y cinco en ambos ejes.$

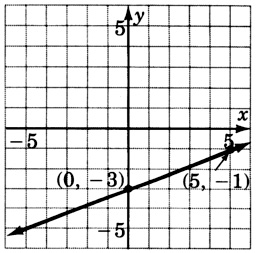
Contestar: $Una gráfica de una línea que pasa por dos puntos con coordenadas cero, negativo tres y cinco, negativo uno.$

Ejercicio$\PageIndex{21}$

$4(x+y)=8$

$Un plano xy con líneas de cuadrícula, etiquetado negativo cinco y cinco en ambos ejes.$

Contestar

$4(x+y)=8$

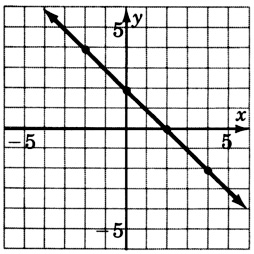
$Gráfica de una línea que pasa por cuatro puntos con coordenadas negativas dos, cuatro; cero, dos; dos, cero; y cuatro, negativas dos.$

Ejercicio$\PageIndex{22}$

$\dfrac{3}{2}y + 2 = 0$

$Un plano xy con líneas de cuadrícula, etiquetado negativo cinco y cinco en ambos ejes.$

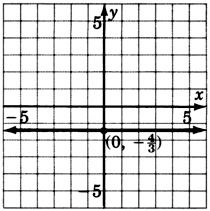
Contestar: $Una gráfica de una línea paralela al eje x y pasando por un punto con coordenadas cero, negativas cuatro sobre tres.$

Ejercicio$\PageIndex{23}$

$x=−2$

$Un plano xy con líneas de cuadrícula, etiquetado negativo cinco y cinco en ambos ejes.$

Contestar

$x=−2$

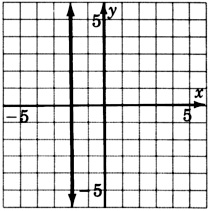
$Un gráfico de una línea paralela al eje y en un plano xy. La línea cruza el eje x en x es igual a dos negativos.$

Ejercicio$\PageIndex{24}$

$2x+3y>6$

$Un plano xy con líneas de cuadrícula, etiquetado negativo cinco y cinco en ambos ejes.$

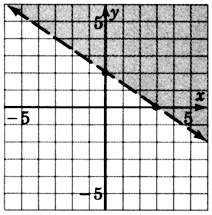
Contestar: $Una línea discontinua en un plano xy que pasa por dos puntos con coordenadas cero, dos y tres, cero. La región por encima de la línea está sombreada.$

Ejercicio$\PageIndex{25}$

Al leer solo de la gráfica, determinar la ecuación de la línea.

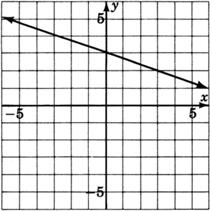
$Una gráfica de una línea inclinada hacia arriba y hacia la izquierda.$

Contestar: $y = -\dfrac{1}{3}x + 3$

Search

Ejercicio\(\PageIndex{1}\)

Ejercicio\(\PageIndex{2}\)

Ejercicio\(\PageIndex{3}\)

Ejercicio\(\PageIndex{4}\)

Ejercicio\(\PageIndex{5}\)

Ejercicio\(\PageIndex{6}\)

Ejercicio\(\PageIndex{7}\)

Ejercicio\(\PageIndex{8}\)

Ejercicio\(\PageIndex{9}\)

Ejercicio\(\PageIndex{10}\)

Ejercicio\(\PageIndex{11}\)

Ejercicio\(\PageIndex{12}\)

Ejercicio\(\PageIndex{13}\)

Ejercicio\(\PageIndex{14}\)

Ejercicio\(\PageIndex{15}\)

Ejercicio\(\PageIndex{16}\)

Ejercicio\(\PageIndex{17}\)

Ejercicio\(\PageIndex{18}\)

Ejercicio\(\PageIndex{19}\)

Ejercicio\(\PageIndex{20}\)

Ejercicio\(\PageIndex{21}\)

Ejercicio\(\PageIndex{22}\)

Ejercicio\(\PageIndex{23}\)

Ejercicio\(\PageIndex{24}\)

Ejercicio\(\PageIndex{25}\)