10.8: Graficar soluciones cuadráticas

Última actualización
Guardar como PDF

Page ID: 112069

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Parabolas

Ahora estudiaremos las gráficas de ecuaciones cuadráticas en dos variables con forma general

$y = ax^2 + bx + c, a \not= 0$. $a, b, c$son números reales.

Parábola

Todas esas gráficas tienen una forma similar. La gráfica de una ecuación cuadrática de este tipo Parábola se denomina parábola y asumirá una de las siguientes formas.

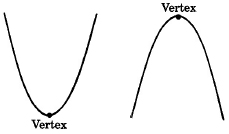
$Dos parábola, una abierta hacia arriba y otra hacia abajo. El punto más bajo de la apertura de la parábola hacia arriba y el punto más alto de la apertura de la parábola hacia abajo están etiquetados como 'Vértice'.$

Vértice

El punto alto o punto bajo de una parábola se llama el vértice de la parábola.

Construyendo Gráficas de Parábola

Construiremos la gráfica de una parábola eligiendo varios valores x, calculando para encontrar los valores y correspondientes, trazando estos pares ordenados, luego dibujando una curva suave a través de ellos.

Conjunto de Muestras A

Ejemplo$\PageIndex{1}$

Gráfica$y = x^2$. Construir una tabla para exhibir varios pares ordenados.

$x$	$y=x^2$
0	0
1	1
2	4
3	9
−1	1
−2	4
−3	9

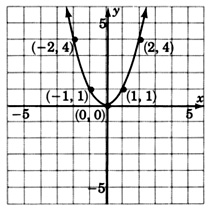
$Gráfica de una parábola que pasa por cinco puntos con coordenadas negativas dos, cuatro; negativo uno, uno; cero, cero; uno, uno; y dos, cuatro.$

Esta es la parábola más básica. Si bien otras parabolas pueden ser más anchas, más estrechas, movidas hacia arriba o hacia abajo, movidas hacia la izquierda o hacia la derecha, o invertidas, todas tendrán esta misma forma básica. Tendremos que trazar tantos pares ordenados como sea necesario para asegurar esta forma básica.

Ejemplo$\PageIndex{2}$

Gráfica$y = x^2 - 2$. Construir una tabla de pares ordenados.

$x$	$y=x^2 -2$
0	−2
1	−1
2	2
3	7
−1	−1
−2	2
−3	7

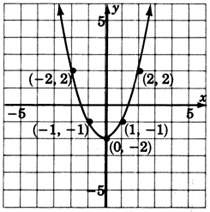
$Gráfica de una parábola que pasa por cinco puntos con coordenadas negativas dos, dos; negativo uno, negativo uno; cero, negativo dos, uno, negativo uno; y dos, dos.$

Observe que la gráfica de$y = x^2 - 2$ es precisamente la gráfica de$y = x^2$ pero tradujo 2 unidades hacia abajo. Comparar las ecuaciones de$y = x^2$ y$y = x^2 - 2$. ¿Ves qué causa la traducción descendente de 2 unidades?

Conjunto de práctica A

Problema de práctica$\PageIndex{1}$

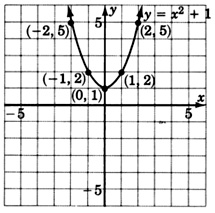
Usa la idea sugerida en el Conjunto de Muestras A para bosquejar (de forma rápida y quizás no perfectamente precisa) las gráficas de

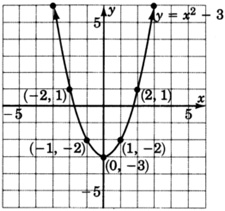
$y = x^2 + 1$y$y = x^2 - 3$

$Un plano de coordenadas xy con líneas de cuadrícula, etiquetado como cinco negativos y cinco con incrementos de una unidad en ambos ejes.$

Contestar

$Una gráfica de una ecuación cuadrática y es igual a x cuadrado más uno que pasa por cinco puntos con coordenadas negativas dos, cinco; negativas uno, dos; cero, uno; uno, dos; y dos, cinco.$

$Una gráfica de una ecuación cuadrática y es igual a x cuadrado menos tres pasando por cinco puntos con coordenadas negativas dos, uno; negativo uno, negativo dos; cero, negativo tres; uno, negativo dos; y dos, uno.$

Conjunto de Muestras B

Ejemplo$\PageIndex{1}$

Gráfica$y = (x + 2)^2$.

¿Esperamos que la gráfica sea similar a la gráfica de$y = x^2$? Hacer una mesa de pares ordenados.

$x$	$y$
0	4
1	9
−1	1
−2	0
−3	1
−4	4

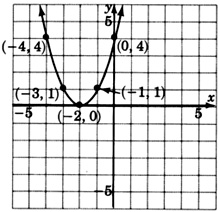
$Gráfica de una parábola que pasa por cinco puntos con coordenadas negativas cuatro, cuatro; negativo tres, uno; negativo dos, cero; negativo uno, uno; y cero, cuatro.$

Observe que la gráfica de$y = (x + 2)^2$ es precisamente la gráfica de$y = x^2$ pero traducida 2 unidades a la izquierda. El$+2$ interior de los paréntesis mueve$y = x^2$ dos unidades hacia la izquierda. Un valor negativo dentro de los paréntesis hace un movimiento hacia la derecha.

Set de práctica B

Problema de práctica$\PageIndex{1}$

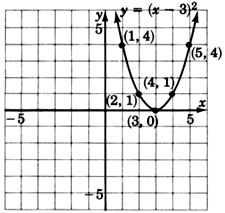
Usa la idea sugerida en el Conjunto de Muestras B para esbozar las gráficas de

$y = (x-3)^2$y$y = (x + 1)^2$

$Un plano de coordenadas xy con líneas de cuadrícula, etiquetado como cinco negativos y cinco con incrementos de una unidad en ambos ejes.$

Contestar: $Una gráfica de una ecuación cuadrática y es igual a x menos tres el cuadrado completo pasando por cinco puntos con las coordenadas uno, cuatro; dos, uno; tres, cero; cuatro, uno; y cinco, cuatro.$

Problema de práctica$\PageIndex{3}$

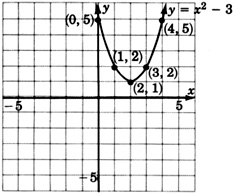
Gráfica$y = (x-2)^2 + 1$

$Un plano de coordenadas xy con líneas de cuadrícula, etiquetado como cinco negativos y cinco con incrementos de una unidad en ambos ejes.$

Contestar: $Una gráfica de una ecuación cuadrática y es igual a x cuadrado menos tres pasando por cinco puntos con las coordenadas cero, cinco; uno, dos; dos, uno; tres, dos; y cuatro, cinco.$

Ejercicios

Para los siguientes problemas, graficar las ecuaciones cuadráticas.

Ejercicio$\PageIndex{1}$

$y = x^2$

$Un plano de coordenadas xy con líneas de cuadrícula, etiquetado como cinco negativos y cinco con incrementos de una unidad en ambos ejes.$

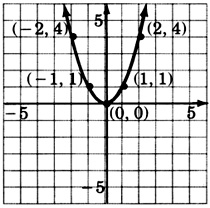
Contestar: $Gráfica de una parábola que pasa por cinco puntos con coordenadas negativas dos, cuatro; negativo uno, uno; cero, cero, uno, uno; y dos, cuatro.$

Ejercicio$\PageIndex{2}$

$y = -x^2$

$Un plano de coordenadas xy con líneas de cuadrícula, etiquetado como cinco negativos y cinco con incrementos de una unidad en ambos ejes.$

Ejercicio$\PageIndex{3}$

$y = (x-1)^2$

$Un plano de coordenadas xy con líneas de cuadrícula, etiquetado como cinco negativos y cinco con incrementos de una unidad en ambos ejes.$

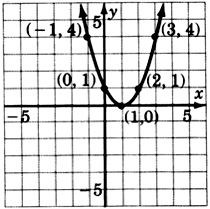
Contestar: $Gráfica de una parábola que pasa por cinco puntos con coordenadas negativas uno, cuatro; cero, uno; uno, cero, dos, uno; y tres, cuatro.$

Ejercicio$\PageIndex{4}$

$y = (x-2)^2$

$Un plano de coordenadas xy con líneas de cuadrícula, etiquetado como cinco negativos y cinco con incrementos de una unidad en ambos ejes.$

Ejercicio$\PageIndex{5}$

$y = (x + 3)^2$

$Un plano de coordenadas xy con líneas de cuadrícula, etiquetado como cinco negativos y cinco con incrementos de una unidad en ambos ejes.$

Ejercicio$\PageIndex{6}$

$y = (x + 3)^2$

$Un plano de coordenadas xy con líneas de cuadrícula, etiquetado como cinco negativos y cinco con incrementos de una unidad en ambos ejes.$

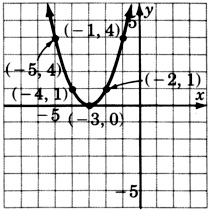
Contestar: $Gráfico de una parábola que pasa por cinco puntos con coordenadas negativas cinco, cuatro; negativo cuatro, uno; negativo tres, cero; negativo dos, uno; y negativo uno, cuatro.$

Ejercicio$\PageIndex{7}$

$y = (x + 1)^2$

$Un plano de coordenadas xy con líneas de cuadrícula, etiquetado como cinco negativos y cinco con incrementos de una unidad en ambos ejes.$

Ejercicio$\PageIndex{8}$

$y = x^2 - 3$

$Un plano de coordenadas xy con líneas de cuadrícula, etiquetado como cinco negativos y cinco con incrementos de una unidad en ambos ejes.$

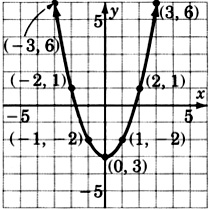
Contestar: $Gráfico de una parábola que pasa por siete puntos con coordenadas negativas tres, seis; negativas dos, uno; negativo uno, negativo dos; cero, negativo tres; uno, negativo dos; dos, uno; y tres, seis.$

Ejercicio$\PageIndex{9}$

$y = x^2 - 1$

$Un plano de coordenadas xy con líneas de cuadrícula, etiquetado como cinco negativos y cinco con incrementos de una unidad en ambos ejes.$

Ejercicio$\PageIndex{10}$

$y = x^2 + 2$

$Un plano de coordenadas xy con líneas de cuadrícula, etiquetado como cinco negativos y cinco con incrementos de una unidad en ambos ejes.$

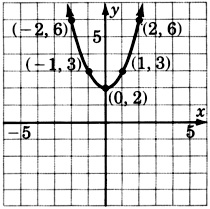
Contestar: $Gráfico de una parábola que pasa por cinco puntos con coordenadas negativas dos, seis; negativas uno, tres; cero, dos; uno, tres; y dos, seis.$

Ejercicio$\PageIndex{11}$

$y = x^2 + \dfrac{1}{2}$

$Un plano de coordenadas xy con líneas de cuadrícula, etiquetado como cinco negativos y cinco con incrementos de una unidad en ambos ejes.$

Ejercicio$\PageIndex{12}$

$y = x^2 - \dfrac{1}{2}$

$Un plano de coordenadas xy con líneas de cuadrícula, etiquetado como cinco negativos y cinco con incrementos de una unidad en ambos ejes.$

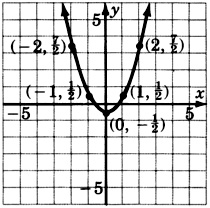
Contestar: $Gráfico de una parábola que pasa por cinco puntos con coordenadas negativas dos, siete sobre dos; negativo uno, uno sobre dos; cero, negativo uno sobre dos; uno, uno sobre dos; y dos, siete sobre dos.$

Ejercicio$\PageIndex{13}$

$y = -x^2 + 1$(comparar con el problema 2)

$Un plano de coordenadas xy con líneas de cuadrícula, etiquetado como cinco negativos y cinco con incrementos de una unidad en ambos ejes.$

Ejercicio$\PageIndex{14}$

$y = -x^2 - 1$(comparar con el problema 1)
$Un plano de coordenadas xy con líneas de cuadrícula, etiquetado como cinco negativos y cinco con incrementos de una unidad en ambos ejes.$

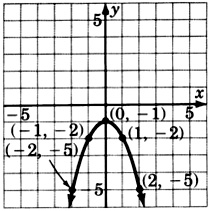
Contestar: $Gráfica de una parábola que pasa por cinco puntos con coordenadas negativas dos, negativas cinco; negativo uno, negativo dos; cero, negativo uno, uno, negativo dos; y dos, negativo cinco.$

Ejercicio$\PageIndex{15}$

$y = (x-1)^2 - 1$

$Un plano de coordenadas xy con líneas de cuadrícula, etiquetado como cinco negativos y cinco con incrementos de una unidad en ambos ejes.$

Ejercicio$\PageIndex{16}$

$y = (x + 3)^2 + 2$

$Un plano de coordenadas xy con líneas de cuadrícula, etiquetado como cinco negativos y cinco con incrementos de una unidad en ambos ejes.$

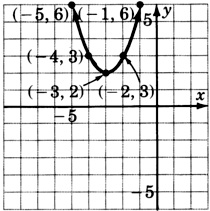
Contestar: $Gráfico de una parábola que pasa por cinco puntos con coordenadas negativas cinco, seis; negativo cuatro, tres; negativo tres, dos; negativo dos, tres; y negativo uno, seis.$

Ejercicio$\PageIndex{17}$

$y = -(x + 1)^2$

$Un plano de coordenadas xy con líneas de cuadrícula, etiquetado como cinco negativos y cinco con incrementos de una unidad en ambos ejes.$

Ejercicio$\PageIndex{18}$

$y = -(x + 3)^2$

$Un plano de coordenadas xy con líneas de cuadrícula, etiquetado como cinco negativos y cinco con incrementos de una unidad en ambos ejes.$

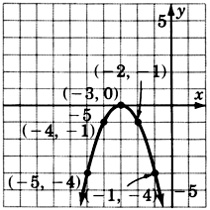
Contestar: $Gráfica de una parábola que pasa por cinco puntos con coordenadas negativas cinco, negativas cuatro; negativas cuatro, negativas una; negativas tres, cero; negativas dos, negativas una; y negativas una, cuatro negativas.$

Ejercicio$\PageIndex{19}$

$y = 2x^2$

$Un plano de coordenadas xy con líneas de cuadrícula, etiquetado como cinco negativos y cinco con incrementos de una unidad en ambos ejes.$

Ejercicio$\PageIndex{20}$

$y = 3x^2$

$Un plano de coordenadas xy con líneas de cuadrícula, etiquetado como cinco negativos y cinco con incrementos de una unidad en ambos ejes.$

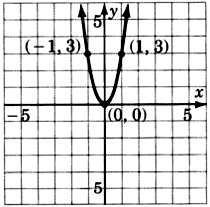
Contestar: $Gráfico de una parábola que pasa por tres puntos con coordenadas negativas uno, tres; cero, cero; y uno, tres.$

Ejercicio$\PageIndex{21}$

$y = \dfrac{1}{2}x^2$

$Un plano de coordenadas xy con líneas de cuadrícula, etiquetado como cinco negativos y cinco con incrementos de una unidad en ambos ejes.$

Para los siguientes problemas, trate de adivinar la ecuación cuadrática que corresponde a la gráfica dada.

Ejercicio$\PageIndex{22}$

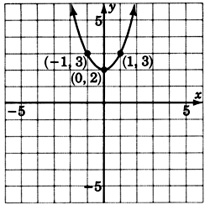
$Gráfica de una ecuación cuadrática que pasa por tres puntos con coordenadas negativas uno, tres; cero, dos; y uno, tres.$

Ejercicio$\PageIndex{23}$

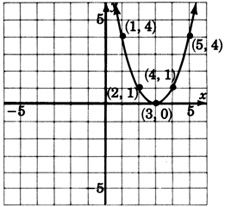
$Gráfica de una ecuación cuadrática que pasa por tres puntos con las coordenadas uno, cuatro; dos, uno; tres, cero; cuatro, uno y cinco, cuatro.$

Contestar: $y = (x-3)^2$

Ejercicio$\PageIndex{24}$

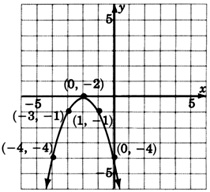
$Gráfica de una ecuación cuadrática que pasa por cinco puntos con coordenadas negativas cuatro, negativas cuatro; negativas tres, negativas una; negativas dos, cero; negativas una, negativas una; y cero, cuatro negativas.$

Ejercicio$\PageIndex{25}$

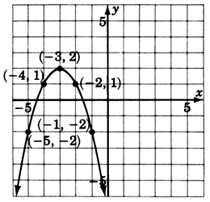
$Gráfica de una ecuación cuadrática que pasa por cinco puntos con coordenadas negativas cinco, negativas dos; negativas cuatro, uno; negativas tres, dos; negativas dos, uno; y negativo uno, negativo dos.$

Contestar: $y = -(x + 3)^2 + 2$

Ejercicios para revisión

Ejercicio$\PageIndex{26}$

Simplifica y escribe$(x^{-4}y^5)^{-3}(x^{-6}y^4)^2$ para que solo aparezcan exponentes positivos.

Ejercicio$\PageIndex{27}$

Factor$y^2 - y - 42$

Contestar: $(y+6)(y−7)$

Ejercicio$\PageIndex{28}$

Encuentra la suma:$\dfrac{2}{a - 3} + \dfrac{3}{a + 3} + \dfrac{18}{a^2 - 9}$

Ejercicio$\PageIndex{29}$

Simplificar$\dfrac{2}{4 + \sqrt{5}}$

Contestar: $\dfrac{8 - 2\sqrt{5}}{11}$

Ejercicio$\PageIndex{30}$

Cuatro se agrega a un entero y esa suma se duplica. Cuando este resultado se multiplica por el entero original, el producto es$-6$. Encuentra el entero.

Parabolas

Construyendo Gráficas de Parábola

Conjunto de Muestras A

Ejemplo\(\PageIndex{1}\)

Ejemplo\(\PageIndex{2}\)

Conjunto de práctica A

Problema de práctica\(\PageIndex{1}\)

Conjunto de Muestras B

Ejemplo\(\PageIndex{1}\)

Set de práctica B

Problema de práctica\(\PageIndex{1}\)

Problema de práctica\(\PageIndex{3}\)

Ejercicios

Ejercicio\(\PageIndex{1}\)

Ejercicio\(\PageIndex{2}\)

Ejercicio\(\PageIndex{3}\)

Ejercicio\(\PageIndex{4}\)

Ejercicio\(\PageIndex{5}\)

Ejercicio\(\PageIndex{6}\)

Ejercicio\(\PageIndex{7}\)

Ejercicio\(\PageIndex{8}\)

Ejercicio\(\PageIndex{9}\)

Ejercicio\(\PageIndex{10}\)

Ejercicio\(\PageIndex{11}\)

Ejercicio\(\PageIndex{12}\)

Ejercicio\(\PageIndex{13}\)

Ejercicio\(\PageIndex{14}\)

Ejercicio\(\PageIndex{15}\)

Ejercicio\(\PageIndex{16}\)

Ejercicio\(\PageIndex{17}\)

Ejercicio\(\PageIndex{18}\)

Ejercicio\(\PageIndex{19}\)

Ejercicio\(\PageIndex{20}\)

Ejercicio\(\PageIndex{21}\)

Ejercicio\(\PageIndex{22}\)

Ejercicio\(\PageIndex{23}\)

Ejercicio\(\PageIndex{24}\)

Ejercicio\(\PageIndex{25}\)

Ejercicios para revisión

Ejercicio\(\PageIndex{26}\)

Ejercicio\(\PageIndex{27}\)

Ejercicio\(\PageIndex{28}\)

Ejercicio\(\PageIndex{29}\)

Ejercicio\(\PageIndex{30}\)