1.3: Multiplicar y dividir enteros

Última actualización
Guardar como PDF

Page ID: 110103

Anonymous
LibreTexts

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Objetivos de aprendizaje

Multiplicar y dividir los enteros con signo.
Traducir frases en inglés que impliquen multiplicación y división en declaraciones matemáticas.
Determinar la factorización primo de los números compuestos.
Interpretar los resultados de cocientes que implican cero.

Multiplicación y división

Comenzamos con una revisión de lo que significa multiplicar y dividir números firmados. El resultado de multiplicar números reales se llama producto y el resultado de dividir se llama cociente. Recordemos que la multiplicación equivale a sumar:

$3 \cdot 4 = 4+4+4 = 12$

Claramente, el producto de dos números positivos es positivo. De igual manera, el producto de un número positivo y un número negativo se puede escribir como se muestra:

Vemos que el producto de un número positivo y un número negativo es negativo. A continuación, explore los resultados de multiplicar dos números negativos. Considere los productos en la siguiente ilustración e intente identificar el patrón:

\ [\ begin {align*}
&\ left. \ begin {aligned}
3 (-3) &=-9\\
2 (-3) &=-6\\
1 (-3) &=-3
\ end {alineado}
\ right\}
&&\ qquad\ color {cerúleo} {Los\ productos\ aumentan\ por\ 3.}\\\\
&\ 0 (-3) = 0 &&\ qquad\ color {cerúleo} {Cero\ veces\ cualquiera\ real\ número\ es\ cero.}\\\\\
&\ izquierda. \ begin {alineado}
(-1) (-3) &=3\\
(-2) (-3) &=6\\
(-3) (-3) &=9
\ end {alineado}
\ right\}
&&\ qquad\ color {cerúleo} {El\ patrón\ continúa\ aumentando\ los\ productos\ por\ 3.}
\ end {alinear*}\]

Esto demuestra que el producto de dos números negativos es positivo. Para resumir,

\ [\ begin {alinear*}
\ color {cerúleo} {positivo}\\ color {Negro} {\ veces}\\ color {cerúleo} {positivo}\ &\ color {Negro} {=}\\ color {cerúleo} {positivo}\
\ color {cerúleo} {positivo}\\ color {negro} {\ veces}\\ color {cerúleo} {negativo}\ &\ color {Negro} {=}\\ color {cerúleo} {negativo }\\
\ color {cerúleo} {negativo}\\ color {Negro} {\ veces}\\ color {cerúleo} {negativo}\ &\ color {Negro} {=}\\ color {cerúleo} {negativo}
\ final {alinear*}\]

Las reglas para la división son las mismas porque la división siempre se puede reescribir como multiplicación:

Las reglas de multiplicación y división no deben confundirse con el hecho de que la suma de dos números negativos es negativa.

Ejemplo$\PageIndex{1}$

Simplificar:

a.$(-3)+(-5)$

b.$(-3)(-5)$

Solución

Aquí sumamos y multiplicamos los mismos dos números negativos.

a. El resultado de sumar dos números negativos es negativo.

\ [\ begin {align*}
(-3) + (-5) &= -3-5\\
&= -8\\
\ end {alinear*}\]

b. El resultado de multiplicar dos números negativos es positivo.

$(-3)(-5)=15$

Contestar

a,$-8$ b.$15$

Dados los números reales$a$$b$,$c$, y, tenemos las siguientes propiedades de multiplicación:

Propiedad de factor cero:	$a \cdot 0 = 0 \cdot a = 0$
Propiedad de identidad multiplicativa:	$a \cdot 1 = 1 \cdot a = a$
Propiedad asociativa:	$(a \cdot b) \cdot c = a \cdot (b \cdot c)$
Propiedad conmutativa:	$a \cdot b = b \cdot a$

Ejemplo$\PageIndex{2}$

Simplificar:

a.$5 \cdot 0$

b.$10 \cdot 1$

Solución

a. Multiplicar por cero resulta en cero.

$5 \cdot 0 = 0$

b. Multiplicar cualquier número real por uno da como resultado el mismo número real.

$10 \cdot 1 = 10$

Respuestas:

a.$0$ b.$10$

Ejemplo$\PageIndex{3}$

Simplificar:

a.$(3 \cdot 7) \cdot 2$

b.$3 \cdot (7 \cdot 2) $

Solución

\ [\ begin {align*}
(\ color {cerúleo} {3\ cdot 7}\ color {Negro} {)}\ cdot 2 &= 21\ cdot 2\\
&= 42
\ end {align*}\]

\ [\ begin {align*}
3\ cdot (\ color {cerúleo} {7\ cdot 2}\ color {Negro} {)} &= 3\ cdot 14\\
&= 42
\ end {align*}\]

El valor de cada expresión es 42. Cambiar la agrupación de los números no cambia el resultado.

$(\color{Cerulean}{3 \cdot 7} \color{Black}{)} \cdot 2 = 3 \cdot (\color{Cerulean}{7 \cdot 2} \color{Black}{)} = 42$

Contestar

a.$42$ b.$42$

En este punto, destacamos que la multiplicación es conmutativa: el orden en que nos multiplicamos no importa y arroja el mismo resultado.

\ [\ begin {align*}
2\ cdot 9 &= 9\ cdot 2\\
18 &= 18
\ end {alinear*}\]

Por otro lado, la división no es conmutativa.

\ [\ begin {align*}
10\ div 5 &\ neq 5\ div 10\\
2 &\ neq\ frac {1} {2}
\ end {align*}\]

Utilice estas propiedades para realizar operaciones secuenciales que impliquen multiplicación y división. Al hacerlo, es importante realizar estas operaciones en orden de izquierda a derecha.

Ejemplo$\PageIndex{4}$

Simplificar:$3(-2)(-5)(-1)$

Solución

Multiplique dos números a la vez de la siguiente manera:

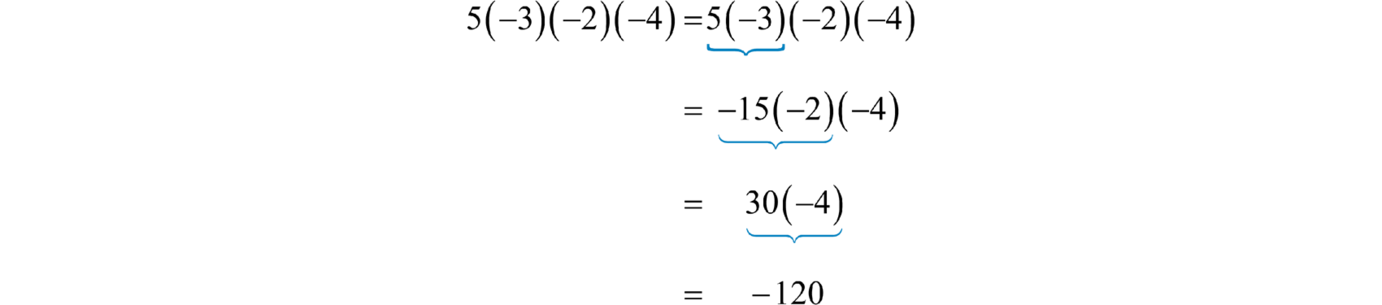
Contestar

$−120$

Debido a que la multiplicación es conmutativa, el orden en que nos multiplicamos no afecta la respuesta final. Cuando las operaciones secuenciales implican multiplicación y división, el orden sí importa; de ahí que debemos trabajar las operaciones de izquierda a derecha para obtener un resultado correcto.

Ejemplo$\PageIndex{5}$

Simplificar:$10 \div (-2)(-5)$

Solución

Realizar primero la división; de lo contrario el resultado será incorrecto.

Observe que el orden en que multiplicamos y dividimos sí afecta el resultado. Por lo tanto, es importante realizar las operaciones de multiplicación y división tal como aparecen de izquierda a derecha.

Contestar

$25$

Observe que el orden en que multiplicamos y dividimos sí afecta el resultado final. Por lo tanto, es importante realizar las operaciones de multiplicación y división tal como aparecen de izquierda a derecha.

Ejemplo$\PageIndex{6}$

Simplificar:$-6(3) \div (-2)(-3)$

Solución

Trabajar las operaciones una a la vez de izquierda a derecha.

\ [\ begin {align*}
&-6 (2)\ div (-2) (-3)\\
= &-18\ div (-2) (-3)\\
= & 9 (-3)\\
= &-27
\ end {align*}
\]

Ejemplo$\PageIndex{7}$

¡Prueba esto! Simplificar:$-5 \div 5 \cdot 2(-3)$

Solución de video:

(haga clic para ver el video)

Dentro de las aplicaciones basadas en texto, el símbolo utilizado para la multiplicación es el asterisco (*) y el símbolo utilizado para la división es la diagonal hacia adelante (/).

$5 * 3$y$14/2=7$

El conjunto de enteros pares es el conjunto de todos los enteros que son uniformemente divisibles por$2$. También podemos obtener el conjunto de enteros pares multiplicando cada entero por$2$.

$\{ \dots, -6, -4, -2, 0, 2, 4, 6, \dots\} \quad \color{Cerulean}{Even\ integers}$

El conjunto de enteros impares es el conjunto de todos los enteros que no son uniformemente divisibles por$2$.

$\{ \dots, -5, -3, -1, 1, 3, 5, \dots\} \quad \color{Cerulean}{Odd\ integers}$

Un número primo es un entero mayor que 1 que es divisible solo por$1$ y por sí mismo. El número primo más pequeño es 2 y el resto son necesariamente impares.

$\{2, 3, 5, 7, 11, 13, 17, 19, 23, \dots\} \quad \color{Cerulean}{Prime\ numbers}$

Cualquier entero mayor$1$ que eso no sea primo se llama número compuesto y puede escribirse como un producto de primos. Cuando un número compuesto, tal como$30$, se escribe como un producto$30=2 \cdot 15$,, decimos que$2 \cdot 15$ es una factorización de$30$ y eso$2$ y$15$ son factores. Tenga en cuenta que los factores dividen el número de manera uniforme. Podemos seguir escribiendo factores compuestos como productos hasta que solo quede un producto de primos.

La factorización principal de$30$ es$2 \cdot 3 \cdot 5$.

Ejemplo$\PageIndex{8}$

Determinar la factorización principal de$70$.

Solución

Comience por escribir$70$ como producto con$2$ como factor. Entonces exprese cualquier factor compuesto como producto de números primos.

\ [\ begin {align*}
70 &= 2\ cdot 35\\
&= 2\ cdot 5\ cdot 7
\ end {align*}\]

Dado que la factorización prima es única, no importa cómo elegimos factorizar inicialmente el número porque el resultado final es el mismo.

\ [\ begin {align*}
70 &= 7\ cdot 10\\
&= 7\ cdot 2\ cdot 5\\
&= 2\ cdot 5\ cdot 7
\ end {align*}\]

Contestar

La factorización principal de$70$ es$2 \cdot 5 \cdot 7$.

Algunas pruebas (llamadas pruebas de divisibilidad) útiles para encontrar factores primos de números compuestos siguen:

Si el entero es par, entonces$2$ es un factor.
Si la suma de los dígitos es uniformemente divisible por$3$, entonces$3$ es un factor.
Si el último dígito es a$5$ o$0$, entonces$5$ es un factor.

A menudo encontramos la necesidad de traducir frases en inglés que incluyen términos de multiplicación y división a declaraciones matemáticas. A continuación se enumeran algunas palabras clave que se traducen a la operación dada.

Palabras clave	Operación
Producto, multiplicado por, de, veces	* o ⋅
Cociente, dividido por, ratio, per	/o ÷

Ejemplo$\PageIndex{9}$

Calcular el cociente de$20$ y$−10$.

Solución

La palabra clave “cociente” implica que debemos dividir.

$20 \div (-10) = -2$

Respuesta:

El cociente de$20$ y$-10$ es$-2$.

Ejemplo$\PageIndex{10}$

¿Cuál es el producto de los tres primeros enteros pares positivos?

Solución

Los tres primeros enteros pares positivos son {2, 4, 6} y la palabra clave “producto” implica que debemos multiplicar.

\ [\ begin {align*}
2\ cdot 4\ cdot 6 &= 8\ cdot 6\\
&= 48
\ end {align*}\]

Contestar

El producto de los tres primeros enteros pares positivos es$48$.

Ejemplo$\PageIndex{11}$

Joe es capaz de conducir$342$ millas con$18$ galones de gasolina. ¿Cuántas millas por galón de gasolina es esta?

Solución

La palabra clave “per” indica que debemos dividir el número de millas recorridas por el número de galones utilizados:

$\frac{342\ \text{miles}}{18\ \text{gallons}} = 19\ \text{miles per gallon (mpg)}$

Contestar

Joe obtiene$19$ millas por galón de su vehículo.

En la vida cotidiana, a menudo deseamos utilizar un único valor que tipifique un conjunto de valores. Una forma de hacerlo es usar lo que se llama la media aritmética o promedio. Para calcular un promedio, divida la suma de los valores en el conjunto por el número de valores en ese conjunto.

Ejemplo$\PageIndex{12}$

Un alumno gana$75$,$86$, y$94$ en sus tres primeros exámenes. ¿Cuál es el promedio de la prueba del alumno?

Solución

Agrega las puntuaciones y divide la suma por$3$.

\ [\ begin {align*}
\ frac {75+86+94} {3} &=\ frac {255} {3}\\
&= 85
\ end {align*}\]

Contestar

El promedio de prueba del alumno es$85$.

Cero y División

Recordemos la relación entre multiplicación y división:

En este caso, el dividendo$12$ se divide equitativamente por el divisor$6$ para obtener el cociente,$2$. Es cierto en general que si multiplicamos el divisor por el cociente obtenemos el dividendo. Ahora consideremos el caso donde el dividendo es cero y el divisor es distinto de cero:

$0 \div 6 = 0$Desde$6 \cdot 0 = 0$

Esto demuestra que el cero dividido por cualquier número real distinto de cero debe ser cero. Ahora considere un número distinto de cero dividido por cero:

$12 \div 0 = \color{Cerulean}{?}$o$0 \cdot \color{Cerulean}{?}\ \color{Black}{=\ }0$

Aquí cualquier número real parece funcionar. Por ejemplo,$0 \cdot 5=0$ y$0⋅3=0$. Por lo tanto, el cociente es incierto o indeterminado.

$0 \div 0 = \frac{0}{0}\ \color{Cerulean}{Is\ indeterminate.}$

En este curso, afirmamos que$0 \div 0$ es indefinido.

Claves para llevar

Un número positivo multiplicado por un número negativo es negativo. Un número negativo multiplicado por un número negativo es positivo.
La multiplicación es conmutativa y la división no lo es.
Al simplificar, trabajar las operaciones de multiplicación y división en orden de izquierda a derecha.
Los enteros pares son números que son uniformemente divisibles por$2$ o múltiplos de$2$, y todos los demás números enteros son impares.
Un número primo es un número entero mayor que$1$ eso es divisible solo por$1$ y por sí mismo.
Los números compuestos son enteros mayores que los$1$ que no son primos. Los números compuestos se pueden escribir únicamente como un producto de primos.
La factorización prima de un número compuesto se encuentra al continuar dividiéndolo en factores hasta que solo quede un producto de primos.
Para calcular un promedio de un conjunto de números, divida la suma de los valores en el conjunto por el número de valores en el conjunto.
El cero dividido por cualquier número distinto de cero es cero. Cualquier número dividido por cero no está definido.

Ejercicio$\PageIndex{1}$

Multiplicar y dividir.

$5(−7)$
$−3(−8)$
$2(−4)(−9)$
$−3 \cdot 2 \cdot 5$
$−12(3)(0)$
$0(−12)(−5)$
$(−1)(−1)(−1)(−1)$
$(−1)(−1)(−1)$
$−100÷25$
$25 \div 5(−5)$
$−15(−2)÷10(−3)$
$−5⋅10÷2(−5)$
$(−3)(25)÷(−5)$
$6*(−3)/(−9)$
$20/(−5)*2$
$−50/2*5$
Determinar el producto de$11$ y$−3$.
Determinar el producto de$−7$ y$−22$.
Encuentra el producto de 5 y$−12$.
Encuentra el cociente de veinticinco y cinco negativos.
Determinar el cociente de$−36$ y$3$.
Determinar el cociente de$26$ y$−13$.
Calcular el producto de$3$ y$−8$ dividido por$−2$.
Calcular el producto de$−1$ y$−3$ dividido por$3$.
Determinar el producto de los tres primeros enteros pares positivos.
Determinar el producto de los tres primeros enteros impares positivos.

Contestar

1:$−35$

3:$72$

5:$0$

7:$1$

9:$−4$

11:$−9$

13:$15$

15:$−8$

17:$−33$

19:$−60$

21:$−12$

23:$12$

25:$48$

Ejercicio$\PageIndex{2}$

Determinar la factorización prima de los siguientes números enteros.

$105$
$78$
$138$
$154$
$165$
$330$

Contestar

1:$3⋅5⋅7$

3:$2⋅3⋅23$

5:$3⋅5⋅11$

Ejercicio$\PageIndex{3}$

Calcular el promedio de los números en cada uno de los siguientes conjuntos.

$\{50, 60, 70\}$
$\{9, 12, 30\}$
$\{3, 9, 12, 30, 36\}$
$\{72, 84, 69, 71\}$
Los primeros cuatro enteros pares positivos.
Los primeros cuatro enteros impares positivos.

Contestar

1:$60$

2:$18$

5:$5$

Ejercicio$\PageIndex{4}$

La distancia recorrida$D$ es igual a la tasa promedio$r$ multiplicada por el tiempo recorrido$t$ a ese ritmo:$D=rt$. Determinar la distancia recorrida dada la tasa y el tiempo.

$60$millas por hora por$3$ horas
$55$millas por hora por$3$ horas
$15$millas por hora por$5$ horas
$75$pies por segundo por$5$ segundos
$60$kilómetros por hora por$10$ horas
$60$metros por segundo por$30$ segundos
Un club de estudiantes dirigía una recaudación de fondos en el quad vendiendo hot dogs. Los estudiantes vendieron comidas para perritos$122$ calientes para$$3.00$ cada uno. Sus costos incluyen$$50.00$ para los hot dogs y bollos,$$25.00$ para paquetes de papas fritas envueltos individualmente y$$35.00$ para los refrescos. ¿Cuál fue su ganancia?
Un hombre de$230$ -libra pierde$4$ libras cada semana durante$8$ semanas. ¿Cuánto pesa al final de las$8$ semanas?
Mary descubrió que era capaz de conducir$264$ millas con$12$ galones de gasolina. ¿Cuántas millas por galón recibe su auto?
Después de llenar su auto con gasolina, Bill señaló que su lectura del odómetro era$45,346$ millas. Después de usar su auto durante una semana, llenó su tanque con$14$ galones de gasolina y señaló que su odómetro leía$45,724$ millas. En esa semana, ¿cuántas millas por galón obtuvo el auto de Bill?

Contestar

1:$180$ millas

3:$75$ millas

5:$600$ kilómetros

7:$$256.00$

9:$22$ millas por galón

11:$0$

Ejercicio$\PageIndex{5}$

Realizar las operaciones.

$0÷9$
$15÷0$
$4(−7)÷0$
$7(0)÷(−15)$
$−5(0)÷9(0)$
$5⋅2(−3)(−5)$
$−8−5+(−13)$
$−4(−8)÷16(−2)$
$50÷(−5)÷(−10)$
$49÷7÷(−1)$
$3⋅4÷12$
$0−(−8)−12$
$−8⋅4(−3)÷2$
$0/(−3*8*5)$
$(−4*3)/(2*(−3))$
$−16/(−2*2)*3$
$−44/11*2$
$−5*3/(−15)$
$4*3*2/6$
$−6*7/( −2)$
Durante días$5$ consecutivos de invierno, los mínimos diarios fueron$−7°$$−3°$,$0°$,$−5°$, y$−10°$. Calcular la temperatura media baja.
En un día muy frío se registró la temperatura cada 4 horas con los siguientes resultados:$−16°$,$−10°$,$2°$,$6°$,$−5°$, y$−13°$. Determinar la temperatura promedio.
Un estudiante gana$9$$8$,$10$,$7$, y$6$ puntos en los primeros cuestionarios de$5$ química. ¿Cuál es el promedio de su cuestionario?
Un sitio web rastreó los éxitos en su página principal durante las vacaciones de Acción de Gracias El número de aciertos por cada día del jueves al domingo fue$12,250$;$4,400$;$7,750$; y$10,200$, respectivamente. ¿Cuál fue el promedio de aciertos diarios durante el periodo vacacional?

Contestar

1:$0$

3: Sin definir

5:$0$

7:$−26$

9:$1$

11:$1$

13:$48$

15:$2$

17:$−8$

19:$4$

21:$−5°$

23:$8$ puntos

Ejercicio$\PageIndex{1}$

Temas de Mesa de Discusión.

Demostrar la propiedad asociativa de la multiplicación con tres números reales cualesquiera.
Demostrar que la división no es conmutativa.
Discutir la importancia de trabajar las operaciones de multiplicación y división de izquierda a derecha. Haz un ejemplo donde el orden sí importa y comparte la solución.
Discutir la división que involucra$0$. Con ejemplos, explica por qué el resultado es a veces$0$ y por qué a veces es indefinido.
Investigar y discutir el teorema fundamental de la aritmética.
Investigar y discutir otras pruebas de divisibilidad. Proporcione un ejemplo para cada prueba.
La media aritmética es una forma de tipificar un conjunto de valores. Investigar otros métodos utilizados para tipificar un conjunto de valores

Propiedad de factor cero:	\(a \cdot 0 = 0 \cdot a = 0\)
Propiedad de identidad multiplicativa:	\(a \cdot 1 = 1 \cdot a = a\)
Propiedad asociativa:	\((a \cdot b) \cdot c = a \cdot (b \cdot c)\)
Propiedad conmutativa:	\(a \cdot b = b \cdot a\)