3.7: Multiplicar y dividir enteros (Parte 1)
- Page ID
- 114213
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Multiplicar enteros
- Dividir enteros
- Simplificar expresiones con enteros
- Evaluar expresiones variables con números enteros
- Traducir frases de palabras a expresiones algebraicas
Antes de comenzar, toma este cuestionario de preparación.
- Traducir el cociente de\(20\) y\(13\) en una expresión algebraica. Si te perdiste este problema, revisa el Ejemplo 1.5.12.
- Agregar:\(−5 + (−5) + (−5)\). Si te perdiste este problema, revisa el Ejemplo 3.2.8.
- Evaluar\(n + 4\) cuándo\(n = −7\). Si te perdiste este problema, revisa el Ejemplo 3.2.10.
Multiplicar enteros
Dado que la multiplicación es una taquigrafía matemática para la suma repetida, nuestro modelo de contador se puede aplicar fácilmente para mostrar la multiplicación de números enteros. Veamos este modelo concreto para ver qué patrones notamos. Usaremos los mismos ejemplos que usamos para sumar y restar.
Recordamos que eso\(a • b\) significa sumar\(a\),\(b\) tiempos. Aquí, estamos utilizando el modelo que se muestra en la Figura\(\PageIndex{1}\) solo para ayudarnos a descubrir el patrón.
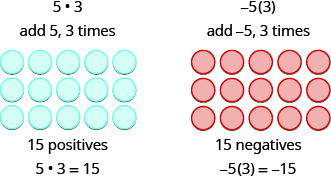
Figura\(\PageIndex{1}\)
Ahora considera lo que significa multiplicar\(5\) por\(−3\). Significa restar\(5\),\(3\) tiempos. Mirar la resta como quitar, significa llevar\(5\),\(3\) tiempos. Pero no hay nada que quitar, así que empezamos por sumar pares neutros como se muestra en la Figura\(\PageIndex{2}\).
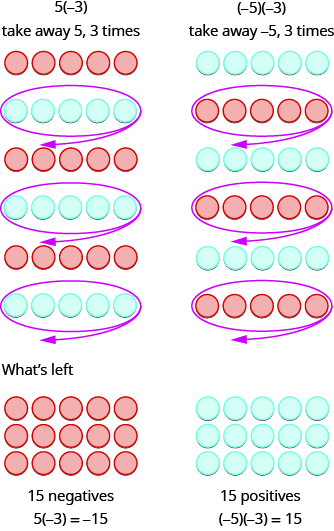
Figura\(\PageIndex{2}\)
En ambos casos, empezamos con pares\(15\) neutros. En el caso de la izquierda, nos llevamos\(5\),\(3\) tiempos y el resultado fue\(−15\). Para multiplicar\((−5)(−3)\), nos llevamos\(−5\),\(3\) tiempos y el resultado fue\(15\). Así que encontramos que
| 5 (3) = 15 | -5 (3) = -15 |
| 5 (-3) = -15 | (-5) (-3) = 15 |
Observe que para la multiplicación de dos números firmados, cuando los signos son iguales, el producto es positivo, y cuando los signos son diferentes, el producto es negativo.
El signo del producto de dos números depende de sus signos.
| Mismos signos | Producto |
|---|---|
| Dos positivos | Positivo |
| Dos negativos | Positivo |
| Distintas señales | Producto |
|---|---|
| Positivo • negativo | Negativo |
| Negativo • positivo | Negativo |
Multiplique cada uno de los siguientes:
- \(−9 • 3\)
- \(−2(−5)\)
- \(4(−8)\)
- \(7 • 6\)
Solución
| Multiplicar, señalando que los signos son diferentes y así el producto es negativo. | —9 • 3 = —27 |
| Multiplicar, señalando que los signos son los mismos y así el producto es positivo. | —2 (—5) = 10 |
| Multiplicar, señalando que los signos son diferentes y así el producto es negativo. | 4 (—8) = —32 |
| Los signos son los mismos, por lo que el producto es positivo. | 7 • 6 = 42 |
Multiplicar:
- \(−6 • 8\)
- \(−4(−7)\)
- \(9(−7)\)
- \(5 • 12\)
- Contestar a
-
\(-48\)
- Respuesta b
-
\(28\)
- Respuesta c
-
\(-63\)
- Respuesta d
-
\(60\)
Multiplicar:
- \(−8 • 7\)
- \(−6(−9)\)
- \(7(−4)\)
- \(3 • 13\)
- Contestar a
-
\(-56\)
- Respuesta b
-
\(54\)
- Respuesta c
-
\(-28\)
- Respuesta d
-
\(39\)
Cuando multiplicamos un número por\(1\), el resultado es el mismo número. ¿Qué pasa cuando multiplicamos un número por\(−1\)? Multipliquemos un número positivo y luego un número negativo por\(−1\) para ver qué obtenemos.
| −1 • 4 | −1 (−3) |
| −4 | 3 |
| −4 es lo opuesto a 4 | 3 es lo opuesto a −3 |
Cada vez que multiplicamos un número por\(−1\), obtenemos su opuesto.
Multiplicar un número por\(−1\) da su opuesto.
\[-1 \cdot a = -a \]
Multiplique cada uno de los siguientes:
- \(−1 • 7\)
- \(−1(−11)\)
Solución
| Los signos son diferentes, por lo que el producto será negativo. | −1 • 7 |
| Observe que −7 es lo opuesto a 7. | −7 |
| Los signos son los mismos, por lo que el producto será positivo. | −1 (−11) |
| Observe que 11 es lo opuesto a −11. | 11 |
Multiplicar.
- \(−1 • 9\)
- \(−1 • (−17)\)
- Contestar a
-
\(-9\)
- Respuesta b
-
\(17\)
Multiplicar.
- \(−1 • 8\)
- \(−1 • (−16)\)
- Contestar a
-
\(-8\)
- Respuesta b
-
\(16\)
Dividir enteros
La división es la operación inversa de la multiplicación. Entonces,\(15 ÷ 3 = 5\) porque\(5 • 3 = 15\) En palabras, esta expresión dice que se\(15\) pueden dividir en\(3\) grupos de\(5\) cada uno porque sumar cinco tres veces da\(15\). Si nos fijamos en algunos ejemplos de multiplicar enteros, podríamos averiguar las reglas para dividir enteros.
| 5 • 3 = 15 entonces 15 ÷ 3 = 5 | −5 (3) = −15 entonces −15 ÷ 3 = −5 |
| (−5) (−3) = 15 entonces 15 ÷ (−3) = −5 | 5 (−3) = −15 entonces −15 ÷ −3 = 5 |
La división de los números firmados sigue las mismas reglas que la multiplicación. Cuando los signos son los mismos, el cociente es positivo, y cuando los signos son diferentes, el cociente es negativo.
El signo del cociente de dos números depende de sus signos.
| Mismos signos | Cociente |
|---|---|
| Dos positivos | Positivo |
| Dos negativos | Positivo |
| Distintas señales | Cociente |
|---|---|
| Positivo y negativo | Negativo |
| Negativo y positivo | Negativo |
Recuerda, siempre puedes verificar la respuesta a un problema de división multiplicando.
Divida cada uno de los siguientes:
- \(−27 ÷ 3\)
- \(−100 ÷ (−4)\)
Solución
| Dividir, señalando que los signos son diferentes y así el cociente es negativo. | —27 ÷ 3 = —9 |
| Dividir, señalando que los signos son los mismos y así el cociente es positivo. | —100 ÷ (—4) = 25 |
Dividir:
- \(−42 ÷ 6\)
- \(−117 ÷ (−3)\)
- Contestar a
-
\(-7\)
- Respuesta b
-
\(39\)
Dividir:
- \(−63 ÷ 7\)
- \(−115 ÷ (−5)\)
- Contestar a
-
\(-9\)
- Respuesta b
-
\(23\)
Así como vimos con la multiplicación, cuando dividimos un número por\(1\), el resultado es el mismo número. ¿Qué pasa cuando dividimos un número por\(−1\)? Dividamos un número positivo y luego un número negativo por\(−1\) para ver qué obtenemos.
| 8 ÷ (−1) | −9 ÷ (−1) |
| −8 | 9 |
| −8 es lo opuesto a 8 | 9 es lo opuesto a −9 |
Cuando dividimos un número por,\(−1\) obtenemos su opuesto.
Dividir un número por\(−1\) da su opuesto.
\[a \div (-1) = -a\]
Divida cada uno de los siguientes:
- \(16 ÷ (−1)\)
- \(−20 ÷ (−1)\)
Solución
| El dividendo, 16, se está dividiendo por —1. | 16 ÷ (—1) |
| Dividir un número por —1 da su opuesto. | —16 |
Observe que los signos fueron diferentes, por lo que el resultado fue negativo.
| El dividendo, —20, está siendo dividido por —1. | —20 ÷ (—1) |
| Dividir un número por —1 da su opuesto. | 20 |
Observe que los signos fueron los mismos, por lo que el cociente fue positivo.
Dividir:
- \(6 ÷ (−1)\)
- \(−36 ÷ (−1)\)
- Contestar a
-
\(-6\)
- Respuesta b
-
\(36\)
Dividir:
- \(28 ÷ (−1)\)
- \(−52 ÷ (−1)\)
- Contestar a
-
\(-28\)
- Respuesta b
-
\(52\)
Simplificar expresiones con números enteros
Ahora simplificaremos las expresiones que usan las cuatro operaciones (suma, resta, multiplicación y división) con números enteros. Recuerda seguir el orden de las operaciones.
Simplificar:\(7(−2) + 4(−7) − 6\).
Solución
Utilizamos el orden de las operaciones. Multiplica primero y luego suma y resta de izquierda a derecha.
| Multiplicar primero. | −14 + (−28) −6 |
| Agregar. | −42 − 6 |
| Restar. | −48 |
Simplificar:\(8(−3) + 5(−7)−4\)
- Contestar
-
\(-63\)
Simplificar:\(9(−3) + 7(−8) − 1\)
- Contestar
-
\(-84\)
Simplificar:
- \((−2)^4\)
- \(−2^4\)
Solución
El exponente dice cuántas veces para multiplicar la base.
- El exponente es\(4\) y la base es\(−2\). Elevamos\(−2\) a la cuarta potencia.
| Escribir en forma expandida. | (−2) (−2) (−2) (−2) |
| Multiplicar. | 4 (−2) (−2) |
| Multiplicar. | −8 (−2) |
| Multiplicar. | 16 |
- El exponente es\(4\) y la base es\(2\). Elevamos\(2\) a la cuarta potencia y luego tomamos lo contrario.
| Escribir en forma expandida. | − (2 • 2 • 2 • 2) |
| Multiplicar. | − (4 • 2 • 2) |
| Multiplicar. | − (8 • 2) |
| Multiplicar. | −16 |
Simplificar:
- \((−3)^4\)
- \(−3^4\)
- Contestar a
-
\(81\)
- Respuesta b
-
\(-81\)
Simplificar:
- \((−7)^2\)
- \(−7^2\)
- Contestar a
-
\(49\)
- Respuesta b
-
\(-49\)
Simplificar:\(12 − 3(9 − 12)\).
Solución
Según el orden de las operaciones, simplificamos primero entre paréntesis. Entonces vamos a multiplicar y finalmente restaremos.
| Reste primero los paréntesis. | 12 − 3 (−3) |
| Multiplicar. | 12 − (−9) |
| Restar. | 21 |
Simplificar:\(17 − 4(8 − 11)\)
- Contestar
-
\(29\)
Simplificar:\(16 − 6(7 − 13)\)
- Contestar
-
\(52\)
Simplificar:\(8(−9) ÷ (−2)^3\).
Solución
Simplificamos primero el exponente, luego multiplicamos y dividimos.
| Simplifica el exponente. | 8 (−9) ÷ (−8) |
| Multiplicar. | −72 ÷ (−8) |
| Dividir. | 9 |
Simplificar:\(12(−9) ÷ (−3)^3\)
- Contestar
-
\(4\)
Simplificar:\(18(−4) ÷ (−2)^3\)
- Contestar
-
\(9\)
Simplificar:\(−30 ÷ 2 + (−3)(−7)\).
Solución
Primero multiplicaremos y dividiremos de izquierda a derecha. Después agregaremos.
| Dividir. | −15 + (−3) (−7) |
| Multiplicar. | −15 + 21 |
| Agregar. | 6 |
Simplificar:\(−27 ÷ 3 + (−5)(−6)\)
- Contestar
-
\(21\)
Simplificar:\(−32 ÷ 4 + (−2)(−7)\)
- Contestar
-
\(6\)


