Inicio
Matemáticas
Álgebra
Álgebra inicial
3: Graficar líneas
3.4: Gráfica usando la intercepción Y y la pendiente

3.4: Gráfica usando la intercepción Y y la pendiente

Última actualización
Guardar como PDF

Page ID: 110101

Anonymous
LibreTexts

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Objetivos de aprendizaje

Identificar y encontrar la pendiente de una línea.
Grafica una línea usando la pendiente y la$y$ intercepción.

Talud

La inclinación de cualquier inclinación se puede medir como la relación entre el cambio vertical y el cambio horizontal. Por ejemplo, un$5$% de inclinación puede escribirse como$\frac{5}{100}$, lo que significa que por cada$100$ pie adelante, la altura aumenta$5$ los pies.

$Captura de pantalla (569) .png$

Figura$\PageIndex{1}$

En matemáticas, llamamos a la inclinación de una línea la pendiente y usamos la letra$m$ para denotarla. El cambio vertical se llama subida y el cambio horizontal se llama carrera.

\[\color{Cerulean}{Slope}\quad\color{black}{m=\frac{\text{vertical change}}{\text{horizontal change}}=\frac{rise}{run}}\]

El ascenso y la carrera pueden ser positivos o negativos. Una subida positiva corresponde a un cambio vertical hacia arriba y una subida negativa corresponde a un cambio vertical hacia abajo. Una carrera positiva denota un cambio horizontal a la derecha y una carrera negativa corresponde a un cambio horizontal a la izquierda. Dada la gráfica, podemos calcular la pendiente determinando los cambios verticales y horizontales entre dos puntos cualesquiera.

Ejemplo$\PageIndex{1}$

Encuentra la pendiente de la línea dada:

$Captura de pantalla (570) .png$

Figura$\PageIndex{2}$

Solución:

A partir de los puntos dados en la gráfica, contar$3$ unidades hacia abajo y$4$ unidades a la derecha.

$m=\frac{rise}{run}=\frac{-3\:\text{units}}{4\:\text{units}}=-\frac{3}{4}$

Respuesta:

$m=-\frac{3}{4}$

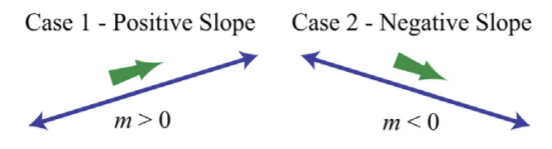
Aquí tenemos una pendiente negativa, lo que significa que por cada$4$ unidad de movimiento hacia la derecha, el cambio vertical es$3$ unidades hacia abajo. Hay cuatro casos geométricos para el valor de la pendiente.

$Captura de pantalla (571) .png$

Figura$\PageIndex{3}$

Al leer la gráfica de izquierda a derecha, vemos que las líneas con una pendiente ascendente tienen pendientes positivas y las líneas con pendiente descendente tienen pendientes negativas.

$Captura de pantalla (572) .png$

Figura$\PageIndex{4}$

Si la línea es horizontal, entonces la subida es$0$:

$m=\frac{rise}{run}=\frac{0}{run}=0$

La pendiente de una línea horizontal es$0$. Si la línea es vertical, entonces la carrera es$0$:

$m=\frac{rise}{run}=\frac{rise}{0}\quad\color{Cerulean}{Undefined}$

La pendiente de una línea vertical es indefinida.

Ejercicio$\PageIndex{1}$

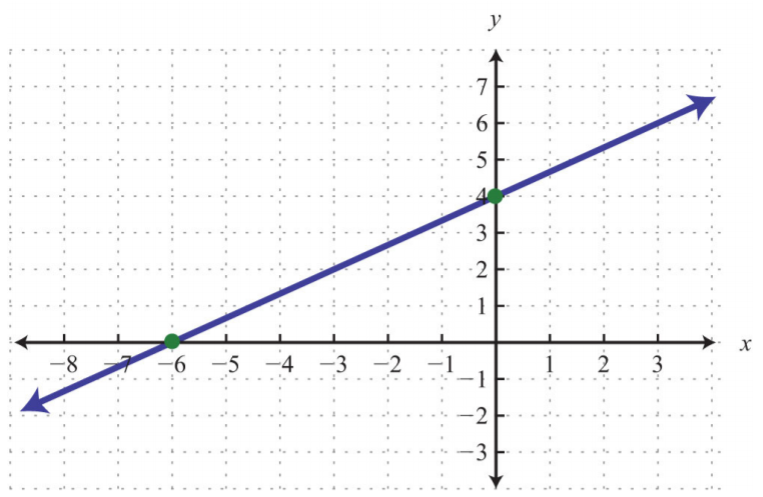
Encuentra la pendiente de la línea dada:

$Captura de pantalla (573) .png$

Figura$\PageIndex{5}$

Contestar: $m=\frac{2}{3}$

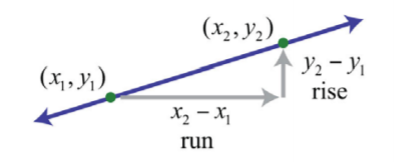
Calcular la pendiente puede ser difícil si la gráfica no tiene puntos con coordenadas enteras. Por lo tanto, a continuación desarrollamos una fórmula que nos permite calcular la pendiente algebraicamente. Dados dos puntos cualesquiera$(x_{1}, y_{1})$ y$(x_{2}, y_{2})$, podemos obtener la subida y correr restando las coordenadas correspondientes.

$Captura de pantalla (574) .png$

Figura$\PageIndex{6}$

Esto nos lleva a la fórmula de pendiente. Dados dos puntos cualesquiera$(x_{1}, y_{1})$ y$(x_{2}, y_{2})$, la pendiente viene dada por

$m=\frac{rise}{run}=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}$

Ejemplo$\PageIndex{2}$

Encuentra la pendiente de la línea que pasa por$(−3, −5)$ y$(2, 1)$.

Solución:

Dado$(−3, −5)$ y$(2, 1)$, calcular la diferencia de los$y$ -valores divididos por la diferencia de los$x$ -valores. Dado que la resta no es conmutativa, tenga cuidado de ser consistente a la hora de restar las coordenadas.

$\begin{array}{cc}{(x_{1},y_{1})}&{(x_{2},y_{2})}\\{(-3,-5)}&{(2,1)}\end{array}$

$\begin{aligned} m&=\frac{y_{2}-y_{1}}{x_{2}-x_{1}} \\ &=\frac{1-(-5)}{2-(-3)} \\ &=\frac{1+5}{2+3} \\ &=\frac{6}{5} \end{aligned}$

Respuesta:

$m=\frac{6}{5}$

Podemos graficar la línea descrita en el ejemplo anterior y verificar que la pendiente es$\frac{6}{5}$.

$Captura de pantalla (575) .png$

Figura$\PageIndex{7}$

Ciertamente la gráfica es opcional; la belleza de la fórmula del talud es que podemos obtener la pendiente, dados dos puntos, utilizando únicamente álgebra.

Ejemplo$\PageIndex{3}$

Encuentra la pendiente de la línea que pasa por$(−4, 3)$ y$(−1, −7)$.

Solución:

$\begin{array}{cc}{(x_{1},y_{1})}&{(x_{2},y_{2})}\\{(-4,3)}&{(-1,-7)} \end{array}$

$m=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}=\frac{-7-(3)}{-1-(-4)}=\frac{-7-3}{-1+4}=\frac{-10}{3}$

Respuesta:

$m=-\frac{10}{3}$

Al usar la fórmula de pendiente, tenga cuidado de ser consistente ya que el orden sí importa. Debe restar las coordenadas del primer punto de las coordenadas del segundo punto tanto para el numerador como para el denominador en el mismo orden.

Ejemplo$\PageIndex{4}$

Encuentra la pendiente de la línea que pasa por$(7, −2)$ y$(−5, −2)$.

Solución:

$\begin{array}{cc}{(x_{1},y_{1})}&{(x_{2},y_{2})}\\{(7,-2)}&{(-5,-2)} \end{array}$

$m=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}=\frac{-2-(-2)}{-5-(7)}=\frac{-2+2}{-5-7}=\frac{0}{-12}=0$

Respuesta:

$m=0$. Como ejercicio, trazar los dos puntos dados y verificar que se encuentran en una línea horizontal.

Ejemplo$\PageIndex{5}$

Encuentra la pendiente de la línea que pasa por$(−4, −3)$ y$(−4, 5)$.

Solución:

$\begin{array}{cc}{(x_{1},y_{1})}&{(x_{2},y_{2})}\\{(-4,-3)}&{(-4,5)} \end{array}$

$m=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}=\frac{5-(-3)}{-4-(-4)}=\frac{5+3}{-4+4}=\frac{8}{0}\quad\color{Cerulean}{Undefined}$

Respuesta:

La pendiente$m$ es indefinida. Como ejercicio, trazar los dos puntos dados y verificar que se encuentran en una línea vertical.

Ejercicio$\PageIndex{2}$

Calcular la pendiente de la línea que pasa por$(−2, 3)$ y$(5, −5)$.

Contestar: $m=-\frac{8}{7}$

Al considerar la pendiente como una tasa de cambio es importante incluir las unidades correctas.

Ejemplo$\PageIndex{6}$

Un Corvette Coupe se compró nuevo en 1970 por alrededor de $$5,200$ y se depreció en valor a lo largo del tiempo hasta que se vendió en 1985 por $$1,300$. En este punto, el auto comenzaba a considerarse un clásico y comenzó a aumentar de valor. En el año 2000, cuando el auto tenía 30 años, se vendía en subasta por $$10,450$. El siguiente gráfico de líneas representa el valor del automóvil a lo largo del tiempo.

$Captura de pantalla (576) .png$

Figura$\PageIndex{8}$

Determinar la tasa a la que el automóvil se depreció en valor de 1970 a 1985.
Determinar la tasa a la que el automóvil se apreció en valor de 1985 a 2000.

Solución:

Observe que el valor depende de la antigüedad del automóvil y que la pendiente mide la tasa en dólares al año.

a. La pendiente del segmento lineal que representa el valor para los primeros 15 años es

$m=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}=\frac{$1,300-$5,200}{15\text{ years}-0\text{ years}}=\frac{-$3,900}{15\text{ years}}=-$260\text{ per year}$

b. La pendiente del segmento lineal que representa el valor para los próximos 15 años es

$m=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}=\frac{$10,450-$1,300}{30\text{ years}-15\text{ years}}=\frac{$9,150}{15\text{ years}}=$610\text{ per year}$

Respuesta:

El valor del automóvil se depreció $$260$ anuales de 1970 a 1985.
El valor del auto se apreció$610$ $ al año de 1985 a 2000.

Forma de Inclinación-Intercepción de una Línea

A este punto, hemos aprendido a graficar líneas trazando puntos y usando las$x$ - y$y$ -intercepciones. Además, hemos visto que sólo necesitamos dos puntos para graficar una línea. En esta sección, delineamos un proceso para determinar fácilmente dos puntos usando la$y$ intersección y la pendiente. La ecuación de cualquier línea no vertical se puede escribir en forma de pendiente-intercepción$y=mx+b$. De esta forma, podemos identificar la pendiente,$m$, y la$y$ -intercepción,$(0, b)$.

Ejemplo$\PageIndex{7}$

Determinar la pendiente y$y$ -interceptar:

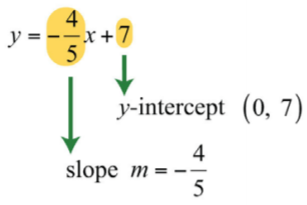
$y=−\frac{4}{5}x+7$.

Solución:

En esta forma, el coeficiente de$x$ es la pendiente, y la constante es el$y$ -valor de la$y$ -intercepción. Por lo tanto, por inspección, tenemos

$Captura de pantalla (577) .png$

Figura$\PageIndex{9}$

Respuesta:

El$y$ -intercepto es$(0, 7)$, y la pendiente es$m=−\frac{4}{5}$.

No siempre ocurre que la ecuación lineal se da en forma de pendiente-intercepción. Cuando se da en forma estándar, primero hay que resolver para$y$ obtener la forma pendiente-intercepción.

Ejemplo$\PageIndex{8}$

Expresar$3x+5y=30$ en forma de pendiente-intersección y luego identificar la pendiente e$y$ -interceptar.

Solución:

Comience resolviendo para$y$. Para ello, aplique las propiedades de igualdad para aislar primero$5y$ y luego dividir ambos lados por$5$.

$\begin{aligned} 3x+5y&=30 \\ 3x+5y\color{Cerulean}{-3x}&=30\color{Cerulean}{-3x} \\ 5y&=-3x+30 \\ \frac{5y}{\color{Cerulean}{5}}&=\frac{-3x+30}{\color{Cerulean}{5}} \\ y&=\frac{-3x}{5}+\frac{30}{5} \\ y&=-\frac{3}{5}x+6 \end{aligned}$

Respuesta:

Forma pendiente-intercepción:$y=−\frac{3}{5}x+6$;$y$ -intercepción:$(0, 6)$; pendiente:$m=−\frac{3}{5}$

Una vez que la ecuación está en forma de pendiente-intersección, inmediatamente tenemos un punto para trazar, el$y$ -intercepto. Desde la intercepción, se puede marcar la pendiente para trazar otro punto en la línea. Del ejemplo anterior tenemos

$y=-\frac{3}{5}x+6$

$y$-interceptar:$(0,6)$

pendiente:$m=-\frac{3}{5}=\frac{-3}{5}=\frac{rise}{run}$

Partiendo del punto$(0, 6)$, usa la pendiente para marcar otras$3$ unidades de punto hacia abajo y$5$ unidades a la derecha.

$Captura de pantalla (578) .png$

Figura$\PageIndex{10}$

No es necesario verificar que el segundo punto, (5, 3), resuelva la ecuación lineal original. No obstante, lo hacemos aquí en aras de la integridad.

$\begin{aligned} 3x+5y&=30 \\ 3(\color{OliveGreen}{5}\color{black}{)+5(}\color{OliveGreen}{3}\color{black}{)}&=30 \\ 15+15&=30 \\ 30&=30\quad\color{Cerulean}{\checkmark} \end{aligned}$

Marcar la pendiente de esta manera produce tantas soluciones de pares ordenadas como deseamos. Observe que si volvemos a marcar la pendiente, desde el punto$(5, 3)$, entonces obtenemos la$x$ -intercepción,$(10, 0)$.

Ejemplo$\PageIndex{9}$

Gráfica:

$−x+2y=4$.

Solución:

En este ejemplo, describimos los pasos generales para graficar una línea usando la forma pendiente-intercepción.

Paso 1: Resolver$y$ para obtener la forma pendiente-intercepción.

$\begin{aligned} -x+2y&=4 \\ -x+2y\color{Cerulean}{+x}&=4\color{Cerulean}{+x} \\ 2y&=x+4 \\ \frac{2y}{\color{Cerulean}{2}}&=\frac{x+4}{\color{Cerulean}{2}} \\ y&=\frac{1x}{2}+\frac{4}{2} \\ y&=\frac{1}{2}x+2 \end{aligned}$

Paso 2: Identificar la$y$ -intercepción y pendiente.

$y$-interceptar:$(0,2)$

pendiente:$m=\frac{1}{2}=\frac{rise}{run}$

Paso 3: Trazar la$y$ -intercepción y utilizar la pendiente para encontrar otra solución de par ordenado. A partir de la$y$ -intercepción, marcar la pendiente e identificar un segundo punto. En este caso, marcar un punto después de una subida de$1$ unidad y una tirada de$2$ unidades.

$Captura de pantalla (579) .png$

Figura$\PageIndex{11}$

Paso 4: Dibuja la línea a través de los dos puntos con una recta.

Respuesta:

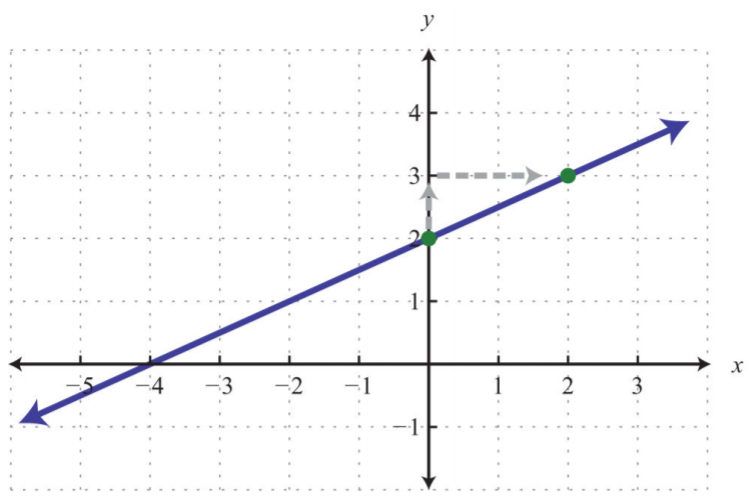$Captura de pantalla (580) .png$

Figura$\PageIndex{12}$

En este ejemplo, notamos que podríamos obtener la$x$ -intercepción marcando la pendiente de una manera diferente pero equivalente. Considere la pendiente como la relación de dos números negativos de la siguiente manera:

$m=\frac{1}{2}=\frac{-1}{-2}=\frac{rise}{run}$

Podríamos obtener otro punto en la línea marcando las$2$ unidades equivalentes de pendiente descendente$1$ e izquierda. Esto lo hacemos dos veces para obtener la$x$ -intercepción,$(−4, 0)$.

$Captura de pantalla (581) .png$

Figura$\PageIndex{13}$

Marcar la pendiente varias veces no necesariamente siempre va a darnos la$x$ -intercepción, pero cuando lo hace, obtenemos un punto valioso con poco esfuerzo. De hecho, es una buena práctica marcar la pendiente varias veces; hacerlo permite obtener más puntos en la línea y producir una gráfica más precisa.

Ejemplo$\PageIndex{10}$

Grafica y encuentra la$x$ -intercepción:

$y=\frac{3}{4}x−2$.

Solución:

La ecuación se da en forma de pendiente-intercepción. Por lo tanto, por inspección, tenemos la$y$ -intercepción y pendiente.

$y$-interceptar:$(0,-2)$

pendiente:$m=\frac{3}{4}=\frac{rise}{run}$

$Captura de pantalla (582) .png$

Figura$\PageIndex{14}$

Podemos ver que el$x$ -valor de la$x$ -intercepción es un número mixto entre$2$ y$3$. Para encontrar algebraicamente$x$ -intercepciones, recordemos que debemos establecer$y = 0$ y resolver para$x$.

Respuesta:

El$x$ -intercepto es$(2\frac{2}{3}, 0)$.

Ejemplo$\PageIndex{11}$

Gráfica:

$x−y=0$.

Solución:

Comience resolviendo para$y$.

$\begin{aligned} x-y&=0\\x-y\color{Cerulean}{-x}&=0\color{Cerulean}{-x} \\ -y&=-x \\ \color{Cerulean}{-1\cdot}\color{black}{(-y)}&=\color{Cerulean}{-1\cdot}\color{black}{(-x)} \\ y&=x \end{aligned}$

La ecuación se$y=x$ puede escribir$y=1x+0$, y tenemos

$y$-interceptar:$(0,0)$

pendiente:$m=1=\frac{1}{1}=\frac{rise}{run}$

Respuesta:

$Captura de pantalla (583) .png$

Figura$\PageIndex{15}$

Ejercicio$\PageIndex{3}$

Grafica$−2x+5y=20$ y etiqueta la$x$ -intercepción.

Contestar

$Captura de pantalla (584) .png$

Figura$\PageIndex{16}$

Claves para llevar

La pendiente mide la inclinación de una línea como subida sobre carrera. Una subida positiva denota un cambio vertical hacia arriba, y una subida negativa denota un cambio vertical hacia abajo. Una ejecución positiva denota un cambio horizontal a la derecha, y una carrera negativa denota un cambio horizontal a la izquierda.
Las líneas horizontales tienen una pendiente de cero y las verticales tienen pendientes indefinidas.
Dados dos puntos cualesquiera en una línea, podemos calcular algebraicamente la pendiente usando la fórmula de pendiente,$m=\frac{rise}{run}=\frac{y_{2}−y_{1}}{x_{2}−x_{1}}$.
Cualquier línea no vertical puede escribirse en forma de pendiente-intersección,$y=mx+b$, a partir de la cual podemos determinar, por inspección, la pendiente$m$ e$y$ -intercepción$(0, b)$.
Si conocemos la$y$ -intercepción y pendiente de una línea, entonces podemos graficarla fácilmente. Primero, traza la$y$ intersección, y a partir de este punto usa la pendiente como subida sobre carrera para marcar otro punto en la línea. Por último, dibuja una línea a través de estos dos puntos con una recta y agrega una flecha en cada extremo para indicar que se extiende indefinidamente.
Podemos obtener tantos puntos en la línea como deseemos marcando la pendiente varias veces.

Ejercicio$\PageIndex{4}$ Slope

Determinar la pendiente y la$y$ -intercepción de la gráfica dada.

$Captura de pantalla (585) .png$

Figura$\PageIndex{17}$

$Captura de pantalla (586) .png$

Figura$\PageIndex{18}$

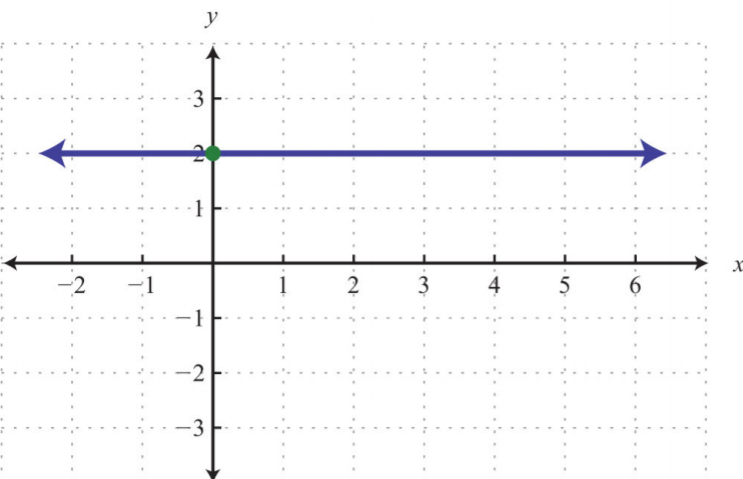$Captura de pantalla (587) .png$

Figura$\PageIndex{19}$

$Captura de pantalla (588) .png$

Figura$\PageIndex{20}$

$Captura de pantalla (589) .png$

Figura$\PageIndex{21}$

$Captura de pantalla (590) .png$

Figura$\PageIndex{22}$

Contestar

1. $y$-intercepción:$(0, 3)$; pendiente:$m = −\frac{3}{4}$

3. $y$-intercepción:$(0, 2)$; pendiente:$m = 0$

5. $y$-intercepción:$(0, 0)$; pendiente:$m = 2$

Ejercicio$\PageIndex{5}$ Slope

Determinar la pendiente, dados dos puntos.

$(3, 2)$y$(5, 1)$
$(7, 8)$y$(−3, 5)$
$(2, −3)$y$(−3, 2)$
$(−3, 5)$y$(7, −5)$
$(−1, −6)$y$(3, 2)$
$(5, 3)$y$(4, 12)$
$(−9, 3)$y$(−6, −5)$
$(−22, 4)$y$(−8, −12)$
$(\frac{1}{2}, −\frac{1}{3})$y$(−\frac{1}{2}, \frac{2}{3})$
$(−\frac{3}{4}, \frac{3}{2})$y$(\frac{1}{4}, −\frac{1}{2})$
$(−\frac{1}{3}, \frac{5}{8})$y$(\frac{1}{2}, −\frac{3}{4})$
$(−\frac{3}{5}, −\frac{3}{2})$y$(\frac{1}{10}, \frac{4}{5})$
$(3, −5)$y$(5, −5)$
$(−3, 1)$y$(−14, 1)$
$(−2, 3)$y$(−2, −4)$
$(−4, −4)$y$(5, 5)$
Un techo baja$4$ pies por cada$12$ pie hacia adelante. Determinar la pendiente de la cubierta.
Un camino baja$300$ pies por cada$5,280$ pie adelante. Determinar la pendiente de la carretera.
La siguiente gráfica da la población estadounidense de personas de 65 años y más. ¿A qué ritmo aumentó esta población de 2000 a 2008?

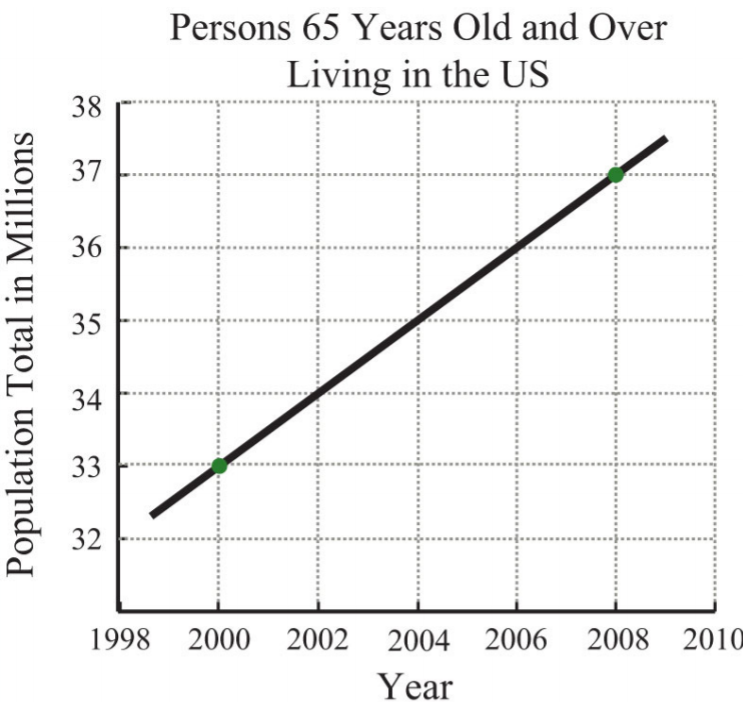$Captura de pantalla (592) .png$

Figura$\PageIndex{23}$: Fuente: Oficina del Censo de Estados Unidos.

20. La siguiente gráfica da crédito al consumo total pendiente en Estados Unidos. ¿A qué tasa aumentó el crédito al consumo de 2002 a 2008?

$Captura de pantalla (593) .png$

Figura$\PageIndex{24}$: Fuente: Oficina del Censo de Estados Unidos.

21. Se compró una camioneta comercial nueva por $$20,000$ y se espera que valga $$4,000$ en 8 años. Determinar la tasa a la que la camioneta se deprecia en valor.

22. Una fotocopiadora de grado comercial se compró nueva por $$4,800$ y se considerará inútil en 6 años. Determinar la tasa a la que la fotocopiadora se deprecia en valor.

23. Encuentra$y$ si la pendiente de la línea que pasa por$(−2, 3)$ y$(4, y)$ es$12$.

24. Encuentra$y$ si la pendiente de la línea que pasa por$(5, y)$ y$(6, −1)$ es$10$.

25. Encuentra$y$ si la pendiente de la línea que pasa por$(5, y)$ y$(−4, 2)$ es$0$.

26. Encuentra$x$ si la pendiente de la línea que pasa por$(−3, 2)$ y$(x, 5)$ es indefinida.

Contestar

1. $−\frac{1}{2}$

3. $−1$

5. $2$

7. $−\frac{8}{3}$

9. $−1$

11. $−\frac{33}{20}$

13. $0$

15. Sin definir

17. $−\frac{1}{3}$

19. $\frac{1}{2}$millones por año

21. $$2,000$ por año

23. $75$

25. $2$

Ejercicio$\PageIndex{6}$ Slope-Intercept Form

Expresar la ecuación lineal dada en forma de pendiente-intersección e identificar la pendiente e$y$ -intercepción.

$6x−5y=30$
$−2x+7y=28$
$9x−y=17$
$x−3y=18$
$2x−3y=0$
$−6x+3y=0$
$\frac{2}{3}x−\frac{5}{4}y=10$
$−\frac{4}{3}x+\frac{1}{5}y=−5$

Contestar

1. $y=\frac{6}{5}x−6$; pendiente:$\frac{6}{5}$;$y$ -intercepción:$(0, −6)$

3. $y=9x−17$; pendiente:$9$;$y$ -intercepción:$(0, −17)$

5. $y=\frac{2}{3}x$; pendiente:$\frac{2}{3}$;$y$ -intercepción:$(0, 0)$

7. $y=\frac{8}{15}x−8$; pendiente:$\frac{8}{15}$;$y$ -intercepción:$(0, −8)$

Ejercicio$\PageIndex{7}$ Slope-Intercept Form

Grafica la línea dada la pendiente y la$y$ -intercepción.

$m=\frac{1}{3}$y$(0, −2)$
$m=−\frac{2}{3}$y$(0, 4)$
$m=3$y$(0, 1)$
$m=−2$y$(0, −1)$
$m=0$y$(0, 5)$
$m$undefined y$(0, 0)$
$m=1$y$(0, 0)$
$m=−1$y$(0, 0)$
$m=−\frac{15}{3}$y$(0, 20)$
$m=−10$y$(0, −5)$

Contestar

$Captura de pantalla (594) .png$

Figura$\PageIndex{25}$

$Captura de pantalla (595) .png$

Figura$\PageIndex{26}$

$Captura de pantalla (596) .png$

Figura$\PageIndex{27}$

$Captura de pantalla (597) .png$

Figura$\PageIndex{28}$

$Captura de pantalla (598) .png$

Figura$\PageIndex{29}$

Ejercicio$\PageIndex{8}$ Slope-Intercept Form

Gráfica usando la pendiente y$y$ -intercepción.

$y=\frac{2}{3}x−2$
$y=−\frac{1}{3}x+1$
$y=−3x+6$
$y=3x+1$
$y=\frac{3}{5}x$
$y=−\frac{3}{7}x$
$y=−8$
$y=7$
$y=−x+2$
$y=x+1$
$y=\frac{1}{2}x+\frac{3}{2}$
$y=−\frac{3}{4}x+\frac{5}{2}$
$4x+y=7$
$3x−y=5$
$5x−2y=10$
$−2x+3y=18$
$x−y=0$
$x+y=0$
$\frac{1}{2}x−\frac{1}{3}y=1$
$−\frac{2}{3}x+\frac{1}{2}y=2$
$3x+2y=1$
$5x+3y=1$
En el mismo conjunto de ejes, grafica las tres líneas, dónde$y=\frac{3}{2}x+b$ y$b = \{−2, 0, 2\}$.
En el mismo conjunto de ejes, grafica las tres líneas, dónde$y=mx+1$ y$m = \{−\frac{1}{2}, 0, \frac{1}{2}\}$.

Contestar

$Captura de pantalla (599) .png$

Figura$\PageIndex{30}$

$Captura de pantalla (600) .png$

Figura$\PageIndex{31}$

$Captura de pantalla (601) .png$

Figura$\PageIndex{32}$

$Captura de pantalla (602) .png$

Figura$\PageIndex{33}$

$Captura de pantalla (603) .png$

Figura$\PageIndex{34}$

11.

$Captura de pantalla (604) .png$

Figura$\PageIndex{35}$

13.

$Captura de pantalla (605) .png$

Figura$\PageIndex{36}$

15.

$Captura de pantalla (606) .png$

Figura$\PageIndex{37}$

17.

$Captura de pantalla (607) .png$

Figura$\PageIndex{38}$

19.

$Captura de pantalla (608) .png$

Figura$\PageIndex{39}$

21.

$Captura de pantalla (609) .png$

Figura$\PageIndex{40}$

23.

$Captura de pantalla (610) .png$

Figura$\PageIndex{41}$

Ejercicio$\PageIndex{9}$ Discussion Board Topics

Nombra tres métodos para graficar líneas. Discutir los pros y los contras de cada método.
Elija una ecuación lineal y gráfiquelo de tres formas diferentes. Escanea el trabajo y compártelo en el panel de discusión.
¿Por qué usamos la letra m para pendiente?
¿Cómo son útiles las fracciones equivalentes cuando se trabaja con pendientes?
¿Podemos graficar una línea conociendo solo su pendiente?
Investigar y discutir la notación alternativa para pendiente:$m=\frac{Δy}{Δx}$.
¿Qué estrategias para graficar líneas se deben llevar a un examen? Explicar

Contestar

1. Las respuestas pueden variar

3. Las respuestas pueden variar

5. Las respuestas pueden variar

7. Las respuestas pueden variar