3.3: Gráfica usando intercepciones
- Page ID
- 110109
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Objetivos de aprendizaje
- Identificar y encontrar\(x\) - e\(y\) -intercepciones de una gráfica.
- Graficar una línea usando\(x\) - y\(y\) -intercepciones
Definición de\(x\) - y\(y\) -intercepciones
El \(x\)-intercept es el punto donde la gráfica de una línea intersecta el\(x\) eje.
El \(y\)-intercept es el punto donde la gráfica de una línea intersecta el\(y\) eje.
Estos puntos tienen la forma\((x,0)\) y\((0,y)\), respectivamente.
.png)
Figura\(\PageIndex{1}\)
Para encontrar las\(y\) intercepciones\(x\) - y -algebraicamente, use el hecho de que todas las\(x\) -intercepciones tienen un\(y\) -valor de cero y todas las\(y\) -intercepciones tienen un\(x\) -valor de cero. Para encontrar la\(y\) -intercepción, establezca\(x=0\) y determine el\(y\) valor -correspondiente. De igual manera, para encontrar la\(x\) -intercepción, establecer\(y=0\) y determinar el\(x\) -valor correspondiente.
Ejemplo\(\PageIndex{1}\)
Encuentra las\(x\) - y\(y\) -intercepciones:
\(−3x+2y=12\).
Solución:
Para encontrar la\(x\) -intercepción, establecer\(y = 0\).
Por lo tanto, la\(x\) -intercepción es\((−4, 0)\). Para encontrar la\(y\) -intercepción, establecer\(x = 0\).
\(\begin{aligned} -3x+2y&=12 &\color{Cerulean}{To\:find\:the\:y-intercept,} \\ \color{Cerulean}{\downarrow}\qquad &&\color{Cerulean}{set\:x=0.} \\ -3(\color{OliveGreen}{0}\color{black}{)+2y}&=12 \\ 2y&=12\\y&=6 \end{aligned}\)
De ahí que la\(y\) -intercepción sea\((0, 6)\). Tenga en cuenta que esta ecuación lineal está graficada arriba.
Respuesta:
\(x\)-interceptar:\((−4, 0)\);\(y\) -interceptar:\((0, 6)\)
Ejemplo\(\PageIndex{2}\)
Encuentra las\(x\) - y\(y\) -intercepciones:
\(y=−3x+9\)
Solución:
Comience por encontrar la\(x\) -intercepción.
\(\begin{aligned} y&=-3x+9 &\color{Cerulean}{Set\:y=0.} \\ \color{Cerulean}{\downarrow}&& \\ \color{OliveGreen}{0}&=-3x+9&\color{Cerulean}{Solve\:for\:x.} \\ 3x&=9 \\ x&=3 \end{aligned}\)
El\(x\) -intercepto es\((3, 0)\). A continuación, determinar la\(y\) -intercepción.
\(\begin{aligned} y&=-3x+9 &\color{Cerulean}{Set\:x=0.}\end{aligned}\)
\( \color{Cerulean}{\downarrow}\qquad\qquad\:\:\:\)
\(\begin{aligned} y&=-3(\color{OliveGreen}{0}\color{black}{)+9} & \color{Cerulean}{Solve\:for\:y.} \\ y&=9 \end{aligned}\)
El\(y\) -intercepto es\((0, 9)\).
Respuesta:
\(x\)-interceptar:\((3, 0)\);\(y\) -interceptar:\((0, 9)\)
Tenga en cuenta que las intercepciones son pares ordenados y no números. En otras palabras, la\(x\) -intercepción no es\(x=2\) sino más bien\((2, 0)\). Además, no todas las gráficas necesariamente tienen ambas intercepciones: por ejemplo,
.png)
Figura\(\PageIndex{2}\)
La línea horizontal graficada arriba tiene una\(y\) -intercepción de\((0, −2)\) y ninguna\(x\) -intercepción.
.png)
Figura\(\PageIndex{3}\)
La línea vertical graficada arriba tiene un\(x\) -intercept\((3, 0)\) y no\(y\) -intercept.
Ejercicio\(\PageIndex{1}\)
Encuentra las\(x\) - y\(y\) -intercepciones:
\(4x−y=2\).
- Contestar
-
\(x\)-interceptar:\((\frac{1}{2}, 0)\);\(y\) -interceptar:\((0, −2)\)
Graficar líneas mediante intercepciones
Dado que dos puntos determinan una línea, podemos usar las\(y\) intercepciones\(x\) - y -para graficar ecuaciones lineales. Acabamos de esbozar un método fácil para encontrar intercepciones; ahora delineamos los pasos para graficar líneas usando las intercepciones.
Ejemplo\(\PageIndex{3}\)
Gráfica usando intercepciones:
\(2x−3y=12\).
Solución:
Paso 1: Encuentra las intercepciones\(x\) - y\(y\) -intercepciones.
\(\begin{array}{c|c}{\underline{\color{Cerulean}{To\:find\:the\:x-intercept,\:set\:y=0.}}}&{\underline{\color{Cerulean}{To\:find\:the\:y-intercept,\:set\:x=0.}}}\\{2x-3y=12}&{2x-3y=12}\\{2x-3(\color{OliveGreen}{0}\color{black}{)=12}}&{2(\color{OliveGreen}{0}\color{black}{)-3y=12}}\\{2x=12}&{-3y=12}\\{x=6}&{y=-4}\\{x-intercept:\:(6,0)}&{y-intercept:\:(0,-4)} \end{array}\)
Paso 2: Traza las intercepciones y dibuja la línea a través de ellas. Usa una recta para crear una bonita línea recta. Agrega una flecha en cada extremo para indicar que la línea continúa indefinidamente en cualquier dirección.
Respuesta:
.png)
Figura\(\PageIndex{4}\)
Ejemplo\(\PageIndex{4}\)
Gráfica usando intercepciones:
\(y=−\frac{1}{5}x+3\).
Solución:
Comience por determinar las intercepciones\(x\) - y\ (y\ -.
\(\begin{array}{c|c}{\underline{\color{Cerulean}{x-intercept}}}&{\underline{\color{Cerulean}{y-intercept}}}\\{y=-\frac{1}{5}x+3}&{y=-\frac{1}{5}x+3}\\{\color{OliveGreen}{0}\color{black}{=-\frac{1}{5}x+3}}&{y=-\frac{1}{5}(\color{OliveGreen}{0}\color{black}{)+3}}\\{\frac{1}{5}x=3}&{y=3}\\{\color{Cerulean}{5\cdot}\color{black}{\frac{1}{5}x=}\color{Cerulean}{5\cdot}\color{black}{3}}&{y-intercept:\:(0,3)}\\{x=15}&{}\\{x-intercept:\:(15,0)}&{} \end{array}\)
A continuación, grafica los dos puntos y dibuja una línea a través de ellos con un borde recto.
Respuesta:
.png)
Figura\(\PageIndex{5}\)
Ejemplo\(\PageIndex{5}\)
Gráfica usando intercepciones:
\(y=−2x\).
Solución:
\(\begin{array}{c|c}{\underline{\color{Cerulean}{x-intercept}}}&{\underline{\color{Cerulean}{y-intercept}}}\\{y=-2x}&{y=-2x}\\{\color{OliveGreen}{0}\color{black}{=-2x}}&{y=-2(\color{OliveGreen}{0}\color{black}{)}}\\{\frac{0}{\color{Cerulean}{-2}}=\frac{-2x}{\color{Cerulean}{-2}}}&{y=0}\\{0=x}&{y-intercept:\:(0,0)}\\{x-intercept:\:(0,0)}&{}\end{array}\)
Aquí las\(x\) - y\(y\) -intercepciones son en realidad el mismo punto, el origen. Vamos a necesitar al menos un punto más para que podamos graficar la línea. Elija cualquier valor para\(x\) y determine el valor correspondiente para\(y\).
.png)
Figura\(\PageIndex{6}\)
Utilice las soluciones de par ordenadas\((0, 0), (−1, 2)\), y\((1, −2)\) para graficar la línea.
Respuesta:
.png)
Figura\(\PageIndex{7}\)
Para resumir, cualquier ecuación lineal se puede graficar encontrando dos puntos y conectándolos con una línea dibujada con una recta. Dos puntos importantes y útiles son los\(x\) - y\(y\) -interceptos; encontrar estos puntos sustituyendo\(y = 0\) y\(x = 0\), respectivamente. Este método para encontrar intercepciones será utilizado a lo largo de nuestro estudio del álgebra.
Ejercicio\(\PageIndex{2}\)
Gráfica usando intercepciones:
\(3x−5y=15\).
- Contestar
-
\(x\)-interceptar:\((5, 0)\);\(y\) -interceptar:\((0, −3)\)
Encontrar intercepciones dada la gráfica
Las\(x\) - y\(y\) -intercepciones son puntos importantes en cualquier gráfica. Este capítulo se centrará en las gráficas de ecuaciones lineales. Sin embargo, en este punto, podemos usar estas ideas para determinar intercepciones de gráficas no lineales. Recuerde que las intercepciones son pares ordenados que indican dónde la gráfica intersecta los ejes.
Ejemplo\(\PageIndex{6}\)
Encuentra las\(x\) - y\(y\) -intercepciones dadas la siguiente gráfica:
.png)
Figura\(\PageIndex{8}\)
Solución:
Vemos que la gráfica cruza el\(x\) eje -en dos lugares. Esta gráfica tiene dos\(x\) -intercepciones, a saber,\((−4, 0)\) y\((2, 0)\). Además, la gráfica cruza el\(y\) eje -en un solo lugar. El único\(y\) -intercepto es\((0, −3)\).
Respuesta:
\(x\)-intercepta:\((−4, 0), (2, 0)\);\(y\) -interceptar:\((0, −3)\)
En nuestro estudio del álgebra, veremos que algunas gráficas tienen muchas intercepciones. Además, veremos que algunas gráficas no tienen ninguna.
Ejemplo\(\PageIndex{7}\)
Dada la siguiente gráfica, encuentre las intercepciones\(x\) - y\(y\) -intercepciones:
.png)
Figura\(\PageIndex{9}\)
Solución:
Esta es una gráfica de un círculo; podemos ver que no se cruza con ninguno de los dos ejes. Por lo tanto, esta gráfica no tiene ninguna interceptación.
Respuesta:
Ninguno
Claves para llevar
- Dado que dos puntos determinan cualquier línea, podemos graficar líneas usando las\(y\) intercepciones\(x\) - y -.
- Para encontrar la\(x\) -intercepción, establecer\(y = 0\) y resolver para\(x\).
- Para encontrar la\(y\) -intercepción, establecer\(x = 0\) y resolver para\(y\).
- Este método de encontrar\(x\) - y\(y\) -intercepciones se utilizará a lo largo de nuestro estudio del álgebra porque funciona para cualquier ecuación.
- Para graficar una línea, encuentra las intercepciones, si existen, y dibuja una línea recta a través de ellas. Use una recta para crear la línea e incluya flechas en cada extremo para indicar que la línea se extiende infinitamente en cualquier dirección.
- Las líneas horizontales y verticales no siempre tienen ambas\(x\) - y\(y\) -intercepciones.
Ejercicio\(\PageIndex{3}\) Intercepts
Dada la gráfica, encuentra las\(x\) - y\(y\) -intercepciones.
1.
.png)
Figura\(\PageIndex{10}\)
2.
.png)
Figura\(\PageIndex{11}\)
3.
.png)
Figura\(\PageIndex{12}\)
4.
.png)
Figura\(\PageIndex{13}\)
5.
.png)
Figura\(\PageIndex{14}\)
6.
.png)
Figura\(\PageIndex{15}\)
- Contestar
-
1. \(y\)-interceptar:\((0, −3)\);\(x\) -interceptar:\((4, 0)\)
3. \(y\)-interceptar:\((0, −3)\);\(x\) -interceptar: ninguno
5. \(y\)-interceptar:\((0, 0)\);\(x\) -interceptar:\((0, 0)\)
Ejercicio\(\PageIndex{4}\) Intercepts
Encuentra las\(x\) - y\(y\) -intercepciones.
- \(5x−4y=20 \)
- \(−2x+7y=−28 \)
- \(x−y=3 \)
- \(−x+y=0 \)
- \(3x−4y=1 \)
- \(−2x+5y=3 \)
- \(\frac{1}{4}x−\frac{1}{3}y=1\)
- \(−\frac{2}{5}x+\frac{3}{4}y=2\)
- \(y=6\)
- \(y=−3\)
- \(x=2\)
- \(x=−1\)
- \(y=mx+b \)
- \(ax+by=c\)
- Contestar
-
1. \(x\)-interceptar:\((4, 0)\);\(y\) -interceptar:\((0, −5) \)
3. \(x\)-interceptar:\((3, 0)\);\(y\) -interceptar:\((0, −3) \)
5. \(x\)-interceptar:\((\frac{1}{3}, 0)\);\(y\) -interceptar:\((0, −\frac{1}{4})\)
7. \(x\)-interceptar:\((4, 0)\);\(y\) -interceptar:\((0, −3) \)
9. \(x\)-interceptar: ninguno;\(y\) -interceptar:\((0, 6) \)
11. \(x\)-interceptar:\((2, 0)\);\(y\) -interceptar: ninguno
13. \(x\)-interceptar:\((−\frac{b}{m}, 0)\);\(y\) -interceptar:\((0, b)\)
Ejercicio\(\PageIndex{5}\) Graph Using Intercepts
Encuentra las intercepciones y graficarlas.
- \(3x+4y=12\)
- \(−2x+3y=6\)
- \(5x−2y=10\)
- \(−4x−8y=16\)
- \(−\frac{1}{2}x+\frac{1}{3}y=1\)
- \(\frac{3}{4}x−\frac{1}{2}y=−3\)
- \(2x−\frac{5}{2}y=10\)
- \(2x−\frac{7}{3}y=−14\)
- \(4x−y=−8\)
- \(6x−y=6\)
- \(–x+2y=1\)
- \(3x+4y=6\)
- \(2x+y=−1\)
- \(−2x+6y=3\)
- \(15x+4y=−60\)
- \(−25x+3y=75\)
- \(4x+2y=0\)
- \(3x−y=0\)
- \(−12x+6y=−4\)
- \(3x+12y=−4\)
- \(y=2x+4\)
- \(y=−x+3\)
- \(y=\frac{1}{2}x+1\)
- \(y=\frac{2}{3}x−3\)
- \(y=−\frac{2}{5}x+1\)
- \(y=−\frac{5}{8}x−\frac{5}{4}\)
- \(y=−\frac{7}{8}x−\frac{7}{2}\)
- \(y=−x+\frac{3}{2}\)
- \(y=3\)
- \(y=\frac{3}{2}\)
- \(x=5\)
- \(x=−2\)
- \(y=5x\)
- \(y=−x\)
- Contestar
-
1.
.png)
Figura\(\PageIndex{16}\)
3.
.png)
Figura\(\PageIndex{17}\)
5.
.png)
Figura\(\PageIndex{18}\)
7.
.png)
Figura\(\PageIndex{19}\)
9.
.png)
Figura\(\PageIndex{20}\)
11.
.png)
Figura\(\PageIndex{21}\)
13.
.png)
Figura\(\PageIndex{22}\)
15.
.png)
Figura\(\PageIndex{23}\)
17.
.png)
Figura\(\PageIndex{24}\)
19.
.png)
Figura\(\PageIndex{25}\)
21.
.png)
Figura\(\PageIndex{26}\)
23.
.png)
Figura\(\PageIndex{27}\)
25.
.png)
Figura\(\PageIndex{28}\)
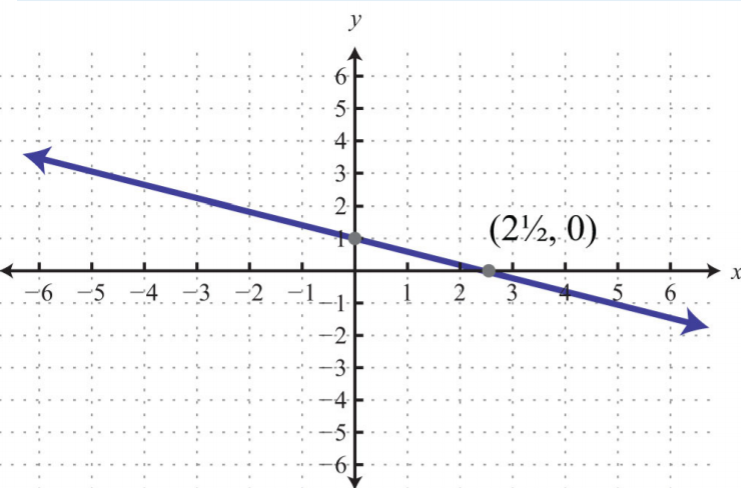
27.
.png)
Figura\(\PageIndex{29}\)
29.
.png)
Figura\(\PageIndex{30}\)
31.
.png)
Figura\(\PageIndex{31}\)
33.
.png)
Figura\(\PageIndex{32}\)
Ejercicio\(\PageIndex{6}\) Intercepts of Nonlinear Graphs
Dada la gráfica encontrar las\(x\) - y\(y\) -intercepciones.
1.
.png)
Figura\(\PageIndex{33}\)
2.
.png)
Figura\(\PageIndex{34}\)
3.
.png)
Figura\(\PageIndex{35}\)
4.
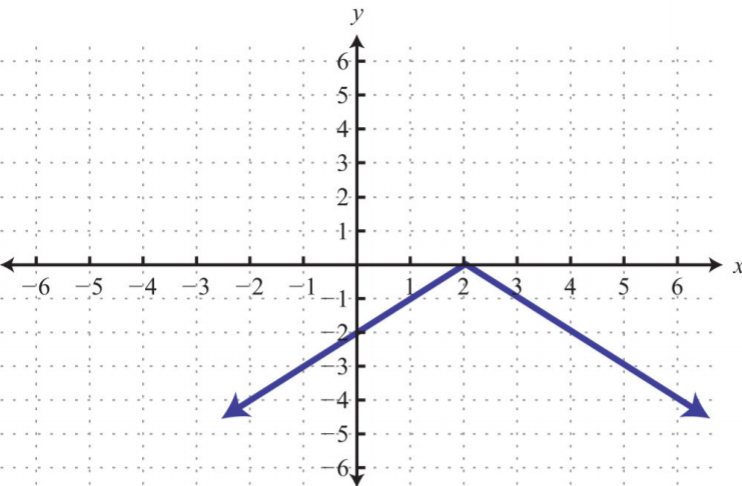.png)
Figura\(\PageIndex{36}\)
5.
.png)
Figura\(\PageIndex{37}\)
6.
.png)
Figura\(\PageIndex{38}\)
7.
.png)
Figura\(\PageIndex{39}\)
8.
.png)
Figura\(\PageIndex{40}\)
9.
.png)
Figura\(\PageIndex{41}\)
10.
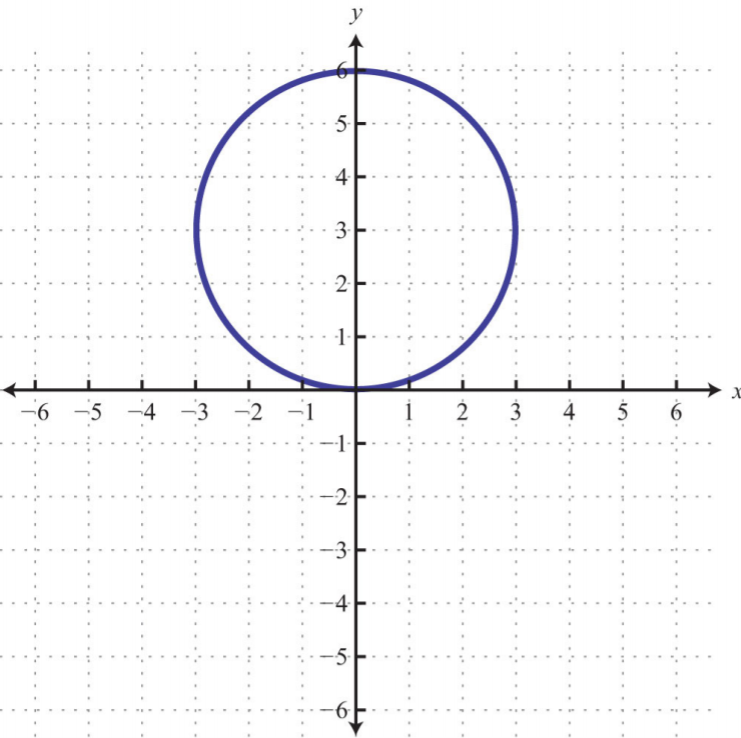.png)
Figura\(\PageIndex{42}\)
- Contestar
-
1. \(x\)-intercepta:\((−3, 0), (3, 0)\);\(y\) -interceptar:\((0, −3)\)
3. \(x\)-intercepta:\((−4, 0), (0, 0)\);\(y\) -interceptar:\((0, 0) \)
5. \(x\)-intercepta:\((−2, 0), (2, 0)\);\(y\) -interceptar:\((0, −1) \)
7. \(x\)-intercepta:\((−3, 0), (0, 0), (2, 0)\);\(y\) -interceptar:\((0, 0) \)
9. \(x\)-intercepta:\((−4, 0), (4, 0)\);\(y\) -intercepta:\((0, −4), (0, 4)\)
Ejercicio\(\PageIndex{7}\) Discussion Board Topics
- ¿Cuáles son las\(x\) -intercepciones de la línea\(y = 0\)?
- ¿Cuáles son las\(y\) -intercepciones de la línea\(x = 0\)?
- ¿Todas las líneas tienen intercepciones?
- ¿Cuántas intercepciones puede tener un círculo? Dibuja círculos que muestren todos los números posibles de intercepciones.
- Investigar y publicar las definiciones de segmento de línea, rayo y línea. ¿Por qué son importantes las flechas?
- Contestar
-
1. Las respuestas pueden variar
3. Las respuestas pueden variar
5. Las respuestas pueden variar


