7.7: Variación

Última actualización
Guardar como PDF

Page ID: 110092

This page is a draft and is under active development.

Anonymous
LibreTexts

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Objetivos de aprendizaje

Resolver aplicaciones que implican variación directa.
Resolver aplicaciones que implican variación inversa.
Resolver aplicaciones que involucran variación articular.

Variación directa

Considera un tren de carga que se mueve a una velocidad constante de 30 millas por hora. La ecuación que expresa la distancia recorrida a esa velocidad en términos de tiempo viene dada por

$D=30t$

Después de$1$ hora el tren ha recorrido$30$ millas, después de$2$ horas el tren ha recorrido$60$ millas, y así sucesivamente. Podemos construir un gráfico y graficar esta relación.

Mesa$\PageIndex{1}$
Tiempo,$t$, en horas	Distancia$D=30t$
\ (t\), en horas">0	\ (D=30t\) ">0
\ (t\), en horas">1	\ (D=30t\) ">30
\ (t\), en horas">2	\ (D=30t\) ">60
\ (t\), en horas">3	\ (D=30t\) ">90
\ (t\), en horas">4	\ (D=30t\) ">120

Captura de pantalla (326) .png — Figura$\PageIndex{1}$

En este ejemplo, podemos ver que la distancia varía con el tiempo como producto de la tasa constante,$30$ millas por hora, y la variable,$t$. Esta relación se describe como variación directa y$30$ se denomina constante de variación. Además, si dividimos ambos lados de$D=30t$ por$t$ tenemos

$\frac{D}{t}=30$

En esta forma, es razonable decir que$D$ es proporcional a$t$, donde$30$ está la constante de proporcionalidad. En general, tenemos

Mesa$\PageIndex{2}$
Palabras clave	Traducción
“$y$varía directamente como$x$”	\[y=kx\]
“$y$es directamente proporcional a$x$”
“$y$es proporcional a$x$”

Aquí$k$ es distinto de cero y se llama la constante de variación o la constante de proporcionalidad.

Ejemplo$\PageIndex{1}$

La circunferencia de un círculo es directamente proporcional a su diámetro, y la constante de proporcionalidad es$π$. Si la circunferencia se mide para ser$20$ pulgadas, entonces ¿cuál es el radio del círculo?

Solución:

Dejar$C$ representar la circunferencia del círculo.

Dejar$d$ representar el diámetro de un círculo.

Utilizar el hecho de que “la circunferencia es directamente proporcional al diámetro” para escribir una ecuación que relacione las dos variables.

$C=kd$

Se nos da que “la constante de la proporcionalidad es”$π$, o$k=π$. Por lo tanto, escribimos

$C=πd$

Ahora usa esta fórmula para encontrar$d$ cuando la circunferencia es$20$ pulgadas.

$\begin{aligned} 20&=\pi d \\ \frac{20}{\color{Cerulean}{\pi}}&=\frac{\pi d}{\color{Cerulean}{\pi}}\\ \frac{20}{\pi}&=d \end{aligned}$

El radio del círculo,$r$, es la mitad de su diámetro.

$\begin{aligned} r&=\frac{d}{2} \\ &=\frac{\color{OliveGreen}{\frac{20}{\pi}}}{2} \\ &=\frac{20}{\pi}\cdot \frac{1}{2} \\ &= \frac{10}{\pi} \end{aligned}$

Respuesta:

El radio es$\frac{10}{π}$ pulgadas, o aproximadamente$3.18$ pulgadas

Por lo general, no se nos dará la constante de variación. En cambio, se nos dará información a partir de la cual se puede determinar.

Ejemplo$\PageIndex{2}$

El peso de un objeto en la tierra varía directamente a su peso en la luna. Si un hombre pesa$180$ libras en la tierra, entonces pesará$30$ libras en la luna. Establecer una ecuación algebraica que exprese el peso en la tierra en términos del peso en la luna y utilízala para determinar el peso de una mujer en la luna si pesa$120$ libras en la tierra.

Solución:

Vamos a$y$ representar el peso en la Tierra.

Vamos a$x$ representar el peso en la Luna.

Se nos da que el “peso en la tierra varía directamente al peso en la luna”.

$y=kx$

Para encontrar la constante de variación$k$, utilice la información dada. Un hombre de$180$ -libra en la tierra pesa$30$ libras en la luna, o$y=180$ cuando$x=30$.

$180 = k \cdot 30$

Resolver para$k$.

$\begin{aligned} \frac{180}{30} &=k \\ 6&=k \end{aligned}$

A continuación, establecer una fórmula que modele la información dada.

$y=6x$

Esto implica que el peso de una persona en la tierra es$6$ multiplicado por su peso en la luna. Para responder a la pregunta, usa el peso de la mujer en la tierra,$y=120$ libras, y resuelve para$x$.

$\begin{aligned} 120&=6x \\ \frac{120}{6} &=x \\ 20&=x \end{aligned}$

Respuesta:

La mujer pesa$20$ libras en el estado de ánimo.

Variación inversa

A continuación, considere la relación entre el tiempo y la tasa,

$r=\frac{D}{t}$

Si deseamos recorrer una distancia fija, entonces podemos determinar la velocidad promedio requerida para recorrer esa distancia en una cantidad de tiempo determinada. Por ejemplo, si deseamos conducir 240 millas en 4 horas, podemos determinar la velocidad promedio requerida de la siguiente manera:

$r=\frac{240}{4}=6$

La velocidad promedio requerida para conducir 240 millas en 4 horas es de 60 millas por hora. Si queremos conducir las 240 millas en 5 horas, entonces determinar la velocidad requerida usando una ecuación similar:

$r=\frac{240}{5}=48$

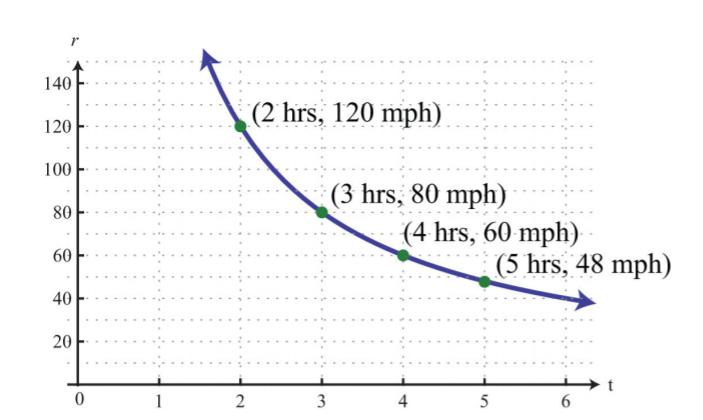
En este caso, solo tendríamos que promediar 48 millas por hora. Podemos hacer un gráfico y ver esta relación en una gráfica.

Mesa$\PageIndex{3}$
Tiempo$t$ en horas	Velocidad$r=\frac{240}{t}$
\ (t\) en horas">2	\ (r=\ frac {240} {t}\) ">120
\ (t\) en horas">3	\ (r=\ frac {240} {t}\) ">80
\ (t\) en horas">4	\ (r=\ frac {240} {t}\) ">60
\ (t\) en horas">5	\ (r=\ frac {240} {t}\) ">48

Captura de pantalla (327) .png — Figura$\PageIndex{2}$

Este es un ejemplo de una relación inversa. Decimos que$r$ es inversamente proporcional al tiempo$t$, donde$240$ está la constante de proporcionalidad. En general, tenemos

Mesa$\PageIndex{4}$
Palabras clave	Traducción
“$y$varía inversamente como$x$”	\[y=\frac{k}{x}\]
“$y$es inversamente proporcional a$x$”	\[y=\frac{k}{x}\]

Nuevamente,$k$ es distinto de cero y se llama la constante de variación o la constante de proporcionalidad.

Ejemplo$\PageIndex{3}$

Si$y$ varía inversamente como$x$ y$y=5$ cuándo$x=2$, entonces encuentra la constante de proporcionalidad y una ecuación que relaciona las dos variables.

Solución:

Si dejamos$k$ representar la constante de proporcionalidad, entonces la afirmación “$y$varía inversamente como$x$” se puede escribir de la siguiente manera:

$y=\frac{k}{x}$

Utilice la información dada,$y=5$ cuándo$x=2$, para encontrar$k$.

$5=\frac{k}{2}$

Resolver para$k$.

$\begin{aligned} \color{Cerulean}{2}\color{black}{\cdot 5}&=\color{Cerulean}{2}\color{black}{\cdot\frac{k}{2}\\10&=k} \end{aligned}$

Por lo tanto, la fórmula que modela el problema es

$y=\frac{10}{x}$

Respuesta:

La constante de proporcionalidad es$10$, y la ecuación es$y=\frac{10}{x}$.

Ejemplo$\PageIndex{4}$

El peso de un objeto varía inversamente como el cuadrado de su distancia desde el centro de la tierra. Si un objeto pesa$100$ libras en la superficie de la tierra (aproximadamente$4,000$ a millas del centro), entonces ¿cuánto pesará a$1,000$ millas por encima de la superficie terrestre?

Solución:

Dejar$w$ representar el peso del objeto.

Vamos a$d$ representar la distancia del objeto desde el centro de la Tierra.

Ya que "$w$varía inversamente como el cuadrado de”$d$, podemos escribir

$w=\frac{k}{d^{2}}$

Utilice la información dada para encontrar$k$. Un objeto pesa$100$ libras en la superficie de la tierra, aproximadamente$4,000$ a millas del centro. En otras palabras,$w = 100$ cuando$d = 4,000$:

$100=\frac{k}{(4000)^{2}}$

Resolver para$k$:

$\begin{aligned} \color{Cerulean}{(4,000)^{2}}\color{black}{\cdot 100}&=\color{Cerulean}{(4,000)^{2}}\color{black}{\cdot\frac{k}{(4,000)^{2}}}\\ 1,600,000,000&=k \\ 1.6\times 10^{9} &=k \end{aligned}$

Por lo tanto, podemos modelar el problema con la siguiente fórmula:

$w=\frac{1.6\times 10^{9}}{d^{2}}$

Para usar la fórmula para encontrar el peso, necesitamos la distancia desde el centro de la tierra. Dado que el objeto está$1,000$ a millas por encima de la superficie, encuentre la distancia desde el centro de la tierra agregando$4,000$ millas:

$d=4,000+1,000=5,000$millas

Para responder a la pregunta, usa la fórmula con$d = 5,000$.

$\begin{aligned} y &= \frac{1.6\times 10^{9}}{(\color{OliveGreen}{5,000}\color{black}{)^{2}}} \\ &=\frac{1.6\times 10^{9}}{25,000,000}\\ &=\frac{1.6\times 10^{9}}{2.5\times 10^{7}}\\ &=0.64\times 10^{2}\\ &=64 \end{aligned}$

Respuesta:

El objeto pesará$64$ libras a una distancia$1,000$ millas sobre la superficie de la tierra.

Variación conjunta

Por último, definimos las relaciones entre múltiples variables. En general, tenemos

Mesa$\PageIndex{5}$
El vocabulario	Traducción
“$y$varía conjuntamente como$x$ y$z$”	\[y=kyz\]
“$y$es conjuntamente proporcional a$x$ y$z$”	\[y=kyz\]

Aquí$k$ es distinto de cero y se llama la constante de variación o la constante de proporcionalidad.

Ejemplo$\PageIndex{5}$

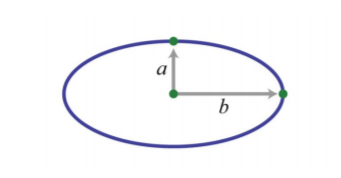
El área de una elipse varía conjuntamente como$a$, la mitad del eje mayor de la elipse y$b$, la mitad del eje menor de la elipse. Si el área de una elipse es$300π \text{cm}^{2}$, donde$a=10$ cm y$b=30$ cm, entonces ¿cuál es la constante de proporcionalidad? Dar una fórmula para el área de una elipse.

Captura de pantalla (328) .png — Figura$\PageIndex{3}$

Solución:

Si dejamos$A$ representar el área de una elipse, entonces podemos usar la declaración “área varía conjuntamente como$a$ y$b$” para escribir

$A=kab$

Para encontrar la constante de variación,$k$, utilizar el hecho de que el área es$300π$ cuándo$a=10$ y$b=30$.

$\begin{aligned} 300\pi &=k(\color{OliveGreen}{10}\color{black}{)(}\color{OliveGreen}{30}\color{black}{)} \\ 300\pi &=300k \\ \pi&=k \end{aligned}$

Por lo tanto, la fórmula para el área de una elipse es

$A=\pi ab$

Respuesta:

La constante de proporcionalidad es$π$, y la fórmula para el área es$A=abπ$.

Ejercicio$\PageIndex{1}$

Dado que$y$ varía directamente como el cuadrado de$x$ e inversamente a$z$, dónde$y = 2$ cuándo$x = 3$ y$z = 27$, encontrar$y$ cuándo$x = 2$ y$z = 16$.

Contestar: $\frac{3}{2}$

Claves para llevar

La configuración de los problemas de variación generalmente requiere múltiples pasos. Primero, identificar las palabras clave para establecer una ecuación y luego usar la información dada para encontrar la constante de variación$k$. Después de determinar la constante de variación, escriba una fórmula que modele el problema. Una vez que se encuentre una fórmula, úsela para responder a la pregunta.

Ejercicio$\PageIndex{2}$ Variation Problems

Traducir las siguientes frases en una fórmula matemática.

La distancia,$D$, un automóvil puede recorrer es directamente proporcional al tiempo,$t$, que recorre a una velocidad constante.
La extensión de un muelle colgante,$d$, es directamente proporcional al peso,$w$, unido a él.
La distancia de rotura de un automóvil$d$,, es directamente proporcional al cuadrado de la velocidad del automóvil,$v$.
El volumen,$V$, de una esfera varía directamente como el cubo de su radio,$r$.
El volumen,$V$, de una masa dada de gas es inversamente proporcional a la presión,$p$, ejercida sobre ella.
La intensidad,$I$, de la luz de una fuente de luz es inversamente proporcional al cuadrado de la distancia,$d$, de la fuente.
Cada partícula de materia en el universo atrae a todas las demás partículas con una fuerza$F$,, que es directamente proporcional al producto de las masas,$m_{1}$ y$m_{2}$, de las partículas e inversamente proporcional al cuadrado de la distancia,$d$, entre ellas.
El interés simple$I$,, es proporcional conjuntamente a la tasa de interés anual$r$,, y el tiempo$t$,, en años se invierte una cantidad fija de dinero.
El periodo,$T$, de un péndulo es directamente proporcional a la raíz cuadrada de su longitud,$L$.
El tiempo,$t$, que tarda un objeto en caer es directamente proporcional a la raíz cuadrada de la distancia$d$,, cae.

Contestar

1. $D=kt$

3. $d=kv^{2}$

5. $V=\frac{k}{p}$

7. $F=\frac{km_{1}⋅m_{2}}{d^{2}}$

9. $T=k\sqrt{L}$

Ejercicio$\PageIndex{3}$ Variation Problems

Construir un modelo matemático dado lo siguiente.

$y$varía directamente como$x$, y$y = 30$ cuando$x = 6$.
$y$varía directamente como$x$, y$y = 52$ cuando$x = 4$.
$y$es directamente proporcional a$x$, y$y = 12$ cuando$x = 3$.
$y$es directamente proporcional a$x$, y$y = 120$ cuando$x = 20$.
$y$varía directamente como$x$, y$y = 14$ cuando$x = 10$.
$y$varía directamente como$x$, y$y = 2$ cuando$x = 8$.
$y$varía inversamente como$x$, y$y = 5$ cuando$x = 7$.
$y$varía inversamente como$x$, y$y = 12$ cuando$x = 2$.
$y$es inversamente proporcional a$x$, y$y = 3$ cuando$x = 9$.
$y$es inversamente proporcional a$x$, y$y = 21$ cuando$x = 3$.
$y$varía inversamente como$x$, y$y = 2$ cuando$x = \frac{1}{8}$.
$y$varía inversamente como$x$, y$y = \frac{3}{2}$ cuando$x = \frac{1}{9}$.
$y$varía conjuntamente como$x$ y$z$, donde$y = 8$ cuando$x = 4$ y$z = \frac{1}{2}$.
$y$varía conjuntamente como$x$ y$z$, donde$y = 24$ cuando$x =\frac{1}{3}$ y$z = 9$.
$y$es conjuntamente proporcional a$x$ y$z$, donde$y = 2$ cuando$x = 1$ y$z = 3$.
$y$es conjuntamente proporcional a$x$ y$z$, donde$y = 15$ cuando$x = 3$ y$z = 7$.
$y$varía conjuntamente como$x$ y$z$, donde$y = \frac{2}{3}$ cuando$x = \frac{1}{2}$ y$z = 12$.
$y$varía conjuntamente como$x$ y$z$, donde$y = 5$ cuando$x = \frac{3}{2}$ y$z = \frac{2}{9}$.
$y$varía directamente como el cuadrado de$x$, donde$y = 45$ cuando$x = 3$.
$y$varía directamente como el cuadrado de$x$, donde$y = 3$ cuando$x = \frac{1}{2}$.
$y$es inversamente proporcional al cuadrado de$x$, donde$y = 27$ cuando$x = \frac{1}{3}$.
$y$es inversamente proporcional al cuadrado de$x$, donde$y = 9$ cuando$x = \frac{2}{3}$.
$y$varía conjuntamente como$x$ y el cuadrado de$z$, donde$y = 54$ cuando$x = 2$ y$z = 3$.
$y$varía conjuntamente como$x$ y el cuadrado de$z$, donde$y = 6$ cuando$x = \frac{1}{4}$ y$z = \frac{2}{3}$.
$y$varía conjuntamente como$x$$z$ e inversamente como el cuadrado de$w$, dónde$y = 30$ cuándo$x = 8, z = 3$, y$w = 2$
$y$varía conjuntamente como$x$ y$z$ e inversamente como el cuadrado de$w$, dónde$y = 5$ cuándo$x= 1, z = 3$, y$w = \frac{1}{2}$.
$y$varía directamente como la raíz cuadrada de$x$ e inversamente como$z$, dónde$y = 12$ cuándo$x= 9$ y$z = 5$.
$y$varía directamente como la raíz cuadrada de$x$ e inversamente como el cuadrado de$z$, dónde$y = 15$ cuándo$x = 25$ y$z = 2$.
$y$varía directamente como el cuadrado de$x$ e inversamente como$z$ y el cuadrado de$w$, donde$y = 14$ cuando$x = 4, w = 2$, y$z = 2$.
$y$varía directamente como la raíz cuadrada de$x$ e inversamente como$z$ y el cuadrado de$w$, dónde$y = 27$ cuándo$x = 9, w = \frac{1}{2}$, y$z = 4$.

Contestar

1. $y=5x$

3. $y=4x$

5. $y=\frac{7}{5}x$

7. $y=\frac{35}{x}$

9. $y=\frac{27}{x}$

11. $y=\frac{1}{4x}$

13. $y=4xz$

15. $y=\frac{2}{3}xz$

17. $y=\frac{1}{9}xz$

19. $y=5x^{2}$

21. $y=3x^{2}$

23. $y=3xz^{2}$

25. $y=\frac{5xz}{w^{2}}$

27. $y=\frac{20x}{\sqrt{z}}$

29. $y=\frac{7x^{2}}{w^{2}z}$

Ejercicio$\PageIndex{4}$ Variation Problems

Aplicaciones que implican variación.

Los ingresos en dólares son directamente proporcionales al número de sudaderas de marca vendidas. Si los ingresos obtenidos por la venta de$25$ sudaderas son $$318.75$, entonces determine los ingresos si se venden$30$ sudaderas.
El impuesto a las ventas sobre la compra de un auto nuevo varía directamente según el precio del auto. Si se compra un auto$18,000$ nuevo $, entonces el impuesto a las ventas es $$1,350$. ¿Cuánto impuesto sobre las ventas se cobra si el auto nuevo tiene un precio de $$22,000$?
El precio de una acción de acciones ordinarias en una empresa es directamente proporcional a las ganancias por acción (EPS) de los 12 meses anteriores. Si el precio de una acción de acciones ordinarias en una empresa es $$22.55$ y el EPS se publica para ser $$1.10$, entonces determinar el valor de la acción si el EPS aumenta en $$0.20$.
La distancia recorrida en un viaje por carretera varía directamente con el tiempo que se pasa en la carretera. Si se puede hacer un viaje de$126$ millas en$3$ horas, entonces ¿qué distancia se puede recorrer en$4$ horas?
La circunferencia de un círculo es directamente proporcional a su radio. Si la circunferencia de un círculo con radio$7$ centímetros se mide como$14π$ centímetros, entonces encuentra la constante de proporcionalidad.
El área de círculo varía directamente como el cuadrado de su radio. Si se determina que el área de un círculo con$7$ centímetros de radio es centímetros$49π$ cuadrados, entonces encuentra la constante de proporcionalidad.
La superficie de una esfera varía directamente como el cuadrado de su radio. Cuando el radio de una esfera mide$2$ metros, la superficie mide metros$16π$ cuadrados. Encuentra el área de superficie de una esfera con$3$ medidores de radio.
El volumen de una esfera varía directamente como el cubo de su radio. Cuando el radio de una esfera mide$3$ metros, el volumen es metros$36π$ cúbicos. Encuentra el volumen de una esfera con$1$ medidor de radio.
Con una altura fija, el volumen de un cono es directamente proporcional al cuadrado del radio en la base. Cuando el radio en la base mide$10$ centímetros, el volumen es centímetros$200$ cúbicos. Determine el volumen del cono si el radio de la base está reducido a la mitad.
La distancia,$d$, un objeto en caída libre cae varía directamente con el cuadrado de la época$t$,, que ha ido cayendo. Si un objeto en caída libre cae$36$ pies en$1.5$ segundos, entonces ¿hasta dónde habrá caído en$3$ segundos?

Contestar

1. $$382.50 $

3. $$26.65 $

5. $2π$

7. $36π$metros cuadrados

9. $50$centímetros cúbicos

Ejercicio$\PageIndex{5}$ Variation Problems

La ley de Hooke sugiere que la extensión de un resorte colgante es directamente proporcional al peso que se le une. La constante de variación se llama constante de resorte.

Si un resorte colgante se estira$5$ pulgadas cuando se le une un peso de$20$ -libra, entonces determine su constante de resorte.
Si un resorte colgante se estira$3$ centímetros cuando se le une un peso de$2$ -kilogramo, entonces determine la constante del resorte.
Si un resorte colgante se estira$3$ pulgadas cuando se adjunta un peso de$2$ -libra, entonces ¿qué tan lejos se estirará con un peso de$5$ -libra unido?
Si un resorte colgante se estira$6$ centímetros cuando se le une un peso de$4$ -kilogramo, entonces ¿qué tan lejos se estirará con un peso de$2$ -kilogramo adherido?

Contestar

1. $\frac{1}{4}$

3. $7.5$pulgadas

Ejercicio$\PageIndex{6}$ Variation Problems

La distancia de rotura de un automóvil es directamente proporcional al cuadrado de su velocidad.

Si se necesitan$36$ pies para detener un automóvil en particular que se mueve a una velocidad de$30$ millas por hora, entonces ¿cuánta distancia de ruptura se requiere si la velocidad es de$35$ millas por hora?
Después de un accidente, se determinó que le costó a un conductor$80$ pies detener su auto. En un experimento en condiciones similares, se necesitan$45$ pies para detener el automóvil que se mueve a una velocidad de$30$ millas por hora. Estimar qué tan rápido se movía el conductor antes del accidente.

Contestar: 1. $49$pies

Ejercicio$\PageIndex{7}$ Variation Problems

La ley de Boyle establece que si la temperatura permanece constante, el volumen,$V$, de una masa de gas dada es inversamente proporcional a la presión,$p$, ejercida sobre ella.

Un globo se llena a un volumen de pulgadas$216$ cúbicas en un bote de buceo bajo$1$ atmósfera de presión. Si el globo se toma bajo el agua aproximadamente$33$ pies, donde la presión mide$2$ atmósferas, entonces ¿cuál es el volumen del globo?
Si un globo se llena a pulgadas$216$ cúbicas bajo una presión de$3$ atmósferas a una profundidad de$66$ pies, entonces ¿cuál sería el volumen en la superficie, donde la presión es la$1$ atmósfera?
Para equilibrar un balancín, la distancia desde el fulcro que debe sentarse una persona es inversamente proporcional a su peso. Si un chico de$72$ -libra está sentado a$3$ pies del fulcro, entonces, ¿qué tan lejos del fulcro debe sentarse un chico$54$ - libra para equilibrar el balancín?
La corriente,$I$, en un conductor eléctrico es inversamente proporcional a su resistencia,$R$. Si la corriente es$\frac{1}{4}$ amperio cuando la resistencia es$100$ ohmios, entonces ¿cuál es la corriente cuando la resistencia es$150$ ohmios?
El número de hombres, representados por$y$, necesarios para colocar un camino de adoquines es directamente proporcional al área,$A$, de la calzada e inversamente proporcional a la cantidad de tiempo,$t$, permitido para completar el trabajo. Por lo general,$3$ los hombres pueden poner pies$1,200$ cuadrados de adoquines en$4$ horas. ¿Cuántos hombres se requerirán para poner pies$2,400$ cuadrados de adoquín dadas$6$ horas?
El volumen de un cilindro circular derecho varía conjuntamente como el cuadrado de su radio y su altura. Un cilindro circular derecho con un radio de$3$ -centímetro y una altura de$4$ centímetros tiene un volumen de centímetros$36π$ cúbicos. Encuentre una fórmula para el volumen de un cilindro circular derecho en términos de su radio y altura.
El periodo,$T$, de un péndulo es directamente proporcional a la raíz cuadrada de su longitud,$L$. Si la longitud de un péndulo es$1$ metro, entonces el periodo es de aproximadamente$2$ segundos. Aproximar el periodo de un péndulo que es$0.5$ metro de longitud.
El tiempo,$t$, que tarda un objeto en caer es directamente proporcional a la raíz cuadrada de la distancia$d$,, cae. Un objeto caído de$4$ pies tardará$\frac{1}{2}$ segundo en chocar contra el suelo. ¿Cuánto tiempo tardará un objeto caído de$16$ pies en chocar contra el suelo?

Contestar

1. $108$pulgadas cúbicas

3. $4$pies

5. $4$hombres

7. $1.4$segundos

Ejercicio$\PageIndex{8}$ Variation Problems

La ley universal de la gravitación de Newton establece que cada partícula de materia en el universo atrae a todas las demás partículas con una fuerza$F$, que es directamente proporcional al producto de las masas,$m_{1}$ y$m_{2}$, de las partículas e inversamente proporcional al cuadrado de la distancia, $d$, entre ellos. La constante de proporcionalidad se llama la constante gravitacional.

Si dos objetos con masas$50$ kilogramos y$100$ kilogramos están separados por$\frac{1}{2}$ metros, entonces producen aproximadamente$1.34×10^{−6}$ newtons (N) de fuerza. Calcular la constante gravitacional.
Utilizar la constante gravitacional del ejercicio anterior para escribir una fórmula que se aproxime a la fuerza$F$,, en newtons entre dos masas$m_{1}$ y$m_{2}$, expresada en kilogramos, dada la distancia$d$ entre ellas en metros.
Calcular la fuerza en newtons entre la tierra y la luna, dado que la masa de la luna es aproximadamente$7.3×10^{22}$ kilogramos, la masa de tierra es aproximadamente$6.0×10^{24}$ kilogramos, y la distancia entre ellos es en$1.5×10^{11}$ metros promedio.
Calcular la fuerza en newtons entre la tierra y el sol, dado que la masa del sol es aproximadamente$2.0×10^{30}$ kilogramos, la masa de tierra es aproximadamente$6.0×10^{24}$ kilogramos, y la distancia entre ellos es en$3.85×10^{8}$ metros promedio.
Si$y$ varía directamente como el cuadrado de$x$, entonces ¿cómo$y$ cambia si$x$ se duplica?
Si$y$ varía inversamente como cuadrado de$t$, entonces ¿cómo$y$ cambia si$t$ se duplica?
Si$y$ varía directamente como el cuadrado de$x$ e inversamente como el cuadrado de$t$, entonces ¿cómo$y$ cambia si ambos$x$ y$t$ se duplican?

Contestar

1. $6.7×10^{−11} \frac{N m^{2}}{kg^{2}}$

3. $1.98×10^{20}$N

5. $y$cambios por un factor de$4$

7. $y$permanece sin cambios

Palabras clave	Traducción
“\(y\)varía directamente como\(x\)”	\[y=kx\]
“\(y\)es directamente proporcional a\(x\)”
“\(y\)es proporcional a\(x\)”

Palabras clave	Traducción
“\(y\)varía inversamente como\(x\)”	\[y=\frac{k}{x}\]
“\(y\)es inversamente proporcional a\(x\)”	\[y=\frac{k}{x}\]

El vocabulario	Traducción
“\(y\)varía conjuntamente como\(x\) y\(z\)”	\[y=kyz\]
“\(y\)es conjuntamente proporcional a\(x\) y\(z\)”	\[y=kyz\]