7.1: Simplificar expresiones racionales

Última actualización
Guardar como PDF

Page ID: 110085

Anonymous
LibreTexts

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Objetivos de aprendizaje

Determinar las restricciones al dominio de una expresión racional.
Simplifica las expresiones racionales.
Simplifica expresiones con factores binomiales opuestos.
Simplificar y evaluar las funciones racionales.

Expresiones racionales, evaluación y restricciones

Un número racional, o fracción$\frac{a}{b}$, es un número real definido como un cociente de dos enteros a y b, donde$b≠0$. Del mismo modo, definimos una expresión racional, o fracción algebraica$\frac{P}{Q}$, como el cociente de dos polinomios P y Q, donde$Q≠0$. Algunos ejemplos de expresiones racionales siguen:

El ejemplo$\frac{x+3}{x-5}$ consiste en expresiones lineales tanto en el numerador como en el denominador. Debido a que el denominador contiene una variable, esta expresión no está definida para todos los valores de x.

Ejemplo$\PageIndex{1}$

Evaluar$\frac{x+3}{x-5}$ para el conjunto de valores x$\{-3,4,5\}$.

Solución:

Sustituir los valores en por x.

$\begin{array}{c|c}{x=-3} & {x=4} & {x=5} \\ \hline \frac{x+3}{x-5}=\frac{(\color{OliveGreen}{-3}\color{black}{)}+3}{(\color{OliveGreen}{-3}\color{black}{)}-5} & {\frac{x+3}{x-5}=\frac{(\color{OliveGreen}{4}\color{black}{)}+3}{(\color{OliveGreen}{4}\color{black}{)}-5}} & {\frac{x+3}{x-5}=\frac{(\color{OliveGreen}{5}\color{black}{)}+3}{(\color{OliveGreen}{5}\color{black}{)}-5}} \\ {=\frac{0}{-8}}&{=\frac{7}{-1}}&{=\frac{8}{0}\:\:\color{Cerulean}{Undefined}}\\{=0}&{=-7}&{}\end{array}$

Respuesta:

Cuando$x=−3$, el valor de la expresión racional es$0$; cuándo$x=4$, el valor de la expresión racional es$−7$; y cuándo$x=5$, el valor de la expresión racional es indefinido.

Este ejemplo ilustra que las variables están restringidas a valores que no hacen que el denominador sea igual a 0. El dominio de una expresión racional es el conjunto de números reales para los que se define, y las restricciones son los números reales para los que no se define la expresión. A menudo expresamos el dominio de una expresión racional en términos de sus restricciones.

Ejemplo$\PageIndex{2}$

Encuentra el dominio de lo siguiente:

$\frac{x+7}{2 x^{2}+x-6}$

Solución:

En este ejemplo, el numerador$x+7$ es una expresión lineal y el denominador$2x^{2}+x−6$ es una expresión cuadrática. Si factorizamos el denominador, entonces obtendremos una expresión equivalente.

$\frac{x+7}{2 x^{2}+x-6}=\frac{x+7}{(2 x-3)(x+2)}$

Debido a que las expresiones racionales son indefinidas cuando el denominador es 0, deseamos encontrar los valores para x que lo hacen 0. Para ello, aplique la propiedad cero del producto. Establezca cada factor en el denominador igual a 0 y resuelva.

$(2 x-3)(x+2)=0$

$\begin{array}{ll}{2 x-3=0} & {\text { or } \quad x+2=0} \\ {2 x=3} &\qquad\quad {x=-2} \\ {x=\frac{3}{2}}\end{array}$

Concluimos que la expresión original se define para cualquier número real excepto$\frac{3}{2}$ y$−2$. Estos dos valores son las restricciones al dominio. Es importante señalar que no$−7$ es una restricción al dominio porque la expresión se define como 0 cuando el numerador es 0.

$\begin{aligned} \frac{x+7}{2 x^{2}+x-6} &=\frac{(\color{OliveGreen}{-7}\color{black}{)}+7}{2(\color{OliveGreen}{-7}\color{black}{)}^{2}+(\color{OliveGreen}{-7}\color{black}{)}-6} \\ &=\frac{0}{98-7-6} \\ &=\frac{0}{85} \\ &=0 \end{aligned}$

Respuesta:

El dominio consiste en cualquier número real x, donde$x≠\frac{3}{2}$ y$x≠−2$.

Podemos expresar el dominio del ejemplo anterior usando la notación de la siguiente manera:

$\begin{array}{cc}{\color{Cerulean} { Set-builder\: notation}} & {\color{Cerulean} {Interval\: notation}} \\ {\left\{x | x \neq-2, \frac{3}{2}\right\}} & {(-\infty,-2) \cup\left(-2, \frac{3}{2}\right) \cup\left(\frac{3}{2}, \infty\right)}\end{array}$

Las restricciones al dominio de una expresión racional están determinadas por el denominador. Ignorar el numerador al encontrar esas restricciones.

Ejemplo$\PageIndex{3}$

Determine el dominio:

$\frac{x^{4}+x^{3}-2x^{2}-x}{x^{2}-1}$

Solución:

Para encontrar las restricciones al dominio, establezca el denominador igual a 0 y resuelva:

$\begin{array}{r}{x^{2}-1=0} \\ {(x+1)(x-1)=0}\end{array}$

$\begin{array}{rlrl}{x+1} & {=0} & {\text { or }} & {x-1=0} \\ {x} & {=-1} & &{x=1}\end{array}$

Estos dos valores hacen que el denominador sea 0. De ahí que estén restringidos del dominio.

Respuesta:

El dominio consiste en cualquier número real x, donde$x≠±1$.

Ejemplo$\PageIndex{4}$

Determine el dominio:

$\frac{x^{2}-25}{4}$

Solución:

No hay ninguna variable en el denominador y por lo tanto no hay restricción al dominio.

Respuesta:

El dominio consta de todos los números reales, R.

Simplificación de expresiones racionales

Al simplificar fracciones, busque factores comunes que cancelen. Por ejemplo,

$\frac{12}{60}=\frac{1 \cdot \color{Cerulean}{\cancel{\color{black}{12}}}}{5 \cdot \color{Cerulean}{\cancel{\color{black}{12}}}}\color{black}{=}\frac{1}{5}$

Decimos que la fracción$\frac{12}{60}$ es equivalente a$\frac{1}{5}$. Las fracciones están en forma más simple si el numerador y el denominador no comparten otro factor común que no sea$1$. De igual manera, al trabajar con expresiones racionales, busque factores para cancelar. Por ejemplo,

$\frac{x+4}{(x-3)(x+4)}=\frac{1 \cdot\color{Cerulean}{\cancel{\color{black}{(x+4)}}}}{(x-3)\color{Cerulean}{\cancel{\color{black}{(x+4)}}}}=\frac{1}{x-3}$

La expresión racional resultante es equivalente si comparte el mismo dominio. Por lo tanto, debemos tomar nota de las restricciones y escribir

$\frac{x+4}{(x-3)(x+4)}=\frac{1}{x-3}, \text { where } x \neq 3 \text { and } x \neq-4$

En palabras,$\frac{x+4}{(x-3)(x+4)}$ es equivalente a$\frac{1}{x-3}$, si$x≠3$ y$x≠−4$. Podemos verificar esto eligiendo unos valores con los que evaluar ambas expresiones para ver si los resultados son los mismos. Aquí elegimos$x=7$ y evaluamos de la siguiente manera:

$\begin{aligned} \frac{x+4}{(x-3)(x+4)} &=\frac{1}{x-3} \\ \frac{(\color{OliveGreen}{7}\color{black}{)}+4}{(\color{OliveGreen}{7}\color{black}{-}3)(\color{OliveGreen}{7}\color{black}{+}4)} &=\frac{1}{(\color{OliveGreen}{7}\color{black}{)}-3} \\ \frac{11}{(4)(11)} &=\frac{1}{4} \\ \frac{1}{4} &=\frac{1}{4}\:\:\color{Cerulean}{\checkmark} \end{aligned}$

Es importante exponer las restricciones antes de simplificar las expresiones racionales porque la expresión simplificada puede definirse para restricciones del original. En este caso, las expresiones no son equivalentes. Aquí −4 se define para el equivalente simplificado pero no para el original, como se ilustra a continuación:

$\begin{aligned} \frac{x+4}{(x-3)(x+4)} &=\frac{1}{x-3} \\ \frac{(\color{OliveGreen}{-4}\color{black}{)}+4}{(\color{OliveGreen}{-4}\color{black}{-}3)(\color{OliveGreen}{-4}\color{black}{+}4)} &=\frac{1}{(\color{OliveGreen}{-4}\color{black}{)}-3} \\ \frac{0}{(-7)(0)} &=\frac{1}{-7} \\ \frac{0}{0} &=-\frac{1}{7} \quad \color{red}{x} \end{aligned}$

Ejemplo$\PageIndex{5}$

Simplifique y establezca la restricción:

$\frac{25 x^{2}}{15 x^{3}}$

Solución:

En este ejemplo, la expresión es indefinida cuando x es 0.

$\frac{25 x^{2}}{15 x^{3}}=\frac{25(\color{OliveGreen}{0}\color{black}{)}^{2}}{15(\color{OliveGreen}{0}\color{black}{)}^{3}}=\frac{0}{0}\:\:\color{Cerulean}{Undefined}$

Por lo tanto, el dominio consiste en todos los números reales x, donde$x≠0$. Con este entendimiento, podemos cancelar factores comunes.

$\begin{aligned} \frac{25 x^{2}}{15 x^{3}} &=\frac{5 \cdot \color{Cerulean}{\cancel{\color{black}{5 x^{2}}}}}{3 x \cdot \color{Cerulean}{\cancel{\color{black}{5 x^{2}}}}} \\ &=\frac{5}{3 x} \end{aligned}$

Respuesta:

$\frac{5}{3 x}$, donde$x\neq 0$

Ejemplo$\PageIndex{6}$

Declarar las restricciones y simplificar:

$\frac{3x(x-5)}{(2x-1)(x-5)}$

Solución:

Para determinar las restricciones, establezca el denominador igual a 0 y resuelva.

$(2 x+1)(x-5)=0$

$\begin{array}{rlrl}{2 x+1} & {=0} & {\text { or }} & {x-5=0} \\ {2 x} & {=-1} & &{x=5} \\ {x} & {=-\frac{1}{2}}\end{array}$

El dominio consta de todos los números reales excepto por$−\frac{1}{2}$ y$5$. A continuación, encontramos una expresión equivalente al cancelar factores comunes.

$\begin{aligned} \frac{3 x(x-5)}{(2 x+1)(x-5)} &=\frac{3 x \color{Cerulean}{\cancel{\color{black}{(x-5)}}}}{(2 x+1)\color{Cerulean}{\cancel{\color{black}{(x-5)}}}} \\ &=\frac{3 x}{2 x+1} \end{aligned}$

Respuesta:

$\frac{3 x}{2 x+1}$, donde$x\neq -\frac{1}{2}$ y$x\neq 5$

Por lo general, las expresiones racionales no se dan en forma factorizada. Si este es el caso, factorizar primero y luego cancelar. Los pasos se describen en el siguiente ejemplo.

Ejemplo$\PageIndex{7}$

Declarar las restricciones y simplificar:

$\frac{3 x+6}{x^{2}+x-2}$

Solución:

Paso 1: Factorizar completamente el numerador y denominador.

$\frac{3 x+6}{x^{2}+x-2}=\frac{3(x+2)}{(x-1)(x+2)}$

Paso 2: Determinar las restricciones al dominio. Para ello, establece el denominador igual a 0 y resuelve.

$(x-1)(x+2)=0$

$\begin{array}{rlrl}{x-1} & {=0} & {\text { or }} & {x+2=0} \\ {x} & {=1} && {x=-2}\end{array}$

El dominio consta de todos los números reales excepto$−2$ y$1$.

Paso 3: Cancelar factores comunes, si los hubiere.

$\begin{aligned} \frac{3 x+6}{x^{2}+x-2} &=\frac{3\color{Cerulean}{\cancel{\color{black}{(x+2)}}}}{(x-1)\color{Cerulean}{\cancel{\color{black}{(x+2)}}}} \\ &=\frac{3}{x-1} \end{aligned}$

Respuesta:

$\frac{3}{x-1}$, donde$x\neq 1$ y$x\neq -2$

Ejemplo$\PageIndex{8}$

Declarar las restricciones y simplificar:

Solución:

Primero, factorizar el numerador y el denominador.

Cualquier valor de x que resulte en un valor de$0$ en el denominador es una restricción. Por inspección, determinamos que el dominio consta de todos los números reales excepto$4$ y$3$. A continuación, cancelar factores comunes.

$\begin{array}{l}{=\color{black}{\frac{\color{Cerulean}{\cancel{\color{black}{(x-3)}}}\color{black}{(x+10)}}{(x-4)\color{Cerulean}{\cancel{\color{black}{(x-3)}}}}}} \\ {=\frac{x+10}{x-4}}\end{array}$

Respuesta:

$\frac{x+10}{x-4}$, donde$x\neq 3$ y$x\neq 4$

Es importante recordar que solo podemos cancelar factores de un producto. Un error común es cancelar términos. Por ejemplo,

Ejercicio$\PageIndex{1}$

Declarar las restricciones y simplificar:

$\frac{x^{2}-16}{5x^{2}-20x}$

Contestar: $\frac{x+4}{5 x}$, donde$x\neq 0$ y$x\neq 4$

En algunos ejemplos, haremos una suposición amplia de que el denominador es distinto de cero. Cuando hacemos esa suposición, no necesitamos determinar las restricciones.

Ejemplo$\PageIndex{9}$

Simplificar:

(Supongamos que todos los denominadores son distintos de cero.)

Solución:

Factorizar el numerador por agrupación. Factorizar el denominador usando la fórmula para una diferencia de cuadrados.

A continuación, cancelar factores comunes.

$\begin{array}{l}{=\frac{\color{Cerulean}{\cancel{\color{black}{(x+y)}}}\color{black}{(y-3)}}{\color{Cerulean}{\cancel{\color{black}{(x+y)}}}\color{black}{(x-y)}}} \\ {=\frac{y-3}{x-y}}\end{array}$

Respuesta:

$\frac{y-3}{x-y}$

Factores Binomiales Opuestos

Recordemos que lo opuesto al número real a es −a. Del mismo modo, podemos definir lo opuesto de un polinomio P para que sea −P. Primero consideramos lo contrario del binomio$a−b$:

\[-(a-b)=-a+b=b-a\]

Esto nos lleva a la propiedad binomial opuesta:

\[-(a-b)=(b-a)\]

Esto equivale a factorizar un$–1$.

\[(b-a)=-1(a-b)\]

Si$a≠b$, entonces podemos dividir ambos lados por$(a−b)$ y obtener lo siguiente:

$\frac{b-a}{a-b}=-1$

Ejemplo$\PageIndex{10}$

Declarar las restricciones y simplificar:

$\frac{3-x}{x-3}$

Solución:

Por inspección, podemos ver que el denominador es$0$ si$x=3$. Por lo tanto,$3$ es la restricción al dominio. Aplicar la propiedad binomial opuesta al numerador y luego cancelar.

Respuesta:

$\frac{3-x}{x-3}$, donde$x\neq 3$

Dado que la adición es conmutativa, tenemos

\[(a+b)=(b+a)\]

$\frac{b+a}{a+b}=1$

Tenga cuidado de no confundir esto con la propiedad binomial opuesta. Además, es importante recordar que

$\frac{-a}{b}=-\frac{a}{b}=\frac{a}{-b}$

Es decir, mostrar una fracción negativa colocando el signo negativo en el numerador, frente a la barra de fracciones, o en el denominador. Generalmente, se evitan los denominadores negativos.

Ejemplo$\PageIndex{11}$

Simplifique y establezca las restricciones:

$\frac{4-x^{2}}{x^{2}+3 x-10}$

Solución:

Comience por factorizar el numerador y el denominador.

$\begin{aligned} \frac{4-x^{2}}{x^{2}+3 x-10} &=\frac{(2+x)\color{Cerulean}{(2-x)}}{\color{Cerulean}{(x-2)}\color{black}{(}x+5)}\qquad\qquad\quad\color{Cerulean}{The\:restrictions\:are\:x\neq2\:and\:x\neq-5.} \\ &=\frac{(2+x) \cdot(-1)\color{Cerulean}{\cancel{\color{black}{(x-2)}}}}{\color{Cerulean}{\cancel{\color{black}{(x-2)}}}\color{black}{(x+5)}}\quad\:\color{Cerulean}{Apply\:the\:opposite\:binomial\:property,\:then\:cancel.} \\ &=\frac{(2+x) \cdot(-1)}{(x+5)} \\ &=-\frac{2+x}{x+5} \quad \text { or } \quad=-\frac{x+2}{x+5} \end{aligned}$

Respuesta:

$-\frac{x+2}{x+5}$, donde$x\neq 2$ y$x\neq -5$

Ejercicio$\PageIndex{2}$

Simplifique y establezca las restricciones:

Contestar: $\frac{-2x+3}{x+5}$, donde$x\neq\pm 5$

Funciones racionales

Las funciones racionales tienen la forma

\[r(x)=\frac{p(x)}{q(x)}\],

donde p (x) y q (x) son polinomios y q (x) ≠ 0. El dominio de una función racional consiste en todos los números reales x tales que el denominador q (x) ≠ 0.

Ejemplo$\PageIndex{12}$

Simplificar:$r(x)=\frac{2 x^{2}+5 x-3}{6 x^{2}+18 x}$.
Declarar el dominio.
Calcular$r(-2)$.

Solución:

a. Para simplificar la función racional, primero factorizar y luego cancelar.

$\begin{aligned} r(x) &=\frac{2 x^{2}+5 x-3}{6 x^{2}+18 x} \\ &=\frac{(2 x-1)\color{Cerulean}{\cancel{\color{black}{(x+3)}}}}{6 x\color{Cerulean}{\cancel{\color{black}{(x+3)}}}} \\ &=\frac{2 x-1}{6 x} \end{aligned}$

b. para determinar las restricciones, establecer el denominador de la función original igual a 0 y resolver.

$\begin{array}{l}{6 x^{2}+18 x=0} \\ {6 x(x+3)=0}\end{array}$

$\begin{array}{cc}{6 x=0} & {\text { or } \quad x+3=0} \\ {x=0} & {x=-3}\end{array}$

El dominio consta de todos los números reales x, donde$x≠0$ y$x≠−3$.

c. Como no$−2$ es una restricción, sustituirla por la variable x usando la forma simplificada.

$\begin{aligned} r(x) &=\frac{2 x-1}{6 x} \\ r(-2) &=\frac{2(\color{OliveGreen}{-2}\color{black}{)}-1}{6(\color{OliveGreen}{-2}\color{black}{)}} \\ &=\frac{-4-1}{-12} \\ &=\frac{-5}{-12} \\ &=\frac{5}{12} \end{aligned}$

Respuesta:

a.$\frac{2 x-1}{6 x}$ b. El dominio es todo números reales excepto$0$ y$−3$. c.$r(-2) = \frac{5}{12}$

Si una función de costo$C(x)$ representa el costo de producir x unidades, entonces el costo promedio$c(x)$ es el costo dividido por el número de unidades producidas.

\[\color{Cerulean}{Average\:cost}\color{black}{:} c(x)=\frac{C(x)}{x}\]

Ejemplo$\PageIndex{13}$

El costo en dólares de producir camisetas con el logotipo de una empresa viene dado por$C(x)=7x+200$, donde x representa el número de camisas producidas. Determinar el costo promedio de producción

40 playeras
250 playeras
1,000 playeras

Solución:

Configura una función que represente el costo promedio.

$c(x)=\frac{C(x)}{x}=\frac{7 x+200}{x}$

A continuación, calcule c (40), c (250) y c (1000).

$\begin{aligned} c(40) &=\frac{7(\color{OliveGreen}{40}\color{black}{)}+200}{\color{OliveGreen}{40}}=\frac{280+200}{40}=\frac{480}{40}=12.00 \\ c(250) &=\frac{7(\color{OliveGreen}{250}\color{black}{)}+200}{\color{OliveGreen}{250}}=\frac{1750+200}{250}=\frac{1950}{250}=7.80 \\ c(1000) &=\frac{7(\color{OliveGreen}{1000}\color{black}{)}+200}{\color{OliveGreen}{1000}}=\frac{7000+200}{1000}=\frac{7200}{1000}=7.20 \end{aligned}$

Respuesta:

Si se producen 40 playeras, entonces el costo promedio por camiseta es de $12.00.
Si se producen 250 playeras, entonces el costo promedio por camiseta es de $7.80.
Si se producen mil playeras, entonces el costo promedio por camiseta es de $7.20.

Claves para llevar

Las expresiones racionales generalmente no se definen para todos los números reales. Los números reales que dan un valor de 0 en el denominador no forman parte del dominio. Estos valores se llaman restricciones.
Simplificar expresiones racionales es similar a simplificar fracciones. Primero, factorizar el numerador y el denominador y luego cancelar los factores comunes. Las expresiones racionales se simplifican si no hay factores comunes distintos de 1 en el numerador y el denominador.
Las expresiones racionales simplificadas son equivalentes para valores en el dominio de la expresión original. Asegúrese de indicar las restricciones si no se asume que los denominadores son distintos de cero.
Utilice la propiedad binomial opuesta para cancelar los factores binomiales que implican sustracción. Utilízalo$−(a−b)=b−a$ para reemplazar factores que luego cancelarán. No confundas esto con factores que involucren adición, como$(a+b)=(b+a)$.

Ejercicio$\PageIndex{3}$ Rational Expressions

Evaluar para el conjunto dado de valores x.

$5x; {−1, 0, 1}$
$\frac{4x^{3}}{x^{2}}; {−1, 0, 1} $
$\frac{1}{x+9}; {−10, −9, 0} $
$\frac{x+6}{x−5}; {−6, 0, 5}$
$\frac{3x(x−2)}{2x−1}; {0, \frac{1}{2}, 2}$
$\frac{9x^{2}−1}{x−7}; {0, \frac{1}{3}, 7} $
$5x^{2}−9; {−3, 0, 3}$
$\frac{x^{2}−2}{5x^{2}−3x−10}; {−5, −4, 5}$
Rellena la siguiente tabla:
$Captura de pantalla (308) .png$
Figura$\PageIndex{1}$
Rellena la siguiente tabla:
$Captura de pantalla (309) .png$
Figura$\PageIndex{2}$
Rellena la siguiente tabla:
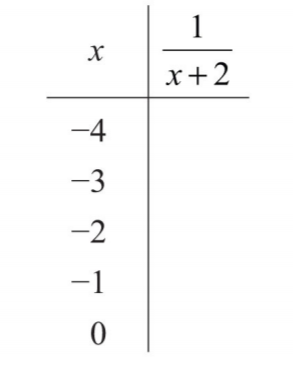$Captura de pantalla (310) .png$
Figura$\PageIndex{3}$
Rellena la siguiente tabla:
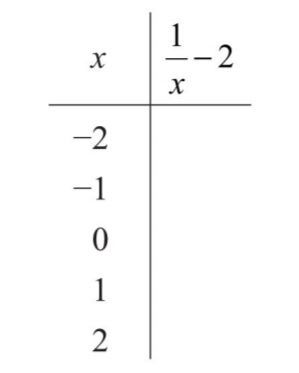$Captura de pantalla (311) .png$
Figura$\PageIndex{4}$

Contestar

1. $−5$, indefinido,$5$

3. $−1$, indefinido,$\frac{1}{9}$

5. $0$, indefinido,$0$

7. Sin definir,$−\frac{5}{9}$, indefinido

Captura de pantalla (312) .png — Figura$\PageIndex{5}$

11.

Captura de pantalla (313) .png — Figura$\PageIndex{6}$

Ejercicio$\PageIndex{4}$ Rational Expressions

El peso de un objeto depende de su altura sobre la superficie de la tierra. Si un objeto pesa 120 libras en la superficie de la tierra, entonces su peso en libras, W, x millas por encima de la superficie se aproxima por la fórmula

$W=\frac{120\cdot 4000^{2}}{(4000+x)^{2}}$

Para cada problema a continuación, aproxime el peso de un objeto de 120 libras a la altura dada sobre la superficie de la tierra. (1 milla = 5,280 pies)

100 millas
1,000 millas
44,350 pies
90,000 pies

Contestar

1. 114 libras

3. 119.5 libras

Ejercicio$\PageIndex{5}$ Rational Expressions

La relación precio-ganancias (P/E) es una métrica utilizada para comparar las valoraciones de empresas similares que cotizan en bolsa. La relación P/E se calcula utilizando el precio de las acciones y las ganancias por acción (EPS) durante el periodo anterior de 12 meses de la siguiente manera:

P/E=Precio por acción ganancias por acción

Si cada acción de una empresa tiene un precio de 22.40 dólares, entonces calcule la relación P/E dados los siguientes valores para las ganancias por acción.

$1.40
$1.21
¿Qué sucede con la relación P/E cuando disminuyen las ganancias?
¿Qué sucede con la relación P/E cuando aumentan las ganancias?

Contestar

1. 16

3. La relación P/E aumenta.

Ejercicio$\PageIndex{6}$ Rational Expressions

Declarar las restricciones al dominio.

$\frac{1}{3x}$
$\frac{3x^{2}}{7x^{5}}$
$\frac{3x(x+1)}{x+4}$
$\frac{2x^{2}(x−3)}{x−1}$
$\frac{1}{5x−1}$
$\frac{x−2}{3x−2}$
$\frac{x−9}{5x(x−2)}$
$\frac{1}{(x−3)(x+6)}$
$\frac{x}{1−x^{2}}$
$\frac{x^{2}−9}{x^{2}−36}$
$\frac{1}{2x(x+3)(2x−1)}$
$\frac{x−3}{(3x−1)(2x+3)}$
$\frac{4x(2x+1)}{12x^{2}+x−1}$
$\frac{x−5}{3x^{2}−15x}$

Contestar

1. $x≠0$

3. $x≠−4$

5. $x≠\frac{1}{5}$

7. $x≠0$y$x≠2$

9. $x≠±1$

11. $x≠0$,$x≠−3$, y$x≠\frac{1}{2}$

13. $x≠−\frac{1}{3}$y$x≠\frac{1}{4}$

Ejercicio$\PageIndex{7}$ Simplifying Rational Expressions

Declarar las restricciones y luego simplificar.

$\frac{5x^{2}}{20x^{3}}$
$\frac{12x^{6}}{60x}$
$\frac{3x^{2}(x−2)}{9x(x−2)}$
$\frac{20(x−3)(x−5)}{6(x−3)(x+1)}$
$\frac{6x^{2}(x−8)}{36x(x+9)(x−8)}$
$\frac{16x^{2}−1}{(4x+1)^{2}}$
$\frac{9x^{2}−6x+1}{(3x−1)^{2}}$
$\frac{x−7}{x^{2}−49}$
$\frac{x^{2}−64}{x^{2}+8x}$
$\frac{x+10}{x^{2}−100}$
$\frac{2x^{3}−12x^{2}}{5x^{2}−30x}$
$\frac{30x^{5}+60x^{4}}{2x^{3}−8x}$
$\frac{2x−12}{x^{2}+x−6}$
$\frac{x^{2}−x−6}{3x^{2}−8x−3}$
$\frac{6x^{2}−25x+25}{3x^{2}+16x−35}$
$\frac{3x^{2}+4x−1}{5x^{2}−9}$
$\frac{x^{2}−10x+21}{x^{2}−4x−21}$
$\frac{x^{3}−1}{x^{2}−1}$
$\frac{x^{3}+8}{x^{2}−4}$
$\frac{x^{4}−1}{6x^{2}−4}$

Contestar

1. $\frac{1}{4x}; x≠0$

3. $\frac{x}{3}; x≠0, 2$

5. $\frac{x}{6(x+9)}; x≠0,−9, 8$

7. $1; x≠\frac{1}{3}$

9. $\frac{x−8}{x}; x≠0,−8$

11. $\frac{2x}{5}; x≠0, 6$

13. $\frac{2x−12}{x^{2}+x−6}\; x≠−2, \frac{3}{2}$

15. $\frac{2x−5}{x+7}; x≠−7, \frac{5}{3}$

17. $\frac{x−3}{x+3}; x≠−3, 7$

19. $\frac{x^{2}-2 x+4}{x-2} ; x≠±2$

Ejercicio$\PageIndex{8}$ Simplifying Rational Expressions with Opposite Binomial Factors

Declarar las restricciones y luego simplificar.

$\frac{x−9}{9−x}$
$\frac{3x−2}{2−3x}$
$\frac{x+6}{6+x}$
$\frac{3x+1}{1+3x}$
$\frac{(2x−5)(x−7)}{(7−x)(2x−1)}$
$\frac{(3x+2)(x+5)}{(x−5)(2+3x)}$
$\frac{x^{2}−4}{(2−x)^{2}}$
$\frac{16−9x^{2}}{(3x+4)^{2}}$
$\frac{4x^{2}(10−x)}{3x^{3}−300x}$
$−\frac{2x+1}{4x^{3}−49x}$
$\frac{2x^{2}−7x−4}{1−4x^{2}}$
$\frac{9x^{2}−4}{4x−6x^{2}}$
$\frac{x^{2}−5x−14}{7−15x+2x^{2}}$
$\frac{2x^{3}+x^{2}−2x−1}{1+x−2x^{2}}$
$\frac{x^{3}+2 x-3 x^{2}-6}{2+x^{2}}$
$\frac{27+x^{3}}{x^{2}+6x+9}$
$\frac{64−x^{3}}{x^{2}−8x+16}$
$\frac{x^{2}+4}{4−x^{2}}$

Contestar

1. $−1; x≠9 $

3. $1; x≠−6 $

5. $\frac{−2x−5}{2x−1}; x≠\frac{1}{2},7$

7. $\frac{x+2}{x−2}; x≠2$

9. $−\frac{4x}{3(x+10)}; x≠±10, 0$

11. $\frac{x−4}{1−2x}; x≠±\frac{1}{2}$

13. $\frac{x+2}{2x−1}; x≠\frac{1}{2},7$

15. $x−3$; ninguno

17. $\frac{−16+4x+x^{2}}{x−4}; x≠4$

Ejercicio$\PageIndex{9}$ Simplifying Rational Expressions with Opposite Binomial Factors

Simplificar. (Supongamos que todos los denominadores son distintos de cero.)

$−\frac{15x^{3}y^{2}}{5xy^{2}(x+y)}$
$\frac{14x^{7}y^{2}(x−2y)^{4}}{7x^{8}y(x−2y)^{2}}$
$\frac{y+x}{x^{2}−y^{2}}$
$\frac{y−x}{x^{2}−y^{2}}$
$\frac{x^{2}−y^{2}}{(x−y)^{2}}$
$\frac{a^{2}−ab−6b^{2}}{a^{2}−6ab+9b^{2}}$
$\frac{2a^{2}−11a+12}{−32+2a^{2}}$
$\frac{a^{2}b−3a^{2}}{3a^{2}−3ab}$
$\frac{x y^{2}-x+y^{3}-y}{x-x y^{2}}$
$\frac{x^{3}−xy^{2}−x^{2}y+y}{3x^{2}−2xy+y^{2}}$
$\frac{x^{3}−27}{x^{2}+3x+9}$
$\frac{x^{2}−x+1}{x^{3}+1}$

Contestar

1. $−\frac{3x^{2}}{x+y}$

3. $\frac{1}{x−y}$

5. $\frac{x+y}{x−y}$

7. $\frac{2 a-3}{2(a+4)}$

9. $-\frac{x+y}{x}$

11. $x−3$

Ejercicio$\PageIndex{10}$ Rational Functions

Calcula lo siguiente.

$f(x)=\frac{5x}{x−3}; f(0), f(2), f(4)$
$f(x)=\frac{x+7}{x^{2}+1}; f(−1), f(0), f(1) $
$g(x)=\frac{x^{3}}{(x−2)^{2}}; g(0), g(2), g(−2) $
$g(x)=\frac{x^{2}−9}{9−x^{2}}; g(−2), g(0), g(2) $
$g(x)=\frac{x^{3}}{x^{2}+1}; g(−1), g(0), g(1)$
$g(x)=\frac{5x+1}{x^{2}−25}; g(−\frac{1}{5}), g(−1), g(−5)$

Contestar

1. f (0) =0, f (2) =−10, f (4) =20

3. g (0) =0, g (2) indefinido, g (−2) =−$\frac{1}{2}$

5. g (−1) =−$\frac{1}{2}$, g (0) =0, g (1) =$\frac{1}{2}$

Ejercicio$\PageIndex{11}$ Rational Functions

Declarar las restricciones al dominio y luego simplificar.

$f(x)=−\frac{3x^{2}−6x}{x^{2}+4x+4}$
$f(x)=\frac{x^{2}+6x+9}{2x^{2}+5x−3 }$
$g(x)=\frac{9−x}{x^{2}−81}$
$g(x)=\frac{x^{3}−27}{3−x}$
$g(x)=\frac{3x−15}{10−2x}$
$g(x)=\frac{25−5x}{4x−20}$
El costo en dólares de producir tazas de café con el logotipo de una empresa viene dado por$C(x)=x+40$, donde x representa el número de tazas producidas. Calcular el costo promedio de producir 100 tazas y el costo promedio de producir 500 tazas.
El costo en dólares de rentar un camión de mudanza para el día viene dado por$C(x)=0.45x+90$, donde x representa el número de millas recorridas. Calcula el costo promedio por milla si el camión es conducido 250 millas en un día.
El costo en dólares de producir sudaderas con un diseño personalizado en la espalda viene dado por$C(x)=1200+(12−0.05x)x$, donde x representa el número de sudaderas producidas. Calcula el costo promedio de producir 150 sudaderas personalizadas.
El costo en dólares de producir una pieza moldeada inyectada personalizada viene dado por$C(x)=500+(3−0.001x)x$, donde x representa el número de piezas producidas. Calcular el costo promedio de producir 1,000 piezas personalizadas.

Contestar

1. $f(x)=−\frac{3x}{x+2}; x≠−2 $

3. $g(x)=−\frac{1}{x+9}; x≠±9 $

5. $g(x)=−\frac{3}{2}; x≠5 $

7. El costo promedio de producir 100 tazas es de $1.40 por taza. El costo promedio de producir 500 tazas es de $1.08 por taza.

9. $12.50

Ejercicio$\PageIndex{12}$ Discussion Board

Explique por qué$\frac{b−a}{a−b}=−1$ e ilustre este hecho sustituyendo algunas variables por números.
Explique por qué$\frac{b+a}{a+b}=1$ e ilustre este hecho sustituyendo algunas variables por números.
Explique por qué no podemos cancelar x en la expresión$\frac{x}{x+1}$.

Contestar

1. Las respuestas pueden variar

3. Las respuestas pueden variar

Search

Text Color

Text Size

Margin Size

Font Type

Simplificación de expresiones racionales

Factores Binomiales Opuestos

Funciones racionales

Claves para llevar