7.6: Aplicaciones de ecuaciones racionales
- Page ID
- 110084
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Objetivos de aprendizaje
- Resolver aplicaciones que involucran relaciones entre números reales.
- Resolver aplicaciones que implican movimiento uniforme (problemas de distancia).
- Resolver aplicaciones de tasa de trabajo.
Problemas numéricos
Recordemos que el recíproco de un número distinto de cero\(n\) es\(\frac{1}{n}\). Por ejemplo, el recíproco de\(5\) es\(\frac{1}{5}\) y\(5\cdot \frac{1}{5} = 1\). En esta sección, las aplicaciones a menudo involucrarán la palabra clave “recíproco”. Cuando este es el caso, veremos que la configuración algebraica da como resultado una ecuación racional.
Ejemplo\(\PageIndex{1}\)
Un entero positivo es\(4\) menor que otro. La suma de los recíprocos de los dos enteros positivos es\(\frac{10}{21}\). Encuentra los dos enteros.
Solución:
Comience asignando variables a las incógnitas.
Let\(n\) representar el entero positivo más grande.
Let\(n-4\) representa el entero positivo más pequeño.
A continuación, utilizar los recíprocos\(\frac{1}{n}\) y\(\frac{1}{n−4}\) traducir las oraciones en una ecuación algebraica.
\(\begin{array}{ccc}{\color{Cerulean} { the\:sum\:of\:the\:reciprocals }} & {\color{Cerulean} { is }} \\ {\qquad \frac{1}{n}+\frac{1}{n-4}} & {=} & {\frac{10}{21}}\end{array}\)
Podemos resolver esta expresión racional multiplicando ambos lados de la ecuación por el mínimo denominador común (LCD). En este caso, la pantalla LCD es\(21n(n−4)\).
\(\begin{array}{cl}{\frac{1}{n}+\frac{1}{n-4}=\frac{10}{21}}&{} \\ {\color{Cerulean}{21n(n-4)} \color{black}{\cdot \left(\frac{1}{n}+\frac{1}{n-4} \right)}=\color{Cerulean}{21n(n-4)}\color{black}{ \cdot\left(\frac{10}{21}\right)}}&{\color{Cerulean}{Multiply\:both\:sides}}\\{}&{\color{Cerulean}{by\:the\:LCD.}} \\ {\color{Cerulean}{21n (n-4)}\color{black}{ \cdot \frac{1}{n}+}\color{Cerulean}{21n (n-4)}\color{black}{ \cdot \frac{1}{n-4}}=\color{Cerulean}{21n (n-4)}\color{black}{ \cdot\left(\frac{10}{21}\right)}}&{\color{Cerulean}{Distribute\:and}}\\{}&{\color{Cerulean}{then\:cancel.}} \\ {21(n-4)+21n =10 n(n-4)}\end{array}\)
Resolver la ecuación cuadrática resultante.
\(\begin{array}{rlrl}{5 n-6} & {=0} & {\text { or }} & {n-7=0} \\ {5 n} & {=6} && {n=7} \\ {n} & {=\frac{6}{5}}\end{array}\)
La pregunta pide enteros y la única solución entera es\(n=7\). De ahí el desprecio\(\frac{6}{5}\). Usa la expresión\(n−4\) para encontrar el entero más pequeño.
\(n-4=7-4=3\)
Respuesta:
Los dos enteros positivos son\(3\) y\(7\). El cheque se deja al lector.
Ejemplo\(\PageIndex{2}\)
Un entero positivo es\(4\) menor que otro. Si el recíproco del entero más pequeño se resta del doble del recíproco del mayor, entonces el resultado es\(\frac{1}{30}\). Encuentra los dos enteros.
Solución:
Let\(n\) representar el entero positivo más grande.
Let\(n-4\) representa el entero positivo más pequeño.
Establecer una ecuación algebraica.
Resuelve esta expresión racional multiplicando ambos lados por la LCD. El LCD es\(30n(n−4)\).
\(\begin{aligned}\frac{2}{n}-\frac{1}{n-4}&=\frac{1}{30} \\ \color{Cerulean}{30 n(n-4)}\color{black}{ \cdot\left(\frac{2}{n}-\frac{1}{n-4}\right)}&=\color{Cerulean}{30 n(n-4)}\color{black}{ \cdot\left(\frac{1}{30}\right)} \\ \color{Cerulean}{30 n(n-4)}\color{black}{ \cdot \frac{2}{n}-}\color{Cerulean}{30 n(n-4)}\color{black}{ \cdot \frac{1}{n-4}}&=\color{Cerulean}{30 n(n-4)}\color{black}{ \cdot\left(\frac{1}{30}\right)}\end{aligned}\)
\(\begin{array}{rlrl}{n-10} & {=0 \quad \text { or }} & {n-24} & {=0} \\ {n} & {=10} & { n=24}\end{array}\)
Aquí tenemos dos posibilidades viables para el entero más grande. Por ello, vamos a tener dos soluciones a este problema.
Si\(n=10\), entonces\(n-4=10-4=6\).
Si\(n=24\), entonces\(n-4=24-4=20\).
A modo de comprobación, realizar las operaciones indicadas en el problema.
\(\begin{array}{r|r}{\text { Check } 6 \text { and } 10 .} &{\text{Check} \:20\:\text{and}\:24.}\\{2\left(\frac{1}{\color{OliveGreen}{10}}\right)-\frac{1}{\color{OliveGreen}{6}}=\frac{1}{5}-\frac{1}{6}}&{2\left(\frac{1}{\color{OliveGreen}{24}}\right)-\frac{1}{\color{OliveGreen}{20}}=\frac{1}{12}-\frac{1}{20}}\\{=\frac{6}{30}-\frac{5}{30}}&{=\frac{5}{60}-\frac{3}{60}}\\{=\frac{1}{30}\quad\color{Cerulean}{\checkmark}}&{=\frac{1}{30}\quad\color{Cerulean}{\checkmark}} \end{array}\)
Respuesta:
Dos conjuntos de enteros positivos resuelven este problema: {\(6, 10\)} y {\(20, 24\)}.
Ejercicio\(\PageIndex{1}\)
La diferencia entre los recíprocos de dos enteros impares positivos consecutivos es\(\frac{2}{15}\). Encuentra los enteros.
- Contestar
-
Los números enteros son\(3\) y\(5\).
Problemas de movimiento uniforme
Los problemas de movimiento uniforme, también conocidos como problemas de distancia, implican la fórmula
\[D=rt\]
donde la distancia,\(D\), se da como el producto de la tasa promedio,\(r\), y el tiempo,\(t\), recorrida a ese ritmo. Si dividimos ambos lados por la tasa promedio\(r\),, entonces obtenemos la fórmula
\[t=\frac{D}{r}\]
Por esta razón, cuando la cantidad desconocida es el tiempo, la configuración algebraica para problemas de distancia a menudo resulta en una ecuación racional. Del mismo modo, cuando la cantidad desconocida es la tasa, la configuración también puede resultar en una ecuación racional.
Comenzamos cualquier problema de movimiento uniforme organizando primero nuestros datos con un gráfico. Utilice esta información para configurar una ecuación algebraica que modele la aplicación.
Ejemplo\(\PageIndex{5}\)
Mary pasó las primeras 120 millas de su viaje por carretera en el tráfico. Cuando el tráfico se despejó, pudo conducir el doble de rápido durante las 300 millas restantes. Si el viaje total tardó 9 horas, entonces ¿qué tan rápido se movía en el tráfico?
Solución:
Primero, identificar la cantidad desconocida y organizar los datos.
\(x\)Representemos la velocidad promedio de Mary (millas por hora) en el tráfico.
Dejar\(2x\) representar su velocidad promedio después de que el tráfico se despejara.
.png)
Para evitar introducir dos variables más para la columna de tiempo, utilice la fórmula\(t=\frac{D}{r}\). Aquí el tiempo para cada tramo del viaje se calcula de la siguiente manera:
\(\begin{array}{c} {\color{Cerulean} { Time\:spent\:in\:traffic:}\:\:\color{black}{ t=\frac{D}{r}=\frac{120}{x}}} \\{\color{Cerulean}{Time\:clear\:of\:traffic:}\:\:\color{black}{t=\frac{D}{r}}=\frac{300}{2x}} \end{array}\)
Utilice estas expresiones para completar el gráfico.
.png)
La configuración algebraica está definida por la columna de tiempo. Suma los tiempos de cada tramo del viaje para obtener un total de 9 horas:
\(\begin{array}{ccccc}{\color{Cerulean}{time\:spent\:in\:traffic}}&{}&{\color{Cerulean}{time\:clear\:of\:traffic}}&{}&{\color{Cerulean}{total\:time\:of\:trip}} \\ {\overbrace{\frac{120}{x}}}&{+}&{\overbrace{\frac{300}{2x}}}&{=}&{\overbrace{9}} \end{array}\)
Comenzamos a resolver esta ecuación multiplicando primero ambos lados por la LCD,\(2x\).
\(\begin{aligned} \frac{120}{x}+\frac{300}{2 x} &=9 \\ \color{Cerulean}{2x }\color{black}{ \cdot\left(\frac{120}{x}+\frac{300}{2 x}\right)} &=\color{Cerulean}{2 x}\color{black}{ \cdot 9} \\ \color{Cerulean}{2 x}\color{black}{ \cdot \frac{120}{x}+}\color{Cerulean}{2 x}\color{black}{ \cdot \frac{300}{2 x}} &=\color{Cerulean}{2 x}\color{black}{ \cdot 9} \\ 240+300 &=18 x \\ 540 &=18 x \\ 30 &=x \end{aligned}\)
Respuesta:
Mary promedió 30 millas por hora en el tráfico.
Ejemplo\(\PageIndex{6}\)
Un tren de pasajeros puede viajar, en promedio,\(20\) millas por hora más rápido que un tren de carga. Si el tren de pasajeros cubre\(390\) millas al mismo tiempo que tarda el tren de carga en cubrir\(270\) millas, entonces ¿qué tan rápido es cada tren?
Solución:
Primero, identificar las cantidades desconocidas y organizar los datos.
Dejar\(x\) representar la velocidad promedio del tren de carga.
Dejar\(x+20\) representar la velocidad del tren de pasajeros.
A continuación, organice los datos dados en un gráfico.
.png)
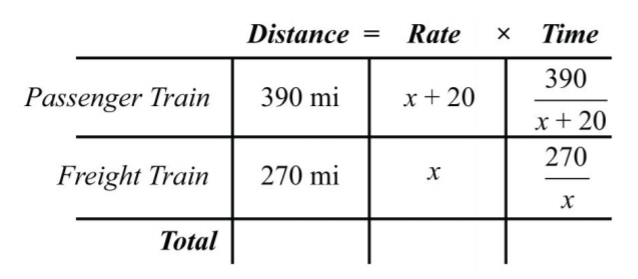
Usa la fórmula\(t=\frac{D}{r}\) para rellenar la columna de tiempo para cada tren.
\(\begin{array}{c} {\color{Cerulean} { Passenger\: train: }\:\:\color{black}{ t=\frac{D}{r}=\frac{390}{x+20}}} \\ {\color{Cerulean}{Freight\:train:}\:\:\color{black}{t=\frac{D}{r}=\frac{270}{x}}} \end{array}\)
.png)
Debido a que los trenes viajan la misma cantidad de tiempo, termina la configuración algebraica equiparando las expresiones que representan los tiempos:
\(\frac{390}{x+20}=\frac{270}{x}\)
Resolver esta ecuación multiplicando primero ambos lados por la LCD,\(x(x+20)\).
\(\begin{aligned} \color{Cerulean}{x(x+20)}\color{black}{ \cdot\left(\frac{390}{x+20}\right)} &=\color{Cerulean}{x(x+20)}\color{black}{ \cdot\left(\frac{270}{x}\right) }\\ 390 x &=270(x+20) \\ 390 x &=270 x+5400 \\ 120 x &=5400 \\ x &=45 \end{aligned}\)
Utilízalo\(x+20\) para encontrar la velocidad del tren de pasajeros.
\(x+20=\color{OliveGreen}{45}\color{black}{+20=65}\)
Respuesta:
La velocidad del tren de pasajeros es de\(65\) millas por hora y la velocidad del tren de carga es de\(45\) millas por hora.
Ejemplo\(\PageIndex{7}\)
Brett vive en el río\(8\) a millas río arriba de la ciudad. Cuando la corriente es de\(2\) millas por hora, puede remar su bote río abajo a la ciudad en busca de suministros y retroceder en\(3\) horas. ¿Cuál es su velocidad promedio de remo en agua sin gas?
Solución:
\(x\)Representemos la velocidad promedio de remo de Brett en agua sin gas.
Remando río abajo, la corriente aumenta su velocidad, y su tasa es de\(x + 2\) millas por hora. Remando aguas arriba, la corriente disminuye su velocidad, y su tasa es de\(x − 2\) millas por hora. Comience por organizar los datos en la siguiente tabla:
.png)
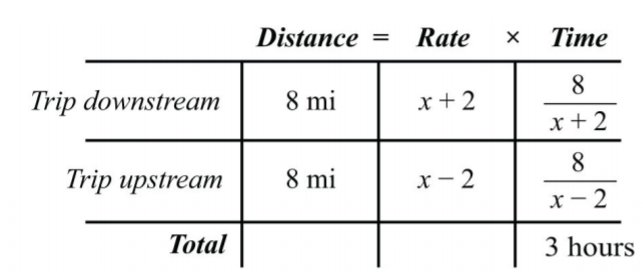
Usa la fórmula\(t=\frac{D}{r}\) para rellenar la columna de tiempo para cada tramo del viaje.
\(\begin{array}{c} {\color{Cerulean} { Trip\: downstream: } \:\:\color{black}{ t=\frac{D}{r}=\frac{8}{x+2}}}\\{\color{Cerulean}{Trip\:upstream:}\:\:\color{black}{t=\frac{D}{r}=\frac{8}{x-2}}} \end{array}\)
.png)
La configuración algebraica está definida por la columna de tiempo. Suma los tiempos de cada tramo del viaje para obtener un total de 3 horas:
\(\begin{array}{ccccc}{\color{Cerulean}{time\:rowing\:downstream}}&{}&{\color{Cerulean}{time\:rowing\:upstream}}&{}&{\color{Cerulean}{total\:time\:of\:trip}}\\{\overbrace{\frac{8}{x+2}}}&{+}&{\overbrace{\frac{8}{x-2}}}&{=}&{\overbrace{3}} \end{array}\)
Resolver esta ecuación multiplicando primero ambos lados por la LCD,\((x+2)(x−2)\).
A continuación, resolver la ecuación cuadrática resultante.
\(\begin{array}{rlrl}{3 x+2} & {=0} & {\text { or }} & {x-6=0} \\ {3 x} & {=-2} & {} & {x=6} \\ {x} & {=\frac{-2}{3}}\end{array}\)
Use solo la solución positiva,\(x=6\) millas por hora.
Respuesta:
Su velocidad de remo es de\(6\) millas por hora.
Ejercicio\(\PageIndex{2}\)
Dwayne condujo\(18\) millas hasta el aeropuerto para recoger a su padre y luego regresó a casa. En el viaje de regreso pudo conducir un promedio de\(15\) millas por hora más rápido que en el viaje allí. Si el tiempo total de manejo era de\(1\) hora, entonces ¿cuál era su velocidad promedio conduciendo al aeropuerto?
- Contestar
-
Su velocidad promedio al conducir al aeropuerto era de\(30\) millas por hora.
Problemas de tasa de trabajo
La velocidad a la que se puede realizar una tarea se denomina tasa de trabajo.
Ejemplo\(\PageIndex{8}\)
Por ejemplo, si un pintor puede pintar una habitación en 8 horas, entonces la tarea es pintar la habitación, y podemos escribir
\(\frac{1 \text { task }}{8 \text { hours }} \quad \color{Cerulean} { Work\: rate }\)
Es decir, el pintor puede completar\(\frac{1}{8}\) la tarea por hora.
Solución
Si trabaja menos de 8 horas, entonces realizará una fracción de la tarea. Por ejemplo,
\(\begin{array}{cc} {\color{Cerulean}{work\:rate}\color{black}{\times}\color{Cerulean}{time}\color{black}{=}\color{Cerulean}{work\:completed}}&{}\\{\frac{1}{8}\times 2\text{hrs}=\frac{1}{4}}&{\color{Cerulean}{One-quarter\:of\:the\:room\:painted}}\\{\frac{1}{8}\times 4\text{hrs}=\frac{1}{2}}&{\color{Cerulean}{One-half\:of\:the\:room\:painted}}\\{\frac{1}{8}\times 8\text{hrs}=1}&{\color{Cerulean}{One\:whole\:room\:painted}} \end{array}\)
Obtener la cantidad de la tarea completada multiplicando la tasa de trabajo por la cantidad de tiempo que trabaja el pintor. Por lo general, los problemas de tasa de trabajo involucran a personas que trabajan juntas para completar tareas. Cuando este es el caso, podemos organizar los datos en un gráfico, tal como lo hemos hecho con los problemas de distancia.
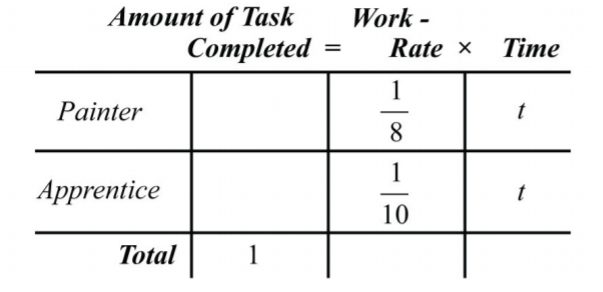
Supongamos que un aprendiz de pintor puede pintar la misma habitación solo en\(10\) horas. Entonces decimos que puede completar\(\frac{1}{10}\) la tarea por hora.
Vamos a\(t\) representar el tiempo que tardan los dos pintores, trabajando juntos, en pintar la habitación.
.png)
Para completar el gráfico, multiplique la tasa de trabajo por el tiempo para cada persona.
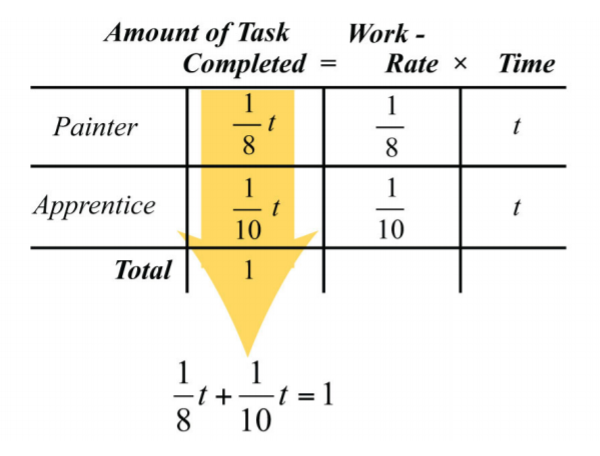
La porción de la habitación que cada uno puede pintar se suma a un total de\(1\) tarea completada.
Esto se representa por la ecuación obtenida de la primera columna del gráfico:
.png)
Esta configuración da como resultado una ecuación racional que puede resolverse\(t\) multiplicando ambos lados por la LCD,\(40\).
\(\begin{aligned} \frac{1}{8}t+\frac{1}{10}t &=1 \\ \color{Cerulean}{40}\color{black}{\cdot \left(\frac{1}{8}t+\frac{1}{10}t\right)}&=\color{Cerulean}{40}\color{black}{\cdot 1} \\ \color{Cerulean}{40}\color{black}{\cdot\frac{t}{8}+}\color{Cerulean}{40}\color{black}{\cdot\frac{t}{10}}&=\color{Cerulean}{40}\color{black}{\cdot 1}\\ 5t+4t &=40 \\ 9t & =40 \\ t & = \frac{40}{9} \\ t & = 4 \frac{4}{9} \end{aligned}\)
Por lo tanto, los dos pintores, trabajando juntos, completan la tarea en\(4 \frac{4}{9}\) horas.
En general, tenemos la siguiente fórmula de tasa de trabajo:
\[\frac{1}{t_{1}}t + \frac{1}{t_{2}}t = 1\]
Aquí\(\frac{1}{t_{1}}\) y\(\frac{1}{t_{2}}\) están las tasas de trabajo individuales y\(t\) es el tiempo que lleva completar una tarea trabajando juntos. Si facetamos el tiempo\(t\), y luego dividimos ambos lados por\(t\), obtenemos una fórmula equivalente de tasa de trabajo:
\(\begin{array}{c} {\frac{1}{t_{1}}t + \frac{1}{t_{2}}t = 1} \\ {t\left( \frac{1}{t_{1}}+\frac{1}{t_{2}} \right)=1} \\ {\frac{1}{t_{1}}+\frac{1}{t_{2}}=\frac{1}{t}} \end{array}\)
En resumen, tenemos las siguientes fórmulas equivalentes de tasa de trabajo:
\(\begin{array}{ccccc}{}&{}&{\color{Cerulean}{Work\:rate\:formulas:}}&{}&{} \\ {\frac{1}{t_{1}}t}&{\text{or}}&{\frac{t}{t_{1}}+\frac{t}{t_{2}}=1}&{\text{or}}&{\frac{1}{t_{1}}+\frac{1}{t_{2}}=\frac{1}{t}}\end{array}\)
Ejemplo\(\PageIndex{9}\)
Trabajando solo, el papá de Billy puede completar el trabajo de jardín en 3 horas. Si Billy ayuda a su papá, entonces el trabajo de jardín toma 2 horas. ¿Cuánto tiempo le tomaría a Billy trabajar solo para completar el trabajo de jardín?
Solución:
La información dada nos dice que el papá de Billy tiene una tasa de trabajo individual de\(\frac{1}{3}\) tarea por hora. Si dejamos\(x\) representar el tiempo que le toma a Billy trabajar solo para completar el trabajo de jardín, entonces la tasa de trabajo individual de Billy es\(\frac{1}{x}\), y podemos escribir
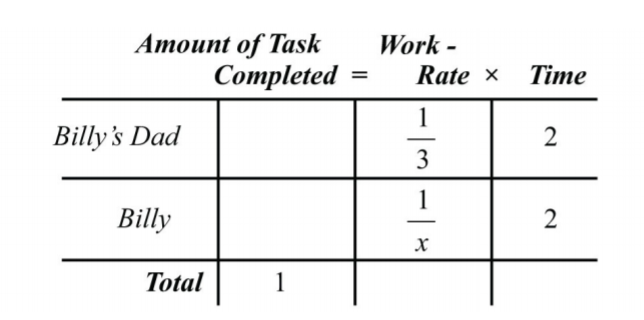.png)
Trabajando juntos, pueden completar la tarea en\(2\) horas. Multiplique las tarifas de trabajo individuales por\(2\) horas para rellenar la tabla.
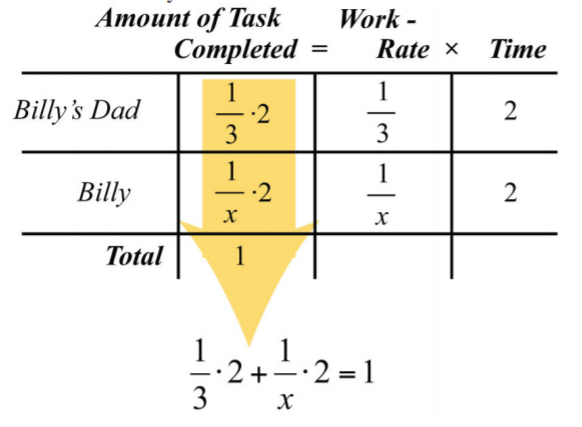.png)
El monto de la tarea que cada uno complete totalizará 1 tarea completada. Para resolver\(x\), primero multiplicamos ambos lados por la pantalla LCD,\(3x\).
\(\begin{aligned} \frac{1}{3}\cdot 2+\frac{1}{x}\cdot 2 &=1 \\ \color{Cerulean}{3x}\color{black}{\cdot \left(\frac{2}{3}+\frac{2}{x} \right)}&=\color{Cerulean}{3x}\color{black}{\cdot1} \\ \color{Cerulean}{3x}\color{black}{\cdot \frac{2}{3} +}\color{Cerulean}{3x}\color{black}{\cdot \frac{2}{x}}&=\color{Cerulean}{3x}\color{black}{\cdot 1} \\ 2x+6&=3x \\ 6&=x \end{aligned}\)
Respuesta:
A Billy le toma\(6\) horas completar el trabajo en el patio solo.
Por supuesto, la unidad de tiempo para la tasa de trabajo no necesita ser siempre en horas.
Ejemplo\(\PageIndex{10}\)
Trabajando juntos, dos equipos de construcción pueden construir un cobertizo en\(5\) días. Trabajando por separado, la tripulación menos experimentada tarda el doble en construir un cobertizo que la tripulación más experimentada. Trabajando por separado, ¿cuánto tiempo tarda cada tripulación en construir un cobertizo?
Solución:
Vamos a\(x\) representar el tiempo que lleva a la tripulación más experimentada construir un cobertizo.
Vamos a\(2x\) representar el tiempo que lleva a la tripulación menos experimentada construir un cobertizo.
Trabajando en conjunto, el trabajo se completa en\(5\) días. Esto da la siguiente configuración:
.png)
La primera columna del gráfico nos da una ecuación algebraica que modela el problema:
\(\begin{aligned} \frac{1}{x}\cdot 5+\frac{1}{2x}\cdot 5 &=1 \\ \frac{5}{x}+\frac{5}{2x}&=1 \end{aligned}\)
Resuelve la ecuación multiplicando ambos lados por\(2x\).
\(\begin{aligned} \color{Cerulean}{2x}\color{black}{\cdot \left(\frac{5}{x}+\frac{5}{2x} \right)}&=\color{Cerulean}{2x}\color{black}{\cdot 1}\\ \color{Cerulean}{2x}\color{black}{\cdot \frac{5}{x} +}\color{Cerulean}{2x}\color{black}{\cdot \frac{5}{2x}}&=\color{Cerulean}{2x}\color{black}{\cdot 1} \\ 10+5&=2x \\ 15&=2x \\ \frac{15}{2}&=x \quad\text{or}\quad x=7\frac{1}{2}\:\text{days} \end{aligned}\)
Para determinar el tiempo que tarda la tripulación menos experimentada, utilizamos\(2x\):
\(\begin{aligned} 2x&= 2\color{black}{\left(\color{OliveGreen}{\frac{15}{2}} \right) } \\ &= 15\:\text{days} \end{aligned}\)
Respuesta:
Trabajando por separado, la tripulación experimentada tarda\(7\frac{1}{2}\) días en construir un cobertizo, y la tripulación menos experimentada tarda\(15\) días en construir un cobertizo.
Ejercicio\(\PageIndex{3}\)
La manguera de jardín Joe's llena la piscina en\(12\) horas. Su vecino tiene una manguera más delgada que llena la alberca en\(15\) horas. ¿Cuánto tiempo tardará en llenar la piscina usando ambas mangueras?
- Contestar
-
Ambas mangueras tardarán\(6\frac{2}{3}\) horas en llenar la alberca.
Claves para llevar
- En esta sección se aplican todos los pasos señalados para resolver problemas generales de palabras. Busca la nueva palabra clave “recíproca”, que indica que debes escribir la cantidad en el denominador de una fracción con numerador\(1\).
- Al resolver problemas de distancia donde se desconoce el elemento tiempo, utilice la forma equivalente de la fórmula de movimiento uniforme\(t=\frac{D}{r}\),, para evitar introducir más variables.
- Al resolver problemas de tasa de trabajo, multiplique la tasa de trabajo individual por el tiempo para obtener la parte de la tarea completada. La suma de las porciones de la tarea da como resultado la cantidad total de trabajo completado.
Ejercicio\(\PageIndex{4}\) Number Problems
Utilice álgebra para resolver las siguientes aplicaciones.
- Un entero positivo es dos veces otro. La suma de los recíprocos de los dos enteros positivos es\(\frac{3}{10}\). Encuentra los dos enteros.
- Un entero positivo es dos veces otro. La suma de los recíprocos de los dos enteros positivos es\(\frac{3}{12}\). Encuentra los dos enteros.
- Un entero positivo es dos veces otro. La diferencia de los recíprocos de los dos enteros positivos es\(\frac{1}{8}\). Encuentra los dos enteros.
- Un entero positivo es dos veces otro. La diferencia de los recíprocos de los dos enteros positivos es\(\frac{1}{18}\). Encuentra los dos enteros.
- Un entero positivo es\(2\) menor que otro. Si la suma del recíproco del menor y el doble del recíproco del mayor es\(\frac{5}{12}\), entonces encuentra los dos enteros.
- Un entero positivo es\(2\) más que otro. Si la suma del recíproco del menor y el doble del recíproco del mayor es\(\frac{17}{35}\), entonces encuentra los dos enteros.
- La suma de los recíprocos de dos enteros pares positivos consecutivos es\(\frac{11}{60}\). Encuentra los dos enteros pares.
- La suma de los recíprocos de dos enteros impares positivos consecutivos es\(\frac{16}{63}\). Encuentra los enteros.
- La diferencia de los recíprocos de dos enteros pares positivos consecutivos es\(\frac{1}{24}\). Encuentra los dos enteros pares.
- La diferencia de los recíprocos de dos enteros impares positivos consecutivos es\(\frac{2}{99}\). Encuentra los enteros.
- Si\(3\) veces el recíproco del mayor de dos enteros consecutivos se resta de\(2\) veces el recíproco del menor, entonces el resultado es\(\frac{1}{2}\). Encuentra los dos enteros.
- Si\(3\) veces el recíproco del menor de dos enteros consecutivos se resta de\(7\) veces el recíproco del mayor, entonces el resultado es\(\frac{1}{2}\). Encuentra los dos enteros.
- Un entero positivo es\(5\) menor que otro. Si el recíproco del entero más pequeño se resta de\(3\) veces el recíproco del mayor, entonces el resultado es\(\frac{1}{12}\). Encuentra los dos enteros.
- Un entero positivo es\(6\) menor que otro. Si el recíproco del entero más pequeño se resta de\(10\) veces el recíproco del mayor, entonces el resultado es\(\frac{3}{7}\). Encuentra los dos enteros.
- Contestar
-
1. {\(5, 10\)}
3. {\(4, 8\)}
5. {\(6, 8\)}
7. {\(10, 12\)}
9. {\(6, 8\)}
11. {\(1, 2\)} o {\(−4, −3\)}
13. {\(4, 9\)} o {\(15, 20\)}
Ejercicio\(\PageIndex{5}\) Uniform Motion Problems
Utilice álgebra para resolver las siguientes aplicaciones.
- James puede trotar el doble de rápido que puede caminar. Pudo correr los primeros\(9\) kilómetros hasta la casa de su abuela, pero luego se cansó y caminó los\(1.5\) kilómetros restantes. Si el viaje total tardó\(2\) horas, entonces ¿cuál era su velocidad promedio de trote?
- En un viaje de negocios, un ejecutivo viajó\(720\) millas en avión a reacción y luego otras\(80\) millas en helicóptero. Si el jet promediaba\(3\) veces la velocidad del helicóptero y el viaje total tardaba\(4\) horas, entonces ¿cuál era la velocidad promedio del jet?
- Sally pudo conducir un promedio de\(20\) millas por hora más rápido en su automóvil después de que el tráfico se despejó. Condujo\(23\) millas en el tráfico antes de que despejara y luego condujo otros\(99\) kilómetros. Si el viaje total tardó\(2\) horas, entonces ¿cuál era su velocidad promedio en el tráfico?
- Harry viajó\(15\) millas en el autobús y luego otras\(72\) millas en un tren. Si el tren era\(18\) millas por hora más rápido que el autobús y el viaje total tardaba\(2\) horas, entonces ¿cuál era la velocidad promedio del tren?
- Un autobús promedia\(6\) millas por hora más rápido que un tranvía. Si el autobús recorre\(90\) millas en el mismo tiempo que toma el tranvía recorrer\(75\) millas, entonces, ¿cuál es la velocidad de cada uno?
- Un automóvil de pasajeros promedia\(16\) millas por hora más rápido que el autobús. Si el autobús recorre\(56\) millas en el mismo tiempo que tarda el carro de pasajeros en recorrer\(84\) millas, entonces, ¿cuál es la velocidad de cada uno?
- Un avión ligero viaja\(2\) millas por hora menos del doble de rápido que un automóvil de pasajeros. Si el automóvil de pasajeros puede recorrer\(231\) millas en el mismo tiempo que tarda la aeronave en recorrer\(455\) millas, entonces, ¿cuál es la velocidad promedio de cada uno?
- Mary puede correr\(1\) milla por hora más del doble de rápido que Bill puede caminar. Si Bill puede caminar\(3\) millas al mismo tiempo que le toma a Mary correr\(7.2\) millas, entonces, ¿cuál es la velocidad promedio de caminar de Bill?
- Un avión que viaja con viento de cola\(20\) de -milla por hora cubre\(270\) millas. En el viaje de regreso contra el viento, cubre\(190\) millas en la misma cantidad de tiempo. ¿Cuál es la velocidad del avión en el aire quieto?
- Un avión a reacción que viaja con viento de cola de\(30\) -milla por hora cubre\(525\) millas en la misma cantidad de tiempo que puede viajar\(495\) millas después de que el viento de cola se relaja a\(10\) millas por hora. ¿Cuál es la velocidad del avión en el aire quieto?
- Un barco promedia\(16\) millas por hora en agua sin gas. Con la corriente, el barco puede recorrer\(95\) millas al mismo tiempo que recorre\(65\) millas en su contra. ¿Cuál es la velocidad de la corriente?
- Un barco turístico por el río promedia\(7\) millas por hora en agua sin gas. Si el recorrido total\(24\) de millas río abajo y\(24\) millas atrás lleva\(7\) horas, entonces, ¿qué tan rápido es la corriente del río?
- Si la corriente del río fluye a un promedio de\(3\) millas por hora, entonces un bote turístico hace el recorrido\(9\) de millas aguas abajo con la corriente y retrocede las\(9\) millas contra la corriente en\(4\) horas. ¿Cuál es la velocidad promedio de la embarcación en aguas sin gas?
- Jane remó su canoa contra una\(1\) milla por hora corriente arriba\(12\) millas y luego regresó las\(12\) millas río abajo. Si el viaje total tardó\(5\) horas, entonces ¿a qué velocidad puede Jane remar en agua sin gas?
- José condujo\(15\) millas para recoger a su hermana y luego regresó a su casa. En el viaje de regreso, pudo promediar\(15\) millas por hora más rápido que en el viaje para recogerla. Si el viaje total tardó\(1\) una hora, entonces ¿cuál era la velocidad promedio de José en el viaje de regreso?
- Barry condujo los\(24\) kilómetros hasta la ciudad y luego regresó en\(1\) una hora. En el viaje de regreso, pudo promediar\(14\) millas por hora más rápido de lo que promedió en el viaje a la ciudad. ¿Cuál fue su velocidad promedio en el viaje a la ciudad?
- Jerry remó su kayak río arriba contra una corriente de\(1\) -milla por hora durante\(12\) millas. El viaje de regreso aguas abajo con la corriente\(1\) de -milla por hora tomó\(1\) hora menos tiempo. ¿Qué tan rápido puede Jerry remar el kayak en agua sin gas?
- Se necesita una\(1\) hora de avión ligero más tiempo para volar\(360\) millas contra un\(30\) viento de cabeza de milla por hora que volar a la misma distancia con él. ¿Cuál es la velocidad de la aeronave en aire tranquilo?
- Contestar
-
1. \(6\)millas por hora
3. \(46\)millas por hora
5. Trolley:\(30\) millas por hora; autobús:\(36\) millas por hora
7. Automóvil de pasajeros:\(66\) millas por hora; avión:\(130\) millas por hora
9. \(115\)millas por hora
11. \(3\)millas por hora
13. \(6\)millas por hora
15. \(40\)millas por hora
17. \(5\)millas por hora
Ejercicio\(\PageIndex{6}\) Work-Rate Problems
Utilice álgebra para resolver las siguientes aplicaciones.
- James puede pintar la oficina solo en\(7\) horas. Manny pinta la oficina en\(10\) horas. ¿Cuánto tiempo les llevará pintar la oficina trabajando juntos?
- Barry puede poner un camino de entrada de ladrillos solo en\(12\) horas. Robert hace el mismo trabajo en\(10\) horas. ¿Cuánto tiempo les llevará colocar la entrada de ladrillos trabajando juntos?
- Jerry puede detallar un auto solo en\(50\) minutos. Sally hace el mismo trabajo en\(1\) horas. ¿Cuánto tiempo les llevará detallar un auto trabajando juntos?
- José puede construir un pequeño cobertizo solo en\(26\) horas. Alex construye el mismo pequeño cobertizo en\(2\) días. ¿Cuánto tiempo les llevaría construir el cobertizo trabajando juntos?
- Allison puede completar una ruta de ventas por sí misma en\(6\) horas. Trabajando con una asociada, ella completa la ruta en\(4\) horas. ¿Cuánto tiempo tardaría su asociada en completar la ruta por sí misma?
- James puede preparar y pintar una casa solo en\(5\) días. Trabajando con su hermano, Bryan, pueden hacerlo en\(3\) días. ¿Cuánto tiempo le tomaría a Bryan preparar y pintar la casa solo?
- Joe puede armar una computadora por sí mismo en\(1\) horas. Al trabajar con un asistente, puede armar una computadora en\(40\) cuestión de minutos. ¿Cuánto tiempo le tomaría a su asistente armar una computadora trabajando solo?
- El asistente del maestro puede calificar las tareas de clase por sí misma en\(1\) horas. Si el profesor ayuda, entonces la calificación se puede completar en\(20\) minutos. ¿Cuánto tiempo tardaría el profesor en calificar los trabajos trabajando solo?
- Una tubería más grande llena un tanque de agua dos veces más rápido que una tubería más pequeña. Cuando se utilizan ambas tuberías, llenan el tanque en\(5\) horas. Si se deja la tubería más grande, entonces ¿cuánto tiempo tardaría la tubería más pequeña en llenar el tanque?
- Una impresora más nueva puede imprimir el doble de rápido que una impresora más antigua. Si ambas impresoras que trabajan juntas pueden imprimir un lote de volantes en\(45\) minutos, entonces, ¿cuánto tiempo tardaría la impresora más nueva en imprimir el lote trabajando sola?
- Trabajando solo, Henry tarda\(9\) horas más que Mary en limpiar las alfombras de toda la oficina. Trabajando juntos, limpian las alfombras en\(6\) horas. ¿Cuánto tiempo le tomaría a Mary limpiar las alfombras de la oficina si Henry no estuviera ahí para ayudar?
- Trabajando sola, Monique tarda\(4\) horas más que Audrey en registrar el inventario de toda la tienda. Trabajando juntos, hacen inventario en\(1.5\) horas. ¿Cuánto tardaría Audrey en registrar el inventario trabajando sola?
- Jerry puede poner un piso de baldosas en\(3\) horas menos tiempo que Jake. Si trabajan juntos, el uso de la palabra toma\(2\) horas. ¿Cuánto tardaría Jerry en poner la palabra solo?
- Jeremy puede construir un avión modelo en\(5\) horas menos tiempo que su hermano. Trabajando juntos, necesitan\(6\) horas para construir el avión. ¿Cuánto tiempo le tomaría a Jeremy construir el modelo de avión trabajando solo?
- Harry puede pintar un cobertizo solo en\(6\) horas. Jeremy puede pintar el mismo cobertizo solo en\(8\) horas. ¿Cuánto tiempo les llevará pintar dos cobertizos trabajando juntos?
- Joe ensambla una computadora por sí mismo en\(1\) horas. Al trabajar con un asistente, puede armar\(10\) computadoras en\(6\) horas. ¿Cuánto tiempo le tomaría a su asistente armar\(1\) computadora trabajando solo?
- Jerry puede poner un piso de baldosas en\(3\) horas, y su asistente puede hacer el mismo trabajo en\(4\) horas. Si Jerry inicia el trabajo y su asistente se une a él 1 hora después, entonces ¿cuánto tiempo tardará en poner el piso?
- Trabajando sola, Monique tarda\(6\) horas en registrar el inventario de toda la tienda, mientras que Audrey tarda solo\(4\) horas en hacer el mismo trabajo. ¿Cuánto tiempo les llevará trabajar juntos si Monique se va\(2\) horas antes?
- Contestar
-
1. \(4 \frac{2}{17}\)horas
3. \(27 \frac{3}{11}\)minutos
5. \(12\)horas
7. \(2\)horas
9. \(15\)horas
11. \(9\)horas
13. \(3\)horas
15. \(6\frac{6}{7}\)horas
17. \(2 \frac{1}{7}\)horas


