8.4: Multiplicar y dividir expresiones radicales
- Page ID
- 110121
Objetivos de aprendizaje
- Multiplicar expresiones radicales.
- Dividir expresiones radicales.
- Racionalizar el denominador.
Multiplicar expresiones radicales
Al multiplicar expresiones radicales con el mismo índice, usamos la regla de producto para radicales. Si a y b representan números reales positivos,
\[\sqrt[n]{a} \cdot \sqrt[n]{b}=\sqrt[n]{a \cdot b}\]
Ejemplo\(\PageIndex{1}\)
Multiplicar:
\(\sqrt{2} \cdot \sqrt{6}\)
Solución:
Este problema es producto de dos raíces cuadradas. Aplica la regla del producto para los radicales y luego simplifica.
\(\begin{aligned} \sqrt{2} \cdot \sqrt{6} &=\sqrt{2 \cdot 6}\qquad\color{Cerulean}{Multiply\:the\:radicands.} \\ &=\sqrt{12}\qquad\:\:\:\color{Cerulean}{Simplify.} \\ &=\sqrt{2^{2} \cdot 3} \\ &=2 \sqrt{3} \end{aligned}\)
Respuesta:
\(2\sqrt{3}\)
Ejemplo\(\PageIndex{2}\)
Multiplicar:
\(\sqrt[3]{9} \cdot \sqrt[3]{6}\)
Solución:
Este problema es producto de las raíces cubicas. Aplica la regla del producto para los radicales y luego simplifica.
\(\begin{aligned} \sqrt[3]{9} \cdot \sqrt[3]{6} &=\sqrt[3]{9 \cdot 6}\qquad\color{Cerulean}{Multiply\:the\:radiands.} \\ &=\sqrt[3]{54}\qquad\:\color{Cerulean}{Simplify.} \\ &=\sqrt[3]{3^{3} \cdot 2} \\ &=3 \sqrt[3]{2} \end{aligned}\)
Respuesta:
\(3\sqrt[3]{2}\)
A menudo habrá coeficientes frente a los radicales.
Ejemplo\(\PageIndex{3}\)
Multiplicar:
\(2 \sqrt{3} \cdot 5 \sqrt{2}\)
Solución:
Usando la regla del producto para los radicales y el hecho de que la multiplicación es conmutativa, podemos multiplicar los coeficientes y los radicandos de la siguiente manera.
\(\begin{aligned} 2 \sqrt{3} \cdot 5 \sqrt{2} &=2 \cdot 5 \cdot \sqrt{3} \cdot \sqrt{2}\qquad\color{Cerulean}{Multiplication\:is\:commutative.} \\ &=10 \cdot \sqrt{6}\qquad\qquad\:\:\:\color{Cerulean}{Multiply\:the\:coefficients\:and\:the\:radicands.} \\ &=10 \sqrt{6} \end{aligned}\)
Por lo general, no se muestra el primer paso que implica la aplicación de la propiedad conmutativa.
Respuesta:
\(10\sqrt{6}\)
Ejemplo\(\PageIndex{4}\)
Multiplicar:
Solución:
Respuesta:
\(-30x\)
Utilice la propiedad distributiva al multiplicar expresiones racionales con más de un término.
Ejemplo\(\PageIndex{5}\)
Multiplicar:
Solución:
Aplicar la propiedad distributiva y multiplicar cada término por\(4\sqrt{3}\).
Respuesta:
Ejemplo\(\PageIndex{6}\)
Multiplicar:
Solución:
Aplicar la propiedad distributiva y luego simplificar el resultado.
Respuesta:
El proceso para multiplicar expresiones radicales con múltiples términos es el mismo proceso que se utiliza al multiplicar polinomios. Aplicar la propiedad distributiva, simplificar cada radical, y luego combinar términos similares.
Ejemplo\(\PageIndex{7}\)
Multiplicar:
\((\sqrt{5}+2)(\sqrt{5}-4)\)
Solución:
Comience por aplicar la propiedad distributiva.
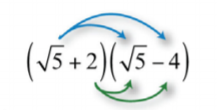.png)
Respuesta:
\(-3-2\sqrt{5}\)
Ejemplo\(\PageIndex{8}\)
Multiplicar:
\((3 \sqrt{x}-\sqrt{y})^{2}\)
Solución:
Respuesta:
\(9x-6\sqrt{xy}+y\)
Ejercicio\(\PageIndex{1}\)
Multiplicar:
\((2\sqrt{3}+5\sqrt{2})(\sqrt{3}-2\sqrt{6})\)
- Responder
-
\(6-12\sqrt{2}+5\sqrt{6}-20\sqrt{3}\)
Las expresiones\((a+b)\) y\((a−b)\) se llaman conjugados. Al multiplicar conjugados, la suma de los productos de los términos interno y externo resulta en 0.
Ejemplo\(\PageIndex{9}\)
Multiplicar:
\((\sqrt{2}+\sqrt{5})(\sqrt{2}-\sqrt{5})\)
Solución:
Aplicar la propiedad distributiva y luego combinar términos similares.
Respuesta:
\(-3\)
Es importante señalar que al multiplicar expresiones radicales conjugadas, obtenemos una expresión racional. Esto es cierto en general y es de uso frecuente en nuestro estudio del álgebra.
\(\begin{aligned}(\sqrt{a}+\sqrt{b})(\sqrt{a}-\sqrt{b}) &=\sqrt{a^{2}}-\sqrt{a b}+\sqrt{a b}-\sqrt{b^{2}} \\ &=a-b \end{aligned}\)
Por lo tanto, para los números reales no negativos a y b, tenemos la siguiente propiedad:
\[(\sqrt{a}+\sqrt{b})(\sqrt{a}-\sqrt{b})=a-b\]
Dividir expresiones radicales (racionalizar el denominador)
Para dividir expresiones radicales con el mismo índice, usamos la regla del cociente para los radicales. Si a y b representan números no negativos, donde\(b≠0\), entonces tenemos
\[\frac{\sqrt[n]{a}}{\sqrt[n]{b}}=\sqrt[n]{\frac{a}{b}}\]
Ejemplo\(\PageIndex{10}\)
Dividir:
\(\frac{\sqrt{80}}{\sqrt{10}}\)
Solución:
En este caso, podemos ver que 10 y 80 tienen factores comunes. Si aplicamos la regla del cociente para los radicales y la escribimos como una sola raíz cuadrada, podremos reducir el radicado fraccional.
\(\begin{aligned} \frac{\sqrt{80}}{\sqrt{10}} &=\sqrt{\frac{80}{10}}\qquad\color{Cerulean}{Apply\:the\:quotient\:rule\:for\:radicals\:and\:reduce\:the\:radicand.} \\ &=\sqrt{8}\qquad\quad\color{Cerulean}{Simplify.} \\ &=\sqrt{4 \cdot 2} \\ &=2 \sqrt{2} \end{aligned}\)
Respuesta:
\(2\sqrt{2}\)
Ejemplo\(\PageIndex{11}\)
Dividir:
\(\frac{\sqrt{16 x^{5} y^{4}}}{\sqrt{2 x y}}\)
Solución:
\(\begin{aligned} \frac{\sqrt{16 x^{5} y^{4}}}{\sqrt{2 x y}} &=\sqrt{\frac{16 x^{5} y^{4}}{2 x y}} \qquad\qquad\qquad\color{Cerulean}{Apply\:the\:quotient\:rule\:for\:radicals\:and\:cancel.}\\ &=\sqrt{8 x^{4} y^{3}} \qquad\qquad\qquad\quad\color{Cerulean}{Simplify.}\\ &=\sqrt{4 \cdot 2 \cdot\left(x^{2}\right)^{2} \cdot y^{2} \cdot y} \\ &=2 x^{2} y \sqrt{2 y} \end{aligned}\)
Respuesta:
\(2 x^{2} y \sqrt{2 y}\)
Ejemplo\(\PageIndex{12}\)
Dividir:
\(\frac{\sqrt[3]{54 a^{3} b^{5}}}{\sqrt[3]{16 a^{2} b^{2}}}\)
Solución:
\(\begin{aligned}\frac{\sqrt[3]{54a^{3}b^{5}}}{\sqrt[3]{16a^{2}b^{2}}} &=\sqrt[3]{\frac{54 \cdot a^{3} b^{5}}{16 a^{2} b^{2}}}\qquad\color{Cerulean}{Apply\:the\:quotient\:rule\:for\:radicals\:and\:then\:cancel.} \\ &=\sqrt[3]{\frac{27 a b^{3}}{8}}\qquad\:\:\:\color{Cerulean}{Replace\:27\:and\:8\:with\:their\:prime\:factorizations.} \\&=\sqrt[3]{\frac{3^{3}ab^{3}}{2^{3}}}\qquad\:\:\:\color{Cerulean}{Simplify.} \\&=\frac{\sqrt[3]{3^{3}ab^{3}}}{\sqrt[3]{2^{3}}} \\&=\frac{3b\sqrt[3]{a}}{2}\end{aligned}\)
Respuesta:
\(\frac{3 b \sqrt[3]{a}}{2}\)
Cuando el divisor de una expresión radical contiene un radical, es una práctica común encontrar una expresión equivalente donde el denominador es un número racional. Encontrar tal expresión equivalente se llama racionalizar el denominador.
\(\begin{aligned}\color{Cerulean}{ Radical} &\:\color{Cerulean}{expression} &\color{Cerulean}{ Rational}& \:\color{Cerulean}{denominator} \\ &\frac{1}{\sqrt{3}} &=&\frac{\sqrt{3}}{3} \end{aligned}\)
Para ello, multiplica la fracción por una forma especial de 1 para que el radicando en el denominador pueda escribirse con una potencia que coincida con el índice. Después de hacer esto, simplificar y eliminar el radical en el denominador. Por ejemplo,
\(\frac{1}{\sqrt{3}}=\frac{1}{\sqrt{3}} \cdot \color{Cerulean}{\frac{\sqrt{3}}{\sqrt{3}}}\color{black}{=}\frac{\sqrt{3}}{\sqrt{3^{2}}}=\frac{\sqrt{3}}{3}\)
Recuerda, para obtener una expresión equivalente, debes multiplicar el numerador y el denominador por exactamente el mismo factor distinto de cero.
Ejemplo\(\PageIndex{13}\)
Racionalizar el denominador:
\(\frac{\sqrt{3}}{\sqrt{2}}\)
Solución:
El objetivo es encontrar una expresión equivalente sin un radical en el denominador. En este ejemplo, multiplique por 1 en la forma\(\color{Cerulean}{\frac{\sqrt{2}}{\sqrt{2}}}\).
\(\begin{aligned} \frac{\sqrt{3}}{\sqrt{2}} &=\frac{\sqrt{3}}{\sqrt{2}} \cdot\color{Cerulean}{ \frac{\sqrt{2}}{\sqrt{2}}}\qquad\color{Cerulean}{Multiply\:by\:\frac{\sqrt{2}}{\sqrt{2}}.} \\ &=\frac{\sqrt{6}}{\sqrt{2^{2}}}\qquad\qquad\color{Cerulean}{Simplify.} \\ &=\frac{\sqrt{6}}{2}\qquad\qquad\:\color{Cerulean}{Rational\:denominator.} \end{aligned}\)
Respuesta:
\(\frac{\sqrt{6}}{2}\)
Ejemplo\(\PageIndex{14}\)
Racionalizar el denominador:
\(\frac{1}{2 \sqrt{3 x}}\)
Solución:
El radicando en el denominador determina los factores que se necesitan utilizar para racionalizarlo. En este ejemplo, multiplique por 1 en la forma\(\frac{1}{2 \sqrt{3 x}}\).
\(\begin{aligned} \frac{1}{2 \sqrt{3 x}} &=\frac{1}{2 \sqrt{3 x}} \cdot \color{Cerulean}{ \frac{\sqrt{3 x}}{\sqrt{3 x}}}\qquad\color{Cerulean}{Multiply\:by\:\frac{\sqrt{3x}}{\sqrt{3x}}.} \\ &=\frac{\sqrt{3 x}}{2 \sqrt{3^{2} x^{2}}}\qquad\qquad\color{Cerulean}{Simplify.} \\ &=\frac{\sqrt{3 x}}{2 \cdot 3 x} \\ &=\frac{\sqrt{3 x}}{6 x} \end{aligned}\)
Respuesta:
\(\frac{\sqrt{3 x}}{6 x}\)
Normalmente, encontraremos la necesidad de reducir, o cancelar, después de racionalizar el denominador.
Ejemplo\(\PageIndex{15}\)
Racionalizar el denominador:
\(\frac{5 \sqrt{2}}{\sqrt{5 a b}}\)
Solución
En este ejemplo, vamos a multiplicar por 1 en la forma\(\frac{\sqrt{5 a b}}{\sqrt{5 a b}}\).
\(\begin{aligned} \frac{5 \sqrt{2}}{\sqrt{5 a b}} &=\frac{5 \sqrt{2}}{\sqrt{5 a b}} \cdot \color{Cerulean}{\frac{\sqrt{5 a b}}{\sqrt{5 a b}}} \\ &=\frac{5 \sqrt{10 a b}}{\sqrt{25 a^{2} b^{2}}}\qquad\quad\color{Cerulean}{Simplify.} \\ &=\frac{5 \sqrt{10 a b}}{5 a b}\qquad\quad\:\color{Cerulean}{Cancel.} \\ &=\frac{\sqrt{10 a b}}{a b} \end{aligned}\)
Observe que a y b no cancelan en este ejemplo. No canceles factores dentro de un radical con los que están afuera.
Respuesta:
\(\frac{\sqrt{10 a b}}{a b}\)
Ejercicio\(\PageIndex{2}\)
Racionalizar el denominador:
\(\sqrt{\frac{4a}{3b}}\)
- Responder
-
\(\frac{2\sqrt{3ab}}{3b}\)
Hasta este punto, hemos visto que multiplicar un numerador y un denominador por una raíz cuadrada con exactamente el mismo radicando da como resultado un denominador racional. En general, esto es cierto sólo cuando el denominador contiene una raíz cuadrada. Sin embargo, este no es el caso de una raíz cubo. Por ejemplo,
\(\frac{1}{\sqrt[3]{x}} \cdot\color{Cerulean}{ \frac{\sqrt[3]{x}}{\sqrt[3]{x}}}\color{black}{=}\frac{\sqrt[3]{x}}{\sqrt[3]{x^{2}}}\)
Obsérvese que multiplicar por el mismo factor en el denominador no lo racionaliza. En este caso, si multiplicamos por 1 en forma de\(\frac{\sqrt[3]{x^{2}}}{\sqrt[3]{x^{2}}}\), entonces podemos escribir el radicando en el denominador como una potencia de 3. Al simplificar el resultado se obtiene un denominador racionalizado. Por ejemplo,
\(\frac{1}{\sqrt[3]{x}}=\frac{1}{\sqrt[3]{x}} \cdot \color{Cerulean}{\frac{\sqrt[3]{x^{2}}}{\sqrt[3]{x^{2}}}}\color{black}{=}\frac{\sqrt[3]{x^{2}}}{\sqrt[3]{x^{3}}}=\frac{\sqrt[3]{x^{2}}}{x}\)
Por lo tanto, para racionalizar el denominador de expresiones radicales con un término radical en el denominador, comienza por factorizar el radicando del denominador. Los factores de este radicando y el índice determinan por qué debemos multiplicar. Multiplique el numerador y el denominador por la raíz n ésima de factores que producen n poderes de todos los factores en el radicando del denominador.
Ejemplo\(\PageIndex{16}\)
Racionalizar el denominador:
\(\frac{1}{\sqrt[3]{25}}\)
Solución:
El radical en el denominador es equivalente a\(\sqrt[3]{5^{2}}\). Para racionalizar el denominador, debería serlo\(\sqrt[3]{5^{3}}\). Para obtener esto, necesitamos un factor más de 5. Por lo tanto, multiplicar por 1 en forma de\(\frac{\sqrt[3]{5}}{\sqrt[3]{5}}\).
\(\begin{aligned} \frac{1}{\sqrt[3]{25}} &=\frac{1}{\sqrt[3]{5^{2}}} \cdot\color{Cerulean}{ \frac{\sqrt[3]{5}}{\sqrt[3]{5}}}\qquad\color{Cerulean}{Multiply\:by\:the\:cube\:root\:of\:factors\:that\:result\:in\:powers\:of\:3.} \\ &=\frac{\sqrt[3]{5}}{\sqrt[3]{5^{3}}}\qquad\qquad\:\:\color{Cerulean}{Simplify.} \\ &=\frac{\sqrt[3]{5}}{5} \end{aligned}\)
Respuesta:
\(\frac{\sqrt[3]{5}}{5}\)
Ejemplo\(\PageIndex{17}\)
Racionalizar el denominador:
\(\sqrt[3]{\frac{27 a}{2 b^{2}}}\)
Solución:
En este ejemplo, vamos a multiplicar por 1 en la forma\(\frac{\sqrt[3]{2^{2} b}}{\sqrt[3]{2^{2} b}}\).
\(\begin{aligned} \sqrt[3]{\frac{27 a}{2 b^{2}}} &=\frac{\sqrt[3]{3^{3} a}}{\sqrt[3]{2 b^{2}}}\qquad\qquad\quad\color{Cerulean}{Apply\:the\:quotient\:rule\:for\:radicals.} \\ &=\frac{3 \sqrt[3]{a}}{\sqrt[3]{2 b^{2}}} \cdot\color{Cerulean}{ \frac{\sqrt[3]{2^{2} b}}{\sqrt[3]{2^{2} b}}} \quad\:\:\:\color{Cerulean}{Multiply\:by\:the\:cube\:root\:of\:factors\:that\:result\:in\:powers\:of\:3.}\\ &=\frac{3 \sqrt[3]{2^{2} a b}}{\sqrt[3]{2^{3} b^{3}}}\qquad\qquad\color{Cerulean}{Simplify.} \\ &=\frac{3 \sqrt[3]{4 a b}}{2 b} \end{aligned}\)
Respuesta:
\(\frac{3 \sqrt[3]{4 a b}}{2 b}\)
Ejemplo\(\PageIndex{18}\)
Racionalizar el denominador:
\(\frac{1}{\sqrt[5]{4 x^{3}}}\)
Solución:
En este ejemplo, vamos a multiplicar por 1 en la forma\(\frac{\sqrt[5]{2^{3} x^{2}}}{\sqrt[5]{2^{3} x^{2}}}\).
\(\begin{aligned} \frac{1}{\sqrt[5]{4 x^{3}}} &=\frac{1}{\sqrt[5]{2^{2} x^{3}}} \cdot \color{Cerulean}{\frac{\sqrt[5]{2^{3} x^{2}}}{\sqrt[5]{2^{3} x^{2}}}}\qquad\color{Cerulean}{Multiply\:by\:the\:fifth\:root\:of\:factors\:that\:result\:in\:powers\:of\:5.} \\ &=\frac{\sqrt[5]{2^{3} x^{5}}}{\sqrt[5]{2^{5} x^{5}}}\qquad\qquad\qquad\color{Cerulean}{Simplify.} \\ &=\frac{\sqrt[5]{8 x^{2}}}{2 x} \end{aligned}\)
Respuesta:
\(\frac{\sqrt[5]{8 x^{2}}}{2 x}\)
Cuando dos términos que involucran raíces cuadradas aparecen en el denominador, podemos racionalizarlo usando una técnica muy especial. Esta técnica implica multiplicar el numerador y el denominador de la fracción por el conjugado del denominador. Recordemos que multiplicar una expresión radical por su conjugado produce un número racional.
Ejemplo\(\PageIndex{19}\)
Racionalizar el denominador:
\(\frac{1}{\sqrt{3}-\sqrt{2}}\)
Solución:
En este ejemplo, el conjugado del denominador es\(\sqrt{3}+\sqrt{2}\). Por lo tanto, multiplicar por 1 en la forma\(\frac{(\sqrt{3}+\sqrt{2})}{(\sqrt{3}+\sqrt{2})}\).
\(\begin{aligned} \frac{1}{\sqrt{3}-\sqrt{2}} &=\frac{1}{(\sqrt{3}-\sqrt{2})}\color{Cerulean}{ \frac{(\sqrt{3}+\sqrt{2})}{(\sqrt{3}+\sqrt{2})}}\qquad\color{Cerulean}{Multiply\:numerator\:and\:denominator\:by\:the\:conjugate\:of\:the\:denominator.} \\ &=\frac{\sqrt{3}+\sqrt{2}}{\sqrt{9}+\sqrt{6}-\sqrt{6}-\sqrt{4}}\qquad\:\:\:\color{Cerulean}{Simplify.} \\ &=\frac{\sqrt{3}+\sqrt{2}}{3-2} \\ &=\frac{\sqrt{3}+\sqrt{2}}{1} \\ &=\sqrt{3}+\sqrt{2} \end{aligned}\)
Respuesta:
\(\sqrt{3}+\sqrt{2}\)
Observe que los términos que involucran la raíz cuadrada en el denominador se eliminan multiplicando por el conjugado. Podemos utilizar la propiedad\(\frac{(\sqrt{a}+\sqrt{b})}{(\sqrt{a}-\sqrt{b})}=a-b\) para agilizar el proceso de multiplicar las expresiones en el denominador.
Ejemplo\(\PageIndex{20}\)
Racionalizar el denominador:
\(\frac{\sqrt{2}-\sqrt{6}}{\sqrt{2}+\sqrt{6}}\)
Solución:
Multiplicar por 1 en la forma\(\frac{(\sqrt{2}-\sqrt{6})}{(\sqrt{2}-\sqrt{6})}\)
Respuesta:
\(-2+\sqrt{3}\)
Ejemplo\(\PageIndex{21}\)
Racionalizar el denominador:
\(\frac{\sqrt{x}-\sqrt{y}}{\sqrt{x}+\sqrt{y}}\)
Solución:
En este ejemplo, vamos a multiplicar por 1 en la forma\(\frac{(\sqrt{x}-\sqrt{y})}{(\sqrt{x}-\sqrt{y})}\).
Respuesta:
Ejercicio\(\PageIndex{3}\)
Racionalizar el denominador:
\(\frac{3 \sqrt{5}+5}{2 \sqrt{5}-3}\)
- Responder
-
\(\frac{45+19 \sqrt{5}}{11}\)
Claves para llevar
- Para multiplicar dos expresiones radicales de un solo término, multiplicar los coeficientes y multiplicar los radicandos. Si es posible, simplifique el resultado.
- Aplicar la propiedad distributiva al multiplicar expresiones radicales con múltiples términos. Entonces simplifica y combina todos como radicales.
- Multiplicar una expresión radical de dos términos que involucra raíces cuadradas por su conjugado da como resultado una expresión racional.
- Es práctica común escribir expresiones radicales sin radicales en el denominador. El proceso de encontrar tal expresión equivalente se llama racionalizar el denominador.
- Si una expresión tiene un término en el denominador que involucra a un radical, entonces racionalizarlo multiplicando numerador y denominador por la enésima raíz de factores del radicando para que sus poderes sean iguales al índice.
- Si una expresión radical tiene dos términos en el denominador que involucran raíces cuadradas, entonces racionalizarla multiplicando el numerador y el denominador por su conjugado.
Ejercicio\(\PageIndex{4}\) multiplying radical expressions
Multiplicar. (Supongamos que todas las variables son no negativas.)
- \(\sqrt{3}\cdot\sqrt{5}\)
- \(\sqrt{7}\cdot\sqrt{3}\)
- \(\sqrt{2}\cdot\sqrt{6}\)
- \(\sqrt{5}\cdot\sqrt{15}\)
- \(\sqrt{7}\cdot\sqrt{7}\)
- \(\sqrt{12}\cdot\sqrt{12}\)
- \(2\sqrt{5}\cdot 7\sqrt{10}\)
- \(3\sqrt{15}\cdot 2\sqrt{6}\)
- \((2\sqrt{5})^{2}\)
- \((6\sqrt{2})^{2}\)
- \(\sqrt{2x}\cdot\sqrt{2x}\)
- \(\sqrt{5y}\cdot\sqrt{5y}\)
- \(\sqrt{3a}\cdot\sqrt{12}\)
- \(\sqrt{3a}\cdot\sqrt{2a}\)
- \(4\sqrt{2x}\cdot 3\sqrt{6x}\)
- \(5\sqrt{10y}\cdot 2\sqrt{2y}\)
- \(\sqrt[3]{5} \cdot \sqrt[3]{25}\)
- \(\sqrt[3]{4}\cdot\sqrt[3]{2}\)
- \(\sqrt[3]{4}\cdot\sqrt[3]{10}\)
- \(\sqrt[3]{18}\cdot\sqrt[3]{6}\)
- \((5\sqrt[3]{9})(2\sqrt[3]{6})\)
- \((2\sqrt[3]{4})(3\sqrt[3]{4})\)
- \((2\sqrt[3]{2})^{3}\)
- \((3\sqrt[3]{4})^{3}\)
- \(\sqrt[3]{3a^{2}}\cdot\sqrt[3]{9a}\)
- \(\sqrt[3]{7b}\cdot\sqrt[3]{49b^{2}}\)
- \(\sqrt[3]{6x^{2}}\cdot\sqrt[3]{4x^{2}}\)
- \(\sqrt[3]{12y}\cdot\sqrt[3]{9y^{2}}\)
- \(\sqrt[3]{20x^{2}y}\cdot\sqrt[3]{10x^{2}y^{2}}\)
- \(\sqrt[3]{63xy}\cdot\sqrt[3]{12x^{4}y^{2}}\)
- \(\sqrt{5}( 3 − \sqrt{5})\)
- \(\sqrt{2}(\sqrt{3}−\sqrt{2})\)
- \(3\sqrt{7}(2\sqrt{7} − \sqrt{3})\)
- \(2\sqrt{5}(6−3\sqrt{10})\)
- \(\sqrt{6}(\sqrt{3}−\sqrt{2})\)
- \(\sqrt{15}(\sqrt{5}+\sqrt{3})\)
- \(\sqrt{x}(\sqrt{x}+\sqrt{xy})\)
- \(\sqrt{y}(\sqrt{xy}+\sqrt{y})\)
- \(\sqrt{2ab}(\sqrt{14a}−2\sqrt{10b})\)
- \(\sqrt{6ab}(5\sqrt{2a}−\sqrt{3b})\)
- \((\sqrt{2}−\sqrt{5})(\sqrt{3}+\sqrt{7})\)
- \((\sqrt{3}+\sqrt{2})(\sqrt{5}−\sqrt{7})\)
- \((2\sqrt{3}−4)(3\sqrt{6}+1)\)
- \((5−2\sqrt{6})(7−2\sqrt{3})\)
- \((\sqrt{5}−\sqrt{3})^{2}\)
- \((\sqrt{7}−\sqrt{2})^{2}\)
- \((2\sqrt{3}+\sqrt{2})(2\sqrt{3}−\sqrt{2})\)
- \((\sqrt{2}+3\sqrt{7})(\sqrt{2}−3\sqrt{7})\)
- \((\sqrt{a}−\sqrt{2b})^{2}\)
- \((\sqrt{ab}+1)^{2}\)
- ¿Cuáles son el perímetro y el área de un rectángulo con longitud de\(5\sqrt{3}\) centímetros y ancho de\(3\sqrt{2}\) centímetros?
- ¿Cuáles son el perímetro y el área de un rectángulo con longitud de\(2\sqrt{6}\) centímetros y ancho de\(\sqrt{3}\) centímetros?
- Si la base de un triángulo mide\(6\sqrt{2}\) metros y la altura mide\(3\sqrt{2}\) metros, entonces ¿cuál es el área?
- Si la base de un triángulo mide\(6\sqrt{3}\) metros y la altura mide\(3\sqrt{6}\) metros, entonces ¿cuál es el área?
- Responder
-
1. \(\sqrt{15}\)
3. \(2\sqrt{3}\)
5. \(7\)
7. \(70\sqrt{2}\)
9. \(20\)
11. \(2x\)
13. \(6\sqrt{a}\)
15. \(24x\sqrt{3}\)
17. \(5\)
19. \(2 \sqrt[3]{5}\)
21. \(30 \sqrt[3]{2}\)
23. \(16\)
25. \(3a\)
27. \(2 \sqrt[3]{3}\left(x^{2}\right)^{\frac{2}{3}}\)
29. \(2xy\sqrt[3]{25x}\)
31. \(3\sqrt{5}−5\)
33. \(42-3 \sqrt{21}\)
35. \(3\sqrt{2}−2\sqrt{3}\)
37. \(x+x\sqrt{y}\)
39. \(\sqrt{2}(\sqrt{14} \sqrt{a}-2 \sqrt{10} \sqrt{b}) \sqrt{a b}\)
41. \(\sqrt{6}+\sqrt{14}-\sqrt{15}-\sqrt{35}\)
43. \(18 \sqrt{2}+2 \sqrt{3}-12 \sqrt{6}-4\)
45. \(8-2 \sqrt{15}\)
47. \(10\)
49. \((\sqrt{a}-\sqrt{2b} )^{2}\)
51. Perímetro:\((10\sqrt{3}+6\sqrt{2})\) centímetros; área: centímetros\(15\sqrt{6}\) cuadrados
53. \(18\)metros cuadrados
Ejercicio\(\PageIndex{5}\) dividing radical expressions
Dividir.
- \(\frac{\sqrt{75}}{\sqrt{3}}\)
- \(\frac{\sqrt{360}}{\sqrt{10}}\)
- \(\frac{\sqrt{72}}{\sqrt{75}}\)
- \(\frac{\sqrt{90}}{\sqrt{98}}\)
- \(\frac{\sqrt{90 x^{5}}}{\sqrt{2 x}}\)
- \(\frac{\sqrt{96 y^{3}}}{\sqrt{3 y}}\)
- \(\frac{\sqrt{162 x^{7} y^{5}}}{\sqrt{2 x y}}\)
- \(\frac{\sqrt{363 x^{4} y^{9}}}{\sqrt{3 x y}}\)
- \(\frac{\sqrt[3]{16 a^{5} b^{2}}}{\sqrt[3]{2 a^{2} b^{2}}}\)
- \(\frac{\sqrt[3]{192 a^{2} b^{7}}}{\sqrt[3]{2 a^{2} b^{2}}}\)
- Responder
-
1. \(5\)
3. \(\frac{2 \sqrt{6}}{5}\)
5. \(3 \sqrt{5} x^{2}\)
7. \(9 x^{3} y^{2}\)
9. \(2a\)
Ejercicio\(\PageIndex{6}\) dividing radical expressions
Racionalizar el denominador
- \(\sqrt{\frac{1}{5}}\)
- \(\sqrt{\frac{1}{6}}\)
- \(\frac{\sqrt{2}}{\sqrt{3}}\)
- \(\frac{\sqrt{3}}{\sqrt{7}}\)
- \(\sqrt{\frac{52}{10}}\)
- \(\sqrt{\frac{3}{56}}\)
- \(\frac{\sqrt{3}-\sqrt{5}}{\sqrt{3}}\)
- \(\frac{\sqrt{6}-\sqrt{2}}{\sqrt{2}}\)
- \(\sqrt{\frac{1}{7 x}}\)
- \(\sqrt{\frac{1}{3y}}\)
- \(a \sqrt{\frac{5}{a b}} \)
- \ (\ 3 b^ {2}\ sqrt {\ frac {23} {a b}})
- 236−√3
- 147√3
- 14x−√3
- 13y2−−−√3
- 9x2√39xy2−−−−−√3
- 5y2x−−√35x2y−−−−−√3
- 3a2 3a2b2−−−−−√3
- 25n3 25m2n−−−−−−−√3
- 327x2y−−−−−√5
- 216xy2−−−−−−√5
- ab9a3b−−−−√5
- abcab2c3−−−−−√5
- 310−√−3
- 26√−2
- 15√+3√
- 17√−2√
- 3√3√+6√
- 5√5√+15−√
- 105−35√
- −22√4−32√
- 3√+5√3√−5√
- 10−√−2√10−−√+2√
- 23√−32√43√+2√
- 65√+225√−2√
- x+y√x−y√
- x−y√x+y√
- a√−b√a√+b√
- ab−−√+2√ab −√−√−2√
- x−−√5−2x−√ 106. 1x−−√−y
- Responder
-
1. \(\frac{\sqrt{5}}{5}\)
3. \(\frac{\sqrt{6}}{3}\)
5. \(\frac{\sqrt{130}}{5}\)
7. \(\frac{3-\sqrt{15}}{3}\)
9. \(\frac{\sqrt{7x}}{7 x}\)
11. \(a \frac{\sqrt{5a b}}{a b}\)
13. 6√33
15. 2x2−−−−√32x
17. 3 6x2y−−−−−√3y
19. 9ab−−−√32b
21. 9x3y4−−−−−−−√5xy
23. 27a2b4−−−−−−−√53
25. 310−√+9
27. 5√−3√2
29. −1+2√
31. −5−35√2
33. −4−15−√
35. 15−76√23
37. x2+2xy√+yx2−y
39. a−2ab−√+ba−b
41. 5x−√+2x25−4x
Ejercicio\(\PageIndex{7}\) discussion
- Investigar y discutir algunas de las razones por las que es una práctica común racionalizar el denominador.
- Explica con tus propias palabras cómo racionalizar el denominador.
- Responder
-
1. La respuesta puede variar


