3.2: Resolver sistemas lineales con dos variables

Última actualización
Guardar como PDF

Page ID: 109856

Anonymous
LibreTexts

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Objetivos de aprendizaje

Resolver sistemas lineales utilizando el método de sustitución.
Resolver sistemas lineales utilizando el método de eliminación.
Identificar las fortalezas y debilidades de cada método.

El Método de Sustitución

En esta sección, revisamos una técnica completamente algebraica para resolver sistemas, el método de sustitución ¹¹. La idea es resolver una ecuación para una de las variables y sustituir el resultado por la otra ecuación. Después de realizar este paso de sustitución, nos quedamos con una sola ecuación con una variable, la cual se puede resolver usando álgebra.

Ejemplo\(\PageIndex{1}\):

Resolver por sustitución:\(\left\{ \begin{array} { l } { 2 x + y = - 3 } \\ { 3 x - 2 y = - 8 } \end{array} \right.\).

Solución

Resuelve para cualquiera de las variables en cualquiera de las ecuaciones. Si eliges la primera ecuación, puedes aislar\(y\) en un solo paso.

\(\begin{aligned} 2 x + y & = - 3 \\ y & = - 2 x - 3 \end{aligned}\)

Sustituir la expresión\(-2x-3\) por la variable\(y\) en la otra ecuación.

\(3 x - 2 ( - \color{OliveGreen}{2 x - 3}\color{Black}{ )} = - 8\)

Esto nos deja con una ecuación equivalente con una variable, que puede resolverse utilizando las técnicas aprendidas hasta este punto. Resolver para la variable restante.

\(\begin{aligned} 3 x - 2 ( \color{OliveGreen}{- 2 x - 3}\color{Black}{ )} & = - 8 \\ 3 x + 4 x + 6 & = - 8 \\ 7 x + 6 & = - 8 \\ 7 x & = - 14 \\ x & = - 2 \end{aligned}\)

Volver sustituir ¹² para encontrar la otra coordenada. Sustituir\(x = −2\) en cualquiera de las ecuaciones originales o sus equivalentes. Normalmente, usamos la ecuación equivalente que encontramos al aislar una variable en el primer paso.

\(\begin{aligned} y & = - 2 x - 3 \\ & = - 2 ( \color{OliveGreen}{- 2}\color{Black}{ )} - 3 \\ & = 4 - 3 \\ & = 1 \end{aligned}\)

Recuerde presentar la solución como un par ordenado:\((−2, 1)\). Verifique que estas coordenadas resuelvan ambas ecuaciones del sistema original:

Mesa\(\PageIndex{1}\)
Comprobar:\((-2,1)\)
Ecuación 1	Ecuación 2
\(\begin{array} { r } { 2 x + y = - 3 } \\ { 2 ( \color{Cerulean}{- 2} \color{Black}{)} + (\color{Cerulean}{ 1} \color{Black}{)} = - 3 } \\ { - 4 + 1 = - 3 } \\ { - 3 = - 3 } \:\:\color{Cerulean}{✓}\end{array}\)	\(\begin{array} { r } { 3 x - 2 y = - 8 } \\ { 3 ( - 2 ) \color{Cerulean}{- 2}\color{Black}{ (}\color{Cerulean}{ 1}\color{Black}{ )} = - 8 } \\ { - 6 - 2 = - 8 } \\ { - 8 = - 8 } \:\:\color{Cerulean}{✓} \end{array}\)

La gráfica de este sistema lineal sigue:

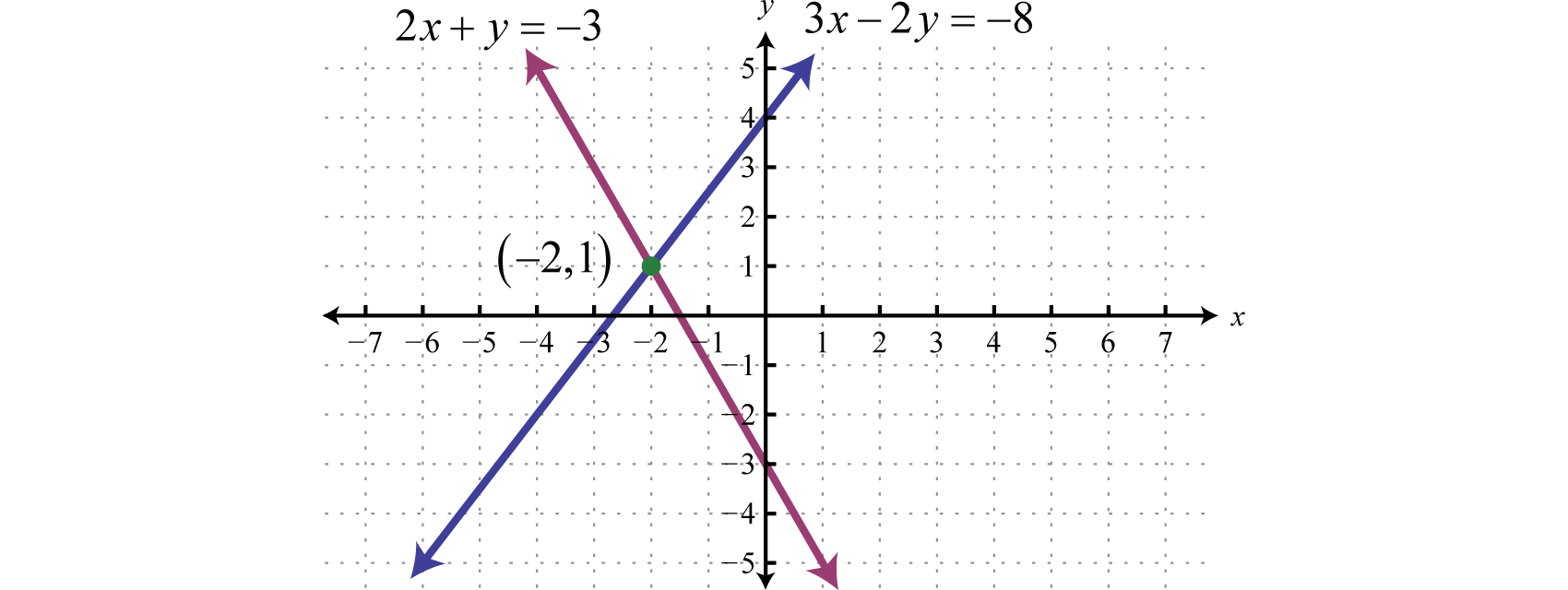
El método de sustitución para resolver sistemas es un método completamente algebraico. Por lo tanto, no se requiere graficar las líneas.

Respuesta:

\((-2, 1)\)

Ejemplo\(\PageIndex{2}\):

Resolver por sustitución:\(\left\{ \begin{array} { l } { 3 x - 5 y = 9 } \\ { 4 x + 2 y = - 1 } \end{array} \right.\).

Solución

No importa qué variable elegimos aislar primero. En este caso, comience por resolver para\(x\) en la primera ecuación.

\(\begin{aligned} 3 x - 5 y & = 9 \\ 3 x & = 5 y + 9 \\ x & = \frac { 5 y + 9 } { 3 } \\ x & = \frac { 5 } { 3 } y + 3 \end{aligned}\)

\(\left\{ \begin{array} { c } { 3 x - 5 y = 9 \Longrightarrow \color{Cerulean}{x}\color{Black}{ =} \frac { 5 } { 3 } y + 3 } \\ { 4\color{Cerulean}{ x}\color{Black}{ +} 2 y = - 1 } \end{array} \right.\)

A continuación, sustituya en la segunda ecuación y resuelva para\(y\).

\(\begin{aligned} 4 \left( \frac { 5 } { 3 } y + 3 \right) + 2 y & = - 1 \\ \frac { 20 } { 3 } y + 12 + 2 y & = - 1 \\ \frac { 26 } { 3 } y & = - 13 \\ y & = - 13 \left( \frac { 3 } { 26 } \right) \\ y & = - \frac { 3 } { 2 } \end{aligned}\)

Volver a sustituir en la ecuación utilizada en el paso de sustitución:

\(\begin{aligned} x & = \frac { 5 } { 3 } y + 3 \\ & = \frac { 5 } { 3 } \left( \color{Cerulean}{- \frac { 3 } { 2 }} \right) + 3 \\ & = - \frac { 5 } { 2 } + 3 \\ & = \frac { 1 } { 2 } \end{aligned}\)

Respuesta:

\(\left( \frac { 1 } { 2 } , - \frac { 3 } { 2 } \right)\)

Ejercicio\(\PageIndex{1}\)

Resolver por sustitución:\(\left\{ \begin{array} { l } { 5 x - 4 y = 3 } \\ { x + 2 y = 2 } \end{array} \right.\).

Contestar

\(\left( 1 , \frac { 1 } { 2 } \right)\)

www.youtube.com/v/gzphthhkeda

Como sabemos, no todos los sistemas lineales tienen solo una solución de par ordenado. A continuación, exploramos lo que sucede cuando se utiliza el método de sustitución para resolver un sistema dependiente.

Ejemplo\(\PageIndex{3}\):

Resolver por sustitución:\(\left\{ \begin{array} { l } { - 5 x + y = - 1 } \\ { 10 x - 2 y = 2 } \end{array} \right.\).

Solución

Dado que la primera ecuación tiene un término con coeficiente\(1\), elegimos resolver para eso primero.

\(\left\{ \begin{array} { l } { - 5 x + y = - 1 \quad \Rightarrow \quad \color{Cerulean}{y}\color{Black}{ =} 5 x - 1 } \\ { 10 x - 2\color{Cerulean}{ y}\color{Black}{ =} 2 } \end{array} \right.\)

A continuación, sustituya esta expresión por\(y\) en la segunda ecuación.

\(\begin{aligned} 10 x - 2 y & = 2 \\ 10 x - 2 ( \color{OliveGreen}{5 x - 1}\color{Black}{ )} & = 2 \\ 10 x - 10 x + 2 & = 2 \\ 2 & = 2\quad \color{Cerulean}{True} \end{aligned}\)

Este proceso condujo a una afirmación verdadera; de ahí que la ecuación sea una identidad y cualquier número real es una solución. Esto indica que el sistema es dependiente. Las soluciones simultáneas toman la forma\((x, mx + b)\), o en este caso,\((x, 5x − 1)\), donde\(x\) está cualquier número real.

Respuesta:

\(( x , 5 x - 1 )\)

Para tener una mejor comprensión del ejemplo anterior, reescribe ambas ecuaciones en forma de pendiente-intercepción y graficarlas en el mismo conjunto de ejes.

\(\left\{ \begin{array} { l } { - 5 x + y = - 1 } \\ { 10 x - 2 y = 2 } \end{array} \right. \Rightarrow \left\{ \begin{array} { l } { y = 5 x - 1 } \\ { y = 5 x - 1 } \end{array} \right.\)

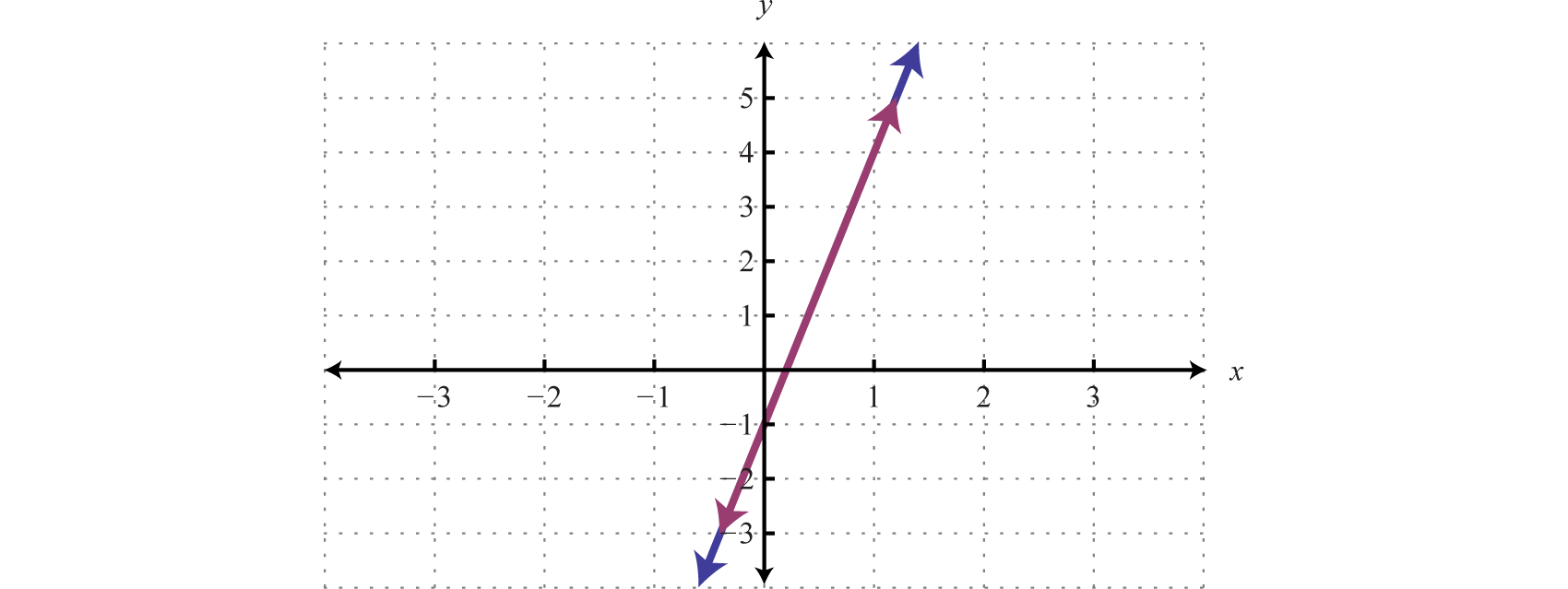
Podemos ver que ambas ecuaciones representan la misma línea, y así el sistema es dependiente. Ahora explora lo que sucede al resolver un sistema inconsistente usando el método de sustitución.

Ejemplo\(\PageIndex{4}\):

Resolver por sustitución:\(\left\{ \begin{array} { l } { - 7 x + 3 y = 3 } \\ { 14 x - 6 y = - 16 } \end{array} \right.\).

Solución

Resuelve para\(y\) en la primera ecuación.

\(\begin{aligned} - 7 x + 3 y & = 3 \\ - 7 x + 3 y & = 3 \\ 3 y & = 7 x + 3 \\ y & = \frac { 7 x + 3 } { 3 } \\ y & = \frac { 7 } { 3 } x + 1 \end{aligned}\)

\(\left\{ \begin{array} { l l } { - 7 x + 3 y = 3 } & { \Rightarrow \quad \color{Cerulean}{y}\color{Black}{ =} \frac { 7 } { 3 } x + 1 } \\ { 14 x - 6\color{Cerulean}{ y}\color{Black}{ =} - 16 } \end{array} \right. \)

Sustituir en la segunda ecuación y resolver.

\(\begin{aligned} 14 x - 6 y & = - 16 \\ 14x-6 \left( \color{OliveGreen}{\frac { 7 } { 3 } x + 1} \right) & = - 16 \\ 14x - \overset{\color{Cerulean}{2}}{\color{Black}{\cancel{6}}} \cdot \frac { 7 } { \underset{\color{Cerulean}{1}}{\cancel{3} }} x - 6 & = - 16 \\14 x - 14 x - 6 & = - 16 \\ - 6 &= - 16\quad\color{red}{False} \end{aligned}\)

Resolver conduce a una declaración falsa. Esto indica que la ecuación es una contradicción. No hay solución para\(x\) y por lo tanto ninguna solución para el sistema.

Respuesta:

\(\varnothing\)

Una declaración falsa indica que el sistema es inconsistente, o en términos geométricos, que las líneas son paralelas y no se cruzan. Para ilustrar esto, determine la forma pendiente-intercepción de cada línea y gráfiquelas en el mismo conjunto de ejes.

\(\left\{ \begin{array} { l l } { - 7 x + 3 y = 3 } \\ { 14 x - 6 y = - 16 } \end{array} \right. \Rightarrow \left\{ \begin{array} { l } { y = \frac { 7 } { 3 } x + 1 } \\ { y = \frac { 7 } { 3 } x + \frac { 8 } { 3 } } \end{array} \right.\)

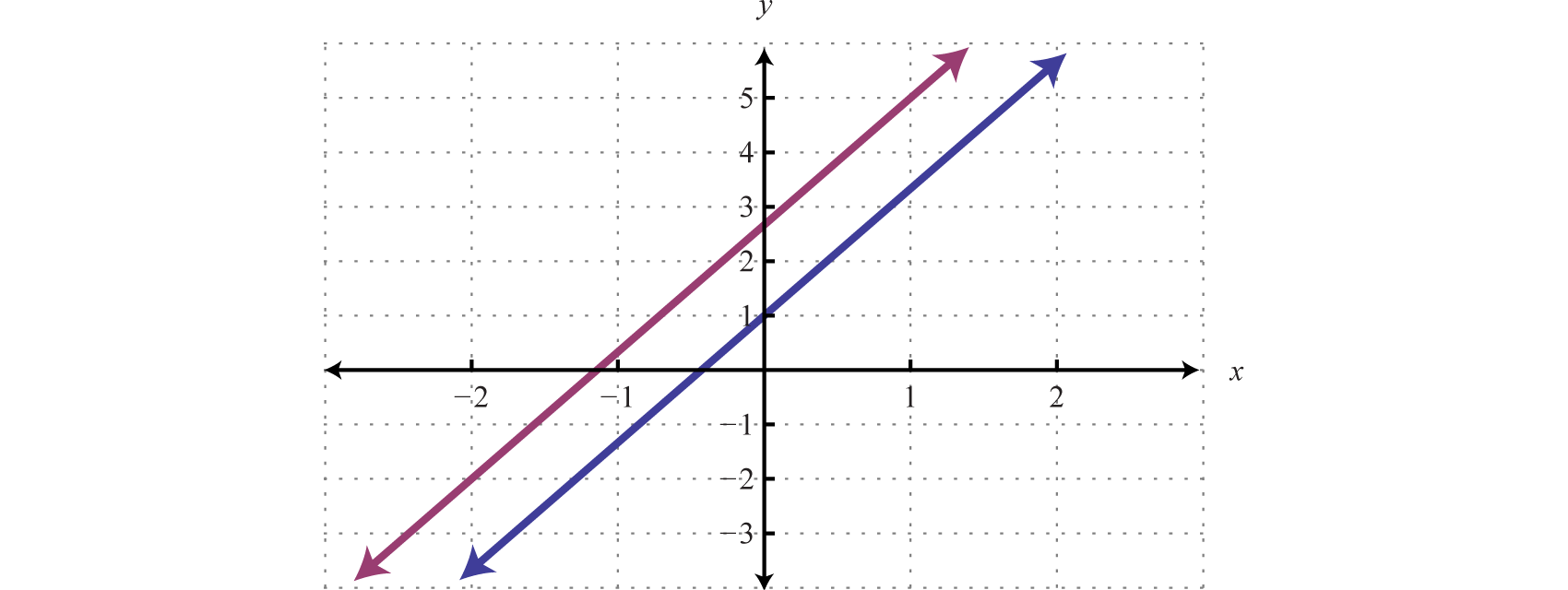
En forma de pendiente-intercepción, es fácil ver que las dos líneas tienen la misma pendiente pero diferentes\(y\) -intercepciones.

Ejercicio\(\PageIndex{2}\)

Resolver por sustitución:\(\left\{ \begin{array} { r } { 2 x - 5 y = 3 } \\ { 4 x - 10 y = 6 } \end{array} \right.\).

Contestar

\(\left( x , \frac { 2 } { 5 } x - \frac { 3 } { 5 } \right)\)

www.youtube.com/v/jkx9m-l9wow

El método de eliminación

En esta sección, el objetivo es revisar otro método completamente algebraico para resolver un sistema de ecuaciones lineales denominado método de eliminación ¹³ o método de adición ¹⁴. Este método depende de la propiedad de suma de las ecuaciones ¹⁵: dadas las expresiones algebraicas A, B, C y D tenemos

\(\text{If} \:A = B \text { and } C = D , \text { then } A + C = B + D\)

Podemos sumar las ecuaciones juntas para eliminar la variable\(y\).

\(\begin{aligned} x \color{red}{+ y}\color{Black}{ =} 5 \\ \pm \frac { x \color{red}{- y} = 1 } { 2 x \:\:\:= \:\:\: 6 }\end{aligned}\)

Esto nos deja con una ecuación lineal con una variable que se puede resolver fácilmente:

\(\begin{aligned} 2 x & = 6 \\ x & = 3 \end{aligned}\)

En este punto, tenemos la\(x\) coordenada -de la solución simultánea, por lo que todo lo que queda por hacer es volver a sustituir para encontrar el\(y\) -valor correspondiente.

\(\begin{array} { r } { x + y = 5 } \\ { \color{OliveGreen}{3} \color{Black}{+} y = 5 } \\ { y = 2 } \end{array}\)

La solución al sistema es\((3, 2)\). Por supuesto, la variable no siempre se elimina tan fácilmente. Normalmente, tenemos que encontrar un sistema equivalente aplicando la propiedad de multiplicación de igualdad a una o ambas ecuaciones como medio para alinear una de las variables a eliminar. El objetivo es disponer que o bien los\(x\) términos o los\(y\) términos sean opuestos, para que cuando se agreguen las ecuaciones, los términos eliminen.

Ejemplo\(\PageIndex{5}\):

Resolver por eliminación:\(\left\{ \begin{array} { l } { 5 x - 3 y = - 1 } \\ { 3 x + 2 y = 7 } \end{array} \right.\).

Solución

Elegimos eliminar los términos con variable\(y\) porque los coeficientes tienen signos diferentes. Para ello, primero determinamos el múltiplo menos común de los coeficientes; en este caso, el\(LCM(3, 2)\) es\(6\). Por lo tanto, multiplique ambos lados de ambas ecuaciones por los valores apropiados para obtener coeficientes de\(−6\) y\(6\). Esto da como resultado el siguiente sistema equivalente:

\(\left\{ \begin{array} { l l } { 5 x - 3 y = - 1 } & { \stackrel { x 2 } { \Rightarrow } } \\ { 3 x + 2 y = 7 } & { \stackrel { x3 } { \Rightarrow } } \end{array} \right. \left\{ \begin{array} { c } { 10 x - 6 y = - 2 } \\ { 9 x + 6 y = 21 } \end{array} \right.\)

Los términos que involucran ahora\(y\) están alineados para eliminar. Sumar las ecuaciones juntas y resolver para\(x\).

\(\begin{aligned} 10 x \color{red}{- 6 y} & \color{Black}{=} - 2 \\ + \quad 9 x \color{red}{+ 6 y} & \color{Black}{=} 21 \\ \hline 19 x & = 19 \\ x & = 1 \end{aligned}\)

Sustituto de espalda.

\(\begin{aligned} 3 x + 2 y & = 7 \\ 3 ( \color{OliveGreen}{1}\color{Black}{ )} + 2 y & = 7 \\ 3 + 2 y & = 7 \\ 2 y & = 4 \\ y & = 2 \end{aligned}\)

Por lo tanto la solución simultánea es\((1, 2)\). A continuación se indica el cheque.

Mesa\(\PageIndex{2}\)
Comprobar:\((1, 2)\)
Ecuación 1:	Ecuación 2:
\(\begin{aligned} 5 x - 3 y & = - 1 \\ 5 ( \color{Cerulean}{1}\color{Black}{ )} - 3 ( \color{Cerulean}{2}\color{Black}{ )} & = - 1 \\ 5 - 6 & = - 1 \\ - 1 & = - 1 \:\:\color{Cerulean}{✓}\end{aligned}\)	\(\begin{array} { r } { 3 x + 2 y = 7 } \\ { 3 ( \color{Cerulean}{1}\color{Black}{ )} + 2 ( \color{Cerulean}{2}\color{Black}{ )} = 7 } \\ { 3 + 4 = 7 } \\ { 7 = 7 } \:\:\color{Cerulean}{✓}\end{array}\)

Respuesta:

\((1, 2)\)

A veces los sistemas lineales no se dan en forma estándar\(ax + by = c\). Cuando este es el caso, lo mejor es reorganizar las ecuaciones antes de comenzar los pasos para resolver por eliminación. Además, podemos eliminar cualquiera de las variables. El objetivo es obtener una solución para una de las variables y luego volver a sustituirla para encontrar una solución para la otra.

Ejemplo\(\PageIndex{6}\):

Resolver por eliminación:\(\left\{ \begin{aligned} 12 x + 5 y & = 11 \\ 3 x & = 4 y + 1 \end{aligned} \right.\).

Solución:

Primero, reescribir la segunda ecuación en forma estándar.

\(\begin{aligned} 3 x & = 4 y + 1 \\ 3 x - 4 y & = 1 \end{aligned}\)

Esto da como resultado un sistema equivalente en forma estándar, donde términos similares se alinean en columnas.

\(\left\{ \begin{array} { c c } { 12 x + 5 y = 11 } \\ { 3 x = 4 y + 1 } \end{array} \right. \Rightarrow \left\{ \begin{array} { c } { 12 x + 5 y = 11 } \\ { 3 x - 4 y = 1 } \end{array} \right.\)

Podemos eliminar el término con variable\(x\) si multiplicamos la segunda ecuación por\(−4\).

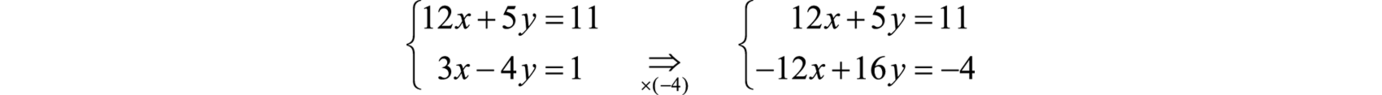
A continuación, sumamos las ecuaciones juntas,

\(\begin{aligned} \color{red}{12 x} \color{Black}{+5 y} & \color{Black}{=} 11 \\ + \quad \color{red}{-12x} \color{Black}{+ 16 y} & \color{Black}{=} -4 \\ \hline 21y & = 7 \\ y & = \frac{7}{21} = \frac{1}{3} \end{aligned}\)

Sustituto de espalda.

\(\begin{array} { l } { 3 x = 4 y + 1 } \\ { 3 x = 4 \left( \color{OliveGreen}{\frac { 1 } { 3 }} \right) + 1 } \\ { 3 x = \frac { 4 } { 3 } + 1 } \\ { 3 x = \frac { 7 } { 3 } } \\ { x = \frac { 7 } { 3 } \cdot \frac { 1 } { 3 } } \\ { x = \frac { 7 } { 9 } } \end{array}\)

Respuesta:

\(\left( \frac { 7 } { 9 } , \frac { 1 } { 3 } \right)\)

Ejercicio\(\PageIndex{3}\)

Resolver por eliminación:\(\left\{ \begin{array} { l } { 2 x + 5 y = 5 } \\ { 3 x + 2 y = - 9 } \end{array} \right.\).

Contestar

\((-5, 3)\)

www.youtube.com/v/fx90hfggjbi

En este punto, exploramos lo que sucede al resolver sistemas dependientes e inconsistentes utilizando el método de eliminación.

Ejemplo\(\PageIndex{7}\):

Resolver por eliminación:\(\left\{ \begin{array} { c } { 3 x - y = 7 } \\ { 6 x - 2 y = 14 } \end{array} \right.\).

Solución

Para eliminar la variable\(x\), podríamos multiplicar la primera ecuación por\(−2\).

Ahora sumando las ecuaciones que tenemos

\(\begin{aligned} -6 x + \color{red}{2 y} & \color{Black}{=} -14 \\ \pm \quad \color{black}{6x}- \color{red}{2 y} & \color{Black}{=} 14 \\ \hline 0 & = 0\quad\color{Cerulean}{True} \end{aligned}\)

Una afirmación verdadera indica que se trata de un sistema dependiente. Las líneas coinciden, y necesitamos\(y\) en términos de\(x\) presentar el conjunto de soluciones en la forma\((x, mx + b)\). Elige una de las ecuaciones originales y resuelve para\(y\). Dado que las ecuaciones son equivalentes, no importa cuál escojamos.

\(\begin{aligned} 3 x - y & = 7 \\ - y & = - 3 x + 7 \\ \color{Cerulean}{- 1}\color{Black}{ (} - y ) & = \color{Cerulean}{- 1}\color{Black}{ (} - 3 x + 7 ) \\ y & = 3 x - 7 \end{aligned}\)

Respuesta:

\(( x , 3 x - 7 )\)

Ejercicio\(\PageIndex{4}\)

Resolver por eliminación:\(\left\{ \begin{array} { l } { 3 x + 15 y = - 15 } \\ { 2 x + 10 y = 30 } \end{array} \right.\).

Contestar

Sin solución,\(\varnothing\)

www.youtube.com/v/e4b0lmleliy

Dado un sistema lineal donde las ecuaciones tienen coeficientes fraccionarios, suele ser mejor borrar las fracciones antes de comenzar el método de eliminación.

Ejemplo\(\PageIndex{8}\):

Resolver:\(\left\{ \begin{array} { l } { - \frac { 1 } { 10 } x + \frac { 1 } { 2 } y = \frac { 4 } { 5 } } \\ { \frac { 1 } { 7 } x + \frac { 1 } { 3 } y = - \frac { 2 } { 21 } } \end{array} \right.\).

Solución

Recordemos que podemos borrar fracciones multiplicando ambos lados de una ecuación por el mínimo común múltiplo de los denominadores (LCD). Tenga cuidado de distribuir y luego simplificar.

Mesa\(\PageIndex{3}\)
Ecuación 1	Ecuación 2
\(\begin{array} { r } { \color{Cerulean}{10}\color{Black}{ \left( - \frac { 1 } { 10 } x + \frac { 1 } { 2 } y \right)} = \color{Cerulean}{10}\color{Black}{ \left( \frac { 4 } { 5 } \right) }} \\ { \color{Cerulean}{10} \color{Black}{\cdot} \left( - \frac { 1 } { 10 } x \right) + \color{Cerulean}{10}\color{Black}{ \cdot} \frac { 1 } { 2 } y = \color{Cerulean}{10}\color{Black}{ \cdot} \frac { 4 } { 5 } } \\ { - x + 5 y = 8 } \end{array}\)	\(\begin{array} { c } { \color{Cerulean}{21}\color{Black}{ \left( \frac { 1 } { 7 } x + \frac { 1 } { 3 } y \right)} = \color{Cerulean}{21}\color{Black}{ \left( - \frac { 2 } { 21 } \right) }} \\ { \color{Cerulean}{21}\color{Black}{ \cdot} \frac { 1 } { 7 } x + \color{Cerulean}{21}\color{Black}{ \cdot} \frac { 1 } { 3 } y = \color{Cerulean}{21}\color{Black}{ \left( - \frac { 2 } { 21 } \right) }} \\ { 3 x + 7 y = - 2 } \end{array}\)

Esto da como resultado un sistema equivalente donde las ecuaciones tienen coeficientes enteros,

\(\left\{ \begin{array} { l l } { -\frac{1}{10} x + \frac{1}{2}y = \frac{4}{5} } & { \stackrel { x 10 } { \Rightarrow } } \\ { \frac{1}{7} x + \frac{1}{3} y = -\frac{2}{21} } & { \stackrel { x21 } { \Rightarrow } } \end{array} \right. \left\{ \begin{array} { c } { - x +5y = 8 } \\ { 3 x + 7 y = -2 } \end{array} \right.\)

Resuelve usando el método de eliminación.

Figura\(\PageIndex{7}\)

\(\begin{aligned} \color{red}{-3 x} + \color{black}{15 y} & \color{Black}{=} 24 \\ \pm \quad \color{red}{3x}+ \color{black}{7 y} & \color{Black}{=} -2 \\ \hline 22y & = 22 \\ y&=1 \end{aligned}\)

Sustituto de espalda.

\(\begin{aligned} 3 x + 7 y & = - 2 \\ 3 x + 7 ( \color{OliveGreen}{1}\color{Black}{ )} & = - 2 \\ 3 x + 7 & = - 2 \\ 3 x & = - 9 \\ x & = - 3 \end{aligned}\)

Respuesta:

\((-3,1)\)

Podemos usar una técnica similar para borrar decimales antes de resolver.

Ejercicio\(\PageIndex{5}\)

Resolver usando eliminación:\(\left\{ \begin{array} { l } { \frac { 1 } { 3 } x - \frac { 2 } { 3 } y = 3 } \\ { \frac { 1 } { 3 } x - \frac { 1 } { 2 } y = \frac { 8 } { 3 } } \end{array} \right.\).

Contestar

\((5, -2)\)

www.youtube.com/v/ujlpep7nake

Resumen de los métodos para resolver sistemas lineales

Hemos revisado tres métodos para resolver sistemas lineales de dos ecuaciones con dos variables. Cada método es válido y puede producir el mismo resultado correcto. En esta sección, resumimos las fortalezas y debilidades de cada método.

El método de graficar es útil para entender qué es un sistema de ecuaciones y cómo deben ser las soluciones. Cuando las ecuaciones de un sistema están graficadas en el mismo conjunto de ejes, podemos ver que la solución es el punto donde se cruzan las gráficas. La gráfica se facilita cuando las ecuaciones están en forma de pendiente-intersección. Por ejemplo,

\(\left\{ \begin{array} { l } { y = 5 x + 15 } \\ { y = - 5 x + 5 } \end{array} \right.\)

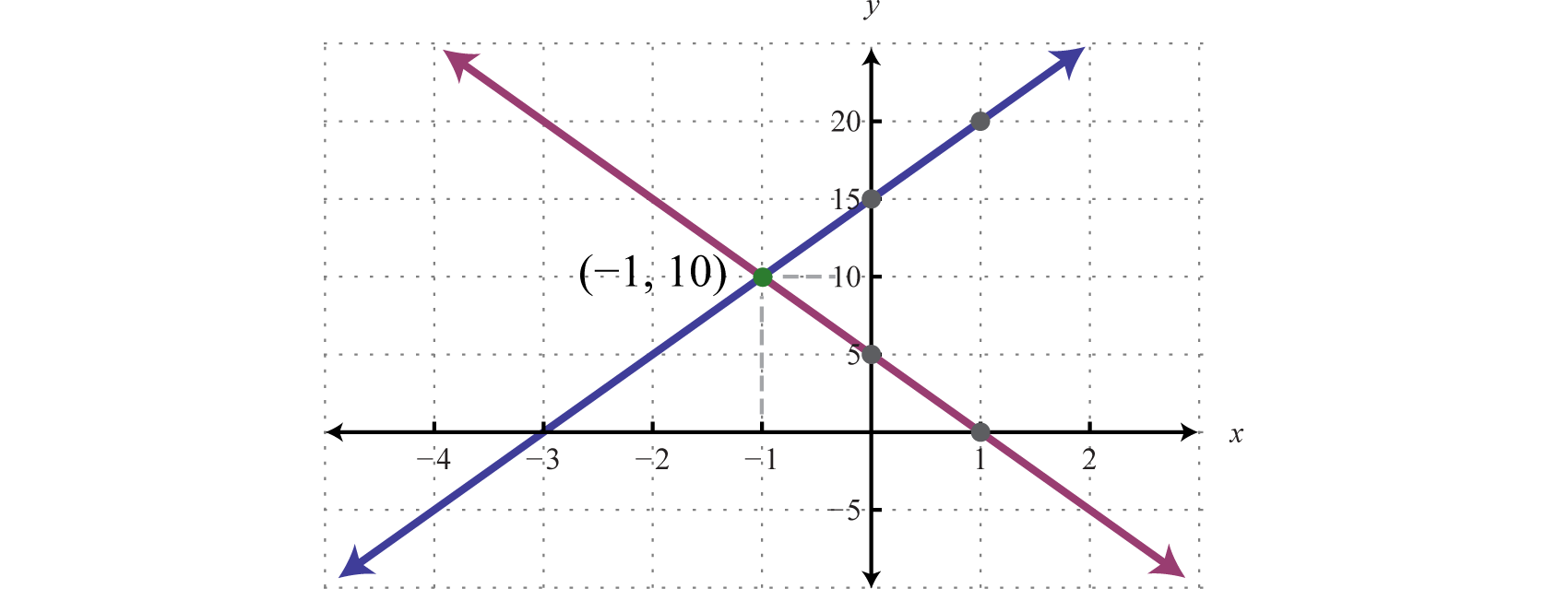
La solución simultánea\((−1, 10)\) corresponde al punto de intersección. Un inconveniente de este método es que es muy inexacto. Cuando las coordenadas de la solución no son números enteros, el método es prácticamente inutilizable. Si tenemos una opción, normalmente evitamos este método en favor de las técnicas algebraicas más precisas.

El método de sustitución, por otro lado, es un método completamente algebraico. Requiere que resuelvas una de las variables y sustituyas el resultado en la otra ecuación. La ecuación resultante tiene una variable para la cual se puede resolver. Este método es particularmente útil cuando existe una variable dentro del sistema con coeficiente de\(1\). Por ejemplo,

\(\left\{ \begin{array} { l } { 10 x + y = 20 } \\ { 7 x + 5 y = 14 } \end{array} \right. \color{Cerulean}{Choose\: the\: substitution\: method.} \quad\)

En este caso, es fácil de resolver\(y\) en la primera ecuación y luego sustituir el resultado por la otra ecuación. Un inconveniente de este método es que a menudo conduce a ecuaciones equivalentes con coeficientes fraccionarios, con los que resulta tedioso trabajar. Si no hay un coeficiente de\(1\), entonces generalmente es mejor elegir el método de eliminación.

El método de eliminación es un método completamente algebraico que hace uso de la propiedad de adición de ecuaciones. Multiplicamos una o ambas ecuaciones para obtener ecuaciones equivalentes donde se elimina una de las variables si las sumamos juntas. Por ejemplo,

\(\left\{ \begin{array} { l } { 2 x - 3 y = 9 } \\ { 5 x - 8 y = - 16 } \end{array} \color{Cerulean}\:\:{Choose\: the\:elimination\: method.}\right. \quad\)

Para eliminar los términos que implican\(x\), multiplicaríamos ambos lados de la primera ecuación por\(5\) y ambos lados de la segunda ecuación por\(−2\). Esto da como resultado un sistema equivalente donde la variable\(x\) se elimina cuando sumamos las ecuaciones juntas. Por supuesto, hay otras combinaciones de números que logran el mismo resultado. Incluso podríamos optar por eliminar la variable\(y\). No importa qué variable se elimine primero, la solución será la misma. Obsérvese que el método de sustitución, en este caso, requeriría cálculos tediosos con coeficientes fraccionarios. Una debilidad del método de eliminación, como veremos más adelante en nuestro estudio del álgebra, es que no siempre funciona para sistemas no lineales.

Claves para llevar

El método de sustitución requiere que resolvamos una de las variables y luego sustituimos el resultado por la otra ecuación. Después de realizar la etapa de sustitución, la ecuación resultante tiene una variable y se puede resolver utilizando las técnicas aprendidas hasta este punto.
El método de eliminación es otro método completamente algebraico para resolver un sistema de ecuaciones. Multiplique una o ambas ecuaciones en un sistema por ciertos números para obtener un sistema equivalente donde al menos una variable en ambas ecuaciones tenga coeficientes opuestos. Al sumar estas ecuaciones equivalentes se elimina esa variable, y la ecuación resultante tiene una variable para la cual se puede resolver.
Es una buena práctica reescribir primero las ecuaciones en forma estándar antes de comenzar el método de eliminación.
Las soluciones a sistemas de dos ecuaciones lineales con dos variables, si existen, son pares ordenados\((x, y)\).
Si el proceso de resolver un sistema de ecuaciones conduce a una declaración falsa, entonces el sistema es inconsistente y no hay solución,\(Ø\).
Si el proceso de resolver un sistema de ecuaciones conduce a una identidad, entonces el sistema es dependiente y hay infinitamente muchas soluciones que se pueden expresar usando la forma\((x, mx + b)\).

Ejercicio\(\PageIndex{6}\)

Resolver por sustitución.

\(\left\{ \begin{array} { l } { y = - 5 x + 1 } \\ { 4 x - 3 y = - 41 } \end{array} \right.\)
\(\left\{ \begin{array} { l } { x = 2 y - 3 } \\ { x + 3 y = - 8 } \end{array} \right.\)
\(\left\{ \begin{array} { l } { y = x } \\ { 2 x + 3 y = 10 } \end{array} \right.\)
\(\left\{ \begin{array} { l } { y = \frac { 1 } { 2 } x + \frac { 1 } { 3 } } \\ { x - 6 y = 4 } \end{array} \right.\)
\(\left\{ \begin{array} { l } { y = 4 x + 1 } \\ { - 4 x + y = 2 } \end{array} \right.\)
\(\left\{ \begin{array} { l } { y = - 3 x + 5 } \\ { 3 x + y = 5 } \end{array} \right.\)
\(\left\{ \begin{array} { l } { y = 2 x + 3 } \\ { 2 x - y = - 3 } \end{array} \right.\)
\(\left\{ \begin{array} { l } { y = \frac { 2 } { 3 } x - 1 } \\ { 6 x - 9 y = 0 } \end{array} \right.\)
\(\left\{ \begin{array} { l } { y = - 2 } \\ { - 2 x - y = - 6 } \end{array} \right.\)
\(\left\{ \begin{array} { l } { y = - \frac { 1 } { 5 } x + 3 } \\ { 7 x - 5 y = 9 } \end{array} \right.\)
\(\left\{ \begin{array} { l } { x + y = 1 } \\ { 3 x - 5 y = 19 } \end{array} \right.\)
\(\left\{ \begin{array} { l } { x - y = 3 } \\ { - 2 x + 3 y = - 2 } \end{array} \right.\)
\(\left\{ \begin{array} { l } { 2 x + y = 2 } \\ { 3 x - 2 y = 17 } \end{array} \right.\)
\(\left\{ \begin{array} { l } { x - 3 y = - 11 } \\ { 3 x + 5 y = - 5 } \end{array} \right.\)
\(\left\{ \begin{array} { l } { x + 2 y = - 3 } \\ { 3 x - 4 y = - 2 } \end{array} \right.\)
\(\left\{ \begin{array} { l } { 5 x - y = 12 } \\ { 9 x - y = 10 } \end{array} \right.\)
\(\left\{ \begin{array} { l } { x + 2 y = - 6 } \\ { - 4 x - 8 y = 24 } \end{array} \right.\)
\(\left\{ \begin{array} { l } { x + 3 y = - 6 } \\ { - 2 x - 6 y = - 12 } \end{array} \right.\)
\(\left\{ \begin{array} { l } { - 3 x + y = - 4 } \\ { 6 x - 2 y = - 2 } \end{array} \right.\)
\(\left\{ \begin{array} { l } { x - 5 y = - 10 } \\ { 2 x - 10 y = - 20 } \end{array} \right.\)
\(\left\{ \begin{array} { l } { 3 x - y = 9 } \\ { 4 x + 3 y = - 1 } \end{array} \right.\)
\(\left\{ \begin{array} { l } { 2 x - y = 5 } \\ { 4 x + 2 y = - 2 } \end{array} \right.\)
\(\left\{ \begin{array} { l } { 2 x - 5 y = 1 } \\ { 4 x + 10 y = 2 } \end{array} \right.\)
\(\left\{ \begin{array} { l } { 3 x - 7 y = - 3 } \\ { 6 x + 14 y = 0 } \end{array} \right.\)
\(\left\{ \begin{array} { l } { 10 x - y = 3 } \\ { - 5 x + \frac { 1 } { 2 } y = 1 } \end{array} \right.\)
\(\left\{ \begin{array} { l } { - \frac { 1 } { 3 } x + \frac { 1 } { 6 } y = \frac { 2 } { 3 } } \\ { \frac { 1 } { 2 } x - \frac { 1 } { 3 } y = - \frac { 3 } { 2 } } \end{array} \right.\)
\(\left\{ \begin{array} { l } { \frac { 1 } { 3 } x + \frac { 2 } { 3 } y = 1 } \\ { \frac { 1 } { 4 } x - \frac { 1 } { 3 } y = - \frac { 1 } { 12 } } \end{array} \right.\)
\(\left\{ \begin{array} { l } { \frac { 1 } { 7 } x - y = \frac { 1 } { 2 } } \\ { \frac { 1 } { 4 } x + \frac { 1 } { 2 } y = 2 } \end{array} \right.\)
\(\left\{ \begin{array} { l } { - \frac { 3 } { 5 } x + \frac { 2 } { 5 } y = \frac { 1 } { 2 } } \\ { \frac { 1 } { 3 } x - \frac { 1 } { 12 } y = - \frac { 1 } { 3 } } \end{array} \right.\)
\(\left\{ \begin{array} { l } { \frac { 1 } { 2 } x = \frac { 2 } { 3 } y } \\ { x - \frac { 2 } { 3 } y = 2 } \end{array} \right.\)
\(\left\{ \begin{array} { l } { - \frac { 1 } { 2 } x + \frac { 1 } { 2 } y = \frac { 5 } { 8 } } \\ { \frac { 1 } { 4 } x + \frac { 1 } { 2 } y = \frac { 1 } { 4 } } \end{array} \right.\)
\(\left\{ \begin{array} { l } { x - y = 0 } \\ { - x + 2 y = 3 } \end{array} \right.\)
\(\left\{ \begin{array} { l } { y = 3 x } \\ { 2 x - 3 y = 0 } \end{array} \right.\)
\(\left\{ \begin{array} { l } { - 3 x + 4 y = 20 } \\ { 2 x + 8 y = 8 } \end{array} \right.\)
\(\left\{ \begin{array} { l } { 5 x - 3 y = - 1 } \\ { 3 x + 2 y = 7 } \end{array} \right.\)
\(\left\{ \begin{array} { l } { - 3 x + 7 y = 2 } \\ { 2 x + 7 y = 1 } \end{array} \right.\)
\(\left\{ \begin{array} { l } { x = 5 } \\ { x = - 2 } \end{array} \right.\)
\(\left\{ \begin{array} { l } { y = 4 } \\ { 5 y = 20 } \end{array} \right.\)

Contestar

1. \((-2,11)\)

3. \((2,2)\)

5. \(\varnothing\)

7. \(( x , 2 x + 3 )\)

9. \(( 4 , - 2 )\)

11. \(( 3 , - 2 )\)

13. \(( 3 , - 4 )\)

15. \(\left( - \frac { 8 } { 5 } , - \frac { 7 } { 10 } \right)\)

17. \(\left( x , - \frac { 1 } { 2 } x - 3 \right)\)

19. \(\varnothing\)

21. \(( 2 , - 3 )\)

23. \(\left( \frac { 1 } { 2 } , 0 \right)\)

25. \(\varnothing\)

27. \(( 1,1 )\)

29. \(\left( - \frac { 11 } { 10 } , - \frac { 2 } { 5 } \right)\)

31. \(\left( - \frac { 1 } { 2 } , \frac { 3 } { 4 } \right)\)

33. \((0,0)\)

35. \((1, 2)\)

37. \(\varnothing\)

Ejercicio\(\PageIndex{7}\)

Resolver por eliminación.

\(\left\{ \begin{array} { l } { 6 x + y = 3 } \\ { 3 x - y = 0 } \end{array} \right.\)
\(\left\{ \begin{array} { l } { x + y = 3 } \\ { 2 x - y = 9 } \end{array} \right.\)
\(\left\{ \begin{array} { l } { x - y = - 6 } \\ { 5 x + y = - 18 } \end{array} \right.\)
\(\left\{ \begin{array} { l } { x + 3 y = 5 } \\ { - x - 2 y = 0 } \end{array} \right.\)
\(\left\{ \begin{array} { l } { - x + 4 y = 4 } \\ { x - y = - 7 } \end{array} \right.\)
\(\left\{ \begin{array} { l } { - x + y = 2 } \\ { x - y = - 3 } \end{array} \right.\)
\(\left\{ \begin{array} { l } { 3 x - y = - 2 } \\ { 6 x + 4 y = 2 } \end{array} \right.\)
\(\left\{ \begin{array} { l } { 5 x + 2 y = - 3 } \\ { 10 x - y = 4 } \end{array} \right.\)
\(\left\{ \begin{array} { l } { - 2 x + 14 y = 28 } \\ { x - 7 y = 21 } \end{array} \right.\)
\(\left\{ \begin{array} { l } { - 2 x + y = 4 } \\ { 12 x - 6 y = - 24 } \end{array} \right.\)
\(\left\{ \begin{array} { l } { x + 8 y = 3 } \\ { 3 x + 12 y = 6 } \end{array} \right.\)
\(\left\{ \begin{array} { l } { 2 x - 3 y = 15 } \\ { 4 x + 10 y = 14 } \end{array} \right.\)
\(\left\{ \begin{array} { l } { 4 x + 3 y = - 10 } \\ { 3 x - 9 y = 15 } \end{array} \right.\)
\(\left\{ \begin{array} { l } { - 4 x - 5 y = - 3 } \\ { 8 x + 3 y = - 15 } \end{array} \right.\)
\(\left\{ \begin{array} { l } { - 2 x + 7 y = 56 } \\ { 4 x - 2 y = - 112 } \end{array} \right.\)
\(\left\{ \begin{array} { l } { - 9 x - 15 y = - 15 } \\ { 3 x + 5 y = - 10 } \end{array} \right.\)
\(\left\{ \begin{array} { l } { 6 x - 7 y = 4 } \\ { 2 x + 6 y = - 7 } \end{array} \right.\)
\(\left\{ \begin{array} { l } { 4 x + 2 y = 4 } \\ { - 5 x - 3 y = - 7 } \end{array} \right.\)
\(\left\{ \begin{array} { l } { 5 x - 3 y = - 1 } \\ { 3 x + 2 y = 7 } \end{array} \right.\)
\(\left\{ \begin{array} { l } { 7 x + 3 y = 9 } \\ { 2 x + 5 y = - 14 } \end{array} \right.\)
\(\left\{ \begin{array} { l } { 9 x - 3 y = 3 } \\ { 7 x + 2 y = - 15 } \end{array} \right.\)
\(\left\{ \begin{array} { l } { 5 x - 3 y = - 7 } \\ { - 7 x + 6 y = 11 } \end{array} \right.\)
\(\left\{ \begin{array} { l } { 2 x + 9 y = 8 } \\ { 3 x + 7 y = - 1 } \end{array} \right.\)
\(\left\{ \begin{array} { l } { 2 x + 2 y = 5 } \\ { 3 x + 3 y = - 5 } \end{array} \right.\)
\(\left\{ \begin{array} { l } { - 3 x + 6 y = - 12 } \\ { 2 x - 4 y = 8 } \end{array} \right.\)
\(\left\{ \begin{array} { l } { 25 x + 15 y = - 1 } \\ { 15 x + 10 y = - 1 } \end{array} \right.\)
\(\left\{ \begin{array} { l } { 2 x - 3 y = 2 } \\ { 18 x - 12 y = 5 } \end{array} \right.\)
\(\left\{ \begin{array} { l } { y = - 2 x - 3 } \\ { - 3 x - 2 y = 4 } \end{array} \right.\)
\(\left\{ \begin{array} { l } { 28 x + 6 y = 9 } \\ { 6 y = 4 x - 15 } \end{array} \right.\)
\(\left\{ \begin{array} { l } { y = 5 x + 15 } \\ { y = - 5 x + 5 } \end{array} \right.\)
\(\left\{ \begin{array} { l } { 2 x - 3 y = 9 } \\ { 5 x - 8 y = - 16 } \end{array} \right.\)
\(\left\{ \begin{array} { l } { \frac { 1 } { 2 } x - \frac { 1 } { 3 } y = \frac { 1 } { 6 } } \\ { \frac { 5 } { 2 } x + y = \frac { 7 } { 2 } } \end{array} \right.\)
\(\left\{ \begin{array} { l } { \frac { 1 } { 4 } x - \frac { 1 } { 9 } y = 1 } \\ { x + y = \frac { 3 } { 4 } } \end{array} \right.\)
\(\left\{ \begin{array} { l } { \frac { 1 } { 2 } x - \frac { 1 } { 4 } y = \frac { 1 } { 3 } } \\ { \frac { 1 } { 4 } x + \frac { 1 } { 2 } y = - \frac { 19 } { 6 } } \end{array} \right.\)
\(\left\{ \begin{array} { l } { - \frac { 14 } { 3 } x + 2 y = 4 } \\ { - \frac { 1 } { 3 } x + \frac { 1 } { 7 } y = \frac { 4 } { 21 } } \end{array} \right.\)
\(\left\{ \begin{array} { l } { 0.025 x + 0.1 y = 0.5 } \\ { 0.11 x + 0.04 y = - 0.2 } \end{array} \right.\)
\(\left\{ \begin{array} { l } { 1.3 x + 0.1 y = 0.35 } \\ { 0.5 x + y = - 2.75 } \end{array} \right.\)
\(\left\{ \begin{array} { l } { x + y = 5 } \\ { 0.02 x + 0.03 y = 0.125 } \end{array} \right.\)

Contestar

1. \(\left( \frac { 1 } { 3 } , 1 \right)\)

3. \((-4,2)\)

5. \((-8,-1)\)

7. \(\left( - \frac { 1 } { 3 } , 1 \right)\)

9. \(\varnothing\)

11. \(\left( 1 , \frac { 1 } { 4 } \right)\)

13. \((-1,-2)\)

15. \((-28,0)\)

17. \(\left( - \frac { 1 } { 2 } , - 1 \right)\)

19. \((1,2)\)

21. \((-1,-4)\)

23. \((-5,2)\)

25. \(\left( x , \frac { 1 } { 2 } x - 2 \right)\)

27. \(\left( - \frac { 3 } { 10 } , - \frac { 13 } { 15 } \right)\)

29. \(\left( \frac { 3 } { 4 } , - 2 \right)\)

31. \((120,77)\)

33. \(\left( 3 , - \frac { 9 } { 4 } \right)\)

35. \(\varnothing\)

37. \(( 0.5 , - 3 )\)

Ejercicio\(\PageIndex{8}\)

Resuelve usando cualquier método.

\(\left\{ \begin{array} { l } { 6 x = 12 y + 7 } \\ { 6 x + 24 y + 5 = 0 } \end{array} \right.\)
\(\left\{ \begin{array} { l } { y = 2 x - 3 } \\ { 3 x + y = 12 } \end{array} \right.\)
\(\left\{ \begin{array} { l } { x + 3 y = - 5 } \\ { y = \frac { 1 } { 3 } x + 5 } \end{array} \right.\)
\(\left\{ \begin{array} { l } { y = 1 } \\ { x = - 4 } \end{array} \right.\)
\(\left\{ \begin{array} { l } { y = \frac { 1 } { 2 } } \\ { x + 9 = 0 } \end{array} \right.\)
\(\left\{ \begin{array} { l } { y = x } \\ { - x + y = 1 } \end{array} \right.\)
\(\left\{ \begin{array} { l } { y = 5 x } \\ { y = - 10 } \end{array} \right.\)
\(\left\{ \begin{array} { l } { y = - \frac { 3 } { 2 } x + 1 } \\ { - 2 y + 2 = 3 x } \end{array} \right.\)
\(\left\{ \begin{array} { l } { 7 y = - 2 x - 1 } \\ { 7 x = 2 y + 23 } \end{array} \right.\)
\(\left\{ \begin{array} { l } { 5 x + 9 y - 14 = 0 } \\ { 3 x + 2 y - 5 = 0 } \end{array} \right.\)
\(\left\{ \begin{array} { l } { y = - \frac { 5 } { 16 } x + 10 } \\ { y = \frac { 5 } { 16 } x - 10 } \end{array} \right.\)
\(\left\{ \begin{array} { l } { y = - \frac { 6 } { 5 } x + 12 } \\ { x = 6 } \end{array} \right.\)
\(\left\{ \begin{array} { l } { 2 ( x - 3 ) + y = 0 } \\ { 3 ( 2 x + y - 1 ) = 15 } \end{array} \right.\)
\(\left\{ \begin{array} { l } { 3 - 2 ( x - y ) = - 3 } \\ { 4 x - 3 ( y + 1 ) = 8 } \end{array} \right.\)
\(\left\{ \begin{array} { l } { 2 ( x + 1 ) = 3 ( 2 y - 1 ) - 21 } \\ { 3 ( x + 2 ) = 1 - ( 3 y - 2 ) } \end{array} \right.\)
\(\left\{ \begin{array} { l } { \frac { x } { 2 } - \frac { y } { 3 } = - 7 } \\ { \frac { x } { 3 } - \frac { y } { 2 } = - 8 } \end{array} \right.\)
\(\left\{ \begin{array} { l } { - \frac { 1 } { 7 } x + y = - \frac { 2 } { 3 } } \\ { - \frac { 1 } { 14 } x + \frac { 1 } { 2 } y = \frac { 1 } { 3 } } \end{array} \right.\)
\(\left\{ \begin{array} { l } { \frac { x } { 4 } - \frac { y } { 2 } = \frac { 3 } { 4 } } \\ { \frac { x } { 3 } + \frac { y } { 6 } = \frac { 1 } { 6 } } \end{array} \right.\)
\(\left\{ \begin{array} { l } { y = - \frac { 5 } { 3 } x + \frac { 1 } { 2 } } \\ { \frac { 1 } { 3 } x + \frac { 1 } { 5 } y = \frac { 1 } { 10 } } \end{array} \right.\)
\(\left\{ \begin{array} { l } { \frac { 1 } { 15 } x - \frac { 1 } { 12 } y = \frac { 1 } { 3 } } \\ { - \frac { 3 } { 10 } x + \frac { 3 } { 8 } y = - \frac { 3 } { 2 } } \end{array} \right.\)
\(\left\{ \begin{array} { l } { 0.2 x - 0.05 y = 0.43 } \\ { 0.3 x + 0.1 y = - 0.3 } \end{array} \right.\)
\(\left\{ \begin{array} { l } { 0.1 x + 0.3 y = 0.3 } \\ { 0.05 x - 0.5 y = - 0.63 } \end{array} \right.\)
\(\left\{ \begin{array} { l } { 0.15 x - 0.25 y = - 0.3 } \\ { - 0.75 x + 1.25 y = - 4 } \end{array} \right.\)
\(\left\{ \begin{array} { l } { - 0.15 x + 1.25 y = 0.4 } \\ { - 0.03 x + 0.25 y = 0.08 } \end{array} \right.\)

Contestar

1. \(\left( \frac { 1 } { 2 } , - \frac { 1 } { 3 } \right)\)

3. \(\left( - 10 , \frac { 5 } { 3 } \right)\)

5. \(\left( - 9 , \frac { 1 } { 2 } \right)\)

7. \(( - 2 , - 10 )\)

9. \(( 3 , - 1 )\)

11. \(( 32,0 )\)

13. \(( x , - 2 x + 6 )\)

15. \(( - 4,3 )\)

17. \(\varnothing\)

19. \(\left( x - \frac { 5 } { 3 } x + \frac { 1 } { 2 } \right)\)

21. \(( 0.8 , - 5.4 )\)

23. \(\varnothing\)

Ejercicio\(\PageIndex{9}\)

Explicar a un estudiante principiante de álgebra cómo elegir un método para resolver un sistema de dos ecuaciones lineales. Además, explica cómo son las soluciones y por qué.
Configura tu propio sistema lineal con dos variables y resolverlo usando los tres métodos. Explique qué método era preferible en su ejercicio.

Contestar: 1. La respuesta puede variar

Notas al pie

¹¹ Un medio para resolver un sistema lineal resolviendo una de las variables y sustituyendo el resultado por la otra ecuación.

¹² Una vez que se encuentra un valor para una variable, sustituirlo de nuevo por una de las ecuaciones originales, o su equivalente, para determinar el valor correspondiente de la otra variable.

¹³ Un medio para resolver un sistema mediante la adición de ecuaciones equivalentes de tal manera que se elimine una variable.

¹⁴ A menudo se usa cuando se hace referencia al método de eliminación para resolver sistemas.

¹⁵ Si\(A, B, C\), y\(D\) son expresiones algebraicas, donde\(A = B\) y\(C = D\), entonces\(A + C = B + D\).