3.3: Aplicaciones de Sistemas Lineales con Dos Variables
( \newcommand{\kernel}{\mathrm{null}\,}\)
Objetivos de aprendizaje
- Configurar y resolver aplicaciones que involucren relaciones entre dos variables.
- Configurar y resolver problemas de mezcla.
- Configure y resuelva problemas de movimiento uniforme (problemas de distancia).
Problemas que involucran relaciones entre dos variables
Si traducimos una aplicación a una configuración matemática usando dos variables, entonces necesitamos formar un sistema lineal con dos ecuaciones. Establecer problemas verbales con dos variables a menudo simplifica todo el proceso, particularmente cuando las relaciones entre las variables no son tan claras.
Ejemplo3.3.1:
La suma de4 veces un entero más grande y5 veces un entero más pequeño es7. Cuando se resta el doble del número entero menor de3 veces el mayor, el resultado es11. Encuentra los enteros.
Solución
Comience asignando variables al entero mayor y menor.
Letx representar el entero más grande.
Lety representar el entero más pequeño.
Al usar dos variables, necesitamos establecer dos ecuaciones. La primera frase describe una suma y la segunda frase describe una diferencia.


Esto lleva al siguiente sistema:
{4x+5y=73x−2y=11
Resuelve usando el método de eliminación. Para eliminar la variabley multiplicar la primera ecuación por2 y la segunda por5.
{4x+5y=7×2⇒3x−2y=11⇒×5{8x+10y=1415x−10y=55
Sumar las ecuaciones en el sistema equivalente y resolver parax.
8x+10y=14±15x−10y=5523x=99x=6923x=3
Volver sustituto para encontrary.
4x+5y=74(3)+5y=712+5y=75y=−5y=−1
Respuesta:
El entero más grande es3 y el entero más pequeño es−1.
Ejercicio3.3.1
Un entero es1 menos del doble que el de otro. Si su suma es20, encuentra los enteros.
- Responder
-
Los dos enteros son7 y13.
www.youtube.com/v/lnzo1_J4x20
A continuación considere aplicaciones que involucren simples intereses y dinero.
Ejemplo3.3.1:
Un total de$12,800 se invirtió en dos cuentas. Parte se invirtió en un CD a una tasa de interés anual318% y parte se invirtió en un fondo del mercado monetario a una tasa de interés434% anual. Si el interés simple total de un año fue$465, entonces ¿cuánto se invirtió en cada cuenta?
Solución
Comience por identificar dos variables.
Dejarx representar la cantidad invertida en318%=3.125%=0.03125.
Dejary representar la cantidad invertida en434%=4.75% =0.0475.
El monto total en ambas cuentas se puede expresar como
x+y=12,800
Para establecer una segunda ecuación, utilice el hecho de que el interés total fue$465. Recordemos que el interés por un año es la tasa de interés multiplicada por el principal(I=prt=pr⋅1=p). Use esto para agregar los intereses en ambas cuentas. Asegúrese de que r utilice los equivalentes decimales para las tasas de interés dadas como porcentajes.
interestfromtheCD+interestfromthefund=totalinterest0.03125x+0.0475y=465
Estas dos ecuaciones juntas forman el siguiente sistema lineal:
{x+y=12,8000.03125x+0.0475y=465
Eliminarx multiplicando la primera ecuación por−0.03125.
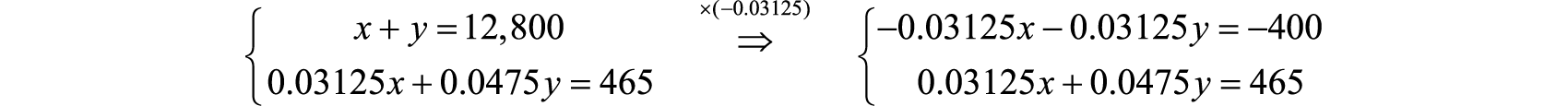
A continuación, agregue las ecuaciones resultantes.
−0.03125x−0.03125y=−400±0.03125x+0.0475y=4650.01625y=65y=650.01635y=4,000
Volver sustituto para encontrarx.
x+y=12,800x+4000=12,800x=8,800
Respuesta:
$4,000se invirtió en434% y$8,800 se invirtió en318%.
Ejemplo3.3.3:
Un frasco que consta de solo monedas de cinco centavos y diez centavos contiene58 monedas. Si el valor total es$4.20, ¿cuántas de cada moneda hay en el frasco?
Solución
Dejarn representar el número de monedas de cinco centavos en el frasco.
Dejard representar el número de monedas de diez centavos en el frasco.
El número total de monedas en el frasco se puede expresar usando la siguiente ecuación:
n+d=58
A continuación, utilice el valor de cada moneda para determinar el valor total$4.20.
valueofnickels+valueofdimes=totalvalue0.05n+0.10d=4.20
Esto nos lleva al siguiente sistema lineal:
{n+d=580.05n+0.10d=4.20
Aquí resolveremos usando el método de sustitución. En la primera ecuación, podemos resolver paran.

Sustituirn=58−d en la segunda ecuación y resolver parad.
0.05(58−d)+0.10d=4.202.9−0.05d+0.10d=4.202.9+0.05d=4.200.05d=1.3d=26
Ahora vuelve sustituto para encontrar el número de nickels.
n=58−d=58−26=32
Respuesta:
Hay32 monedas de cinco y26 diez centavos en el frasco.
Ejercicio3.3.2
Joey tiene un frasco lleno de40 monedas que consta de solo cuartos y monedas de cinco centavos. Si el valor total es$5.00, ¿cuántas de cada moneda tiene Joey?
- Responder
-
Joey tiene15 cuartos y monedas de25 cinco centavos.
www.youtube.com/v/41bxt_tthka
Problemas de mezcla
Los problemas de mezcla suelen incluir un porcentaje y alguna cantidad total. Es importante hacer una distinción entre estos dos tipos de cantidades. Por ejemplo, si un problema indica que un recipiente de20 -onza se llena con una solución salina (sal)2%, entonces esto significa que el recipiente se llena con una mezcla de sal y agua de la siguiente manera:
| Porcentaje | Monto | |
|---|---|---|
| Sal | 2=0.02 | 0.02(20)=0.4onzas onzas |
| Agua | 98%=0.98 | 0.98(20)=19.6onzas onzas |
Es decir, multiplicamos el porcentaje por el total para obtener la cantidad de cada parte de la mezcla.
Ejemplo3.3.4:
Se debe combinar una solución salina en1.8% y mezclarse con una solución salina3.2% para producir35 onzas de una solución salina2.2%. ¿Cuánto de cada uno se necesita?
Solución
Dejarx representar la cantidad de1.8% de solución salina necesaria.
Dejary representar la cantidad de3.2% de solución salina necesaria.
La cantidad total de solución salina necesaria es de35 onzas. Esto lleva a una ecuación,
x+y=35
La segunda ecuación suma la cantidad de sal en los porcentajes correctos. La cantidad de sal se obtiene multiplicando el porcentaje por la cantidad, donde las variablesx yy representan las cantidades de las soluciones. La cantidad de sal en la solución final es2.2% de las35 onzas, o.022(35).
saltin1.8%solution+saltin3.2%solution=saltintheendsolution0.018x+0.032y=0.022(35)
La configuración algebraica consiste en ambas ecuaciones presentadas como un sistema:
{x+y=350.018x+0.032y=0.022(35)
Resolver.
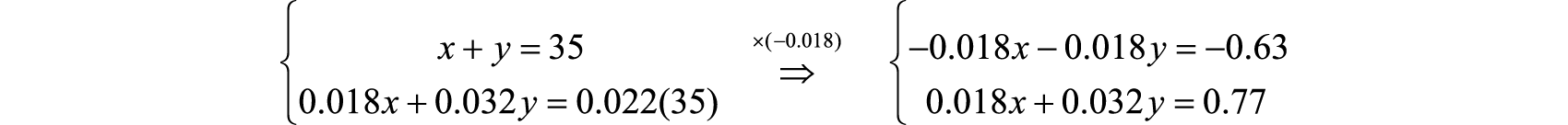
Sumar las ecuaciones resultantes juntas
−0.018x−0.018y=−0.63±0.018x+0.032y=0.770.014y=0.14y=0.140.014y=10
Volver sustituto para encontrarx.
x+y=35x+10=35x=25
Respuesta:
Necesitamos25 onzas del1.8% de solución salina y10 onzas de la solución salina3.2%.
Ejemplo3.3.5:
Un concentrado80% anticongelante se va a mezclar con agua para producir una mezcla de48 -litros que contiene25% anticongelante. ¿Cuánta agua y concentrado anticongelante se necesita?
Solución
Dejarx representar la cantidad de80% de concentrado anticongelante necesario.
Dejary representar la cantidad de agua necesaria.
La cantidad total de la mezcla debe ser de48 litros.
x+y=48
La segunda ecuación suma la cantidad de anticongelante de cada solución en los porcentajes correctos. La cantidad de anticongelante en el resultado final es25% de48 litros, o0.25(48).
antifreezein80%concentrate+antrifreezeinwater=antifreezeintheendmixture0.018x+0.032y=0.022(35)
Ahora podemos formar un sistema de dos ecuaciones lineales y dos variables de la siguiente manera:
{x+y=480.80x=0.25(48)⇒{x+y=480.80x=12
Usa la segunda ecuación para encontrarx:
0.80x=12x=120.80x=15
Volver sustituto para encontrary.
x+y=4815+y=48y=33
Respuesta:
Necesitamos mezclar33 litros de agua con15 litros de concentrado anticongelante.
Ejercicio3.3.3
Un químico desea crear100 ml de una solución con12% de contenido de ácido. Utiliza dos tipos de soluciones madre, una con30% de contenido de ácido y otra con10% de contenido de ácido. ¿Cuánto de cada uno necesita?
- Responder
-
El químico necesitará mezclar10 ml de la solución30% ácida con90 ml de la solución10% ácida.
www.youtube.com/v/nxbyjne9mww
Problemas de movimiento uniforme (problemas de distancia)
Recordemos que la distancia recorrida es igual a la tasa promedio multiplicada por el tiempo recorrido a ese ritmo,D=r⋅t. Estos problemas de movimiento uniforme suelen tener muchos datos, por lo que ayuda a organizar primero esos datos en un gráfico y luego configurar un sistema lineal. En esta sección, se le anima a utilizar dos variables.
Ejemplo3.3.6:
Un ejecutivo viajó un total de4 horas y875 millas en automóvil y en avión. Conduciendo al aeropuerto en automóvil, promedió50 millas por hora. En el aire, el avión promedió320 millas por hora. ¿Cuánto tiempo le tomó conducir hasta el aeropuerto?
Solución
Se nos pide encontrar el tiempo que le lleva conducir hasta el aeropuerto; esto indica que el tiempo es la cantidad desconocida.
Vamos ax representar el tiempo que tardó en conducir hasta el aeropuerto. Dejary representar el tiempo pasado en el aire.
Rellene la tabla con la información dada.

Usa la fórmulaD=r⋅t para rellenar las distancias desconocidas.
Distance traveled in the car: D=r⋅t=50⋅x Distance traveled in the air: D=r⋅t=320⋅y

La columna de distancia y la columna de tiempo del gráfico nos ayudan a configurar el siguiente sistema lineal.
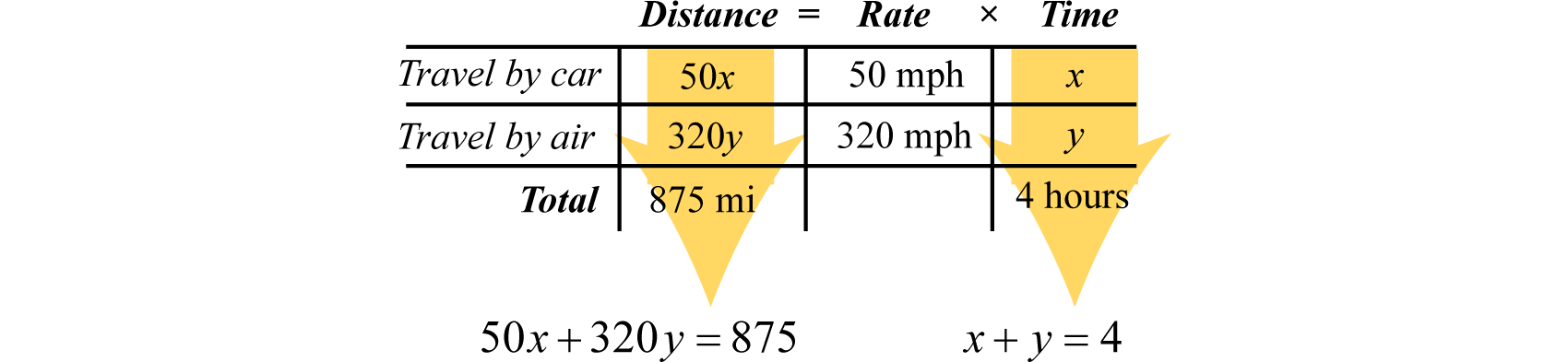
{x+y=4←totaltimetraveled50x+320y=875←totaldistancetraveled
Resolver.
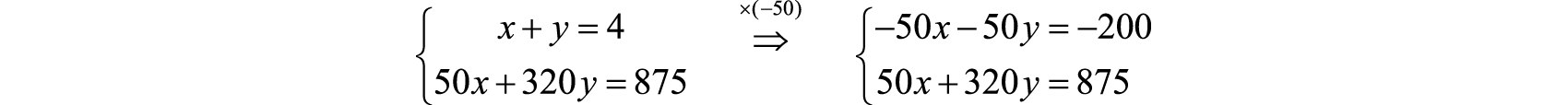
−50x−50y=−200±50x+320y=875270y=675y=675270y=52
Ahora vuelve sustituto para encontrar el tiempox que tardó en conducir hasta el aeropuerto:
x+y=4x+52=4x=82−52x=32
Respuesta:
Le tomó112 horas conducir hasta el aeropuerto.
No siempre ocurre que el tiempo es la cantidad desconocida. Lee el problema detenidamente e identifica lo que te piden que encuentres; esto define tus variables.
Ejemplo3.3.7:
Volando con el viento, un avión ligero viajó240 millas en2 horas. El avión giró entonces contra el viento y recorrió otras135 millas en112 horas. Encuentra la velocidad del avión y la velocidad del viento.
Solución
Comience por identificar variables.
Dejarx representar la velocidad del avión.
Dejarw representar la velocidad del viento.
Utilice la siguiente tabla para organizar los datos:

Con el viento, la velocidad total del avión esx+w. Volando contra el viento, la velocidad total esx−w.

Utilice las filas del gráfico junto con la fórmulaD=r⋅t para construir un sistema lineal que modele este problema. Tenga cuidado de agrupar entre paréntesis las cantidades que representan la tasa.
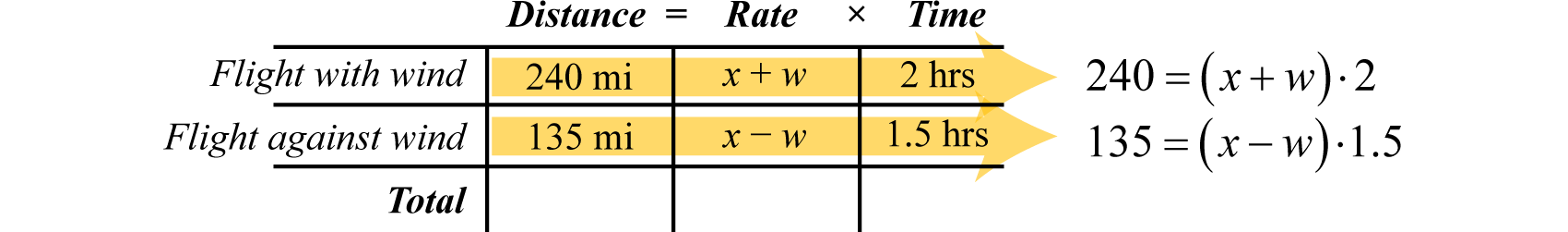
{240=(x+w)⋅2←distancetraveledwiththewind135=(x−w)⋅1.5←distancetraveledagainstthewind
Si dividimos ambos lados de la primera ecuación por2 y ambos lados de la segunda ecuación por1.5, entonces obtenemos el siguiente sistema equivalente:
{240=(x+w)⋅2÷2⟹135=(x−w)⋅1.5⟹÷1.5{120=x+w90=x−w
Aquíw está alineado para eliminar.
x+w=120±x−w=902x=210x=2102x=105
Sustituto de espalda
x+w=120105+w=120w=15
Respuesta:
La velocidad del avión es de105 millas por hora y la velocidad del viento es de15 millas por hora.
Ejercicio3.3.4
Un barco viajó27 millas río abajo en2 horas. En el viaje de regreso, que fue contra la corriente, el barco sólo pudo recorrer21 millas en2 horas. ¿Cuáles fueron las velocidades de la embarcación y de la corriente?
- Responder
-
La velocidad de la embarcación era de12 millas por hora y la velocidad de la corriente era de1.5 millas por hora.
www.youtube.com/V/evdjqTfsUSS
Claves para llevar
- Utilice dos variables como medio para simplificar la configuración algebraica de aplicaciones donde la relación entre incógnitas no está clara.
- Lee atentamente el problema varias veces. Si se utilizan dos variables, entonces recuerde que necesita configurar dos ecuaciones lineales para resolver el problema.
- Asegúrese de responder la pregunta en forma de oración e incluya las unidades correctas para la respuesta.
Ejercicio3.3.5
Configura un sistema lineal y resuelve.
- La suma de dos enteros es45. El entero más grande es3 menos del doble del menor. Encuentra los dos enteros.
- La suma de dos enteros es126. Cuanto más grande es18 menor que5 veces más pequeño. Encuentra los dos enteros.
- La suma de dos enteros es41. Cuando los3 tiempos más pequeños se resta de cuanto mayor es el resultado17. Encuentra los dos enteros.
- La suma de dos enteros es46. Cuando cuanto más grande se resta del doble de menor es el resultado2. Encuentra los dos enteros.
- La diferencia de dos enteros es11. Cuando el doble de mayor se resta de3 veces más pequeño, el resultado es3. Encuentra los enteros.
- La diferencia de dos enteros es6. La suma del doble de menor y mayor es72. Encuentra los enteros.
- La suma de3 veces un entero mayor y2 veces un menor es15. Cuando3 el número entero más pequeño se resta del doble del mayor, el resultado es23. Encuentra los enteros.
- La suma de dos veces un entero mayor y3 veces un menor es10. Cuando las4 veces que se agrega el entero más pequeño al mayor, el resultado es0. Encuentra los enteros.
- La diferencia de dos veces un número entero menor y7 veces un mayor es4. Cuando las5 veces el entero más grande se resta de3 veces el menor, el resultado es−5. Encuentra los enteros.
- La diferencia de un entero menor y dos veces mayor es0. Cuando las3 veces el entero más grande se resta de2 veces el menor, el resultado es−5. Encuentra los enteros.
- La longitud de un rectángulo es5 más del doble de su ancho. Si el perímetro mide46 metros, entonces encuentra las dimensiones del rectángulo.
- El ancho de un rectángulo es2 centímetros menos de la mitad de su longitud. Si el perímetro mide62 centímetros, entonces encuentra las dimensiones del rectángulo.
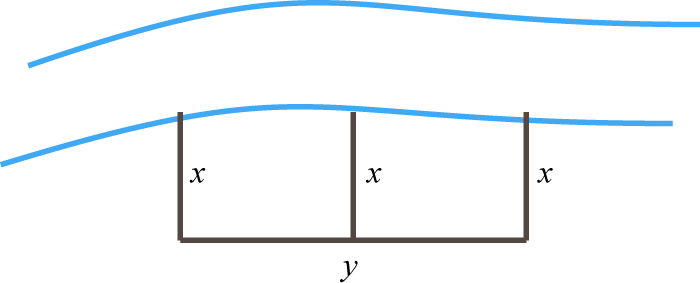
- Se construye un corral rectangular particionado junto a un río con un total de136 pies de cercado (ver ilustración). Si la esgrima exterior mide114 pies, entonces encuentra las dimensiones de la pluma.
14. Se construye una pluma rectangular particionada con un total de168 pies de cercado (ver ilustración). Si el perímetro mide138 pies, entonces encuentra las dimensiones de la pluma.

15. Encontrara yb tal que el sistema{ax+by=8bx+ay=7 tenga solución(2,1). (Pista: Sustituir losy valoresx - y -dados y resolver el sistema lineal resultante en términos dea yb.)
16. Encontrara yb tal que el sistema{ax−by=11bx+ay=13 tenga solución(3,−1).
17. Una línea pasa por dos puntos(5,−9) y(−3,7). Utilizar estos puntos yy=mx+b construir un sistema de dos ecuaciones lineales en términos demb y resolverlo.
18. Una línea pasa por dos puntos(2,7) y(12,−2). Utilizar estos puntos yy=mx+b construir un sistema de dos ecuaciones lineales en términos demb y resolverlo.
19. Un$5,200 principal se invierte en dos cuentas, una ganando3% de interés y otra ganando6% de interés. Si el interés total del año es$210, entonces ¿cuánto se invierte en cada cuenta?
20. El$2,200 ahorro de Harry está en dos cuentas. Una cuenta gana2% de interés anual y la otra gana4%. Su interés total para el año es$69. ¿Cuánto tiene en cada cuenta?
21. Janine tiene dos cuentas de ahorro por un total$6,500. Una cuenta gana234% de interés anual y la otra gana312%. Si su interés total para el año es$211, entonces ¿cuánto hay en cada cuenta?
22. Margaret tiene sus ahorros totales de$24,200 en dos cuentas de CD diferentes. Un CD gana4.6% interés y otro gana3.4% interés. Si su interés total para el año es$1,007.60, entonces ¿cuánto tiene en cada cuenta de CD?
23. El año pasado Mandy ganó el doble de interés en su fondo del Mercado Monetario que en su cuenta de ahorros regular. El interés total de las dos cuentas fue$246. ¿Cuánto interés ganó en cada cuenta?
24. Una pequeña empresa invirtió$120,000 en dos cuentas. La cuenta que gana4% de interés anual arrojó el doble de interés que la cuenta que ganaba3% de interés anual. ¿Cuánto se invirtió en cada cuenta?
25. Sally gana$1,000 por mes más una comisión del2% de ventas. Jane gana$200 por mes más6% de sus ventas. ¿En qué cifra de ventas mensuales tanto Sally como Jane ganarán la misma cantidad de pago?
26. El costo de producir estantes especiales para libros incluye una tarifa inicial de instalación$1,200 más un adicional$20 por unidad producida. Cada repisa se puede vender$60 por unidad. Encuentra el número de unidades que se deben producir y vender donde los costos equivalen a los ingresos generados.
27. Jim pudo comprar una pizza para$12.35 con cuartos y monedas de diez centavos. Si usa71 monedas para comprar la pizza, entonces ¿cuántos de cada uno tenía?
28. Una caja registradora contiene$5 facturas y$10 facturas con un valor total de$350. Si hay46 facturas totales, entonces ¿cuántos de cada uno contiene el registro?
29. Dos familias compraron boletos para el partido de basquetbol en casa. Una familia ordenó boletos2 para adultos y boletos para4 niños por un total de$36.00. Otra familia ordenó boletos3 para adultos y boletos para2 niños por un total de$32.00. ¿Cuánto costó cada boleto?
30. Dos amigos encontraron camisas y pantalones cortos a la venta en un mercadillo. Uno compró4 camisas y2 pantalones cortos por un total de$28.00. El otro compró3 camisas y3 pantalones cortos por un total de$30.75. ¿Cuánto costaba cada camisa y cada par de pantalones cortos?
31. Un teatro comunitario vendió140 boletos para el musical vespertino por un total de$1,540. Cada boleto de adulto se vendió para$12 y cada boleto infantil se vendió para$8. ¿Cuántos boletos de adulto se vendieron?
32. La librería del campus vende calculadoras gráficas para$110 y calculadoras científicas para$16. El primer día de clases se vendieron50 calculadoras por un total de$1,646. ¿Cuántos de cada uno se vendieron?
33. Un frasco que consta de solo monedas de cinco centavos y cuartos contiene70 monedas. Si el valor total es$9.10, ¿cuántas de cada moneda hay en el frasco?
34. Jill tiene$9.20 valor de dimes y cuartos. Si hay68 monedas en total, ¿cuántas de cada una tiene?
- Responder
-
1. Los enteros son16 y29.
3. Los enteros son6 y35.
5. Los enteros son25 y36.
7. Los enteros son−3 y7.
9. Los enteros son−5 y−2.
11. Largo:17 metros; ancho:6 metros
13. Ancho:22 pies; largo:70 pies
15. a=3,b=2
17. m=−2,b=1
19. $3,400al3% y$1,800 al6%
21. $2,200al234% y$4,300 al312%
23. Ahorro:$82; Mercado Monetario:$164.
25. $20,000
27. 35cuartos y36 dimes
29. Adultos$7.00 cada uno y niños$5.50 cada uno.
31. 105Se vendieron boletos para adultos.
33. El frasco contiene42 monedas de níquel y28 cuartos.
Ejercicio3.3.6
Configura un sistema lineal y resuelve.
- Se debe mezclar una solución17% ácida con una solución9% ácida para producir8 galones de una solución10% ácida. ¿Cuánto de cada uno se necesita?
- Una enfermera desea obtener28 onzas de un1.5% de solución salina. ¿Cuánto de un1% de solución salina debe mezclar con un4.5% de solución salina para lograr la mezcla deseada?
- Un cliente ordenó4 libras de un producto mixto de maní que contenía12% de anacardos. El inventario consta de sólo dos mezclas que contienen10% y26% de anacardos. ¿Cuánto de cada tipo se debe mezclar para llenar el pedido?
- Una solución de alcohol contiene10% de alcohol y otra contiene25% de alcohol. ¿Cuánto de cada uno debe mezclarse para obtener2 galones de una solución de13.75% de alcohol?
- ¿Cuánto concentrado de líquido limpiador, con60% de contenido de alcohol, debe mezclarse con agua para obtener una mezcla de24 -onza con15% de contenido de alcohol?
- ¿Cuántas libras de maní puro se deben combinar con una mezcla de20% de maní para producir2 libras de una mezcla de50% de maní?
- Un concentrado de50% de jugo de frutas se puede comprar al por mayor. El mejor sabor se logra cuando se mezcla agua con el concentrado de tal manera que se obtenga una mezcla de15% de jugo de fruta. ¿Cuánta agua y concentrado se necesita para hacer una bebida de jugo de frutas de60 -onza?
- El azúcar puro se debe mezclar con una ensalada de frutas que contenga10% de azúcar para producir65 onzas de una ensalada que contenga18% de azúcar. ¿Cuánto azúcar puro se requiere?
- Se crea una aleación de aluminio personalizada mezclando150 gramos de una aleación de aluminio15% y350 gramos de una aleación de aluminio55%. ¿Qué porcentaje de aluminio hay en la mezcla resultante?
- Un asistente de investigación mezcló500 mililitros de una solución que contenía un12% de ácido con300 mililitros de agua. ¿Qué porcentaje de ácido hay en la solución resultante?
- Responder
-
1. 7galones de la solución de9% ácido y1 galón de la solución17% de ácido
3. 3.5libras de la mezcla de10% de anacardo y0.5 libras de la mezcla de26% de anacardo
5. 6onzas de concentrado de líquido limpiador
7. 18onzas de concentrado de jugo de frutas y42 onzas de agua
9. 43%
Ejercicio3.3.7
Configura un sistema lineal y resuelve.
- Las dos piernas de un viaje432 de milla tardaron8 horas. La velocidad promedio para el primer tramo del viaje fue de52 millas por hora y la velocidad promedio para el segundo tramo del viaje fue de60 millas por hora. ¿Cuánto tiempo duró cada tramo del viaje?
- Jerry tomó dos autobuses en el viaje de una265 milla de Los Ángeles a Las Vegas. El primer autobús promedió55 millas por hora y el segundo autobús pudo promediar50 millas por hora. Si el viaje total tardó5 horas, entonces ¿cuánto tiempo se pasó en cada autobús?
- Una ejecutiva pudo promediar48 millas por hora hasta el aeropuerto en su automóvil y luego abordar un avión que promedió210 millas por hora. El viaje de negocios de549 -milla tomó3 horas. ¿Cuánto tiempo le tomó conducir hasta el aeropuerto?
- Joe pasa1 una hora cada mañana haciendo ejercicio trotando y luego en bicicleta por un total de15 millas. Él es capaz de promediar6 millas por hora trotar y18 millas por hora en bicicleta. ¿Cuánto tiempo pasa trotando cada mañana?
- Nadar con el Jack actual puede nadar2.5 millas en12 hora. Nadando hacia atrás, contra la misma corriente, sólo puede nadar2 millas en la misma cantidad de tiempo. ¿Qué tan rápido es la corriente?
- Un avión ligero que vuela con el viento puede recorrer180 millas en112 horas. El avión puede volar la misma distancia contra el viento en2 horas. Encuentra la velocidad del viento.
- Un avión ligero que vuela con el viento puede recorrer600 millas en4 horas. En el viaje de regreso, contra el viento, tomará5 horas. ¿Cuáles son las velocidades del avión y del viento?
- Un barco puede recorrer15 millas con la corriente aguas abajo en114 horas. Al regresar río arriba contra la corriente, el barco solo puede recorrer834 millas en la misma cantidad de tiempo. Encuentra la velocidad de la corriente.
- Mary recorrió el sendero desde su auto hasta la cabina a razón de6 millas por hora. Luego caminó de regreso a su automóvil a razón de4 millas por hora. Si todo el viaje tardó1 una hora, entonces ¿cuánto tiempo le tomó caminar de regreso a su auto?
- Dos trenes salen de la estación viajando en direcciones opuestas. Un tren es8 millas por hora más rápido que el otro y en212 horas están230 a millas de distancia. Determinar la velocidad promedio de cada tren.
- Dos trenes salen de la estación viajando en direcciones opuestas. Un tren es12 millas por hora más rápido que el otro y en3 horas están300 a millas de distancia. Determinar la velocidad promedio de cada tren.
- Un corredor puede mantener una tasa promedio de carrera de8 millas por hora a su destino y6 millas por hora en el viaje de regreso. Encuentra la distancia total que corrió el jogger si el tiempo total de carrera fue de134 hora.
- Responder
-
1. El partido de ida del viaje tomó6 horas y el de vuelta tomó2 horas.
3. Le tomó12 una hora conducir hasta el aeropuerto.
5. 0.5millas por hora.
7. Avión:135 millas por hora; viento:15 millas por hora
9. 35hora
11. Un tren promedió44 millas por hora y el otro promedió56 millas por hora.
Ejercicio3.3.8
- Redacte un problema de número o dinero propio y compártelo en el tablero de discusión.
- Redacte un problema de mezcla propio y compártelo en el tablero de discusión.
- Redacte un problema de movimiento uniforme propio y compártelo en el tablero de discusión.
- Responder
-
1. La respuesta puede variar
3. La respuesta puede variar


