3.7: Resolviendo Sistemas de Desigualdades con Dos Variables
- Page ID
- 109836
Objetivos de aprendizaje
- Verificar soluciones a sistemas de desigualdades con dos variables.
- Grapar conjuntos de soluciones de sistemas de desigualdades.
Soluciones a Sistemas de Desigualdades
Un sistema de desigualdades 33 consiste en un conjunto de dos o más desigualdades con las mismas variables. Las desigualdades definen las condiciones que deben considerarse simultáneamente. Por ejemplo,
\(\left\{ \begin{array} { l } { y > x - 2 } \\ { y \leq 2 x + 2 } \end{array} \right.\)
Sabemos que cada desigualdad en el conjunto contiene infinitamente muchas soluciones de pares ordenados definidas por una región en un plano de coordenadas rectangulares. Al considerar dos de estas desigualdades juntas, la intersección de estos conjuntos definirá el conjunto de soluciones simultáneas de pares ordenados. Cuando graficamos cada una de las desigualdades anteriores por separado tenemos:
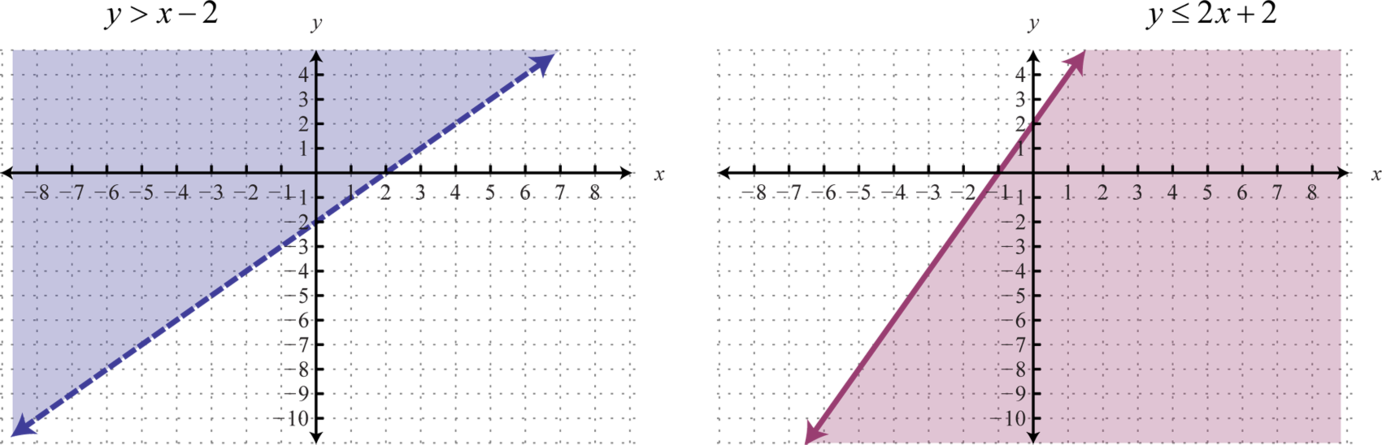
Y cuando se grafica en el mismo conjunto de ejes, se puede determinar la intersección.
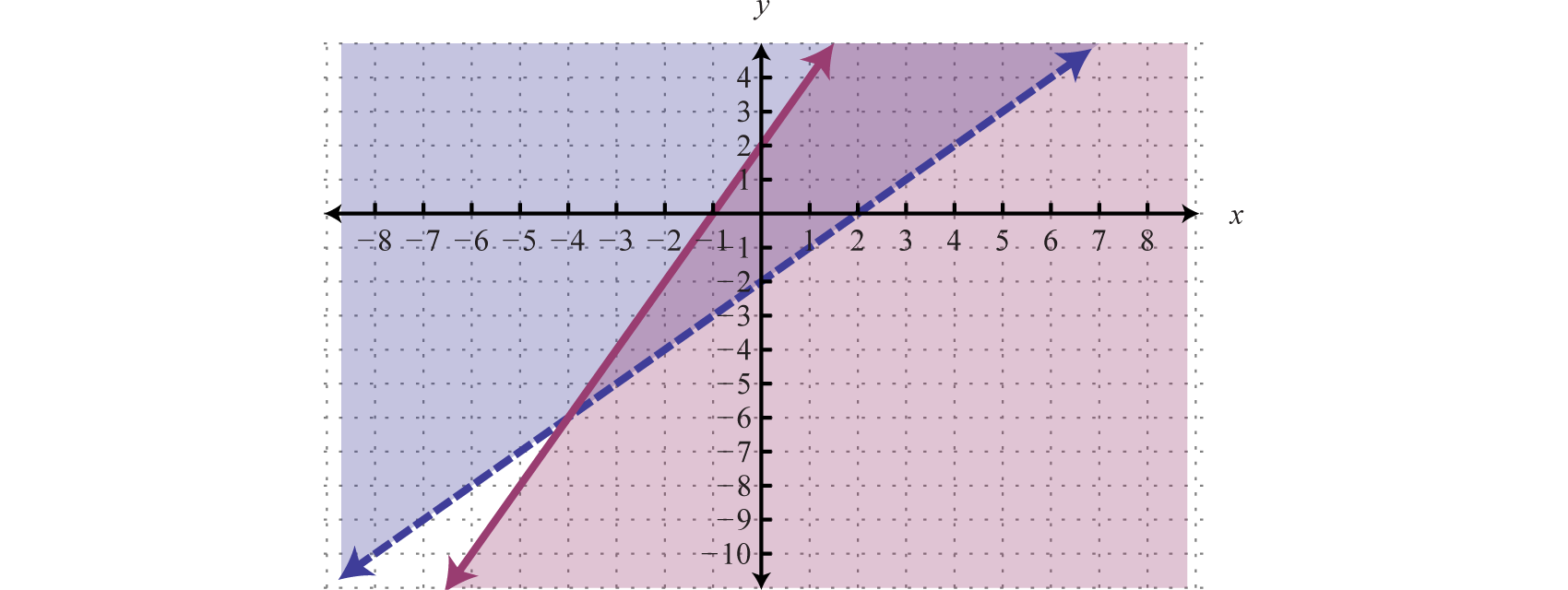
La intersección está sombreada más oscura y la gráfica final del conjunto de soluciones se presentará de la siguiente manera:
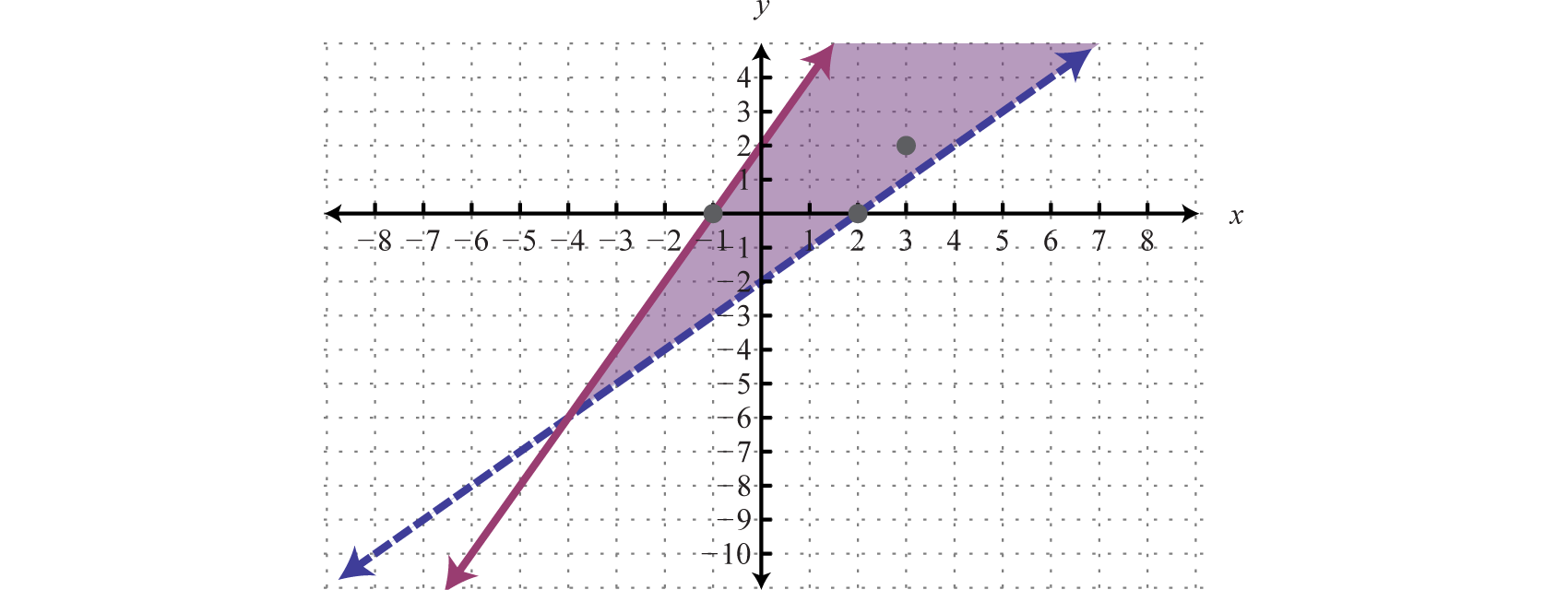
El gráfico sugiere que\((3, 2)\) es una solución porque está en la intersección. Para verificar esto, podemos demostrar que resuelve ambas desigualdades originales de la siguiente manera:
| \(\color{Cerulean}{Check :}\:\:\color{YellowOrange}{(3,2)}\) | |
|
Desigualdad\(1\): \(\begin{array} { l } { y > x - 2 } \\ { \color{Cerulean}{2}\color{black}{ >}\color{Cerulean}{ 3}\color{black}{ -} 2 } \\ { 2 > 1 }\:\: \color{Cerulean}{✓} \end{array}\) |
Desigualdad\(2\): \(\begin{array} { l } { y \leq 2 x + 2 } \\ { \color{Cerulean}{2}\color{black}{ \leq} 2 (\color{Cerulean}{ 3}\color{black}{ )} + 2 } \\ { 2 \leq 8 } \:\:\color{Cerulean}{✓} \end{array}\) |
Los puntos en el límite sólido se incluyen en el conjunto de soluciones simultáneas y los puntos en el límite discontinua no lo están. Considere el punto\((−1, 0)\) en el límite sólido definido por\(y = 2x + 2\) y verifique que resuelve el sistema original:
| \(\color{Cerulean}{Check :}\:\:\color{YellowOrange}{(-1,0)}\) | |
|
Desigualdad\(1\): \(\begin{array} { l } { y > x - 2 } \\ { \color{Cerulean}{0}\color{black}{ >}\color{Cerulean}{ -1}\color{black}{ -} 2 } \\ { 0 > -3 }\:\: \color{Cerulean}{✓} \end{array}\) |
Desigualdad\(2\): \(\begin{array} { l } { y \leq 2 x + 2 } \\ { \color{Cerulean}{0}\color{black}{ \leq} 2 (\color{Cerulean}{ -1}\color{black}{ )} + 2 } \\ { 0 \leq 0 } \:\:\color{Cerulean}{✓} \end{array}\) |
Observe que este punto satisface ambas desigualdades y así se incluye en el conjunto de soluciones. Ahora considere el punto\((2, 0)\) en el límite discontinuas definido por\(y = x − 2\) y verifique que no resuelva el sistema original:
| \(\color{Cerulean}{Check :}\:\:\color{YellowOrange}{(2,0)}\) | |
|
Desigualdad\(1\): \(\begin{array} { l } { y > x - 2 } \\ { \color{Cerulean}{0}\color{black}{ >}\color{Cerulean}{ 2}\color{black}{ -} 2 } \\ { 0 > 0 } \:\:\color{red}{✗}\end{array}\) |
Desigualdad\(2\): \(\begin{array} { l } { y \leq 2 x + 2 } \\ {\color{Cerulean}{ 0}\color{black}{ \leq} 2 (\color{Cerulean}{ 2}\color{black}{ )} + 2 } \\ { 0 \leq 6 } \:\:\color{Cerulean}{✓}\end{array}\) |
Este punto no satisface ambas desigualdades y por lo tanto no se incluye en el conjunto de soluciones.
Ejemplo\(\PageIndex{1}\)
Determine si\((-3,3)\) es o no una solución al siguiente sistema:
\(\left\{ \begin{aligned} 2 x + 6 y \leq 6 \\ - \frac { 1 } { 3 } x - y \leq 3 \end{aligned} \right.\)
Solución
Sustituir las coordenadas de\((x, y) = (−3, 3)\) en ambas desigualdades.
| \(\color{Cerulean}{Check :}\:\:\color{YellowOrange}{(-3,3)}\) | |
|
Desigualdad\(1\): \(\begin{aligned} 2 x + 6 y \leq 6 \\ 2 ( \color{Cerulean}{- 3}\color{black}{ )} + 6 ( \color{Cerulean}{3}\color{black}{ )} \leq 6 \\ - 6 + 18 \leq 6 \\ 12 \leq 6 \:\:\color{red}{✗}\end{aligned}\) |
Desigualdad\(2\): \(\begin{aligned} - \frac { 1 } { 3 } x - y & \leq 3 \\ - \frac { 1 } { 3 } ( \color{Cerulean}{- 3}\color{black}{ )} - (\color{Cerulean}{ 3}\color{black}{ )} & \leq 3 \\ 1 - 3 & \leq 3 \\ - 2 & \leq 3 \:\:\color{Cerulean}{✓}\end{aligned}\) |
Responder
\((-3,3)\)no es una solución; no satisface ambas desigualdades.
Podemos graficar de manera similar las soluciones de sistemas que contienen desigualdades no lineales. Por ejemplo, ambos conjuntos de soluciones de las siguientes desigualdades se pueden graficar en el mismo conjunto de ejes:
\(\left\{ \begin{array} { l } { y < \frac { 1 } { 2 } x + 4 } \\ { y \geq x ^ { 2 } } \end{array} \right.\)
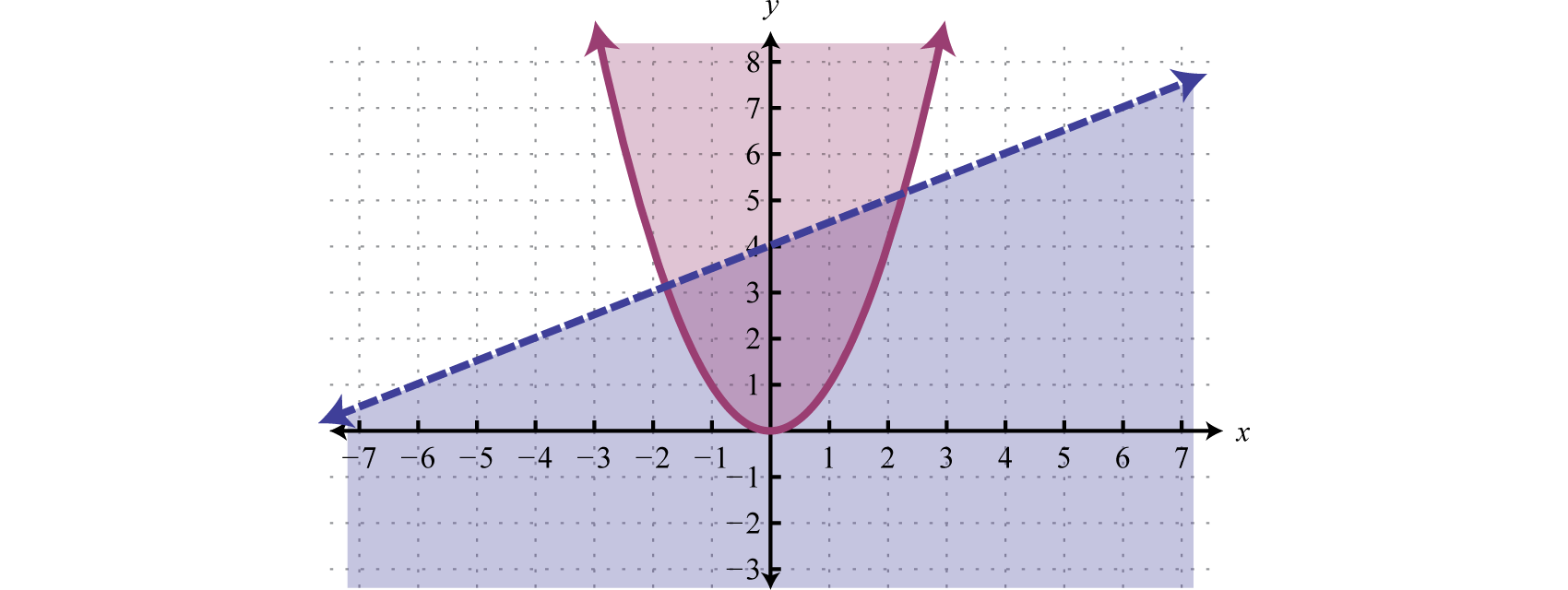
Y la intersección de ambas regiones contiene la región de soluciones simultáneas de pares ordenados.
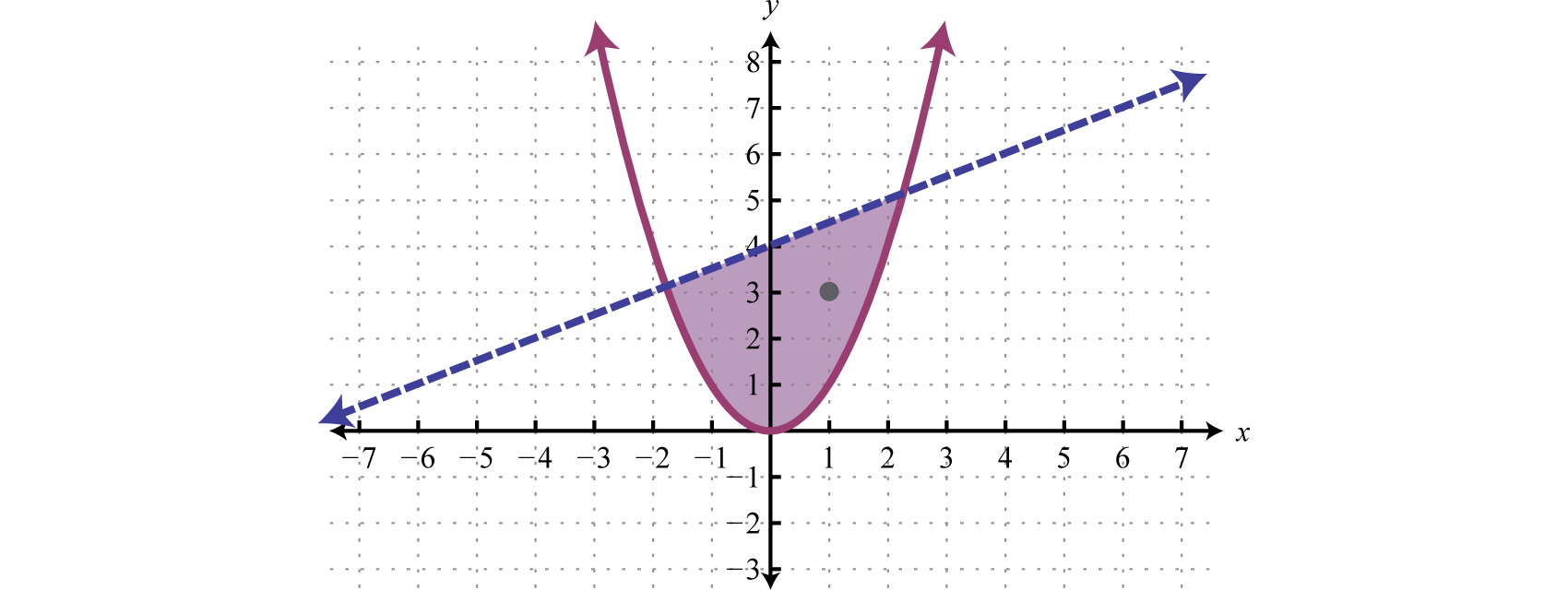
De la gráfica, esperamos que el par\((1, 3)\) ordenado resuelva ambas desigualdades.
| \(\color{Cerulean}{Check :}\:\:\color{black}{(1,3)}\) | |
|
Desigualdad\(1\): \(\begin{array} { l } { y < \frac { 1 } { 2 } x + 4 } \\ { \color{Cerulean}{3}\color{black}{ <} \frac { 1 } { 2 } ( \color{Cerulean}{1}\color{black}{ )} + 4 } \\ { 3 < 4 \frac { 1 } { 2 } \quad } \:\:\color{Cerulean}{✓}\end{array}\) |
Desigualdad\(2\): \(\begin{array} { l } { y \geq x ^ { 2 } } \\ { \color{Cerulean}{3}\color{black}{ \geq} ( \color{Cerulean}{1}\color{black}{ )} ^ { 2 } } \\ { 3 \geq 1 } \:\:\color{Cerulean}{✓}\end{array}\) |
Graficando Soluciones a Sistemas de Desigualdades
Las soluciones a un sistema de desigualdades son los pares ordenados que resuelven todas las desigualdades en el sistema. Por lo tanto, para resolver estos sistemas graficamos los conjuntos de soluciones de las desigualdades en un mismo conjunto de ejes y determinamos dónde se cruzan. Esta intersección, o superposición, definirá la región de las soluciones comunes de pares ordenados.
Ejemplo\(\PageIndex{2}\):
Grafique el conjunto de soluciones:\(\left\{ \begin{array} { l } { - 2 x + y > - 4 } \\ { 3 x - 6 y \geq 6 } \end{array} \right.\).
Solución
Para facilitar el proceso de graficación, primero resolvemos para\(y\).
\(\left\{ \begin{array} { l l } { - 2 x + y > - 4 } \\ { 3 x - 6 y \geq 6 } \end{array} \right. \quad\Rightarrow\quad \left\{ \begin{array} { l } { y > 2 x - 4 } \\ { y \leq \frac { 1 } { 2 } x - 1 } \end{array} \right.\)
Para la primera desigualdad, usamos un límite discontinuas definido por\(y = 2x − 4\) y sombreamos todos los puntos por encima de la línea. Para la segunda desigualdad, utilizamos un límite sólido definido por\(y = \frac{1}{ 2} x − 1\) y sombreamos todos los puntos a continuación. La intersección está oscurecida.
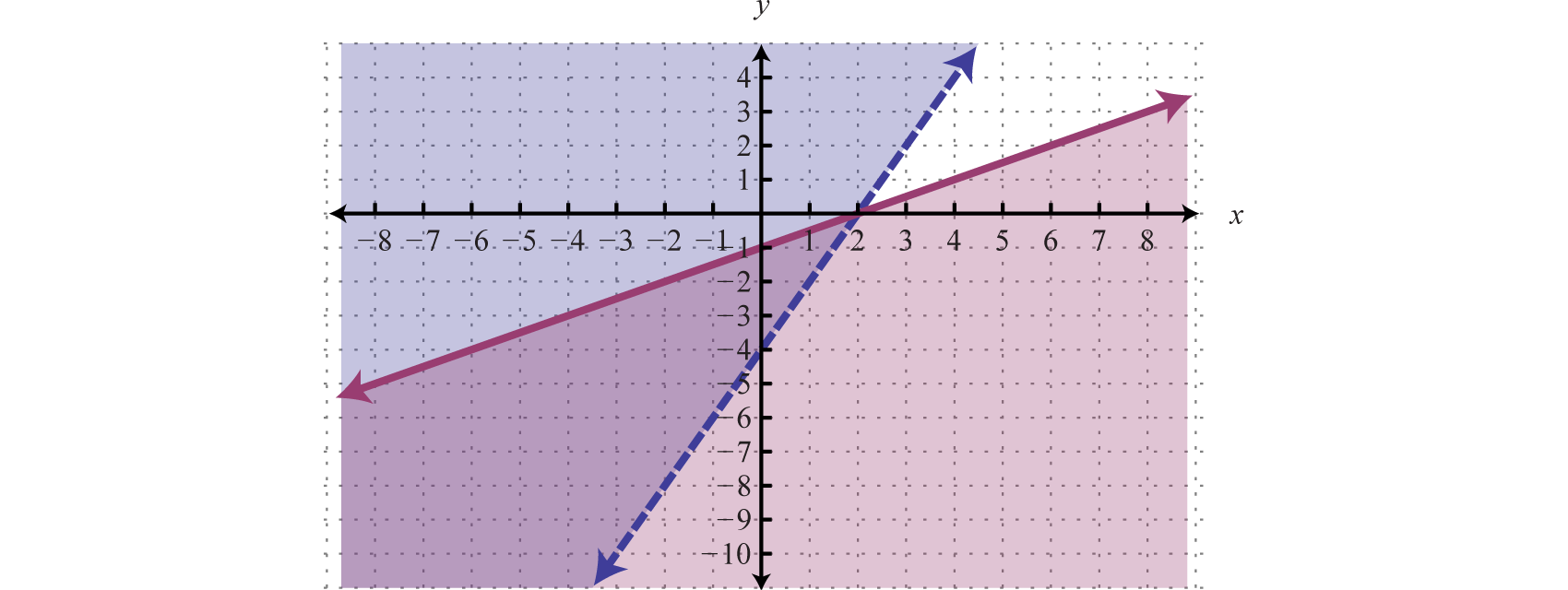
Ahora presentamos nuestra solución con solo la intersección sombreada.
Respuesta:
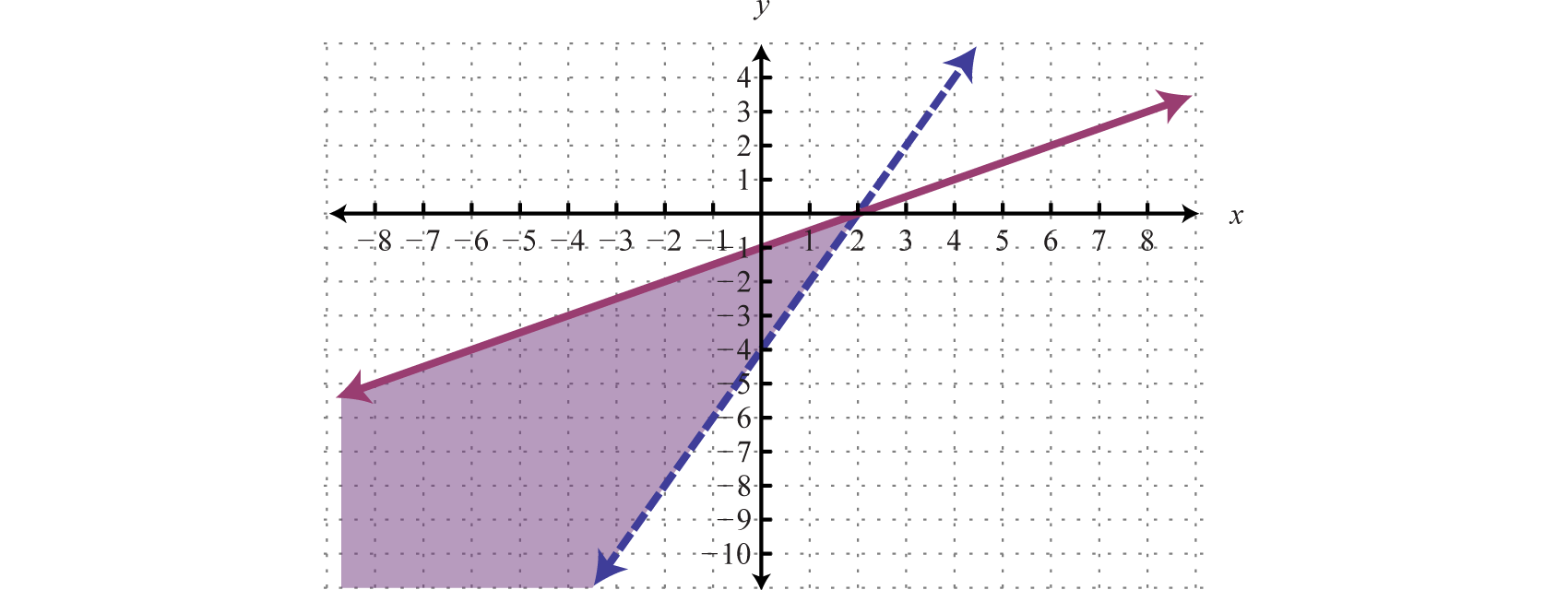
Ejemplo\(\PageIndex{3}\):
Grafique el conjunto de soluciones:\(\left\{ \begin{array} { l } { - 3 x + 2 y > 6 } \\ { 6 x - 4 y > 8 } \end{array} \right.\).
Solución
Comenzamos por resolver ambas desigualdades para\(y\).
\(\left\{ \begin{array} { l } { - 3 x + 2 y > 6 } \\ { 6 x - 4 y > 8 } \end{array} \right. \quad\Rightarrow\quad \left\{ \begin{array} { l } { y > \frac { 3 } { 2 } x + 3 } \\ { y < \frac { 3 } { 2 } x - 2 } \end{array} \right.\)
Debido a las estrictas desigualdades, usaremos una línea discontinua para cada límite. Para la primera desigualdad sombree todos los puntos por encima del límite y para la segunda desigualdad sombree todos los puntos por debajo del límite.
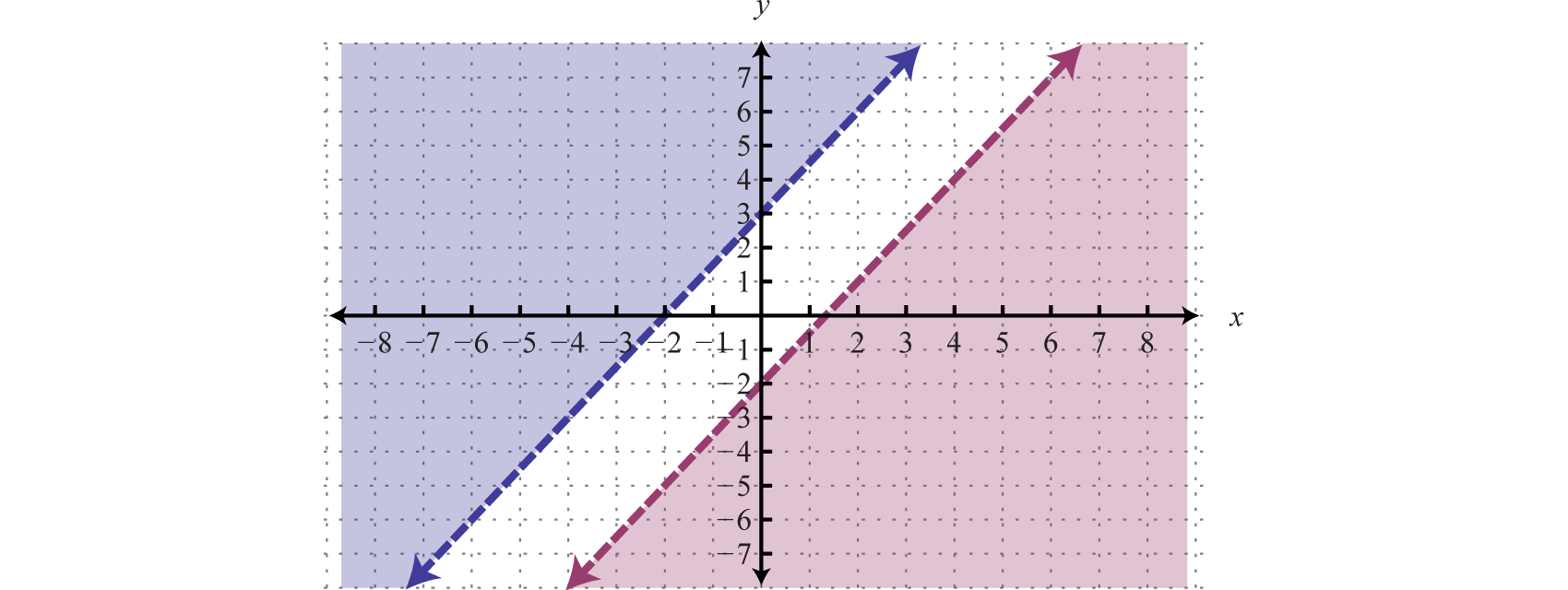
Como podemos ver, no hay intersección de estas dos regiones sombreadas. Por lo tanto, no hay soluciones simultáneas.
Respuesta:
\(\varnothing\)
Ejemplo\(\PageIndex{4}\):
Grafique el conjunto de soluciones:\(\left\{ \begin{array} { l } { y \geq - 4 } \\ { y < x + 3 } \\ { y \leq - 3 x + 3 } \end{array} \right.\)
Solución
Comience por graficar los conjuntos de soluciones a las tres desigualdades.
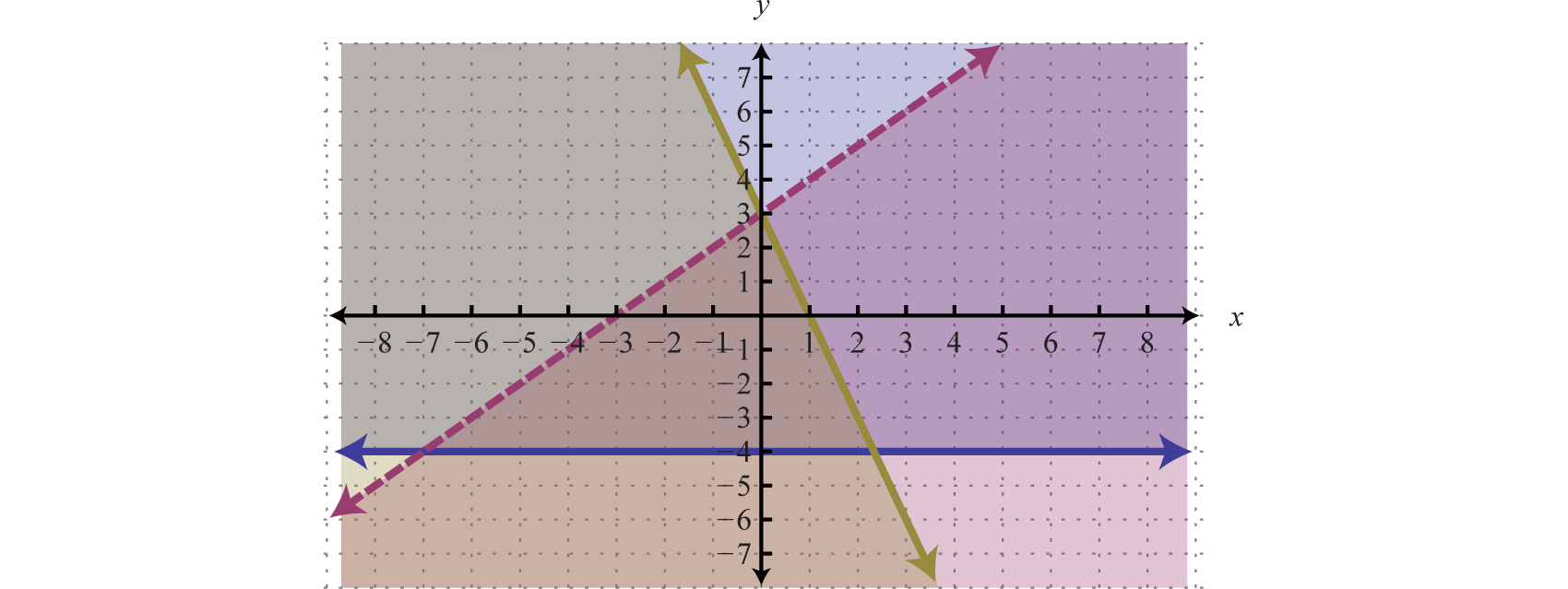
Después de graficar las tres desigualdades en el mismo conjunto de ejes, determinamos que la intersección se encuentra en la región triangular que se muestra a continuación.
Respuesta:
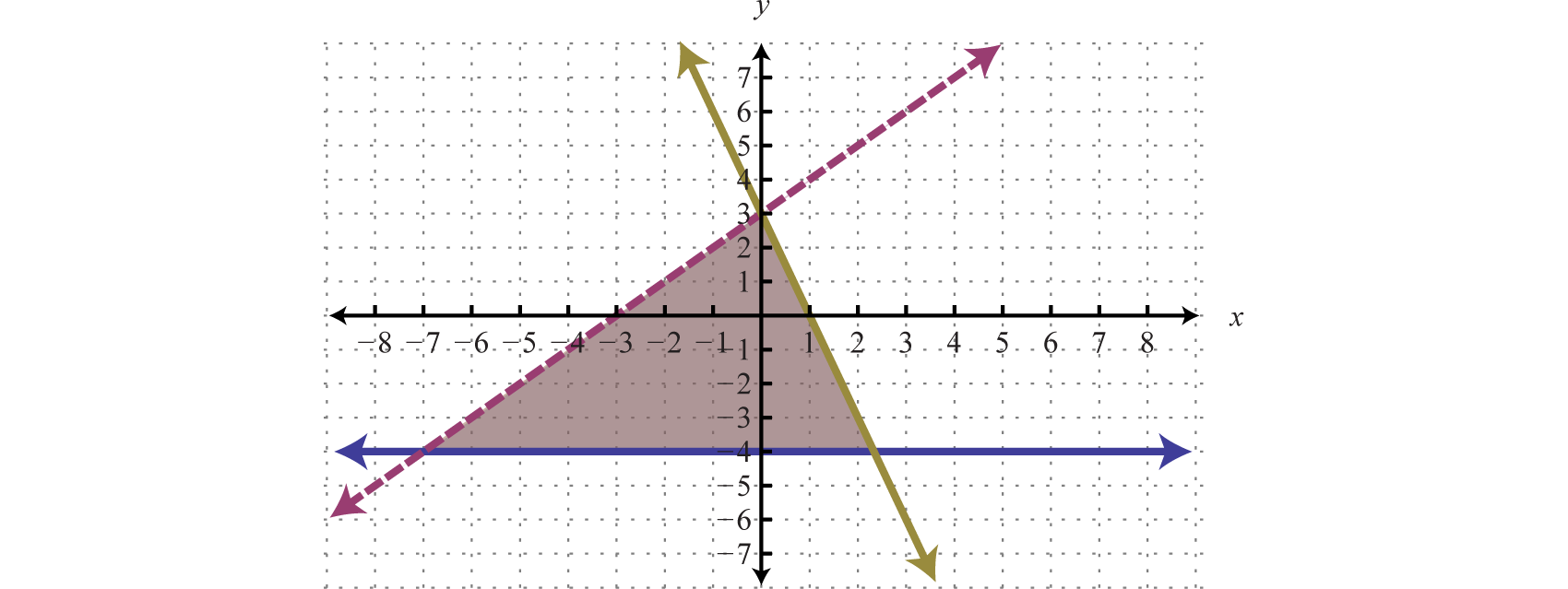
El gráfico sugiere que\((−1, 1)\) es una solución simultánea. Como cheque, podríamos sustituir ese punto en las desigualdades y verificar que resuelve las tres condiciones.
| \(\color{Cerulean}{Check:}\:\:\color{black}{(-1,1)}\) | ||
|
Desigualdad\(1\): \(\begin{array} { l } { y \geq - 4 } \\ { \color{Cerulean}{1}\color{black}{ \geq} - 4 }\:\:\color{Cerulean}{✓} \end{array}\) |
Desigualdad\(2\): \(\begin{array} { l } { y < x + 3 } \\ { \color{Cerulean}{1}\color{black}{ <}\color{Cerulean}{ - 1}\color{black}{ +} 3 } \\ { 1 < 2 } \:\:\color{Cerulean}{✓} \end{array}\) |
Desigualdad\(3\): \(\begin{array} { l } { y \leq -3x + 3 } \\ { \color{Cerulean}{1}\color{black}{\leq} -3(\color{Cerulean}{ - 1}\color{black}{ )+} 3 } \\ { 1 \leq 3+3 } \\{1 \leq 6}\:\:\color{Cerulean}{✓} \end{array}\) |
Utilice la misma técnica para graficar los conjuntos de soluciones a sistemas de desigualdades no lineales.
Ejemplo\(\PageIndex{5}\):
Grafique el conjunto de soluciones:\(\left\{ \begin{array} { l } { y < ( x + 1 ) ^ { 2 } } \\ { y \leq - \frac { 1 } { 2 } x + 3 } \end{array} \right.\).
Solución
La primera desigualdad tiene un límite parabólico. Este límite es una traslación horizontal de la función básica\(y = x^{2}\) a la\(1\) unidad izquierda. Debido a la estricta desigualdad, el límite se discontinua, lo que indica que no está incluido en el conjunto de soluciones. La segunda desigualdad es lineal y se graficará con un límite sólido. Los conjuntos de soluciones para ambos se representan a continuación.
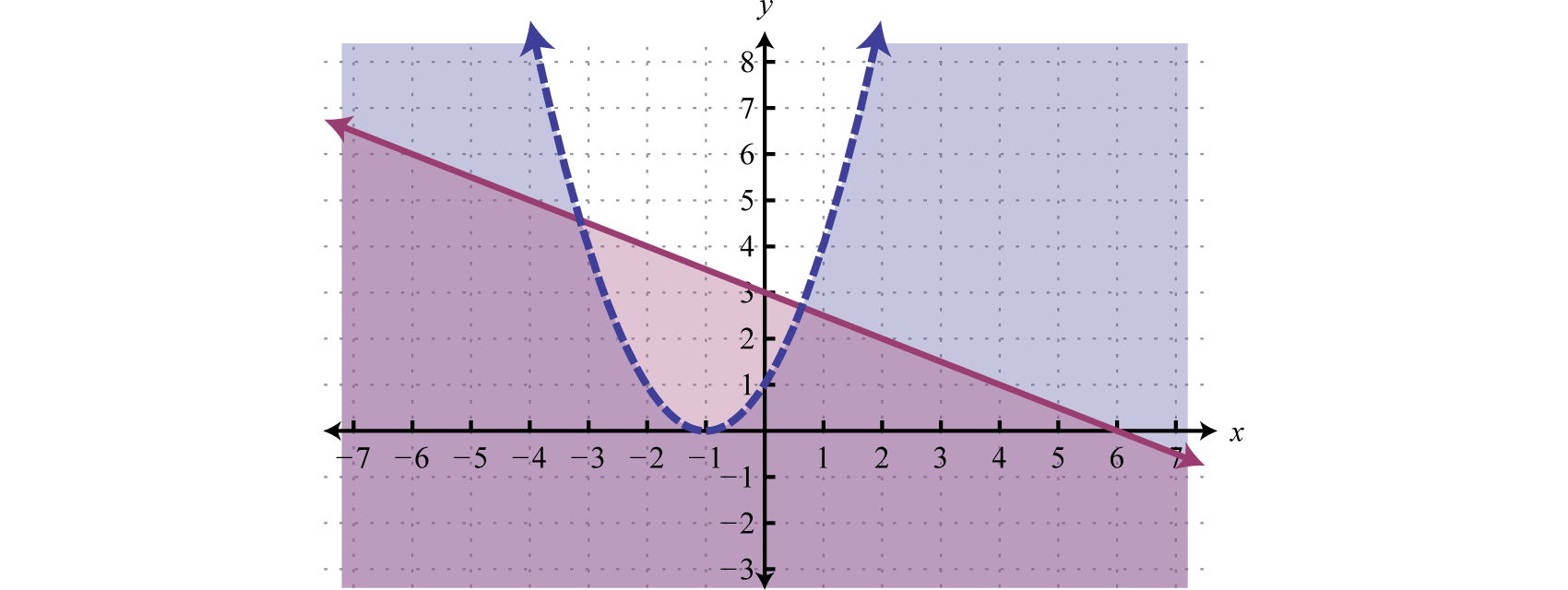
Después de graficar las desigualdades en el mismo conjunto de ejes, determinamos que la intersección se encuentra en la región que se muestra a continuación.
Respuesta:
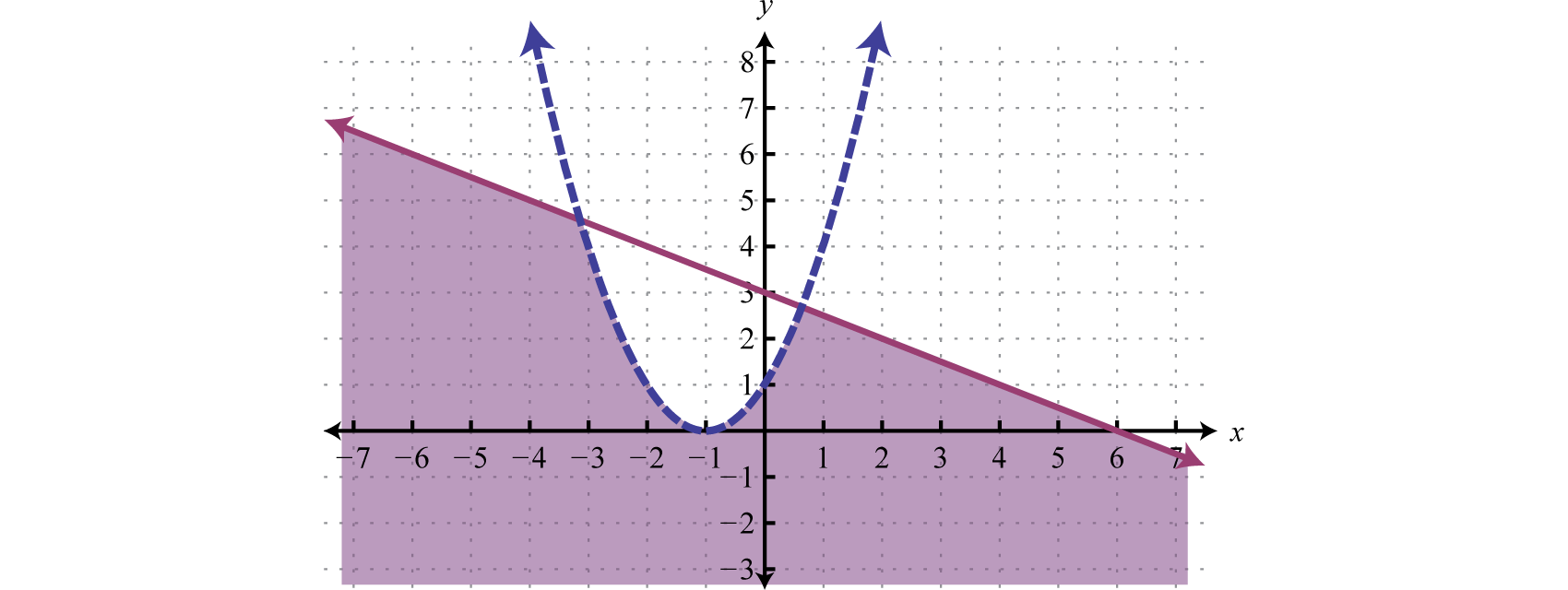
Ejercicio\(\PageIndex{1}\)
Grafique el conjunto de soluciones:\(\left\{ \begin{array} { l } { y \geq - | x + 1 | + 3 } \\ { y \leq 2 } \end{array} \right.\).
- Responder
-
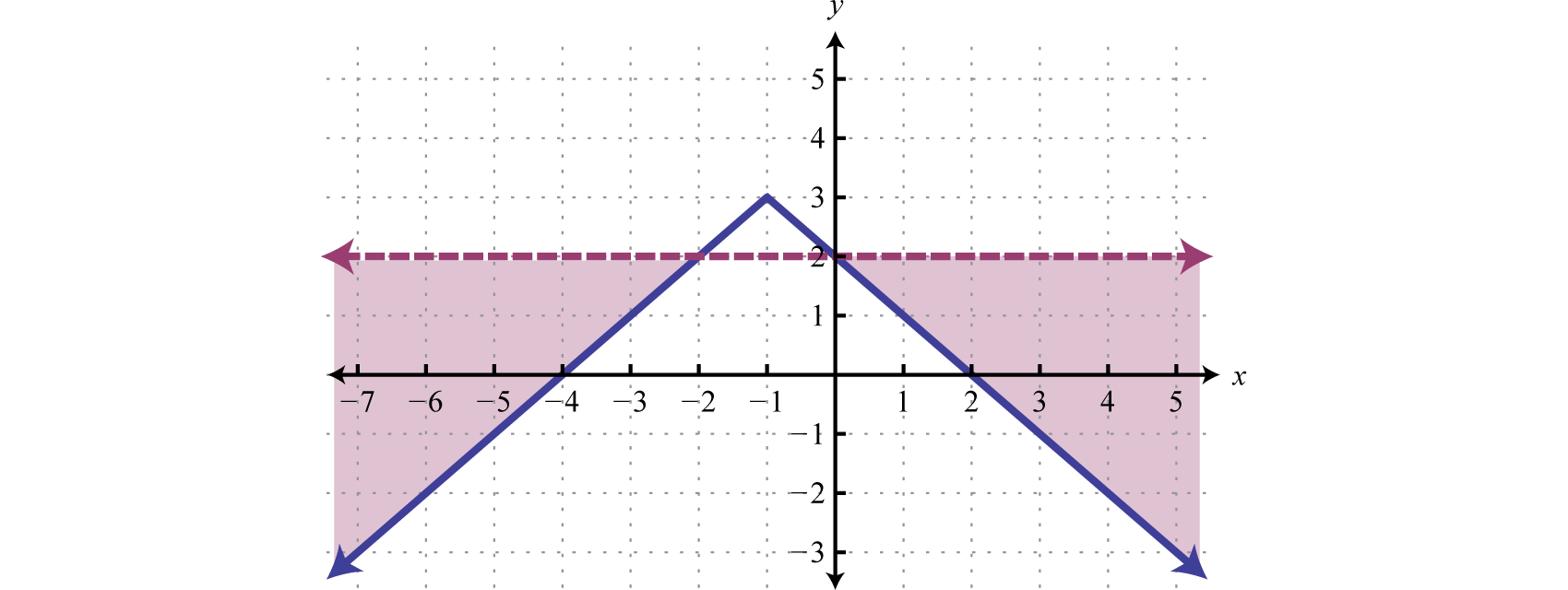
Figura\(\PageIndex{13}\) www.youtube.com/v/9z87e7iw9je
Claves para llevar
- Para graficar soluciones a sistemas de desigualdades, graficar los conjuntos de soluciones de cada desigualdad en un mismo conjunto de ejes y determinar dónde se cruzan.
- Puedes verificar tu respuesta eligiendo algunos valores dentro y fuera de la región sombreada para ver si satisfacen las desigualdades o no. Si bien esto no es una prueba, hacerlo dará una buena indicación de que ha graficado la región correcta.
Ejercicio\(\PageIndex{2}\)
Determinar si el punto dado es o no una solución al sistema de desigualdades dado.
1. \((-2,1)\);
\(\left\{ \begin{array} { l } { y > 3 x + 5 } \\ { y \leq - x + 1 } \end{array} \right.\)
2. \((-1,-3)\);
\(\left\{ \begin{array} { l } { y \geq 3 x - 1 } \\ { y < - 2 x } \end{array} \right.\)
3. \((-2,-1)\);
\(\left\{ \begin{array} { l } { x - 2 y > - 1 } \\ { 3 x - y < - 3 } \end{array} \right.\)
4. \((0,-5)\);
\(\left\{ \begin{array} { c } { 5 x - y \geq 5 } \\ { 3 x + 2 y < - 1 } \end{array} \right.\)
5. \((-\frac{1}{2} ,0)\);
\(\left\{ \begin{array} { l } { - 8 x + 5 y \geq 3 } \\ { 2 x - 3 y < 0 } \end{array} \right.\)
6. \((-1, \frac{1}{2})\);
\(\left\{ \begin{array} { l } { 2 x - 9 y < - 1 } \\ { 3 x - 6 y > - 2 } \end{array} \right.\)
7. \((-1,-2)\);
\(\left\{ \begin{array} { c } { 2 x - y \geq - 1 } \\ { x - 3 y < 6 } \\ { 2 x - 3 y > - 1 } \end{array} \right.\)
8. \((-5,2)\);
\(\left\{ \begin{array} { c } { - x + 5 y > 10 } \\ { 2 x + y < 1 } \\ { x + 3 y < - 2 } \end{array} \right.\)
9. \((0,3)\);
\(\left\{ \begin{array} { l } { y + 4 \geq 0 } \\ { \frac { 1 } { 2 } x + \frac { 1 } { 3 } y \leq 1 } \\ { - 3 x + 2 y \leq 6 } \end{array} \right.\)
10. \((1,1)\);
\(\left\{ \begin{array} { l } { y \leq - \frac { 3 } { 4 } x + 2 } \\ { y \geq - 5 x + 2 } \\ { y \geq \frac { 1 } { 3 } x - 1 } \end{array} \right.\)
11. \((-1,2)\);
\( \left\{ \begin{array} { l } { y \geq x ^ { 2 } + 1 } \\ { y < - 2 x + 3 } \end{array} \right.\)
12. \((4,5)\);
\(\left\{ \begin{array} { l } { y < ( x - 1 ) ^ { 2 } - 1 } \\ { y > \frac { 1 } { 2 } x - 1 } \end{array} \right.\)
13. \((-2,-3)\);
\(\left\{ \begin{array} { l } { y < 0 } \\ { y \geq - | x | + 4 } \end{array} \right.\)
14. \((1,2)\);
\(\left\{ \begin{array} { l } { y < | x - 3 | + 2 } \\ { y \geq 2 } \end{array} \right.\)
15. \(\left( - \frac { 1 } { 2 } , - 5 \right)\);
\(\left\{ \begin{array} { l } { y \leq - 3 x - 5 } \\ { y > ( x - 1 ) ^ { 2 } - 10 } \end{array} \right.\)
16. \((-4,1)\)
\(\left\{ \begin{array} { l } { x \geq - 5 } \\ { y < ( x + 3 ) ^ { 2 } - 2 } \end{array} \right.\)
17. \(\left( - \frac { 3 } { 2 } , \frac { 1 } { 3 } \right)\);
\(\left\{ \begin{array} { l } { x - 2 y \leq 4 } \\ { y \leq | 3 x - 1 | + 2 } \end{array} \right.\)
18,\(\left( - 3 , - \frac { 3 } { 4 } \right)\);
\(\left\{ \begin{array} { l } { 3 x - 4 y < 24 } \\ { y < ( x + 2 ) ^ { 2 } - 1 } \end{array} \right.\)
19. \((4,2)\);
\(\left\{ \begin{array} { l } { y < ( x - 3 ) ^ { 2 } + 1 } \\ { y < - \frac { 3 } { 4 } x + 5 } \end{array} \right.\)
20. \((\frac{5}{2}, 1)\)
\(\left\{ \begin{array} { l } { y \geq - 1 } \\ { y < - ( x - 2 ) ^ { 2 } + 3 } \end{array} \right.\)
- Responder
-
1. Sí
3. Sí
5. Sí
7. Sí
9. Sí
11. Sí
13. No
15. Sí
17. Sí
19. No
Ejercicio\(\PageIndex{3}\)
Grafique el conjunto de soluciones.
- \(\left\{ \begin{array} { l } { y \geq \frac { 2 } { 3 } x - 3 } \\ { y < - \frac { 1 } { 3 } x + 3 } \end{array} \right.\)
- \(\left\{ \begin{array} { l } { y \geq - \frac { 1 } { 4 } x + 1 } \\ { y < \frac { 1 } { 2 } x - 2 } \end{array} \right.\)
- \(\left\{ \begin{array} { l } { y > \frac { 2 } { 3 } x + 1 } \\ { y > \frac { 4 } { 3 } x - 5 } \end{array} \right.\)
- \(\left\{ \begin{array} { l } { y \leq - 5 x + 4 } \\ { y < \frac { 4 } { 3 } x - 2 } \end{array} \right.\)
- \(\left\{ \begin{array} { l } { x - y \geq - 3 } \\ { x + y \geq 3 } \end{array} \right.\)
- \(\left\{ \begin{array} { l } { 3 x + y < 4 } \\ { 2 x - y \leq 1 } \end{array} \right.\)
- \(\left\{ \begin{array} { l } { - x + 2 y \leq 0 } \\ { 3 x + 5 y < 15 } \end{array} \right.\)
- \(\left\{ \begin{array} { c } { 2 x + 3 y < 6 } \\ { - 4 x + 3 y \geq - 12 } \end{array} \right.\)
- \(\left\{ \begin{array} { l } { 3 x + 2 y > 1 } \\ { 4 x - 2 y > 3 } \end{array} \right.\)
- \(\left\{ \begin{array} { l } { x - 4 y \geq 2 } \\ { 8 x + 4 y \leq 3 } \end{array} \right.\)
- \(\left\{ \begin{array} { l } { 5 x - 2 y \leq 6 } \\ { - 5 x + 2 y < 2 } \end{array} \right.\)
- \(\left\{ \begin{array} { l } { 12 x + 10 y > 20 } \\ { 18 x + 15 y < - 15 } \end{array} \right.\)
- \(\left\{ \begin{array} { l } { x + y < 0 } \\ { y + 4 > 0 } \end{array} \right.\)
- \(\left\{ \begin{array} { l } { x > - 3 } \\ { y < 1 } \end{array} \right.\)
- \(\left\{ \begin{array} { l } { 2 x - 2 y < 0 } \\ { 3 x - 3 y > 3 } \end{array} \right.\)
- \(\left\{ \begin{array} { l } { y + 1 \leq 0 } \\ { y + 3 \geq 0 } \end{array} \right.\)
- Construir un sistema de desigualdades lineales que describa todos los puntos del primer cuadrante.
- Construir un sistema de desigualdades lineales que describa todos los puntos del segundo cuadrante.
- Construir un sistema de desigualdades lineales que describa todos los puntos del tercer cuadrante.
- Construir un sistema de desigualdades lineales que describa todos los puntos del cuarto cuadrante.
- Responder
-
1.
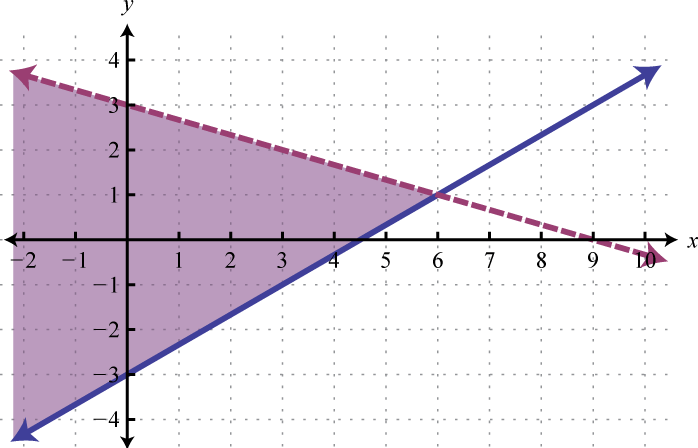
Figura\(\PageIndex{14}\) 3.
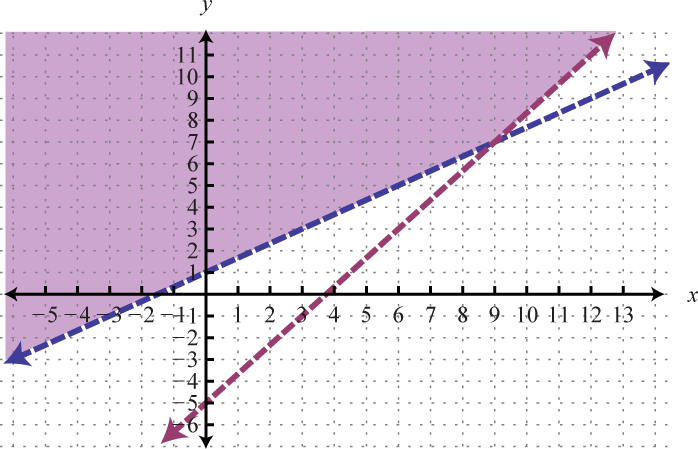
Figura\(\PageIndex{15}\) 5.
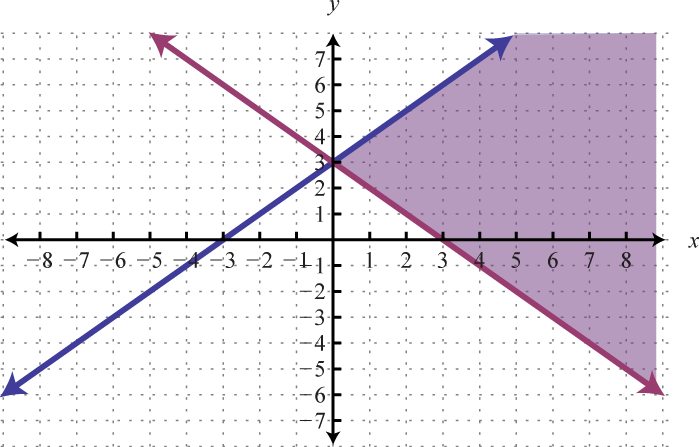
Figura\(\PageIndex{16}\) 7.
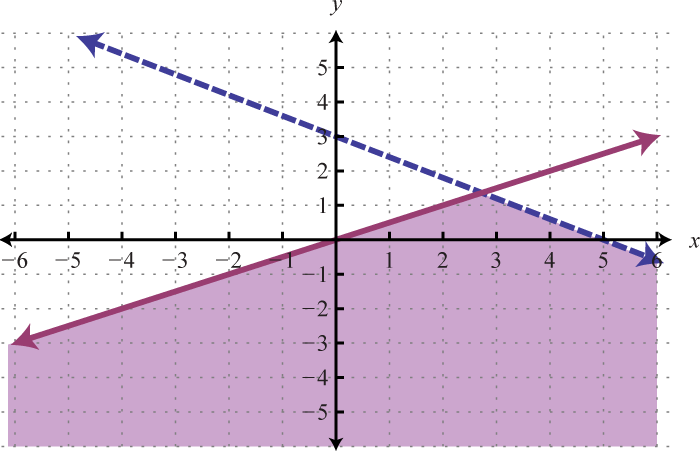
Figura\(\PageIndex{17}\) 9.
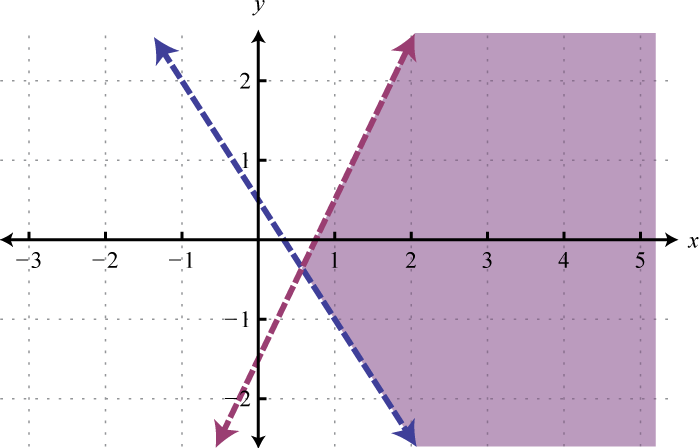
Figura\(\PageIndex{18}\) 11.
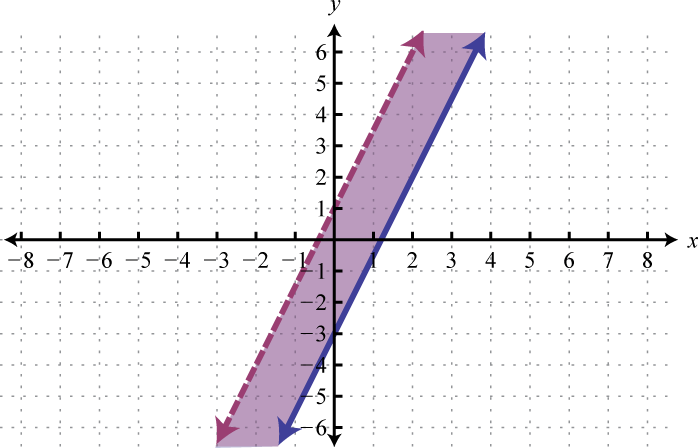
Figura\(\PageIndex{19}\) 13.
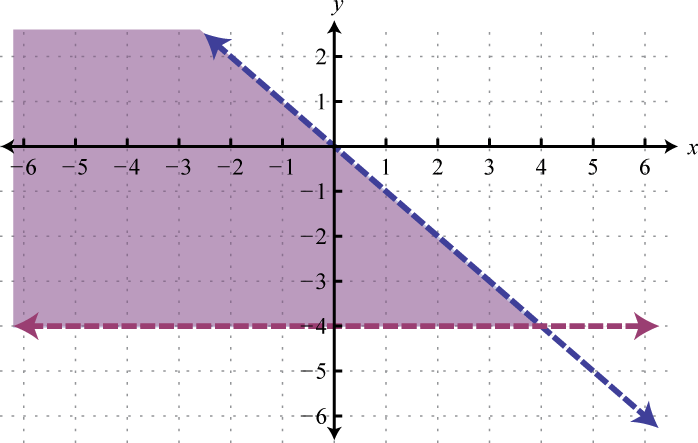
Figura\(\PageIndex{20}\) 15. \(\varnothing\)
17. \(\left\{ \begin{array} { l } { x > 0 } \\ { y > 0 } \end{array} \right.\)
19. \(\left\{ \begin{array} { l } { x < 0 } \\ { y < 0 } \end{array} \right.\)
Ejercicio\(\PageIndex{4}\)
Grafique el conjunto de soluciones.
- \(\left\{ \begin{array} { l } { y \geq - \frac { 1 } { 2 } x + 3 } \\ { y \geq \frac { 3 } { 2 } x - 3 } \\ { y \leq \frac { 3 } { 2 } x + 1 } \end{array} \right.\)
- \(\left\{ \begin{array} { l } { y \leq - \frac { 3 } { 4 } x + 2 } \\ { y \geq - 5 x + 2 } \\ { y \geq \frac { 1 } { 3 } x - 1 } \end{array} \right.\)
- \(\left\{ \begin{array} { l } { 3 x - 2 y > 6 } \\ { 5 x + 2 y > 8 } \\ { - 3 x + 4 y \leq 4 } \end{array} \right.\)
- \(\left\{ \begin{array} { l } { 3 x - 5 y > - 15 } \\ { 5 x - 2 y \leq 8 } \\ { x + y < - 1 } \end{array} \right.\)
- \(\left\{ \begin{array} { l } { 3 x - 2 y < - 1 } \\ { 5 x + 2 y > 7 } \\ { y + 1 > 0 } \end{array} \right.\)
- \(\left\{ \begin{array} { l } { 3 x - 2 y < - 1 } \\ { 5 x + 2 y < 7 } \\ { y + 1 > 0 } \end{array} \right.\)
- \(\left\{ \begin{array} { l } { 4 x + 5 y - 8 < 0 } \\ { y > 0 } \\ { x + 3 > 0 } \end{array} \right.\)
- \(\left\{ \begin{array} { l } { y - 2 < 0 } \\ { y + 2 > 0 } \\ { 2 x - y \geq 0 } \end{array} \right.\)
- \(\left\{ \begin{array} { l } { \frac { 1 } { 2 } x + \frac { 1 } { 2 } y < 1 } \\ { x < 3 } \\ { - \frac { 1 } { 2 } x + \frac { 1 } { 2 } y \leq 1 } \end{array} \right.\)
- \(\left\{ \begin{array} { l } { \frac { 1 } { 2 } x + \frac { 1 } { 3 } y \leq 1 } \\ { y + 4 \geq 0 } \\ { - \frac { 1 } { 2 } x + \frac { 1 } { 3 } y \leq 1 } \end{array} \right.\)
- \(\left\{ \begin{array} { l } { y < x + 2 } \\ { y \geq x ^ { 2 } - 3 } \end{array} \right.\)
- \(\left\{ \begin{array} { l } { y \geq x ^ { 2 } + 1 } \\ { y > - \frac { 3 } { 4 } x + 3 } \end{array} \right.\)
- \(\left\{ \begin{array} { l } { y \leq ( x + 2 ) ^ { 2 } } \\ { y \leq \frac { 1 } { 3 } x + 4 } \end{array} \right.\)
- \(\left\{ \begin{array} { l } { y < ( x - 3 ) ^ { 2 } + 1 } \\ { y < - \frac { 3 } { 4 } x + 5 } \end{array} \right.\)
- \(\left\{ \begin{array} { l } { y \geq - 1 } \\ { y < - ( x - 2 ) ^ { 2 } + 3 } \end{array} \right.\)
- \(\left\{ \begin{array} { l } { y < - ( x + 1 ) ^ { 2 } - 1 } \\ { y < \frac { 3 } { 2 } x - 2 } \end{array} \right.\)
- \(\left\{ \begin{array} { l } { y \leq \frac { 1 } { 3 } x + 3 } \\ { y \geq | x + 3 | - 2 } \end{array} \right.\)
- \(\left\{ \begin{array} { l } { y \leq - x + 5 } \\ { y > | x - 1 | + 2 } \end{array} \right.\)
- \(\left\{ \begin{array} { l } { y > - | x - 2 | + 5 } \\ { y > 2 } \end{array} \right.\)
- \(\left\{ \begin{array} { l } { y \leq - | x | + 3 } \\ { y < \frac { 1 } { 4 } x } \end{array} \right.\)
- \(\left\{ \begin{array} { l } { y > | x | + 1 } \\ { y \leq x - 1 } \end{array} \right.\)
- \(\left\{ \begin{array} { l } { y \leq | x | + 1 } \\ { y > x - 1 } \end{array} \right.\)
- \(\left\{ \begin{array} { l } { y \leq | x - 3 | + 1 } \\ { x \leq 2 } \end{array} \right.\)
- \(\left\{ \begin{array} { l } { y > | x + 1 | } \\ { y < x - 2 } \end{array} \right.\)
- \(\left\{ \begin{array} { l } { y < x ^ { 3 } + 2 } \\ { y \leq x + 3 } \end{array} \right.\)
- \(\left\{ \begin{array} { l } { y \leq 4 } \\ { y \geq ( x + 3 ) ^ { 3 } + 1 } \end{array} \right.\)
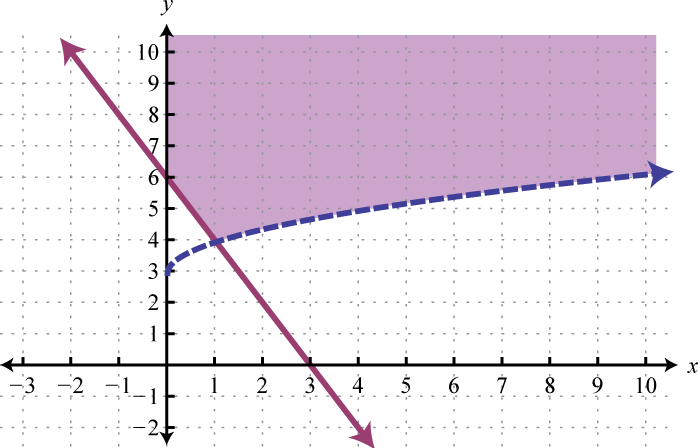
- \(\left\{ \begin{array} { l } { y \geq - 2 x + 6 } \\ { y > \sqrt { x } + 3 } \end{array} \right.\)
- \(\left\{ \begin{array} { l } { y \leq \sqrt { x + 4 } } \\ { x \leq - 1 } \end{array} \right.\)
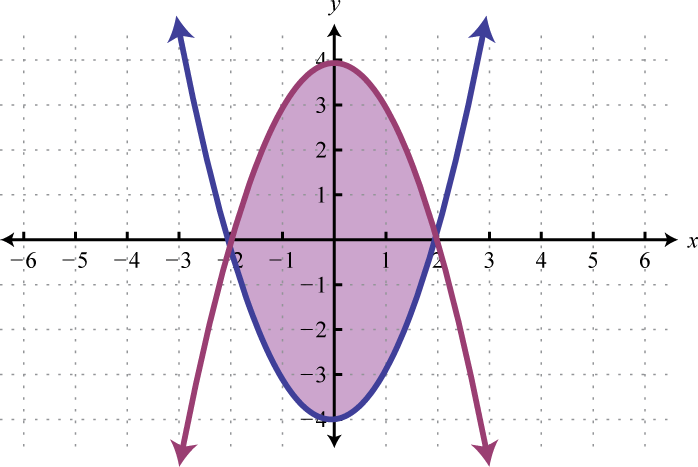
- \(\left\{ \begin{array} { l } { y \leq - x ^ { 2 } + 4 } \\ { y \geq x ^ { 2 } - 4 } \end{array} \right.\)
- \(\left\{ \begin{array} { l } { y \geq | x - 1 | - 3 } \\ { y \leq - | x - 1 | + 3 } \end{array} \right.\)
- Responder
-
1.
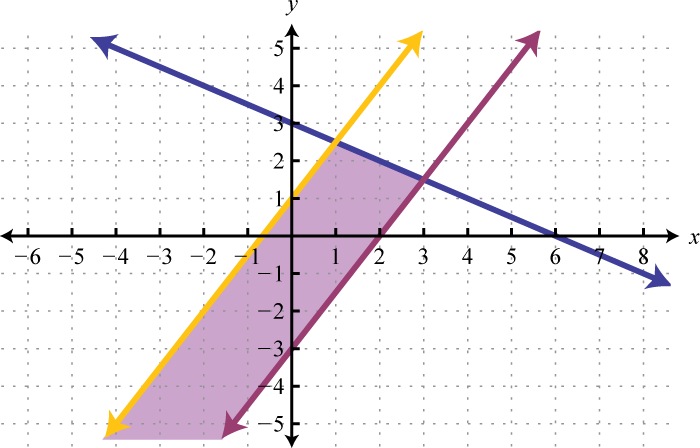
Figura\(\PageIndex{21}\) 3.
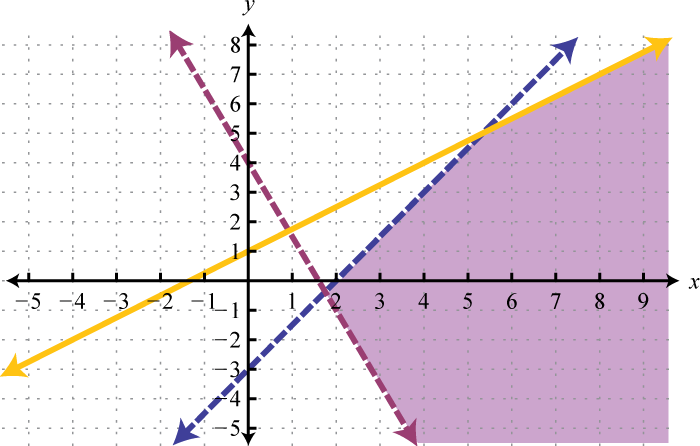
Figura\(\PageIndex{22}\) 5.
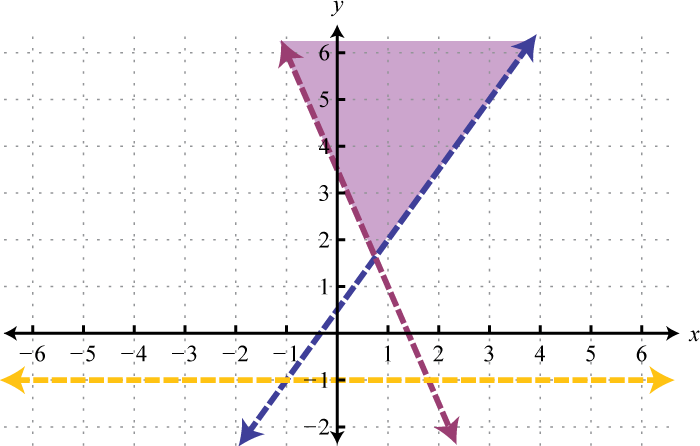
Figura\(\PageIndex{23}\) 7.
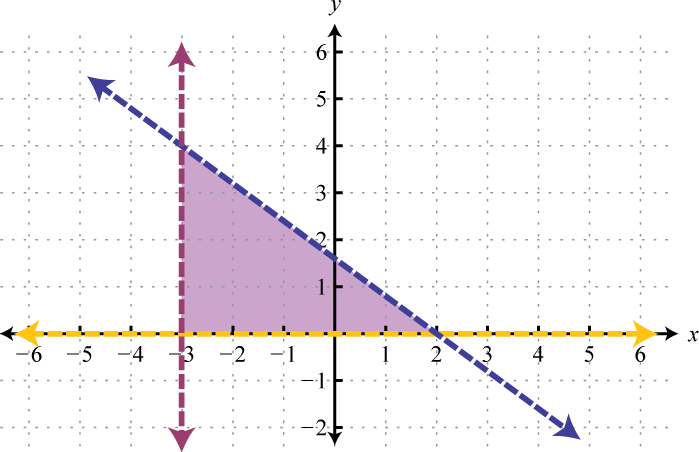
Figura\(\PageIndex{24}\) 9.
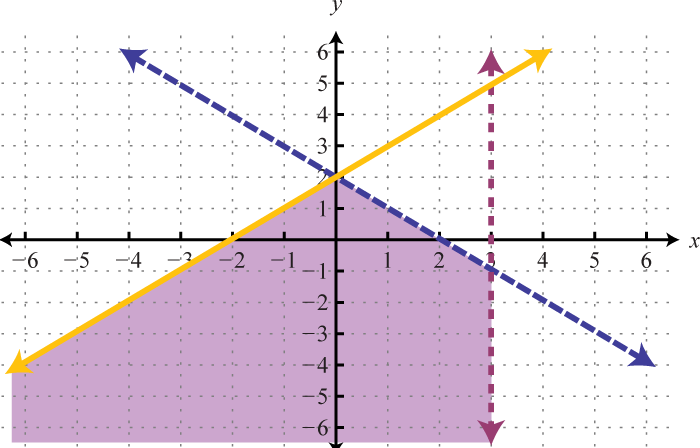
Figura\(\PageIndex{25}\) 11.
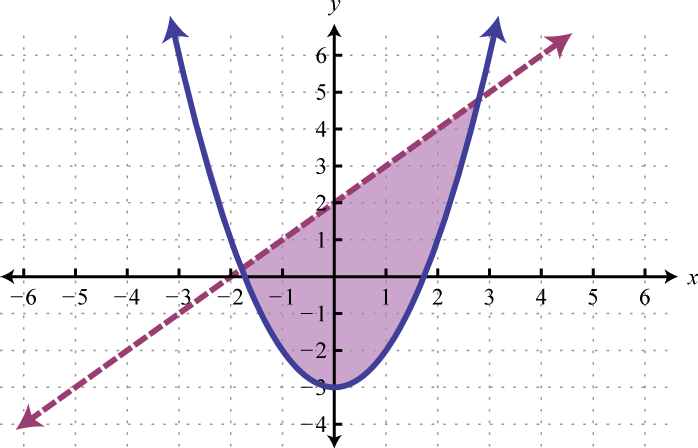
Figura\(\PageIndex{26}\) 13.
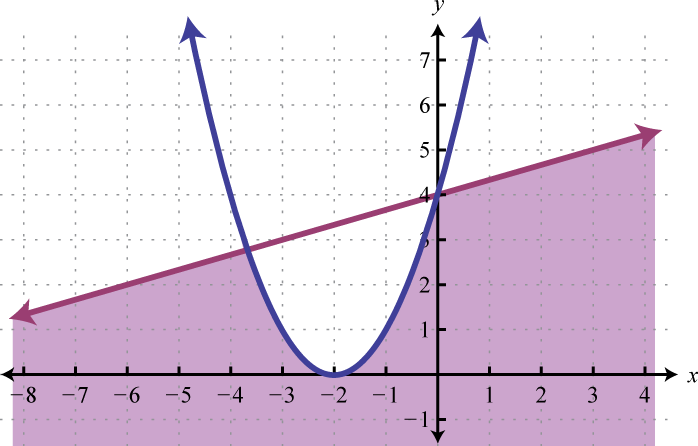
Figura\(\PageIndex{27}\) 15.
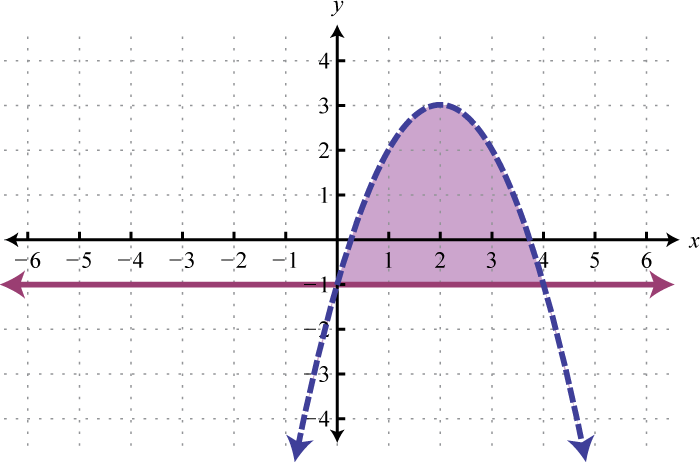
Figura\(\PageIndex{28}\) 17.
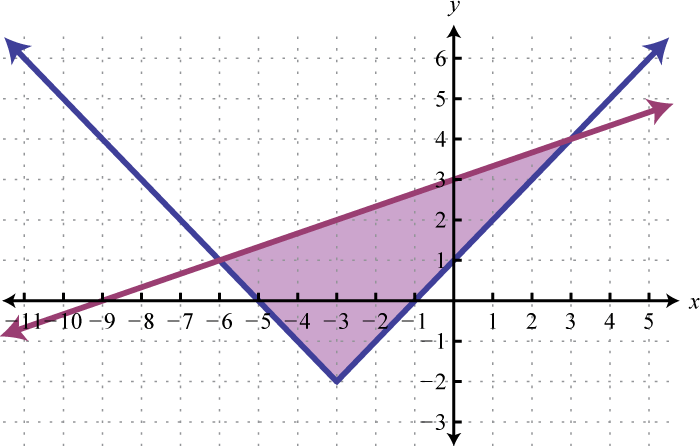
Figura\(\PageIndex{29}\) 19.
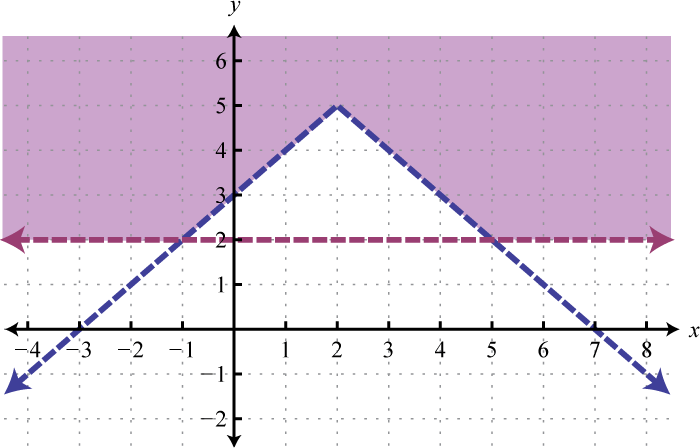
Figura\(\PageIndex{30}\) 21. \(\varnothing\)
23.
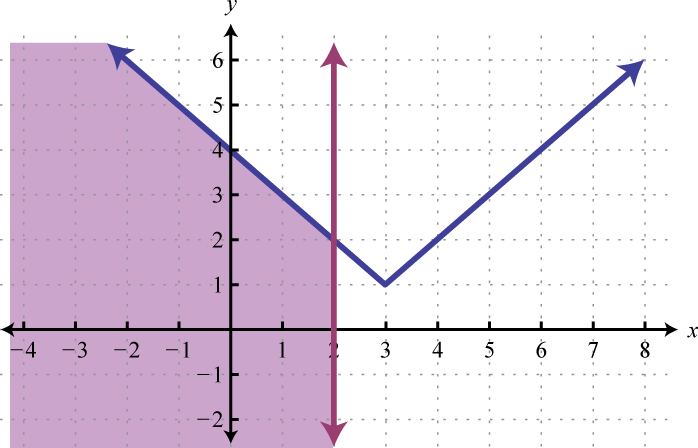
Figura\(\PageIndex{31}\) 25.
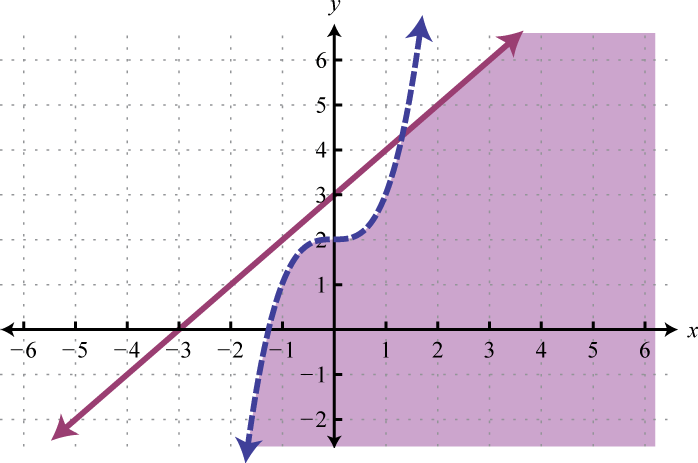
Figura\(\PageIndex{32}\) 27.
Figura\(\PageIndex{33}\) 29.
Figura\(\PageIndex{34}\)
Notas al pie
33 Un conjunto de dos o más desigualdades con las mismas variables.


