6.6: Resolviendo Desigualdades Polinómicas y Racionales

Objetivos de aprendizaje

• Resolver desigualdades polinomiales.
• Resolver desigualdades racionales.

Resolviendo Desigualdades Polinómicas

Una desigualdad polinómica ¹⁸ es una declaración matemática que relaciona una expresión polinómica como menor o mayor que otra. Podemos usar gráficos de signos para resolver desigualdades polinomiales con una variable.

Ejemplo\(\PageIndex{1}\)

Resolver\(x(x+3)^{2}(x-4)<0\).

Solución

Comience por encontrar los números críticos. Para una desigualdad polinómica en forma estándar, con cero en un lado, los números críticos son las raíces. Debido a que\(f (x) = x(x + 3)^{2} (x − 4)\) se da en su forma factorizada las raíces son aparentes. Aquí las raíces son:\(0, −3\), y\(4\). Debido a la estricta desigualdad, graficarlos usando puntos abiertos en una recta numérica.

Figura\(\PageIndex{1}\)

En este caso, los números críticos particionan la recta numérica en cuatro regiones. Pruebe valores en cada región para determinar si f es positivo o negativo. Aquí elegimos valores de prueba\(−5, −1, 2\), y\(6\). Recuerda que solo nos preocupa el signo\((+\) o\(−)\) el resultado.

\(\begin{aligned} f(\color{OliveGreen}{-5}\color{black}{)}&=(\color{OliveGreen}{-5}\color{black}{)}(\color{OliveGreen}{-5}\color{black}{+}3)^{2}(\color{OliveGreen}{-5}\color{black}{-}4) =(-)(-)^{2}(-)&=+\color{Cerulean} { Positive} \\ f(\color{OliveGreen}{-1}\color{black}{)}&=(\color{OliveGreen}{-1}\color{black}{)}(\color{OliveGreen}{-1}\color{black}{+}3)^{2}(\color{OliveGreen}{-1}\color{black}{-}4) =(-)(+)^{2}(-)&=+\color{Cerulean} { Positive } \\ f(\color{OliveGreen}{2}\color{black}{)}&=(\color{OliveGreen}{2}\color{black}{)}(\color{OliveGreen}{2}\color{black}{+}3)^{2}(\color{OliveGreen}{2}\color{black}{-}4) =(+)(+)^{2}(-)&=-\color{Cerulean} { Negative } \\ f(\color{OliveGreen}{6}\color{black}{)}&=(\color{OliveGreen}{6}\color{black}{)}(\color{OliveGreen}{6}\color{black}{+}3)^{2}(\color{OliveGreen}{6}\color{black}{-}4) =(+)(+)^{2}(+)&=+\color{Cerulean} { Positive } \end{aligned}\)

Después de probar los valores podemos completar un gráfico de signos.

Figura\(\PageIndex{2}\)

La pregunta nos pide encontrar los valores donde\(f (x) < 0\), o donde la función es negativa. Del gráfico de signos podemos ver que la función es negativa para\(x\) -valores intermedios\(0\) y\(4\).

Figura\(\PageIndex{3}\)

Podemos expresar este conjunto de soluciones de dos maneras:

\(\begin{aligned}\{x | 0<&x<4\} &\color{Cerulean} { Set\: notation } \\ (0,&4) &\color{Cerulean} { Interval\: notation }\end{aligned}\)

En este libro de texto continuaremos presentando conjuntos de soluciones usando notación de intervalos.

Respuesta:

\((0,4)\)

Graficar polinomios como el del ejemplo anterior está más allá del alcance de este libro de texto. Sin embargo, la gráfica de esta función se proporciona a continuación. Compara la gráfica con su gráfica de signos correspondiente.

Figura\(\PageIndex{4}\)

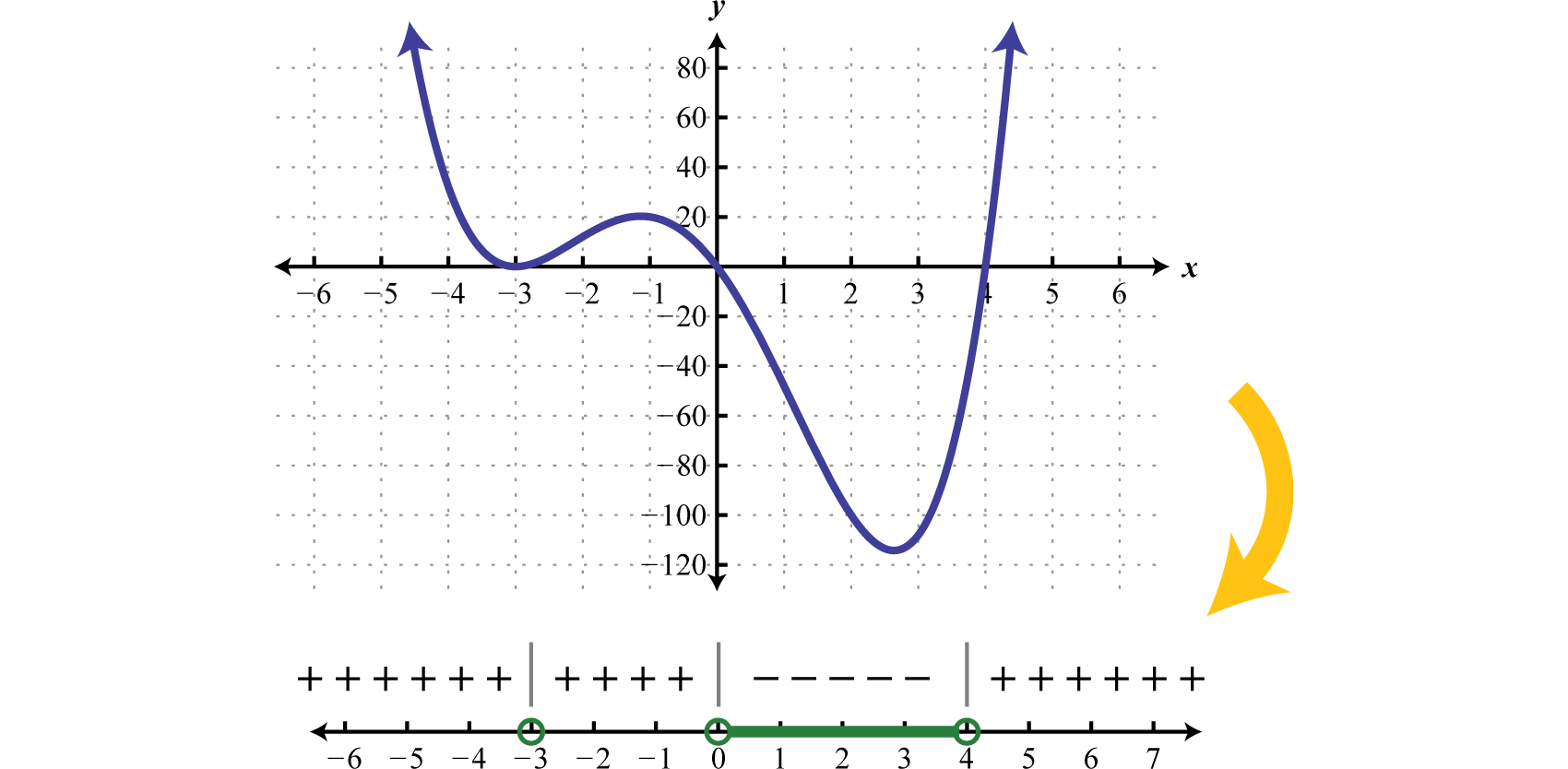
Ciertamente puede no darse el caso de que el polinomio sea factorizado ni que tenga cero en un lado de la desigualdad. Para modelar una función usando un gráfico de signos, todos los términos deben estar en un lado y cero en el otro. Los pasos generales para resolver una desigualdad polinómica se enumeran en el siguiente ejemplo.

Ejemplo\(\PageIndex{2}\):

Resolver:\(2 x^{4}>3 x^{3}+9 x^{2}\).

Solución

Paso 1: Obtener cero en un lado de la desigualdad. En este caso, restar para obtener un polinomio en el lado izquierdo en estándar de.

\(\begin{aligned}2 x^{4}&>3 x^{3}+9 x^{2} \\ 2 x^{4}-3 x^{3}-9 x^{2}&>0\end{aligned}\)

Paso 2: Encuentra los números críticos. Aquí podemos encontrar los ceros por factorización.

\(2 x^{4}-3 x^{3}-9 x^{2}=0 \)
\(x^{2}\left(2 x^{2}-3 x-9\right)=0 \)
\(x^{2}(2 x+3)(x-3)=0 \)

Hay tres soluciones, de ahí, tres números críticos\(−\frac{3}{2}, 0\), y\(3\). La estricta desigualdad indica que debemos usar puntos abiertos.

Figura\(\PageIndex{5}\)

Paso 3: Crear un gráfico de señales. En este caso use\(f (x) = x^{2} (2x + 3) (x − 3) \) y pruebe valores\(−2, −1, 1\), y\(4\) para determinar el signo de la función en cada intervalo.

\(\begin{aligned} f(\color{OliveGreen}{-2}\color{black}{)} &=(\color{OliveGreen}{-2}\color{black}{)}^{2}[2(\color{OliveGreen}{-2}\color{black}{)}+3](\color{OliveGreen}{-2}\color{black}{-}3)&=(-)^{2}(-)(-)=+\\ f(\color{OliveGreen}{-1}\color{black}{)} &=(\color{OliveGreen}{-1}\color{black}{)}^{2}[2(\color{OliveGreen}{-1}\color{black}{)}+3](\color{OliveGreen}{-1}\color{black}{-}3)&=(-)^{2}(+)(-)=-\\ f(\color{OliveGreen}{1}\color{black}{)} &=(\color{OliveGreen}{1}\color{black}{)}^{2}[2(\color{OliveGreen}{1}\color{black}{)}+3](\color{OliveGreen}{1}\color{black}{-}3) &=(+)^{2}(+)(-)=-\\ f(\color{OliveGreen}{4}\color{black}{)} &=(\color{OliveGreen}{4}\color{black}{)}^{2}[2(\color{OliveGreen}{4}\color{black}{)}+3](\color{OliveGreen}{4}\color{black}{-}3) &=(+)^{2}(+)(+)=+\end{aligned}\)

Con esta información podemos completar el gráfico de señales.

Figura\(\PageIndex{6}\)

Paso 4: Usa el gráfico de señales para responder a la pregunta. Aquí la solución consiste en todos los valores para los cuales\(f (x) > 0\). Sombra en los valores que producen resultados positivos y luego expresan este conjunto en notación de intervalos.

Figura\(\PageIndex{7}\)

Respuesta:

\(\left(-\infty,-\frac{3}{2}\right) \cup(3, \infty)\)

Ejemplo\(\PageIndex{3}\)

Resolver:\(x^{3}+x^{2} \leq 4(x+1)\).

Solución

Comience por reescribir la desigualdad en forma estándar, con cero en un lado.

\(\begin{aligned}x^{3}+x^{2} &\leq 4(x+1) \\ x^{3}+x^{2} &\leq 4 x+4 \\ x^{3}+x^{2}-4 x-4 &\leq 0\end{aligned}\)

A continuación, encuentre los números críticos de\(f(x)=x^{3}+x^{2}-4 x-4\):

\(\begin{aligned} x^{3}+x^{2}-4 x-4 &=0 \quad\color{Cerulean} { Factor\: by\: grouping.} \\ x^{2}(x+1)-4(x+1) &=0 \\(x+1)\left(x^{2}-4\right) &=0 \\(x+1)(x+2)(x-2) &=0 \end{aligned}\)

Los números críticos son\(−2, −1\), y\(2\). Debido a la desigualdad inclusiva los\((≤)\) trazaremos usando puntos cerrados.

Figura\(\PageIndex{8}\)

Utilice los valores de prueba\(-3\),\(-\frac{3}{2}\),\(0\), y\(3\) para crear un gráfico de signos.

\(\begin{aligned} f(\color{OliveGreen}{-3}\color{black}{)}&=(\color{OliveGreen}{-3}\color{black}{+}1)(\color{OliveGreen}{-3}\color{black}{+}2)(\color{OliveGreen}{-3}\color{black}{-}2) &=(-)(-)(-)=- \\ f(\color{OliveGreen}{-\frac{3}{2}}\color{black}{)}&=(\color{OliveGreen}{-\frac{3}{2}}\color{black}{+}1)(\color{OliveGreen}{-\frac{3}{2}}\color{black}{+}2)(\color{OliveGreen}{-\frac{3}{2}}\color{black}{-}2) &=(-)(+)(-)=+\\ f(\color{OliveGreen}{0}\color{black}{)}&=(\color{OliveGreen}{0}\color{black}{+}1)(\color{OliveGreen}{0}\color{black}{+}2)(\color{OliveGreen}{0}\color{black}{-}2)&=(+)(+)(-)=- \\ f(\color{OliveGreen}{3}\color{black}{)}&=(\color{OliveGreen}{3}\color{black}{+}1)(\color{OliveGreen}{3}\color{black}{+}2)(\color{OliveGreen}{3}\color{black}{-}2)&=(+)(+)(+)=+\end{aligned}\)

Y tenemos

Figura\(\PageIndex{9}\)

Usa el gráfico de signos para sombrear los valores que tienen resultados negativos\((f (x) ≤ 0)\).

Figura\(\PageIndex{10}\)

Responder

\((-\infty,-2] \cup[-1,2]\)

Ejercicio\(\PageIndex{1}\)

Resolver\(-3 x^{4}+12 x^{3}-9 x^{2}>0\).

Responder

\((1,3)\)

www.youtube.com/v/expe_0lzbsy

Resolver desigualdades racionales

Una desigualdad racional ¹⁹ es una afirmación matemática que relaciona una expresión racional como menor o mayor que otra. Debido a que las funciones racionales tienen restricciones al dominio debemos tener cuidado a la hora de resolver las desigualdades racionales. Además de los ceros, incluiremos las restricciones al dominio de la función en el conjunto de números críticos.

Ejemplo\(\PageIndex{4}\)

Resolver:\(\frac{(x-4)(x+2)}{(x-1)} \geq 0\)

Solución

Los ceros de una función racional ocurren cuando el numerador es cero y los valores que producen cero en el denominador son las restricciones. En este caso,

\(\begin{array}{c | c}{\text { Roots (Numerator) }} & {\text{Restriction(Denominator)}} \\ {x-4=0 \text { or } x+2=0} & {x-1=0} \\ {\:\:\quad\quad\quad\: x=4 \quad\quad x=-2}& {x=1}\end{array}\)

Por lo tanto los números críticos son\(−2, 1\), y\(4\). Debido a la desigualdad inclusiva\((≥)\) usa un punto cerrado para las raíces\({−2, 4}\) y siempre usa un punto abierto para las restricciones\({1}\). Las restricciones nunca se incluyen en el conjunto de soluciones.

Figura\(\PageIndex{11}\)

Usar valores de prueba\(x = −4, 0, 2, 6\).

\(\begin{aligned} f(\color{OliveGreen}{-4}\color{black}{)} &=\frac{(\color{OliveGreen}{-4}\color{black}{-}4)(\color{OliveGreen}{-4}\color{black}{+}2)}{(\color{OliveGreen}{-4}\color{black}{-}1)}&=\frac{(-)(-)}{(-)}=-\\ f(\color{OliveGreen}{0}\color{black}{)} &=\frac{(\color{OliveGreen}{0}\color{black}{-}4)(\color{OliveGreen}{0}\color{black}{+}2)}{(\color{OliveGreen}{0}\color{black}{-}1)}&=\frac{(-)(+)}{(-)}=+\\ f(\color{OliveGreen}{2}\color{black}{)} &=\frac{(\color{OliveGreen}{2}\color{black}{-}4)(\color{OliveGreen}{2}\color{black}{+}2)}{(\color{OliveGreen}{2}\color{black}{-}1)}&=\frac{(-)(+)}{(+)}=-\\ f(\color{OliveGreen}{6}\color{black}{)} &=\frac{(\color{OliveGreen}{6}\color{black}{-}4)(\color{OliveGreen}{6}\color{black}{+}2)}{(\color{OliveGreen}{6}\color{black}{-}1)}&=\frac{(+)(+)}{(+)}=+\end{aligned}\)

Y luego completar el gráfico de señales.

Figura\(\PageIndex{12}\)

La pregunta nos pide encontrar los valores para los cuales\(f (x) ≥ 0\), es decir, positivos o cero. Sombra en las regiones apropiadas y presentar la solución establecida en notación de intervalos.

Figura\(\PageIndex{13}\)

Responder

\([-2,1) \cup[4, \infty)\)

Graficar funciones tan racionales como la del ejemplo anterior está fuera del alcance de este libro de texto. Sin embargo, la gráfica de esta función se proporciona a continuación. Compara la gráfica con su gráfica de signos correspondiente.

Figura\(\PageIndex{14}\)

Observe que la restricción\(x = 1\) corresponde a una asíntota vertical que limita regiones donde la función cambia de positiva a negativa. Si bien no se incluye en el conjunto de soluciones, la restricción es un número crítico. Antes de crear un gráfico de señales debemos asegurarnos de que la desigualdad tenga un cero en un lado. Los pasos generales para resolver una desigualdad racional se describen en el siguiente ejemplo.

Ejemplo\(\PageIndex{5}\):

Resolver\(\frac{7}{x+3}<2\).

Solución

Paso 1: Comienza por obtener cero en el lado derecho.

\(\begin{aligned}\frac{7}{x+3}&<2 \\ \frac{7}{x+3}-2&<0\end{aligned}\)

Paso 2: Determinar los números críticos. Los números críticos son los ceros y las restricciones. Comience simplificando a una sola fracción algebraica.

\(\begin{aligned}\frac{7}{x+3}-\frac{2}{1}&<0 \\ \frac{7-2(x+3)}{x+3}&<0 \\ \frac{7-2 x-6}{x+3}&<0 \\ \frac{-2 x+1}{x+3}&<0\end{aligned}\)

A continuación encuentra los números críticos. Establece el numerador y el denominador iguales a cero y resuelve.

\(\begin{array}{c|c} {\text{Root}}&{\text{Restriction}}\\ {-2x+1=0}\\{-2x=-1}&{x+3=0}\\{x=\frac{1}{2}}&\quad\quad\:\:{x=-3} \end{array}\)

En este caso, la estricta desigualdad indica que debemos usar un punto abierto para la raíz.

Figura\(\PageIndex{15}\)

Paso 3: Crear un gráfico de señales. Elija los valores de prueba\(−4, 0\), y\(1\).

\(\begin{aligned} f(\color{OliveGreen}{-4}\color{black}{)} &=\frac{-2(\color{OliveGreen}{-4}\color{black}{)}+1}{\color{OliveGreen}{-4}\color{black}{+}3}&=\frac{+}{-}=-\\ f(\color{OliveGreen}{0}\color{black}{)} &=\frac{-2(\color{OliveGreen}{0}\color{black}{)}+1}{\color{OliveGreen}{0}\color{black}{+}3}&=\frac{+}{+}=+\\ f(\color{OliveGreen}{1}\color{black}{)} &=\frac{-2(\color{OliveGreen}{1}\color{black}{)}+1}{\color{OliveGreen}{1}\color{black}{+}3}&=\frac{-}{+}=-\end{aligned}\)

Y tenemos

Figura\(\PageIndex{16}\)

Paso 4: Usa el gráfico de señales para responder a la pregunta. En este ejemplo estamos buscando los valores para los que la función es negativa,\(f (x) < 0\). Sombra los valores apropiados y luego presente su respuesta usando notación de intervalo.

Figura\(\PageIndex{17}\)

Respuesta:

\((-\infty,-3) \cup\left(\frac{1}{2}, \infty\right)\)

Ejemplo\(\PageIndex{6}\):

Resolver:\(\frac{1}{x^{2}-4} \leq \frac{1}{2-x}\).

Solución

Comienza por obtener cero en el lado derecho.

\(\begin{aligned}\frac{1}{x^{2}-4} &\leq \frac{1}{2-x} \\ \frac{1}{x^{2}-4}-\frac{1}{2-x} &\leq 0\end{aligned}\)

Siguiente simplificar el lado izquierdo a una sola fracción algebraica.

\(\begin{array}{r}{\frac{1}{x^{2}-4}-\frac{1}{2-x} \leq 0} \\ {\frac{1}{(x+2)(x-2)}-\frac{1}{-(x-2)} \leq 0} \\ {\frac{1}{(x+2)(x-2)}+\frac{1\color{Cerulean}{(x+2)}}{\color{black}{(x-2)}\color{Cerulean}{(x+2)}}\color{black}{ \leq} 0} \\ {\frac{1+x+2}{(x+2)(x-2)} \leq 0} \\ {\frac{x+3}{(x+2)(x-2)} \leq 0}\end{array}\)

Los números críticos son\(−3, −2\), y\(2\). Tenga en cuenta que\(±2\) son restricciones y así usaremos puntos abiertos al trazarlos en una recta numérica. Debido a la desigualdad inclusiva usaremos un punto cerrado en la raíz\(−3\).

Figura\(\PageIndex{18}\)

Elija los valores de prueba\(-4, -2\frac{1}{2} = -\frac{5}{2}, 0\), y\(3\).

\(\begin{aligned}f(\color{OliveGreen}{-4}\color{black}{)}&= \frac{\color{OliveGreen}{-4}\color{black}{+}3}{(\color{OliveGreen}{-4}\color{black}{+}2)(\color{OliveGreen}{-4}\color{black}{-}2)}&=\frac{(-)}{(-)(-)}=- \\ f(\color{OliveGreen}{-\frac{5}{2}}\color{black}{)} &= \frac{\color{OliveGreen}{-\frac{5}{2}}\color{black}{+}3}{(\color{OliveGreen}{-\frac{5}{2}}\color{black}{+}2)(\color{OliveGreen}{-\frac{5}{2}}\color{black}{-}2)}&=\frac{(+)}{(-)(-)}=+\\ f(\color{OliveGreen}{0}\color{black}{)}&=\frac{\color{OliveGreen}{0}\color{black}{+}3}{(\color{OliveGreen}{0}\color{black}{+}2)(\color{OliveGreen}{0}\color{black}{-}2)}&=\frac{(+)}{(+)(-)}=- \\ f(\color{OliveGreen}{3}\color{black}{)}&=\frac{\color{OliveGreen}{3}\color{black}{+}3}{(\color{OliveGreen}{3}\color{black}{+}2)(\color{OliveGreen}{3}\color{black}{-}2)} &=\frac{(+)}{(+)(+)}=+\end{aligned}\)

Construye un gráfico de señales.

Figura\(\PageIndex{19}\)

Contesta la pregunta; en este caso, encuentra\(x\) dónde\(f(x) \leq 0\).

Figura\(\PageIndex{20}\)

Responder

\((-\infty,-3] \cup(-2,2)\)

Ejercicio\(\PageIndex{2}\)

Resolver:\(\frac{2 x^{2}}{2 x^{2}+7 x-4} \geq \frac{x}{x+4}\).

Responder

\((-4,0] \cup\left(\frac{1}{2}, \infty\right)\)

www.youtube.com/v/3ljchjqexby

Claves para llevar

• Cuando una desigualdad polinómica está en forma estándar, con cero en un lado, las raíces del polinomio son los números críticos. Crea un gráfico de signos que modele la función y luego úsalo para responder a la pregunta.
• Cuando una desigualdad racional se escribe como una sola fracción algebraica, con cero en un lado, las raíces así como las restricciones son los números críticos. Los valores que producen cero en el numerador son las raíces, y los valores que producen cero en el denominador son las restricciones. Siempre use puntos abiertos para las restricciones, independientemente de la desigualdad dada, porque las restricciones no forman parte del dominio. Crea un gráfico de signos que modele la función y luego úsalo para responder a la pregunta.

Ejercicio\(\PageIndex{3}\)

Resolver. Presentar respuestas usando notación de intervalos.

1. \(x(x+1)(x-3)>0\)
2. \(x(x-1)(x+4)<0\)
3. \((x+2)(x-5)^{2}<0\)
4. \((x-4)(x+1)^{2} \geq 0\)
5. \((2 x-1)(x+3)(x+2) \leq 0\)
6. \((3 x+2)(x-4)(x-5) \geq 0\)
7. \(x(x+2)(x-5)^{2}<0\)
8. \(x(2 x-5)(x-1)^{2}>0\)
9. \(x(4 x+3)(x-1)^{2} \geq 0\)
10. \((x-1)(x+1)(x-4)^{2}<0\)
11. \((x+5)(x-10)(x-5)^{2} \geq 0\)
12. \((3 x-1)(x-2)(x+2)^{2} \leq 0\)
13. \(-4 x(4 x+9)(x-8)^{2}>0\)
14. \(-x(x-10)(x+7)^{2}>0\)

Responder

1. \((-1,0) \cup(3, \infty)\)

3. \((-\infty,-2)\)

5. \((-\infty,-3] \cup\left[-2, \frac{1}{2}\right]\)

7. \((-2,0)\)

9. \(\left(-\infty,-\frac{3}{4}\right] \cup[0, \infty)\)

11. \((-\infty,-5] \cup[5,5] \cup[10, \infty)\)

13. \(\left(-\frac{9}{4}, 0\right)\)

Ejercicio\(\PageIndex{4}\)

Resolver.

1. \(x^{3}+2 x^{2}-24 x \geq 0\)
2. \(x^{3}-3 x^{2}-18 x \leq 0\)
3. \(4 x^{3}-22 x^{2}-12 x<0\)
4. \(9 x^{3}+30 x^{2}-24 x>0\)
5. \(12 x^{4}+44 x^{3}>80 x^{2}\)
6. \(6 x^{4}+12 x^{3}<48 x^{2}\)
7. \(x\left(x^{2}+25\right)<10 x^{2}\)
8. \(x^{3}>12 x(x-3)\)
9. \(x^{4}-5 x^{2}+4 \leq 0\)
10. \(x^{4}-13 x^{2}+36 \geq 0\)
11. \(x^{4}>3 x^{2}+4\)
12. \(4 x^{4}<3-11 x^{2}\)
13. \(9 x^{3}-3 x^{2}-81 x+27 \leq 0\)
14. \(2 x^{3}+x^{2}-50 x-25 \geq 0\)
15. \(x^{3}-3 x^{2}+9 x-27>0\)
16. \(3 x^{3}+5 x^{2}+12 x+20<0\)

Responder

1. \([-6,0] \cup[4, \infty)\)

3. \(\left(-\infty,-\frac{1}{2}\right) \cup(0,6)\)

5. \((-\infty,-5) \cup\left(\frac{4}{3}, \infty\right)\)

7. \((-\infty, 0)\)

9. \([-2,-1] \cup[1,2]\)

11. \((-\infty,-2) \cup(2, \infty)\)

13. \((-\infty,-3] \cup\left[\frac{1}{3}, 3\right]\)

15. \((3, \infty)\)

Ejercicio\(\PageIndex{5}\)

Resolver.

1. \(\frac{x}{x-3}>0\)
2. \(\frac{x-5}{x}>0\)
3. \(\frac{(x-3)(x+1)}{x}<0\)
4. \(\frac{(x+5)(x+4)}{(x-2)}<0\)
5. \(\frac{(2 x+1)(x+5)}{(x-3)(x-5)} \leq 0\)
6. \(\frac{(3 x-1)(x+6)}{(x-1)(x+9)} \geq 0\)
7. \(\frac{(x-8)(x+8)}{-2 x(x-2)} \geq 0\)
8. \(\frac{(2 x+7)(x+4)}{x(x+5)} \leq 0\)
9. \(\frac{x^{2}}{(2 x+3)(2 x-3)} \leq 0\)
10. \(\frac{(x-4)^{2}}{-x(x+1)}>0\)
11. \(\frac{-5 x(x-2)^{-}}{(x+5)(x-6)} \geq 0\)
12. \(\frac{(3 x-4)(x+5)}{x(x-4)^{2}} \geq 0\)
13. \(\frac{1}{(x-5)^{4}}>0\)
14. \(\frac{1}{(x-5)^{4}}<0\)

Responder

1. \((-\infty,-0) \cup(3, \infty)\)

3. \((-\infty,-1) \cup(0,3)\)

5. \(\left[-5,-\frac{1}{2}\right] \cup(3,5)\)

7. \([-8,0) \cup(2,8]\)

9. \(\left(-\frac{3}{2}, \frac{3}{2}\right)\)

11. \((-\infty,-5) \cup[0,6)\)

13. \((-\infty, 5) \cup(5, \infty)\)

Ejercicio\(\PageIndex{6}\)

Resolver.

1. \(\frac{x^{2}-11 x-12}{x+4}<0\)
2. \(\frac{x^{2}-10 x+24}{x-2}>0\)
3. \(\frac{x^{2}+x-30}{2 x+1} \geq 0\)
4. \(\frac{2 x^{2}+x-3}{x-3} \leq 0\)
5. \(\frac{3 x^{2}-4 x+1}{x^{2}-9} \leq 0\)
6. \(\frac{x^{2}-16}{2 x^{2}-3 x-2} \geq 0\)
7. \(\frac{x^{2}-12 x+20}{x^{2}-10 x+25}>0\)
8. \(\frac{x^{2}+15 x+36}{x^{2}-8 x+16}<0\)
9. \(\frac{8 x^{2}-2 x-1}{2 x^{2}-3 x-14} \leq 0\)
10. \(\frac{4 x^{2}-4 x-15}{x^{2}+4 x-5} \geq 0\)
11. \(\frac{1}{x+5}+\frac{5}{x-1}>0\)
12. \(\frac{5}{x+4}-\frac{1}{x-4}<0\)
13. \(\frac{1}{x+7}>1\)
14. \(\frac{1}{x-1}<-5\)
15. \(x \geq \frac{30}{x-1}\)
16. \(x \leq \frac{1-2 x}{x-2}\)
17. \(\frac{1}{x-1} \leq \frac{2}{x}\)
18. \(\frac{3}{x+1}>-\frac{1}{x}\)
19. \(\frac{4}{x-3} \leq \frac{1}{x+3}\)
20. \(\frac{2 x-9}{x}+\frac{49}{x-8}<0\)
21. \(\frac{x}{2(x+2)}-\frac{1}{x+2} \leq \frac{12}{x(x+2)}\)
22. \(\frac{1}{2 x+1}-\frac{9}{2 x-1}>2\)
23. \(\frac{3 x}{x^{2}-4}-\frac{2}{x-2}<0\)
24. \(\frac{x}{2 x+1}+\frac{4}{2 x^{2}-7 x-4}<0\)
25. \(\frac{x+1}{2 x^{2}+5 x-3} \geq \frac{x}{4 x^{2}-1}\)
26. \(\frac{x^{2}-14}{2 x^{2}-7 x-4} \leq \frac{5}{1+2 x}\)

Responder

1. \((-\infty,-4) \cup(-1,12)\)

3. \(\left[-6,-\frac{1}{2}\right) \cup[5, \infty)\)

5. \(\left(-3, \frac{1}{3}\right] \cup[1,3)\)

7. \((-\infty, 2) \cup(10, \infty)\)

9. \(\left(-2,-\frac{1}{4}\right] \cup\left[\frac{1}{2}, \frac{7}{2}\right)\)

11. \((-5,-4) \cup(1, \infty)\)

13. \((-7,-6)\)

15. \([-5,1) \cup[6, \infty)\)

17. \((0,1) \cup[2, \infty)\)

19. \((-\infty, 5] \cup(-3,3)\)

21. \([-4,-2) \cup(0,6]\)

23. \((-\infty,-2) \cup(2,4)\)

25. \(\left(-3,-\frac{1}{2}\right) \cup\left(\frac{1}{2}, \infty\right)\)

Ejercicio\(\PageIndex{7}\)

1. ¿Siempre se alterna el gráfico de signos para alguna función polinómica o racional dada? Explica e ilustra tu respuesta con algunos ejemplos.
2. Escribe tus propios pasos para resolver una desigualdad racional e ilustrarlos con un ejemplo. ¿Tus pasos también funcionan para una desigualdad polinómica? Explique.

Responder

1. La respuesta puede variar

Notas al pie

¹⁸ Una declaración matemática que relaciona una expresión polinómica como menor o mayor que otra.

¹⁹ Una afirmación matemática que relaciona una expresión racional como menor o mayor que otra.