6.5: Resolver desigualdades cuadráticas
- Page ID
- 109897
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Objetivos de aprendizaje
- Comprobar soluciones a desigualdades cuadráticas con una variable.
- Comprender la relación geométrica entre las soluciones a las desigualdades cuadráticas y sus gráficas.
- Resolver desigualdades cuadráticas.
Soluciones a las desigualdades cuadráticas
Una desigualdad cuadrática 15 es una afirmación matemática que relaciona una expresión cuadrática como menor o mayor que otra. A continuación se presentan algunos ejemplos de desigualdades cuadráticas resueltas en esta sección.
| \(x^{2}-2 x-11 \leq 0\) | \(2 x^{2}-7 x+3>0\) | \(9-x^{2}>0\) |
Una solución a una desigualdad cuadrática es un número real que producirá una declaración verdadera cuando se sustituya por la variable.
Ejemplo\(\PageIndex{1}\):
Son\(-3\),\(-2\), y\(-1\) soluciones para\(x^{2}-x-6 \leq 0 \)?
Solución
Sustituir el valor dado en por\(x\) y simplificar.
\(\begin{array} {r | r | r} {x^{2}-x-6\leq0}&{x^{2}-x-6\leq0}&{x^{2}-x-6\leq0} \\ {(\color{OliveGreen}{-3}\color{black}{)}^{2}-(\color{OliveGreen}{-3}\color{black}{)}-6\leq0}&{(\color{OliveGreen}{-2}\color{black}{)}^{2}-(\color{OliveGreen}{-2}\color{black}{)}-6\leq0}&{(\color{OliveGreen}{-1}\color{black}{)}^{2}-(\color{OliveGreen}{-1}\color{black}{)}-6\leq0} \\ {9+3-6\leq0}&{4+2-6\leq0}&{1+1-6\leq0} \\ {6\leq0\:\:\color{red}{✗}}&{0\leq0\:\:\color{Cerulean}{✓}}&{-4\leq0\:\:\color{Cerulean}{✓}} \end{array}\)
Respuesta:
\(-2\)y\(-1\) son soluciones y no\(-3\) lo es.
Las desigualdades cuadráticas pueden tener infinitamente muchas soluciones, una solución o ninguna solución. Si hay infinitamente muchas soluciones, grafique el conjunto de soluciones en una línea numérica y/o exprese la solución usando la notación de intervalos. Graficando la función definida por\(f (x) = x^{2} − x − 6\) encontrada en el ejemplo anterior tenemos
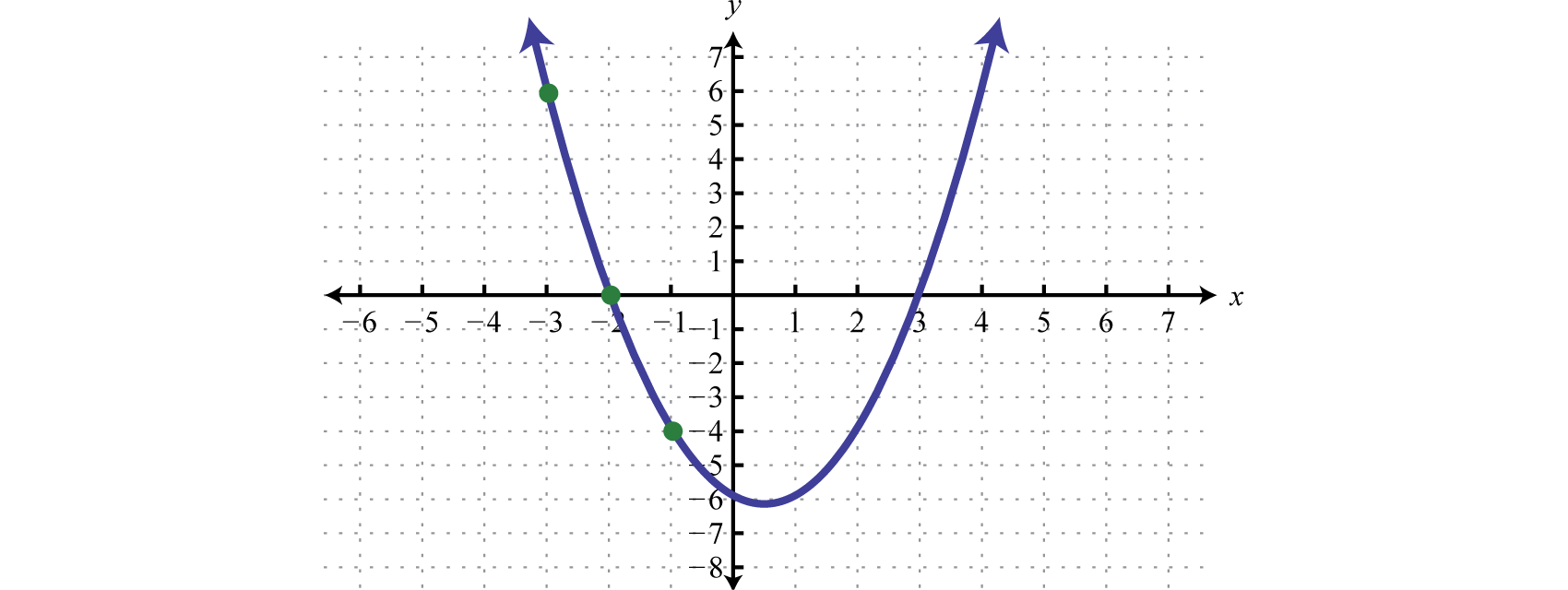
El resultado de evaluar para cualquier\(x\) -valor será negativo, cero o positivo.
\(\begin{aligned} f(-3)&=6 &\color{Cerulean}{Positive \:f(x)>0} \\ f(-2)&=0 &\color{Cerulean}{Zero \:f(x)\:=0} \\f(-1)&=-4 &\color{Cerulean}{Negative \:f(x)<0} \end{aligned}\)
Los valores en el dominio de una función que separan regiones que producen resultados positivos o negativos se denominan números críticos 16. En el caso de una función cuadrática, los números críticos son las raíces, a veces llamadas ceros. Por ejemplo,\(f (x) = x^{2} − x − 6 = (x + 2) (x − 3)\) tiene raíces\(−2\) y\(3\). Estos valores enlazan las regiones donde la función es positiva (por encima del\(x\) eje -) o negativa (por debajo del\(x\) eje -).
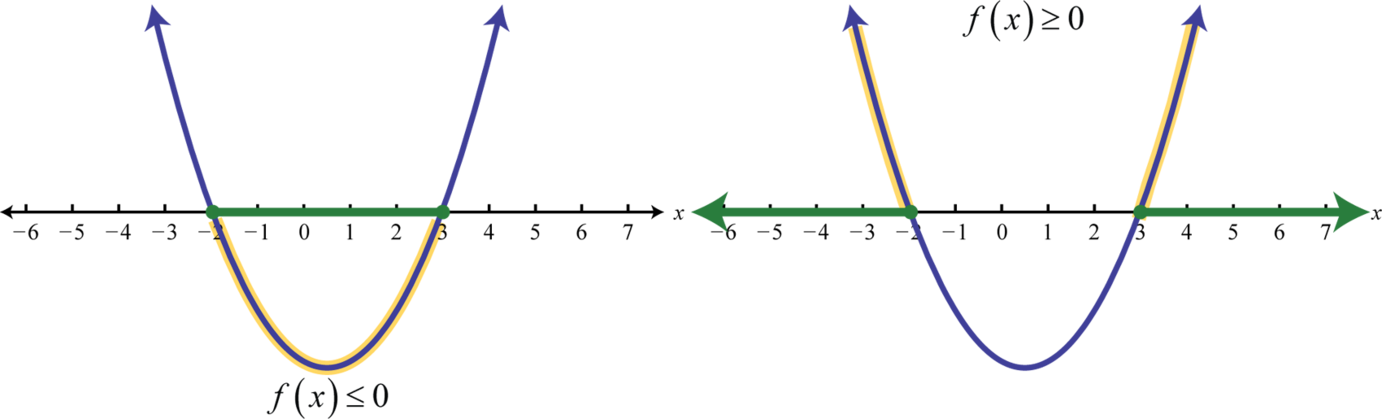
Por lo tanto\(x^{2} − x − 6 ≤ 0\) tiene soluciones donde\(−2 ≤ x ≤ 3\), usando notación de intervalos\([−2, 3]\). Además,\(x^{2} − x − 6 ≥ 0\) tiene soluciones donde\(x ≤ −2\) o\(x ≥ 3\), usando notación de intervalos\((−∞, −2] ∪ [−3, ∞)\).
Ejemplo\(\PageIndex{2}\):
Dada la gráfica de\(f\) determinar las soluciones para\(f(x)>0\):
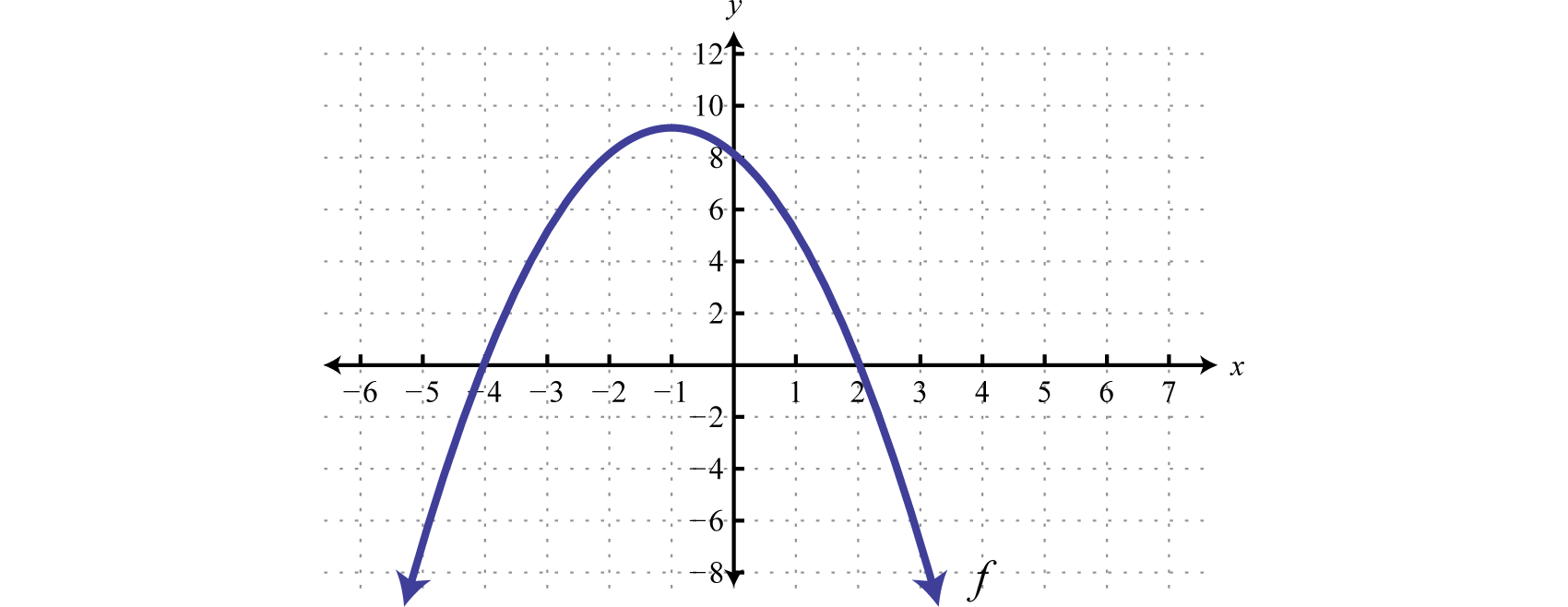
Debido a la estricta desigualdad, el conjunto de soluciones se sombrea con un punto abierto en cada uno de los límites. Esto indica que estos números críticos no están realmente incluidos en el conjunto de soluciones. Este conjunto de soluciones se puede expresar de dos maneras,
\(\begin{aligned}\{x |-4<&x<2\} &\color{Cerulean} { Set\: Notation } \\ (-4,&2) &\color{Cerulean} { Interval\: Notation }\end{aligned}\)
En este libro de texto, seguiremos presentando respuestas en notación de intervalos.
Respuesta:
\((-4,2)\)
Ejercicio\(\PageIndex{1}\)
Dada la gráfica de\(f\) determinar las soluciones para\(f (x) < 0\):
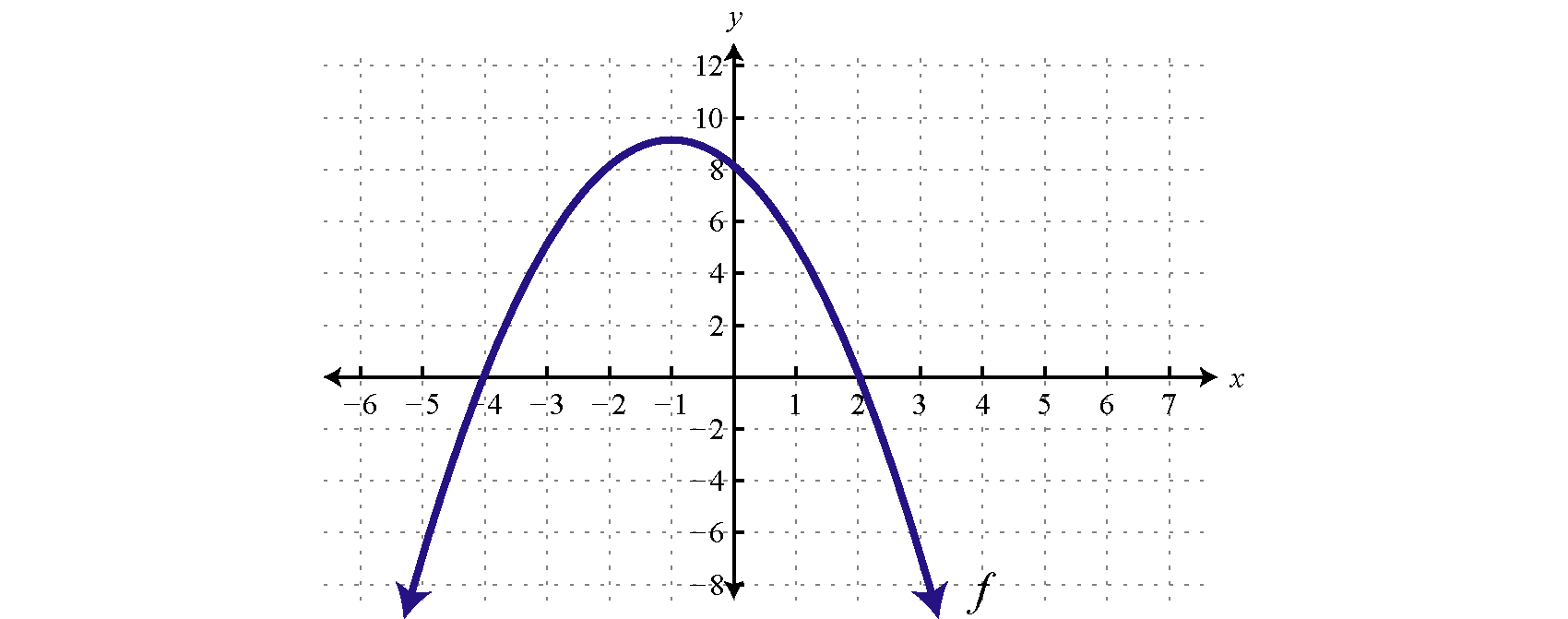
- Contestar
-
\((-\infty,-4) \cup(2, \infty)\)
www.youtube.com/V/kkbaom8bubo
Resolviendo desigualdades cuadráticas
A continuación se esboza una técnica utilizada para resolver desigualdades cuadráticas sin graficar la parábola. Para ello hacemos uso de un gráfico de signos 17 que modela una función utilizando una línea numérica que representa el\(x\) eje -y los signos\((+\) o\(−)\) para indicar donde la función es positiva o negativa. Por ejemplo,
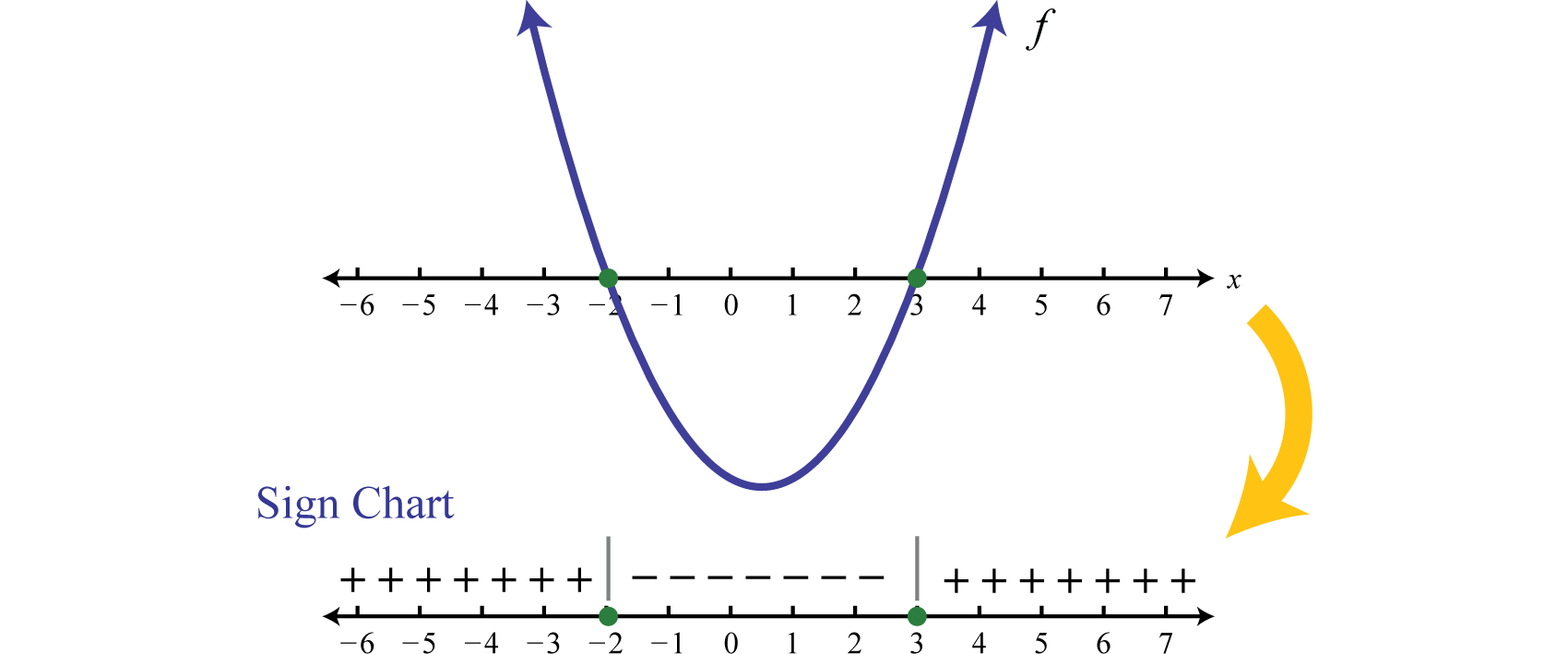
Los signos más indican que la función es positiva en la región. Los signos negativos indican que la función es negativa en la región. Los límites son los números críticos,\(−2\) y\(3\) en este caso. Los gráficos de señales son útiles cuando no se necesita una imagen detallada de la gráfica y se utilizan ampliamente en matemáticas de nivel superior. Los pasos para resolver una desigualdad cuadrática con una variable se describen en el siguiente ejemplo.
Ejemplo\(\PageIndex{3}\):
Resolver:\(-x^{2}+6 x+7 \geq 0\).
Solución
Es importante señalar que esta desigualdad cuadrática se encuentra en forma estándar, con cero en un lado de la desigualdad.
Paso 1: Determinar los números críticos. Para una desigualdad cuadrática en forma estándar, los números críticos son las raíces. Por lo tanto, establezca la función igual a cero y resuelva.
\(-x^{2}+6 x+7=0 \)
\(-\left(x^{2}-6 x-7\right)=0 \)
\(-(x+1)(x-7)=0 \)
\(\begin{aligned}x+1&=0 \:\:\:\:\text { or } &x-7=0 \\ x&=-1 &x=7\end{aligned}\)
Los números críticos son\(-1\) y\(7\).
Paso 2: Crear un gráfico de señales. Dado que los números críticos enlazan las regiones donde la función es positiva o negativa, solo necesitamos probar un solo valor en cada región. En este caso los números críticos particionan la recta numérica en tres regiones y elegimos valores de prueba\(x = −3, x = 0\), y\(x = 10\).
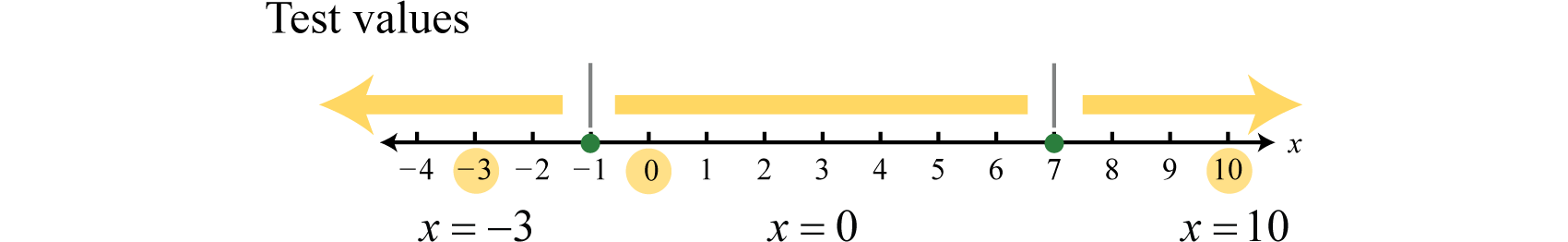
Los valores de las pruebas pueden variar. De hecho, solo necesitamos determinar el signo\((+\) o\(−)\) del resultado a la hora de evaluar\(f (x) = −x^{2} + 6x + 7 = − (x + 1) (x − 7)\). Aquí evaluamos usando la forma factorizada.
\(\begin{aligned} f(\color{OliveGreen}{-3}\color{black}{)}&=-(\color{OliveGreen}{-3}\color{black}{+}1)(\color{OliveGreen}{-3}\color{black}{-}7) =-(-2)(-10)&=-\color{Cerulean} {Negative} \\ f(\color{OliveGreen}{0}\color{black}{)}&=-(\color{OliveGreen}{0}\color{black}{+}1)(\color{OliveGreen}{0}\color{black}{-}7) =-(1)(-7)&=+\color{Cerulean} { Positive } \\ f(\color{OliveGreen}{10}\color{black}{)}&=-(\color{OliveGreen}{10}\color{black}{+}1)(\color{OliveGreen}{10}\color{black}{-}7) =-(11)(3)&=-\color{Cerulean} {Negative} \end{aligned}\)
Dado que el resultado de la evaluación\(−3\) fue negativo, colocamos los signos negativos por encima de la primera región. El resultado de la evaluación\(0\) fue positivo, por lo que colocamos signos positivos por encima de la región media. Finalmente, el resultado de evaluar para\(10\) fue negativo, por lo que colocamos los signos negativos por encima de la última región, y el gráfico de signos está completo.
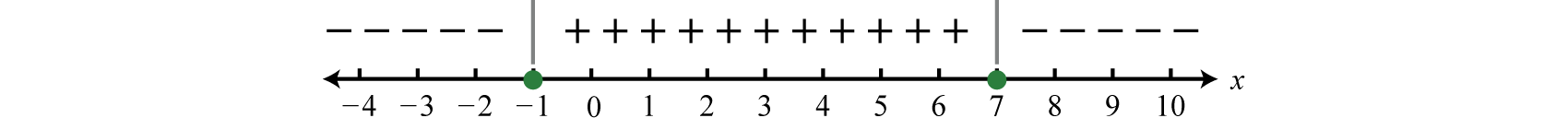
Paso 3: Usa el gráfico de señales para responder a la pregunta. En este caso, se nos pide determinar dónde\(f (x) ≥ 0\), o dónde la función es positiva o cero. A partir del gráfico de signos vemos que esto ocurre cuando\(x\) -valores están inclusivamente entre\(−1\) y\(7\).

Usando la notación de intervalos, la región sombreada se expresa como\([−1, 7]\). No se requiere la gráfica; sin embargo, en aras de la integridad se proporciona a continuación.
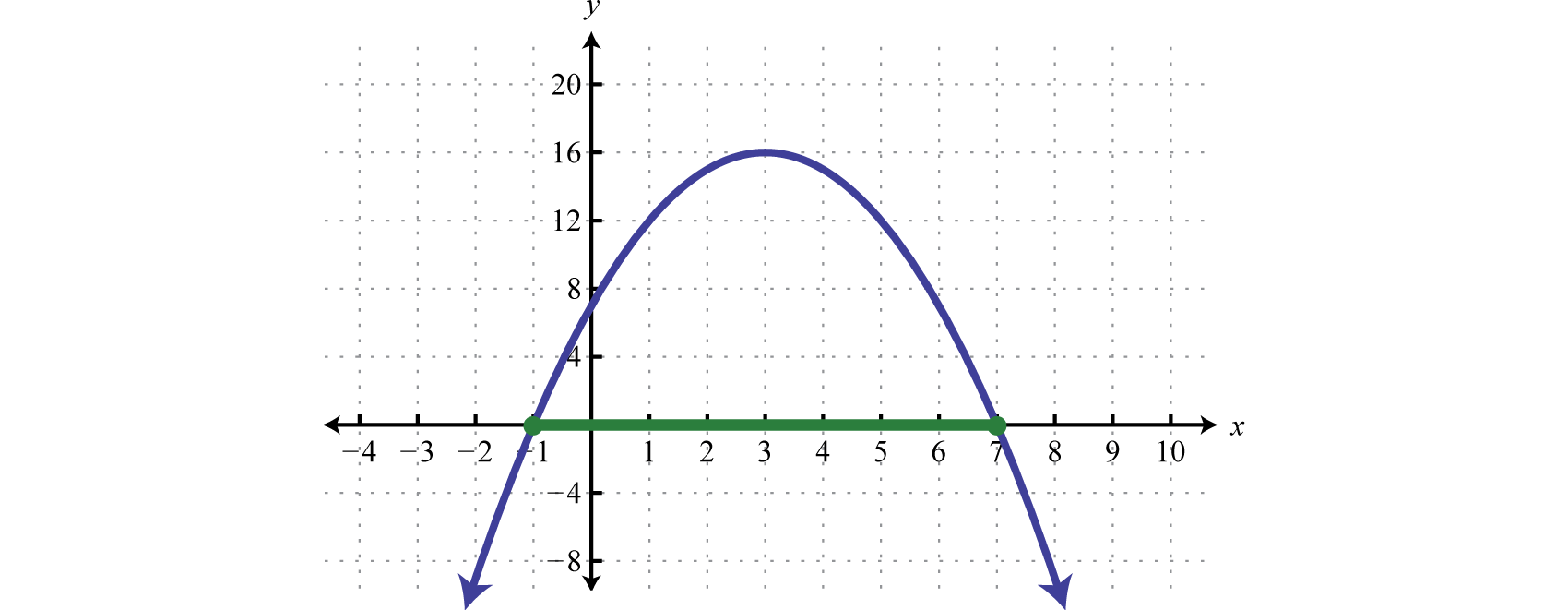
De hecho la función es mayor o igual a cero, por encima o en el\(x\) eje -eje, para\(x\) -valores en el intervalo especificado.
Respuesta:
\([-1,7]\)
Ejemplo\(\PageIndex{4}\):
Resolver:\(2 x^{2}-7 x+3>0\).
Solución
Comience por encontrar los números críticos, en este caso, las raíces de\(f(x)=2 x^{2}-7 x+3\).
\(\begin{aligned}2 x^{2}-7 x+3&=0 \\ (2 x-1)(x-3)&=0\end{aligned}\)
\(\begin{aligned} 2 x-1 &=0 \:\:\:\:\:\text { or }& x-3=0 \\ 2 x &=1 \quad &x=3 \\ x &=\frac{1}{2} \end{aligned}\)
Los números críticos son\(\frac{1}{2}\) y\(3\). Por la estricta desigualdad > usaremos puntos abiertos.

A continuación, elija un valor de prueba en cada región y determine el signo después de evaluar\(f (x) = 2x^{2} − 7x + 3 = (2x − 1) (x − 3)\). Aquí elegimos valores de prueba\(−1, 2\), y\(5\).
\(\begin{aligned} f(\color{OliveGreen}{-1}\color{black}{)} &=[2(\color{OliveGreen}{-1}\color{black}{)}-1](\color{OliveGreen}{-1}\color{black}{-}3)&=(-)(-)=+\\ f(\color{OliveGreen}{2}\color{black}{)} &=[2(\color{OliveGreen}{2}\color{black}{)}-1](\color{OliveGreen}{2}\color{black}{-}3)&=(+)(-)=-\\ f(\color{OliveGreen}{5}\color{black}{)} &=[2(\color{OliveGreen}{5}\color{black}{)}-1](\color{OliveGreen}{5}\color{black}{-}3)&=(+)(+)=+\end{aligned}\)
Y podemos completar el gráfico de señales.

La pregunta nos pide encontrar los\(x\) -valores que producen resultados positivos (mayores que cero). Por lo tanto, sombra en las regiones con un\(+\) sobre ellos. Este es el conjunto de soluciones.

Respuesta:
\(\left(-\infty, \frac{1}{2}\right) \cup(3, \infty)\)
A veces la función cuadrática no factoriza. En este caso podemos hacer uso de la fórmula cuadrática.
Ejemplo\(\PageIndex{5}\):
Resolver:\(x^{2}-2 x-11 \leq 0\)
Solución
Encuentra los números críticos.
\(x^{2}-2 x-11=0\)
Identificar\(a, b\), y\(c\) para su uso en la fórmula cuadrática. Aquí\(a = 1, b = −2\), y\(c = −11\). Sustituir los valores apropiados en la fórmula cuadrática y luego simplificar.
\(\begin{aligned} x &=\frac{-b \pm \sqrt{b^{2}-4 a c}}{2 a} \\ &=\frac{-(\color{OliveGreen}{-2}\color{black}{)} \pm \sqrt{(\color{OliveGreen}{-2}\color{black}{)}^{2}-4(\color{OliveGreen}{1}\color{black}{)}(\color{OliveGreen}{-11}\color{black}{)}}}{2(\color{OliveGreen}{1}\color{black}{)}} \\ &=\frac{2 \pm \sqrt{48}}{2} \\ &=\frac{2 \pm 4 \sqrt{3}}{2} \\ &=1 \pm 2 \sqrt{3} \end{aligned}\)
Por lo tanto los números críticos son\(1-2 \sqrt{3} \approx-2.5\) y\(1+2 \sqrt{3} \approx 4.5\). Use un punto cerrado en el número para indicar que estos valores se incluirán en el conjunto de soluciones.

Aquí usaremos valores de prueba\(−5, 0\), y\(7\).
\(\begin{aligned} f(\color{OliveGreen}{-5}\color{black}{)}&=(\color{OliveGreen}{-5}\color{black}{)}^{2}-2(\color{OliveGreen}{-5}\color{black}{)}-11 =25+10-11&=+\\ f(\color{OliveGreen}{0}\color{black}{)}&=(\color{OliveGreen}{0}\color{black}{)}^{2}-2(\color{OliveGreen}{0}\color{black}{)}-11 =0+0-11&=-\\ f(\color{OliveGreen}{7}\color{black}{)}&=(\color{OliveGreen}{7}\color{black}{)}^{2}-2(\color{OliveGreen}{7}\color{black}{)}-11 =49-14-11&=+\end{aligned}\)
Después de completar la sombra del gráfico de signos en los valores donde la función es negativa como lo indica la pregunta\((f (x) ≤ 0)\).

Respuesta:
\([1-2 \sqrt{3}, 1+2 \sqrt{3}]\)
Ejercicio\(\PageIndex{2}\)
Resolver:\(9-x^{2}>0\).
- Contestar
-
\((-3,3)\)
www.youtube.com/v/7gmj8guvasw
Puede darse el caso de que no haya números críticos.
Ejemplo\(\PageIndex{6}\):
Resolver:\(x^{2}-2 x+3>0\).
Solución
Para encontrar los números críticos resuelven,
\(x^{2}-2 x+3=0\)
Sustituir\(a = 1, b = −2\), y\(c = 3\) en la fórmula cuadrática y luego simplificar.
\(\begin{aligned} x &=\frac{-b \pm \sqrt{b^{2}-4 a c}}{2 a} \\ &=\frac{-(\color{OliveGreen}{-2}\color{black}{)} \pm \sqrt{(\color{OliveGreen}{-2}\color{black}{)}^{2}-4(\color{OliveGreen}{1}\color{black}{)}(\color{OliveGreen}{3}\color{black}{)}}}{2(\color{OliveGreen}{1}\color{black}{)}} \\ &=\frac{2 \pm \sqrt{-8}}{2} \\ &=\frac{2 \pm 2 i \sqrt{2}}{2} \\ &=1+i \sqrt{2} \end{aligned}\)
Debido a que las soluciones no son reales, concluimos que no hay raíces reales; de ahí que no haya números críticos. Cuando este es el caso, la gráfica no tiene\(x\) -intercepciones y está completamente por encima o por debajo del\(x\) eje. Podemos probar cualquier valor para crear un gráfico de signos. Aquí elegimos\(x = 0\).
\(f(0)=(0)^{2}-2(0)+3=+\)
Debido a que el valor de la prueba produjo un resultado positivo, el gráfico de signos se ve como sigue:
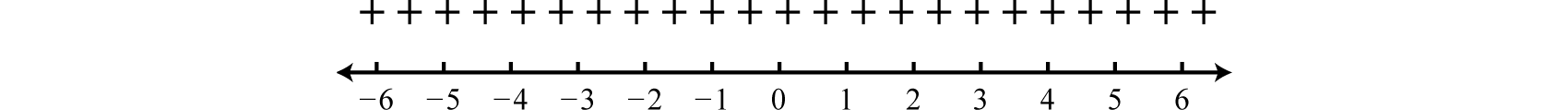
Estamos buscando los valores donde\(f (x) > 0\); el gráfico de signos implica que cualquier número real para\(x\) satisfará esta condición.

Respuesta:
\((-\infty, \infty)\)
La función en el ejemplo anterior se grafica a continuación.
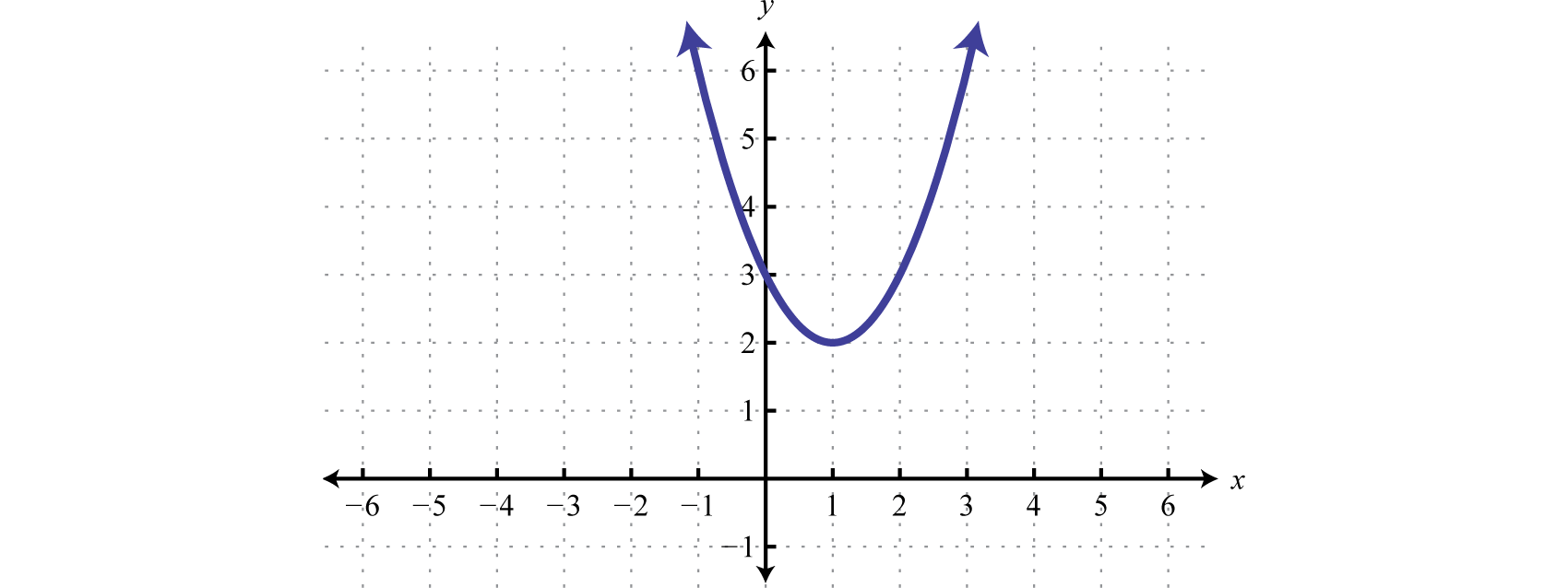
Podemos ver que no tiene\(x\) -intercepciones y siempre está por encima del\(x\) eje -( positivo). Si la pregunta fuera a resolver\(x^{2} − 2x + 3 < 0\), entonces la respuesta no habría sido ninguna solución. La función nunca es negativa.
Ejercicio\(\PageIndex{3}\)
Resolver:\(9 x^{2}-12 x+4 \leq 0\)
- Contestar
-
Una solución,\(\frac{2}{3}\).
www.youtube.com/v/e7vCoyvv_DS
Ejemplo\(\PageIndex{7}\):
Encuentra el dominio:\(f(x)=\sqrt{x^{2}-4}\).
Solución
Recordemos que el argumento de una función de raíz cuadrada debe ser no negativo. Por lo tanto, el dominio consiste en todos los números reales para\(x\) tal que\(x^{2} − 4\) sea mayor o igual a cero.
\(x^{2}-4 \geq 0\)
Debe quedar claro que\(x^{2} − 4 = 0\) tiene dos soluciones\(x = ±2\); estos son los valores críticos. Elija valores de prueba en cada intervalo y evalúe\(f (x) = x^{2} − 4\).
\(\begin{aligned} f(-3) &=(-3)^{2}-4=9-4=+\\ f(0) &=(0)^{2}-4=0-4=-\\ f(3) &=(3)^{2}-4=9-4=+\end{aligned}\)
Sombra en los\(x\) valores -que producen resultados positivos.

Respuesta:
Dominio:\((-\infty,-2] \cup[2, \infty)\)
Claves para llevar
- Las desigualdades cuadráticas pueden tener infinitamente muchas soluciones, una solución o ninguna solución.
- Podemos resolver las desigualdades cuadráticas gráficamente reescribiendo primero la desigualdad en forma estándar, con cero en un lado. Grafica la función cuadrática y determina dónde está por encima o por debajo del\(x\) eje. Si la desigualdad implica “menos que”, entonces determine los\(x\) -valores donde la función está por debajo del\(x\) eje -eje. Si la desigualdad implica “mayor que”, entonces determine los\(x\) -valores donde la función está por encima del\(x\) eje -.
- Podemos agilizar el proceso de resolución de desigualdades cuadráticas haciendo uso de un gráfico de signos. Un gráfico de signos nos da una referencia visual que indica dónde está la función por encima del\(x\) eje usando signos positivos o por debajo del\(x\) eje usando signos negativos. Sombra en los valores x apropiados dependiendo de la desigualdad original.
- Para hacer un gráfico de signos, utilice los valores de función y prueba en cada región delimitada por las raíces. Solo nos preocupa si la función es positiva o negativa y por lo tanto no es necesario un cálculo completo.
Ejercicio\(\PageIndex{4}\)
Determinar si el valor dado es o no una solución.
- \(x^{2}-x+1<0 ; x=-1\)
- \(x^{2}+x-1>0 ; x=-2\)
- \(4 x^{2}-12 x+9 \leq 0 ; x=\frac{3}{2}\)
- \(5 x^{2}-8 x-4<0 ; x=-\frac{2}{5}\)
- \(3 x^{2}-x-2 \geq 0 ; x=0\)
- \(4 x^{2}-x+3 \leq 0 ; x=-1\)
- \(2-4 x-x^{2}<0 ; x=\frac{1}{2}\)
- \(5-2 x-x^{2}>0 ; x=0\)
- \(-x^{2}-x-9<0 ; x=-3\)
- \(-x^{2}+x-6 \geq 0 ; x=6\)
- Contestar
-
1. No
3. Sí
5. No
7. Sí
9. Sí
Ejercicio\(\PageIndex{5}\)
Dada la gráfica de\(f\) determinar el conjunto de soluciones.
1. \(f(x) \leq 0\);
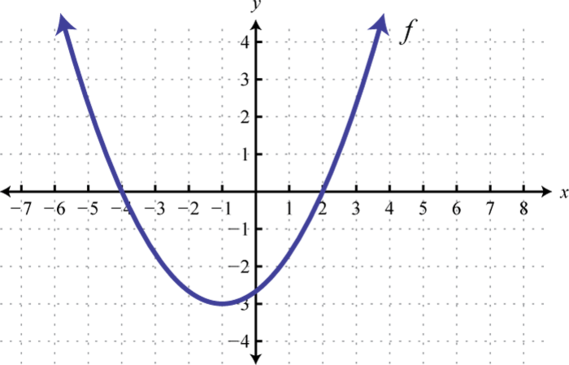
2. \(f(x) \geq 0\);
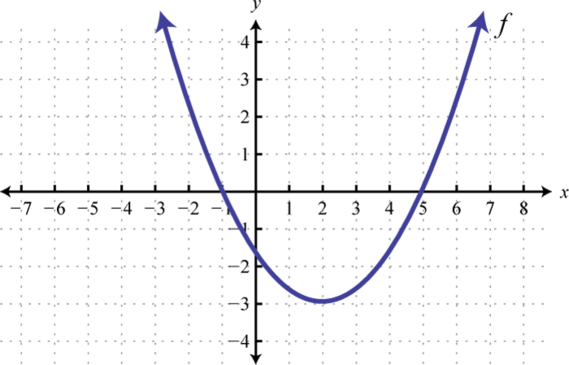
3. \(f(x) \geq 0\);

4. \(f(x) \leq 0\);
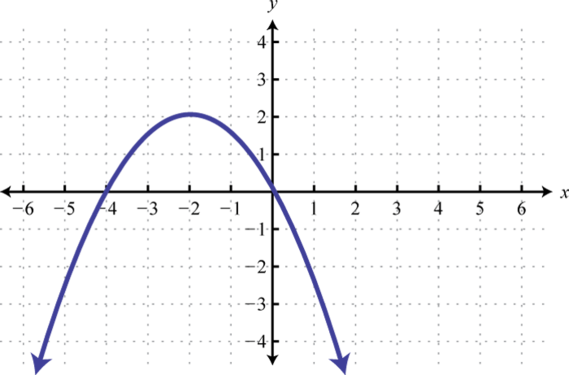
5. \(f(x)>0\);
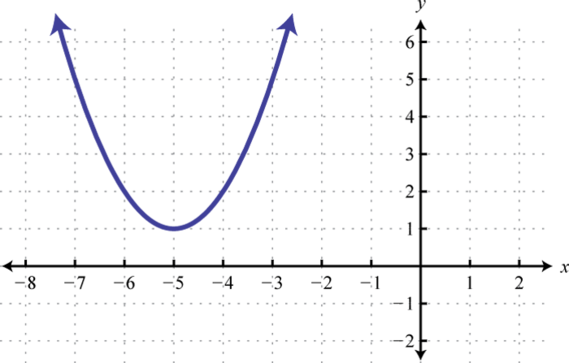
6. \(f(x)<0\);
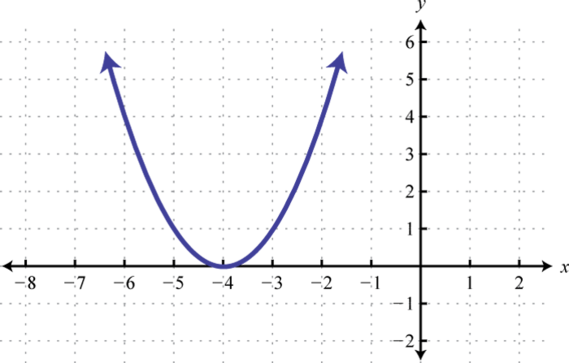
7. \(f(x)>0\);
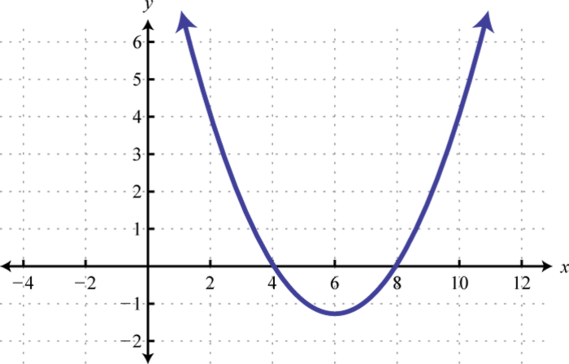
8. \(f(x)<0\);
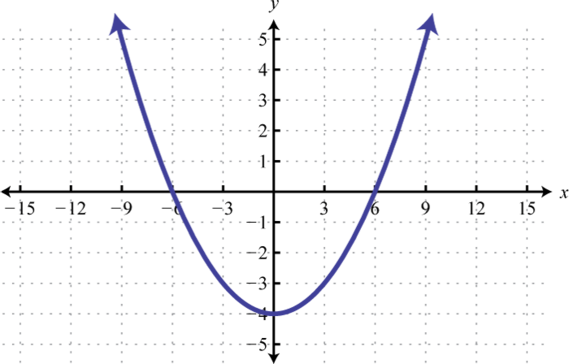
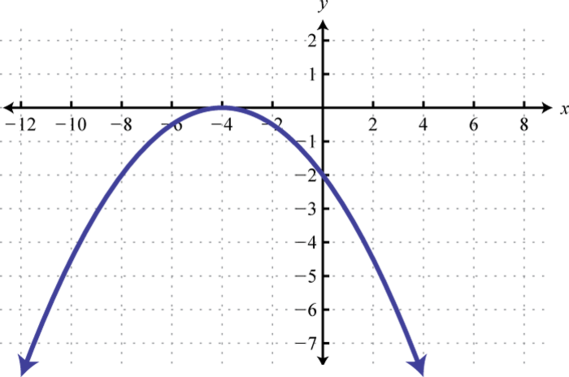
9. \(f(x) \geq 0\);
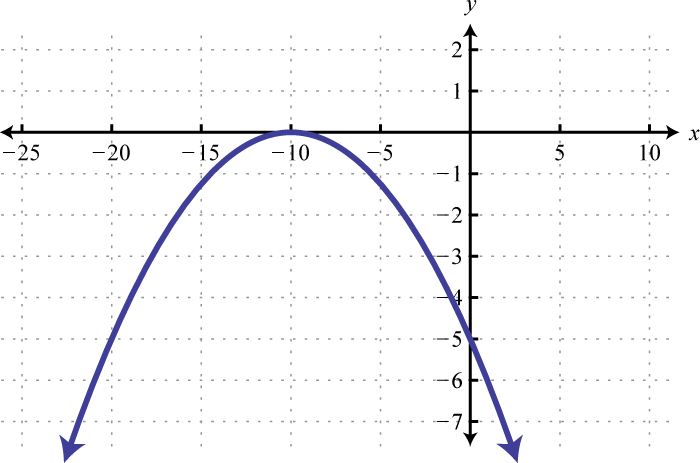
10. \(f(x)<0\);
- Contestar
-
1. \([-4,2]\)
3. \([-1,3]\)
5. \((-\infty, \infty)\)
7. \((-\infty, 4) \cup(8, \infty)\)
9. \(\{-10\}\)
Ejercicio\(\PageIndex{6}\)
Utilice las transformaciones para graficar lo siguiente y luego determinar el conjunto de soluciones.
- \(x^{2}-1>0\)
- \(x^{2}+2>0\)
- \((x-1)^{2}>0\)
- \((x+2)^{2} \leq 0\)
- \((x+2)^{2}-1 \leq 0\)
- \((x+3)^{2}-4>0\)
- \(-x^{2}+4 \geq 0\)
- \(-(x+2)^{2}>0\)
- \(-(x+3)^{2}+1<0\)
- \(-(x-4)^{2}+9>0\)
- Contestar
-
1. \((-\infty,-1) \cup(1, \infty)\)
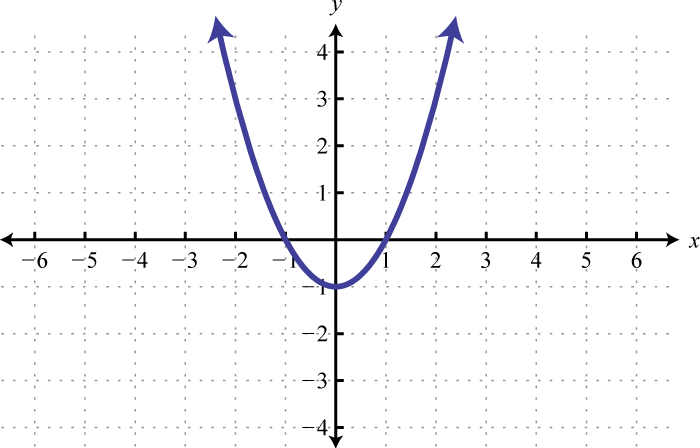
Figura\(\PageIndex{30}\) 3. \((-\infty, 1) \cup(1, \infty)\)
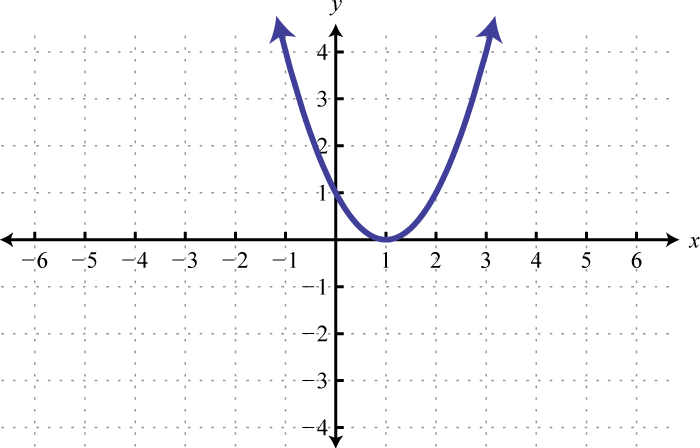
Figura\(\PageIndex{31}\) 5. \([-3,-1]\)
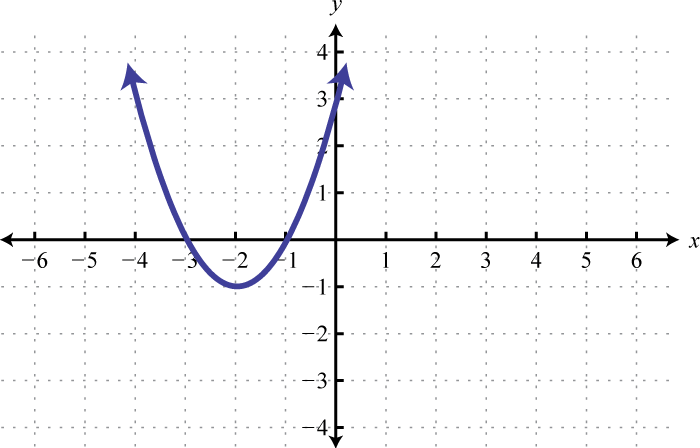
Figura\(\PageIndex{32}\) 7. \([-2,2]\)
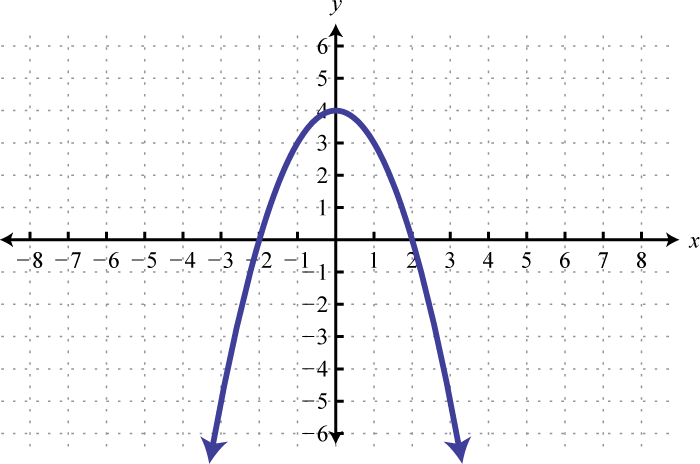
Figura\(\PageIndex{33}\) 9. \((-\infty,-4) \cup(-2, \infty)\)
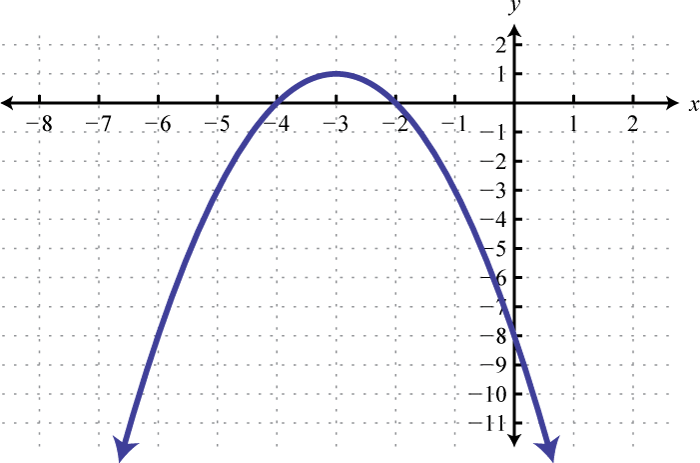
Figura\(\PageIndex{34}\)
Ejercicio\(\PageIndex{7}\)
Utilice un gráfico de señales para resolver y graficar el conjunto de soluciones. Presentar respuestas usando notación de intervalos.
- \(x^{2}-x-12>0\)
- \(x^{2}-10 x+16>0\)
- \(x^{2}+2 x-24<0\)
- \(x^{2}+15 x+54<0\)
- \(x^{2}-23 x-24 \leq 0\)
- \(x^{2}-12 x+20 \leq 0\)
- \(2 x^{2}-11 x-6 \geq 0\)
- \(3 x^{2}+17 x-6 \geq 0\)
- \(8 x^{2}-18 x-5<0\)
- \(10 x^{2}+17 x+6>0\)
- \(9 x^{2}+30 x+25 \leq 0\)
- \(16 x^{2}-40 x+25 \leq 0\)
- \(4 x^{2}-4 x+1>0\)
- \(9 x^{2}+12 x+4>0\)
- \(-x^{2}-x+30 \geq 0\)
- \(-x^{2}-6 x+27 \leq 0\)
- \(x^{2}-64<0\)
- \(x^{2}-81 \geq 0\)
- \(4 x^{2}-9 \geq 0\)
- \(16 x^{2}-25<0\)
- \(25-4 x^{2} \geq 0\)
- \(1-49 x^{2}<0\)
- \(x^{2}-8>0\)
- \(x^{2}-75 \leq 0\)
- \(2 x^{2}+1>0\)
- \(4 x^{2}+3<0\)
- \(x-x^{2}>0\)
- \(3 x-x^{2} \leq 0\)
- \(x^{2}-x+1<0\)
- \(x^{2}+x-1>0\)
- \(4 x^{2}-12 x+9 \leq 0\)
- \(5 x^{2}-8 x-4<0\)
- \(3 x^{2}-x-2 \geq 0\)
- \(4 x^{2}-x+3 \leq 0\)
- \(2-4 x-x^{2}<0\)
- \(5-2 x-x^{2}>0\)
- \(-x^{2}-x-9<0\)
- \(-x^{2}+x-6 \geq 0\)
- \(-2 x^{2}+4 x-1 \geq 0\)
- \(-3 x^{2}-x+1 \leq 0\)
- Contestar
-
1. \((-\infty,-3) \cup(4, \infty)\)
3. \((-6,4)\)
5. \([-1,24]\)
7. \(\left(-\infty,-\frac{1}{2}\right] \cup[6, \infty)\)
9. \(\left(-\frac{1}{4}, \frac{5}{2}\right)\)
11. \(-\frac{5}{3}\)
13. \(\left(-\infty, \frac{1}{2}\right) \cup\left(\frac{1}{2}, \infty\right)\)
15. \([-6,5]\)
17. \((-8,8)\)
19. \(\left(-\infty,-\frac{3}{2}\right] \cup\left[\frac{3}{2}, \infty\right)\)
21. \(\left[-\frac{5}{2}, \frac{5}{2}\right]\)
23. \((-\infty,-2 \sqrt{2}) \cup(2 \sqrt{2}, \infty)\)
25. \((-\infty, \infty)\)
27. \((0,1)\)
29. \(\emptyset\)
31. \(\frac{3}{2}\)
33. \(\left(-\infty,-\frac{2}{3}\right] \cup[1, \infty)\)
35. \((-\infty,-2-\sqrt{6}) \cup(-2+\sqrt{6}, \infty)\)
37. \((-\infty, \infty)\)
39. \(\left[\frac{2-\sqrt{2}}{2}, \frac{2+\sqrt{2}}{2}\right]\)
Ejercicio\(\PageIndex{8}\)
Encuentra el dominio de la función.
- \(f(x)=\sqrt{x^{2}-25}\)
- \(f(x)=\sqrt{x^{2}+3 x}\)
- \(g(x)=\sqrt{3 x^{2}-x-2}\)
- \(g(x)=\sqrt{12 x^{2}-9 x-3}\)
- \(h(x)=\sqrt{16-x^{2}}\)
- \(h(x)=\sqrt{3-2 x-x^{2}}\)
- \(f(x)=\sqrt{x^{2}+10}\)
- \(f(x)=\sqrt{9+x^{2}}\)
- Una empresa de fabricación de robótica ha determinado que su ganancia semanal en miles de dólares está modelada por\(P (n) = −n^{2} + 30n − 200\) donde\(n\) representa el número de unidades que produce y vende. Cuántas unidades debe producir y vender la empresa para mantener la rentabilidad. (Pista: La rentabilidad ocurre cuando el beneficio es mayor que cero.)
- La altura en pies de un proyectil disparado directo al aire viene dada por\(h (t) = −16t^{2} + 400t\) donde\(t\) representa el tiempo en segundos después de ser disparado. ¿En qué intervalos de tiempo está el proyectil bajo\(1,000\) los pies? Redondear a la décima de segundo más cercana.
- Contestar
-
1. \((-\infty,-5] \cup[5, \infty)\)
3. \(\left(-\infty,-\frac{2}{3}\right] \cup[1, \infty)\)
5. \([-4,4]\)
7. \((-\infty, \infty)\)
9. La compañía debe producir y vender más de\(10\) unidades y menos de\(20\) unidades cada semana.
Ejercicio\(\PageIndex{9}\)
- ¿El gráfico de signos para alguna función cuadrática dada siempre se alterna? Explica e ilustra tu respuesta con algunos ejemplos.
- Investigar y discutir otros métodos para resolver una desigualdad cuadrática.
- Explicar la diferencia entre una ecuación cuadrática y una desigualdad cuadrática. ¿Cómo podemos identificar y resolver cada uno? ¿Cuál es la interpretación geométrica de cada uno?
- Contestar
-
1. La respuesta puede variar
3. La respuesta puede variar
Notas al pie
15 Una declaración matemática que relaciona una expresión cuadrática como menor o mayor que otra.
16 Los valores en el dominio de una función que separan regiones que producen resultados positivos o negativos.
17 Un modelo de una función usando una línea numérica y signos\((+\) o\(−)\) para indicar regiones en el dominio donde la función es positiva o negativa.


