8.1: Distancia, punto medio y la parábola

Objetivos de aprendizaje

• Aplicar las fórmulas de distancia y punto medio.
• Grafica una parábola usando su ecuación dada en estándar de.
• Determinar la forma estándar para la ecuación de una parábola dada forma general.

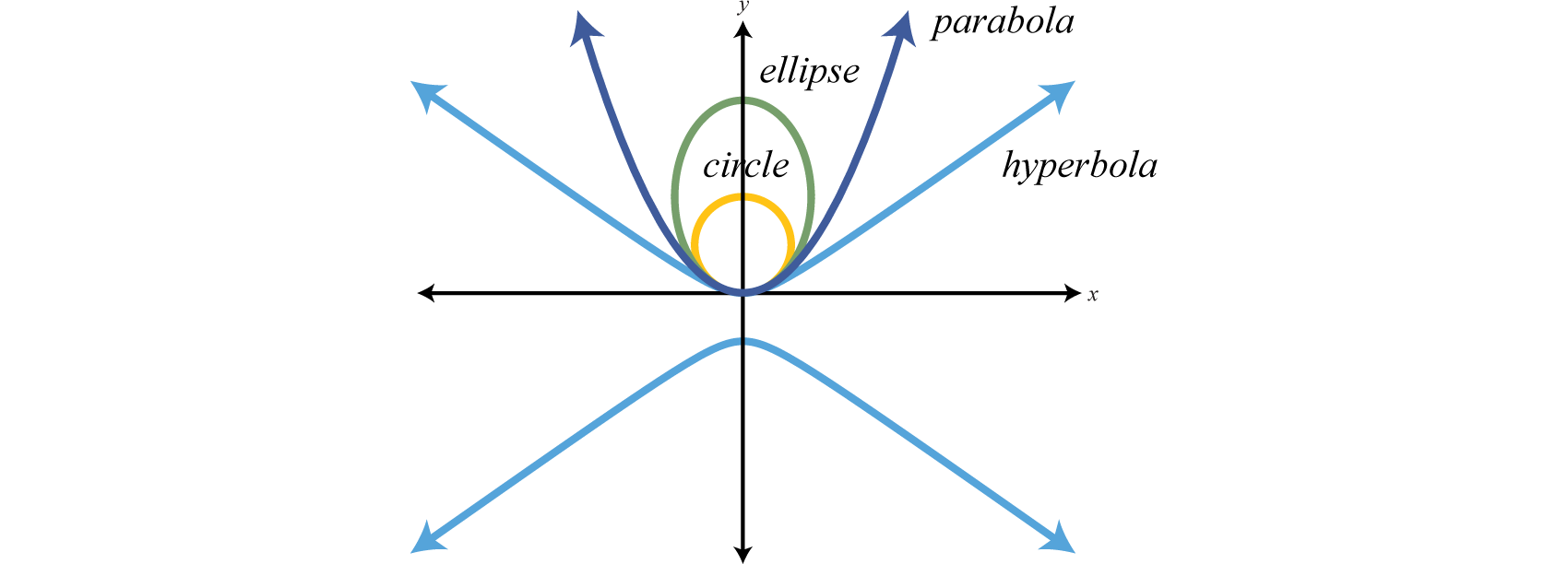
Secciones Cónicas

Una sección cónica ¹ es una curva obtenida de la intersección de un cono circular derecho y un plano. Las secciones cónicas son la parábola, círculo, elipse e hipérbola.

Figura\(\PageIndex{1}\)

El objetivo es esbozar estas gráficas en un plano de coordenadas rectangulares.

Figura\(\PageIndex{2}\)

Las fórmulas de distancia y punto medio

Comenzamos con una revisión de la fórmula de distancia ². Dados dos puntos\((x_{1},  y_{1})\) y\(( x_{2},  y_{2})\) en un plano de coordenadas rectangulares, la distancia\(d\) entre ellos viene dada por la fórmula de distancia,

\(d=\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\)

Además, el punto que bisecta el segmento lineal formado por estos dos puntos se denomina punto medio ³ y viene dado por la fórmula,

\(\left(\frac{x_{1}+x_{2}}{2}, \frac{y_{1}+y_{2}}{2}\right)\)

El punto medio es un par ordenado formado por el promedio de los\(x\) -valores y el promedio de los\(y\) -valores.

Ejemplo\(\PageIndex{1}\):

Dado\((−2,−5)\) y\((−4,−3)\) calcular la distancia y el punto medio entre ellos.

Solución:

En este caso, utilizaremos las fórmulas con los siguientes puntos:

\(\begin{array}{c c}{\left(x_{1}, y_{1}\right)} &{\left(x_{2}, y_{2}\right)} \\ {\color{black}{(\color{Cerulean}{-2}\color{black}{,}\color{OliveGreen}{-5})}}&{\color{black}{(\color{Cerulean}{-4}\color{black}{,}\color{OliveGreen}{-3})}}\end{array}\)

Es una buena práctica incluir la fórmula en su forma general antes de sustituir valores por las variables; esto mejora la legibilidad y reduce la probabilidad de cometer errores.

\(\begin{aligned} d &=\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}} \\ &=\sqrt{[\color{Cerulean}{-4}\color{black}{-}(\color{Cerulean}{-2}\color{black}{)}]^{2}+[\color{OliveGreen}{-3}\color{black}{-}(\color{OliveGreen}{-5}\color{black}{)}]^{2}} \\ &=\sqrt{(-4+2)^{2}+(-3+5)^{2}} \\ &=\sqrt{(-2)^{2}+(2)^{2}} \\ &=\sqrt{4+4} \\ &=\sqrt{8} \\ &=2 \sqrt{2} \end{aligned}\)

A continuación determinar el punto medio.

\(\begin{aligned}\left(\frac{x_{1}+x_{2}}{2}, \frac{y_{1}+y_{2}}{2}\right) &=\left(\frac{-2+(-4)}{2}, \frac{-5+(-3)}{2}\right) \\ &=\left(\frac{-6}{2}, \frac{-8}{2}\right) \\ &=(-3,-4) \end{aligned}\)

Trazar estos puntos en una gráfica tenemos,

Figura\(\PageIndex{3}\)

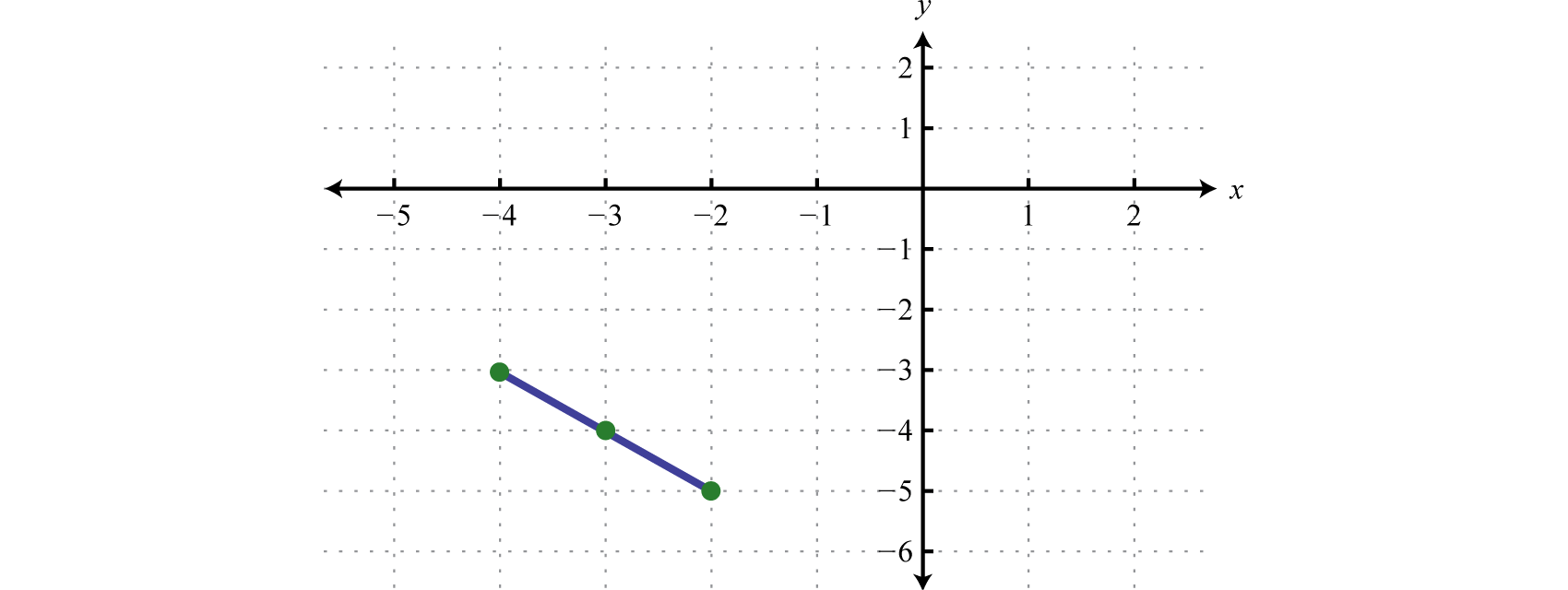
Respuesta:

Distancia:\(2\sqrt{2}\) unidades; punto medio:\((−3,−4)\)

Ejemplo\(\PageIndex{2}\):

El diámetro de un círculo se define por los dos puntos\((−1,2)\) y\((1,−2)\). Determine el radio del círculo y utilízelo para calcular su área.

Solución

Encuentra el diámetro usando la fórmula de distancia.

\(\begin{aligned} d &=\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}} \\ &=\sqrt{\left[\color{Cerulean}{1}\color{black}{-}(\color{Cerulean}{-1}\color{black}{)}^{2}+(\color{OliveGreen}{-2}\color{black}{-}\color{OliveGreen}{2}\color{black}{)}^{2}\right.} \\ &=\sqrt{[2)^{2}+(-4)^{2}} \\&=\sqrt{4+16} \\&=\sqrt{20} \\ &=2 \sqrt{5} \end{aligned}\)

Recordemos que el radio de un círculo es la mitad del diámetro del círculo. Por lo tanto, si\(d=2\sqrt{5}\) las unidades, entonces

\(r=\frac{d}{2}=\frac{2 \sqrt{5}}{2}=\sqrt{5}\)

El área de un círculo viene dada por la fórmula\(A=πr^{2}\) y tenemos

\(\begin{aligned} A &=\pi(\sqrt{5})^{2} \\ &=\pi \cdot 5 \\ &=5 \pi \end{aligned}\)

El área se mide en unidades cuadradas.

Respuesta:

Radio:\(\sqrt{5}\) unidades; área: unidades\(5π\) cuadradas

Ejercicio\(\PageIndex{1}\)

Dado\((0,0)\) y\((9,−3)\) calcular la distancia y el punto medio entre ellos.

Contestar

Distancia:\(3\sqrt{10}\) unidades; punto medio:\(\left(\frac{9}{2},-\frac{3}{2}\right)\)

www.youtube.com/v/6kqnaCocpw0

La Parábola

Una parábola ⁴ es el conjunto de puntos en un plano equidistante de una línea dada, llamada directrix, y un punto que no está en la línea, llamado foco. En otras palabras, si se le da una línea\(L\) la directrix, y un punto\(F\) el foco, entonces\((x,y)\) es un punto en la parábola si la distancia más corta de ella al foco y de ella a la línea es igual como se muestra a continuación:

Figura\(\PageIndex{4}\)

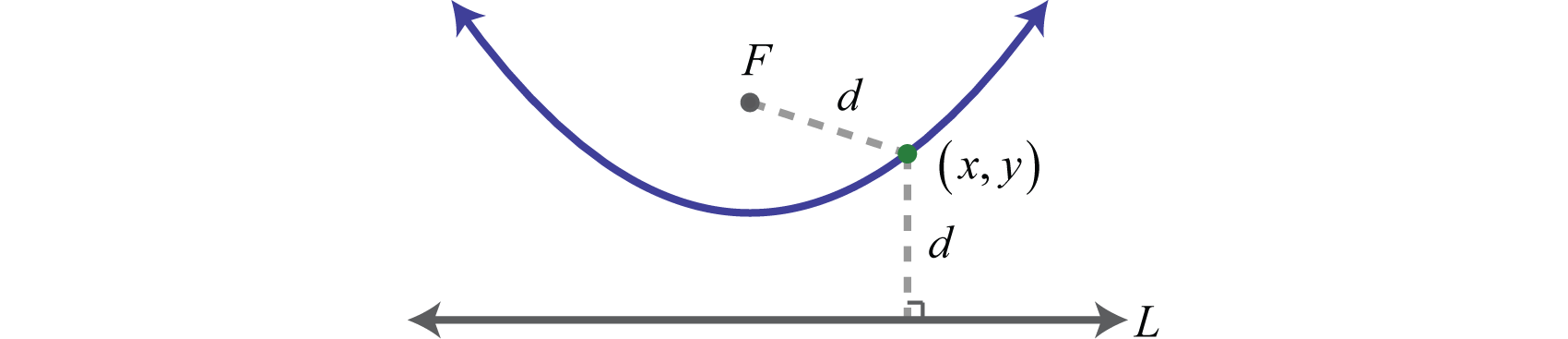
El vértice de la parábola es el punto donde la distancia más corta a la directrix es mínima. Además, una parábola está formada por la intersección de un cono con un plano oblicuo que es paralelo al lado del cono:

Figura\(\PageIndex{5}\)

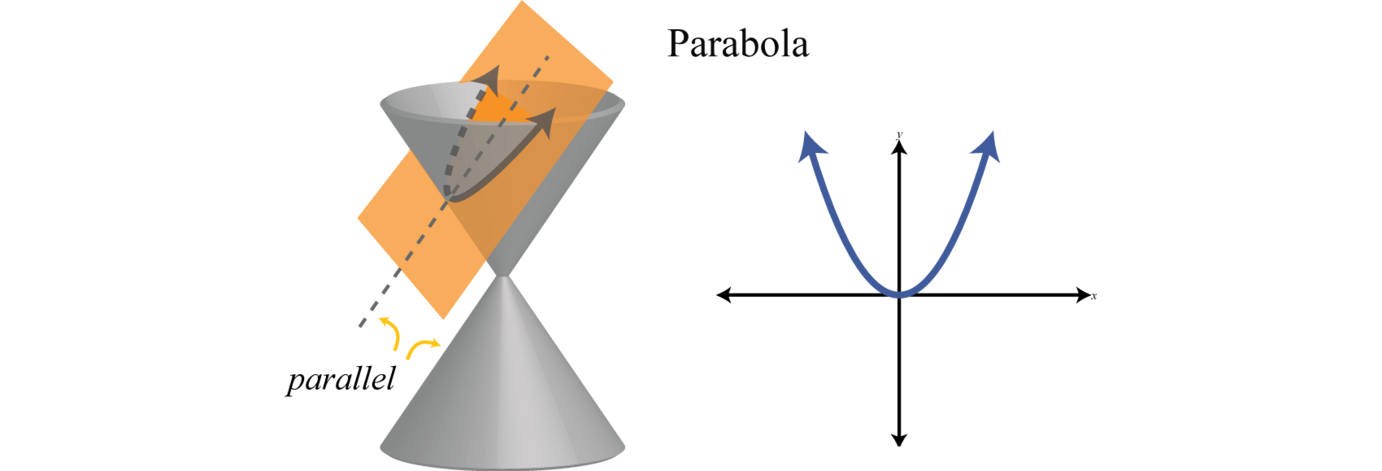
Recordemos que la gráfica de una función cuadrática, una función polinómica de grado 2, es parabólica. Podemos escribir la ecuación de una parábola en forma general ⁵ o podemos escribir la ecuación de una parábola en forma estándar ⁶:

\(\begin{array}{cc}{\color{Cerulean} { General\: Form }} & {\color{Cerulean} { Standard\: Form }} \\ {y=a x^{2}+b x+c} & {y=a(x-h)^{2}+k}\end{array}\)

Ambas formas son útiles para determinar la forma general de la gráfica. No obstante, en esta sección nos enfocaremos en obtener la forma estándar, que a menudo se denomina forma de vértice ⁷. Dada una función cuadrática en forma estándar, el vértice es\((h,k)\). Para ver que este es el caso, considere graficar\(y=(x+3)^{2}+2\) usando transformaciones.

\(\begin{array}{ll}{y=x^{2}} & {\color{Cerulean} { Basic\: squaring\: function. }} \\ {y=(x+3)^{2}} & {\color{Cerulean} {Horizontal\: shift\: left\: 3\: units. }} \\ {y=(x+3)^{2}+2} & {\color{Cerulean} { Vertical\: shift\: up\: 2\: units. }}\end{array}\)

Usa estas traducciones para bosquejar la gráfica,

Figura\(\PageIndex{6}\)

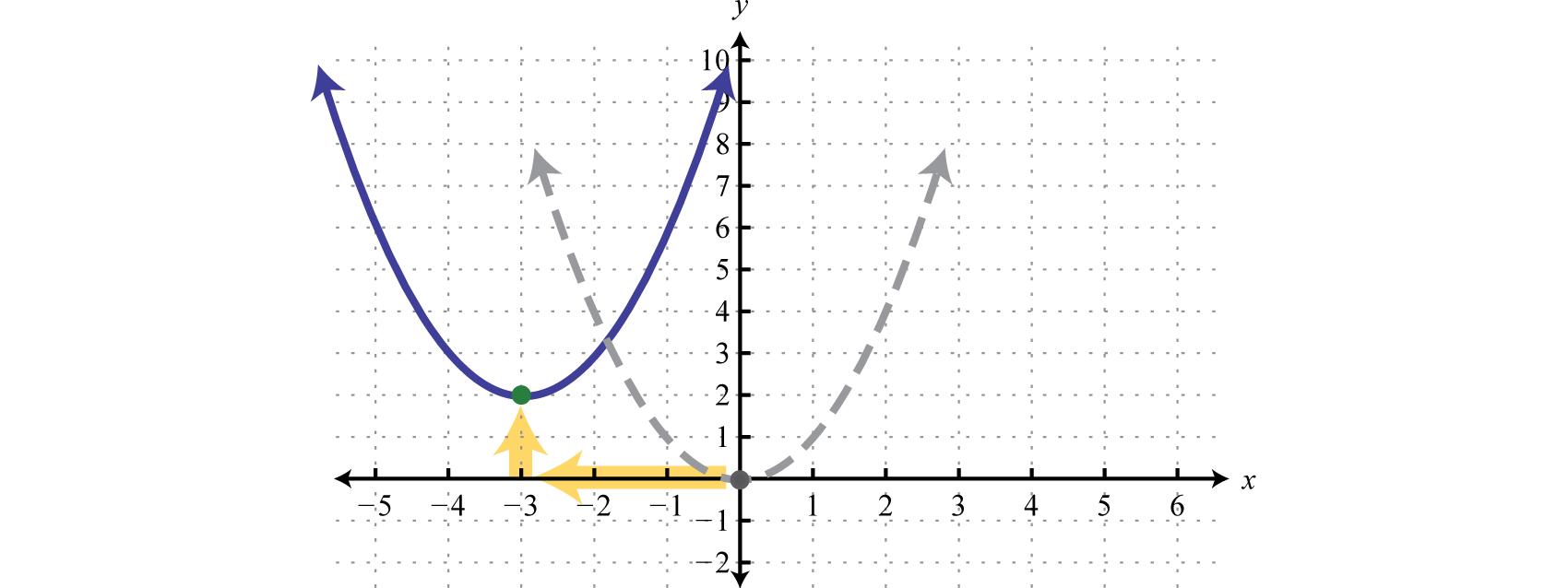
Aquí podemos ver que el vértice es\((−3,2)\). Esto se puede determinar directamente a partir de la ecuación en forma estándar,

\(\begin{array}{l}{y=a(x-h)^{2}\:+\:\:k} \\\color{Cerulean}{\quad\quad\quad\quad\:\downarrow \quad\quad\: \color{Cerulean}{\downarrow}} \\ {y=[x-(-3)]^{2}+2}\end{array}\)

Escrito en esta forma podemos ver que el vértice es\((−3,2)\). Sin embargo, la ecuación normalmente no se da en forma estándar. Transformar la forma general a forma estándar, completando el cuadrado, es el proceso principal por el cual esbozaremos todas las secciones cónicas.

Ejemplo\(\PageIndex{3}\):

Reescribe la ecuación en forma estándar y determina el vértice de su gráfica:\(y=x^{2}-8 x+15\).

Solución

Comience por dejar espacio para el término constante que completa la plaza.

\(\begin{aligned} y &=x^{2}-8 x+15 \\ &=x^{2}-8 x \color{Cerulean}{+ \_\_\_ }\color{black}{+}15 \color{Cerulean}{- \_\_\_}\end{aligned}\)

La idea es sumar y restar el valor que completa el cuadrado,\(\left(\frac{b}{2}\right)^{2}\), y luego factorizar. En este caso, sumar y restar\(\left(\frac{b}{2}\right)^{2}=\left(\frac{-8}{2}\right)^{2}=(-4)^{2}=16\).

\(\begin{aligned} y &=x^{2}-8 x+15 \quad\quad\quad\quad\quad\quad\:\:\color{Cerulean}{Add\:and\:subtract\:16.} \\ &=\color{black}{\left(x^{2}-8 x\color{Cerulean}{+16}\right)}+15\color{Cerulean}{-16}\quad\color{Cerulean}{Factor.} \\ &=(x-4)(x-4)-1 \\ &=(x-4)^{2}-1 \end{aligned}\)

Sumar y restar el mismo valor dentro de una expresión no lo cambia. Hacerlo equivale a sumar\(0\). Una vez que la ecuación está en esta forma, podemos determinar fácilmente el vértice.

\(\begin{array}{l}{y=a(x-h)^{2}\:+\:k} \\\quad\quad\quad\quad\:\color{Cerulean}{\downarrow}\quad\quad\color{Cerulean}{\downarrow} \\ {y=(x\:-\:4)^{2}+(-1)}\end{array}\)

Aquí tenemos una traducción a las\(4\) unidades adecuadas y abajo\(1\) unidad. De ahí,\(h = 4\) y\(k = −1\).

Respuesta:

\(y=(x-4)^{2}-1\); vértice:\((4,−1)\)

Si hay un coeficiente principal distinto de\(1\), entonces comience por factorizar ese coeficiente principal a partir de los dos primeros términos del trinomio.

Ejemplo\(\PageIndex{4}\):

Reescribe la ecuación en forma estándar y determina el vértice de la gráfica:\(y=-2 x^{2}+12 x-16\).

Solución

Ya que\(a=−2\), factorizar esto de los dos primeros términos para completar el cuadrado. Deja espacio dentro de los paréntesis para sumar y restar el valor que completa el cuadrado.

\(\begin{aligned} y &=-2 x^{2}+12 x-16 \\ &=-2\color{black}{\left(x^{2}-6 x\color{Cerulean}{+\_\_\_-\_\_\_}\right)-}16\end{aligned}\)

Ahora usa\(−6\) para determinar el valor que completa el cuadrado. En este caso,\(\left(\frac{b}{2}\right)^{2}=\left(\frac{-6}{2}\right)^{2}=(-3)^{2}=9\). Sumar y restar\(9\) y factorizar de la siguiente manera:

\(\begin{aligned} y &=-2 x^{2}+12 x-16 \\ &=-2\color{black}{\left(x^{2}-6 x\color{Cerulean}{+\_\_\_-\_\_\_}\right)}-16\quad\color{Cerulean}{Add\:and\:subtract\:9.} \\ &=-2\color{black}{\left(x^{2}-6 x\color{Cerulean}{+9-9}\right)-}16\quad\quad\:\:\quad\color{Cerulean}{Factor.} \\ &=-2[(x-3)(x-3)-9]-16\ \\ &=-2\left[(x-3)^{2}-9\right]-16\quad\quad\quad\quad\:\:\color{Cerulean}{Distribute\:the\:-2.} \\ &=-2(x-3)^{2}+18-16 \\ &=-2(x-3)^{2}+2 \end{aligned}\)

De esta forma, podemos determinar fácilmente el vértice.

\(\begin{array}{l}{y=a\:(x\:-\:h)^{2}+k}\\\quad\quad\quad\quad\quad\color{Cerulean}{\downarrow}\quad\:\:\color{Cerulean}{\downarrow} \\ {y=-2(x-3)^{2}+2}\end{array}\)

Aquí\(h = 3\) y\(k = 2\).

Respuesta:

y=−2 (x−3) 2+2y=−2 (x−3) 2+2; vértice: (3,2) (3,2)

Hacer uso tanto de la forma general como de la forma estándar al bosquejar la gráfica de una parábola.

Ejemplo\(\PageIndex{5}\):

Gráfica:\(y=-2 x^{2}+12 x-16\).

Solución:

Del ejemplo anterior tenemos dos formas equivalentes de esta ecuación,

\(\begin{array}{c} {\color{Cerulean}{General\:Form}}&{\color{Cerulean}{Standard\:Form}}\\{y=-2 x^{2}+12 x-16}&{ y=-2(x-3)^{2}+2}\end{array}\)

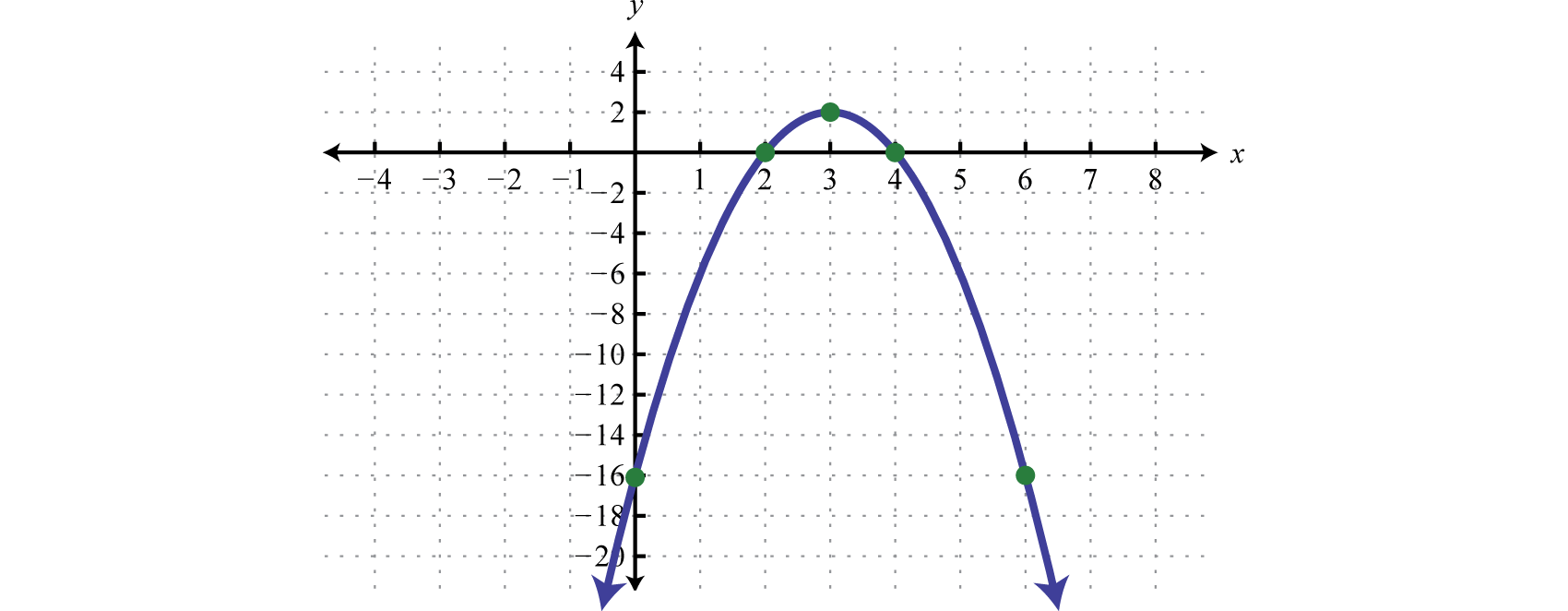
Recordemos que si el coeficiente principal\(a>0\) la parábola se abre hacia arriba y si\(a<0\) la parábola se abre hacia abajo. En este caso,\(a=−2\) y concluimos que la parábola se abre hacia abajo. Utilice la forma general para determinar la\(y\) -intercepción. Cuando\(x=0\) podemos ver que la\(y\) -intercepción es\((0,−16)\). A partir de la ecuación en forma estándar, podemos ver que el vértice es\((3,2)\). Para encontrar la\(x\) -intercepción podríamos usar cualquiera de las dos formas. En este caso, utilizaremos la forma estándar para determinar los\(x\) valores -donde\(y=0\),

\(\begin{aligned} y &=-2(x-3)^{2}+2\quad\color{Cerulean}{Set\:y=0\:and\:solve.} \\ 0 &=-2(x-3)^{2}+2 \\-2 &=-2(x-3)^{2} \\ & 1=(x-3)^{2}\quad\quad\quad\:\:\color{Cerulean}{Apply\:the\:square\:root\:property.} \\ \pm 1 &=x-3 \\ 3 \pm 1 &=x \end{aligned}\)

Aquí\(x=3−1=2\) o\(x=3+1=4\) y por lo tanto los\(x\) -interceptos son\((2,0)\) y\((4,0)\). Usa esta información para bosquejar la gráfica.

Respuesta:

Figura\(\PageIndex{7}\)

Hasta el momento hemos estado dibujando parábolas que se abren hacia arriba o hacia abajo porque estas gráficas representan funciones. En este punto ampliamos nuestro estudio para incluir parábolas que se abren a derecha o izquierda. Si tomamos la ecuación que define la parábola en el ejemplo anterior,

\(y=-2(x-3)^{2}+2\)

y cambiar los valores x e y que obtenemos

\(x=-2(y-3)^{2}+2\)

Esto produce una nueva gráfica con simetría sobre la línea\(y=x\).

Figura\(\PageIndex{8}\)

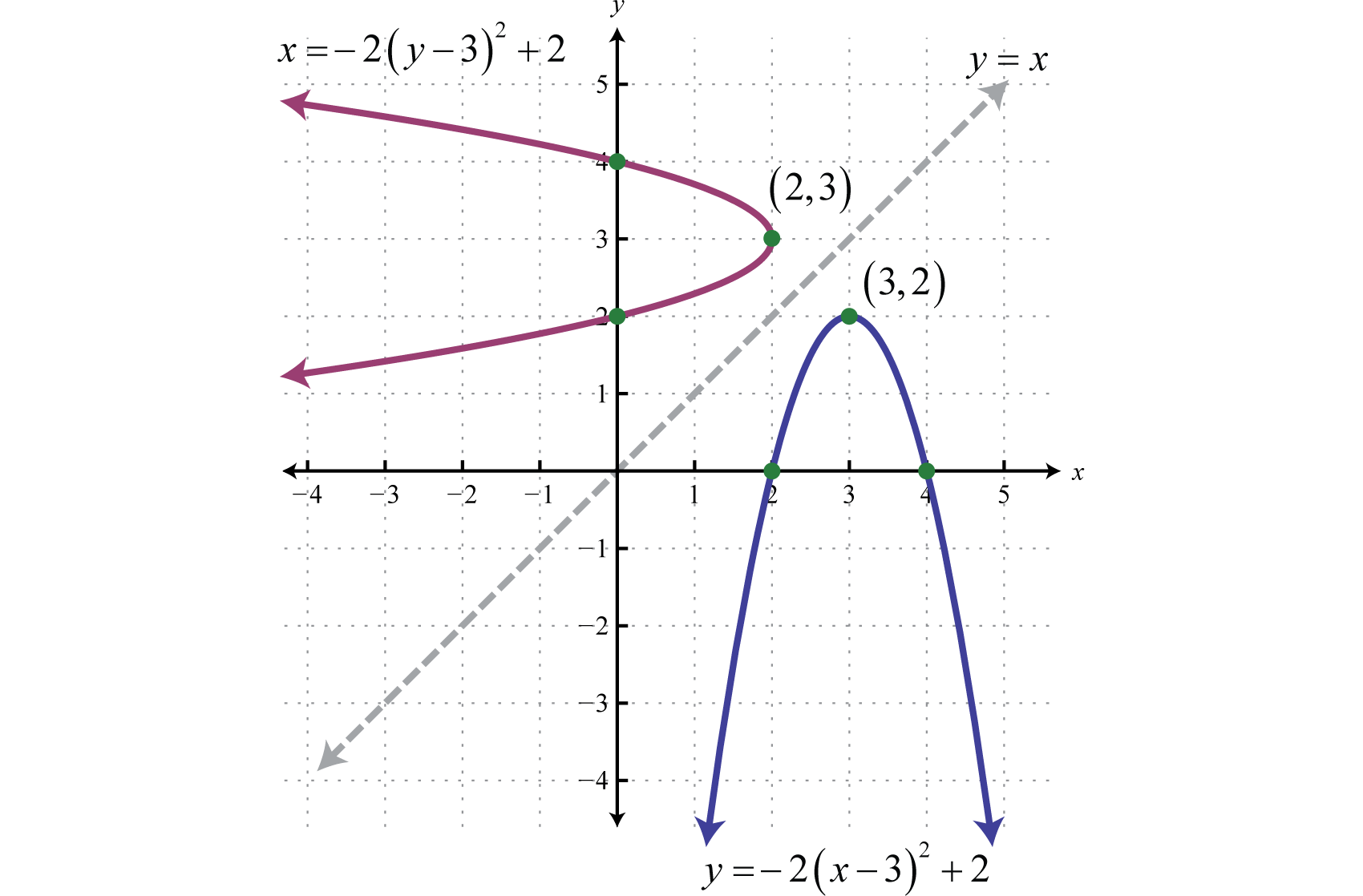
Tenga en cuenta que la gráfica resultante no es una función. Sin embargo, sí tiene la misma forma parabólica general que se abre a la izquierda. Podemos reconocer ecuaciones de parábolas que se abren a la izquierda o a la derecha al notar que son cuadráticas en\(y\) lugar de\(x\). Graficar parábolas que se abren a izquierda o derecha es similar a graficar parábolas que se abren hacia arriba y hacia abajo. En general, tenemos

Figura\(\PageIndex{9}\)

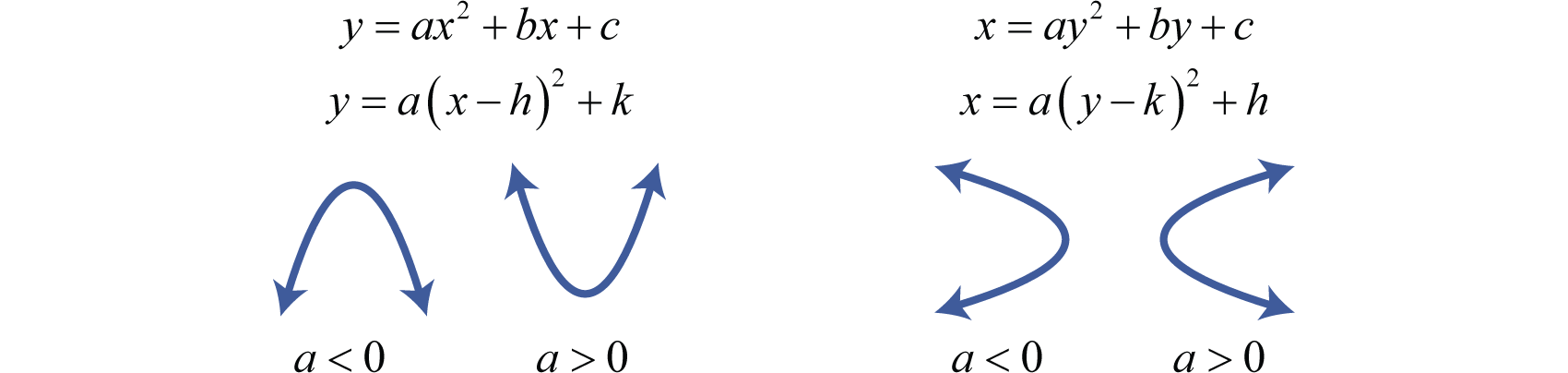
En todos los casos, el vértice es\((h,k)\). Tenga cuidado de anotar la ubicación de\(h\) y\(k\) en cada ecuación.

Ejemplo\(\PageIndex{6}\):

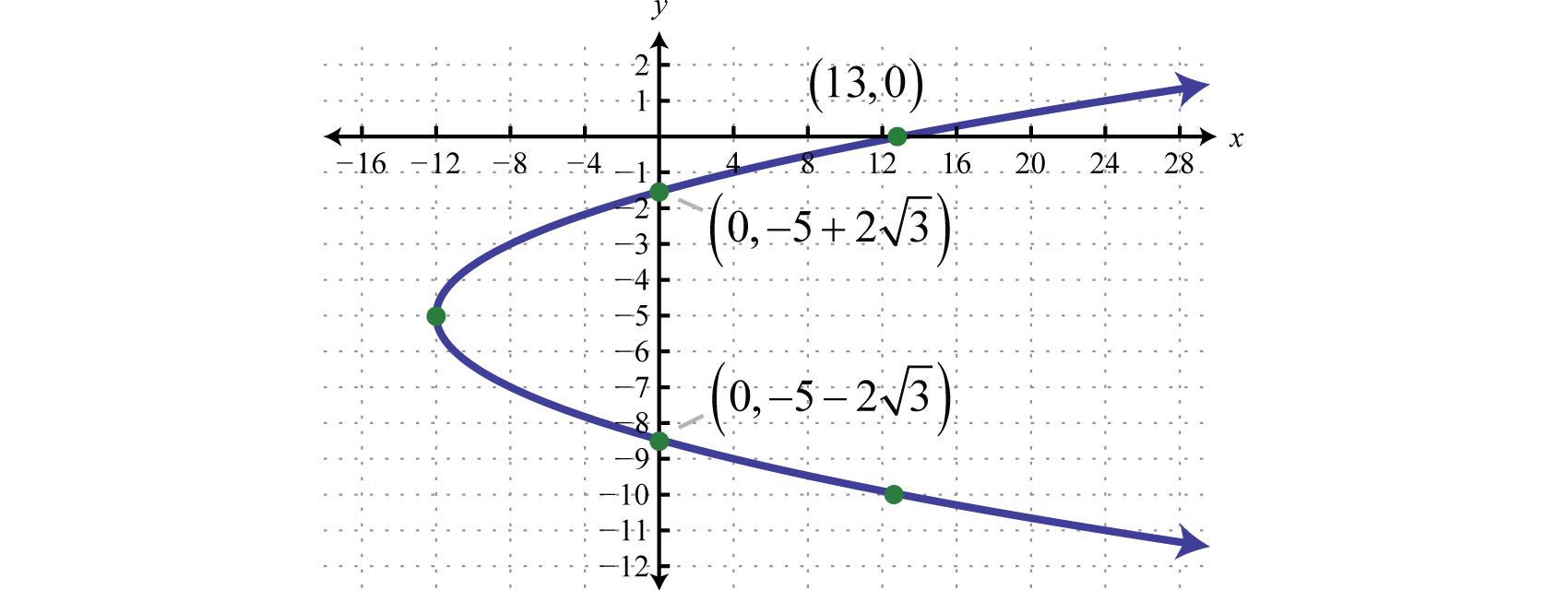
Gráfica:\(x=y^{2}+10 y+13\).

Solución

Debido a que el coeficiente de\(y^{2}\) es positivo\(a=1\),, concluimos que la gráfica es una parábola que se abre a la derecha. Además, cuando\(y=0\) es claro que\(x=13\) y por lo tanto la\(x\) -intercepción es\((13,0)\). Complete el cuadrado para obtener la forma estándar. Aquí sumaremos y restaremos\(\left(\frac{b}{2}\right)^{2}=\left(\frac{10}{2}\right)^{2}=(5)^{2}=25\).

\(\begin{aligned} x &=y^{2}+10 y+13 \\ &=y^{2}+10 y\color{Cerulean}{+25-25}\color{black}{+}13 \\ &=(y+5)(y+5)-12 \\ &=(y+5)^{2}-12 \end{aligned}\)

Por lo tanto,

\(\begin{array}{l}{x=a\:(y\:-\:k)^{2}\:\:\:+\:\:\:\:h}\\ \quad\quad\quad\quad\quad\color{Cerulean}{\downarrow}\quad\quad\quad\color{Cerulean}{\downarrow} \\ {x=(y-(-5))^{2}+(-12)}\end{array}\)

De esto podemos ver que el vértice\((h,k)=(−12,−5)\). A continuación, use el formulario estándar para encontrar las\(y\) intercepciones mediante la configuración\(x=0\).

\(\begin{aligned} x &=(y+5)^{2}-12 \\ 0 &=(y+5)^{2}-12 \\ 12 &=(y+5)^{2} \\ \pm \sqrt{12} &=y+5 \\ \pm 2 \sqrt{3} &=y+5 \\-5 \pm 2 \sqrt{3} &=y \end{aligned}\)

Los\(y\) -interceptos son\((0,-5-2 \sqrt{3})\) y\((0,-5+2 \sqrt{3})\). Usa esta información para bosquejar la gráfica.

Contestar

Figura\(\PageIndex{10}\)

Ejemplo\(\PageIndex{7}\)

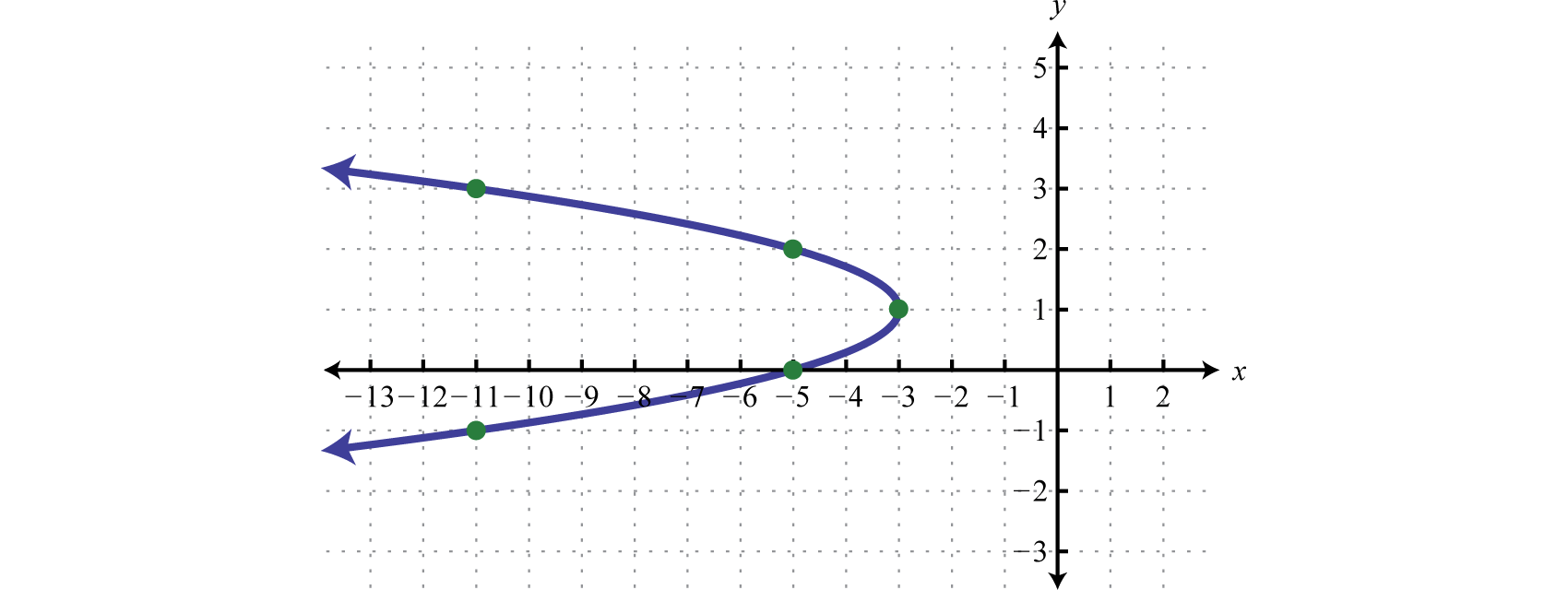
Gráfica:\(x=-2 y^{2}+4 y-5\).

Solución

Debido a que el coeficiente de\(y^{2}\) es\(a=−2\), concluimos que la gráfica es una parábola que se abre a la izquierda. Además, cuando\(y=0\) es claro que\(x=−5\) y por lo tanto la\(x\) -intercepción es\((−5,0)\). Comience por factorizar el coeficiente principal de la siguiente manera:

\(\begin{aligned} x &=-2 y^{2}+4 y-5 \\ &=-2\left(y^{2}-2 y+\_\_\_-\_\_\_\right)-5\end{aligned}\)

Aquí sumaremos y restaremos\(\left(\frac{b}{2}\right)^{2}=\left(\frac{-2}{2}\right)^{2}=(-1)^{2}=1\).

\(\begin{aligned} x &=-2 y^{2}+4 y-5 \\ &=-2\color{black}{\left(y^{2}-2 y\color{Cerulean}{+1-1}\right)-}5 \\ &=-2\left[(y-1)^{2}-1\right]-5 \\ &=-2(y-1)^{2}+2-5 \\ &=-2(y-1)^{2}-3 \end{aligned}\)

Por lo tanto, a partir de la forma de vértice\(x=-2(y-1)^{2}-3\),, podemos ver que el vértice es\((h,k)=(−3,1)\). Debido a que el vértice está en\((−3,1)\) y la parábola se abre a la izquierda, podemos concluir que no hay\(y\) -intercepciones. Ya que solo tenemos dos puntos, elige algunos\(y\) -valores y encuentra los\(x\) -valores correspondientes.

Mesa\(\PageIndex{1}\)

\(x\)	\(y\)	\(x=-2(y-1)^{2}-3\)
\(\color{Cerulean}{-11}\)	\(-1\)	\(x=-2(-1-1)^{2}-3=-2(-2)^{2}-3=-11\)
\(\color{Cerulean}{-5}\)	\(2\)	\(x=-2(2-1)^{2}-3=-2(1)^{2}-3=-5\)
\(\color{Cerulean}{-11}\)	\(3\)	\(x=-2(3-1)^{2}-3=-2(2)^{2}-3=-11\)

Respuesta:

Figura\(\PageIndex{11}\)

Ejercicio\(\PageIndex{2}\):

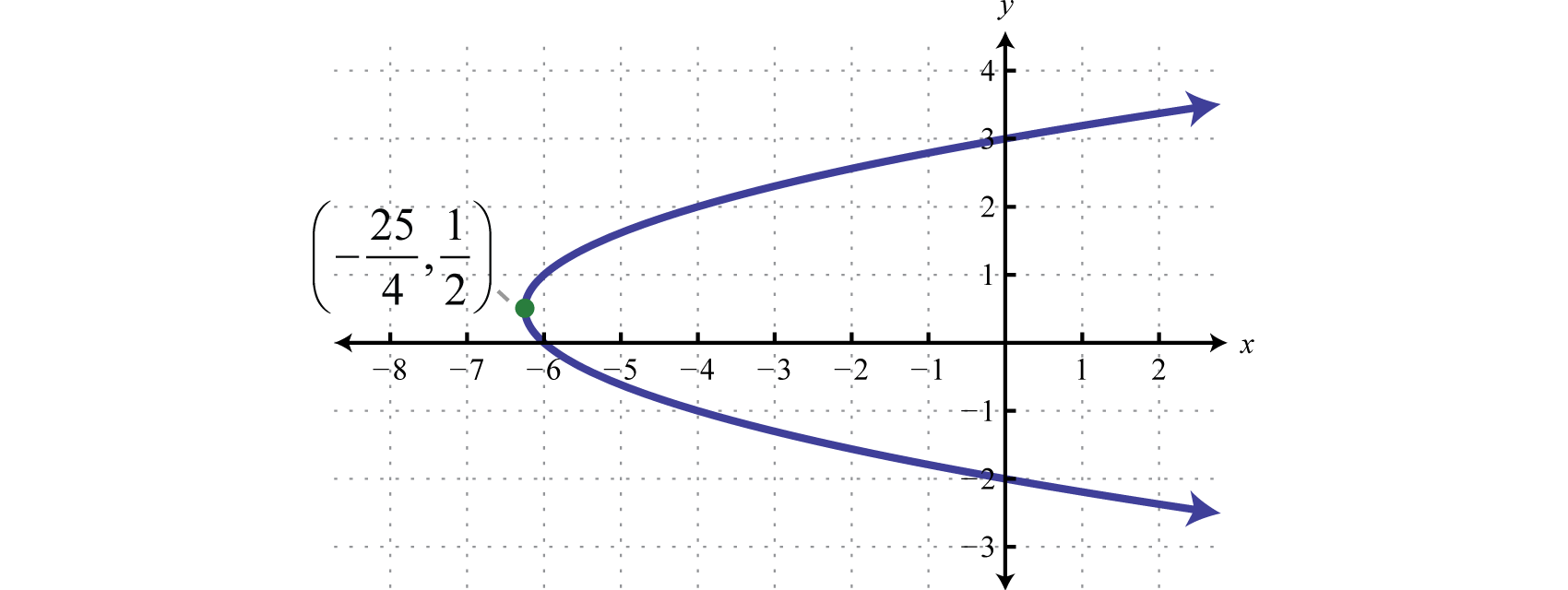
Gráfica:\(x= y^{2}−y−6\).

Respuesta:

Figura\(\PageIndex{12}\)

www.youtube.com/v/pxge96nhsci

Claves para llevar

• Utilice la fórmula de distancia para determinar la distancia entre dos puntos dados. Utilice la fórmula de punto medio para determinar el punto medio entre dos puntos dados cualquiera.
• Una parábola puede abrirse hacia arriba o hacia abajo, en cuyo caso, es una función. En esta sección, ampliamos nuestro estudio de las parábolas para incluir aquellas que se abren a la izquierda o a la derecha. Tales gráficas no representan funciones.
• La ecuación de una parábola que se abre hacia arriba o hacia abajo es cuadrática en\(x, y=ax^{2}+bx+c\). Si\(a>0\), entonces la parábola se abre hacia arriba y si a<0a<0, entonces la parábola se abre hacia abajo.
• La ecuación de una parábola que se abre a la izquierda o a la derecha es cuadrática en\(y, x=ay^{2}+by+c\). Si\(a>0\), entonces la parábola se abre a la derecha y si\(a<0\), entonces la parábola se abre a la izquierda.
• La ecuación de una parábola en forma general\(y=ax^{2}+bx+c\) o\(x=ay^{2}+by+c\) puede transformarse a forma estándar\(y=a(x−h)^{2}+k\) o\(x=a(y−k)^{2}+h\) completando el cuadrado.
• Al completar el cuadrado, asegúrese de que el coeficiente inicial de la agrupación de variables sea\(1\) antes de sumar y restar el valor que completa el cuadrado.
• Tanto las formas generales como las estándar son útiles a la hora de graficar parábolas. Dada la forma estándar, el vértice es aparente\((h,k)\). Para encontrar el conjunto\(x\) -intercept\(y=0\) y resolver para\(x\) y para encontrar el conjunto\(y\) -intercept\(x=0\) y resolver para\(y\).

Ejercicio\(\PageIndex{3}\)

Calcular la distancia y el punto medio entre los dos puntos dados.

1. \((-1,-3)\)y\((5,-11)\)
2. \((-3,2)\)y\((1,-1)\)
3. \((4,-2)\)y\((-2,-6)\)
4. \((-5,-6)\)y\((-3,-4)\)
5. \((10,-1)\)y\((9,6)\)
6. \((-6,-4)\)y\((-12,1)\)
7. \((0,0)\)y\((\sqrt{2}, \sqrt{3})\)
8. \((0,0)\)y\((2 \sqrt{2},-\sqrt{3})\)
9. \((\sqrt{5},-\sqrt{3})\)y\((2 \sqrt{5},-\sqrt{3})\)
10. \((3 \sqrt{10}, \sqrt{6})\)y\((\sqrt{10},-5 \sqrt{6})\)
11. \(\left(\frac{1}{2},-1\right)\)y\(\left(-2, \frac{3}{2}\right)\)
12. \(\left(-\frac{4}{3}, 2\right)\)y\(\left(-\frac{1}{3},-\frac{1}{2}\right)\)
13. \(\left(\frac{1}{5},-\frac{9}{5}\right)\)y\(\left(\frac{3}{10},-\frac{5}{2}\right)\)
14. \(\left(-\frac{1}{2}, \frac{4}{3}\right)\)y\(\left(-\frac{2}{3}, \frac{5}{6}\right)\)
15. \((a, b)\)y\((0,0)\)
16. \((0,0)\)y\((a \sqrt{2}, 2 \sqrt{a})\)

Contestar

1. Distancia:\(10\) unidades; punto medio:\((2, −7)\)

3. Distancia:\(2\sqrt{13}\) unidades; punto medio:\((1, −4)\)

5. Distancia:\(5\sqrt{2}\) unidades; punto medio:\((\frac{19}{2},\frac{5}{2})\)

7. Distancia:\(\sqrt{5}\) unidades; punto medio:\(\left(\frac{\sqrt{2}}{2}, \frac{\sqrt{3}}{2}\right)\)

9. Distancia:\(\sqrt{5}\) unidades; punto medio:\(\left(\frac{3 \sqrt{5}}{2},-\sqrt{3}\right)\)

11. Distancia:\(\frac{5 \sqrt{2}}{2}\) unidades; punto medio:\((−\frac{3}{4}, \frac{1}{4})\)

13. Distancia:\(\frac{\sqrt{2}}{2}\) unidades; punto medio:\(\left(\frac{1}{4},-\frac{43}{20}\right)\)

15. Distancia:\(\sqrt{a^{2}+b^{2}}\) unidades; punto medio:\(\left(\frac{a}{2}, \frac{b}{2}\right)\)

Ejercicio\(\PageIndex{4}\)

Determinar el área de un círculo cuyo diámetro está definido por los dos puntos dados.

1. \((-8,12)\)y\((-6,8)\)
2. \((9,5)\)y\((9,-1)\)
3. \((7,-8)\)y\((5,-10)\)
4. \((0,-5)\)y\((6,1)\)
5. \((\sqrt{6}, 0)\)y\((0,2 \sqrt{3})\)
6. \((0, \sqrt{7})\)y\((\sqrt{5}, 0)\)

Contestar

1. \(5π\)unidades cuadradas

3. \(2π\)unidades cuadradas

5. \(\frac{9}{2} π\)unidades cuadradas

Ejercicio\(\PageIndex{5}\)

Determinar el perímetro del triángulo dadas las coordenadas de los vértices.

1. \((5,3),(2,-3),\)y\((8,-3)\)
2. \((-3,2),(-4,-1),\)y\((-1,0)\)
3. \((3,3),(5,3-2 \sqrt{3}),\)y\((7,3)\)
4. \((0,0),(0,2 \sqrt{2}),\)y\((\sqrt{2}, 0)\)

Contestar

1. \(6+6 \sqrt{5}\)unidades

3. \(12\)unidades

Ejercicio\(\PageIndex{6}\)

Encuentra\(a\) para que la distancia\(d\) entre los puntos sea igual a la cantidad dada.

1. \((1,2)\)y\((4, a) ; d=5\) unidades
2. \((-3, a)\)y\((5,6) ; d=10\) unidades
3. \((3,1)\)y\((a, 0) ; d=\sqrt{2}\) unidades
4. \((a, 1)\)y\((5,3) ; d=\sqrt{13}\) unidades

Contestar

1. \(-2,6\)

3. \(2,4\)

Ejercicio\(\PageIndex{7}\)

Gráfica. Asegúrate de encontrar el vértice y todas las intercepciones.

1. \(y=x^{2}+3\)
2. \(y=\frac{1}{2}(x-4)^{2}\)
3. \(y=-2(x+1)^{2}-1\)
4. \(y=-(x-2)^{2}+1\)
5. \(y=-x^{2}+3\)
6. \(y=-(x+1)^{2}+5\)
7. \(x=y^{2}+1\)
8. \(x=y^{2}-4\)
9. \(x=(y+2)^{2}\)
10. \(x=(y-3)^{2}\)
11. \(x=-y^{2}+2\)
12. \(x=-(y+1)^{2}\)
13. \(x=\frac{1}{3}(y-3)^{2}-1\)
14. \(x=-\frac{1}{3}(y+3)^{2}-1\)

Contestar

1.

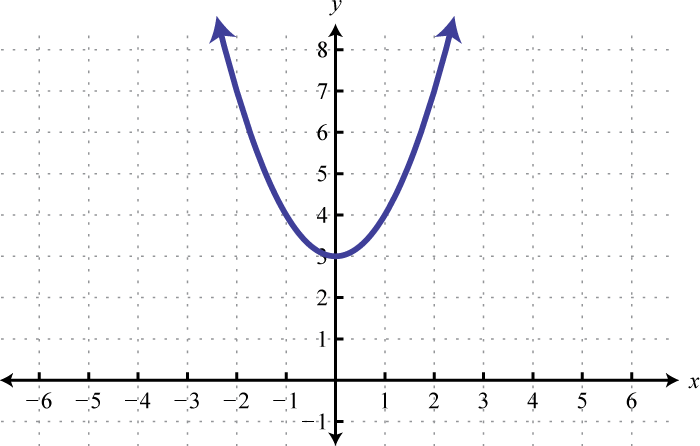
Figura\(\PageIndex{13}\)

3.

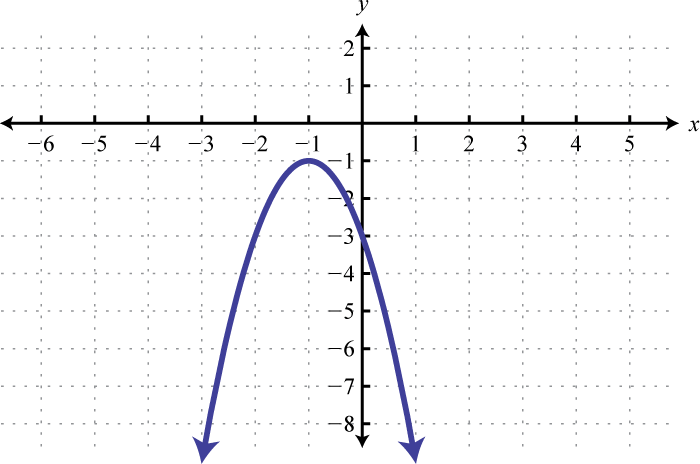
Figura\(\PageIndex{14}\)

5.

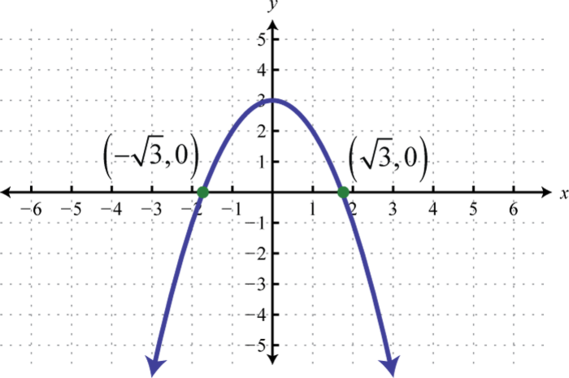
Figura\(\PageIndex{15}\)

7.

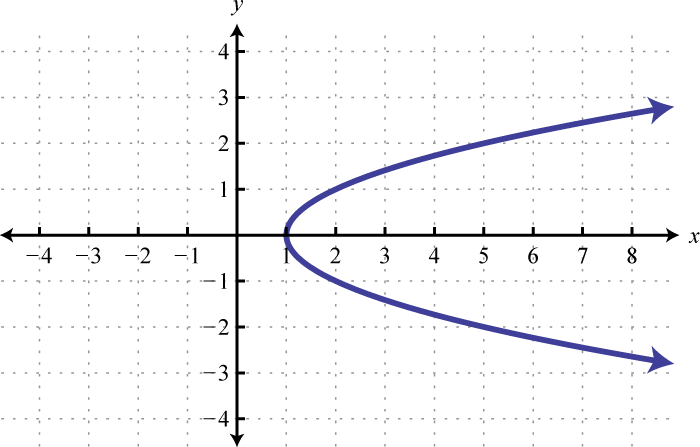
Figura\(\PageIndex{16}\)

9.

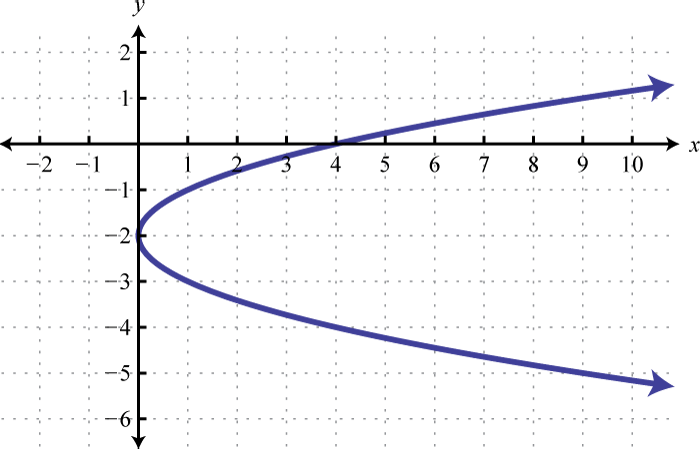
Figura\(\PageIndex{17}\)

11.

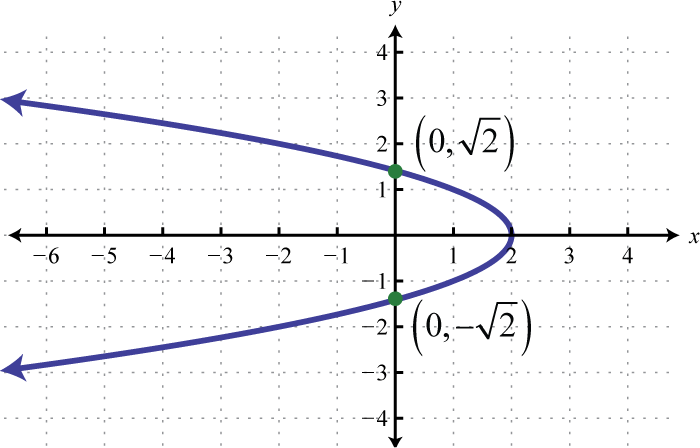
Figura\(\PageIndex{18}\)

13.

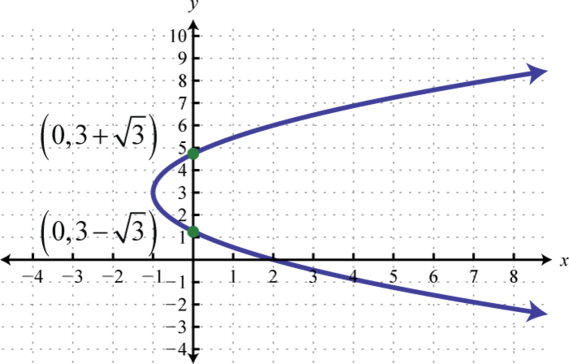
Figura\(\PageIndex{19}\)

Ejercicio\(\PageIndex{8}\)

Reescribe en forma estándar y da el vértice.

1. \(y=x^{2}-6 x+18\)
2. \(y=x^{2}+8 x+36\)
3. \(x=y^{2}+20 y+87\)
4. \(x=y^{2}-10 y+21\)
5. \(y=x^{2}-14 x+49\)
6. \(x=y^{2}+16 y+64\)
7. \(x=2 y^{2}-4 y+5\)
8. \(y=3 x^{2}-30 x+67\)
9. \(y=6 x^{2}+36 x+54\)
10. \(x=3 y^{2}+6 y-1\)
11. \(y=2 x^{2}-2 x-1\)
12. \(x=5 y^{2}+15 y+9\)
13. \(x=-y^{2}+5 y-5\)
14. \(y=-x^{2}+9 x-20\)

Contestar

1. \(y=(x-3)^{2}+9 ;\)vértice:\((3,9)\)

3. \(x=(y+10)^{2}-13 ;\)vértice:\((-13,-10)\)

5. \(y=(x-7)^{2} ;\)vértice:\((7,0)\)

7. \(x=2(y-1)^{2}+3 ;\)vértice:\((3,1)\)

9. \(y=6(x+3)^{2} ;\)vértice:\((-3,0)\)

11. \(y=2\left(x-\frac{1}{2}\right)^{2}-\frac{3}{2} ;\)vértice:\(\left(\frac{1}{2},-\frac{3}{2}\right)\)

13. \(x=-\left(y-\frac{5}{2}\right)^{2}+\frac{5}{4} ;\)vértice:\(\left(\frac{5}{4}, \frac{5}{2}\right)\)

Ejercicio\(\PageIndex{9}\)

Reescribir en forma estándar y gráfica. Asegúrate de encontrar el vértice y todas las intercepciones.

1. \(y=x^{2}-4 x-5\)
2. \(y=x^{2}+6 x-16\)
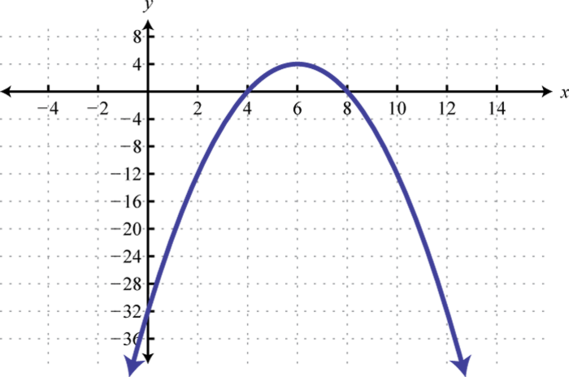
3. \(y=-x^{2}+12 x-32\)
4. \(y=-x^{2}-10 x\)
5. \(y=2 x^{2}+4 x+9\)
6. \(y=3 x^{2}-6 x+4\)
7. \(y=-5 x^{2}+30 x-45\)
8. \(y=-4 x^{2}-16 x-16\)
9. \(x=y^{2}-2 y-8\)
10. \(x=y^{2}+4 y+8\)
11. \(x=y^{2}-2 y-3\)
12. \(x=y^{2}+6 y-7\)
13. \(x=-y^{2}-10 y-24\)
14. \(x=-y^{2}-12 y-40\)
15. \(x=3 y^{2}+12 y+12\)
16. \(x=-2 y^{2}+12 y-18\)
17. \(x=y^{2}-4 y-3\)
18. \(x=y^{2}+6 y+1\)
19. \(x=-y^{2}+2 y+5\)
20. \(y=2 x^{2}-2 x+1\)
21. \(y=-3 x^{2}+2 x+1\)
22. \(y=-x^{2}+3 x+10\)
23. \(x=-4 y^{2}-4 y-5\)
24. \(x=y^{2}-y+2\)
25. \(y=x^{2}+5 x-1\)
26. \(y=2 x^{2}+6 x+3\)
27. \(x=2 y^{2}+10 x+12\)
28. \(x=y^{2}+y-1\)

Contestar

1. \(y=(x-2)^{2}-9\);

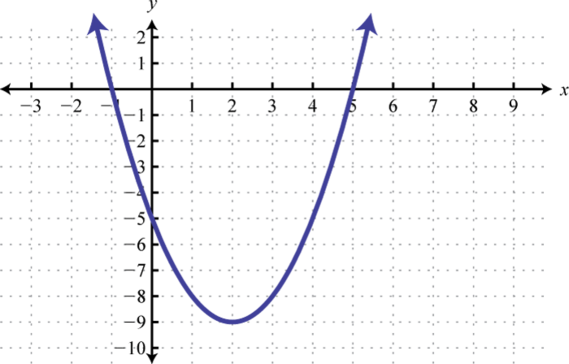
Figura\(\PageIndex{20}\)

3. \(y=-(x-6)^{2}+4\);

Figura\(\PageIndex{21}\)

5. \(y=2(x+1)^{2}+7\);

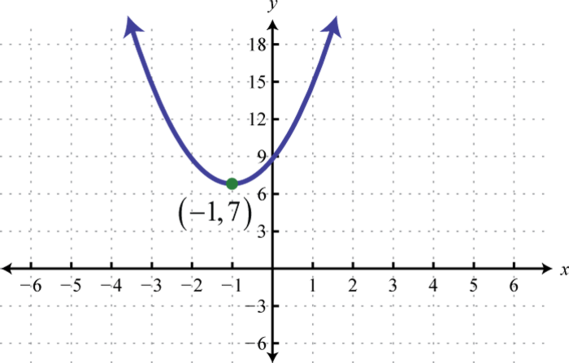
Figura\(\PageIndex{22}\)

7. \(y=-5(x-3)^{2}\);

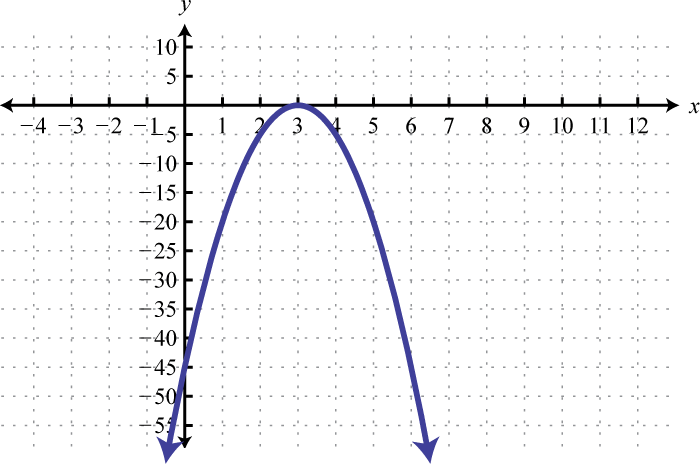
Figura\(\PageIndex{23}\)

9. \(x=(y-1)^{2}-9\);

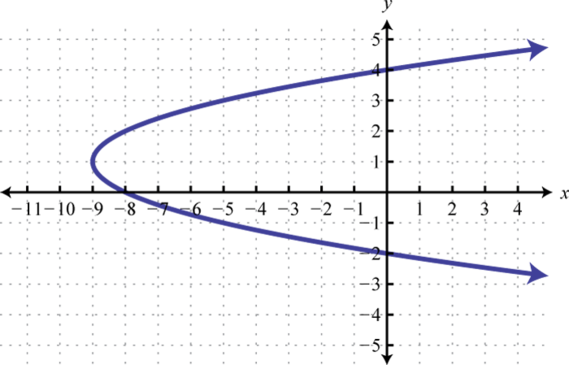
Figura\(\PageIndex{24}\)

11. \(x=(y-1)^{2}-4\);

Figura\(\PageIndex{25}\)

13. \(x=-(y+5)^{2}+1\);

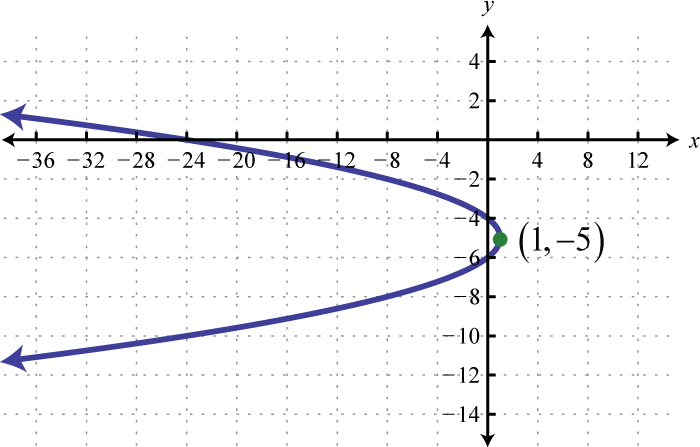
Figura\(\PageIndex{26}\)

15. \(x=3(y+2)^{2}\);

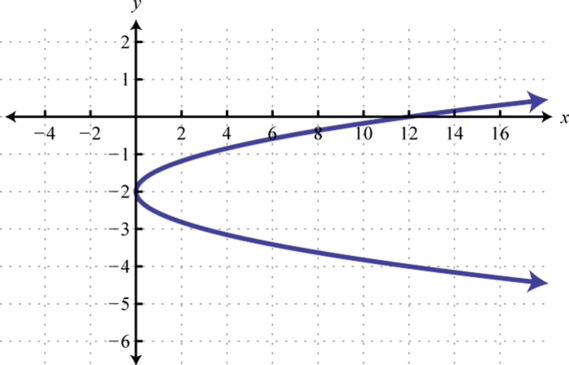
Figura\(\PageIndex{27}\)

17. \(x=(y-2)^{2}-7\);

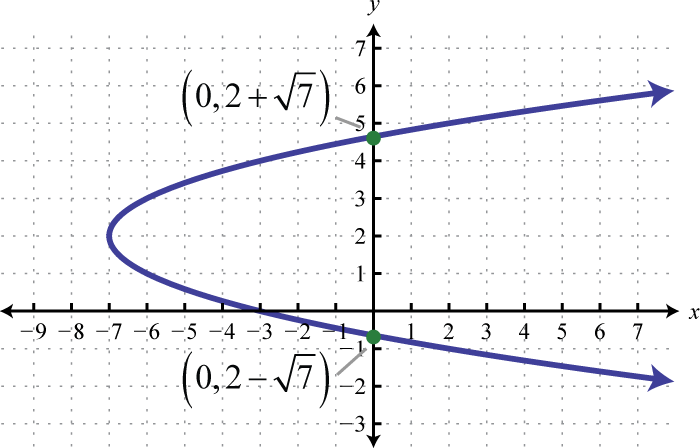
Figura\(\PageIndex{28}\)

19. \(x=-(y-1)^{2}+6\);

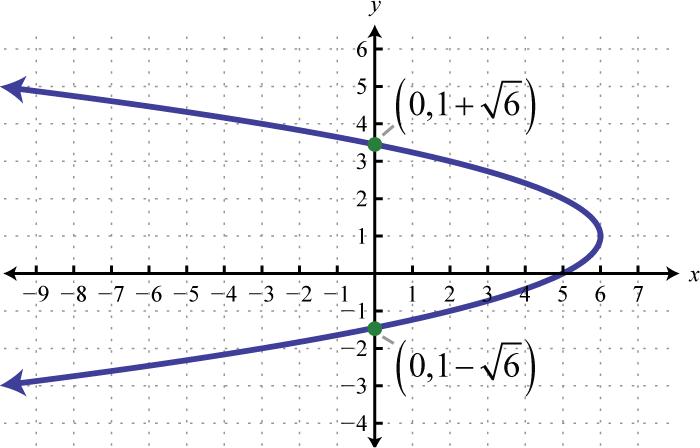
Figura\(\PageIndex{29}\)

21. \(y=-3\left(x-\frac{1}{3}\right)^{2}+\frac{4}{3}\);

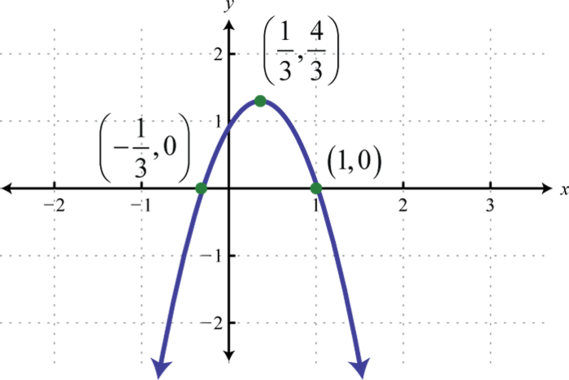
Figura\(\PageIndex{30}\)

23. \(x=-4\left(y+\frac{1}{2}\right)^{2}-4\);

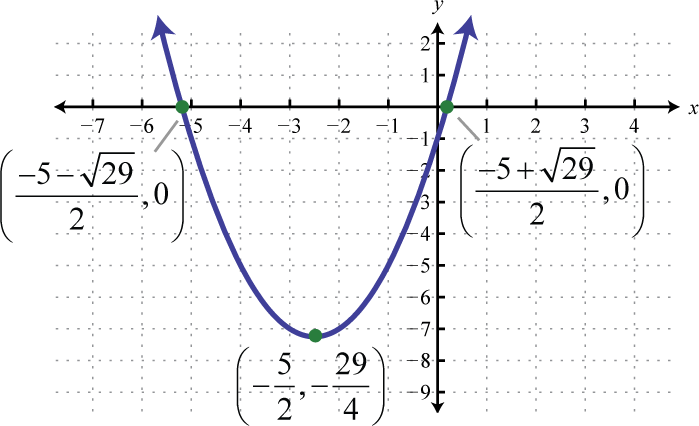
Figura\(\PageIndex{31}\)

25. \(y=\left(x+\frac{5}{2}\right)^{2}-\frac{29}{4}\);

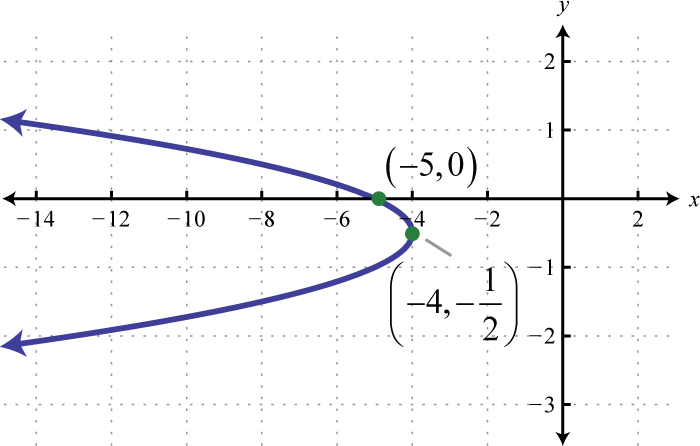
Figura\(\PageIndex{32}\)

27. \(x=2\left(y+\frac{5}{2}\right)^{2}-\frac{1}{2}\);

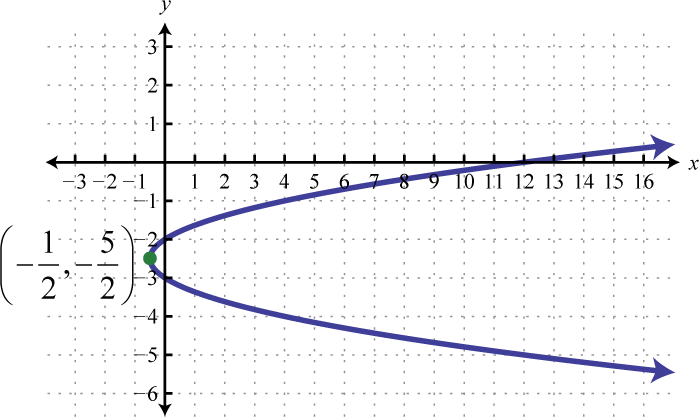
Figura\(\PageIndex{33}\)

Ejercicio\(\PageIndex{10}\)

1. Investigar y discutir aplicaciones del mundo real que involucren una parábola.
2. ¿Todas las parábola tienen\(x\) -intercepciones? Explique.
3. ¿Todas las parábola tienen\(y\) -intercepciones? Explique.
4. Haz tu propia parábola que se abra a la izquierda o a la derecha, escríbalo en forma general y gráficalo.

Contestar

1. La respuesta puede variar

3. La respuesta puede variar

Notas al pie

¹ Curva obtenida de la intersección de un cono circular derecho y un plano.

² Dados dos puntos\((x_{1} , y_{1})\) y\((x_{2}, y_{2})\), la distancia\(d\) entre ellos viene dada por\(d=\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\).

³ Dados dos puntos\((x_{1}, y_{1})\) y\((x_{2}, y_{2})\), el punto medio es un par ordenado dado por\(\left(\frac{x_{1}+x_{2}}{2}, \frac{y_{1}+y_{2}}{2}\right)\).

⁴ El conjunto de puntos en un plano equidistante de una línea dada, llamado directrix, y un punto que no está en la línea, llamado foco.

⁵ La ecuación de una parábola escrita en la forma\(y=a x^{2}+b x+c\) o\(x=a y^{2}+b y+c\), donde\(a, b\), y\(c\) son números reales y\(a ≠ 0\).

⁶ La ecuación de una parábola escrita en la forma\(y=a(x-h)^{2}+k\) o\(x=a(y-k)^{2}+h\).

⁷ La ecuación de una parábola escrita en forma estándar a menudo se llama forma de vértice. En esta forma el vértice es aparente:\((h, k)\).