8.2: Círculos

Objetivos de aprendizaje

• Grafica un círculo en forma estándar.
• Determinar la ecuación de un círculo dada su gráfica.
• Reescribir la ecuación de un círculo en forma estándar.

El círculo en forma estándar

Un círculo ⁸ es el conjunto de puntos en un plano que se encuentran a una distancia fija, llamada radio ⁹, desde cualquier punto, llamado centro. El diámetro ¹⁰ es la longitud de un segmento de línea que pasa por el centro cuyos extremos están en el círculo. Además, se puede formar un círculo por la intersección de un cono y un plano que es perpendicular al eje del cono:

Figura\(\PageIndex{1}\)

En un plano de coordenadas rectangulares, donde\(r\) está el centro de un círculo con radio\((h,k)\), tenemos

Figura\(\PageIndex{2}\)

Calcular la distancia entre\((h,k)\) y\((x,y)\) usando la fórmula de distancia,

\(\sqrt{(x-h)^{2}+(y-k)^{2}}=r\)

Al cuadrar ambos lados nos lleva a la ecuación de un círculo en forma estándar ¹¹,

\((x-h)^{2}+(y-k)^{2}=r^{2}\)

De esta forma, el centro y el radio son aparentes. Por ejemplo, dada la ecuación\((x-2)^{2}+(y+5)^{2}=16\) que tenemos,

\(\begin{array}{l}{(x-h)^{2}\:+\:(x\:-k)^{2}=r^{2}} \\ \quad\quad\color{Cerulean}{\downarrow}\quad\quad\quad\quad\:\color{Cerulean}{\downarrow}\quad\quad\color{Cerulean}{\downarrow} \\ {(x-\color{Cerulean}{2}\color{black}{)}^{2}+[y-(\color{Cerulean}{-5}\color{black}{)}]^{2}=\color{Cerulean}{4}^{\color{black}{2}}}\end{array}\)

En este caso, el centro es\((2,−5)\) y\(r=4\). Más ejemplos siguen:

Mesa\(\PageIndex{1}\)

Ecuación	Centro	Radio
\((x-3)^{2}+(y-4)^{2}=25\)	\((3,4)\)	\(r=5\)
\((x-1)^{2}+(y+2)^{2}=7\)	\((1,-2)\)	\(r=\sqrt{7}\)
\((x+4)^{2}+(y-3)^{2}=1\)	\((-4,3)\)	\(r=1\)
\(x^{2}+(y+6)^{2}=8\)	\((0,-6)\)	\(r=2 \sqrt{2}\)

La gráfica de un círculo está completamente determinada por su centro y radio.

Ejemplo\(\PageIndex{1}\):

Gráfica:\((x-2)^{2}+(y+5)^{2}=16\).

Solución

Escrito en esta forma podemos ver que el centro es\((2,−5)\) y que las\(r=4\) unidades de radio. Desde el centro marca puntos\(4\) unidades arriba y abajo así como\(4\) unidades izquierda y derecha.

Figura\(\PageIndex{3}\)

Después dibuja en el círculo a través de estos cuatro puntos.

Respuesta:

Figura\(\PageIndex{4}\)

Al igual que con cualquier gráfica, nos interesa encontrar las\(x\) -y\(y\) -intercepciones.

Ejemplo\(\PageIndex{2}\):

Encuentra las intercepciones:\((x-2)^{2}+(y+5)^{2}=16\).

Solución

Para encontrar el conjunto\(y\) -intercepts\(x=0\):

\(\begin{aligned}(x-2)^{2}+(y+5)^{2} &=16 \\(\color{Cerulean}{0}\color{black}{-}2)^{2}+(y+5)^{2} &=16 \\ 4+(y+5)^{2} &=16 \end{aligned}\)

Para esta ecuación, podemos resolver extrayendo raíces cuadradas.

\(\begin{aligned}(y+5)^{2} &=12 \\ y+5 &=\pm \sqrt{12} \\ y+5 &=\pm 2 \sqrt{3} \\ y &=-5 \pm 2 \sqrt{3} \end{aligned}\)

Por lo tanto, los\(y\) -interceptos son\((0,-5-2 \sqrt{3})\) y\((0,-5+2 \sqrt{3})\). Para encontrar el conjunto\(x\) -intercepts\(y=0\):

\(\begin{aligned}(x-2)^{2}+(y+5)^{2} &=16 \\(x-2)^{2}+(\color{Cerulean}{0}\color{black}{+}5)^{2} &=16 \\(x-2)^{2}+25 &=16 \\(x-2)^{2} &=-9 \\ x-2 &=\pm \sqrt{-9} \\ x &=2 \pm 3 i \end{aligned}\)

Y debido a que las soluciones son complejas concluimos que no hay\(x\) intercepciones reales. Tenga en cuenta que esto sí tiene sentido dada la gráfica.

Figura\(\PageIndex{5}\)

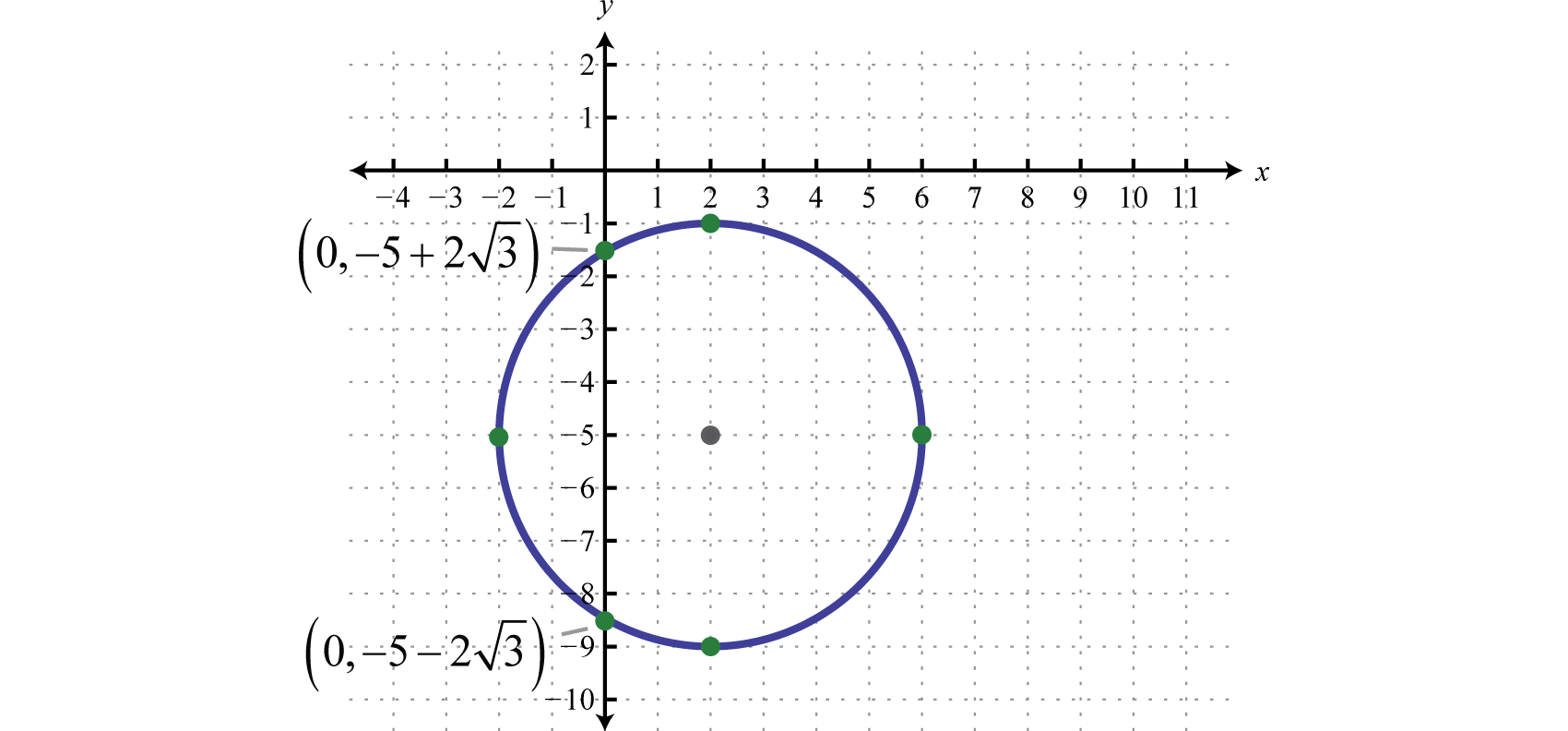
Respuesta:

\(x\)-intercepta: ninguno;\(y\) -intercepta:\((0,-5-2 \sqrt{3})\) y\((0,-5+2 \sqrt{3})\)

Dado el centro y el radio de un círculo, podemos encontrar su ecuación.

Ejemplo\(\PageIndex{3}\):

Grafica el círculo con\(r=3\) unidades de radio centradas en\((−1,0)\). Dar su ecuación en forma estándar y determinar las intercepciones.

Solución:

Dado que el centro es\((−1,0)\) y el radio es,\(r=3\) esbozamos la gráfica de la siguiente manera:

Figura\(\PageIndex{6}\)

Sustituir\(h, k\), y\(r\) encontrar la ecuación en forma estándar. Desde\((h,k)=(−1,0)\) y\(r=3\) tenemos,

\(\begin{aligned} (x-h)^{2}+(y-k)^{2}&=r^{2}\\ [x-(\color{Cerulean}{-1}\color{black}{)}]^{2}+(y-\color{Cerulean}{0}\color{black}{)}^{2}&=\color{Cerulean}{3}\color{black}{^{2}} \\ (x+1)^{2}+y^{2}&=9 \end{aligned}\)

La ecuación del círculo es\((x+1)^{2}+y^{2}=9\), usa esto para determinar las\(y\) -intercepciones.

\(\begin{aligned}(x+1)^{2}+y^{2} &=9 \quad \color{Cerulean} { Set\:x=0\: to\: and\: solve\: for\: y. } \\(\color{Cerulean}{0}\color{black}{+}1)^{2}+y^{2} &=9 \\ 1+y^{2} &=9 \\ y^{2} &=8 \\ y &=\pm \sqrt{8} \\ y &=\pm 2 \sqrt{2} \end{aligned}\)

Por lo tanto, las intercepciones\((0,-2 \sqrt{2})\) y son y\((0,2 \sqrt{2})\). Para encontrar las\(x\) -intercepciones algebraicamente, establecer\(y=0\) y resolver para\(x\); esto se deja para el lector como ejercicio.

Figura\(\PageIndex{7}\)

Respuesta:

Ecuación:\((x+1)^{2}+y^{2}=9\);\(y\) -intercepta:\((0,-2 \sqrt{2})\) y\((0,2 \sqrt{2})\);\(x\) -intercepta:\((−4,0)\) y\((2,0)\)

De particular importancia es el círculo unitario ¹²,

\(x^{2}+y^{2}=1\)

O,

\((x-0)^{2}+(y-0)^{2}=1^{2}\)

En esta forma, debe quedar claro que el centro es\((0,0)\) y que el radio es\(1\) unidad. Además, si resolvemos para\(y\) obtenemos dos funciones:

\(\begin{aligned} x^{2}+y^{2} &=1 \\ y^{2} &=1-x^{2} \\ y &=\pm \sqrt{1-x^{2}} \end{aligned}\)

La función definida por\(y=\sqrt{1-x^{2}}\) es la mitad superior del círculo y la función definida por\(y=-\sqrt{1-x^{2}}\) es la mitad inferior del círculo unitario:

Figura\(\PageIndex{8}\)

Ejercicio\(\PageIndex{1}\):

Grafica y etiqueta las intercepciones:\(x^{2}+(y+2)^{2}=25\).

Respuesta:

Figura\(\PageIndex{9}\)

www.youtube.com/V/KekT9K6IDCK

El Círculo en Forma General

Hemos visto que la gráfica de un círculo está completamente determinada por el centro y el radio que se puede leer a partir de su ecuación en forma estándar. Sin embargo, la ecuación no siempre se da en forma estándar. La ecuación de un círculo en forma general ¹³ sigue:

\(x^{2}+y^{2}+c x+d y+e=0\)

Aquí\(c, d\), y\(e\) están los números reales. Los pasos para graficar un círculo dada su ecuación en forma general siguen.

Ejemplo\(\PageIndex{4}\):

Gráfica:\(x^{2}+y^{2}+6 x-8 y+13=0\).

Solución

Comience por reescribir la ecuación en forma estándar.

Paso 1: Agrupar los términos con las mismas variables y mover la constante hacia el lado derecho. En este caso, restar\(13\) por ambas partes y agrupar los términos que involucran\(x\) y los términos que involucran de la\(y\) siguiente manera.

\(\begin{aligned} x^{2}+y^{2}+6 x-8 y+13 &=0 \\ \left(x^{2}+6 x+\_\_\_\right)+\left(y^{2}-8 y+\_\_\_\right)&=-13 \end{aligned}\)

Paso 2: Completar el cuadrado para cada agrupación. La idea es agregar el valor que completa el cuadrado,\(\left(\frac{b}{2}\right)^{2}\), a ambos lados para ambas agrupaciones, y luego factorizar. Para los términos que implican\(x\) uso\(\left(\frac{6}{2}\right)^{2}=3^{2}=9\) y para los términos que involucran\(y\) uso\(\left(\frac{-8}{2}\right)^{2}=(-4)^{2}=16\).

\(\begin{array}{c}{\color{black}{\left(x^{2}+6 x\color{Cerulean}{+9}\right)+}\color{black}{\left(y^{2}-8 y\color{OliveGreen}{+16}\right)=}-13\color{Cerulean}{+9}\color{OliveGreen}{+16}} \\ {(x+3)^{2}+(y-4)^{2}=12}\end{array}\)

Paso 3: Determinar el centro y el radio a partir de la ecuación en forma estándar. En este caso, el centro es\((−3,4)\) y el radio\(r=\sqrt{12}=2 \sqrt{3}\).

Paso 4: Desde el centro, marca el radio vertical y horizontalmente y luego dibuja el círculo a través de estos puntos.

Figura\(\PageIndex{10}\)

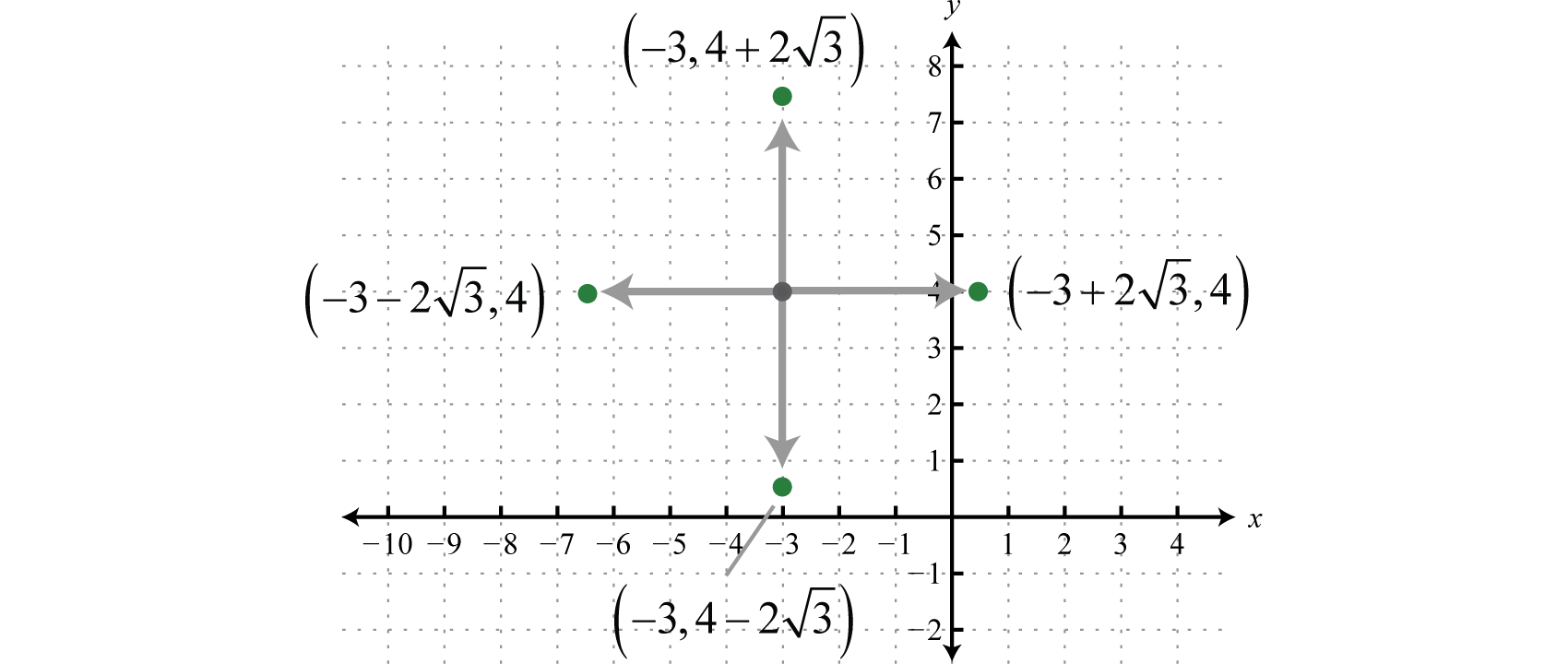
Respuesta:

Figura\(\PageIndex{11}\)

Ejemplo\(\PageIndex{5}\):

Determinar el centro y el radio:\(4 x^{2}+4 y^{2}-8 x+12 y-3=0\).

Solución

Podemos obtener la forma general dividiendo primero ambos lados por\(4\).

\(\frac{4 x^{2}+4 y^{2}-8 x+12 y-3}{4}=\frac{0}{4}\)
\(x^{2}+y^{2}-2 x+3 y-\frac{3}{4}=0\)

Ahora que tenemos la forma general para un círculo, donde ambos términos de grado dos tienen un coeficiente principal de\(1\), podemos usar los pasos para reescribirlo en forma estándar. Comience por agregar\(\frac{3}{4}\) a ambos lados y agrupar variables que sean iguales.

\(\left(x^{2}-2 x+\_\_\_\right)+\left(y^{2}+3 y+\_\_\_\right)=\frac{3}{4}\)

Siguiente completar la plaza para ambas agrupaciones. Utilizar\(\left(\frac{-2}{2}\right)^{2}=(-1)^{2}=1\) para la primera agrupación y\(\left(\frac{3}{2}\right)^{2}=\frac{9}{4}\) para la segunda agrupación.

\(\begin{aligned}\color{black}{\left(x^{2}-2 x\color{Cerulean}{+1}\right)+}\color{black}{\left(y^{2}+3 y\color{OliveGreen}{+\frac{9}{4}}\right)}&=\frac{3}{4}\color{Cerulean}{+1}\color{OliveGreen}{+\frac{9}{4}} \\ (x-1)^{2}+\left(y+\frac{3}{2}\right)^{2} &=\frac{16}{4} \\ (x-1)^{2}+\left(y+\frac{3}{2}\right)^{2}&=4\end{aligned}\)

Respuesta:

Centro:\(\left(1,-\frac{3}{2}\right)\); radio:\(r=2\)

En resumen, para convertir de forma estándar a forma general multiplicamos, y para convertir de forma general a forma estándar completamos el cuadrado.

Figura\(\PageIndex{12}\)

Ejercicio\(\PageIndex{2}\):

Gráfica:\(x^{2}+y^{2}-10 x+2 y+21=0\).

Respuesta:

Figura\(\PageIndex{13}\)

www.youtube.com/V/MS8NNQS6s

Claves para llevar

• La gráfica de un círculo está completamente determinada por su centro y radio.
• La forma estándar para la ecuación de un círculo es\((x-h)^{2}+(y-k)^{2}=r^{2}\). El centro es\((h,k)\) y el radio mide\(r\) unidades.
• Para graficar un círculo marca puntos\(r\) unidades arriba, abajo, izquierda y derecha desde el centro. Dibuja un círculo a través de estos cuatro puntos.
• Si la ecuación de un círculo se da en forma general\(x^{2}+y^{2}+c x+d y+e=0\), agrupe los términos con las mismas variables y complete el cuadrado para ambas agrupaciones. Esto dará como resultado una forma estándar, a partir de la cual podemos leer el centro y el radio del círculo.
• Reconocemos la ecuación de un círculo si es cuadrática en ambas\(x\) y\(y\) donde el coeficiente de los términos cuadrados son los mismos.

Ejercicio\(\PageIndex{3}\)

Determinar el centro y el radio dada la ecuación de un círculo en forma estándar.

1. \((x-5)^{2}+(y+4)^{2}=64\)
2. \((x+9)^{2}+(y-7)^{2}=121\)
3. \(x^{2}+(y+6)^{2}=4\)
4. \((x-1)^{2}+y^{2}=1\)
5. \((x+1)^{2}+(y+1)^{2}=7\)
6. \((x+2)^{2}+(y-7)^{2}=8\)

Contestar

1. Centro:\((5, −4)\); radio:\(r = 8\)

3. Centro:\((0, −6)\); radio:\(r = 2\)

5. Centro:\((−1, −1)\); radio:\(r = \sqrt{7}\)

Ejercicio\(\PageIndex{4}\)

Determinar la forma estándar para la ecuación del círculo dado su centro y radio.

1. Centro\((5, 7)\) con radio\(r = 7\).
2. Centro\((−2, 8)\) con radio\(r = 5\).
3. Centro\((6, −11)\) con radio\(r = \sqrt{2}\).
4. Centro\((−4, −5)\) con radio\(r = \sqrt{6}\).
5. Centro\((0, −1)\) con radio\(r = 2\sqrt{5}\).
6. Centro\((0, 0)\) con radio\(r = 3\sqrt{10}\).

Contestar

1. \((x-5)^{2}+(y-7)^{2}=49\)

3. \((x-6)^{2}+(y+11)^{2}=2\)

5. \(x^{2}+(y+1)^{2}=20\)

Ejercicio\(\PageIndex{5}\)

Gráfica.

1. \((x-1)^{2}+(y-2)^{2}=9\)
2. \((x+3)^{2}+(y-3)^{2}=25\)
3. \((x-2)^{2}+(y+6)^{2}=4\)
4. \((x+6)^{2}+(y+4)^{2}=36\)
5. \(x^{2}+(y-4)^{2}=1\)
6. \((x-3)^{2}+y^{2}=4\)
7. \(x^{2}+y^{2}=12\)
8. \(x^{2}+y^{2}=8\)
9. \((x-7)^{2}+(y-6)^{2}=2\)
10. \((x+2)^{2}+(y-5)^{2}=5\)
11. \((x+3)^{2}+(y-1)^{2}=18\)
12. \((x-3)^{2}+(y-2)^{2}=15\)

Contestar

1.

Figura\(\PageIndex{14}\)

3.

Figura\(\PageIndex{15}\)

5.

Figura\(\PageIndex{16}\)

7.

Figura\(\PageIndex{17}\)

9.

Figura\(\PageIndex{18}\)

11.

Figura\(\PageIndex{19}\)

Ejercicio\(\PageIndex{6}\)

Encuentra los\(x\) - y\(y\) -interceptos.

1. \((x-1)^{2}+(y-2)^{2}=9\)
2. \((x+5)^{2}+(y-3)^{2}=25\)
3. \(x^{2}+(y-4)^{2}=1\)
4. \((x-3)^{2}+y^{2}=18\)
5. \(x^{2}+y^{2}=50\)
6. \(x^{2}+(y+9)^{2}=20\)
7. \((x-4)^{2}+(y+5)^{2}=10\)
8. \((x+10)^{2}+(y-20)^{2}=400\)

Contestar

1. \(x\)-intercepta:\((1 \pm \sqrt{5}, 0)\);\(y\) -intercepta:\((0,2 \pm 2 \sqrt{2})\)

3. \(x\)-intercepta: ninguno;\(y\) -intercepta:\((0, 3), (0, 5)\)

5. \(x\)-intercepta:\((\pm 5 \sqrt{2}, 0)\);\(y\) -intercepta:\((0, \pm 5 \sqrt{2})\)

7. \(x\)-intercepta: ninguno;\(y\) -intercepta: ninguno

Ejercicio\(\PageIndex{7}\)

Encuentra la ecuación del círculo.

1. Círculo con el centro\((1, −2)\) que pasa a través\((3, −4)\).
2. Círculo con el centro\((−4, −1)\) que pasa a través\((0, −3)\).
3. Círculo cuyo diámetro se define por\((5, 1)\) y\((−1, 7)\).
4. Círculo cuyo diámetro se define por\((−5, 7)\) y\((−1, −5)\).
5. Círculo con unidades\(9π\) cuadradas de centro\((5, −2)\) y área.
6. Círculo con unidades\(12π\) cuadradas de centro\((−8, −3)\) y circunferencia.
7. Encuentra el área del círculo con ecuación\((x+12)^{2} \pm(x-5)^{2}=7\).
8. Encuentra la circunferencia del círculo con ecuación\((x+1)^{2}+(y+5)^{2}=8\).

Contestar

1. \((x-1)^{2}+(y+2)^{2}=8\)

3. \((x-2)^{2}+(y-4)^{2}=18\)

5. \((x-5)^{2}+(y+2)^{2}=9\)

7. \(7π\)unidades cuadradas

Ejercicio\(\PageIndex{8}\)

Reescribir en forma estándar y gráfica.

1. \(x^{2}+y^{2}+4 x-2 y-4=0\)
2. \(x^{2}+y^{2}-10 x+2 y+10=0\)
3. \(x^{2}+y^{2}+2 x+12 y+36=0\)
4. \(x^{2}+y^{2}-14 x-8 y+40=0\)
5. \(x^{2}+y^{2}+6 y+5=0\)
6. \(x^{2}+y^{2}-12 x+20=0\)
7. \(x^{2}+y^{2}+8 x+12 y+16=0\)
8. \(x^{2}+y^{2}-20 x-18 y+172=0\)
9. \(4 x^{2}+4 y^{2}-4 x+8 y+1=0\)
10. \(9 x^{2}+9 y^{2}+18 x+6 y+1=0\)
11. \(x^{2}+y^{2}+4 x+8 y+14=0\)
12. \(x^{2}+y^{2}-2 x-4 y-15=0\)
13. \(x^{2}+y^{2}-x-2 y+1=0\)
14. \(x^{2}+y^{2}-x+y-\frac{1}{2}=0\)
15. \(4 x^{2}+4 y^{2}+8 x-12 y+5=0\)
16. \(9 x^{2}+9 y^{2}+12 x-36 y+4=0\)
17. \(2 x^{2}+2 y^{2}+6 x+10 y+9=0\)
18. \(9 x^{2}+9 y^{2}-6 x+12 y+4=0\)

Contestar

1. \((x+2)^{2}+(y-1)^{2}=9\);

Figura\(\PageIndex{20}\)

3. \((x+1)^{2}+(y+6)^{2}=1\);

Figura\(\PageIndex{21}\)

5. \(x^{2}+(y+3)^{2}=4\);

Figura\(\PageIndex{22}\)

7. \((x+4)^{2}+(y+6)^{2}=36\);

Figura\(\PageIndex{23}\)

9. \(\left(x-\frac{1}{2}\right)^{2}+(y+1)^{2}=1\);

Figura\(\PageIndex{24}\)

11. \((x+2)^{2}+(y-4)^{2}=6\);

Figura\(\PageIndex{25}\)

13. \(\left(x-\frac{1}{2}\right)^{2}+(y-1)^{2}=\frac{1}{4}\);

Figura\(\PageIndex{26}\)

15. \((x+1)^{2}+\left(y-\frac{3}{2}\right)^{2}=2\);

Figura\(\PageIndex{27}\)

17. \(\left(x+\frac{3}{2}\right)^{2}+\left(y+\frac{5}{2}\right)^{2}=4\);

Figura\(\PageIndex{28}\)

Ejercicio\(\PageIndex{9}\)

Dado un círculo en forma general, determinar las intercepciones.

1. \(x^{2}+y^{2}-5 x+3 y+6=0\)
2. \(x^{2}+y^{2}+x-2 y-7=0\)
3. \(x^{2}+y^{2}-6 y+2=2\)
4. \(x^{2}+y^{2}-6 x-8 y+5=0\)
5. \(2 x^{2}+2 y^{2}-3 x-9=0\)
6. \(3 x^{2}+3 y^{2}+8 y-16=0\)
7. Determinar el área del círculo cuya ecuación es\(x^{2}+y^{2}-2 x-6 y-35=0\).
8. Determinar el área del círculo cuya ecuación es\(4 x^{2}+4 y^{2}-12 x-8 y-59=0\).
9. Determinar la circunferencia de un círculo cuya ecuación es\(x^{2}+y^{2}-5 x+1=0\).
10. Determinar la circunferencia de un círculo cuya ecuación es\(x^{2}+y^{2}+5 x-2 y+3=0\).
11. Encuentra la forma general de la ecuación de un círculo centrado en el\((−3, 5)\) paso\((1, −2)\).
12. Encuentra la forma general de la ecuación de un círculo centrado en el\((−2, −3)\) paso\((−1, 3)\).

Contestar

1. \(x\)-intercepta:\((2, 0), (3, 0)\);\(y\) -intercepta: ninguna

3. \(x\)-intercepta:\((0, 0)\);\(y\) -intercepta:\((0, 0), (0, 6)\)

5. \(x\)-intercepta:\((−\frac{3}{2}, 0), (3, 0)\);\(y\) -intercepta:\(\left(0, \pm \frac{3 \sqrt{2}}{2}\right)\)

7. \(45π\)unidades cuadradas

9. \(π\sqrt{21}\)unidades

11. \(x^{2}+y^{2}+6 x-10 y-31=0\)

Ejercicio\(\PageIndex{10}\)

Dada la gráfica de un círculo, determinar su ecuación en forma general.

1.

Figura\(\PageIndex{29}\)

2.

Figura\(\PageIndex{30}\)

3.

Figura\(\PageIndex{31}\)

4.

Figura\(\PageIndex{32}\)

Contestar

1. \(x^{2}+y^{2}-6 x+10 y+18=0\)

3. \(x^{2}+y^{2}+2 y=0\)

Ejercicio\(\PageIndex{11}\)

1. ¿El centro de un círculo es parte de la gráfica? Explique.
2. Haz tu propio círculo, escríbalo en forma general y gráficalo.
3. Explicar cómo podemos decir la diferencia entre la ecuación de una parábola en forma general y la ecuación de un círculo en forma general. Dé un ejemplo.
4. ¿Todos los círculos tienen intercepciones? ¿Cuáles son los posibles números de interceptaciones? Ilustra tu explicación con gráficas.

Contestar

1. La respuesta puede variar

3. La respuesta puede variar

Notas al pie

⁸ Un círculo es el conjunto de puntos en un plano que se encuentran a una distancia fija de un punto dado, llamado centro.

⁹ La distancia fija desde el centro de un círculo hasta cualquier punto del círculo.

¹⁰ La longitud de un segmento de línea que pasa por el centro de un círculo cuyos extremos están en el círculo.

¹¹ La ecuación de un círculo escrita en la forma\((x-h)^{2}+(y-k)^{2}=r^{2}\) donde\((h, k)\) está el centro y\(r\) es el radio.

¹² El círculo centrado en el origen con radio\(1\); su ecuación es\(x^{2} + y^{2} = 1\).

¹³ La ecuación de un círculo escrita en la forma\(x^{2} + y^{2} + cx + dy + e = 0\).