9.3: Secuencias geométricas y series

Última actualización
Guardar como PDF

Page ID: 109697

Anonymous
LibreTexts

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Objetivos de aprendizaje

Identificar la proporción común de una secuencia geométrica.
Encuentra una fórmula para el término general de una secuencia geométrica.
Calcular la$n$ ésima suma parcial de una secuencia geométrica.
Calcular la suma de una serie geométrica infinita cuando existe.

Secuencias Geométricas

Una secuencia geométrica ¹⁸, o progresión geométrica ¹⁹, es una secuencia de números donde cada número sucesivo es producto del número anterior y alguna constante$r$.

$a_{n}=r a_{n-1} \quad\color{Cerulean}{Geometric\:Sequence}$

Y porque$\frac{a_{n}}{a_{n-1}}=r$, al factor constante$r$ se le llama el cociente común ²⁰. Por ejemplo, la siguiente es una secuencia geométrica,

$9,27,81,243,729 \ldots$

Aquí$a_{1} = 9$ y la relación entre dos términos sucesivos cualesquiera es$3$. Podemos construir el término general$a_{n}=3 a_{n-1}$ donde,

$\begin{aligned} a_{1} &=9 \\ a_{2} &=3 a_{1}=3(9)=27 \\ a_{3} &=3 a_{2}=3(27)=81 \\ a_{4} &=3 a_{3}=3(81)=243 \\ a_{5} &=3 a_{4}=3(243)=729 \\ & \vdots \end{aligned}$

En general, dado el primer término$a_{1}$ y la relación común$r$ de una secuencia geométrica podemos escribir lo siguiente:

$\begin{aligned} a_{2} &=r a_{1} \\ a_{3} &=r a_{2}=r\left(a_{1} r\right)=a_{1} r^{2} \\ a_{4} &=r a_{3}=r\left(a_{1} r^{2}\right)=a_{1} r^{3} \\ a_{5} &=r a_{3}=r\left(a_{1} r^{3}\right)=a_{1} r^{4} \\ & \vdots \end{aligned}$

De esto vemos que cualquier secuencia geométrica puede escribirse en términos de su primer elemento, su relación común, y el índice de la siguiente manera:

$a_{n}=a_{1} r^{n-1} \quad\color{Cerulean}{Geometric\:Sequence}$

De hecho, cualquier término general que sea exponencial en$n$ es una secuencia geométrica.

Ejemplo$\PageIndex{1}$:

Encuentre una ecuación para el término general de la secuencia geométrica dada y utilízala para calcular su$10^{th}$ término:$3, 6, 12, 24, 48…$

Solución

Comience por encontrar la proporción común,

$r=\frac{6}{3}=2$

Tenga en cuenta que la relación entre dos términos sucesivos cualesquiera es$2$. La secuencia es de hecho una progresión geométrica donde$a_{1} = 3$ y$r = 2$.

$\begin{aligned} a_{n} &=a_{1} r^{n-1} \\ &=3(2)^{n-1} \end{aligned}$

Por lo tanto, podemos escribir el término general$a_{n}=3(2)^{n-1}$ y el$10^{th}$ término se puede calcular de la siguiente manera:

$\begin{aligned} a_{10} &=3(2)^{10-1} \\ &=3(2)^{9} \\ &=1,536 \end{aligned}$

Respuesta:

$a_{n}=3(2)^{n-1} ; a_{10}=1,536$

Los términos entre términos dados de una secuencia geométrica se denominan medias geométricas ²¹.

Ejemplo$\PageIndex{2}$:

Encuentra todos los términos entre$a_{1} = −5$ y$a_{4} = −135$ de una secuencia geométrica. En otras palabras, encontrar todas las medias geométricas entre los$4^{th}$ términos$1^{st}$ y.

Solución

Comience por encontrar la proporción común$r$. En este caso, se nos da el primer y cuarto término:

$\begin{aligned} a_{n} &=a_{1} r^{n-1} \quad\color{Cerulean} { Use \: n=4} \\ a_{4} &=a_{1} r^{4-1} \\ a_{4} &=a_{1} r^{3} \end{aligned}$

Sustituir$a_{1} = −5$ y$a_{4} = −135$ en la ecuación anterior y luego resolver para$r$.

$\begin{aligned}-135 &=-5 r^{3} \\ 27 &=r^{3} \\ 3 &=r \end{aligned}$

A continuación, use el primer término$a_{1} = −5$ y la relación común$r = 3$ para encontrar una ecuación para el término$n$ th de la secuencia.

$\begin{aligned} a_{n} &=a_{1} r^{n-1} \\ a_{n} &=-5(3)^{n-1} \end{aligned}$

Ahora podemos usar$a_{n}=-5(3)^{n-1}$ donde$n$ es un entero positivo para determinar los términos que faltan.

$\left.\begin{array}{l}{a_{1}=-5(3)^{1-1}=-5 \cdot 3^{0}=-5} \\ {a_{2}=-5(3)^{2-1}=-5 \cdot 3^{1}=-15} \\ {a_{3}=-5(3)^{3-1}=-5 \cdot 3^{2}=-45} \\ a_{4}=-5(3)^{4-1}=-5\cdot3^{3}=-135\end{array}\right\} \color{Cerulean}{geometric\:means}$

Respuesta:

$-15,-45$

No se puede dar el primer término de una secuencia geométrica.

Ejemplo$\PageIndex{3}$:

Encuentra el término general de una secuencia geométrica donde$a_{2} = −2$ y$a_{5}=\frac{2}{125}$.

Solución

Para determinar una fórmula para el término general necesitamos$a_{1}$ y$r$. Un sistema no lineal con estas variables se puede formar usando la información dada y$a_{n}=a_{1} r^{n-1} :$:

$\left\{\begin{array}{l}{a_{2}=a_{1} r^{2-1}} \\ {a_{5}=a_{1} r^{5-1}}\end{array}\right. \Longrightarrow \left\{\begin{array}{l}{-2=a_{1} r \quad\:\:\:\color{Cerulean}{Use\:a_{2}=-2.}} \\ {\frac{2}{125}=a_{1} r^{4} \quad\color{Cerulean}{Use\:a_{5}=\frac{2}{125}.}}\end{array}\right.$

Resolver para$a_{1}$ en la primera ecuación,

$-2=a_{1} r \quad \Rightarrow \quad \frac{-2}{r}=a_{1}$
$\frac{2}{125}=a_{1} r^{4}$

Sustituir$a_{1} = \frac{-2}{r}$ en la segunda ecuación y resolver para$r$.

$\frac{2}{125}=a_{1} r^{4}$
$\frac{2}{125}=\left(\frac{-2}{r}\right) r^{4}$
$\frac{2}{125}=-2 r^{3}$
$-\frac{1}{125}=r^{3}$
$-\frac{1}{5}=r$

Volver sustituto para encontrar$a_{1}$:

$\begin{aligned} a_{1} &=\frac{-2}{r} \\ &=\frac{-2}{\left(-\frac{1}{5}\right)} \\ &=10 \end{aligned}$

Por lo tanto,$a_{1} = 10$ y$r = −\frac{1}{5}$.

Respuesta:

$a_{n}=10\left(-\frac{1}{5}\right)^{n-1}$

Ejercicio$\PageIndex{1}$

Encuentre una ecuación para el término general de la secuencia geométrica dada y utilízala para calcular su$6^{th}$ término:$2, \frac{4}{3},\frac{8}{9}, …$

Contestar

$a_{n}=2\left(\frac{2}{3}\right)^{n-1} ; a_{6}=\frac{64}{243}$

www.youtube.com/V/igpel9vloly

Serie Geométrica

Una serie geométrica ²² es la suma de los términos de una secuencia geométrica. Por ejemplo, la suma de los primeros$5$ términos de la secuencia geométrica definida por$a_{n}=3^{n+1}$ lo siguiente:

$\begin{aligned} S_{5} &=\sum_{n=1}^{5} 3^{n+1} \\ &=3^{1+1}+3^{2+1}+3^{3+1}+3^{4+1}+3^{5+1} \\ &=3^{2}+3^{3}+3^{4}+3^{5}+3^{6} \\ &=9+27+81+3^{5}+3^{6} \\ &=1,089 \end{aligned}$

Agregar enteros$5$ positivos es manejable. No obstante, la tarea de sumar un gran número de términos no lo es. Por lo tanto, a continuación desarrollamos una fórmula que se puede utilizar para calcular la suma de los primeros$n$ términos de cualquier secuencia geométrica. En general,

$S_{n}=a_{1}+a_{1} r+a_{1} r^{2}+\ldots+a_{1} r^{n-1}$

Multiplicando ambos lados por$r$ podemos escribir,

$r S_{n}=a_{1} r+a_{1} r^{2}+a_{1} r^{3}+\ldots+a_{1} r^{n}$

Al restar estas dos ecuaciones obtenemos entonces,

$S_{n}-r S_{n}=a_{1}-a_{1} r^{n}$
$S_{n}(1-r)=a_{1}\left(1-r^{n}\right)$

Suponiendo que$r ≠ 1$ dividir ambos lados por nos$(1 − r)$ lleva a la fórmula para la $n$ésima suma parcial de una secuencia geométrica ²³:

$S_{n}=\frac{a_{1}\left(1-r^{n}\right)}{1-r}(r \neq 1)$

En otras palabras, la$n$ ésima suma parcial de cualquier secuencia geométrica se puede calcular utilizando el primer término y la relación común. Por ejemplo, para calcular la suma de los primeros$15$ términos de la secuencia geométrica definida por$a_{n}=3^{n+1}$, utilice la fórmula con$a_{1} = 9$ y$r = 3$.

$\begin{aligned} S_{15} &=\frac{a_{1}\left(1-r^{15}\right)}{1-r} \\ &=\frac{9 \cdot\left(1-3^{15}\right)}{1-3} \\ &=\frac{9(-14,348,906)}{-2} \\ &=64,570,077 \end{aligned}$

Ejemplo$\PageIndex{4}$:

Encuentra la suma de los primeros 10 términos de la secuencia dada:$4, −8, 16, −32, 64,… $

Solución

Determinar si existe o no una relación común entre los términos dados.

$r=\frac{-8}{4}=-2$

Obsérvese que la relación entre dos términos sucesivos cualesquiera es$−2$; por lo tanto, la secuencia dada es una secuencia geométrica. Uso$r = −2$ y el hecho de que$a_{1} = 4$ para calcular la suma de los primeros$10$ términos,

$\begin{aligned} S_{n} &=\frac{a_{1}\left(1-r^{n}\right)}{1-r} \\ S_{10} &=\frac{\color{Cerulean}{4}\color{black}{\left[1-(\color{Cerulean}{-2}\color{black}{)}^{10}\right]}}{1-(\color{Cerulean}{-2}\color{black}{)}} ] \\ &=\frac{4(1-1,024)}{1+2} \\ &=\frac{4(-1,023)}{3} \\ &=-1,364 \end{aligned}$

Respuesta:

$S_{10}=-1,364$

Ejemplo$\PageIndex{5}$:

Evaluar:$\sum_{n=1}^{6} 2(-5)^{n}$.

Solución

En este caso, se nos pide encontrar la suma de los primeros$6$ términos de una secuencia geométrica con término general$a_{n} = 2(−5)^{n}$. Use esto para determinar el$1^{st}$ término y la relación común$r$:

$a_{1}=2(-5)^{1}=-10$

Para demostrar que existe una relación común podemos utilizar términos sucesivos en general de la siguiente manera:

$\begin{aligned} r &=\frac{a_{n}}{a_{n-1}} \\ &=\frac{2(-5)^{n}}{2(-5)^{n-1}} \\ &=(-5)^{n-(n-1)} \\ &=(-5)^{1}\\&=-5 \end{aligned}$

Utilizar$a_{1} = −10$ y$r = −5$ calcular la suma$6^{th}$ parcial.

$\begin{aligned} S_{n} &=\frac{a_{1}\left(1-r^{n}\right)}{1-r} \\ S_{6} &=\frac{\color{Cerulean}{-10}\color{black}{\left[1-(\color{Cerulean}{-5}\color{black}{)}^{6}\right]}}{1-(\color{Cerulean}{-5}\color{black}{)}} \\ &=\frac{-10(1-15,625)}{1+5} \\ &=\frac{-10(-15,624)}{6} \\ &=26,040 \end{aligned}$

Respuesta:

$26,040$

Ejercicio$\PageIndex{2}$

Encuentra la suma de los primeros 9 términos de la secuencia dada:$-2,1,-1 / 2, \dots$

Contestar

$S_{9}=-\frac{171}{128}$

www.youtube.com/V/V-T3P95RWE8

Si la relación común r de una secuencia geométrica infinita es una fracción donde$|r| < 1$ (es decir$−1 < r < 1$), entonces el factor que$(1 − r^{n})$ se encuentra en la fórmula para la$n$ ésima suma parcial tiende hacia a$1$ medida que$n$ aumenta. Por ejemplo, si$r = \frac{1}{10}$ y$n = 2, 4, 6$ tenemos,

$1-\left(\frac{1}{10}\right)^{2}=1-0.01=0.99$
$1-\left(\frac{1}{10}\right)^{4}=1-0.0001=0.9999$
$1-\left(\frac{1}{10}\right)^{6}=1-0.00001=0.999999$

Aquí podemos ver que este factor se acerca cada vez más a 1 para valores cada vez más grandes de$n$. Esto ilustra la idea de un límite, un concepto importante utilizado ampliamente en las matemáticas de nivel superior, que se expresa utilizando la siguiente notación:

$\lim _{n \rightarrow \infty}\left(1-r^{n}\right)=1$donde$|r|<1$

Esto se lee, “el límite de$(1 − r^{n})$ lo que se$n$ acerca al infinito es igual”$1$. Si bien esto da una vista previa de lo que está por venir en su estudio continuo de las matemáticas, en este punto nos preocupa desarrollar una fórmula para series geométricas infinitas especiales. Considere la$n$ suma parcial de cualquier secuencia geométrica,

$S_{n}=\frac{a_{1}\left(1-r^{n}\right)}{1-r}=\frac{a_{1}}{1-r}\left(1-r^{n}\right)$

Si$|r| < 1$ entonces existe el límite de las sumas parciales a medida que n se acerca al infinito y podemos escribir,

$S_{n}=\frac{a_{1}}{1-r}\left(1-r^{n}\right)\quad\color{Cerulean}{\stackrel{\Longrightarrow}{n\rightarrow \infty }} \quad \color{black}{S_{\infty}}=\frac{a_{1}}{1-4}\cdot1$

Por lo tanto, una serie geométrica convergente ²⁴ es una serie geométrica infinita donde$|r| < 1$; su suma se puede calcular usando la fórmula:

$S_{\infty}=\frac{a_{1}}{1-r}$

Ejemplo$\PageIndex{6}$:

Encuentra la suma de la serie geométrica infinita:$\frac{3}{2}+\frac{1}{2}+\frac{1}{6}+\frac{1}{18}+\frac{1}{54}+\dots$

Solución

Determinar la relación común, Dado que la relación común$r = \frac{1}{3}$ es una fracción entre$−1$ y$1$, esta es una serie geométrica convergente. Utilizar el primer término$a_{1} = \frac{3}{2}$ y la relación común para calcular su suma

$\begin{aligned} S_{\infty} &=\frac{a_{1}}{1-r} \\ &=\frac{\frac{3}{2}}{1-\left(\frac{1}{3}\right)} \\ &=\frac{\frac{3}{3}}{\frac{2}{3}} \\ &=\frac{3}{2} \cdot \frac{3}{2} \\ &=\frac{9}{4} \end{aligned}$

Respuesta:

$S_{\infty}=\frac{9}{4}$

Nota

En el caso de una serie geométrica infinita donde$|r| ≥ 1$, la serie diverge y decimos que no hay suma. Por ejemplo, si$a_{n} = (5)^{n−1}$ entonces$r = 5$ y tenemos

$S_{\infty}=\sum_{n=1}^{\infty}(5)^{n-1}=1+5+25+\cdots$

Podemos ver que esta suma crece sin ataduras y no tiene suma.

Ejercicio$\PageIndex{3}$

Encuentra la suma de la serie geométrica infinita:$\sum_{n=1}^{\infty}-2\left(\frac{5}{9}\right)^{n-1}$

Contestar

$-\frac{9}{2}$

www.youtube.com/v/kxspvuyle_a

Un decimal repetido se puede escribir como una serie geométrica infinita cuya relación común es una potencia de$1/10$. Por lo tanto, la fórmula para una serie geométrica convergente se puede utilizar para convertir un decimal repetido en una fracción.

Ejemplo$\PageIndex{7}$:

Escribe como fracción:$1.181818… $

Solución

Comience por identificar los dígitos repetidos a la derecha del decimal y reescribirlo como una progresión geométrica.

$\begin{aligned} 0.181818 \ldots &=0.18+0.0018+0.000018+\ldots \\ &=\frac{18}{100}+\frac{18}{10,000}+\frac{18}{1,000,000}+\ldots \end{aligned}$

En esta forma podemos determinar la relación común,

$\begin{aligned} r &=\frac{\frac{18}{10,000}}{\frac{18}{100}} \\ &=\frac{18}{10,000} \times \frac{100}{18} \\ &=\frac{1}{100} \end{aligned}$

Tenga en cuenta que la relación entre dos términos sucesivos cualesquiera es$\frac{1}{100}$. Usa esto y el hecho de que$a_{1} = \frac{18}{100}$ para calcular la suma infinita:

$\begin{aligned} S_{\infty} &=\frac{a_{1}}{1-r} \\ &=\frac{\frac{18}{100}}{1-\left(\frac{1}{100}\right)} \\ &=\frac{\frac{18}{100}}{\frac{90}{100}} \\ &=\frac{18}{100} \cdot \frac{100}{99} \\ &=\frac{2}{11} \end{aligned}$

Por lo tanto,$0.181818… = \frac{2}{11}$ y tenemos,

$1.181818 \ldots=1+\frac{2}{11}=1 \frac{2}{11}$

Respuesta:

$1 \frac{2}{11}$

Ejemplo$\PageIndex{8}$:

Cierta pelota rebota a dos tercios de la altura de la que cayó. Si esta pelota se cae inicialmente desde$27$ pies, aproxima la distancia total que recorre la pelota.

Solución

Podemos calcular la altura de cada rebote sucesivo:

$\begin{array}{l}{27 \cdot \frac{2}{3}=18 \text { feet } \quad \color{Cerulean} { Height\: of\: the\: first\: bounce }} \\ {18 \cdot \frac{2}{3}=12 \text { feet}\quad\:\color{Cerulean}{ Height \:of\: the\: second\: bounce }} \\ {12 \cdot \frac{2}{3}=8 \text { feet } \quad\:\: \color{Cerulean} { Height\: of\: the\: third\: bounce }}\end{array}$

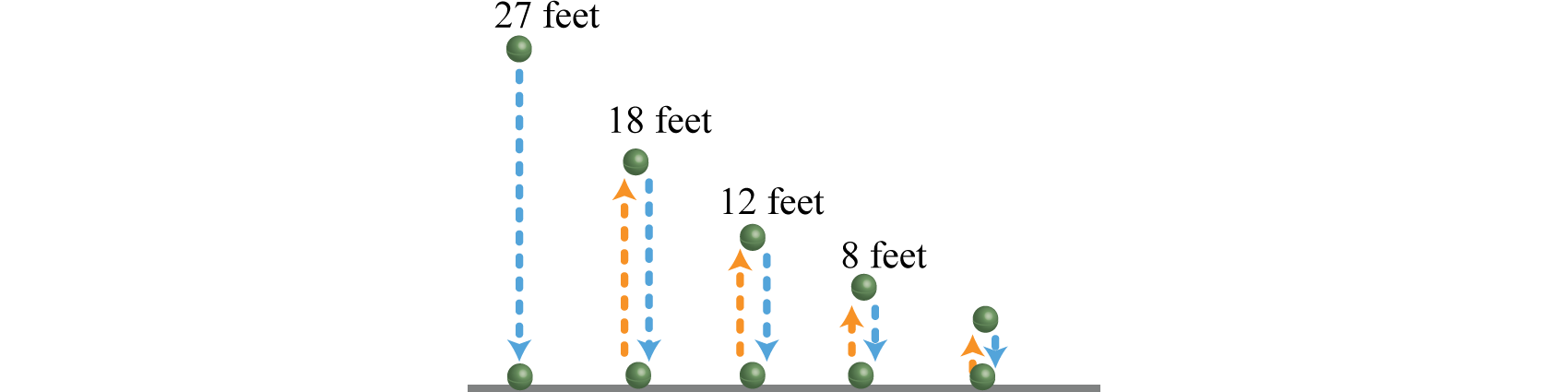
La distancia total que recorre la pelota es la suma de las distancias que la pelota está cayendo y las distancias que la pelota está subiendo. Las distancias que cae la pelota forman una serie geométrica,

$27+18+12+\dots \quad\color{Cerulean}{Distance\:the\:ball\:is\:falling}$

dónde$a_{1} = 27$ y$r = \frac{2}{3}$. Debido a que$r$ es una fracción entre$−1$ y$1$, esta suma se puede calcular de la siguiente manera:

$\begin{aligned} S_{\infty} &=\frac{a_{1}}{1-r} \\ &=\frac{27}{1-\frac{2}{3}} \\ &=\frac{27}{\frac{1}{3}} \\ &=81 \end{aligned}$

Por lo tanto, la pelota está cayendo una distancia total de$81$ pies. Las distancias que sube la pelota forman una serie geométrica,

$18+12+8+\cdots \quad\color{Cerulean}{Distance\:the\:ball\:is\:rising}$

dónde$a_{1} = 18$ y$r = \frac{2}{3}$. Calcule esta suma de manera similar:

$\begin{aligned} S_{\infty} &=\frac{a_{1}}{1-r} \\ &=\frac{18}{1-\frac{2}{3}} \\ &=\frac{18}{\frac{1}{3}} \\ &=54 \end{aligned}$

Por lo tanto, la pelota está subiendo una distancia total de$54$ pies. Aproximar la distancia total recorrida sumando las distancias totales de subida y bajada:

$81+54=135$pies

Respuesta:

$135$pies

Claves para llevar

Una secuencia geométrica es una secuencia donde la relación$r$ entre términos sucesivos es constante.
El término general de una secuencia geométrica se puede escribir en términos de su primer término$a_{1}$, relación común$r$, e índice de la$n$ siguiente manera:$a_{n} = a_{1} r^{n−1}$.
Una serie geométrica es la suma de los términos de una secuencia geométrica.
La$n$ ésima suma parcial de una secuencia geométrica se puede calcular utilizando el primer término$a_{1}$ y la relación común de la$r$ siguiente manera:$S_{n}=\frac{a_{1}\left(1-r^{n}\right)}{1-r}$.
La suma infinita de una secuencia geométrica se puede calcular si la relación común es una fracción entre$−1$ y$1$ (es decir$|r| < 1$) de la siguiente manera:$S_{\infty}=\frac{a_{1}}{1-r}$. Si$|r| ≥ 1$, entonces no existe suma.

Ejercicio$\PageIndex{4}$

Escribir los primeros$5$ términos de la secuencia geométrica dado su primer término y relación común. Encuentra una fórmula para su término general.

$a_{1}=1 ; r=5$
$a_{1}=1 ; r=3$
$a_{1}=2 ; r=3$
$a_{1}=5 ; r=4$
$a_{1}=2 ; r=-3$
$a_{1}=6 ; r=-2$
$a_{1}=3 ; r=\frac{2}{3}$
$a_{1}=6 ; r=\frac{1}{2}$
$a_{1}=1.2 ; r=0.6$
$a_{1}=-0.6 ; r=-3$

Contestar

1. $1,5,25,125,625 ; a_{n}=5^{n-1}$

3. $2,6,18,54,162 ; a_{n}=2(3)^{n-1}$

5. $2,-6,18,-54,162 ; a_{n}=2(-3)^{n-1}$

7. $3,2, \frac{4}{3}, \frac{8}{9}, \frac{16}{27} ; a_{n}=3\left(\frac{2}{3}\right)^{n-1}$

9. $1.2,0.72,0.432,0.2592,0.15552 ; a_{n}=1.2(0.6)^{n-1}$

Ejercicio$\PageIndex{5}$

Dada la secuencia geométrica, encontrar una fórmula para el término general y utilizarla para determinar el$5^{th}$ término en la secuencia.

$7,28,112, \dots$
$-2,-10,-50, \dots$
$2, \frac{1}{2}, \frac{1}{8}, \ldots$
$1, \frac{2}{5}, \frac{4}{25}, \ldots$
$8,4,2, \dots$
$6,2, \frac{2}{3}, \ldots$
$-1, \frac{2}{3},-\frac{4}{9}, \ldots$
$2,-\frac{3}{2}, \frac{9}{8}, \ldots$
$\frac{1}{3},-2,12, \dots$
$\frac{2}{5},-2,10, \dots$
$-3.6,-4.32,-5.184, \dots$
$0.8,-2.08,5.408, \dots$
Encuentra el término general y úsalo para determinar el$20^{th}$ término en la secuencia:$1, \frac{x}{2}, \frac{x^{2}}{4}, \ldots$
Encuentra el término general y úsalo para determinar el$20^{th}$ término en la secuencia:$2,-6 x, 18 x^{2} \ldots$
El número de células en un cultivo de cierta bacteria se duplica cada$4$ hora. Si$200$ las células están inicialmente presentes, escriba una secuencia que muestre la población de células después de$n$ cada período$4$ de hora por un día. Escribe una fórmula que dé el número de celdas después de cualquier periodo de$4$ -hora.
Cierta pelota rebota a la mitad de la altura de la que cayó. Si esta pelota se cae inicialmente de$12$ pies, encuentra una fórmula que le dé la altura de la pelota en el$n$ th rebote y úsela para encontrar la altura de la pelota en el$6^{th}$ rebote.
Dada una secuencia geométrica definida por la relación de recurrencia$a_{n} = 4a_{n−1}$ donde$a_{1} = 2$ y$n > 1$, encontrar una ecuación que dé el término general en términos de$a_{1}$ y la relación común$r$.
Dada la secuencia geométrica definida por la relación de recurrencia$a_{n} = 6a_{n−1}$ donde$a_{1} = \frac{1}{2}$ y$n > 1$, encontrar una ecuación que dé el término general en términos de$a_{1}$ y la relación común$r$.

Contestar

1. $a_{n}=7(4)^{n-1}, a_{5}=1,792$

3. $a_{n}=2\left(\frac{1}{4}\right)^{n-1}, a_{5}=\frac{1}{128}$

5. $a_{n}=8\left(\frac{1}{2}\right)^{n-1}, a_{5}=\frac{1}{2}$

7. $a_{n}=-\left(-\frac{2}{3}\right)^{n-1}, a_{5}=-\frac{16}{81}$

9. $a_{n}=\frac{1}{3}(-6)^{n-1}, a_{5}=432$

11. $a_{n}=-3.6(1.2)^{n-1}, a_{5}=-7.46496$

13. $a_{n}=\left(\frac{x}{2}\right)^{n-1} ; a_{20}=\frac{x^{19}}{2^{19}}$

15. $400$células;$800$ células;$1,600$ células;$3,200$ células;$6,400$ células;$12,800$ células;$p_{n} = 400(2)^{n−1}$ células

17. $a_{n}=2(4)^{n-1}$

Ejercicio$\PageIndex{6}$

Dados los términos de una secuencia geométrica, encontrar una fórmula para el término general.

$a_{1}=-3$y$a_{6}=-96$
$a_{1}=5$y$a_{4}=-40$
$a_{1}=-2$y$a_{8}=-\frac{1}{64}$
$a_{1}=\frac{3}{4}$y$a_{4}=-\frac{1}{36}$
$a_{2}=18$y$a_{5}=486$
$a_{2}=10$y$a_{7}=320$
$a_{4}=-2$y$a_{9}=64$
$a_{3}=-\frac{4}{3}$y$a_{6}=\frac{32}{81}$
$a_{5}=153.6$y$a_{8}=9,830.4$
$a_{4}=-2.4 \times 10^{-3}$y$a_{9}=-7.68 \times 10^{-7}$

Contestar

1. $a_{n}=-3(2)^{n-1}$

3. $a_{n}=-2\left(\frac{1}{2}\right)^{n-1}$

5. $a_{n}=6(3)^{n-1}$

7. $a_{n}=\frac{1}{4}(-2)^{n-1}$

9. $a_{n}=0.6(4)^{n-1}$

Ejercicio$\PageIndex{7}$

Encuentra todas las medias geométricas entre los términos dados.

$a_{1}=2$y$a_{4}=250$
$a_{1}=\frac{1}{3}$y$a_{6}=-\frac{1}{96}$
$a_{2}=-20$y$a_{5}=-20,000$
$a_{3}=49$y$a_{6}=-16,807$

Contestar

1. $10, 50$

3. $-200; -2,000$

Ejercicio$\PageIndex{8}$

Calcular la suma indicada.

$a_{n}=2^{n+1} ; S_{12}$
$a_{n}=(-2)^{n+1} ; S_{12}$
$a_{n}=\left(\frac{1}{2}\right)^{n} ; S_{7}$
$a_{n}=\left(\frac{2}{3}\right)^{n-1} ; S_{6}$
$a_{n}=5(-3)^{n-1} ; S_{5}$
$a_{n}=-7(-4)^{n} ; S_{5}$
$a_{n}=2\left(-\frac{1}{4}\right)^{n} ; S_{5}$
$a_{n}=\frac{1}{3}(2)^{n+1} ; S_{10}$
$\sum_{n=1}^{5} 5^{n}$
$\sum_{n=1}^{6}(-4)^{n}$
$\sum_{k=1}^{10} 2^{k+1}$
$\sum_{k=1}^{14} 2^{k-1}$
$\sum_{k=1}^{10}-2(3)^{k}$
$\sum_{k=1}^{8} 5(-2)^{k}$
$\sum_{n=1}^{5} 2\left(\frac{1}{2}\right)^{n+2}$
$\sum_{n=1}^{4}-3\left(\frac{2}{3}\right)^{n}$
$a_{n}=\left(\frac{1}{5}\right)^{n} ; S_{\infty}$
$a_{n}=\left(\frac{2}{3}\right)^{n-1} ; S_{\infty}$
$a_{n}=2\left(-\frac{3}{4}\right)^{n-1} ; S_{\infty}$
$a_{n}=3\left(-\frac{1}{6}\right)^{n} ; S_{\infty}$
$a_{n}=-2\left(\frac{1}{2}\right)^{n+1} ; S_{\infty}$
$a_{n}=-\frac{1}{3}\left(-\frac{1}{2}\right)^{n} ; S_{\infty}$
$\sum_{n=1}^{\infty} 2\left(\frac{1}{3}\right)^{n-1}$
$\sum_{n=1}^{\infty}\left(\frac{1}{5}\right)^{n}$
$\sum_{n=1}^{\infty} 3(2)^{n-2}$
$\sum_{n=1}^{\infty}-\frac{1}{4}(3)^{n-2}$
$\sum_{n=1}^{\infty} \frac{1}{2}\left(-\frac{1}{6}\right)^{n}$
$\sum_{n=1}^{\infty} \frac{1}{3}\left(-\frac{2}{5}\right)^{n}$

Contestar

1. $16,380$

3. $\frac{127}{128}$

5. $305$

7. $−\frac{205}{512}$

9. $3,905$

11. $4,092$

13. $−177,144$

15. $\frac{31}{64}$

17. $\frac{1}{4}$

19. $\frac{8}{7}$

21. $−1$

23. $3$

25. Sin suma

27. $−\frac{1}{14}$

Ejercicio$\PageIndex{9}$

Escribir como un número mixto.

$1.222…$
$5.777 …$
$2.252525…$
$3.272727…$
$1.999…$
$1.090909…$
Supongamos que accediste a trabajar por centavos al día durante$30$ días. Ganarás$1$ peniques el primer día,$2$ peniques el segundo día,$4$ centavos el tercer día, y así sucesivamente. ¿Cuántos peniques totales habrás ganado al final del periodo del$30$ día? ¿Cuál es el monto en dólares?
Se coloca una apuesta inicial a la ruleta$100$ de $ (en rojo) y se pierde. Para hacer la diferencia, el jugador dobla la apuesta y coloca una$200$ apuesta $ y pierde. Nuevamente, para hacer la diferencia, el jugador dobla la apuesta a $$400$ y pierde. Si el jugador sigue duplicando su apuesta de esta manera y pierde$7$ tiempos seguidos, ¿cuánto habrá perdido en total?
Cierta pelota rebota hasta la mitad de la altura de la que cayó. Si esta pelota se cae inicialmente desde$12$ pies, aproxima la distancia total que recorre la pelota.
Una pelota de golf rebota de una acera de cemento tres cuartas partes de la altura de la que cayó. Si la pelota se cae inicialmente desde$8$ metros, aproxima la distancia total que recorre la pelota.
Una liquidación estructurada arroja una cantidad en dólares cada año, representada por$n$, según la fórmula$p_{n} = 6,000(0.80)^{n−1}$. ¿Cuál es el monto total obtenido de la liquidación después de$10$ años?
Comenzando con un cuadrado, donde cada lado mide$1$ unidad, inscribe otro cuadrado conectando los puntos medios de cada lado. Continuar inscribiendo cuadrados de esta manera indefinidamente, como se muestra en la foto:

Encuentra la suma del área de todos los cuadrados en la figura. (Pista: Comience por encontrar la secuencia formada usando las áreas de cada cuadrado.)

Contestar

1. $1\frac{2}{9}$

3. $2\frac{25}{99}$

5. $2$

7. $1,073,741,823$centavos;$\$ 10,737,418.23$

9. $36$pies

11. $\$ 26,778.77$

Ejercicio$\PageIndex{10}$

Categorizar la secuencia como aritmética, geométrica, o ninguna. Dar la diferencia o proporción común, si existe.

$-12,24,-48, \dots$
$-7,-5,-3, \dots$
$-3,-11,-19, \dots$
$4,9,16, \dots$
$2, \frac{3}{2}, \frac{4}{3}, \dots$
$\frac{4}{3}, \frac{8}{9}, \frac{16}{27}, \dots$
$\frac{1}{6},-\frac{1}{6},-\frac{1}{2}, \ldots$
$\frac{1}{3}, \frac{1}{4}, \frac{3}{16}, \dots$
$\frac{1}{2}, \frac{1}{4}, \frac{1}{6} \dots$
$-\frac{1}{10},-\frac{1}{5},-\frac{3}{10}, \dots$
$1.26,0.252,0.0504, \dots$
$0.02,0.08,0.18, \dots$
$1,-1,1,-1, \ldots$
$0,0,0, \dots$

Contestar

1. Geométrico;$r = −2$

3. Aritmética;$d = −8$

5. Tampoco

7. Aritmética;$d = −\frac{1}{3}$

9. Tampoco

11. Geométrico;$r = 0.2$

13. Geométrico;$r = −1$

Ejercicio$\PageIndex{11}$

Categorizar la secuencia como aritmética o geométrica, y luego calcular la suma indicada.

$a_{n}=3(5)^{n-1} ; S_{8}$
$a_{n}=5-6 n ; S_{22}$
$a_{n}=2 n ; S_{14}$
$a_{n}=2^{n} ; S_{10}$
$a_{n}=-2\left(\frac{1}{7}\right)^{n-1} ; S_{\infty}$
$a_{n}=-2+\frac{1}{7} n ; S_{8}$

Contestar

1. Geométrico;$292,968$

3. Aritmética;$210$

5. Geométrico;$−\frac{7}{3}$

Ejercicio$\PageIndex{12}$

Calcular la suma indicada.

$\sum_{n=1}^{50}(3 n-5)$
$\sum_{n=1}^{25}(4-8 n)$
$\sum_{n=1}^{12}(-2)^{n-1}$
$\sum_{n=1}^{\infty} 5\left(-\frac{1}{2}\right)^{n-1}$
$\sum_{n=1}^{40} 5$
$\sum_{n=1}^{\infty} 0.6^{n}$

Contestar

1. $3,575$

3. $−1,365$

5. $200$

Ejercicio$\PageIndex{13}$

Utilice las técnicas que se encuentran en esta sección para explicar por qué$0.999… = 1$.
Construir una secuencia geométrica donde$r = 1$. Explora$n$ la suma parcial de dicha secuencia. ¿Qué conclusiones podemos sacar?

Contestar: 1. La respuesta puede variar

Notas al pie

¹⁸ Una secuencia de números donde cada número sucesivo es producto del número anterior y alguna constante$r$.

¹⁹ Se utiliza cuando se refiere a una secuencia geométrica.

²⁰ La constante$r$ que se obtiene de dividir cualesquiera dos términos sucesivos de una secuencia geométrica;$\frac{a_{n}}{a_{n-1}}=r$.

²¹ Los términos entre términos dados de una secuencia geométrica.

²² La suma de los términos de una secuencia geométrica.

²³ La suma de los primeros n términos de una secuencia geométrica, dada por la fórmula:$S_{n}=\frac{a_{1}\left(1-r^{n}\right)}{1-r} , r\neq 1$.

²⁴ Una serie geométrica infinita donde$|r| < 1$ cuya suma viene dada por la fórmula:$S_{\infty}=\frac{a_{1}}{1-r}$.