9.4: Teorema Binomial

Objetivos de aprendizaje

• Evaluar expresiones que involucren factoriales.
• Calcular coeficientes binomiales.
• Ampliar poderes de binomios usando el teorema binomial.

Factoriales y el Coeficiente Binomial

Comenzamos definiendo el factorial ²⁵ de un número natural\(n\), denotado\(n!\), como el producto de todos los números naturales menores o iguales a\(n\).

\(n !=n(n-1)(n-2) \cdots 3 \cdot 2 \cdot 1\)

Por ejemplo,

\(\begin{array}{l}{7 !=7 \cdot 6 \cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1=5,040 \quad\color{Cerulean}{Seven\:factorial}} \\[4pt] {5 !=5 \cdot 4 \cdot 3 \cdot 2 \cdot 1=120\quad\quad\quad\quad\:\color{Cerulean}{Five\:factorial}} \\[4pt] {3 !=3 \cdot 2 \cdot 1=6\quad\quad\quad\quad\quad\quad\:\:\:\quad\color{Cerulean}{Three\:factorial}} \\[4pt] {1 !=1=1\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\color{Cerulean}{One\:factorial}}\end{array}\)

Definimos cero factorial ²⁶ para ser igual a\(1\),

\(0 !=1 \quad\color{Cerulean}{Zero\:factorial}\)

No se define el factorial de un número negativo.

En la mayoría de las calculadoras modernas encontrarás una función factorial. Algunas calculadoras no proporcionan un botón dedicado a ello. Sin embargo, por lo general se puede encontrar en el sistema de menús si se proporciona uno.

El factorial también se puede expresar utilizando la siguiente relación de recurrencia,

\(n !=n(n-1) !\)

Por ejemplo, el factorial de se\(8\) puede expresar como el producto de\(8\) y\(7!\):

\(\begin{aligned} 8 ! &=8 \cdot \color{Cerulean}{7 !} \\[4pt] &=8 \cdot \color{Cerulean}{7 \cdot 6 \cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1} \\[4pt] &=40,320 \end{aligned}\)

Cuando se trabaja con ratios que involucran factoriales, a menudo ocurre que muchos de los factores cancelan.

Ejemplo\(\PageIndex{1}\)

Evaluar:\(\frac{12 !}{6 !}\).

Solución

\(\begin{aligned} \frac{12 !}{6 !}&=\frac{12 \cdot 11 \cdot 10 \cdot 9 \cdot 8 \cdot 7 \cdot \color{Cerulean}{6 \cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1}}{\color{Cerulean}{6 \cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1}}\\[4pt] &=\frac{12\cdot11\cdot10\cdot9\cdot8\cdot7 \cdot \cancel{6!}}{\cancel{6!}} \\[4pt] &=12\cdot11\cdot10\cdot9\cdot8\cdot7\\[4pt] &=665,280\end{aligned}\)

Contestar

\(665,280\)

El coeficiente binomial ²⁷, denotado\(_{n} C_{k}=\left( \begin{array}{l}{n} \\[4pt] {k}\end{array}\right)\), se lee “\(n\)elegir\(k\)” y viene dado por la siguiente fórmula:

\(_{n} C_{k}=\left( \begin{array}{l}{n} \\[4pt] {k}\end{array}\right)=\frac{n !}{k !(n-k) !}\)

Esta fórmula es muy importante en una rama de las matemáticas llamada combinatoria. Da la cantidad de formas en que\(k\) los elementos se pueden elegir de un conjunto de\(n\) elementos donde el orden no importa. En esta sección, nos preocupa la capacidad de calcular esta cantidad.

Ejemplo\(\PageIndex{2}\)

Calcular\(\left( \begin{array}{l}{7} \\[4pt] {3}\end{array}\right)\).

Solución

Utilice la fórmula para el coeficiente binomial,

\(\left( \begin{array}{l}{n} \\[4pt] {k}\end{array}\right)=\frac{n !}{k !(n-k) !}\)

dónde\(n = 7\) y\(k = 3\). Después de sustituir, busca factores para cancelar.

\(\begin{aligned} \left( \begin{array}{l}{7} \\[4pt] {3}\end{array}\right) &=\frac{7 !}{3 !(7-3) !} \\[4pt] &=\frac{7 !}{3 ! 4 !} \\[4pt] &=\frac{7\cdot6\cdot5\cdot\cancel{\color{Cerulean}{4!}}}{3! \cancel{\color{Cerulean}{4!}}} \\[4pt]&=\frac{210}{6} \\[4pt] &=35\end{aligned}\)

Respuesta:

\(35\)

Consulta el sistema de menús de tu calculadora para ver una función que calcule esta cantidad. Busque la notación\(_{n} C_{k}\) en la subsección de probabilidad.

Ejercicio\(\PageIndex{1}\)

Calcular\(\left( \begin{array}{l}{8} \\[4pt] {5}\end{array}\right)\).

Contestar

\(56\)

www.youtube.com/v/rpb8kd1hqgc

Consideremos el siguiente binomio elevado al\(3^{rd}\) poder en su forma expandida:

\((x+y)^{3}=x^{3}+3 x^{2} y+3 x y^{2}+y^{3}\)

Compáralo con los siguientes cálculos,

\(\left( \begin{array}{l}{3} \\[4pt] {0}\end{array}\right)=\dfrac{3 !}{0 !(3-0) !}=\frac{3 !}{1 \cdot 3 !}=1\)
\(\left( \begin{array}{l}{3} \\[4pt] {1}\end{array}\right)=d\frac{3 !}{1 !(3-1) !}=\frac{3 \cdot 2 !}{1 \cdot 2 !}=3\)
\(\left( \begin{array}{l}{3} \\[4pt] {2}\end{array}\right)=\dfrac{3 !}{2 !(3-2) !}=\frac{3 \cdot 2 !}{2 !}=3\)
\(\left( \begin{array}{c}{3} \\[4pt] {3}\end{array}\right)=\dfrac{3 !}{3 !(3-3) !}=\frac{3 !}{3 ! 0 !}=1\)

Observe que parece haber una conexión entre estos cálculos y los coeficientes del binomio expandido. Esta observación se generaliza en la siguiente sección.

Teorema binomial

Considere la posibilidad de ampliar\((x+2)^{5} \):

\((x+2)^{5}=(x+2)(x+2)(x+2)(x+2)(x+2)\)

Uno rápidamente se da cuenta de que este es un cálculo muy tedioso que involucra múltiples aplicaciones de la propiedad distributiva. El teorema binomial ²⁸ proporciona un método de expansión de binomios elevados a potencias sin multiplicar directamente cada factor:

\((x+y)^{n}=\left( \begin{array}{c}{n} \\[4pt] {0}\end{array}\right) x^{n} y^{0}+\left( \begin{array}{c}{n} \\[4pt] {1}\end{array}\right) x^{n-1} y^{1}+\left( \begin{array}{c}{n} \\[4pt] {2}\end{array}\right) x^{n-2} y^{2}+\ldots+\left( \begin{array}{c}{n} \\[4pt] {n-1}\end{array}\right) x^{1} y^{n-1}\)

De manera más compacta podemos escribir,

\[(x+y)^{n}=\sum_{k=0}^{n} \left( \begin{array}{l}{n} \\[4pt] {k}\end{array}\right) x^{n-k} y^{k} \quad \color{Cerulean}{Binomial\:theorem} \nonumber\]

Ejemplo\(\PageIndex{3}\)

Expandir usando el teorema binomial:\((x + 2)^{5}\).

Solución

Utilice el teorema binomial donde\(n = 5\) y\(y = 2\).

\((x+2)^{5}=\left( \begin{array}{l}{5} \\[4pt] {0}\end{array}\right) x^{5} 2^{0}+\left( \begin{array}{c}{5} \\[4pt] {1}\end{array}\right) x^{4} 2^{1}+\left( \begin{array}{l}{5} \\[4pt] {2}\end{array}\right) x^{3} 2^{2}+\left( \begin{array}{l}{5} \\[4pt] {3}\end{array}\right) x^{2} 2^{3}+\left( \begin{array}{l}{5} \\[4pt] {4}\end{array}\right) x^{1}2^{4}\)

En ocasiones resulta útil identificar el patrón que resulta de aplicar el teorema binomial. Observe que las potencias de la variable\(x\) comienzan en\(5\) y disminuyen a cero. Los poderes del término constante comienzan en\(0\) y aumentan a\(5\). Los coeficientes binomiales se pueden calcular a un lado y se dejan al lector como ejercicio.

\(\begin{aligned}(x+2)^{5} &=\left( \begin{array}{c}{5} \\[4pt] {0}\end{array}\right) x^{5} 2^{0}+\left( \begin{array}{c}{5} \\[4pt] {1}\end{array}\right) x^{4} 2^{1}+\left( \begin{array}{c}{5} \\[4pt] {2}\end{array}\right) x^{3} 2^{2}+\left( \begin{array}{c}{5} \\[4pt] {3}\end{array}\right) x^{2} 2^{3}+\left( \begin{array}{c}{5} \\[4pt] {4}\end{array}\right) x^{1} 2^{4} \\[4pt] &=1 x^{5} \times 1+5 x^{4} \times 2+10 x^{3} \times 4+10 x^{2} \times 8+5 x^{1} \times 16+1 \times 1 \\[4pt] &=x^{5}+10 x^{4}+40 x^{3}+80 x^{2}+80 x+32 \end{aligned}\)

Contestar

\(x^{5}+10 x^{4}+40 x^{3}+80 x^{2}+80 x+32\)

El binomio puede tener términos negativos, en cuyo caso obtendremos una serie alternante.

Ejemplo\(\PageIndex{4}\)

Expandir usando el teorema binomial:\((u − 2v)^{4}\).

Solución

Utilizar el teorema binomial donde\(n = 4, x = u\),\(y = −2v\) y luego simplificar cada término.

\(\begin{aligned}(u-2 v)^{4} &=\left( \begin{array}{c}{4} \\[4pt] {0}\end{array}\right) u^{4}(-2 v)^{0}+\left( \begin{array}{c}{4} \\[4pt] {1}\end{array}\right) u^{3}(-2 v)^{1}+\left( \begin{array}{c}{4} \\[4pt] {2}\end{array}\right) u^{2}(-2 v)^{2}+\left( \begin{array}{c}{4} \\[4pt] {3}\end{array}\right) u^{1}(-2v)^{3} + \left(\begin{array}{c}4 \\[4pt]4 \end{array} \right)u^{0}(-2v)^{4} \\[4pt] &=1 \times u^{4} \times 1+4 u^{3}(-2 v)+6 u^{2}\left(4 v^{2}\right)+4 u\left(-8 v^{3}\right) + 16v^{4} \\[4pt] &=u^{4}-8 u^{3} v+24 u^{2} v^{2}-32 u v^{3}+16 v^{4} \end{aligned}\)

Contestar

\(u^{4}-8 u^{3} v+24 u^{2} v^{2}-32 u v^{3}+16 v^{4}\)

Ejercicio\(\PageIndex{2}\)

Expandir usando el teorema binomial:\(\left(a^{2}-3\right)^{4}\)

Contestar

\(a^{8}-12 a^{6}+54 a^{4}-108 a^{2}+81\)

www.youtube.com/V/WICBQMoa4t4

A continuación estudiamos los coeficientes de las expansiones de\((x + y)^{n}\) comenzar con\(n = 0\):

\[ \begin{align*} (x+y)^{0} &=1 \\[4pt] (x+y)^{1}&=x+y \\[4pt] (x+y)^{2}&=x+y \\[4pt] (x+y)^{3}&=x^{2}+2 x y+y^{2} \\[4pt] (x+y)^{3}&=x^{3}+3 x^{2} y+3 x y^{2}+y^{3} \\[4pt] (x+y)^{4}&=x^{4}+4 x^{3} y+6 x^{2} y^{2}+4 x y^{3}+y^{4} \end{align*}\]

Escribe los coeficientes en una matriz triangular y observa que cada número a continuación es la suma de los dos números por encima de él, dejando siempre un\(1\) en cada extremo.

Figura\(\PageIndex{1}\)

Este es el triángulo ²⁹ de Pascal; proporciona un método rápido para calcular los coeficientes binomiales. Utilice esto en conjunto con el teorema binomial para agilizar el proceso de expansión de binomios elevados a potencias. Por ejemplo, para\((x − 1)^{6}\) expandirnos necesitaríamos dos filas más del triángulo de Pascal,

Figura\(\PageIndex{2}\)

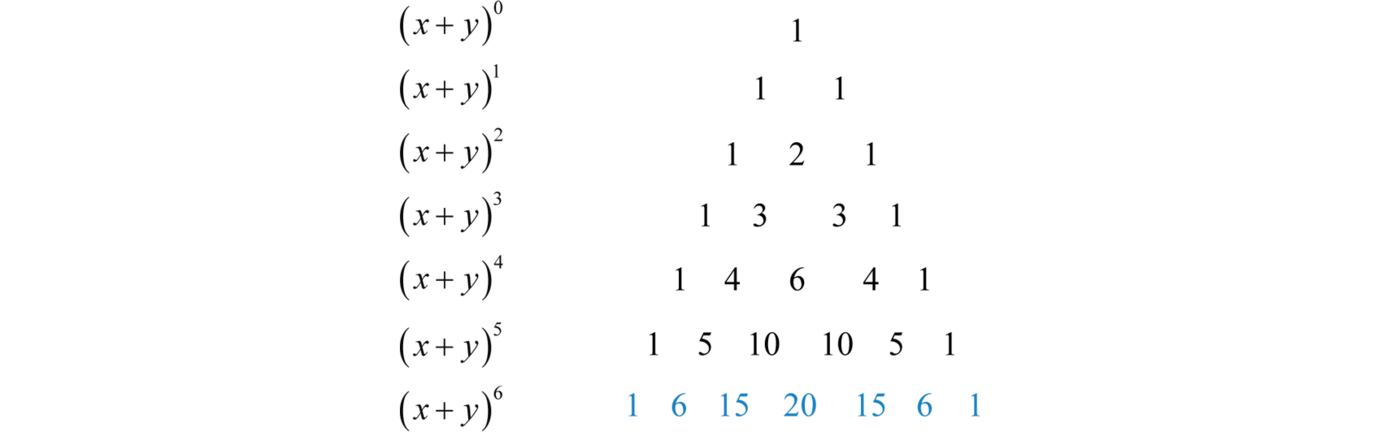
Los coeficientes binomiales que necesitamos están en azul. Usa estos números y el teorema binomial para expandirte rápidamente de la\((x − 1)^{6}\) siguiente manera:

\(\begin{aligned}(x-1)^{6} &=1 x^{6}(-1)^{0}+6 x^{5}(-1)^{1}+15 x^{4}(-1)^{2}+20 x^{3}(-1)^{3}+15 x^{2}(-1)^{4}+6 x(-1)^{5} \\[4pt] &=x^{6}-6 x^{5}+15 x^{4}-20 x^{3}+15 x^{2}-6 x+1 \end{aligned}\)

Ejemplo\(\PageIndex{5}\)

Expandir usando el teorema binomial y el triángulo de Pascal:\((2x − 5)^{4}\).

Solución

Del triángulo de Pascal podemos ver que cuando\(n = 4\) los coeficientes binomiales son\(1, 4, 6, 4\), y\(1\) .Usa estos números y el teorema binomial de la siguiente manera:

\(\begin{aligned}(2 x-5)^{4} &=1(2 x)^{4}(-5)^{0}+4(2 x)^{3}(-5)^{1}+6(2 x)^{2}(-5)^{2}+4(2 x)^{1}(-5)^{3}+(2 x)^{0}(-5)^{4} \\[4pt] &=16 x^{4} \cdot 1+4 \cdot 8 x^{3}(-5)+6 \cdot 4 x^{2} \cdot 25+4 \cdot 2 x(-125)+1 \cdot 625 \\[4pt] &=16 x^{4}-160 x^{3}+600 x^{2}-1,000 x+625 \end{aligned}\)

Respuesta:

\(16 x^{4}-160 x^{3}+600 x^{2}-1,000 x+625\)

Claves para llevar

• Para calcular el factorial de un número natural, multiplique ese número por todos los números naturales menores que éste:\(5! = 5 ⋅ 4 ⋅ 3 ⋅ 2 ⋅ 1 = 120\). Recuerda que hemos definido\(0! = 1\).
• Los coeficientes binomiales son los enteros calculados usando la fórmula:\[\left( \begin{array}{l}{n} \\[4pt] {k}\end{array}\right)=\frac{n !}{k !(n-k) !}. \nonumber\]
• El teorema binomial proporciona un método para expandir binomios elevados a potencias sin multiplicar directamente cada factor:\[(x+y)^{n}=\sum_{k=0}^{n} \left( \begin{array}{l}{n} \\[4pt] {k}\end{array}\right) x^{n-k} y^{k}\nonumber\]
• Utilice el triángulo de Pascal para determinar rápidamente los coeficientes binomiales.

Ejercicio\(\PageIndex{3}\)

Evaluar.

1. \(6!\)
2. \(4!\)
3. \(10!\)
4. \(9!\)
5. \(\frac{6 !}{3 !}\)
6. \(\frac{8 !}{4 !}\)
7. \(\frac{13 !}{9 !}\)
8. \(\frac{15 !}{10 !}\)
9. \(\frac{12 !}{3 ! 7 !}\)
10. \(\frac{10 !}{2 ! 5 !}\)
11. \(\frac{n !}{(n-2) !}\)
12. \(\frac{(n+1) !}{(n-1) !}\)
13. a\(4 !+3 !\)) b\((4+3) !\)
14. a\(4 !-3 !\)) b\((4-3) !\)

Contestar

1. \(720\)

3. \(3,628,800\)

5. \(120\)

7. \(17,160\)

9. \(15,840\)

11. \(n^{2} − n\)

13. a.\(30\) b.\(5,040\)

Ejercicio\(\PageIndex{4}\)

Reescribir usando notación factorial.

1. \(1 \times 2 \times 3 \times 4 \times 5 \times 6 \times 7\)
2. \(1 \times 2 \times 3 \times 4 \times 5\)
3. \(15 \times 14 \times 13\)
4. \(10 \times 9 \times 8 \times 7\)
5. \(13\)
6. \(8 \times 7\)
7. \(n(n-1)(n-2)\)
8. \(1 \times 2 \times 3 \times \cdots \times n \times(n+1)\)

Contestar

1. \(7!\)

3. \(\frac{15 !}{12 !}\)

5. \(\frac{13 !}{12 !}\)

7. \(\frac{n !}{(n-3) !}\)

Ejercicio\(\PageIndex{5}\)

Calcular el coeficiente binomial indicado.

1. \(\left( \begin{array}{l}{6} \\[4pt] {4}\end{array}\right)\)
2. \(\left( \begin{array}{l}{8} \\[4pt] {4}\end{array}\right)\)
3. \(\left( \begin{array}{l}{7} \\[4pt] {2}\end{array}\right)\)
4. \(\left( \begin{array}{l}{9} \\[4pt] {5}\end{array}\right)\)
5. \(\left( \begin{array}{l}{9} \\[4pt] {0}\end{array}\right)\)
6. \(\left( \begin{array}{l}{13} \\[4pt] {12}\end{array}\right)\)
7. \(\left( \begin{array}{l}{n} \\[4pt] {0}\end{array}\right)\)
8. \(\left( \begin{array}{l}{n} \\[4pt] {n}\end{array}\right)\)
9. \(\left( \begin{array}{l}{n} \\[4pt] {1}\end{array}\right)\)
10. \(\left( \begin{array}{c}{n} \\[4pt] {n-1}\end{array}\right)\)
11. \(_{10} C_{8}\)
12. \(_{5} C_{1}\)
13. \(_{12} C_{12}\)
14. \(_{10} C_{5}\)
15. \(_{n} C_{n-2}\)
16. \(_{n} C_{n-3}\)

Contestar

1. \(15\)

3. \(21\)

5. \(1\)

7. \(1\)

9. \(n\)

11. \(45\)

13. \(1\)

15. \(\frac{n^{2}-n}{2}\)

Ejercicio\(\PageIndex{6}\)

Expandir usando el teorema binomial.

1. \((4 x-3)^{3}\)
2. \((2 x-5)^{3}\)
3. \(\left(\frac{x}{2}+y\right)^{3}\)
4. \(\left(x+\frac{1}{y}\right)^{3}\)
5. \((x+3)^{4}\)
6. \((x+5)^{4}\)
7. \((x-4)^{4}\)
8. \((x-2)^{4}\)
9. \(\left(x+\frac{2}{y}\right)^{4}\)
10. \(\left(\frac{x}{3}-y\right)^{4}\)
11. \((x+1)^{5}\)
12. \((x-3)^{5}\)
13. \((x-2)^{6}\)
14. \((x+1)^{6}\)
15. \((x-1)^{7}\)
16. \((x+1)^{7}\)
17. \((5 x-1)^{4}\)
18. \((3 x-2)^{4}\)
19. \((4 u+v)^{4}\)
20. \((3 u-v)^{4}\)
21. \((u-5 v)^{5}\)
22. \((2 u+3 v)^{5}\)
23. \(\left(a-b^{2}\right)^{5}\)
24. \(\left(a^{2}+b^{2}\right)^{4}\)
25. \(\left(a^{2}+b^{4}\right)^{6}\)
26. \(\left(a^{5}+b^{2}\right)^{5}\)
27. \((x+\sqrt{2})^{3}\)
28. \((x-\sqrt{2})^{4}\)
29. \((\sqrt{x}-\sqrt{y})^{4}, x, y \geq 0\)
30. \((\sqrt{x}+2 \sqrt{y})^{5}, x, y \geq 0\)
31. \((x+y)^{7}\)
32. \((x+y)^{8}\)
33. \((x+y)^{9}\)
34. \((x-y)^{7}\)
35. \((x-y)^{8}\)
36. \((x-y)^{9}\)

Contestar

1. \(64 x^{3}-144 x^{2}+108 x-27\)

3. \(\frac{x^{3}}{8}+\frac{3 x^{2} y}{4}+\frac{3 x y^{2}}{2}+y^{3}\)

5. \(x^{4}+12 x^{3}+54 x^{2}+108 x+81\)

7. \(x^{4}-16 x^{3}+96 x^{2}-256 x+256\)

9. \(x^{4}+\frac{8 x^{3}}{y}+\frac{24 x^{2}}{y^{2}}+\frac{32 x}{y^{3}}+\frac{16}{y^{4}}\)

11. \(x^{5}+5 x^{4}+10 x^{3}+10 x^{2}+5 x+1\)

13. \(x^{6}-12 x^{5}+60 x^{4}-160 x^{3}+240 x^{2}-192 x+64\)

15. \(x^{7}-7 x^{6}+21 x^{5}-35 x^{4}+35 x^{3}-21 x^{2}+7 x-1\)

17. \(625 x^{4}-500 x^{3}+150 x^{2}-20 x+1\)

19. \(256 u^{4}+256 u^{3} v+96 u^{2} v^{2}+16 u v^{3}+v^{4}\)

21. \(\begin{array}{l}{u^{5}-25 u^{4} v+250 u^{3} v^{2}-1,250 u^{2} v^{3}} {+3,125 u v^{4}-3,125 v^{5}}\end{array}\)

23. \(a^{5}-5 a^{4} b^{2}+10 a^{3} b^{4}-10 a^{2} b^{6}+5 a b^{8}-b^{10}\)

25. \(\begin{array}{l}{a^{12}+6 a^{10} b^{4}+15 a^{8} b^{8}+20 a^{6} b^{12}} {+15 a^{4} b^{16}+6 a^{2} b^{20}+b^{24}}\end{array}\)

27. \(x^{3}+3 \sqrt{2} x^{2}+6 x+2 \sqrt{2}\)

29. \(x^{2}-4 x \sqrt{x y}+6 x y-4 y \sqrt{x y}+y^{2}\)

31. \(\begin{array}{l}{x^{7}+7 x^{6} y+21 x^{5} y^{2}+35 x^{4} y^{3}} {+35 x^{3} y^{4}+21 x^{2} y^{5}+7 x y^{6}+y^{7}}\end{array}\)

33. \(\begin{array}{l}{x^{9}+9 x^{8} y+36 x^{7} y^{2}+84 x^{6} y^{3}+126 x^{5} y^{4}} {+126 x^{4} y^{5}+84 x^{3} y^{6}+36 x^{2} y^{7}+9 x y^{8}+y^{9}}\end{array}\)

35. \(\begin{array}{l}{x^{8}-8 x^{7} y+28 x^{6} y^{2}-56 x^{5} y^{3}+70 x^{4} y^{4}} {-56 x^{3} y^{5}+28 x^{2} y^{6}-8 x y^{7}+y^{8}}\end{array}\)

Ejercicio\(\PageIndex{7}\)

1. Determinar las factoriales de los enteros\(5, 10, 15, 20\), y\(25\). ¿Cuál crece más rápido, la función exponencial común\(a_{n} = 10^{n}\) o la función factorial\(a_{n} = n!\)? Explique.
2. Investigar y discutir la historia del teorema binomial.

Contestar

1. La respuesta puede variar

Notas al pie

²⁵ El producto de todos los números naturales menores o iguales a un número natural dado, denotado\(n!\).

²⁶ El factorial de cero se define como igual a\(1; 0! = 1\).

²⁷ Un número entero que se calcula usando la fórmula:\(\left( \begin{array}{l}{n} \\[4pt] {k}\end{array}\right)=\frac{n !}{k !(n-k) !}\)

²⁸ Describe la expansión algebraica de binomios elevados a potencias:\((x+y)^{n}=\sum_{k=0}^{n} \left( \begin{array}{l}{n} \\[4pt] {k}\end{array}\right) x^{n-k} y^{k}\).

²⁹ Matriz triangular de números que corresponden a los coeficientes binomiales.