2.3E: Ejercicios
- Page ID
- 110243
La práctica hace la perfección
Resolver ecuaciones con constantes en ambos lados
En los siguientes ejercicios, resuelve las siguientes ecuaciones con constantes en ambos lados.
\(9 x-3=60\)
\(12 x-8=64\)
- Contestar
-
\(x=6\)
\(14 w+5=117\)
\(15 y+7=97\)
- Contestar
-
\(y=6\)
\(2 a+8=-28\)
\(3 m+9=-15\)
- Contestar
-
\(m=-8\)
\(-62=8 n-6\)
\(-77=9 b-5\)
- Contestar
-
\(b=-8\)
\(35=-13 y+9\)
\(60=-21 x-24\)
- Contestar
-
\(x=-4\)
\(-12 p-9=9\)
\(-14 q-2=16\)
- Contestar
-
\(q=-\frac{9}{7}\)
Resolver ecuaciones con variables en ambos lados
En los siguientes ejercicios, resuelve las siguientes ecuaciones con variables en ambos lados.
\(19 z=18 z-7\)
\(21 k=20 k-11\)
- Contestar
-
\(k=-11\)
\(9 x+36=15 x\)
\(8 x+27=11 x\)
- Contestar
-
\(x=9\)
\(c=-3 c-20\)
\(b=-4 b-15\)
- Contestar
-
\(b=-3\)
\(9 q=44-2 q\)
\(5 z=39-8 z\)
- Contestar
-
\(z=3\)
\(6 y+\frac{1}{2}=5 y\)
\(4 x+\frac{3}{4}=3 x\)
- Contestar
-
\(x=-\frac{3}{4}\)
\(-18 a-8=-22 a\)
\(-11 r-8=-7 r\)
- Contestar
-
\(r=-2\)
Resolver ecuaciones con variables y constantes en ambos lados
En los siguientes ejercicios, resuelve las siguientes ecuaciones con variables y constantes en ambos lados.
\(8 x-15=7 x+3\)
\(6 x-17=5 x+2\)
- Contestar
-
\(x=19\)
\(26+13 d=14 d+11\)
\(21+18 f=19 f+14\)
- Contestar
-
\(f=7\)
\(2 p-1=4 p-33\)
\(12 q-5=9 q-20\)
- Contestar
-
\(q=-5\)
\(4 a+5=-a-40\)
\(8 c+7=-3 c-37\)
- Contestar
-
\(c=-4\)
\(5 y-30=-5 y+30\)
\(7 x-17=-8 x+13\)
- Contestar
-
\(x=2\)
\(7 s+12=5+4 s\)
\(9 p+14=6+4 p\)
- Contestar
-
\(p=-\frac{8}{5}\)
\(2 z-6=23-z\)
\(3 y-4=12-y\)
- Contestar
-
\(y=4\)
\(\frac{5}{3} c-3=\frac{2}{3} c-16\)
\(\frac{7}{4} m-7=\frac{3}{4} m-13\)
- Contestar
-
\(m=-6\)
\(8-\frac{2}{5} q=\frac{3}{5} q+6\)
\(11-\frac{1}{5} a=\frac{4}{5} a+4\)
- Contestar
-
\(a=7\)
\(\frac{4}{3} n+9=\frac{1}{3} n-9\)
\(\frac{5}{4} a+15=\frac{3}{4} a-5\)
- Contestar
-
\(a=-40\)
\(\frac{1}{4} y+7=\frac{3}{4} y-3\)
\(\frac{3}{5} p+2=\frac{4}{5} p-1\)
- Contestar
-
\(p=15\)
\(14 n+8.25=9 n+19.60\)
\(13 z+6.45=8 z+23.75\)
- Contestar
-
\(z=3.46\)
\(2.4 w-100=0.8 w+28\)
\(2.7 w-80=1.2 w+10\)
- Contestar
-
\(w=60\)
\(5.6 r+13.1=3.5 r+57.2\)
\(6.6 x-18.9=3.4 x+54.7\)
- Contestar
-
\(x=23\)
Matemáticas cotidianas
Boletos para conciertos En un concierto escolar el valor total de los boletos vendidos fue de $1506. Los boletos de estudiante se venden por $6 y los boletos para adultos se venden por $9. El número de boletos de adulto vendidos fue 5 menos que 3 veces el número de boletos de estudiante. Encuentra el número de boletos de estudiante vendidos, s, resolviendo la ecuación 6s+27s−45=1506. Agrega texto de ejercicios aquí.
Haciendo una barda Jovani tiene 150 pies de cercado para hacer un jardín rectangular en su patio trasero. Quiere que el largo sea 15
pies más que el ancho. Encuentra el ancho, w, resolviendo la ecuación\(150=2 w+30+2 w\).
- Contestar
-
30 pies
Ejercicios de escritura
Resuelve la ecuación\(\frac{6}{5} y-8=\frac{1}{5} y+7\) explicando todos los pasos de tu solución como en los ejemplos de esta sección.
Resuelve la ecuación\(10 x+14=-2 x+38\) explicando todos los pasos de tu solución como en esta sección.
- Contestar
-
\(x=2\)Las justificaciones variarán.
Al resolver una ecuación con variables en ambos lados, ¿por qué suele ser mejor elegir el lado con el coeficiente mayor
de\(x\) ser el lado “variable”?
Es\(x=-2\) una solución a la ecuación\(5-2 x=-4 x+1 ?\) ¿Cómo lo sabes?
- Contestar
-
Sí. Las justificaciones variarán.
Autocomprobación
ⓐ Después de completar los ejercicios, usa esta lista de verificación para evaluar tu dominio de los objetivos de esta sección.
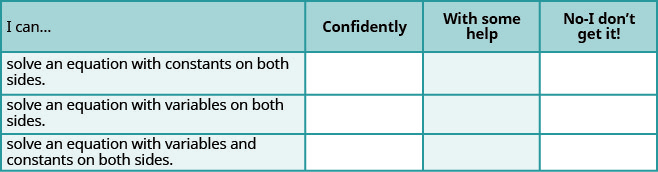
ⓑ ¿Qué te dice esta lista de verificación sobre tu dominio de esta sección? ¿Qué pasos tomarás para mejorar?