2.4: Usar una estrategia general para resolver ecuaciones lineales
- Page ID
- 110229
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Al final de esta sección, podrás:
- Resolver ecuaciones usando una estrategia general
- Clasificar ecuaciones
Antes de comenzar, toma este cuestionario de preparación.
- Simplificar:\(−(a−4)\).
Si te perdiste este problema, revisa Ejercicio 1.10.46 - Multiplicar:\(\frac{3}{2}(12x+20)\)
Si te perdiste este problema, revisa Ejercicio 1.10.34. - Simplificar:\(5−2(n+1)\)
Si te perdiste este problema, revisa Ejercicio 1.10.49. - Multiplicar:\(3(7y+9)\)
Si te perdiste este problema, revisa Ejercicio 1.10.34. - Multiplicar:\((2.5)(6.4)\)
Si te perdiste este problema, revisa Ejercicio 1.8.19.
Resolver ecuaciones usando la estrategia general
Hasta ahora nos hemos ocupado de resolver una forma específica de una ecuación lineal. Ahora es el momento de diseñar una estrategia general que pueda ser utilizada para resolver cualquier ecuación lineal. Algunas ecuaciones que resolvamos no requerirán de todos estos pasos para resolver, pero muchas lo harán.
Empezar simplificando cada lado de la ecuación facilita los pasos restantes.
Resolver:\(-6(x + 3) = 24\).
- Contestar
-
Resolver:\(5(x + 3)=35\)
- Contestar
-
\(x = 4\)
Resolver:\(6(y - 4) = -18\)
- Contestar
-
\(y = 1\)
- Simplifica cada lado de la ecuación tanto como sea posible.
Utilice la Propiedad Distributiva para eliminar cualquier paréntesis.
Combina términos similares. - Recoge todos los términos variables en un lado de la ecuación.
Utilice la Propiedad de Suma o Resta de Igualdad. - Recoge todos los términos constantes del otro lado de la ecuación.
Utilice la Propiedad de Suma o Resta de Igualdad. - Hacer que el coeficiente del término variable sea igual a 1.
Utilizar el Propiedad de Multiplicación o División de Igualdad.
Anotar la solución a la ecuación. - Consulta la solución. Sustituya la solución en la ecuación original para asegurarse de que el resultado es una declaración verdadera.
Resolver:\(-(y + 9) = 8\)
- Contestar
-
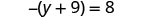
Simplifica cada lado de la ecuación tanto como sea posible distribuyendo.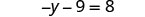 
El único término y está en el lado izquierdo, por lo que todos los términos variables están en el lado izquierdo de la ecuación. Agrega 9 a ambos lados para obtener todos los términos constantes en el lado derecho de la ecuación. 
Simplificar.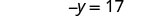 
Reescribe −y como −1y.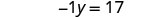 
Hacer que el coeficiente del término variable sea igual a 1 dividiendo ambos lados por −1.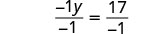 
Simplificar. 
Comprobar: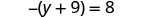 
Deje y=−17.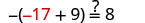 
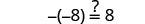
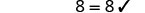
Resolver:\(-(y + 8) = -2\)
- Contestar
-
\(y = -6\)
Resolver:\(-(z + 4) = -12\)
- Contestar
-
\(z = 8\)
Resolver:\(5(a - 3) + 5 = -10\)
- Contestar
-
Simplifica cada lado de la ecuación tanto como sea posible. Distribuir. 
Combina términos similares.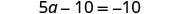 
El único término está en el lado izquierdo, por lo que todos los términos variables están en un lado de la ecuación. Agrega 10 a ambos lados para obtener todos los términos constantes en el otro lado de la ecuación. 
Simplificar.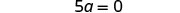 
Hacer que el coeficiente del término variable sea igual a 11 dividiendo ambos lados por 55.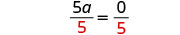 
Simplificar.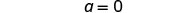 
Comprobar: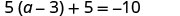 
Dejar a=0.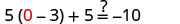 
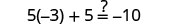
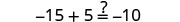
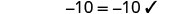
Resolver:\(2(m - 4) + 3 = -1\)
- Contestar
-
\(m = 2\)
Resolver:\(7(n - 3) - 8 = -15\)
- Contestar
-
\(n = 2\)
Resolver:\(\frac{2}{3}(6m - 3) = 8 - m\)
- Contestar
-
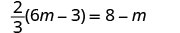
Distribuir.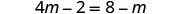 
Agrega m para obtener las variables solo a la izquierda.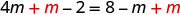 
Simplificar.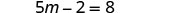 
Agrega 2 para obtener constantes solo a la derecha.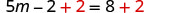 
Simplificar.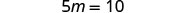 
Dividir por 5.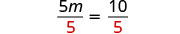 
Simplificar.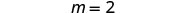 
Comprobar: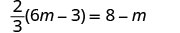 
Dejar m=2.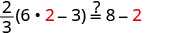 
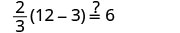
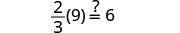
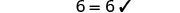
Resolver:\(\frac{1}{3}(6u + 3) = 7 - u\)
- Contestar
-
\(u = 2\)
Resolver:\(\frac{2}{3}(9x - 12) = 8 + 2x\)
- Contestar
-
\(x = 4\)
Resolver:\(8 - 2(3y + 5) = 0\)
- Contestar
-
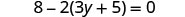
Simplificar: utilice la propiedad distributiva.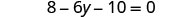 
Combina términos similares.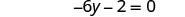 
Agrega 2 a ambos lados para recolectar constantes a la derecha.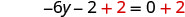 
Simplificar.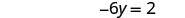 
Divide ambos lados entre −6−6.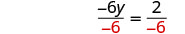 
Simplificar. 
Comprobar: Dejar y=−13.
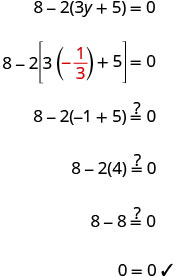
Resolver:\(12 - 3(4j + 3) = -17\)
- Contestar
-
\(j = \frac{5}{3}\)
Resolver:\(-6 - 8(k - 2) = -10\)
- Contestar
-
\(k = \frac{5}{2}\)
Resolver:\(4(x - 1)-2=5(2x+3)+6\)
- Contestar
-
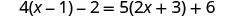
Distribuir.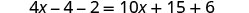 
Combina términos similares.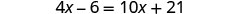 
Restar 4x para obtener las variables sólo en el lado derecho desde\(10>4\). 
Simplificar.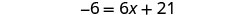 
Resta 21 para obtener las constantes a la izquierda.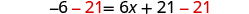 
Simplificar.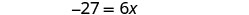 
Dividir por 6.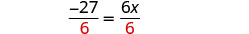 
Simplificar.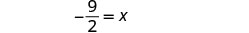 
Comprobar: 
Vamos\(x=-\frac{9}{2}\).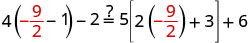 
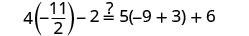
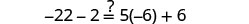
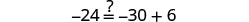
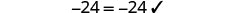
Resolver:\(6(p-3)-7=5(4p+3)-12\)
- Contestar
-
\(p = -2\)
Resolver:\(8(q +1)-5=3(2q-4)-1\)
- Contestar
-
\(q = -8\)
Resolver:\(10[3 - 8(2s-5)] = 15(40 - 5s)\)
- Contestar
-
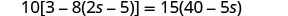
Simplifique primero desde los paréntesis más internos.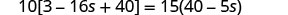 
Combina términos similares entre corchetes.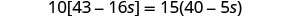 
Distribuir.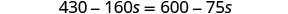 
Agrega 160s para conseguir las s a la derecha.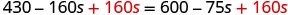 
Simplificar.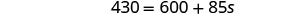 
Resta 600 para obtener las constantes a la izquierda.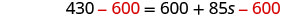 
Simplificar.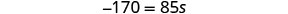 
Dividir.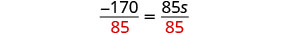 
Simplificar.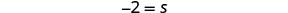 
Comprobar: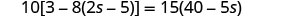 
Sustituir s=−2.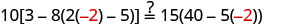 
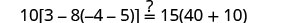
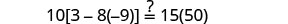
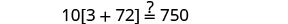
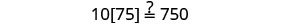
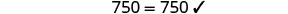
Resolver:\(6[4−2(7y−1)]=8(13−8y)\).
- Contestar
-
\(y = -\frac{17}{5}\)
Resolver:\(12[1−5(4z−1)]=3(24+11z)\).
- Contestar
-
\(z = 0\)
Resolver:\(0.36(100n+5)=0.6(30n+15)\).
- Contestar
-
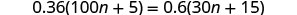
Distribuir.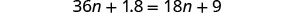 
Restar 18n para obtener las variables a la izquierda.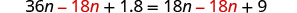 
Simplificar.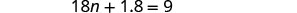 
Restar 1.8 para obtener las constantes a la derecha.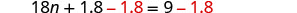 
Simplificar.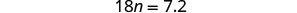 
Dividir.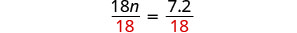 
Simplificar.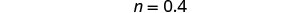 
Comprobar: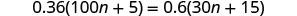 
Dejar n=0.4.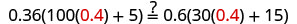 
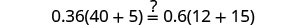
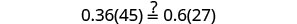
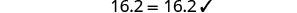
Resolver:\(0.55(100n+8)=0.6(85n+14)\).
- Contestar
-
\(n = 1\)
Resolver:\(0.15(40m−120)=0.5(60m+12)\).
- Contestar
-
\(m = -1\)
Clasificar ecuaciones
Considera la ecuación que resolvimos al inicio de la última sección, 7x+8=−13. La solución que encontramos fue x=−3. Esto significa que la ecuación 7x+8=−13 es verdadera cuando reemplazamos la variable, x, con el valor −3. Esto lo mostramos cuando comprobamos la solución x=−3 y evaluamos 7x+8=−13 para x=−3.
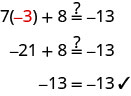
Si evaluamos 7x+8 para un valor diferente de x, el lado izquierdo no será −13.
La ecuación 7x+8=−13 es verdadera cuando reemplazamos la variable, x, con el valor −3, pero no verdadera cuando reemplazamos x por cualquier otro valor. El hecho de que la ecuación 7x+8=−13 sea verdadera o no depende del valor de la variable. Ecuaciones como esta se llaman ecuaciones condicionales.
Todas las ecuaciones que hemos resuelto hasta ahora son ecuaciones condicionales.
Una ecuación que es verdadera para uno o más valores de la variable y falsa para todos los demás valores de la variable es una ecuación condicional.
Ahora consideremos la ecuación 2y+6=2 (y+3). ¿Reconoces que el lado izquierdo y el lado derecho son equivalentes? Veamos qué pasa cuando resolvemos para y.
 |
|
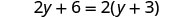| Distribuir. |  |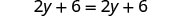
| Restar 2y para obtener las y a un lado. |  |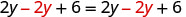
| Simplificar, ¡los y se han ido! |  |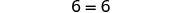
Pero 6=6 es cierto.
Esto significa que la ecuación 2y+6=2 (y+3) es verdadera para cualquier valor de y. Decimos que la solución a la ecuación son todos los números reales. Una ecuación que es verdadera para cualquier valor de la variable así se llama identidad.
Una ecuación que es verdadera para cualquier valor de la variable se llama identidad.
La solución de una identidad son todos los números reales.
¿Qué sucede cuando resolvemos la ecuación 5z=5z−1?
 |
|
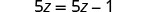| Restar 5z para obtener la constante sola a la derecha. |  |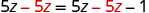
| Simplifica: ¡las z se han ido! |  |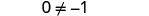
Pero\(0\neq −1\).
Resolver la ecuación 5z=5z−1 condujo a la declaración falsa 0=−1. La ecuación 5z=5z−1 no será cierta para ningún valor de z. No tiene solución. Una ecuación que no tiene solución, o que es falsa para todos los valores de la variable, se llama contradicción.
Una ecuación que es falsa para todos los valores de la variable se llama contradicción.
Una contradicción no tiene solución.
Clasificar la ecuación como una ecuación condicional, una identidad o una contradicción. Entonces exponer la solución.
\(6(2n−1)+3=2n−8+5(2n+1)\)
Responder-
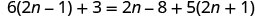
Distribuir.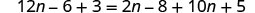 
Combina términos similares.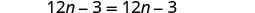 
Restar 12n para conseguir los nn's a un lado.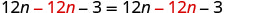 
Simplificar.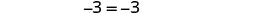 
Esta es una verdadera afirmación. La ecuación es una identidad.
La solución son todos los números reales.
Clasifique la ecuación como una ecuación condicional, una identidad o una contradicción y luego establezca la solución:
\(4+9(3x−7)=−42x−13+23(3x−2)\)
Responder-
identidad; todos los números reales
Clasifique la ecuación como una ecuación condicional, una identidad o una contradicción y luego establezca la solución:
\(8(1−3x)+15(2x+7)=2(x+50)+4(x+3)+1\)
Responder-
identidad; todos los números reales
Clasificar como una ecuación condicional, una identidad o una contradicción. Entonces exponer la solución.
\(10+4(p−5)=0\)
Responder-
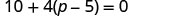
Distribuir.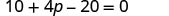 
Combina términos similares.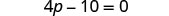 
Agrega 10 a ambos lados. 
Simplificar.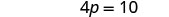 
Dividir.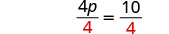 
Simplificar.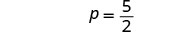 
La ecuación es verdadera cuando\(p = frac{5}{2}\). Esta es una ecuación condicional.
La solución es\(p = frac{5}{2}\).
Clasifique la ecuación como una ecuación condicional, una identidad o una contradicción y luego establezca la solución:\(11(q+3)−5=19\)
- Contestar
-
ecuación condicional;\ (q =\ frac {9} {11}\
Clasifique la ecuación como una ecuación condicional, una identidad o una contradicción y luego establezca la solución:\(6+14(k−8)=95\)
- Contestar
-
ecuación condicional;\(k = \frac{193}{14}\)
Clasificar la ecuación como una ecuación condicional, una identidad o una contradicción. Entonces exponer la solución.
\(5m+3(9+3m)=2(7m−11)\)
Responder-
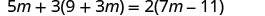
Distribuir.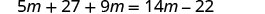 
Combina términos similares.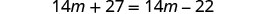 
Restar 14m de ambos lados.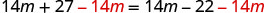 
Simplificar.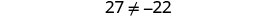 
Pero\(27\neq −22\). La ecuación es una contradicción.
No tiene solución.
Clasifique la ecuación como una ecuación condicional, una identidad o una contradicción y luego establezca la solución:
\(12c+5(5+3c)=3(9c−4)\)
Responder-
contradicción; no hay solución
Clasifique la ecuación como una ecuación condicional, una identidad o una contradicción y luego establezca la solución:
\(4(7d+18)=13(3d−2)−11d\)
Responder-
contradicción; no hay solución
| Tipo de ecuación | ¿Qué pasa cuando lo resuelves? | Solución |
|---|---|---|
| Ecuación Condicional | Verdadero para uno o más valores de las variables y falso para todos los demás valores | Uno o más valores |
| Identidad | True para cualquier valor de la variable | Todos los números reales |
| Contradicción | False para todos los valores de la variable | Sin solución |
Conceptos clave
- Estrategia General para Resolver Ecuaciones Lineales
- Simplifica cada lado de la ecuación tanto como sea posible.
Utilice la Propiedad Distributiva para eliminar cualquier paréntesis.
Combina términos similares. - Recoge todos los términos variables en un lado de la ecuación.
Utilice la Propiedad de Suma o Resta de Igualdad. - Recoge todos los términos constantes del otro lado de la ecuación.
Utilice la Propiedad de Suma o Resta de Igualdad. - Hacer que el coeficiente del término variable sea igual a 1.
Utilizar el Propiedad de Multiplicación o División de Igualdad.
Declarar la solución a la ecuación. - Consulta la solución.
Sustituir la solución por la ecuación original.
- Simplifica cada lado de la ecuación tanto como sea posible.