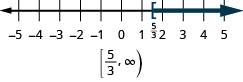Capítulo 2 Ejercicios de revisión
- Page ID
- 110228
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Capítulo 2 Ejercicios de revisión
Resolver ecuaciones usando las propiedades de resta y suma de igualdad
Verificar una Solución de una Ecuación
En los siguientes ejercicios, determine si cada número es una solución a la ecuación.
\(10 x-1=5 x ; x=\frac{1}{5}\)
\(w+2=\frac{5}{8} ; w=\frac{3}{8}\)
- Contestar
-
no
\(-12 n+5=8 n ; n=-\frac{5}{4}\)
\(6 a-3=-7 a, a=\frac{3}{13}\)
- Contestar
-
si
Resolver ecuaciones usando las propiedades de resta y suma de igualdad
En los siguientes ejercicios, resuelve cada ecuación usando la Propiedad de Sustracción de Igualdad.
\(x+7=19\)
\(y+2=-6\)
- Contestar
-
\(y=-8\)
\(a+\frac{1}{3}=\frac{5}{3}\)
\(n+3.6=5.1\)
- Contestar
-
\(n=1.5\)
En los siguientes ejercicios, resuelve cada ecuación usando la Propiedad de Adición de Igualdad.
\(u-7=10\)
\(x-9=-4\)
- Contestar
-
\(x=5\)
\(c-\frac{3}{11}=\frac{9}{11}\)
\(p-4.8=14\)
- Contestar
-
\(p=18.8\)
En los siguientes ejercicios, resuelve cada ecuación.
\(n-12=32\)
\(y+16=-9\)
- Contestar
-
\(y=-25\)
\(f+\frac{2}{3}=4\)
\(d-3.9=8.2\)
- Contestar
-
\(d=12.1\)
Resolver ecuaciones que requieren simplificación
En los siguientes ejercicios, resuelve cada ecuación.
\(y+8-15=-3\)
\(7 x+10-6 x+3=5\)
- Contestar
-
\(x=-8\)
\(6(n-1)-5 n=-14\)
\(8(3 p+5)-23(p-1)=35\)
- Contestar
-
\(p=-28\)
Traducir a una ecuación y resolver
En los siguientes ejercicios, traducir cada oración en inglés a una ecuación algebraica y luego resolverla.
La suma de\(-6\) y\(m\) es 25
Cuatro menos que\(n\) es 13
- Contestar
-
\(n-4=13 ; n=17\)
Traducir y resolver aplicaciones
En los siguientes ejercicios, traduzca en una ecuación algebraica y resuelva.
La hija de Rochelle tiene 11 años. Su hijo es 3 años menor. ¿Cuántos años tiene su hijo?
Tan pesa 146 libras. Minh pesa 15 libras más que Tan. ¿Cuánto pesa Minh?
- Contestar
-
161 libras
Peter pagó 9.75 dólares para ir al cine, que fue 46.25 dólares menos de lo que pagó para ir a un concierto. ¿Cuánto pagó por el concierto?
Elissa ganó\(\$ 152.84\) esta semana, que fue\(\$ 2 . .65\) más de lo que ganó la semana pasada. ¿Cuánto ganó la semana pasada?
- Contestar
-
\(\$ 131.19\)
Resolver Ecuaciones usando las Propiedades de División y Multiplicación de la Igualdad
Resolver ecuaciones usando las propiedades de división y multiplicación de la igualdad
En los siguientes ejercicios, resuelve cada ecuación usando las propiedades de división y multiplicación de la igualdad y comprueba la solución.
\(8 x=72\)
\(13 a=-65\)
- Contestar
-
\(a=-5\)
\(0.25 p=5.25\)
\(-y=4\)
- Contestar
-
\(y=-4\)
\(\frac{n}{6}=18\)
\(\frac{y}{-10}=30\)
- Contestar
-
\(y=-300\)
\(36=\frac{3}{4} x\)
\(\frac{5}{8} u=\frac{15}{16}\)
- Contestar
-
\(u=\frac{3}{2}\)
\(-18 m=-72\)
\(\frac{c}{9}=36\)
- Contestar
-
\(c=324\)
\(0.45 x=6.75\)
\(\frac{11}{12}=\frac{2}{3} y\)
- Contestar
-
\(y=\frac{11}{8}\)
Resolver ecuaciones que requieren simplificación
En los siguientes ejercicios, resuelve cada ecuación que requiere simplificación.
\(5 r-3 r+9 r=35-2\)
\(24 x+8 x-11 x=-7-14\)
- Contestar
-
\(x=-1\)
\(\frac{11}{12} n-\frac{5}{6} n=9-5\)
\(-9(d-2)-15=-24\)
- Contestar
-
\(d=3\)
Traducir a una ecuación y resolver
En los siguientes ejercicios, traduzca a una ecuación y luego resuelva.
143 es producto de\(-11\) y\(y\)
El cociente de\(b\) y y 9 es\(-27\)
- Contestar
-
\(\frac{b}{9}=-27 ; b=-243\)
La suma de q y un cuarto es uno.
La diferencia de s y una doceava es de una cuarta parte.
- Contestar
-
\(s-\frac{1}{12}=\frac{1}{4} ; s=\frac{1}{3}\)
Traducir y resolver aplicaciones
En los siguientes ejercicios, traduzca en una ecuación y resuelva.
Ray pagó $21 por 12 boletos en la feria del condado. ¿Cuál era el precio de cada boleto?
A Janet se le paga\(\$ 24\) por hora. Escuchó que esto es\(\frac{3}{4}\) de lo que le pagan a Adán. ¿Cuánto se paga Adam por hora?
- Contestar
-
$32
Resolver ecuaciones con variables y constantes en ambos lados
Resolver una ecuación con constantes en ambos lados
En los siguientes ejercicios, resuelve las siguientes ecuaciones con constantes en ambos lados.
\(8 p+7=47\)
\(10 w-5=65\)
- Contestar
-
\(w=7\)
\(3 x+19=-47\)
\(32=-4-9 n\)
- Contestar
-
\(n=-4\)
Resolver una ecuación con variables en ambos lados
En los siguientes ejercicios, resuelve las siguientes ecuaciones con variables en ambos lados.
\(7 y=6 y-13\)
\(5 a+21=2 a\)
- Contestar
-
\(a=-7\)
\(k=-6 k-35\)
\(4 x-\frac{3}{8}=3 x\)
- Contestar
-
\(x=\frac{3}{8}\)
Resolver una ecuación con variables y constantes en ambos lados
En los siguientes ejercicios, resuelve las siguientes ecuaciones con variables y constantes en ambos lados.
\(12 x-9=3 x+45\)
\(5 n-20=-7 n-80\)
- Contestar
-
\(n=-5\)
\(4 u+16=-19-u\)
\(\frac{5}{8} c-4=\frac{3}{8} c+4\)
- Contestar
-
\(c=32\)
Usar una estrategia general para resolver ecuaciones lineales
Resolver ecuaciones usando la estrategia general para resolver ecuaciones lineales
En los siguientes ejercicios, resuelve cada ecuación lineal.
\(6(x+6)=24\)
\(9(2 p-5)=72\)
- Contestar
-
\(p=\frac{13}{2}\)
\(-(s+4)=18\)
\(8+3(n-9)=17\)
- Contestar
-
\(n=12\)
\(23-3(y-7)=8\)
\(\frac{1}{3}(6 m+21)=m-7\)
- Contestar
-
\(m=-14\)
\(4(3.5 y+0.25)=365\)
\(0.25(q-8)=0.1(q+7)\)
- Contestar
-
\(q=18\)
\(8(r-2)=6(r+10)\)
\(\begin{array}{l}{5+7(2-5 x)=2(9 x+1)} \\ {-(13 x-57)}\end{array}\)
- Contestar
-
\(x=-1\)
\(\begin{array}{l}{(9 n+5)-(3 n-7)} \\ {=20-(4 n-2)}\end{array}\)
\(\begin{array}{l}{2[-16+5(8 k-6)]} \\ {=8(3-4 k)-32}\end{array}\)
- Contestar
-
\(k=\frac{3}{4}\)
Clasificar ecuaciones
En los siguientes ejercicios, clasifique cada ecuación como una ecuación condicional, una identidad o una contradicción y luego declare la solución.
\(\begin{array}{l}{17 y-3(4-2 y)=11(y-1)} \\ {+12 y-1}\end{array}\)
\(\begin{array}{l}{9 u+32=15(u-4)} \\ {-3(2 u+21)}\end{array}\)
- Contestar
-
contradicción; no hay solución
\(-8(7 m+4)=-6(8 m+9)\)
\(\begin{array}{l}{21(c-1)-19(c+1)} \\ {=2(c-20)}\end{array}\)
- Contestar
-
identidad; todos los números reales
Resolver ecuaciones con fracciones y decimales
Resolver ecuaciones con coeficientes de fracción
En los siguientes ejercicios, resuelve cada ecuación con coeficientes de fracción.
\(\frac{2}{5} n-\frac{1}{10}=\frac{7}{10}\)
\(\frac{1}{3} x+\frac{1}{5} x=8\)
- Contestar
-
\(x=15\)
\(\frac{3}{4} a-\frac{1}{3}=\frac{1}{2} a-\frac{5}{6}\)
\(\frac{1}{2}(k-3)=\frac{1}{3}(k+16)\)
- Contestar
-
\(k=41\)
\(\frac{3 x-2}{5}=\frac{3 x+4}{8}\)
\(\frac{5 y-1}{3}+4=\frac{-8 y+4}{6}\)
- Contestar
-
\(y=-1\)
Resolver ecuaciones con coeficientes decimales
En los siguientes ejercicios, resuelve cada ecuación con coeficientes decimales.
\(0.8 x-0.3=0.7 x+0.2\)
\(0.36 u+2.55=0.41 u+6.8\)
- Responder
-
\(u=-85\)
\(0.6 p-1.9=0.78 p+1.7\)
\(0.6 p-1.9=0.78 p+1.7\)
- Responder
-
\(d=-20\)
Resolver una fórmula para una variable específica
Utilice la fórmula de distancia, tasa y tiempo
En los siguientes ejercicios, resuelve.
Natalie manejó durante 7\(\frac{1}{2}\) horas a 60 millas por hora. ¿Cuánta distancia recorrió?
Mallory toma el autobús de San Luis a Chicago. La distancia es de 300 millas y el autobús viaja a un ritmo constante de 60 millas por hora. ¿Cuánto durará el viaje en autobús?
- Responder
-
5 horas
El amigo de Aaron lo llevó de Búfalo a Cleveland. La distancia es de 187 millas y el viaje duró 2.75 horas. ¿Qué tan rápido conducía el amigo de Aarón?
Link montó su bicicleta a un ritmo constante de 15 millas por hora durante 2\(\frac{1}{2}\) horas. ¿Cuánta distancia recorrió?
- Responder
-
37.5 millas
Resolver una fórmula para una variable específica
En los siguientes ejercicios, resuelve.
Usa la fórmula. d=rt para resolver para t
- cuando d=510 y r=60
- en general
Usa la fórmula. d=rt para resolver para r
- cuando d=451 y t=5.5
- en general
- Responder
-
- r=82mph
- \(r=\frac{D}{t}\)
Usa la fórmula\(A=\frac{1}{2} b h\) para resolver b
- cuando A=390 y h=26
- en general
Usa la fórmula\(A=\frac{1}{2} b h\) para resolver b
- cuando A=153 y b=18
- en general
- Responder
-
- \(h=17\)
- \( h=\frac{2 A}{b}\)
Utilice la fórmula I=Prt para resolver para el principal, P para
- I=$2,501, r= 4.1%, t=5 años
- en general
Resuelve la fórmula 4x+3y=6 para y
- cuando x=−2
- en general
- Responder
-
ⓐ\(y=\frac{14}{3}\) ⓑ\( y=\frac{6-4 x}{3}\)
Resolver\(180=a+b+c\) para\(c\)
Resuelve la fórmula\(V=L W H\) para\(H\)
- Responder
-
\(H=\frac{V}{L W}\)
Resolver desigualdades lineales
Graficar desigualdades en la recta numérica*
En los siguientes ejercicios, grafica cada desigualdad en la recta numérica.
- \(x\leq 4\)
- x>−2
- x<1
- x>0
- x<−3
- \(x\geq −1\)
- Responder
-
En los siguientes ejercicios, grafica cada desigualdad en la recta numérica y escribe en notación de intervalos.
- \(x<-1\)
- \(x \geq-2.5\)
- \(x \leq \frac{5}{4}\)
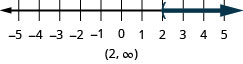
- \(x>2\)
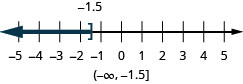
- \(x \leq-1.5\)
- \(x \geq \frac{5}{3}\)
- Responder
-
Resolver desigualdades usando las propiedades de resta y suma de la desigualdad
En los siguientes ejercicios, resuelve cada desigualdad, grafica la solución en la recta numérica y escribe la solución en notación de intervalos.
\(n-12 \leq 23\)
\(m+14 \leq 56\)
- Responder
-
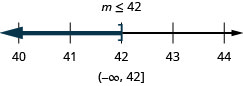
\(a+\frac{2}{3} \geq \frac{7}{12}\)
\(b-\frac{7}{8} \geq-\frac{1}{2}\)
- Responder
-
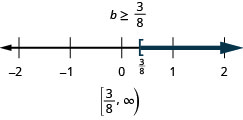
Resolver desigualdades utilizando las propiedades de división y multiplicación de la desigualdad
En los siguientes ejercicios, resuelve cada desigualdad, grafica la solución en la recta numérica y escribe la solución en notación de intervalos.
\(9 x>54\)
\(-12 d \leq 108\)
- Responder
-
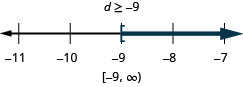
\(\frac{5}{2} j<-60\)
\(\frac{q}{-2} \geq-24\)
- Responder
-
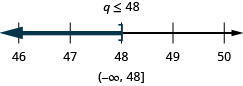
Resolver desigualdades que requieren simplificación
En los siguientes ejercicios, resuelve cada desigualdad, grafica la solución en la recta numérica y escribe la solución en notación de intervalos.
\(6 p>15 p-30\)
\(9 h-7(h-1) \leq 4 h-23\)
- Responder
-
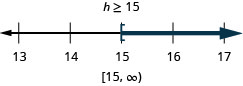
\(5 n-15(4-n)<10(n-6)+10 n\)
\(\frac{3}{8} a-\frac{1}{12} a>\frac{5}{12} a+\frac{3}{4}\)
- Responder
-
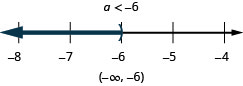
Traducir a una desigualdad y resolver
En los siguientes ejercicios, traduzca y resuelva. Después escribe la solución en notación de intervalos y grafica en la recta numérica.
Cinco más que z es como máximo 19.
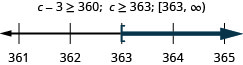
Tres menos que c es al menos 360.
- Responder
-
Nueve veces n supera 42.
Negativo dos veces a no es más de 8.
- Responder
-
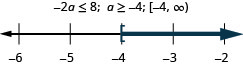
Matemáticas cotidianas
Describe cómo has usado dos temas de este capítulo en tu vida fuera de tu clase de matemáticas durante el mes pasado.
Capítulo 2 Prueba de práctica
Determinar si cada número es una solución a la ecuación\(6 x-3=x+20\)
- 5
- \(\frac{23}{5}\)
- Responder
-
- no
- si
En los siguientes ejercicios, resuelve cada ecuación.
\(n-\frac{2}{3}=\frac{1}{4}\)
\(\frac{9}{2} c=144\)
- Responder
-
c=32
\(4 y-8=16\)
\(-8 x-15+9 x-1=-21\)
- Responder
-
\(x=-5\)
\(-15 a=120\)
\(\frac{2}{3} x=6\)
- Responder
-
\(x=9\)
\(x-3.8=8.2\)
\(10 y=-5 y-60\)
- Responder
-
\(y=-4\)
\(8 n-2=6 n-12\)
\(9 m-2-4 m-m=42-8\)
- Responder
-
\(m=9\)
\(-5(2 x-1)=45\)
\(-(d-9)=23\)
- Responder
-
\(d=-14\)
\(\frac{1}{4}(12 m-28)=6-2(3 m-1)\)
\(2(6 x-5)-8=-22\)
- Responder
-
\(x=-\frac{1}{3}\)
\(8(3 a-5)-7(4 a-3)=20-3 a\)
\(\frac{1}{4} p-\frac{1}{3}=\frac{1}{2}\)
- Responder
-
\(p=\frac{10}{3}\)
\(0.1 d+0.25(d+8)=4.1\)
\(14 n-3(4 n+5)=-9+2(n-8)\)
- Responder
-
contradicción; no hay solución
\(9(3 u-2)-4[6-8(u-1)]=3(u-2)\)
Resolver la fórmula x−2y=5 para y
- cuando x=−3
- en general
- Responder
-
- y=4
- \(y=\frac{5-x}{2}\)
En los siguientes ejercicios, grafica en la recta numérica y escribe en notación de intervalos.
\(x \geq-3.5\)
\(x<\frac{11}{4}\)
- Responder
-
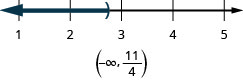
En los siguientes ejercicios,, resolver cada desigualdad, graficar la solución en la recta numéricay escribir la solución en notación de intervalos.
\(8 k \geq 5 k-120\)
\(3 c-10(c-2)<5 c+16\)
- Responder
-
En los siguientes ejercicios, traduzca a una ecuación o desigualdad y resuelva.
4 menos de dos veces x es 16.
Quince más que n es al menos 48.
- Responder
-
\(n+15 \geq 48 ; n \geq 33\)
Samuel pagó 25.82 dólares por gasolina esta semana, lo que fue 3.47 dólares menos de lo que pagó la semana pasada. ¿Cuánto había pagado la semana pasada?
Jenna compró un abrigo a la venta por el\(\$ 120,\) cual era\(\frac{2}{3}\) del precio original. ¿Cuál era el precio original del abrigo?
- Responder
-
\(120=\frac{2}{3} p ;\)El precio original era\(\$ 180\)
Sean tomó el autobús de Seattle a Boise, a una distancia de 506 millas. Si el viaje duró 7\(\frac{2}{3}\) horas, ¿cuál era la velocidad del autobús?