4.1: Usar el Sistema de Coordenadas Rectangulares
- Page ID
- 110263
Al final de esta sección, podrás:
- Trazar puntos en un sistema de coordenadas rectangulares
- Verificar soluciones a una ecuación en dos variables
- Completar una tabla de soluciones a una ecuación lineal
- Encontrar soluciones a una ecuación lineal en dos variables
Antes de comenzar, toma este cuestionario de preparación.
- Evaluar\(x+3\) cuándo\(x=−1\).
Si te perdiste este problema, revisa Ejercicio 1.5.25. - Evaluar\(2x−5y\) cuándo\(x=3\) e y=−2.
Si te perdiste este problema, revisa Ejercicio 1.5.28. - Resuelve para y:\(40−4y=20\)
Si te perdiste este problema, revisa Ejercicio 2.3.1.
Trazar puntos en un sistema de coordenadas rectangulares
Al igual que los mapas utilizan un sistema de cuadrícula para identificar ubicaciones, un sistema de cuadrícula se usa en álgebra para mostrar una relación entre dos variables en un sistema de coordenadas rectangular. El sistema de coordenadas rectangulares también se llama plano xy o 'plano de coordenadas'.
La línea numéricahorizontal se llama eje x. La línea numéricavertical se llama eje y. El eje x y el eje y forman juntos el sistema de coordenadas rectangulares. Estos ejes dividen un plano en cuatro regiones, llamadas cuadrantes. Los cuadrantes se identifican por números romanos, comenzando en la parte superior derecha y procediendo en sentido antihorario. Ver Figura\(\PageIndex{1}\).
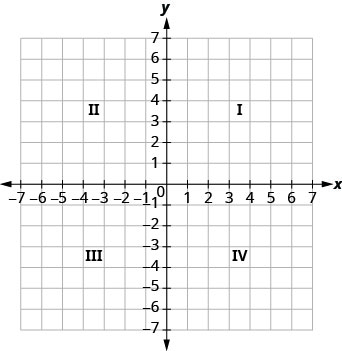
En el sistema de coordenadas rectangulares, cada punto está representado por un par ordenado. El primer número del par ordenado es la coordenada x del punto, y el segundo número es la coordenada y del punto.
Un par ordenado, (x, y) (x, y), da las coordenadas de un punto en un sistema de coordenadas rectangular.
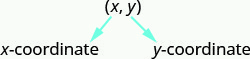
El primer número es la coordenada x.
El segundo número es la coordenada y.
La frase 'par ordenado' significa que el orden es importante. ¿Cuál es el par ordenado del punto donde se cruzan los ejes? En ese punto ambas coordenadas son cero, por lo que su par ordenado lo es\((0,0)\). El punto\((0,0)\) tiene un nombre especial. Se llama el origen.
Al punto\((0,0)\) se le llama el origen. Es el punto donde se cruzan el eje x y el eje y.
Utilizamos las coordenadas para localizar un punto en el plano xy. Vamos a trazar el punto\((1,3)\) como ejemplo. Primero, ubique 1 en el eje x y dibuje ligeramente una línea vertical a través de x=1x=1. Luego, ubique 3 en el eje y y dibuje una línea horizontal a través de y=3y=3. Ahora, encuentra el punto donde se encuentran estas dos líneas, ese es el punto con coordenadas\((1,3)\).
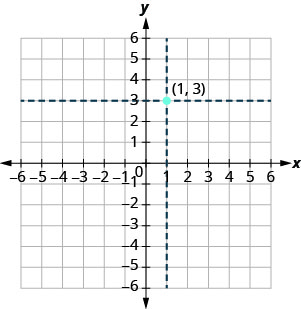
Observe que la línea vertical a través\(x=1\) y la línea horizontal a través no\(y=3\) forman parte de la gráfica. Simplemente los usamos para ayudarnos a localizar el punto\((1,3)\).
Trazar cada punto en el sistema de coordenadas rectangulares e identificar el cuadrante en el que se encuentra el punto:
- (−5,4)
- (−3, −4)
- (2, −3)
- (−2,3)
- \((3, \frac{5}{2})\)
- Contestar
-
El primer número del par de coordenadas es la coordenada x, y el segundo número es la coordenada y.
- Desde x=−5, el punto está a la izquierda del eje y. Además, como y=4, el punto está por encima del eje x. El punto (−5,4) está en el Cuadrante II.
- Desde x=−3, el punto está a la izquierda del eje y. Además, dado que y=−4, el punto está por debajo del eje x. El punto (−3, −4) está en el Cuadrante III.
- Desde x=2, el punto está a la derecha del eje y. Dado que y=−3, el punto está por debajo del eje x. El punto (2, −3) está en el cuadrante lV.
- Desde x=−2, el punto está a la izquierda del eje y. Desde y=3, el punto está por encima del eje x. El punto (−2,3) está en el Cuadrante II.
- Desde x=3, el punto está a la derecha del eje y. Ya que\(y = \frac{5}{2}\), el punto está por encima del eje x. (Puede ser útil escribir\(\frac{5}{2}\) como un número mixto o decimal.) El punto\((3, \frac{5}{2})\) está en el Cuadrante I.
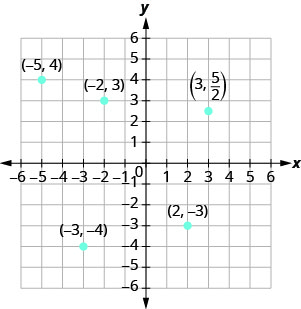
Figura\(\PageIndex{4}\)
Trazar cada punto en un sistema de coordenadas rectangulares e identificar el cuadrante en el que se encuentra el punto:
- (−2,1)
- (−3, −1)
- (4, −4)
- (−4,4)
- \((-4, \frac{3}{2})\)
- Contestar
-
Trazar cada punto en un sistema de coordenadas rectangulares e identificar el cuadrante en el que se encuentra el punto:
- (−4,1)
- (−2,3)
- (2, −5)
- (−2,5)
- \((-3, \frac{5}{2})\)
- Contestar
-
¿Cómo afectan las señales a la ubicación de los puntos? Es posible que hayas notado algunos patrones al graficar los puntos en el ejemplo anterior.
Para el punto en Figura\(\PageIndex{4}\) en el Cuadrante IV, ¿qué nota acerca de los signos de las coordenadas? ¿Y las señales de las coordenadas de puntos en el tercer cuadrante? ¿El segundo cuadrante? ¿El primer cuadrante?
¿Se puede decir con solo mirar las coordenadas en qué cuadrante se encuentra el punto (−2,5)? ¿En qué cuadrante se encuentra (2, −5)?
Podemos resumir los patrones de signos de los cuadrantes de esta manera.
\[\begin{array}{ccc}{\text { Quadrant I }} & {\text { Quadrant II }} & {\text { Quadrant III }} & {\text { Quadrant IV }} \\ {(x, y)} & {(x, y)} & {(x, y)} & {(x, y)} \\ {(+,+)} & {(-,+)} & {(-,-)} & {(+,-)}\end{array}\]
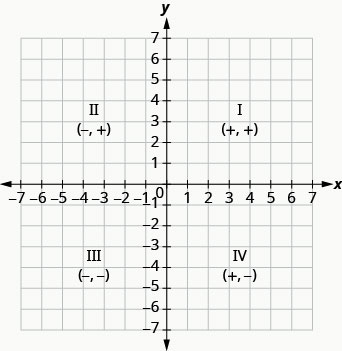
¿Qué pasa si una coordenada es cero como se muestra en la Figura\(\PageIndex{6}\)? ¿Dónde se encuentra el punto (0,4)? ¿Dónde se encuentra el punto (−2,0)?
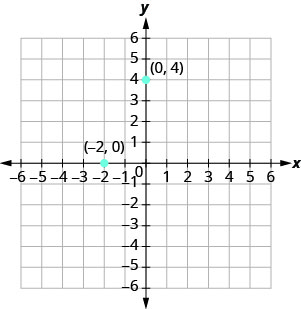
El punto (0,4) está en el eje y y el punto (−2,0) está en el eje x.
Los puntos con una coordenada y igual a 0 están en el eje x, y tienen coordenadas (a,0).
Los puntos con una coordenada x igual a 0 están en el eje y, y tienen coordenadas (0, b).
Trazar cada punto:
- (0,5)
- (4,0)
- (−3,0)
- (0,0)
- (0, −1)
- Contestar
-
- Desde x=0, el punto cuyas coordenadas son (0,5) está en el eje y.
- Desde y=0, el punto cuyas coordenadas son (4,0) está en el eje x.
- Desde y=0, el punto cuyas coordenadas son (−3,0) está en el eje x.
- Desde x=0 e y=0, el punto cuyas coordenadas son (0,0) es el origen.
- Desde x=0, el punto cuyas coordenadas son (0, −1) está en el eje y.
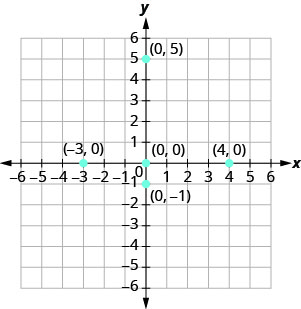
Figura\(\PageIndex{7}\)
Trazar cada punto:
- (4,0)
- (−2,0)
- (0,0)
- (0,2)
- (0, −3).
- Contestar
-
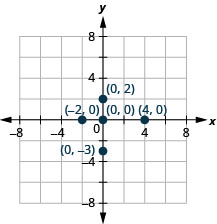
Trazar cada punto:
- (−5,0)
- (3,0)
- (0,0)
- (0, −1)
- (0,4).
- Contestar
-
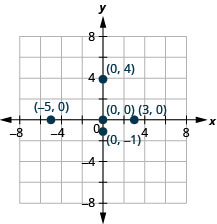
En álgebra, ser capaz de identificar las coordenadas de un punto mostrado en una gráfica es tan importante como poder trazar puntos. Para identificar la coordenada x de un punto en una gráfica, lea el número en el eje x directamente encima o debajo del punto. Para identificar la coordenada y de un punto, lea el número en el eje y directamente a la izquierda o derecha del punto. Recuerda, cuando escribas el par ordenado usa el orden correcto, (x, y).
Nombra el par ordenado de cada punto mostrado en el sistema de coordenadas rectangulares.
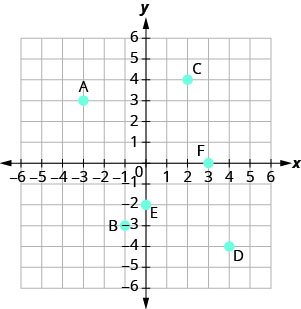
- Contestar
-
El punto A está por encima de −3 en el eje x, por lo que la coordenada x del punto es −3.
El punto está a la izquierda de 3 en el eje y, por lo que la coordenada y del punto es 3. - Las coordenadas del punto son (−3,3).
-
El punto B está por debajo de −1 en el eje x, por lo que la coordenada x del punto es −1.
El punto está a la izquierda de −3 en el eje y, por lo que la coordenada y del punto es −3. - Las coordenadas del punto son (−1, −3).
El punto C está por encima de 2 en el eje x, por lo que la coordenada x del punto es 2.
El punto está a la derecha de 4 en el eje y, por lo que la coordenada y del punto es 4. - Las coordenadas del punto son (2,4).
- El punto D está por debajo de 4 en el eje x, por lo que la coordenada x del punto es 4.
- El punto está a la derecha de −4 en el eje y, por lo que la coordenada y del punto es −4.
- Las coordenadas del punto son (4, −4).
-
El punto E está en el eje y en y=−2. Las coordenadas del punto E son (0, −2).
El punto F está en el eje x en x=3. Las coordenadas del punto F son (3,0).
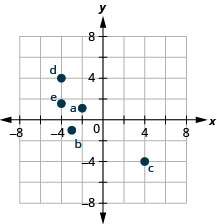
Nombra el par ordenado de cada punto mostrado en el sistema de coordenadas rectangulares.
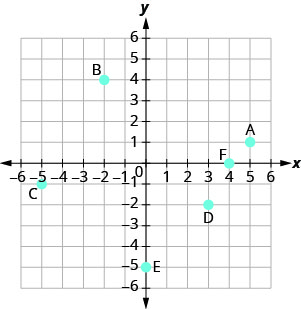
- Contestar
-
A: (5,1) B: (−2,4) C: (−5, −1) D: (3, −2) E: (0, −5) F: (4,0)
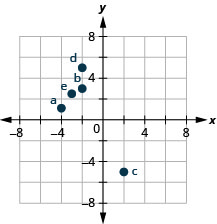
Nombra el par ordenado de cada punto mostrado en el sistema de coordenadas rectangulares.
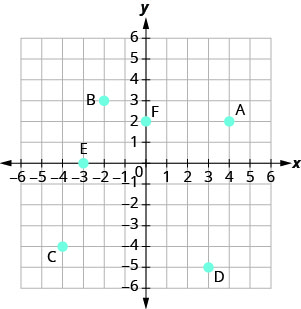
- Contestar
-
A: (4,2) B: (−2,3) C: (−4, −4) D: (3, −5) E: (−3,0) F: (0,2)
Verificar soluciones a una ecuación en dos variables
Hasta ahora, todas las ecuaciones que has resuelto eran ecuaciones con una sola variable. En casi todos los casos, cuando resolviste la ecuación obtuviste exactamente una solución. El proceso de resolución de una ecuación terminó con una declaración como x=4. (Luego, verificó la solución sustituyendo de nuevo a la ecuación).
Aquí hay un ejemplo de una ecuación en una variable, y su única solución.
\[\begin{aligned} 3 x+5 &=17 \\ 3 x &=12 \\ x &=4 \end{aligned}\]
Pero las ecuaciones pueden tener más de una variable. Las ecuaciones con dos variables pueden ser de la forma Ax+By=C. Las ecuaciones de esta forma se denominan ecuaciones lineales en dos variables.
Una ecuación de la forma Ax+By=C, donde A y B no son ambos cero, se denomina ecuación lineal en dos variables.
Observe la línea de palabras en lineal. Aquí hay un ejemplo de una ecuación lineal en dos variables, x e y.
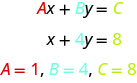
La ecuación y=−3x+5 es también una ecuación lineal. Pero no parece estar en la forma Ax+By=C Podemos usar la Propiedad de Adición de Igualdad y reescribirla en forma Ax+By=C.
\(\begin{array}{llll} {} &{y} &{=} &{-3x + 5} \\ {\text{Add to both sides.}} &{y + 3x } &{=} &{-3x + 5 + 3x} \\{\text{Simplify.}} &{y + 3x} &{=} &{5} \\{\text{Use the Commutative Property to put it in}} &{3x + y} &{=} &{5} \\{Ax+By = C\text{ form.}} &{} &{} &{} \end{array}\)
Al reescribir y=−3x+5 como 3x+y=5, podemos ver fácilmente que es una ecuación lineal en dos variables porque tiene la forma Ax+By=C. Cuando una ecuación está en la forma Ax+By=C, decimos que está en forma estándar.
Una ecuación lineal está en forma estándar cuando se escribe Ax+By=C.
La mayoría de la gente prefiere que A, B y C sean enteros y\(A\geq 0\) al escribir una ecuación lineal en forma estándar, aunque no es estrictamente necesario.
Las ecuaciones lineales tienen infinitamente muchas soluciones. Por cada número que se sustituye por x hay un valor y correspondiente. Este par de valores es una solución a la ecuación lineal y está representado por el par ordenado (x, y). Cuando sustituimos estos valores de x e y en la ecuación, el resultado es una declaración verdadera, porque el valor del lado izquierdo es igual al valor del lado derecho.
Un par ordenado (x, y) es una solución de la ecuación lineal Ax+By=C, si la ecuación es una declaración verdadera cuando los valores x - e y -del par ordenado se sustituyen en la ecuación.
Determinar qué pares ordenados son soluciones a la ecuación x+4y=8.
(a) (0,2)
b) (2, −4)
c) (−4,3)
- Contestar
-
Sustituir los valores x - e y de cada par ordenado en la ecuación y determinar si el resultado es una declaración verdadera.
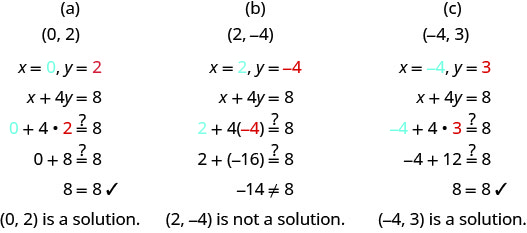
¿Cuáles de los siguientes pares ordenados son soluciones a 2x+3y=6?
- (3,0)
- (2,0)
- (6, −2)
- Contestar
-
1, 3
¿Cuáles de los siguientes pares ordenados son soluciones a la ecuación 4x−y=8?
- (0,8)
- (2,0)
- (1, −4)
- Responder
-
2, 3
¿Cuáles de los siguientes pares ordenados son soluciones a la ecuación y=5x−1?
(a) (0, −1)
b) 1,4
(c) (−2, −7)
- Responder
-
Sustituir los valores x - e y de cada par ordenado en la ecuación y determinar si da como resultado una declaración verdadera.
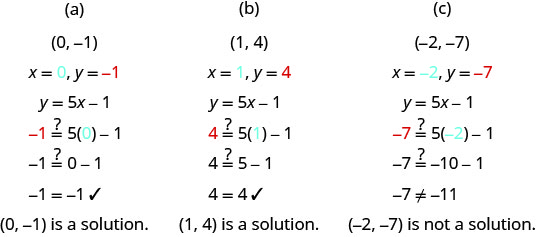
¿Cuáles de los siguientes pares ordenados son soluciones a la ecuación y=4x−3?
- (0,3)
- (1,1)
- (−1, −1)
- Responder
-
2
¿Cuáles de los siguientes pares ordenados son soluciones a la ecuación y=−2x+6?
- (0,6)
- (1,4)
- (−2, −2)
- Responder
-
1, 2
Completar una Tabla de Soluciones a una Ecuación Lineal en Dos Variables
En los ejemplos anteriores, sustituimos los valores x e y de un par ordenado dado para determinar si era o no una solución a una ecuación lineal. Pero, ¿cómo se encuentran los pares ordenados si no se dan? Es más fácil de lo que pensarías, solo puedes elegir un valor para xx y luego resolver la ecuación para yy. O bien, elija un valor para yy y luego resuelva para xx.
Comenzaremos por mirar las soluciones a la ecuación y = 5x−1 que encontramos en Ejercicio\(\PageIndex{13}\). Podemos resumir esta información en una tabla de soluciones, como se muestra en la Tabla\(\PageIndex{1}\).
| y=5x−1 | ||
| x | y | (x, y) |
| 0 | −1 | (0, −1) |
| 1 | 4 | (1,4) |
Para encontrar una tercera solución, dejaremos x=2 y resolveremos para y.
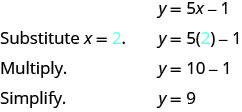
El par ordenado (2,9) es una solución a y=5x−1. Lo agregaremos a Tabla\(\PageIndex{2}\).
| y=5x−1 | ||
| x | y | (x, y) |
| 0 | −1 | (0, −1) |
| 1 | 4 | (1,4) |
| 2 | 9 | (2,9) |
Podemos encontrar más soluciones a la ecuación sustituyendo en cualquier valor de x o cualquier valor de y y resolviendo la ecuación resultante para obtener otro par ordenado que sea una solución. Hay infinitamente muchas soluciones de esta ecuación.
Tabla Completa para encontrar tres soluciones a la ecuación y=4x−2.
| y=4x−2 | ||
| x | y | (x, y) |
| 0 | ||
| −1 | ||
| 2 | ||
- Responder
-
Sustituye x=0, x=−1 y x=2 en y=4x−2.
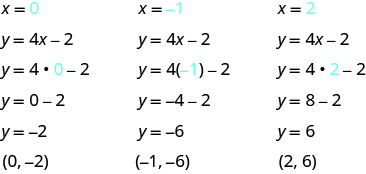
-
Los resultados se resumen en la Tabla\(\PageIndex{4}\).
y=4x−2 x y (x, y) 0 −2 (0, −2) −1 −6 (−1, −6) 2 6 (2,6) Mesa\(\PageIndex{4}\)
Completa la tabla para encontrar tres soluciones a esta ecuación: y=3x−1.
| y=3x−1 | ||
| x | y | (x, y) |
| 0 | ||
| −1 | ||
| 2 | ||
- Responder
-
y=3x−1 x y (x, y) 0 -1 (0, -1) −1 -4 (-1, -4) 2 5 (2, 5) Mesa\(\PageIndex{6}\)
Completa la tabla para encontrar tres soluciones a esta ecuación: y=6x+1.
| y=6x+1 | ||
| x | y | (x, y) |
| -2 | ||
- Responder
-
y=6x+1 x y (x, y) 0 1 (0,1) 1 7 (1,7) −2 −11 (−2, −11) Mesa\(\PageIndex{8}\)
Tabla Completa\(\PageIndex{9}\) para encontrar tres soluciones a la ecuación 5x−4y=20.
| 5x−4y=20 | ||
| x | y | (x, y) |
| 0 | ||
| 5 | ||
- Responder
-
Sustituir el valor dado en la ecuación 5x−4y=20 y resolver para la otra variable. Después, rellena los valores en la tabla.
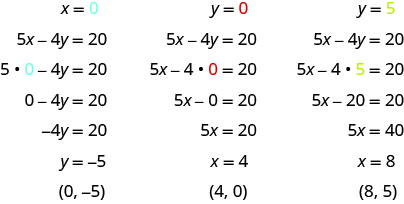
-
Los resultados se resumen en la Tabla\(\PageIndex{10}\).
5x−4y=20 x y (x, y) 0 −5 (0, −5) 4 0 (4,0) 8 5 (8,5) Mesa\(\PageIndex{10}\)
Complete la tabla para encontrar tres soluciones a esta ecuación: 2x−5y=20.
| 2x−5y=20 | ||
| x | y | (x, y) |
| -5 | ||
- Responder
-
2x−5y=20 x y (x, y) 0 −4 (0, −4) 10 0 (10,0) −5 −6 (−5, −6) Mesa\(\PageIndex{12}\)
Complete la tabla para encontrar tres soluciones a esta ecuación: 3x−4y=12.
| 3x−4y=12 | ||
| x | y | (x, y) |
| -4 | ||
- Responder
-
3x−4y=12 x y (x, y) 0 −3 (0, −3) 4 0 (4,0) −4 −6 (−4, −6) Mesa\(\PageIndex{14}\)
Encontrar soluciones a una ecuación lineal
Para encontrar una solución a una ecuación lineal, realmente puedes elegir cualquier número que quieras sustituir en la ecuación por x o y, pero como necesitarás usar ese número para resolver para la otra variable, es una buena idea elegir un número con el que sea fácil trabajar.
Cuando la ecuación está en forma y, con la y por sí misma en un lado de la ecuación, suele ser más fácil elegir valores de x y luego resolver para y.
Encuentra tres soluciones a la ecuación y=−3x+2.
- Responder
-
Podemos sustituir cualquier valor que queramos por x o cualquier valor por y. Dado que la ecuación está en forma y, será más fácil sustituirla en valores de x. Escojamos x=0, x=1 y x=−1.



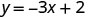
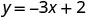
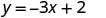
Sustituir el valor en la ecuación. 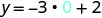
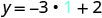
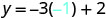
Simplificar. 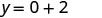
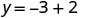
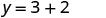
Simplificar. 
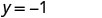

Escribe el par ordenado. (0, 2) (1, -1) (-1, 5) Cheque. y=−3x+2 y=−3x+2 y=−3x+2 \(2 \stackrel{?}{=} -3 \cdot 0 + 2\) \(-1 \stackrel{?}{=} -3 \cdot 1 + 2\) \(5 \stackrel{?}{=} -3 (-1) + 2\) \(2 \stackrel{?}{=} 0 + 2\) \(-1 \stackrel{?}{=} -3 + 2\) \(5 \stackrel{?}{=} -3 + 2\) \(2 = 2\checkmark\) \(-1 = -1\checkmark\) \(5 = 5\checkmark\) - Mesa\(\PageIndex{15}\)
-
Entonces, (0,2), (1, −1) y (−1,5) son todas soluciones a y=−3x+2. Los mostramos en Tabla\(\PageIndex{16}\).
y=−3x+2 x y (x, y) 0 2 (0,2) 1 −1 (1, −1) −1 5 (−1,5) Mesa\(\PageIndex{16}\)
Encuentra tres soluciones a esta ecuación: y=−2x+3.
- Responder
-
Las respuestas variarán.
Encuentra tres soluciones a esta ecuación: y=−4x+1.
- Responder
-
Las respuestas variarán.
Hemos visto como usar cero como un valor de x hace que encontrar el valor de y sea fácil. Cuando una ecuación está en forma estándar, con tanto la x como la y en el mismo lado de la ecuación, suele ser más fácil encontrar primero una solución cuando x=0 encuentra una segunda solución cuando y=0, y luego encontrar una tercera solución.
Encuentra tres soluciones a la ecuación 3x+2y=6.
- Responder
-
Podemos sustituir cualquier valor que queramos por x o cualquier valor por y Dado que la ecuación está en forma estándar, escojamos primero x=0, luego y=0, y luego busquemos un tercer punto.

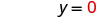

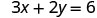
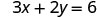
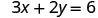
Sustituir el valor en la ecuación. 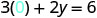
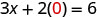
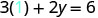
Simplificar. 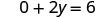
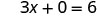
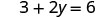
Resolver. 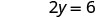
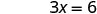
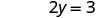
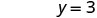

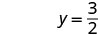
Escribe el par ordenado. (0, 3) (2, 0) \((1,\frac{3}{2})\) Cheque. 3x+2y=6 3x+2y=6 3x+2y=6 \(3\cdot 0 + 2\cdot 3 \stackrel{?}{=} 6\) \(3\cdot 2 + 2\cdot 0 \stackrel{?}{=} 6\) \(3\cdot 1 + 2\cdot \frac{3}{2} \stackrel{?}{=} 6\) \(0 + 6 \stackrel{?}{=} 6\) \(6 + 0 \stackrel{?}{=} 6\) \(3 + 3 \stackrel{?}{=} 6\) \(6 = 6\checkmark\) \(6 = 6\checkmark\) \(6 = 6\checkmark\) Mesa\(\PageIndex{17}\) Entonces (0,3), (2,0), y\((1,\frac{3}{2})\) son todas soluciones a la ecuación 3x+2y=6. Podemos enumerar estas tres soluciones en Table\(\PageIndex{18}\).
3x+2y=63x+2y=6 x y (x, y) 0 3 (0,3) 2 0 (2,0) 1 \(\frac{3}{2}\) \((1, \frac{3}{2})\) Mesa\(\PageIndex{18}\)
Encuentra tres soluciones a la ecuación 2x+3y=6.
- Responder
-
Las respuestas variarán.
Encuentra tres soluciones a la ecuación 4x+2y=8.
- Responder
-
Las respuestas variarán.
Conceptos clave
- Patrones de Signos de los Cuadrantes
\(\begin{array}{ll}{\text { Quadrant I }} & {\text { Quadrant II }} & {\text { Quadrant III }} & {\text { Quadrant IV }} \\ {(x, y)} & {(x, y)} & {(x, y)} & {(x, y)} \\ {(+,+)} & {(-,+)} & {(-,-)} & {(+,-)}\end{array}\) - Puntos en los Ejes
- En el eje x, y=0. Los puntos con una coordenada y igual a 0 están en el eje x, y tienen coordenadas (a,0).
- En el eje y, x=0. Los puntos con una coordenada x igual a 0 están en el eje y, y tienen coordenadas (0, b).
- Solución de una Ecuación Lineal
- Un par ordenado (x, y) es una solución de la ecuación lineal Ax+By=C, si la ecuación es una declaración verdadera cuando los valores x - e y - del par ordenado se sustituyen en la ecuación.
Glosario
- ecuación lineal
- Una ecuación lineal es de la forma Ax+By=C, donde A y B no son ambos cero, se denomina ecuación lineal en dos variables.
- par ordenado
- Un par ordenado (x, y) da las coordenadas de un punto en un sistema de coordenadas rectangular.
- origen
- El punto (0,0) (0,0) se llama origen. Es el punto donde se cruzan el eje x y el eje y.
- cuadrante
- El eje x y el eje y dividen un plano en cuatro regiones, llamadas cuadrantes.
- sistema de coordenadas rectangulares
- Un sistema de cuadrícula se utiliza en álgebra para mostrar una relación entre dos variables; también llamado el plano xy o el 'plano de coordenadas'.
- coordenada x
- El primer número en un par ordenado (x, y).
- coordenada y
- El segundo número en un par ordenado (x, y).


